MG
MG
-
-
w 7
w 7
1
1
NAPR
NAPR
ĘŻ
ĘŻ
ENIA w O
ENIA w O
Ś
Ś
RODKU GRUNTOWYM
RODKU GRUNTOWYM
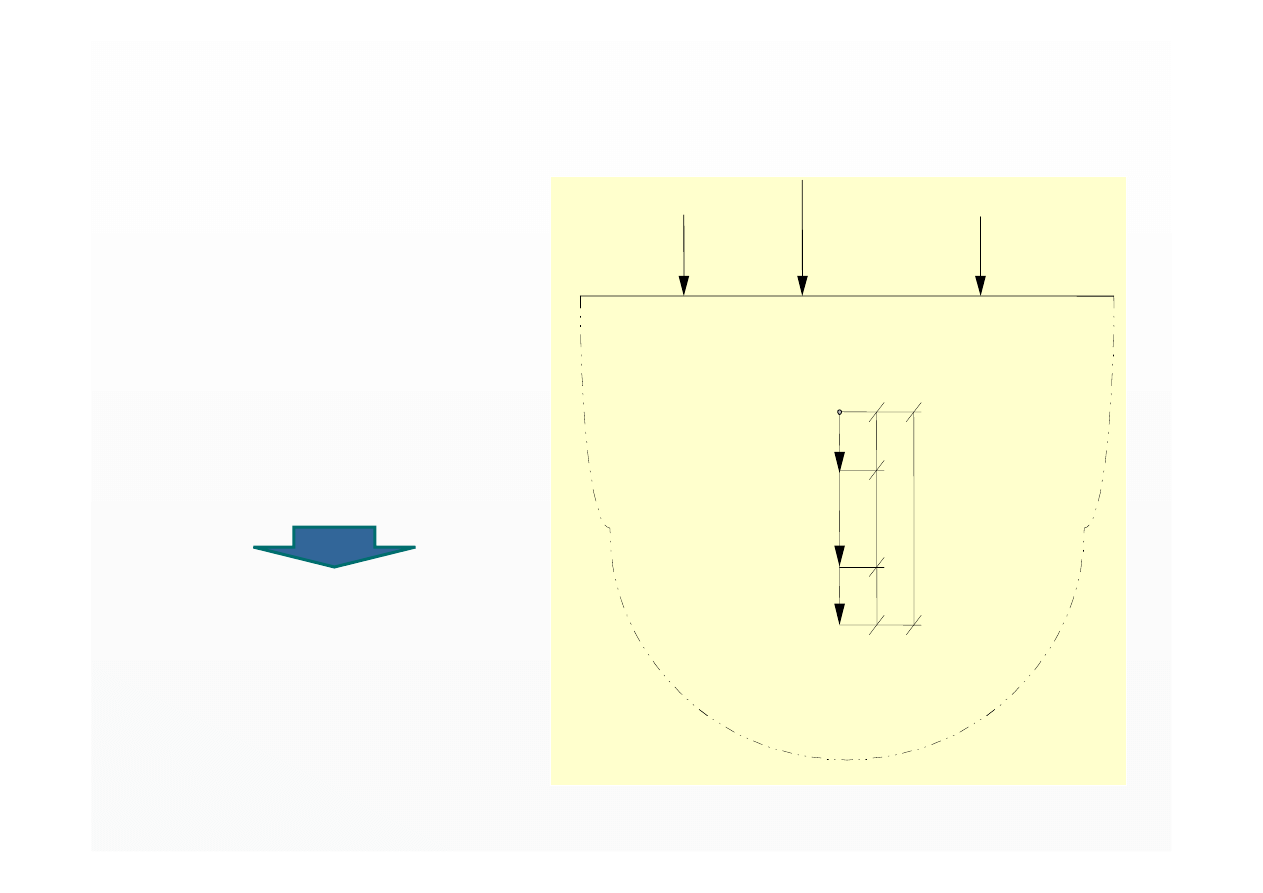
obci
obci
ąż
ąż
enia statyczne
enia statyczne
Założenia
:
ośrodek gruntowy jest:
- półprzestrzenią
- sprężysty
- izotropowy
- jednorodny
obliczając wartości:
odkształceń i naprężeń
stosuje się
zasadę superpozycji
Q
1
Q
2
Q
3
σ
1
σ
2
σ
3
σ
M
półprzestrze
ń
gruntowa
MG
MG
-
-
w 7
w 7
2
2
ROZK
ROZK
Ł
Ł
AD NAPR
AD NAPR
ĘŻ
ĘŻ
E
E
Ń
Ń
od
od
SI
SI
Ł
Ł
Y SKUPIONEJ
Y SKUPIONEJ
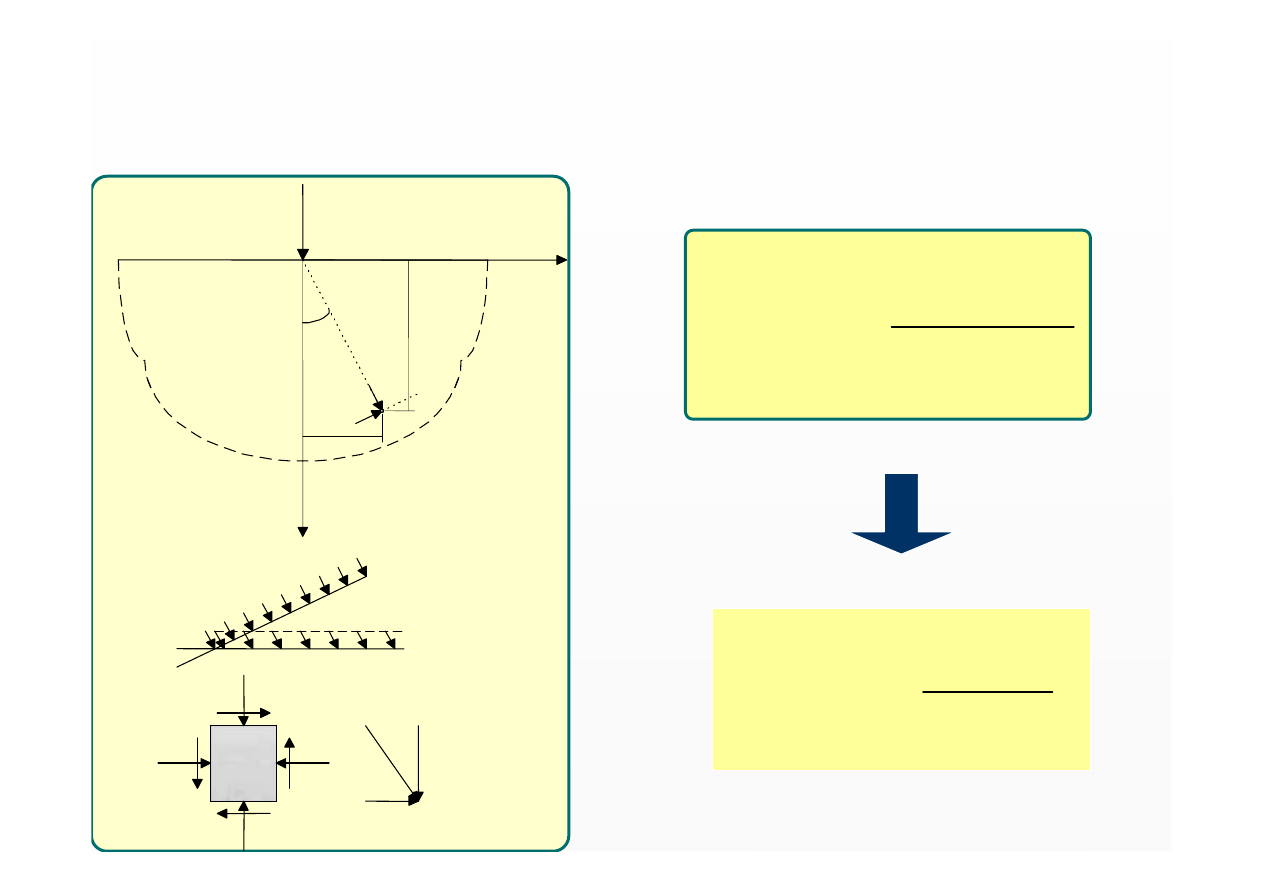
z
r
R
σ
R
τ
f
X
Z
Q
β
σ
R
R
A
A'
β
τ
xz
σ
z
σ
‘
R
a)
b)
M
σ
’
Rozwiązanie Biezuchowa – 1953
2
cos
R
β
Q
k
σ
R
⋅
⋅
=
5
3
R
z
Q
k
σ
z
⋅
⋅
=
MG
MG
-
-
w 7
w 7
3
3
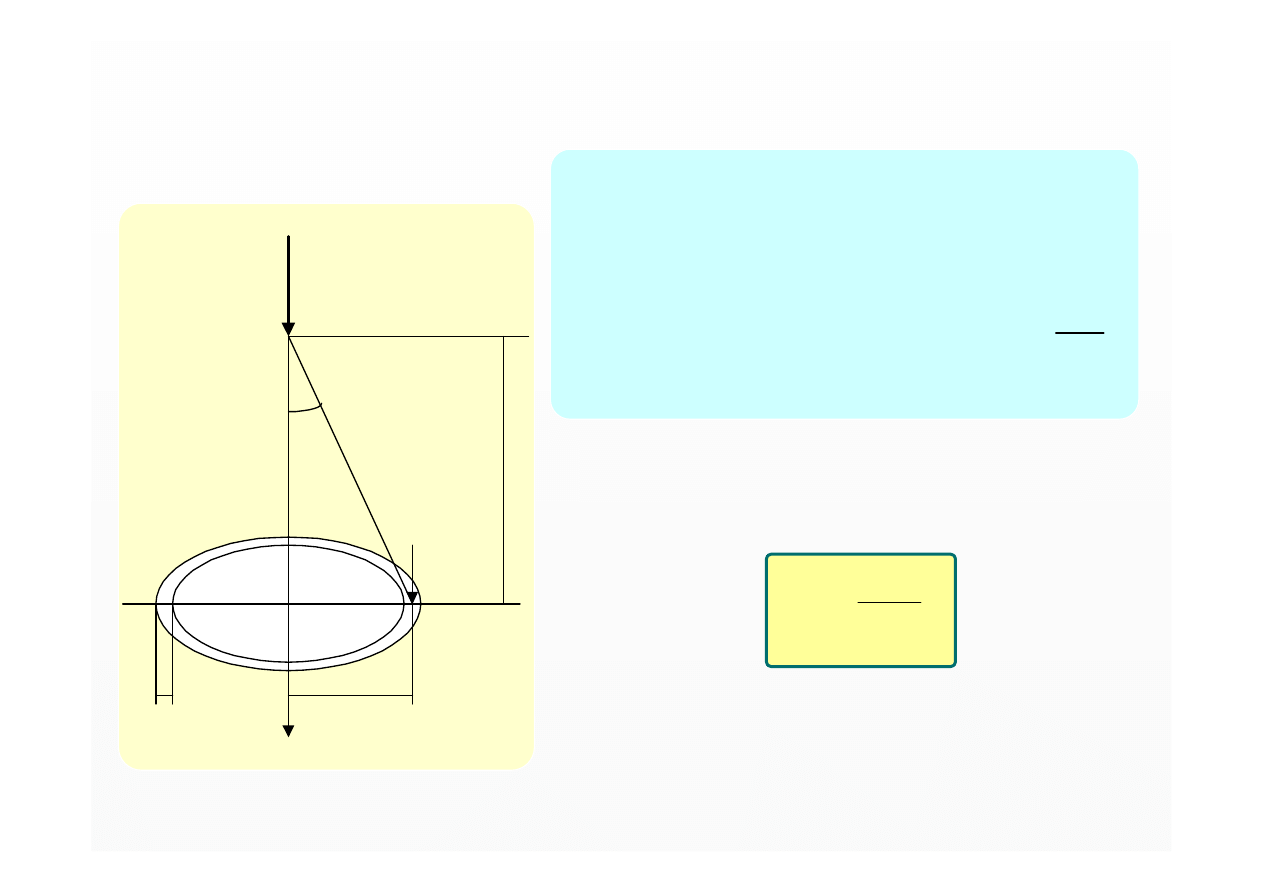
R
z
r
dr
β
Q
z
σ
z
∫
∫
∞
∞
⋅
⋅
⋅
=
⋅
⋅
=
z
z
R
dR
z
k
Q
π
dr
r
σ
π
Q
4
3
0
2
2
dr
r
π
z
σ
dA
z
σ
⋅
⋅
⋅
=
⋅
2
π
k
⋅
=
2
3
MG
MG
-
-
w 7
w 7
4
4
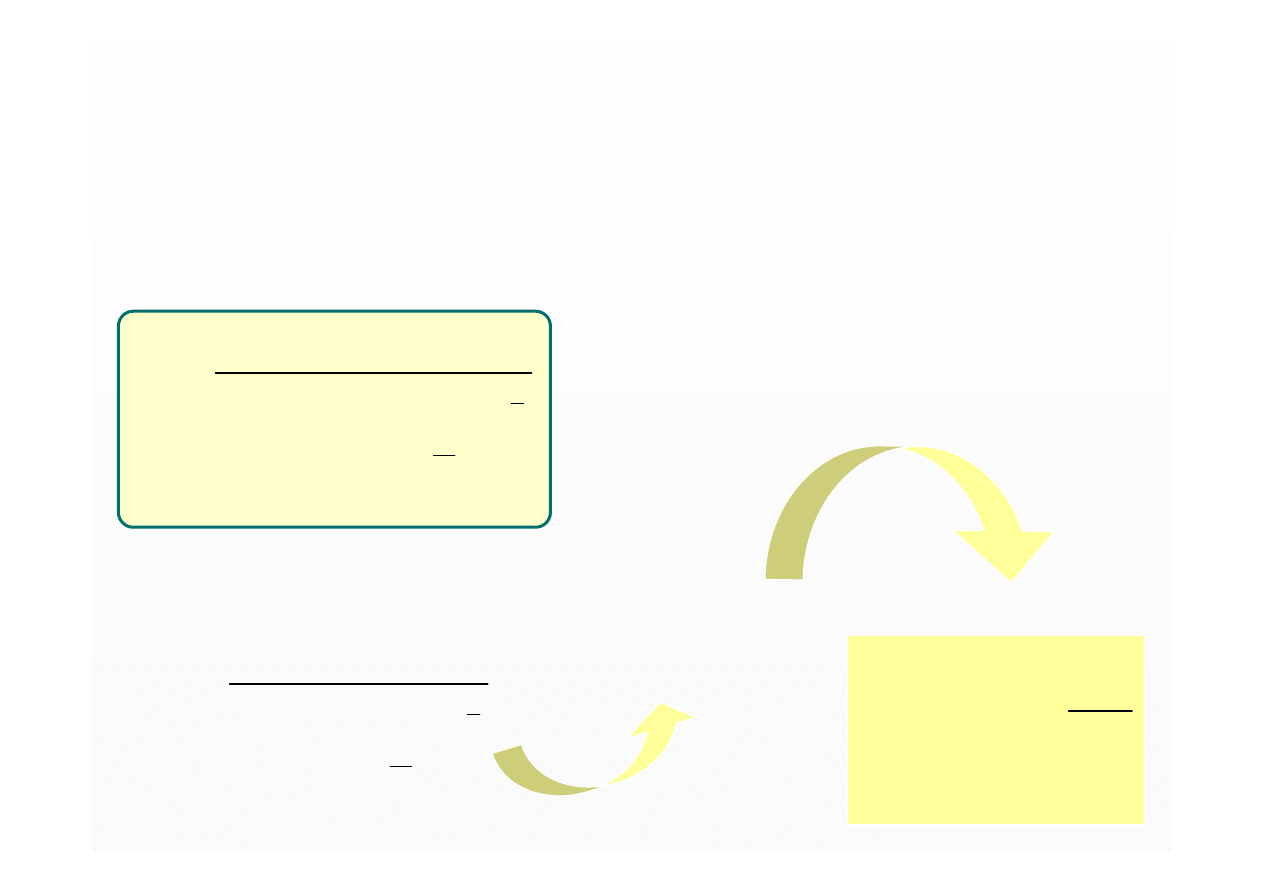
Po podstawieniu wartości współczynnika k, otrzymujemy
wzór na pionowe naprężenia normalne:
2
5
2
2
1
2
3
+
⋅
⋅
⋅
⋅
=
z
r
z
π
Q
σ
z
- wzór Boussinesqe’a
2
5
2
1
2
3
+
⋅
⋅
=
z
r
π
η
Q
2
z
Q
η
σ
Q
z
⋅
=
współczynnik naprężeń
od siły skupionej
MG
MG
-
-
w 7
w 7
5
5
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
2,2
2,4
2,6
2,8
3
3,2
3,4
Q
r
z
R
σ
z
r
z
η
Q
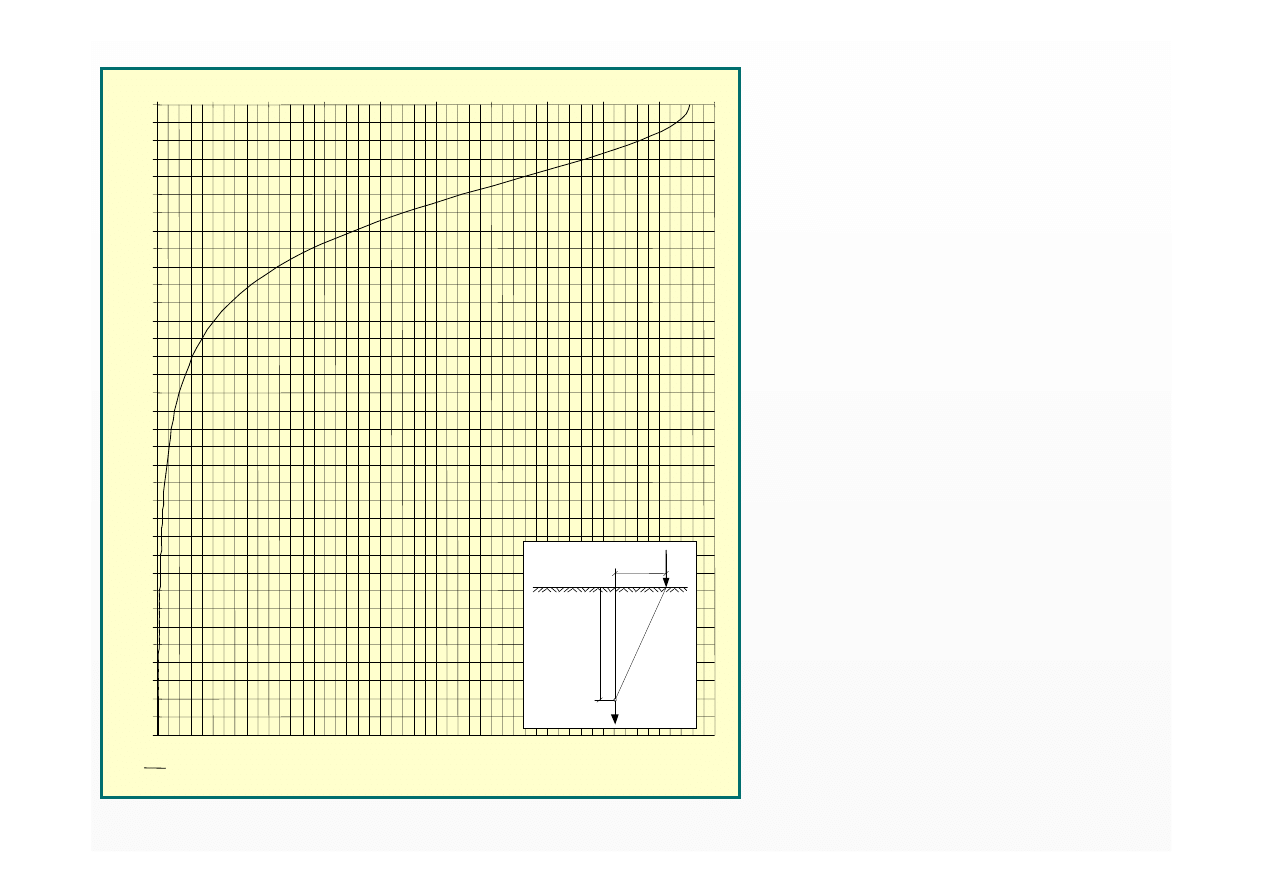
Nomogram
do wyznaczenia
współczynnika
η
Q
MG
MG
-
-
w 7
w 7
6
6
ROZK
ROZK
Ł
Ł
AD NAPR
AD NAPR
ĘŻ
ĘŻ
E
E
Ń
Ń
od OBCI
od OBCI
ĄŻ
ĄŻ
ENIA
ENIA
CI
CI
Ą
Ą
G
G
Ł
Ł
EGO
EGO
„
„
q
q
”
”
L = m·
l
j
B = n·b
i
σ
z
A
11
R
11
r
11
A
nm
Q
11
= q·A
11
q
–
równomiernie rozłożone
na pewnej powierzchni A
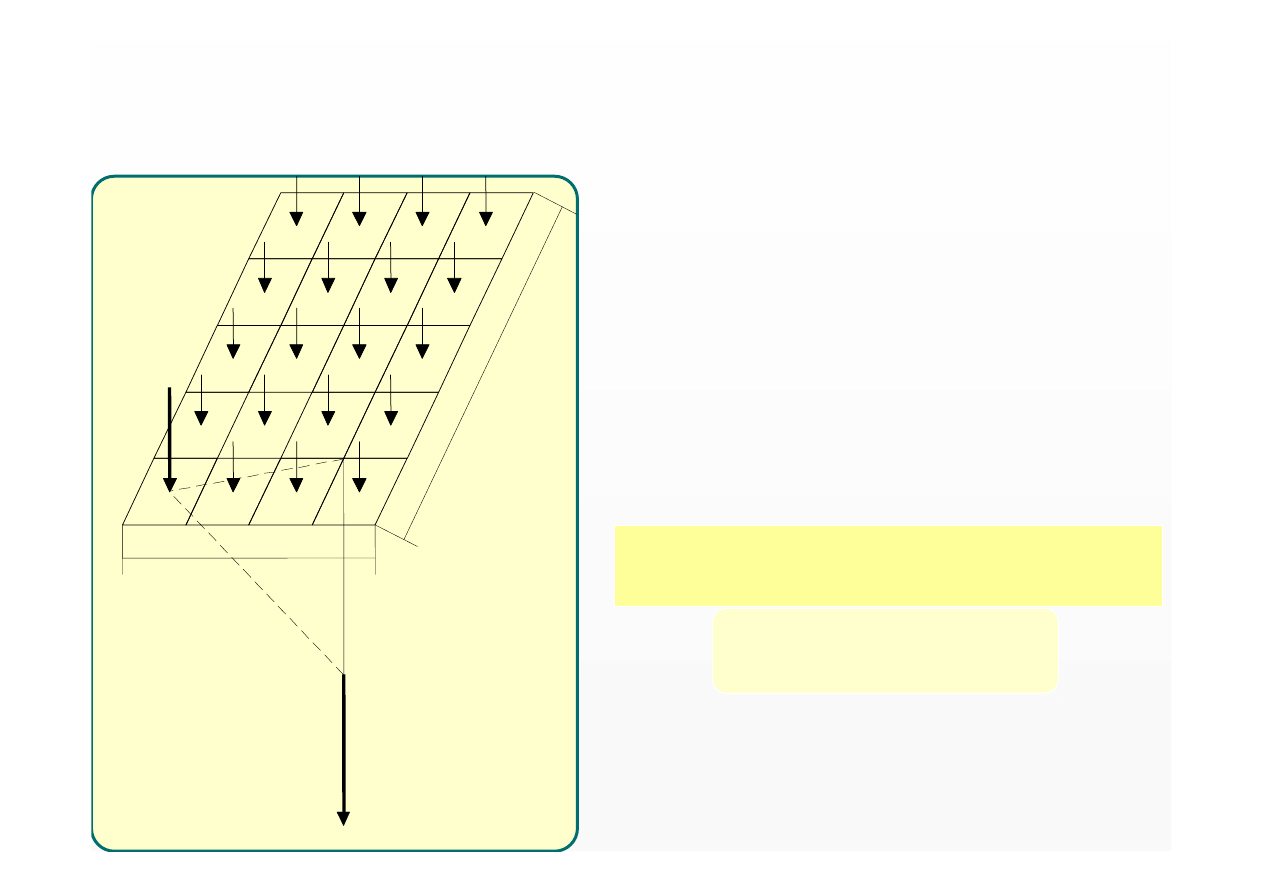
Posługujemy się
wzorami wyprowadzonymi
dla siły skupionej
stosując zasadę superpozycji
σ
z
= Σ
σ
zij
(Q
ij
, r
11
, ..., r
nm
)
z
M
podejście dokładne – wystarczające do celów
praktycznych przy
R
ij
≥
l
i
σ
z
= Q/z
2
· Σ η
Qij
MG
MG
-
-
w 7
w 7
7
7
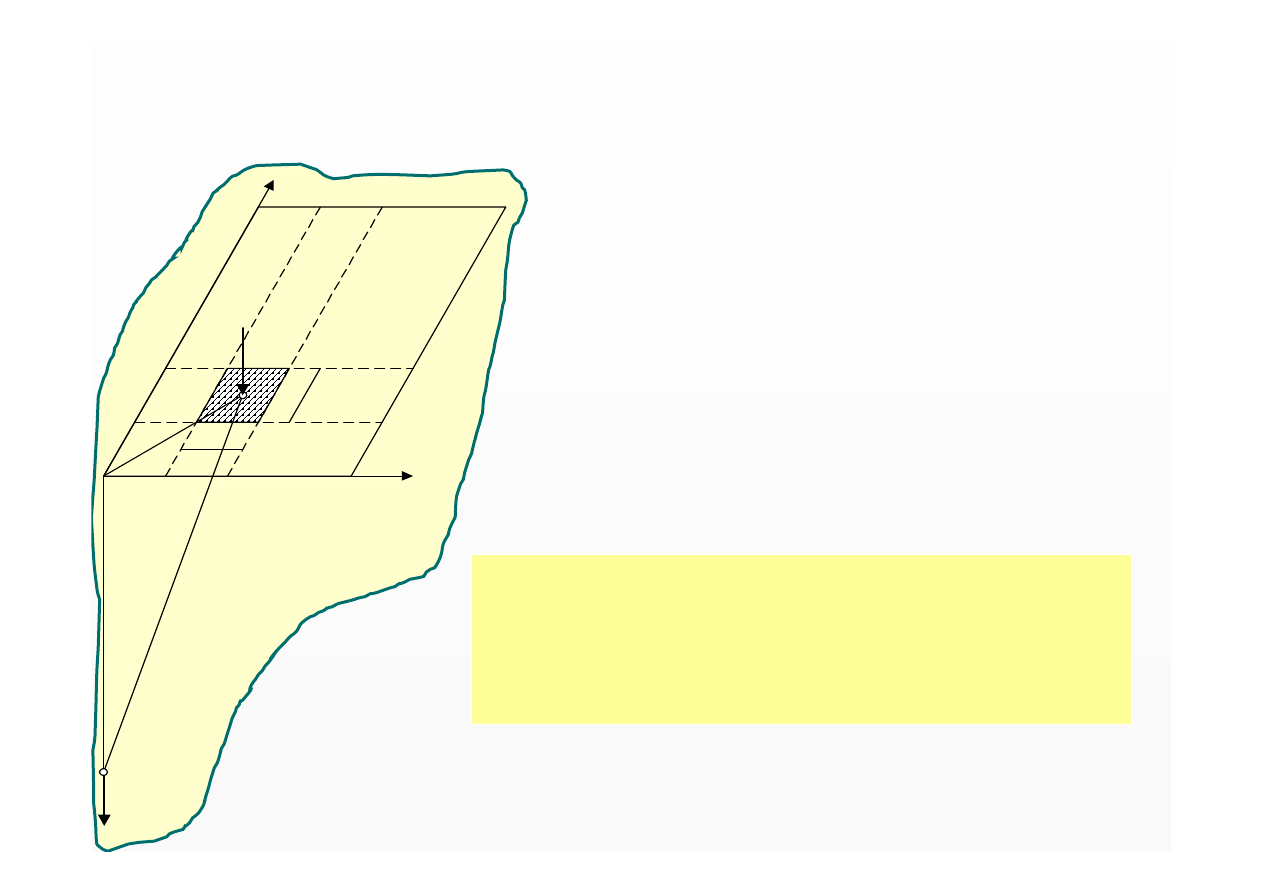
dA = dx·dy –
elementy powierzchni
A
q –
jest równomiernie rozłożone na A
d
Q = q
·
dA –
elementarna siła w A
Naprężenie pionowe w punkcie M ,
zebrane z powierzchni A,
od obciążenia ciągłego q
L B
σ
z
= ∫ ∫
0 0
dQ
d
σ
z
dx
dy
r
x
y
z
B
L
M
3 · q
·
dx
·
dy
2
·
π
·
z
2
·
[
1+ (x
2
+ y
2
)
/
z
2
]
5/2
___________________________

MG
MG
-
-
w 7
w 7
8
8
NAPR
NAPR
ĘŻ
ĘŻ
ENIA pod PROSTOK
ENIA pod PROSTOK
Ą
Ą
TNYM
TNYM
OBSZAREM OBCI
OBSZAREM OBCI
ĄŻ
ĄŻ
ENIA CI
ENIA CI
Ą
Ą
G
G
Ł
Ł
EGO
EGO
Zagadnienie
wyznaczania naprężeń w podłożu gruntowym
:
• pod narożem
prostokątnego obciążonego obszaru
rozwiązał
Steinbrenner
• pod środkiem
obszaru prostokątnego
rozwiązali
Newmark i Polszin
- Wyznaczone rozkłady naprężeń są słuszne przy założeniu
podatności obciążonej powierzchni, tzn.
ugina się ona jednocześnie z odkształceniami gruntu.
-
Przypadki takie zachodzą przy obciążeniach nasypem lub
cienkimi płytami o małej sztywności.

MG
MG
-
-
w 7
w 7
9
9
metoda punkt
metoda punkt
ó
ó
w naro
w naro
ż
ż
nych Steinbrennera
nych Steinbrennera
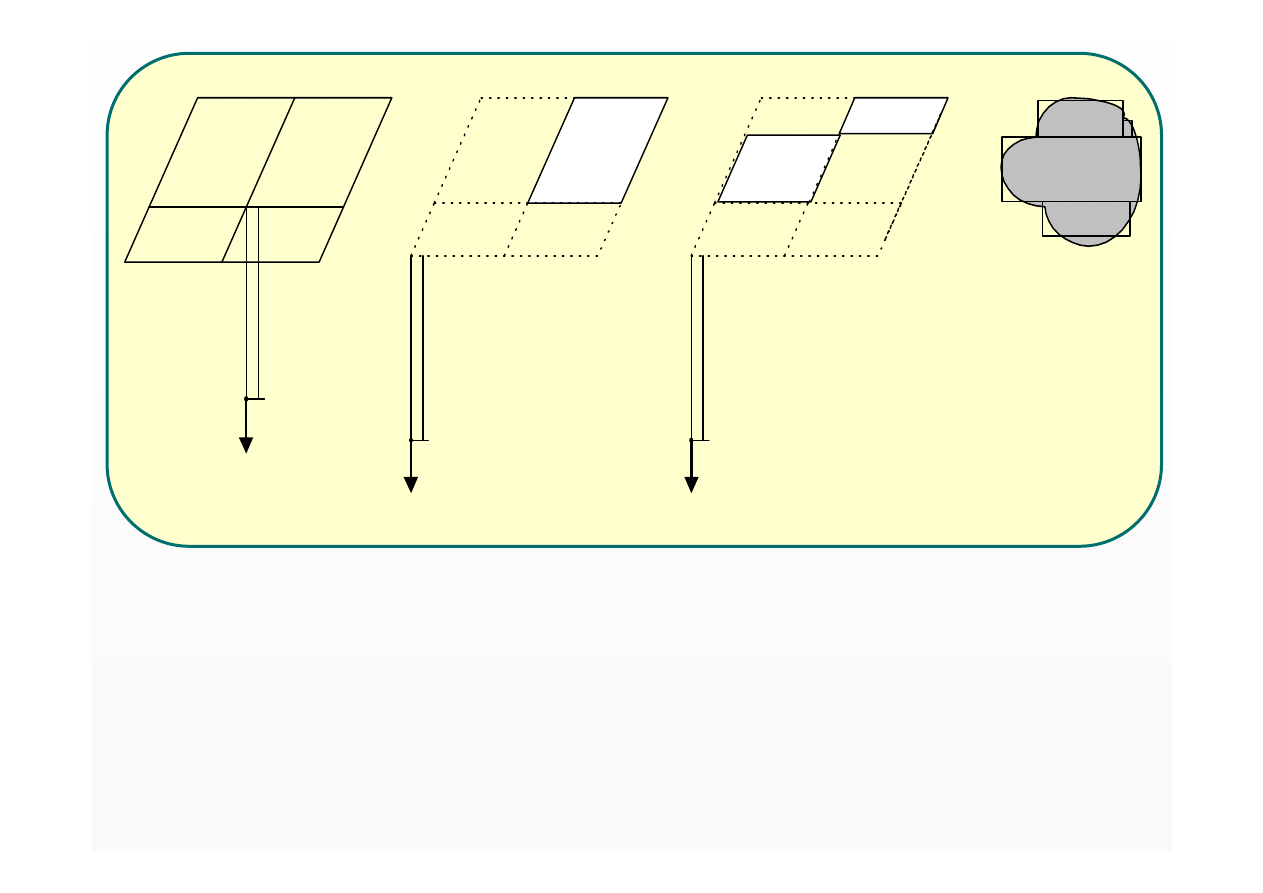
Metoda punktów narożnych (Steinbrennera) umożliwia
wyznaczanie
naprężenia pionowego
oraz
sumy naprężeń
pozwalając na wyznaczanie naprężeń pod następującymi obszarami:
•
według dowolnej linii pionowej przechodzącej
pod obszarem prostokątnym
• według dowolnej linii pionowej przechodzącej
poza obszarem prostokątnym
• w dowolnym punkcie podłoża od obszaru obciążenia
dającego się podzielić na prostokąty
• w dowolnym punkcie podłoża od obszaru obciążenia
dającego się w przybliżeniu podzielić na prostokąty
MG
MG
-
-
w 7
w 7
10
10
I
II
III
IV
z
σ
z
z
σ
z
I
II
III
IV
a)
b)
c)
d)
z
σ
z
I
III
V
VI
II
IV
a) σ
z
=
σ
zI
+
σ
zII
+
σ
zIII
+
σ
zIV
b) σ
z
=
σ
zI÷IV
–
σ
zI,II
–
σ
zI,IV
–
σ
zI
c) σ
z
=
σ
zI,II
–
σ
zI
+
σ
zI÷VI
–
σ
zI÷III
–
σ
zI,II,V,VI
+
σ
zI,II
d) analogicznie jak w przypadku b)
MG
MG
-
-
w 7
w 7
11
11
0
0,05
0,1
0,15
0,2
0
0,3
0,6
0,9
1,2
1,5
1,8
2,1
2,4
2,7
3
3,3
3,6
3,9
4,2
4,5
2
B
L
=
1.5
B
L
=
1
B
L
=
3
B
L
=
5
B
L
=
∞
=
B
L
z
σ
z
q
B
L
ηηηη
n
B
z
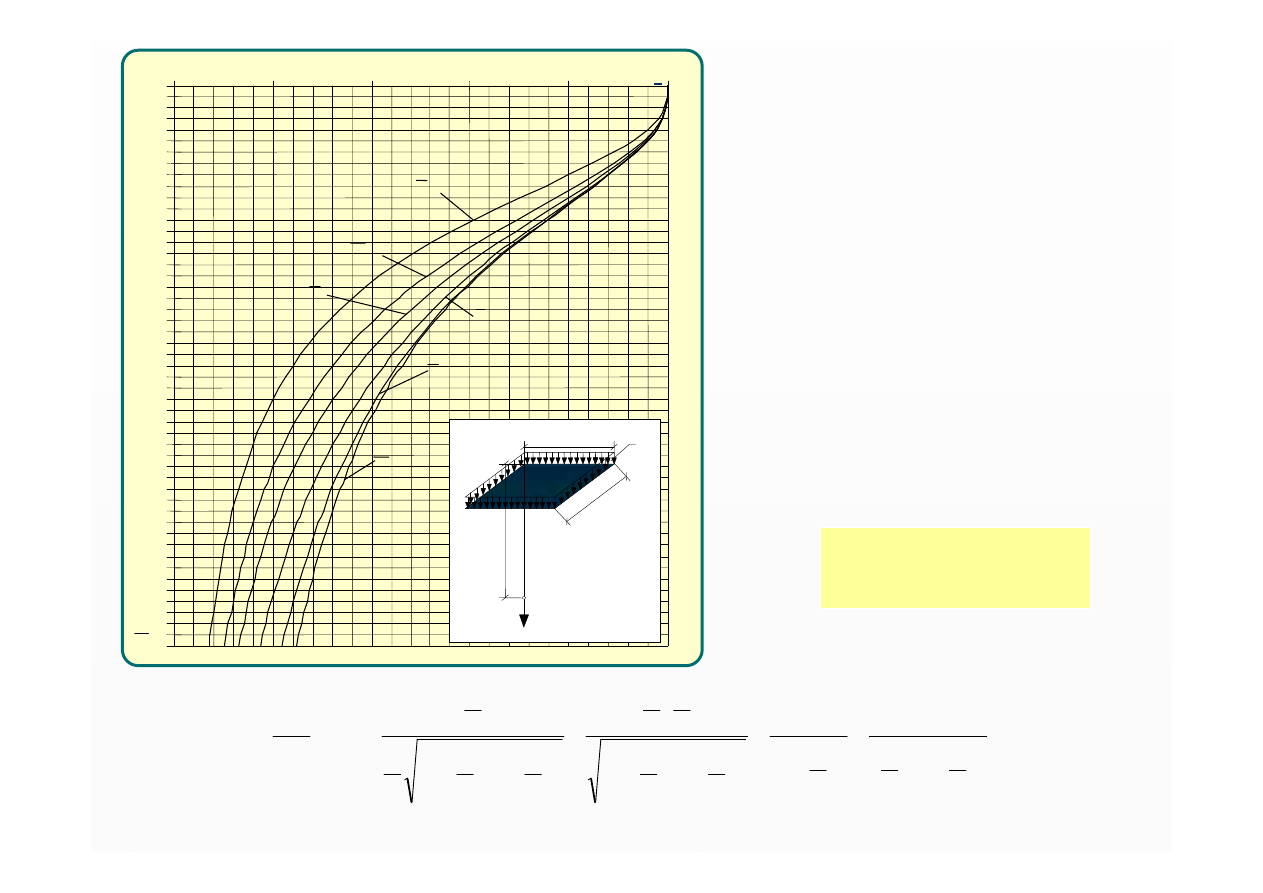
Nomogram do wyznaczania
współczynnika naprężeń
η
n
pod narożem
prostokątnego obszaru
obciążenia ciągłego
równomiernie rozłożonego
+
+
+
⋅
+
+
⋅
+
+
+
⋅
⋅
=
2
2
2
2
2
2
2
1
1
1
1
1
2
1
B
z
B
L
B
z
B
z
B
L
B
z
B
L
B
z
B
L
B
z
B
L
arctg
π
η
n
σ
zn
= q
·
η
n
MG
MG
-
-
w 7
w 7
12
12
metoda punkt
metoda punkt
ó
ó
w
w
ś
ś
rodkowych (Newmark, Polszin)
rodkowych (Newmark, Polszin)
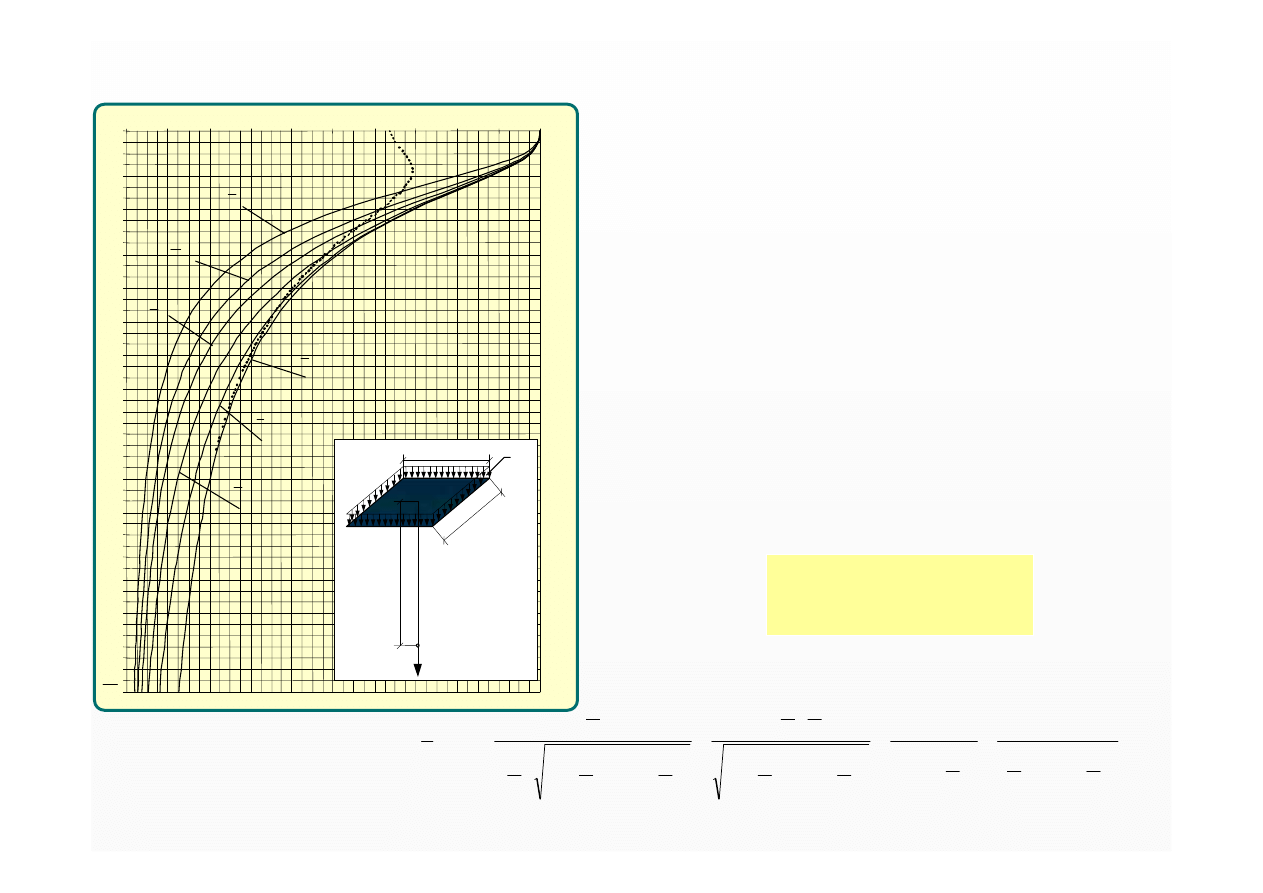
Nomogram do wyznaczania
współczynnika naprężeń
η
m
pod środkiem
prostokątnego obszaru obciążenia
ciągłego równomiernie rozłożonego
pod fundamentem podatnym
pod fundamentem podatnym
σ
zm
= q
·
η
m
⋅
+
+
⋅
+
⋅
⋅
+
+
⋅
⋅
+
⋅
+
+
⋅
⋅
=
2
2
2
2
2
2
2
4
1
4
1
1
4
1
2
4
1
2
2
B
z
B
L
B
z
B
z
B
L
B
z
B
L
B
z
B
L
B
z
B
L
arctg
π
η
m
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
2,2
2,4
2,6
2,8
3
3,2
3,4
3,6
3,8
4
4,2
4,4
4,6
3
B
L
=
5
B
L
=
∞
=
B
L
ηηηη
msz
2
B
L
=
1,5
B
L
=
1
B
L
=
σ
z
q
B
L
z
B
z
ηηηη
m
MG
MG
-
-
w 7
w 7
13
13
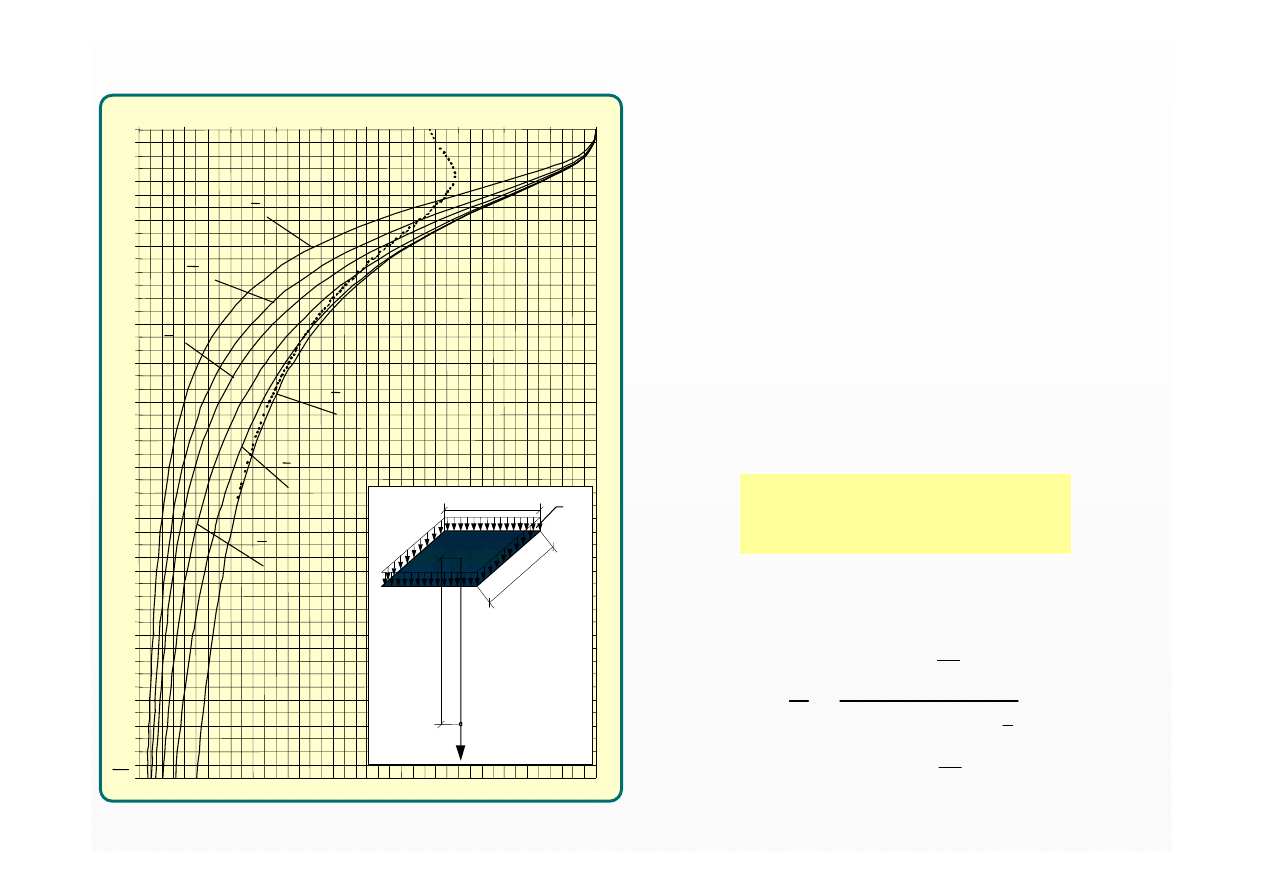
Nomogram do wyznaczania
współczynnika naprężeń
η
msz
pod środkiem
prostokątnego obszaru obciążenia
ciągłego równomiernie rozłożonego
pod fundamentem sztywnym
pod fundamentem sztywnym
σ
zmsz
= q
·
η
msz
⋅
+
+
⋅
=
2
3
2
2
4
1
8
1
2
B
z
B
z
π
η
msz
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
2,2
2,4
2,6
2,8
3
3,2
3,4
3,6
3,8
4
4,2
4,4
4,6
3
B
L
=
5
B
L
=
∞
=
B
L
ηηηη
msz
2
B
L
=
1,5
B
L
=
1
B
L
=
σ
z
q
B
L
z
B
z
ηηηη
m
MG
MG
-
-
w 7
w 7
14
14
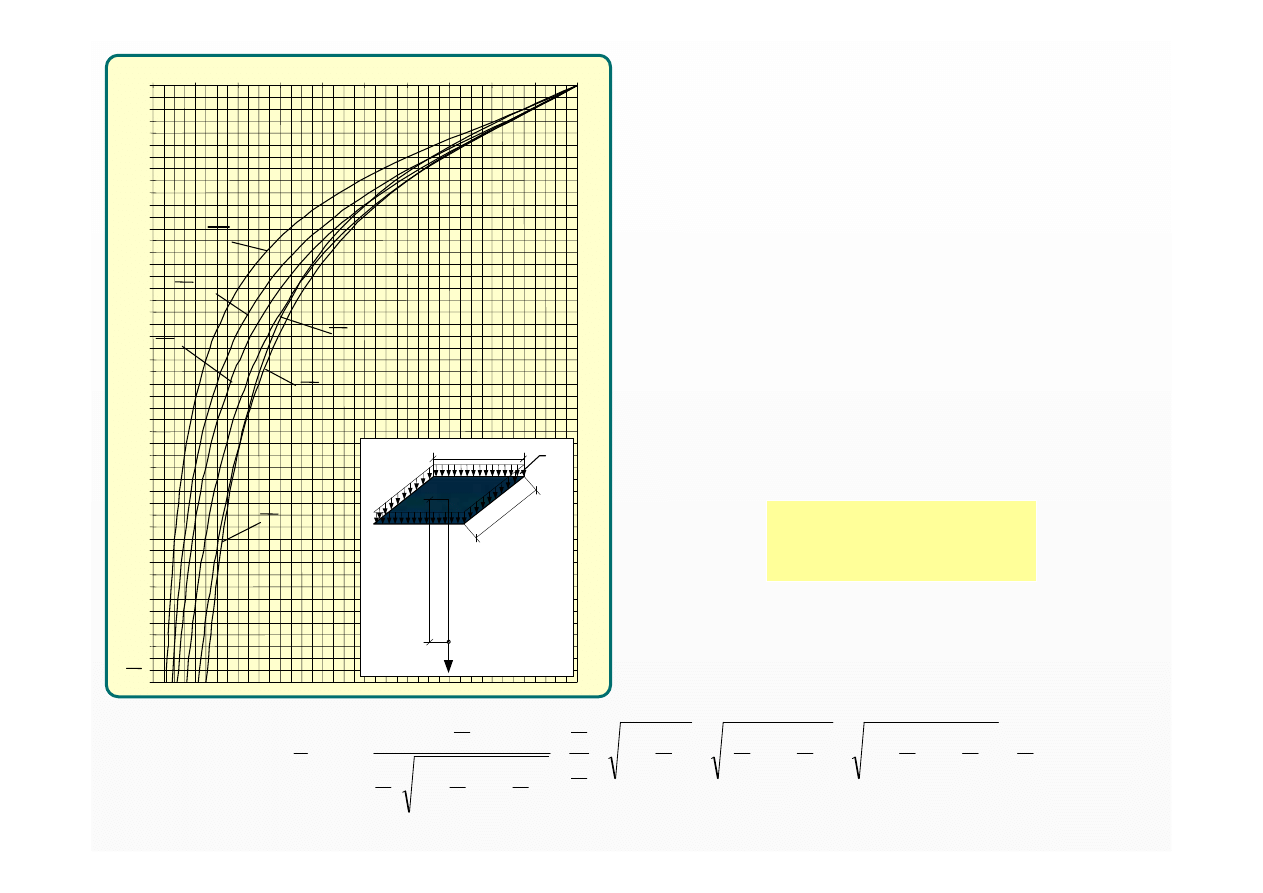
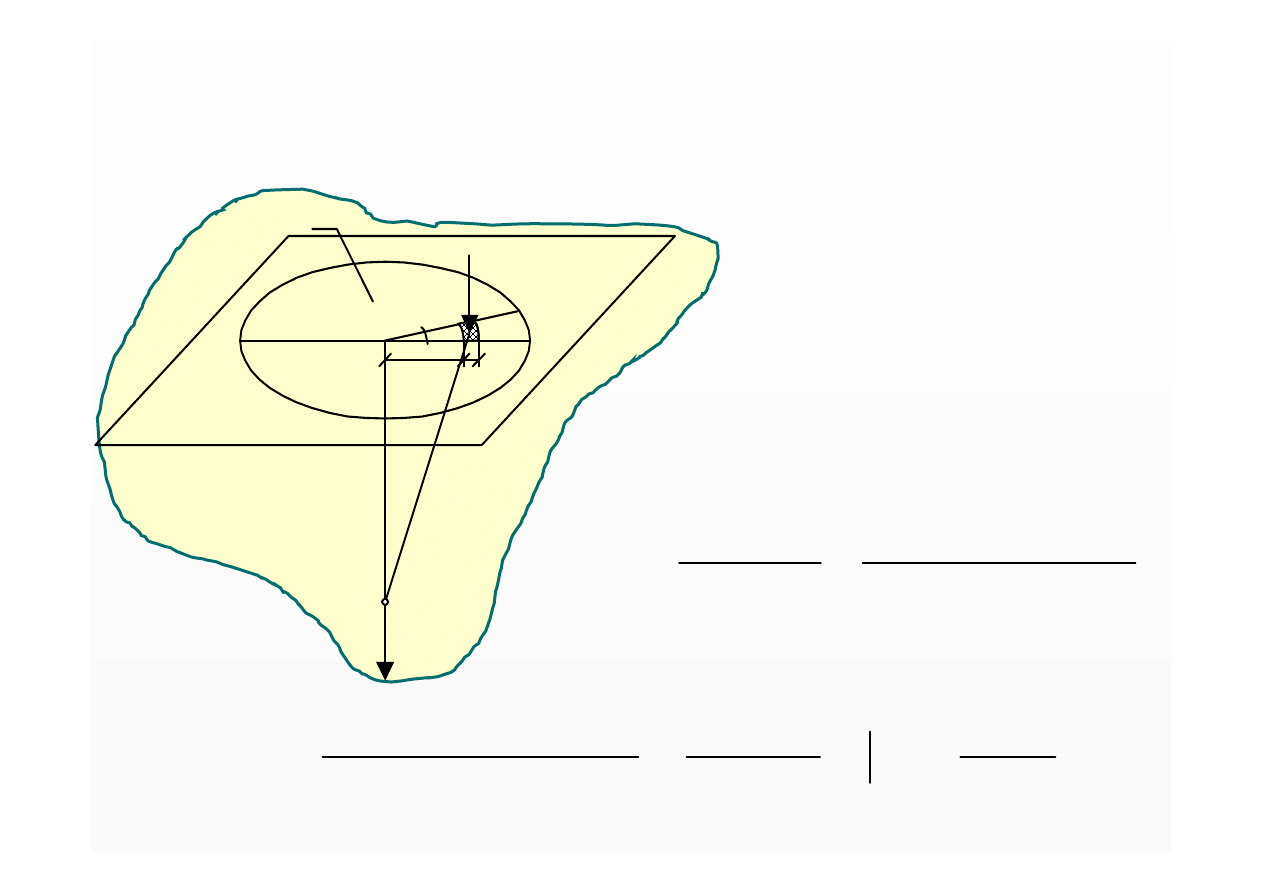
Nomogram do wyznaczania
współczynnika naprężeń
η
s
pod środkiem
prostokątnego obszaru obciążenia
ciągłego równomiernie rozłożonego
σ
zs
= q
·
η
s
−
+
+
−
+
+
+
⋅
+
+
+
⋅
⋅
=
B
z
B
z
B
L
B
z
B
L
B
z
B
L
B
z
B
z
B
L
B
z
B
L
arctg
π
η
s
2
2
2
2
2
2
2
1
1
1
2
B
z
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
2,2
2,4
2,6
2,8
3
3,2
3,4
3,6
3,8
4
4,2
4,4
4,6
1
B
L
=
1,5
B
L
=
2
B
L
=
5
B
L
=
3
B
L
=
∞
=
B
L
ηηηη
s
σ
z
q
B
L
z
MG
MG
-
-
w 7
w 7
15
15
NAPR
NAPR
ĘŻ
ĘŻ
ENIA pod KO
ENIA pod KO
Ł
Ł
OWYM OBSZAREM
OWYM OBSZAREM
OBCI
OBCI
ĄŻ
ĄŻ
ENIA CI
ENIA CI
Ą
Ą
G
G
Ł
Ł
EGO
EGO
(r
(r
ó
ó
wnomiernie roz
wnomiernie roz
ł
ł
o
o
ż
ż
onego)
onego)
r
ρ
d
ρ
d
φ
dQ
q
z
R
d
σ
z
M
dφ
dρ
ρ
dA
⋅
⋅
=
dφ
dρ
ρ
q
dA
q
dQ
⋅
⋅
⋅
=
⋅
=
5
3
5
3
2
3
2
3
R
π
dφ
dρ
ρ
q
z
R
π
z
dQ
dσ
z
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
=
∫
∫ ∫
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
r
π
r
π
z
R
dρ
ρ
φ
π
z
q
R
π
dφ
dρ
ρ
q
z
σ
0
5
2
0
3
0
2
0
5
3
2
3
2
3
MG
MG
-
-
w 7
w 7
16
16
0
0,2
0,4
0,6
0,8
1
0
0,25
0,55
0,85
1,15
1,45
1,75
2,05
2,35
2,65
2,95
3,25
3,55
3,85
4,15
4,45
4,75
ηηηη
0
ηηηη
sz
z
R
σ
z
q
R
z
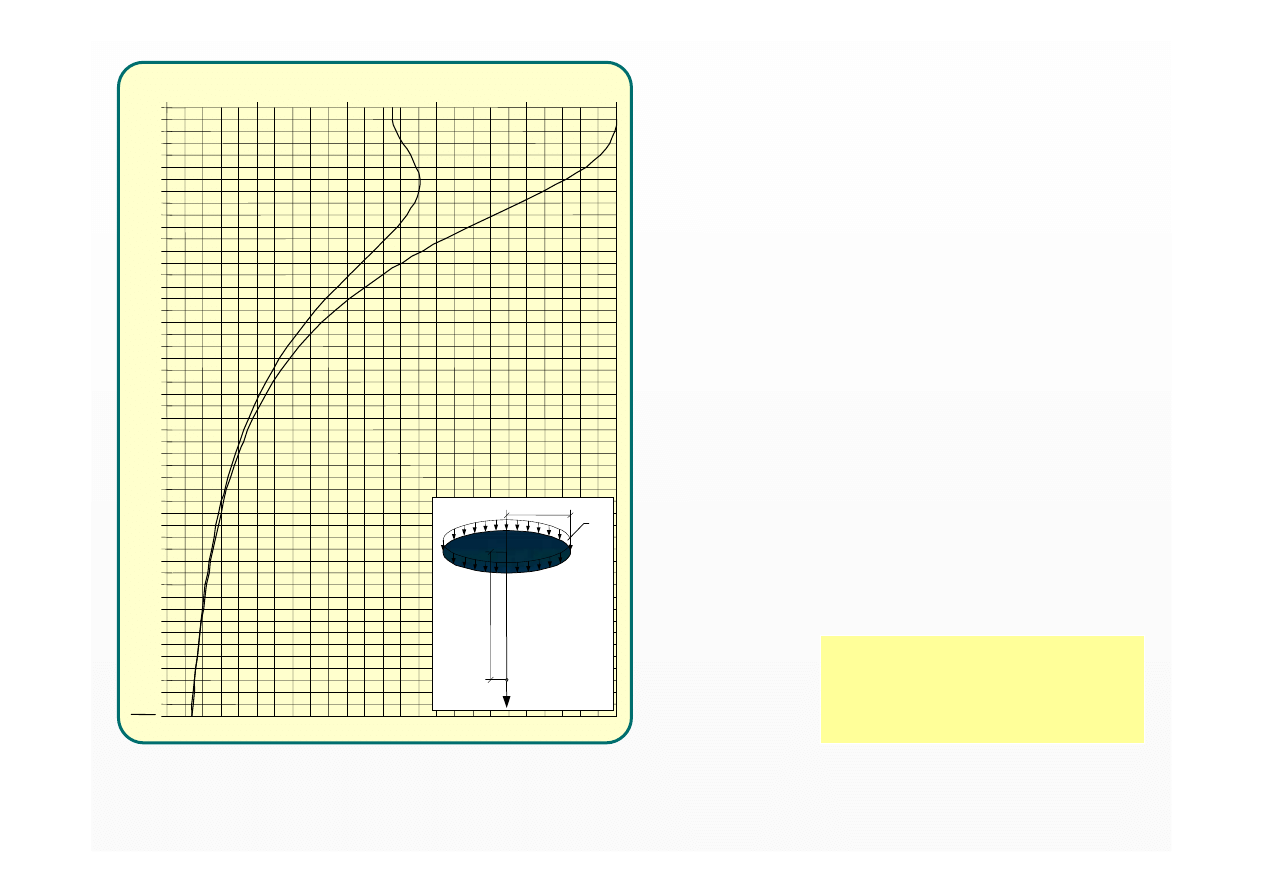
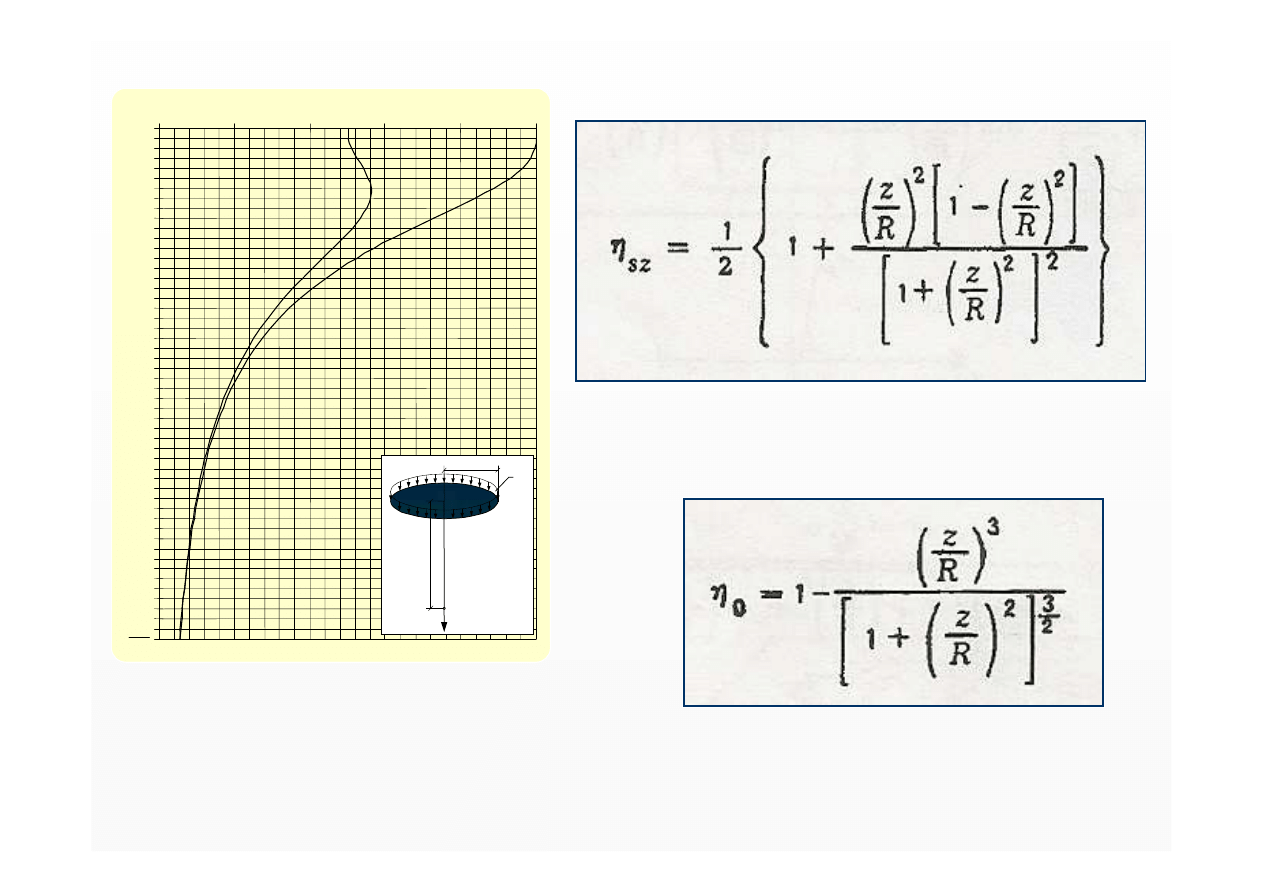
Nomogram do wyznaczania
współczynników naprężenia
η
sz
–
pod fundamentem sztywnym
η
o
–
pod fundamentem podatnym
pod środkiem
kołowego obszaru obciążenia
ciągłego o promieniu R
równomiernie rozłożonego
q
η
σ
sz
z
⋅
=
,
o
ogólnie -
MG
MG
-
-
w 7
w 7
17
17
0
0,2
0,4
0,6
0,8
1
0
0,25
0,55
0,85
1,15
1,45
1,75
2,05
2,35
2,65
2,95
3,25
3,55
3,85
4,15
4,45
4,75
ηηηη
0
ηηηη
sz
z
R
σ
z
q
R
z

MG
MG
-
-
w 7
w 7
18
18
STANY OBCI
STANY OBCI
ĄŻ
ĄŻ
ENIA POD
ENIA POD
Ł
Ł
O
O
Ż
Ż
A
A
GRUNTOWEGO
GRUNTOWEGO
stany obciążenia podłoża gruntowego występujące w trakcie
wykonywania budowli:
• I stan obciążenia –
stan pierwotny
przed rozpoczęciem
robót ziemnych
• II stan obciążenia –
stan obciążenia podłoża gruntowego
po zakończeniu wykonywania wykopu
• III stan obciążenia –
po wykonaniu fundamentów
obiektu
budowlanego i
zasypaniu wykopu
• IV stan obciążenia –
po wykonaniu obiektu budowlanego
i
oddaniu go do eksploatacji

MG
MG
-
-
w 7
w 7
19
19
ROZK
ROZK
Ł
Ł
ADY NAPR
ADY NAPR
ĘŻ
ĘŻ
E
E
Ń
Ń
w POD
w POD
Ł
Ł
O
O
Ż
Ż
U
U
GRUNTOWYM
GRUNTOWYM
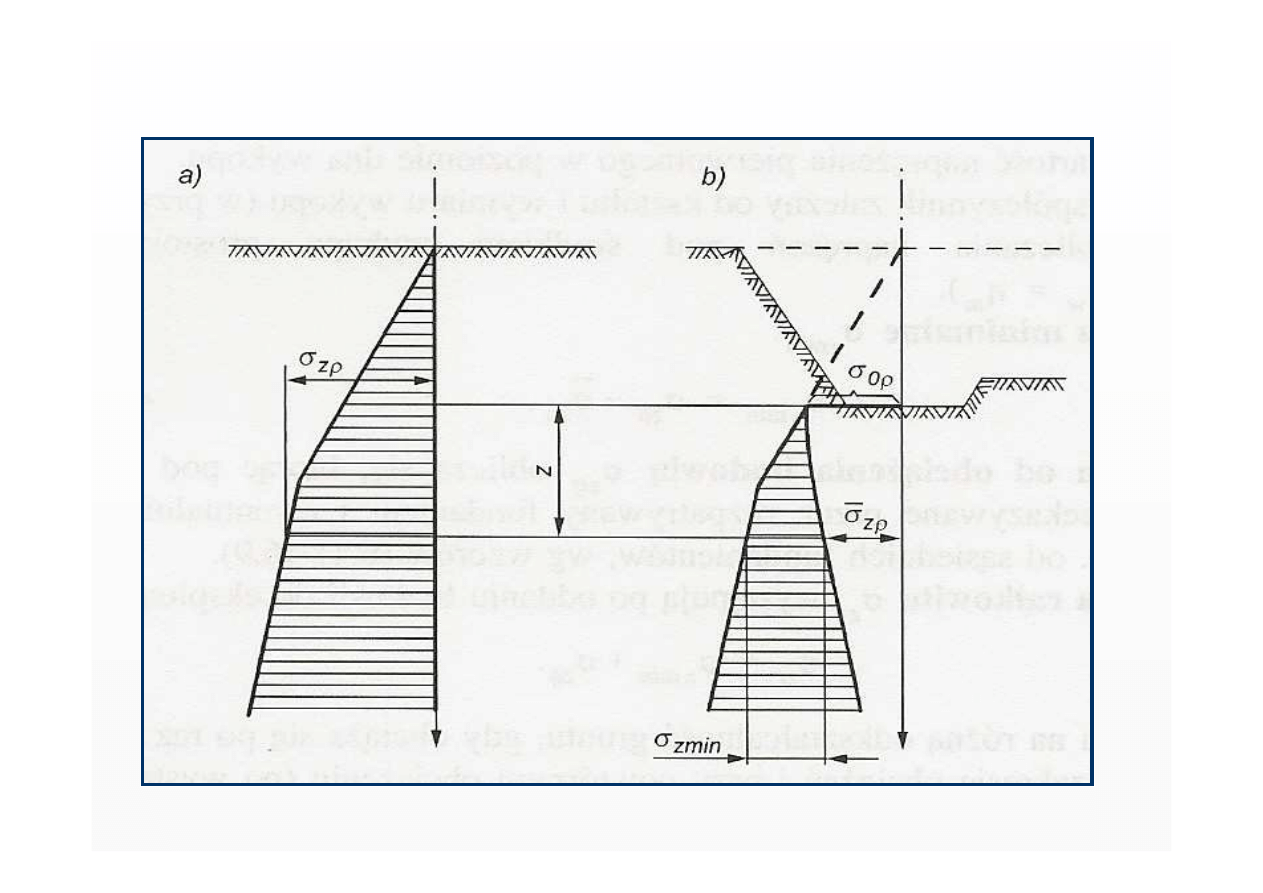
Dla istniejących w podłożu warunków wodno-gruntowych
na granicach warstw obliczeniowych
pod projektowanym fundamentem
dla danego stanu obciążenia
wyznacza się następujące rozkłady naprężeń
:
• naprężeń pierwotnych
• naprężeń minimalnych
po wykonaniu wykopu
• naprężeń wtórnych
• naprężeń dodatkowych
• całkowitych
MG
MG
-
-
w 7
w 7
20
20
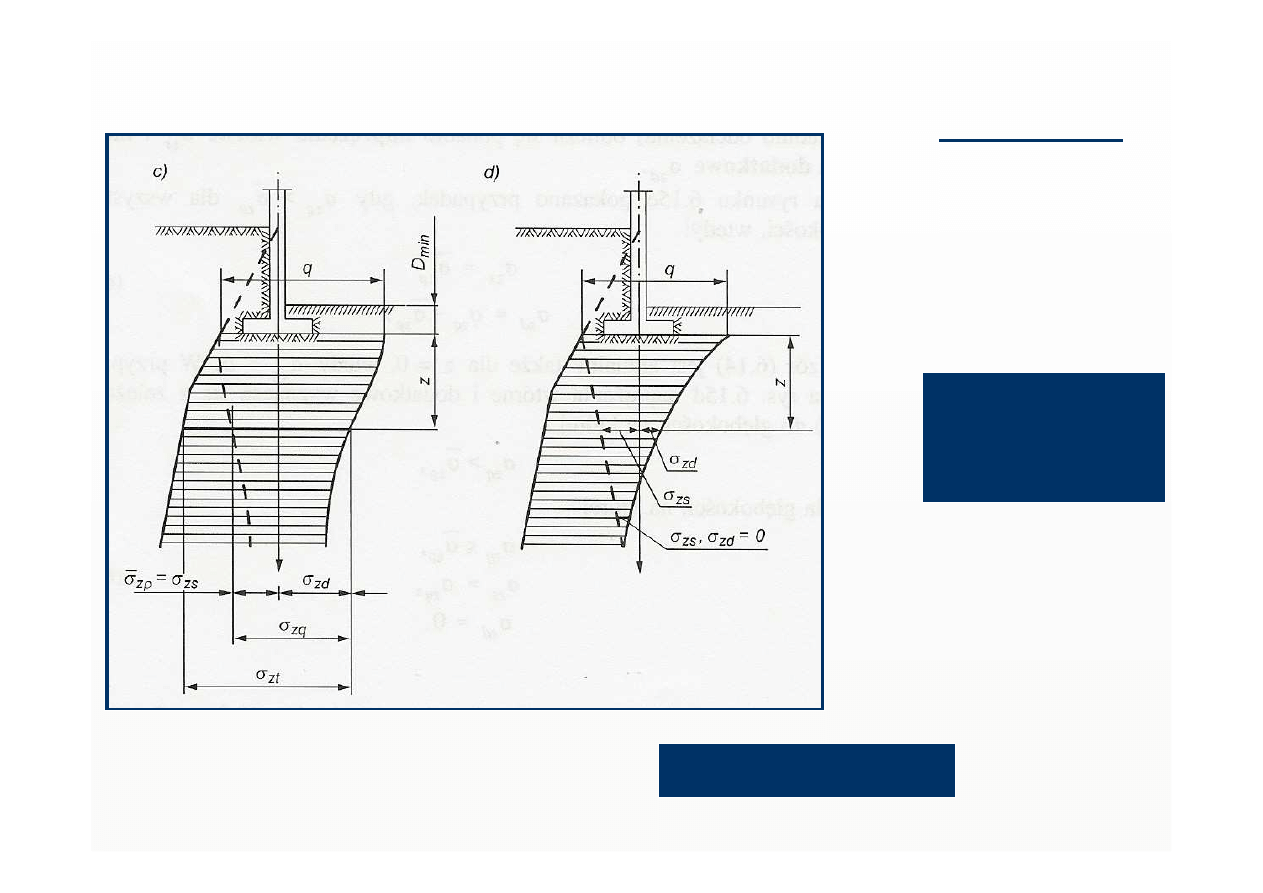
a) napr
a) napr
ęż
ęż
enia pierwotne b) napr
enia pierwotne b) napr
ęż
ęż
enia minimalne
enia minimalne
MG
MG
-
-
w 7
w 7
21
21
napr
napr
ęż
ęż
enia ca
enia ca
ł
ł
kowite
kowite
c) gdy dla wszystkich
gł
ę
boko
ś
ci:
2 przypadki
d)
do gł
ę
boko
ś
ci dla której,
σ
zs
i
σ
zd
wyznaczamy z
zale
ż
no
ś
ci
jak w c)
σ
zq
>
σ
z
ρ
-
wtedy:
σ
zs
=
σ
z
ρ
-
σ
zd
=
σ
z
q
−
σ
z
ρ
-
σ
zq
>
σ
z
ρ
-
za
ś
dla gł
ę
boko
ś
ci, na której
σ
zq
≤
σ
z
ρ
,
σ
zs
=
σ
zq
,
σ
z
d
=
0
-

MG
MG
-
-
w 7
w 7
22
22
Naprężenia pierwotne
oblicza się na podstawie ciężaru
poszczególnych warstw obliczeniowych:
σ
ρzi
= h
i
·
ρ
i
·
g
gdzie:
h
i
– grubość warstwy obliczeniowej
ρ
i
– gęstość objętościowa danej warstwy gruntu
zależnie od rodzaju występującej w nich wody odpowiednio:
ρ
sat ,
ρ‘, ρ’’ dla warstw
g – przyspieszenie ziemskie
następnie
liczymy naprężenia pod poszczególnymi warstwami
sumując naprężenia z warstw położonych powyżej:
σ
ρz
= ∑ σ
zρi
n
i=1

MG
MG
-
-
w 7
w 7
23
23
Odciążenie wykopem – naprężenia minimalne
gdzie:
η
0
– współczynnik rozkładu naprężenia pod
środkiem obszaru prostokątnego obciążonego
równomiernie, zależny od stosunku wymiarów
wykopu
L
w
/ B
w
oraz głębokości
z
∆σ
z
ρ
= σ
z
ρ
D
· η
0
σ
zmin
= σ
zρ
- ∆σ
zρ
MG
MG
-
-
w 7
w 7
24
24
Naprężenia wtórne
σ
zρ
= σ
zmin
+ σ
zs
Przyrost naprężeń od minimalnych
do pierwotnych po posadowieniu
fundamentu i zasypaniu wykopu
Naprężenia całkowite
σ
zq
c
= σ
zq
+σ
zq
s
naprężenia od wznoszonego
obiektu budowlanego
+
naprężenia od obciążeń
sąsiednich

MG
MG
-
-
w 7
w 7
25
25
Naprężenia
pochodzące od wznoszonego obiektu budowlanego
obliczamy zależnie od rodzaju i kształtu fundamentu oraz
wielkości obciążenia, które ma przenieść ten fundament.
Naprężenia
pochodzące od obciążeń sąsiednich
obliczamy metodą punktów narożnych lub nomogramem
Newmarka.

MG
MG
-
-
w 7
w 7
26
26
Jeżeli
odległość obiektu sąsiedniego
>>
>>
>>
>>
od jego wymiarów w planie
,
wartość naprężenia oblicza się
traktując obiekt sąsiedni jako
siłę skupioną
.
σ
ziP
= (1/z
i
2
) · P · K
r
gdzie:
P – wartość siły skupionej
η
Q
= K
r
/z
2
– współczynnik naprężenia zależny od odległości
przyłożenia siły r
=
(x
2
+ y
2
)
1/2
oraz głębokości
obliczeniowej obliczonej zgodnie z [
PN – 81/B – 3020
]
MG
MG
-
-
w 7
w 7
27
27
Naprężenia dodatkowe
σ
zd
= η
0
(q – σ
zρD
)
= η
0
q
naprężenia całkowite
(pochodzące od przyłożonego obciążenia)
pomniejszone o
odciążenie po wykopie
Naprężenia całkowite
σ
zt
= σ
zmin
+ η
0
·q
lub
= σ
zmin
+ η
s
·q
naprężenia minimalne
+
naprężenia dodatkowe
-
q = Q / (L· B)
Q – obciążenie od fundamentu
i obiektu budowlanego
-
MG
MG
-
-
w 7
w 7
28
28
ROZK
ROZK
Ł
Ł
ADY NAPR
ADY NAPR
ĘŻ
ĘŻ
E
E
Ń
Ń
w POD
w POD
Ł
Ł
O
O
Ż
Ż
U GRUNTOWYM
U GRUNTOWYM
Ć
wiczenie rachunkowe
:
:
-
-
napr
napr
ęż
ęż
enia pierwotne,
enia pierwotne,
-
-
napr
napr
ęż
ęż
enia po wykonaniu
enia po wykonaniu
wykopu,
wykopu,
-
-
napr
napr
ęż
ęż
enia po wykonaniu
enia po wykonaniu
fundamentu,
fundamentu,
-
-
napr
napr
ęż
ęż
enia od obiektu
enia od obiektu
s
s
ą
ą
siedniego.
siedniego.
Wyszukiwarka
Podobne podstrony:
mg 2010z 3 w
mg 2010z 4 w
MG-2010z-gęstości, Budownictwo, II rok, Mechanika gruntów
MG 2010z-ćwiczenie rachunkowe-1 (2), Budownictwo, II rok, Mechanika gruntów
mg 2010z 8 w
mg 2010z 1 w
MG 2010z-ćwiczenie rachunkowe-nasze, Budownictwo, II rok, Mechanika gruntów
mg 2010z 6 w
mg 2010z 3 w
MG 2010z ćwiczenie rachunkowe 1 doc
mg 2010z ćwiczenie rachunkowe 2s
MG 2010z cwiczenie rachunkowe 2
mg 2010z ćwiczenie rachunkowe 2
więcej podobnych podstron