Spis treści

Wstęp 9

Część I. Statyka

Wprowadzenie 12

Elementy rachunku wektorowego 13

1. Układy płaskie w przypadku więzów idealnych 16

1.1. Twierdzenie o trzech siłach 16

1.2. Płaski układ sił zbieżnych 25

1.3. Redukcja dowolnego płaskiego układu sił 29

1.4. Równowaga układu sił równoległych 33

1.5. Układy poddane obciążeniom rozłożonym w sposób ciągły 37

1.6. Dowolny płaski układ sił 43

1.7. Kratownice 55

2. Równowaga płaskiego układu sił z uwzględnieniem

sił tarcia 60

3. Przestrzenny układ sił 81

3.1. Wprowadzenie 81

3.2. Redukcja dowolnego przestrzennego układu sił 83

3.3. Układ sił zbieżnych pozostających w równowadze 87

3.4. Dowolny przestrzenny układ sił pozostających w równowadze 91
3.5. Środek sił równoległych i środki ciężkości linii, powierzchni

i brył 99

4. Równowaga wiotkich lin ciężkich — zastosowania

techniczne 113

Część II. Kinematyka

5. Kinematyka punktu 120

Wprowadzenie 120
5.1. Kinematyka punktu we współrzędnych krzywoliniowych 121
5.2. Kinematyka punktu w układzie kartezjańskim 124
5.3. Kinematyka punktu w układzie naturalnym 137
5.4. Kinematyka punktu we współrzędnych krzywoliniowych — układy

biegunowy, cylindryczny, sferyczny, toroidalny 144

6. Ruch obrotowy bryły wokół stałej osi 154

7. Ruch płaski 160

7.1. Wprowadzenie 160
7.2. Przykłady obliczania prędkości punktów ciała w ruchu

płaskim 163

7.3. Przyspieszenie punktów ciała w ruchu płaskim 174

8. Ruch kulisty bryły 211

8.1. Wprowadzenie 211
8.2. Wyznaczanie prędkości kątowych i przyspieszenia kątowego

za pomocą kątów Eulera 213

8.3. Przykłady obliczania prędkości i przyspieszeń punktów ciała

w ruchu kulistym 215

9. Ruch złożony punktu 226

9.1. Wprowadzenie 226
9.2. Przykłady obliczania prędkości bezwzględnych i przyspieszeń

bezwzględnych w ruchu złożonym punktu 228

Część III. Dynamika

10. Dynamika punktu 240

Wprowadzenie 240

10.1. Zadania proste 243
10.2. Zadania odwrotne — całkowanie równań różniczkowych

ruchu 256

10.3. Ruch krzywoliniowy 285
10.4. Drgania o jednym stopniu swobody — drgania własne 293
10.5. Drgania wymuszone 311
10.6. Praca i moc, potencjał pola sił 326
10.7. Zasada równowartości energii kinetycznej i pracy oraz

zasada zachowania energii mechanicznej 333

Spis treści

Spis treści

11. Zadania specjalne dynamiki punktu 350

11.1. Dynamika punktu w ruchu względnym 350

11.2. Ruch punktu w polu środkowym 360

11.3. Wybrane zadania z dynamiki punktu o zmiennej

masie 372

12. Geometria mas 385

12.1. Pojęcia podstawowe 385

12.2. Przykłady znajdowania momentów bezwładności

i momentów dewiacji 389

13. Dynamika układu punktów materialnych 400

13.1. Równania ruchu układu punktów materialnych 400

13.2. Zasada ruchu środka masy 407

13.3. Kręt i zasada krętu dla układu punktów

materialnych 420

14. Ruch obrotowy bryły dookoła stałej osi 427

14.1. Metoda kinetostatyki 427

14.2. Reakcje dynamiczne w ruchu obrotowym bryły dookoła

stałej osi 437

14.3. Równania różniczkowe w ruchu obrotowym dookoła

stałej osi 446

15. Ruch płaski ciała sztywnego 460

16. Przybliżona teoria giroskopu 478

17. Elementy mechaniki analitycznej 486

17.1. Zasada prac przygotowanych 486

17.2. Zasada d'Alamberta i równania Lagrange'a I rodzaju 503

17.3. Równania Lagrange'a II rodzaju 510

18. Wyznaczanie położenia równowagi 538

19. Zderzenia 552

Literatura 575

Wstęp

Podręcznik jest przeznaczony dla studentów studiów magister­

skich i zawodowych kierunków: mechanika i budowa maszyn,

automatyka i robotyka, inżynieria materiałowa i transport. Za­

pewne będzie też przydatny na innych kierunkach studiów,

takich jak budownictwo, wychowanie techniczne, inżynieria

środowiska.

Należytemu zrozumieniu i opanowaniu mechaniki ogólnej

dobrze służą przykłady zastosowań praktycznych.

Książka składa się z trzech części: statyki, kinematyki

i dynamiki. Znajduje się w niej wiele różnorodnych przykła­

dów z mechaniki dobranych w ten sposób, aby Czytelnik mógł

samodzielnie rozwiązywać zadania należące do danego działu

mechaniki. Rozdziały zaczynają się krótkim wstępem zawie­

rającym podstawowe pojęcia i twierdzenia, po czym następują

przykłady z rozwiązaniami. Na końcu każdego rozdziału znaj­

dują się zadania, do rozwiązania których Autor gorąco zachęca

Czytelników.

Zadania i przykłady oznaczone gwiazdką studenci stu­

diów zawodowych mogą pominąć.

Zadania, z którymi spotykamy się w statyce, można podzielić

na dwie grupy. Do grupy pierwszej zaliczamy zadania zwią­

zane z równowagą układu sił, do drugiej — z redukcją ukła­

du sił.

W obydwu przypadkach przy rozwiązywaniu zadań mo­

żemy posługiwać się zarówno metodami analitycznymi, jak

i graficznymi. My będziemy stosować metody anali­

tyczne.

Metody graficzne są nieocenione przy rozwiązywa­

niu płaskich układów prętowych (kratownic), jednak z rozwo­

jem metod komputerowych straciły one na znaczeniu. Omó­

wimy stosowanie metod analitycznych związanych z rozpa­

trywaniem równowagi układu sił. Przed przystąpieniem do

rozwiązania zadania należy:

• zobaczyć, czy mamy do czynienia z układem prostym

(jedno ciało sztywne), czy złożonym (kilka ciał powią­

zanych ze sobą). W tym ostatnim przypadku należy

rozbić myślowo układ złożony na układy proste, pa­

miętając o tym, że siły oddziaływania jednego ciała na

drugie występują zawsze dwójkami zerowymi;

• zaznaczyć wszystkie siły czynne działające na dane

ciało;

• ustalić więzy (ograniczenia nałożone na ruch) bezpo­

średnio działające na dane ciało, a następnie oswobo­

dzić ciało od więzów, zastępując odrzucone myślowo

więzy siłami reakcji;

• zakwalifikować otrzymany układ sił czynnych i bier­

nych działających na dane ciało do odpowiedniej grupy

(układ płaski, przestrzenny, zbieżny, równoległy, do­

wolny);

Elementy rachunku wektorowego

• określić liczbę niezależnych równań równowagi, które

możemy ułożyć dla danego układu;

• rozstrzygnąć, czy mamy do czynienia z układem sta­

tycznie wyznaczalnym, czy liczba niewiadomych reak­

cji nie przekracza liczby równań równowagi;

• wybrać układ współrzędnych tak, aby otrzymać możli­

wie najprostszy układ równań i ułożyć równania rów­

nowagi;

• rozwiązać układ równań ze względu na poszukiwane

wielkości, sprawdzić ich miary, przeprowadzić dyskusję

błędów.

W wielu zadaniach nie można z góry przewidzieć kie­

runku reakcji. W tym przypadku należy reakcję o nieznanym

kierunku rozłożyć na składowe wzdłuż osi układu współrzęd­

nych. Jeżeli z obliczeń otrzymamy składową ujemną, będzie

to oznaczać, że zwrot danej reakcji należy zmienić na prze­

ciwny.

Elementy rachunku wektorowego

Spotykane w naukach fizycznych wielkości są wielkościami

wektorowymi lub skalarnymi. Wielkości skalarne określa się

przez podanie ich wartości. Przykładami takich wielkości są:

masa, praca, moc, energia, czas, potencjał itp. Wielkości wek­
torowe

określa się przez podanie wartości, kierunku i zwrotu.

Przykładami wektorów są: siła, moment siły, prędkość, przy­

spieszenie, pęd, kręt itp.

Wektory reprezentujące wielkości fizyczne oprócz poda­

nych trzech cech powinny mieć określone w danej przestrzeni

położenie. Z tego względu definiuje się trzy typy wek­

torów.

Wektor zaczepiony w dowolnej przestrzeni jest to upo­

rządkowana para punktów (A, B). Geometryczny obraz ta­

kiego wektora jest przedstawiony na rys. 1. Wektor ozna­

czono literą a; można go również oznaczać AB lub (A, B).

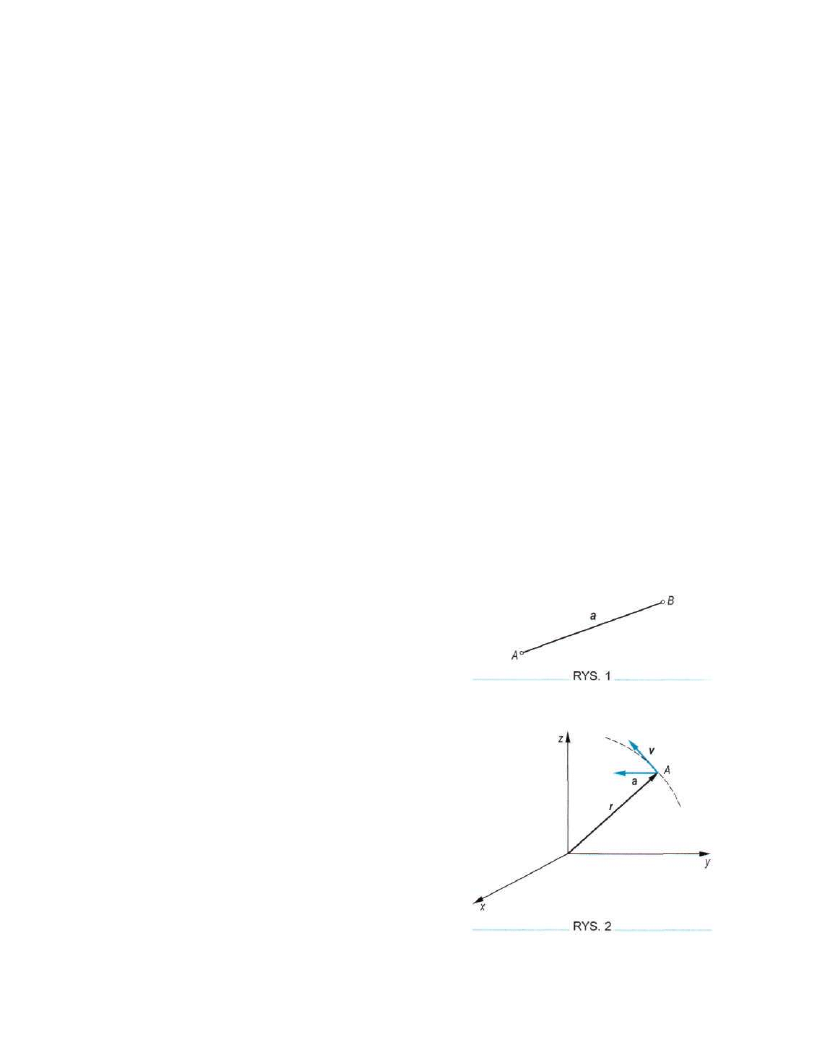
Przykładami wektora zaczepionego mogą być:

• wektor wodzący ruchu punktu, jego prędkość lub przy­

spieszenie (rys. 2)

r = r(t)
v = v(t)

a = a(t)

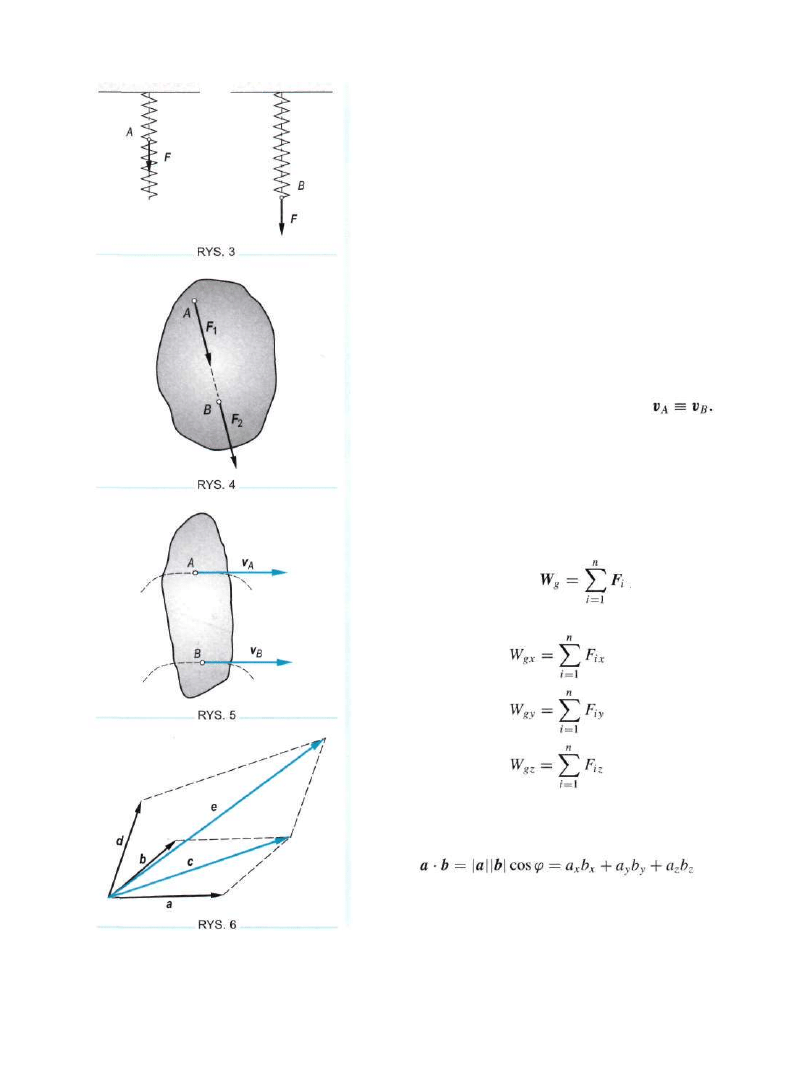
Wprowadzenie

• siła przyłożona do ciała odkształcalnego (rys. 3). Siła

przyłożona do sprężyny w punkcie A spowoduje inny

skutek (odkształcenie) niż siła zaczepiona w punkcie B.\

Wektor przesuwny lub ślizgający się. Istotnymi cechami

takiego wektora są: wartość liczbowa, zwrot i linia działania

(nieistotny jest jego punkt przyłożenia) — rys. 4

|Fi| = | F

2

|

Skutek działania na ciało idealnie sztywne siły Fi zaczepionej

w punkcie A jest taki sam, jak siły F

2

zaczepionej w punk­

cie B Fi = F

2

.

Wektor swobodny. Istotnymi cechami takiego wektora

są: wartość liczbowa, zwrot i kierunek. Przykładami takicl

wektorów mogą być: moment pary sił, prędkość i przyspie­

szenie punktów bryły w ruchu postępowym (rys. 5). Wektory

prędkości punktów A i B są nierozróżnialne

Działania na wektorach
Dodawanie wektorów.

Suma dwóch wektorów a + b jei

wektorem leżącym na przekątnej równoległoboku rozpiętego

na wektorach a i b. Dodawanie wektorów jest przemienni
a+b = b+a

oraz obowiązuje zasada superpozycji a+b+d =

= e = (a + b)+d = c + d (rys. 6). Jeżeli znamy wspoł-

rzędne n wektorów Fi(F

ix

, Fj

y

, F

iz

)

zaczepionych w tym sa

mym punkcie, to ich suma jest wektorem, któ-

rego współrzędne są równe

Iloczyn skalarny

dwóch wektorów jest skalarem (liczbi

(rys. 7) '

Iloczyn wektorowy

dwóch wektorów jest wektorei

(rys. 8) '

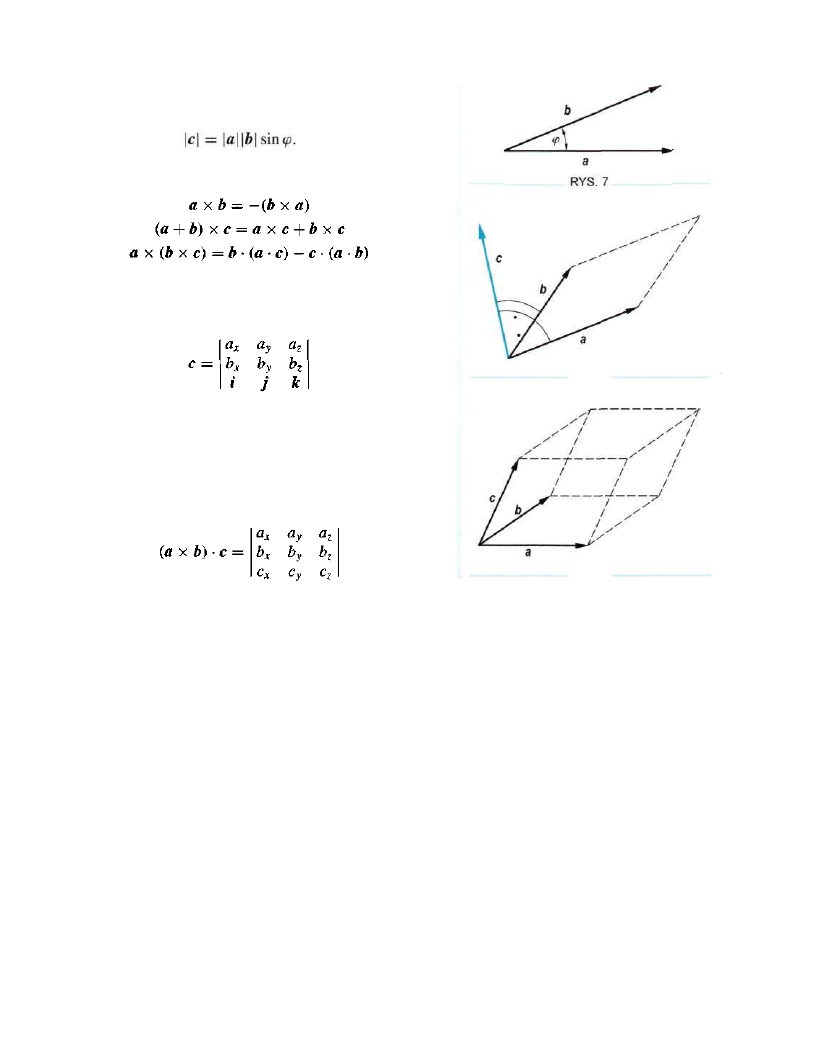
Elementy rachunku wektorowego

15

c

= a x b

Wektor c jest prostopadły do wektorów a i b, jego wartość

gdzie: i, j,k są wersorami (leżącymi odpowiednio na osiach
x, y, z).

Iloczyn mieszany

trzech wektorów (a x b) c jest liczbą. Jej

wartość jest równa objętości równoleglościanu rozpiętego na

tych wektorach (rys. 9). Jeżeli znamy współrzędne wektorów
a, b, c,

to

RYS. 8

RYS. 9

Jeżeli znamy współrzędne dwóch wektorów a(a

x

,a

y

,a

z

)

i b(b

x

,b

y

,b

z

),

to współrzędne wektora c = a x b wyliczamy

z wyznacznika

liczbowa jest równa

Układ wektorów a, b, c tworzy trójkę prawoskrętną. Za­

chodzą związki

1

Układy płaskie w przypadku

więzów idealnych

1.1

Twierdzenie o trzech siłach

Jednym z najprostszych układów płaskich jest układ trzech sił.

Przypomnijmy t w i e r d z e n i e o t r z e c h siłach: warun­

kiem koniecznym i wystarczającym na to, aby układ trzech sił

nierównoległych, leżących w jednej płaszczyźnie pozostawał

w równowadze jest, aby linie działania tych sił przecinały się

w jednym punkcie, a same siły tworzyły trójkąt zamknięty.

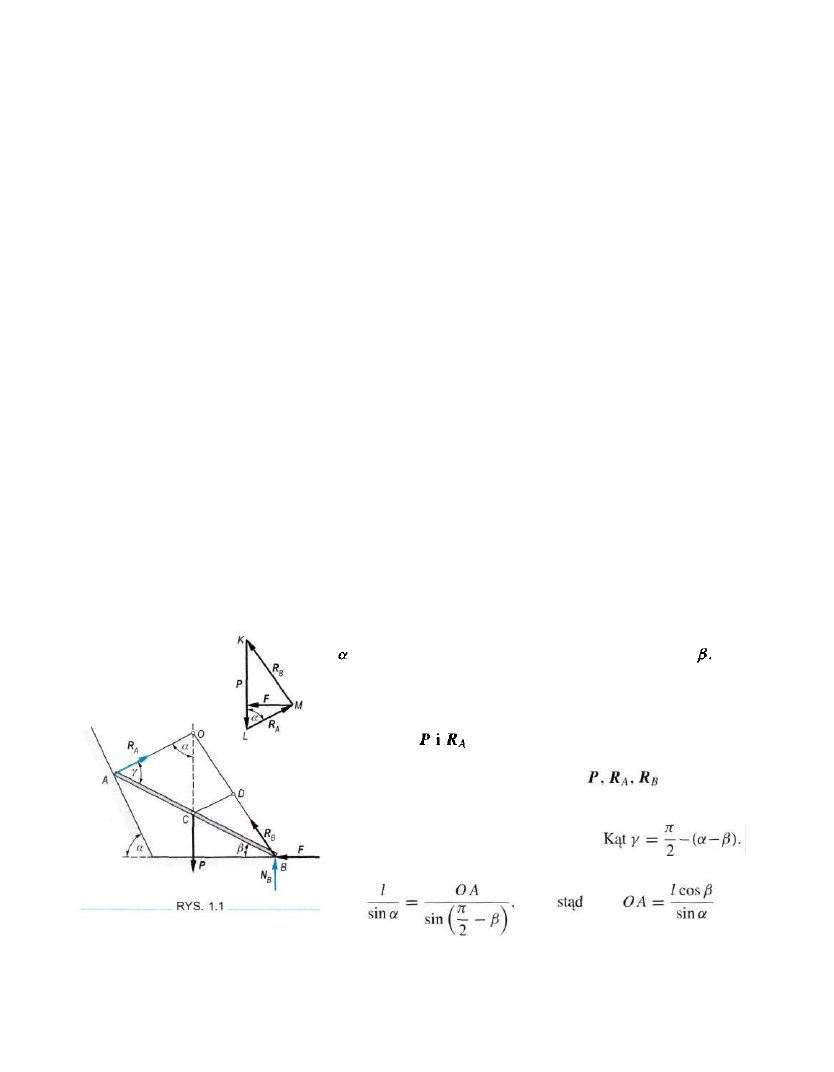
PRZYKŁAD 1.1 Wyznaczyć siłę F utrzymującą jednorodną belkę AB = 21

o ciężarze P w położeniu równowagi. Belka opiera się

o dwie gładkie płaszczyzny: poziomą i nachyloną pod kątem

ROZWIĄZANIE

Na belkę działają trzy siły [P, R

A

, R

B

]

pozostające w równo­

wadze. Siły przecinają się w punkcie O. Zatem kieru­

nek reakcji RB (która składa się z siły F i reakcji płaszczyzny

N

B

)

przechodzi przez punkt O. Siły tworzą trój­

kąt KLM. Poprowadzimy odcinek CD równoległy do odcinka

AO.

Widzimy, że trójkąty OCD i KLM są podobne. Łatwo

możemy wyznaczyć boki trójkąta O AC.

Z twierdzenia sinusów otrzymujemy

(rys. 1.1). Belka tworzy z płaszczyzną poziomą kąt

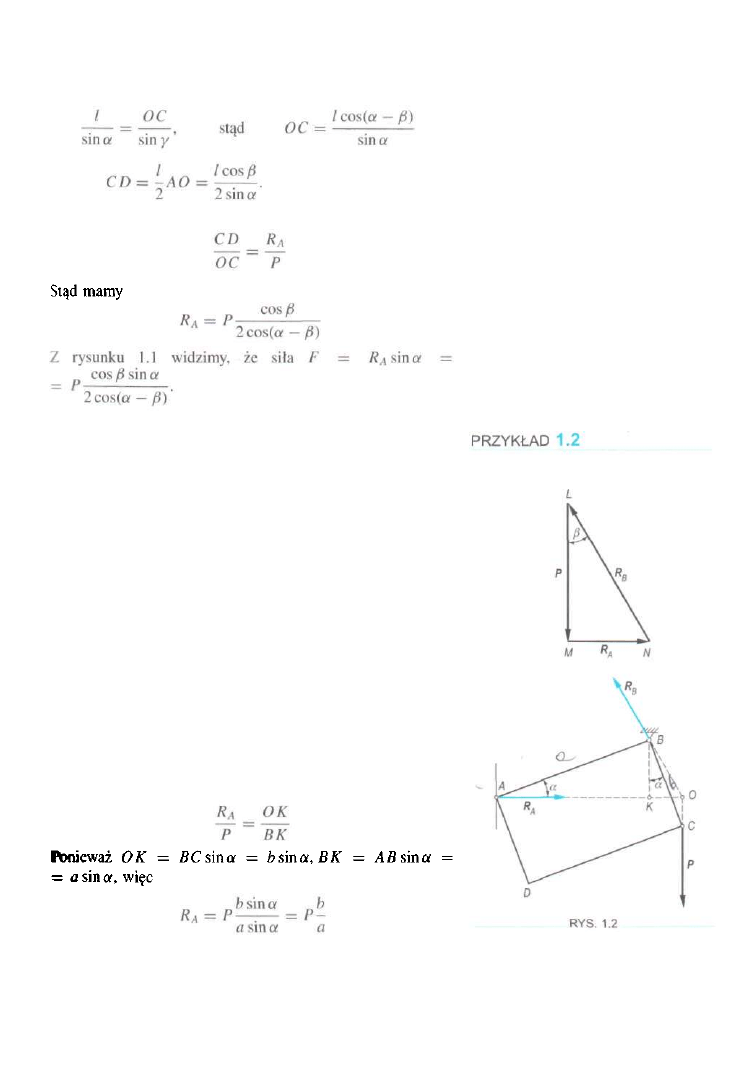
Prostokątna płytka ABCD o bokach AB = a i BC — b jest

umocowana za pomocą przegubu w punkcie B i opiera się

o gładką ścianę w punkcie A. Płytka obciążona jest w punk­

cie C siłą P (rys. 1.2). Zaniedbując ciężar płytki, wyznaczyć

reakcję ściany R

A

i przegubu R

B

.

ROZWIĄZANIE

Na podstawie warunków zadania na ciało działają trzy siły,

z których jedna jest znana. Kierunek reakcji ściany jest rów­

nież znany, jest on prostopadły do ściany. Siły P i R

A

przecinają

się w punkcie O (rys. 1.2). Na podstawie twierdzenia

o trzech siłach przez ten punkt musi przejść również linia

działania trzeciej siły RB, o której wiadomo, że jest zacze­

piona w punkcie B. Kierunek reakcji RB pokrywa się więc

z kierunkiem OB. Układ sił [R

A

, R

B

, P]

będzie w równowa­

dze, jeżeli dodatkowo siły te będą tworzyć trójkąt zamknięty.

Oznaczmy wierzchołki tego trójkąta: L, M, N. Z rysunku wi­

dzimy, że trójkąt LMN jest podobny do trójkąta BKO. Stąd

wynika, że

i podobnie

Odcinek

Z podobieństwa trójkątów OCD i KLM dostajemy

ze związków w trójkącie LMN dostajemy zaś

Jak widać wartości reakcji nie zależą od kąta a.

Jednorodny pręt AB o długości 21 i ciężarze P jest zamoc

wany za pomocą przegubu płaskiego A i utrzymywany w p

łożeniu jak na rys. 1.3 poziomą siłą S. Wyznaczyć reakc

przegubu A oraz kąt a w położeniu równowagi.

ROZWIĄZANIE

Z twierdzenia o trzech siłach wyznaczamy linię działania r

akcji R

A

.

Z trójkąta LMN obliczamy

Belka AB o długości 2/ jest obciążona w środku siłą P, dzia

łającą pod kątem fi — 45° w stosunku do poziomu. Wyzna

czyć reakcje przegubu A i podpory przesuwnej B. Ciężar belki

zaniedbać.

ROZWIĄZANIE

Wszystkie trzy siły przecinają się w punkcie O. Poprowadźr

odcinek BD równoległy do OC. Z rysunku 1.4 widzimy,

1.1. Twierdzenie o trzech siłach 19

Ponieważ

zatem

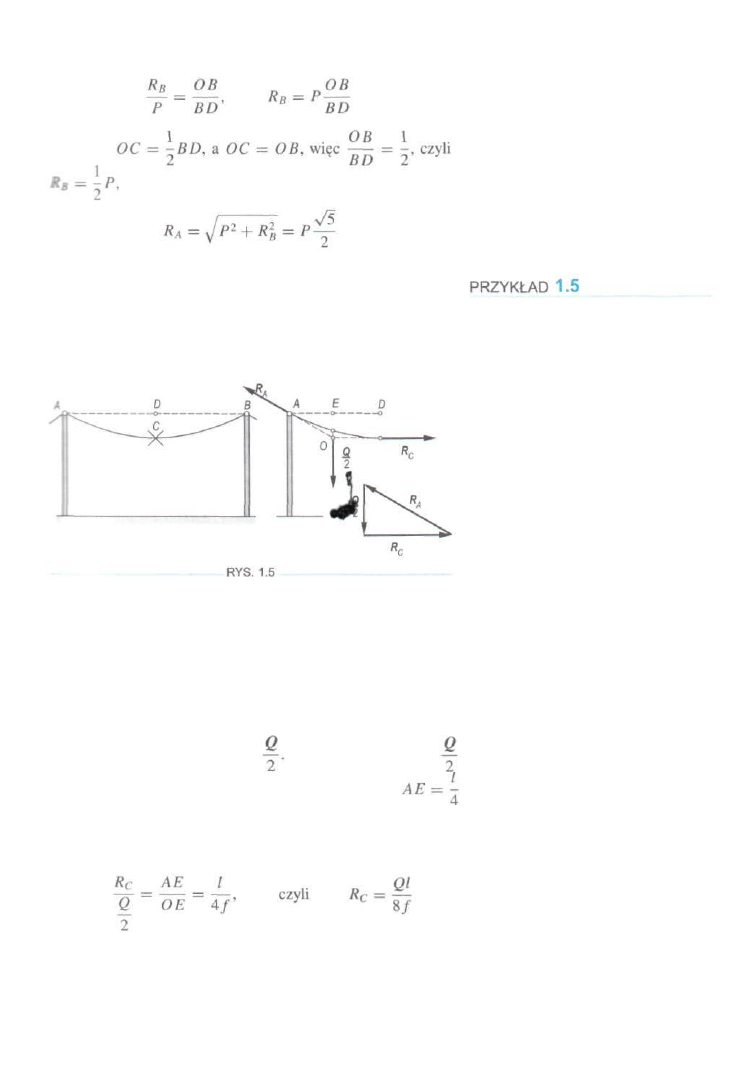
Przewód elektryczny o ciężarze Q jest umocowany na jednym

poziomie do dwóch słupów, pozostających w odległości

AB =1.

Strzałka zwisu przewodu CD — f. Wyznaczyć siłę

rozciągającą przewód w punkcie C oraz reakcje R

A

i R

B

(rys. 1.5).

ROZWIĄZANIE

Przetnijmy myślowo przewód w punkcie C i odrzućmy jego

prawą część. Oddziaływanie tej części na część lewą za­
stępujemy silą Re, której kierunek jest poziomy. Na lewą
część przewodu działa jeszcze dodatkowo silą RĄ O niezna­
nym kierunku i siła pionowa Przyjmujemy, że siła

działa wzdłuż linii odległej od punktu A o odcinek

(rys. 1.5). Linie działania wszystkich trzech sił powinny przeciąć

się w punkcie O. Zamknięty trójkąt sił jest podobny do

trójkąta AOE. Stąd możemy napisać związek

1. Układy płaskie w przypadku więzów idealnych

Jeżeli strzałka zwisu / jest bardzo mała, to siła Rc osiąga

bardzo duże wartości. Wartość reakcji

Ze względu na symetrię całego układu RA = RB

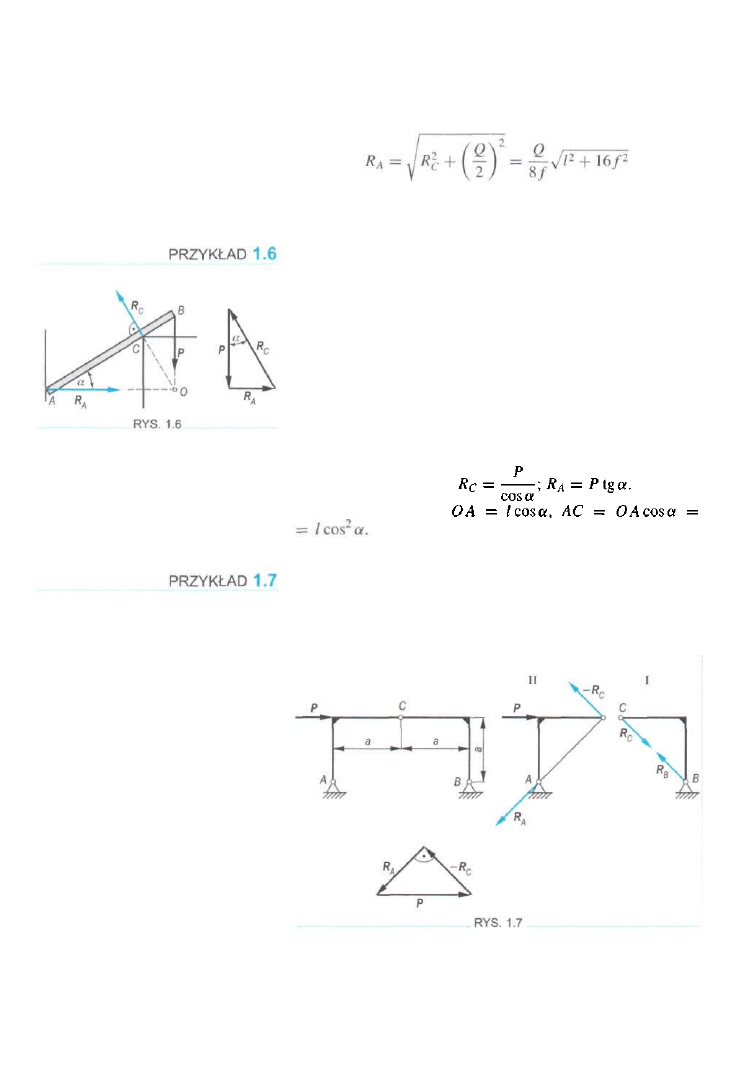
Nieważka belka AB o długości / opiera się jednym koń­

cem A o gładką pionową ścianę, drugim o występ C. Ko­

niec belki obciążono pionową siłą P. Nachylenie belki w sto­

sunku do poziomu równe jest a. Wyznaczyć długość odcinka
AC

oraz wartości reakcji RA i Rc w położeniu równowagi

(rys. 1.6).

ROZWIĄZANIE

Kierunki reakcji RA i Rc w tym przypadku są znane. Przy

zadanym kącie a odległość AC musi być więc tak dobrana,

aby linie działania wszystkich sił przecięły się w punkcie O.
Z trójkąta sił dostajemy

Z rysunku mamy

Wyznaczyć reakcje przegubów A i B ramy, pokazanej na

rys. 1.7, obciążonej poziomą siłą P. Ciężar ramy zaniedbu­

jemy. Rama składa się z dwóch symetrycznych części złączo­

nych płaskim przegubem C.

ROZWIĄZANIE

W zadaniu tym mamy wyznaczyć cztery niewiadome: war­

tości reakcji przegubów A i B oraz ich kierunki. Zadanie

to różni się w sposób zasadniczy od dotychczas rozwiązy­

wanych, gdyż mamy do czynienia już nie z jednym ciałem

sztywnym, lecz z układem dwóch ciał połączonych w tym

przypadku płaskim przegubem C. W tego rodzaju zagadnie­

niach należy układ rozbić na dwa układy proste. Weźmy pod

uwagę układ I. Jest on w równowadze i działają na niego

dwie siły: jedna przyłożona w punkcie B i druga w punk­

cie C. Dwie siły są w równowadze wtedy i tylko wtedy, gdy

tworzą dwójkę zerową. Zatem R

B

i Rc muszą działać wzdłuż

prostej, wyznaczonej przez punkty B i C. Układ I oddziałuje

na układ II siłą — Rc. Przechodząc do układu II, możemy

już wyznaczyć kierunek reakcji RA i z trójkąta sił obliczyć

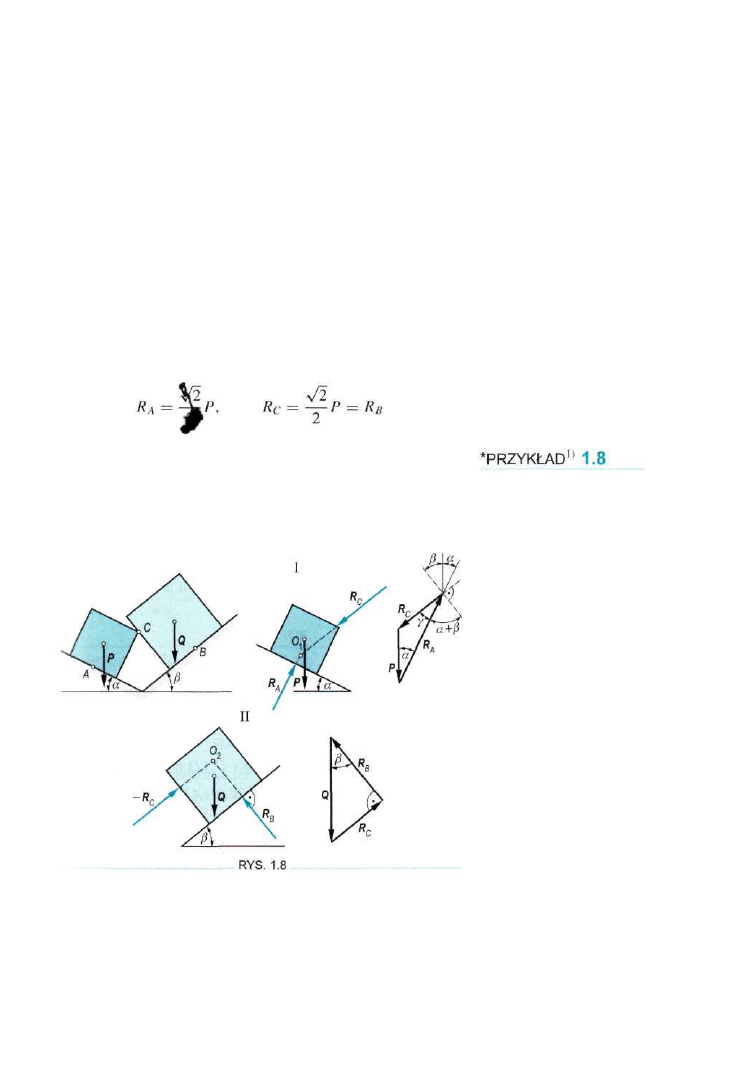
Dwa sześciany o ciężarach P i Q spoczywają na gładkich

równiach nachylonych w stosunku do poziomu pod kątami

a i /3 (rys. 1.8). Znaleźć zależność między siłami P i Q

w położeniu równowagi, naciski sześcianów na równie oraz

siłę oddziaływania jednego sześcianu na drugi.

'Przykłady oznaczone gwiazdką studenci studiów zawodowych

mogą pominąć.

1. Układy płaskie w przypadku więzów idealnych

ROZWIĄZANIE

W tym przypadku mamy również do czynienia z układem

złożonym. Na układ I działają trzy siły i jego równowaga bę­

dzie możliwa, jeżeli ich linie działania przetną się w punkcie

0\.

Podobnie dla układu II linie działania R

B

, Q, Rc

muszą

się przeciąć w punkcie O

2

.

Zbudujemy dwa zamknięte trój­

kąty sił. Po zastosowaniu twierdzenia sinusów z pierwszego

trójkąta dostaniemy

Z drugiego trójkąta otrzymujemy R

c

= Q

sin . Jeżeli

porównamy stronami otrzymane związki, otrzymamy zależ-

ność między siłami P i Q

Podobnie możemy obliczyć

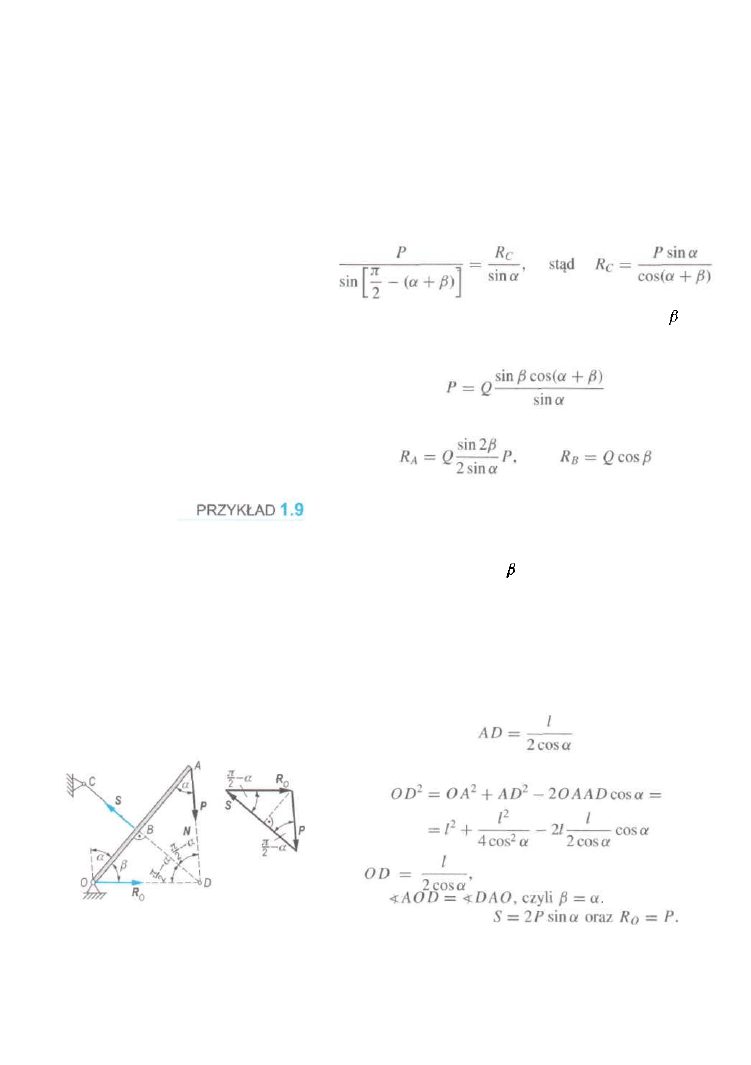
Belka O A jest umocowana przegubem O i przywiązana za

pomocą linki BC do ściany. Belkę obciążono w punkcie A

ciężarem P. Zaniedbując ciężar belki, wyznaczyć wartość re­

akcji przegubu O oraz kąt , który tworzy ona z osią belki.

Wyznaczyć również silę w lince BC, jeżeli jest ona prostopa­

dła do osi belki; przyjąć OB = AB.

ROZWIĄZANIE

Kierunek reakcji Ro powinien przechodzić przez punkt D

(rys. 1.9). Oznaczając długość belki przez / możemy napisać

związek

Ze wzoru Carnota dla trójkąta O AD mamy

czyli

a zatem trójkąt ODA jest równora­

mienny i

Z trójkąta sił mamy:

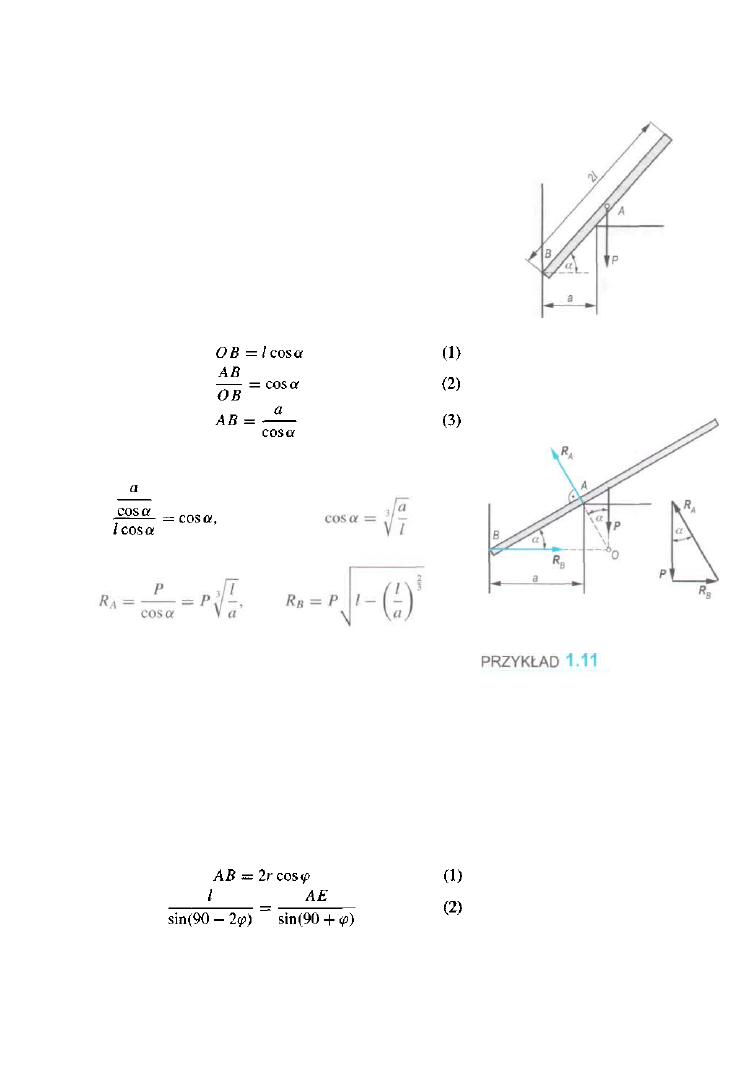
Jednorodny pręt o długości 2/ i ciężarze P opiera się końcen

B

o gładką pionową ścianę. W punkcie A opiera się o występ

znajdujący się w odległości a od ściany. Wyznaczyć reakcj(

w punktach A i B oraz wartość kąta a w położeniu równowag

irys. 1.10).

ROZWIĄZANIE

PRZYKŁAD 1.10

RYS. 1.10

RYS. 1.11

W tym przypadku znamy kierunki działania wszystkich trzech

sił RA, RB, P. Kierunki działania tych sił powinny przecinać

się w jednym punkcie, zatem położenie pręta jak na rys. 1.10

nie może być położeniem równowagi. Narysujmy pręt w po­

łożeniu równowagi (rys. 1.11). Na podstawie tego rysunku

możemy napisać trzy związki

Po podstawieniu zależności (1) i (3) do związku (2) otrzy­

mamy

Z trójkąta sił dostajemy

Jednorodny gładki pręt AD o długości 2/ i ciężarze P znaj­

duje się w półsferycznej czaszy o promieniu r. Wyznaczyć

kąt ę oraz znaleźć reakcje R

A

i R

B

w położeniu równowagi

irys. 1.12).

ROZWIĄZANIE

W zadaniu tym, podobnie jak w poprzednim, znamy kierunki

działania sił R

A

, R

B

, P.

Kierunki te powinny przeciąć się

w jednym punkcie. Na rysunku 1.12 oznaczono ten punkt

przez E. Na podstawie rysunku możemy napisać następujące

zależności geometryczne

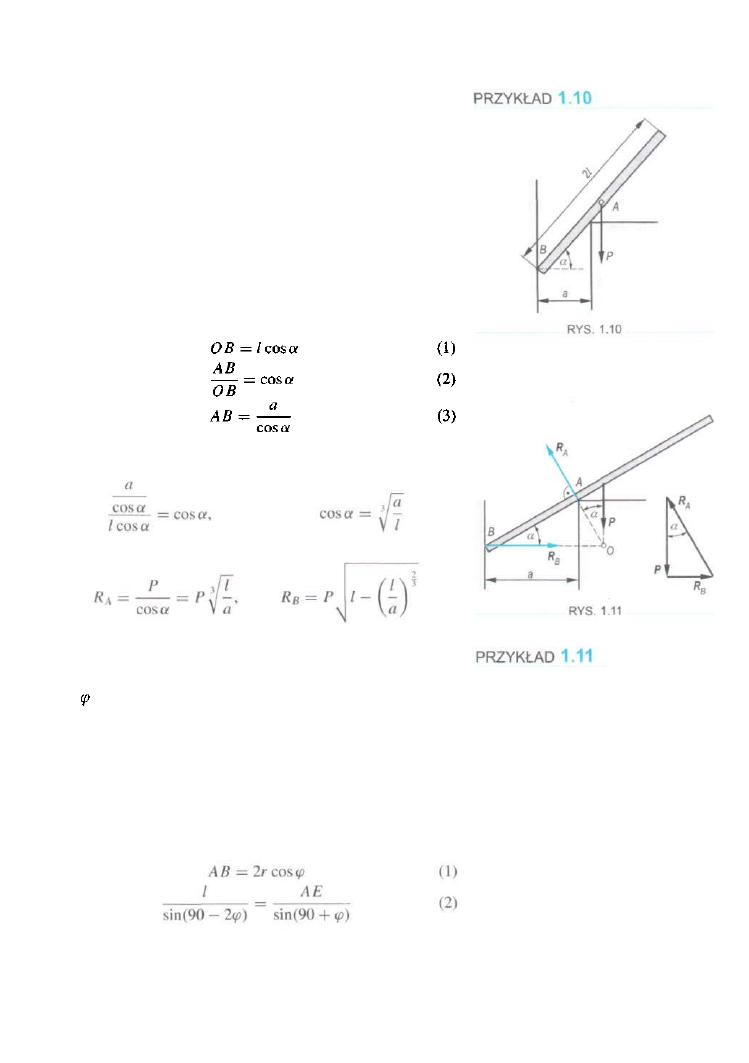
Jednorodny pręt o długości 2/ i ciężarze P opiera się końcem

B

o gładką pionową ścianę. W punkcie A opiera się o występ,

znajdujący się w odległości a od ściany. Wyznaczyć reakcje

w punktach A i B oraz wartość kąta a w położeniu równowagi

irys. 1.10).

ROZWIĄZANIE

W tym przypadku znamy kierunki działania wszystkich trzech

sił RĄ, R

B

, P.

Kierunki działania tych sił powinny przecinać

się w jednym punkcie, zatem położenie pręta jak na rys. 1.10

nie może być położeniem równowagi. Narysujmy pręt w po­

łożeniu równowagi (rys. 1.11). Na podstawie tego rysunku

możemy napisać trzy związki

Po podstawieniu zależności (1) i (3) do związku (2) otrzy­

mamy

stąd

Z trójkąta sił dostajemy

Jednorodny gładki pręt AD o długości 2/ i ciężarze P znaj­

duje się w półsferycznej czaszy o promieniu r. Wyznaczyć

kąt oraz znaleźć reakcje RA i RB w położeniu równowagi

( rys. 1.12).

ROZWIĄZANIE

W zadaniu tym, podobnie jak w poprzednim, znamy kierunki

działania sił R

A

, R

B

, P.

Kierunki te powinny przeciąć się

w jednym punkcie. Na rysunku 1.12 oznaczono ten punkt

przez E. Na podstawie rysunku możemy napisać następujące

zależności geometryczne

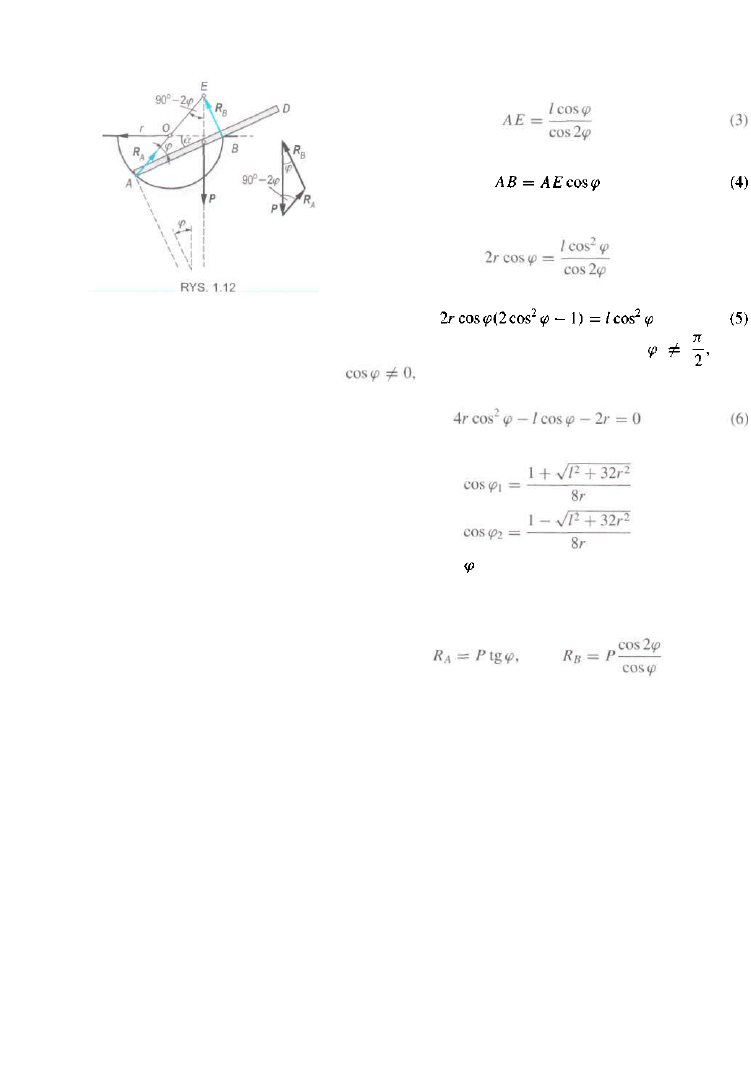
równość (2) wynika z twierdzenia sinusów, stąd mamy

Z rysunku widać, że

Po podstawieniu wzorów (3) i (1) do równania (4) otrzy­

mamy

a po przekształceniu

Ponieważ ze względów fizycznych kąt

więc

a zatem możemy na podstawie zależności (5) na­

pisać równanie

stąd

Ponieważ kąt jest kątem ostrym, drugi pierwiastek rów­

nania (6) nie może być brany pod uwagę.

Korzystając z twierdzenia sinusów, z trójkąta sił wyzna­

czamy poszukiwane reakcje

Na zakończenie podamy kilka uwag m e t o d y c z n y c h :

1. Jeżeli mamy do czynienia z układami prostymi, to

podanymi metodami możemy rozwiązywać zadania, w któ­

rych znamy kierunki działania dwóch sił oraz wartość

jednej z nich. Na podstawie twierdzenia o trzech si­

łach wyznaczamy kierunek działania trzeciej siły (rysu­

nek zasadniczy). Wykreślamy na boku zamknięty trójkąt

sił, w którym znamy tylko jeden bok. Na rysunku zasad­

niczym wyszukujemy trójkąt podobny, którego boki (lub

wzajemne stosunki boków) dadzą się wyznaczyć. Korzy­

stając z podobieństwa tych dwóch trójkątów, wyznaczamy

1.2. Płaski układ sił zbieżnych

25

poszukiwane wartości sił. Tak postępowano w

przykładach 1.1 -- 1.5. Czasami wyszukanie na rysunku

zasadniczym trójkąta podobnego jest kłopotliwe (lub

trudno wyznaczyć wzajemne stosunki jego boków),

wtedy możemy wyznaczyć kąty między poszczególnymi siłami,

a następnie stosując twierdzenie sinusów, obliczyć wartości sił

(przykład 1.9).

2. Jeżeli mamy do czynienia z układem złożonym, należy

go rozbić na układy proste (w miejscu, gdzie ciała sztywne

łączone za pomocą więzów), a następnie rozrysować te

układy i z każdym z nich postąpić tak, jak to podano w p. 1.

Wygodniej jest zacząć od układu łatwiejszego (porównaj przykład

1.7 i 1.8).

3. Jeżeli mamy do czynienia z określeniem położenia równowagi

to wówczas kierunki działania wszystkich trzech sił

a znane. Należy więc w pierwszej kolejności ustawić ciało,

którego równowagę rozpatrujemy, w takim położeniu, by

równowaga mogła zachodzić, tzn. kierunki działania sił przecięły

jednym punkcie (wykonać rysunek zasadniczy), a następnie

postępować tak, jak to podano w p. 1. Ten sposób

zilustrowano w przykładach 1.6, 1.10 i 1.11.

Dla

1.2

Płaski układ sił zbieżnych

dowolnej liczby sił zbieżnych na płaszczyźnie mamy dwa

niezalezne równania równowagi

Lub

Punkty A i B są wybrane dowolnie, lecz nie mogą leżeć

na jednej prostej z punktem 0, w którym przecinają się linie

działania wszystkich sił. Do równań tych wchodzą znane siły

czynne oraz nieznane reakcje. Aby zadanie mogło być statycz-

nie wyznaczalne, liczba niewiadomych nie może przekraczać

dwóch.

Gdy siła P i punkt A leżą na płaszczyźnie, wówczas mo­

tt charakteryzujemy wielkością liczbową M

A

(P)

= ±Ph,

gdzie h jest ramieniem siły (odległością punktu A od linii

działania siły P). Znak „+" przyjmujemy, gdy siła wywo­

łuje obrót w kierunku przeciwnym do ruchu wskazówek ze­
gara.

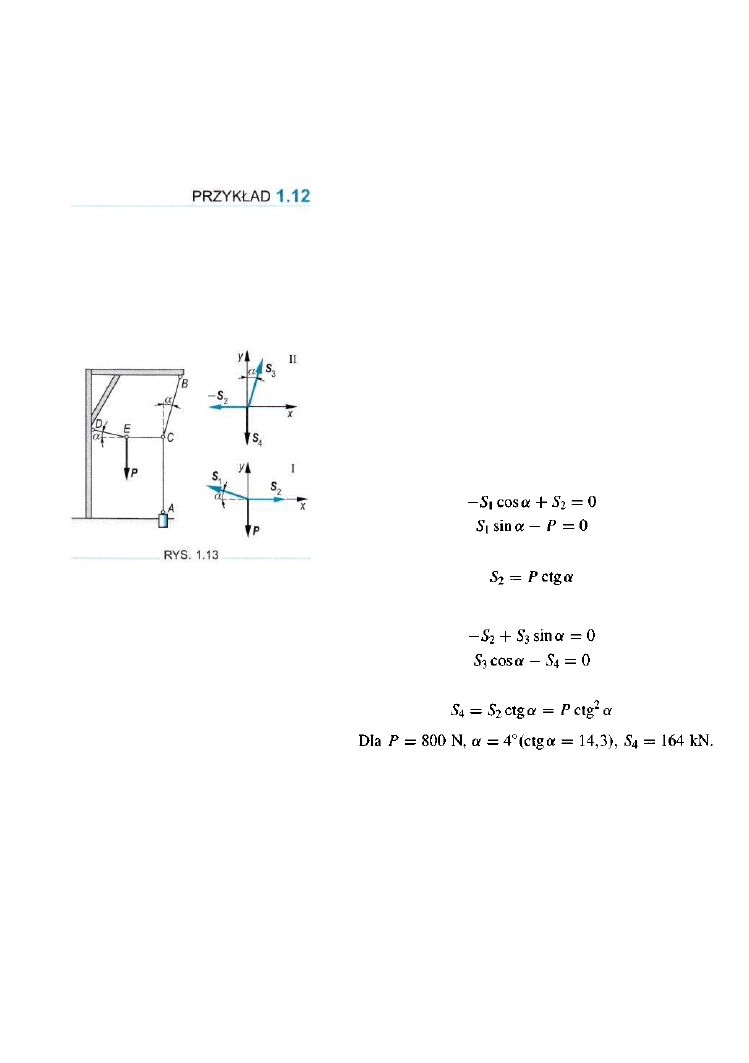
Aby wyciągnąć z ziemi pal, robotnik przywiązał do niego linę

w punkcie A. Po zamocowaniu drugiego końca liny B przy­

wiązał do niej drugą linę w punkcie C, zaczepioną w punkcie

D,

po czym uchwycił rękami linę CD w punkcie E i zawisł

w powietrzu; część AC liny zajęła wtedy położenie pionowe,

a część CE — poziome.

Części CB i DE utworzyły jednakowe kąty a, jedna

z pionem, druga z poziomem (rys. 1.13). Wyznaczyć siłę w li­

nie AC, jeżeli ciężar robotnika jest równy P.

ROZWIĄZANIE

Przecinając linki dostaniemy jeden układ sił zbieżnych

w punkcie E, drugi w punkcie C. Korzystając z warunków

równowagi (1.1), dostaniemy dla układu I następujące równa­
nia

stąd

Podobnie dla układu II otrzymamy

stąd

Na pionowej półkuli jest umieszczona kulka A, która może się

poruszać tylko po okręgu. Kulka jest utrzymywana w równo­

wadze za pomocą nici ABC. Na końcu nici uwieszono ciężar

P.

Ciężar kulki równy jest Q. Znaleźć kąt a, jaki tworzy

odcinek O A z odcinkiem OB w położeniu równowagi, oraz

nacisk kulki na powierzchnię półkuli. Średnicę bloku B za­

niedbać.

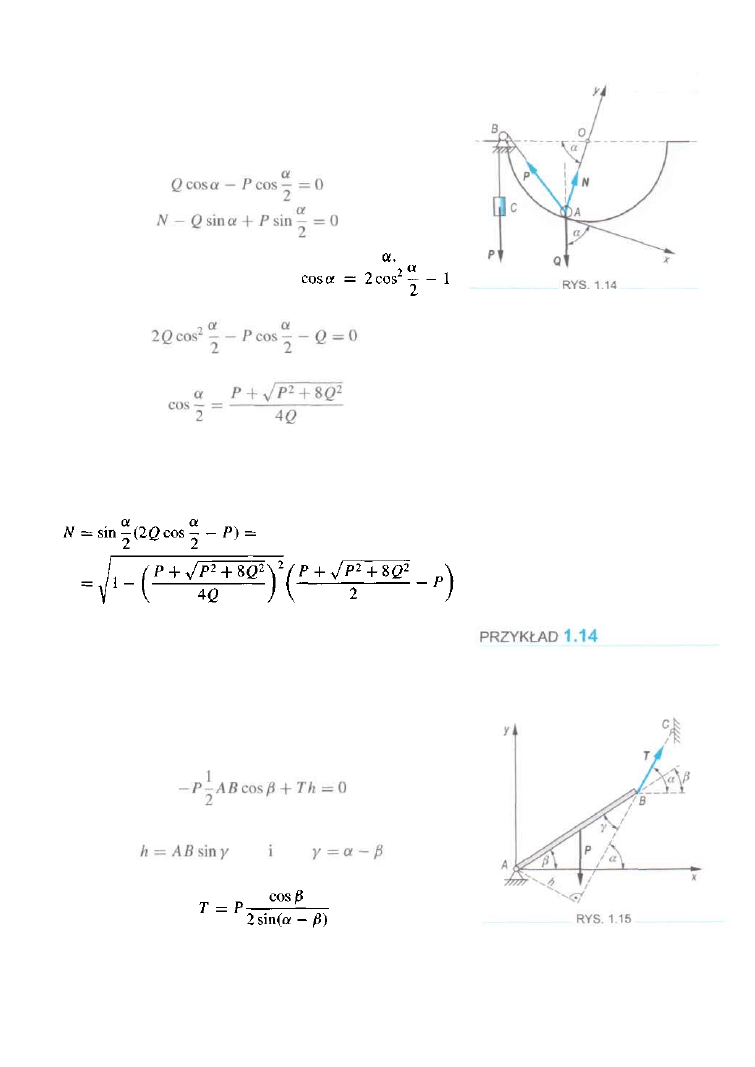
więc

Z rysunku mamy

Jednorodny pręt AB o ciężarze P końcem A jest zamocowany

na przegubie płaskim, koniec B zaś jest zawieszony na lince

BC

(rys. 1.15). Znając kąty a i 8 znaleźć siłę T w lince BC.

ROZWIĄZANIE

Warunek równowagi pręta w postaci (1.2) względem punktu

.4 ma postać

Ponieważ kąt a jest kątem mniejszym niż n, przyjęliśmy

tylko dodatni pierwiastek równania kwadratowego.

Z drugiego równania równowagi można wyznaczyć na­

cisk na półkulę

stąd

Z pierwszego równania można obliczyć kąt Po za­

ROZWIĄZANIE

Przyjmujemy osi układu: x — styczna do półokręgu w punk­

cie A,y — normalna (rys. 1.14). Warunki równowagi kulki

A przyjmą postać

mienieniu cos a zgodnie ze wzorem

dostaiemy równanie

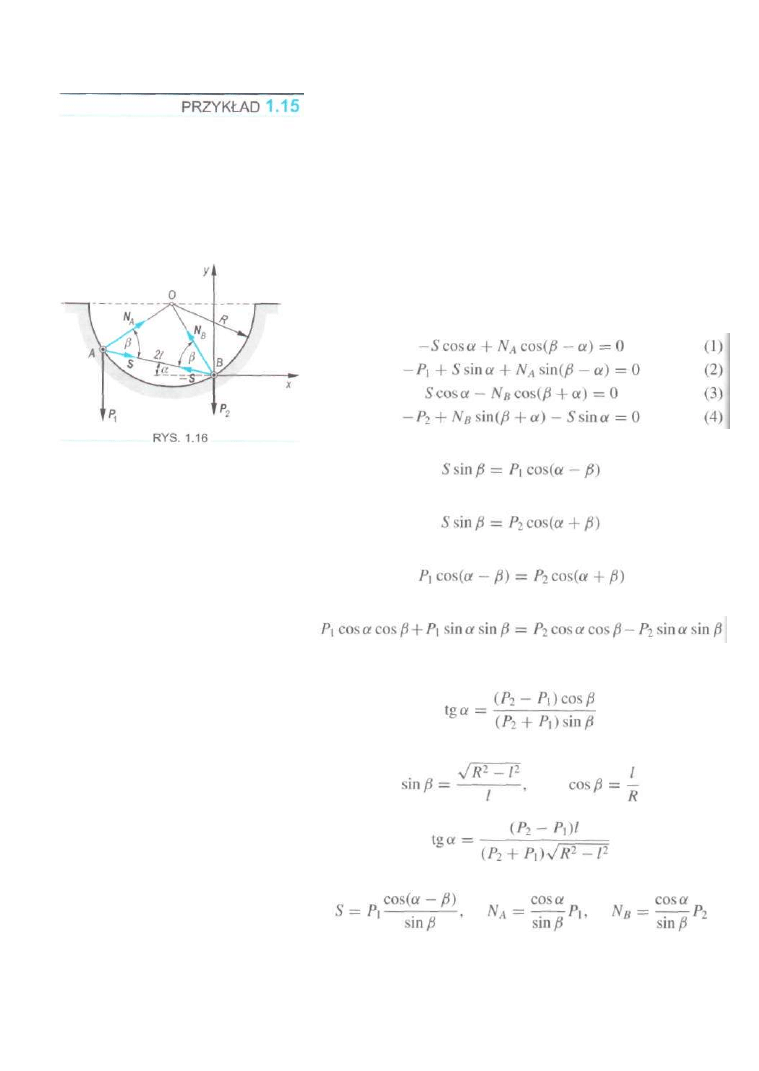
Dwie kulki Ai B o ciężarach P\ i P

2

znajdują się w położeniu

równowagi wewnątrz gładkiej, sferycznej czaszy o promieniu

R.

Kulki są połączone nieważkim prętem o długości AB = 21.

Znaleźć naciski NA i NB kulek na czaszę, siłę S w pręcie

AB

oraz kąt a, jaki tworzy pręt AB z poziomem w położeniu

równowagi (rys. 1.16).

ROZWIĄZANIE

Przecinając myślowo pręt AB, rozdzielamy układ na dwa

układy proste. Siły działające na punkty A i B zaznaczono na

rys. 1.16. Korzystając z warunków równowagi dla punktów A

i fi w postaci (1.1), dostajemy następujące cztery równania

Z równań (1) i (2) otrzymamy

a z równań (3) i (4)

Stad mamy związek

Po rozpisaniu otrzymamy

Po podzieleniu ostatniej równości przez cos a cos /3 i zgrupo­

waniu odpowiednich wyrażeń dostajemy

Na podstawie rys. 1.16 możemy napisać

zatem

Z równań

(1)--(4)

mamy

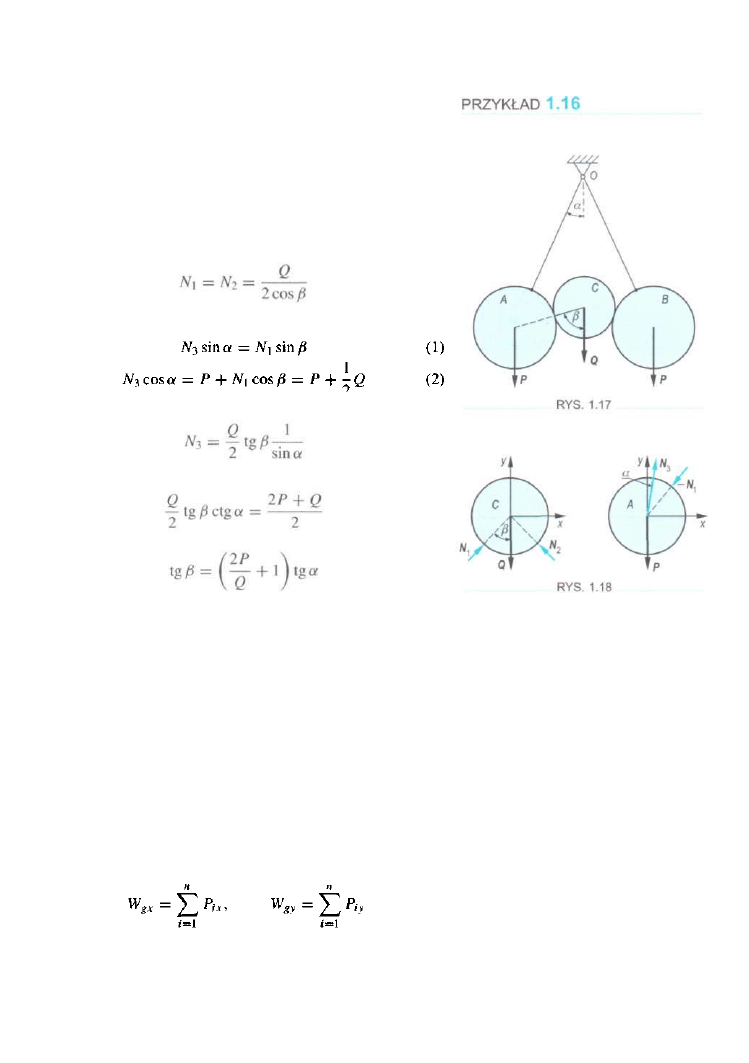
Dwa jednorodne walce A i B, każdy o ciężarze P zawieszono

w punkcie O na nieważkich niciach. Między walcami A i B

położono walec C o ciężarze Q. Znaleźć zależność między

kątami a i 6 w położeniu równowagi (rys. 1.17).

ROZWIĄZANIE

Na walce A i C działają siły przedstawione na rys. 1.18.

Z warunków równowagi walca C mamy

a z warunków równowagi walca A otrzymujemy dwa równania

Wyliczamy

Z drugiego równania dostajemy więc

Zatem

1.3

Redukcja dowolnego płaskiego układu sił

Zredukować dany układ n sił działających na dane ciało

sztywne do wybranego bieguna O oznacza zastąpić układ n

sił układem możliwie najprostszym, przyłożonym w punkcie

O,

równoważnym danemu układowi n sił. Układ równoważny

rozumiemy jako układ wywołujący ten sam skutek.

Z mechaniki wiadomo, że dowolny płaski układ sił re­

dukuje się do wektora głównego W

g

oraz momentu głów­

nego M

g

.

Współrzędne wektora głównego obliczamy ze wzorów

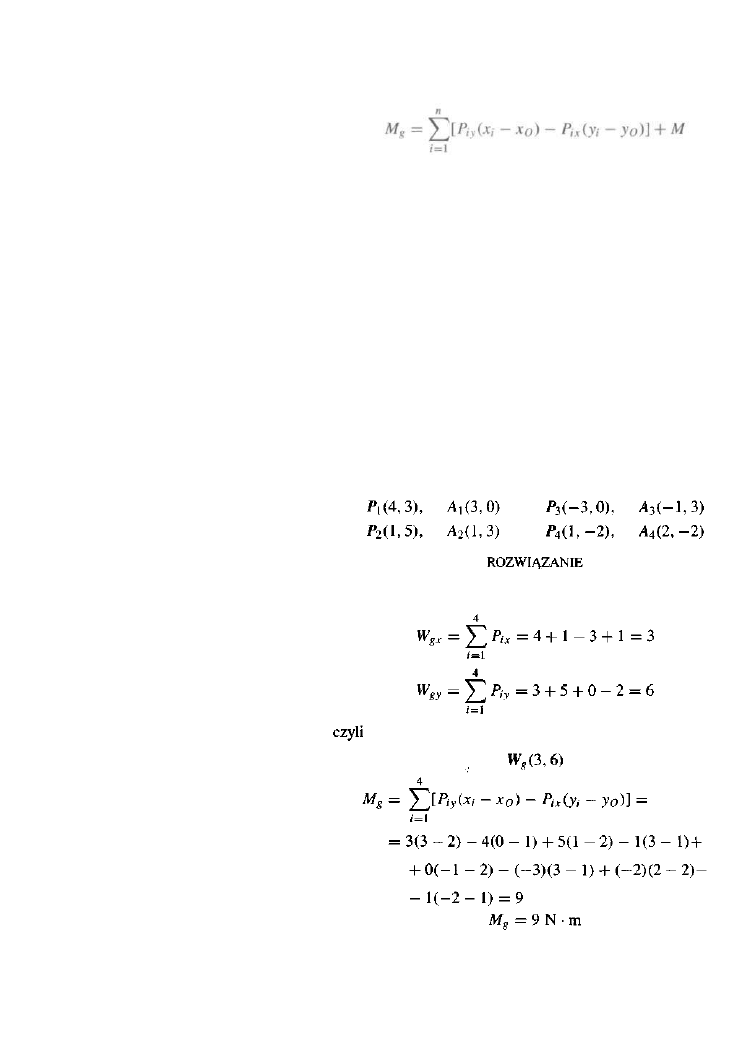
Na podstawie podanych wzorów mamy

PRZYKŁAD 1.17 Zadany układ czterech sił P, zaczepionych w punktach A,

zredukować do bieguna 0(2, 1). Współrzędne sił podano w N,

a współrzędne punktów przyłożenia w m

a moment główny z zależności

gdzie: Pj

x

, Pi

y

— współrzędne i-tej siły układu redukowa­

nego, Xi, yi — współrzędne przyłożenia tej siły, xo,yo —

współrzędne wybranego bieguna redukcji O, M — moment

skupiony działający na dane ciało.

Jak widzimy z tych wzorów, wektor główny nie zależy

od wyboru bieguna redukcji O, będziemy go nazywać nie­

zmiennikiem redukcji.

Moment główny jest funkcją (liniową)

xo, yo,

czyli ze zmianą bieguna jego wartość się zmienia.

Punkt zaczepienia momentu skupionego M jest nieistotny, bo

moment jako wynik działania pary sił jest wektorem swobod­

nym; parę sił możemy dowolnie przemieszczać po płaszczyź­

nie.

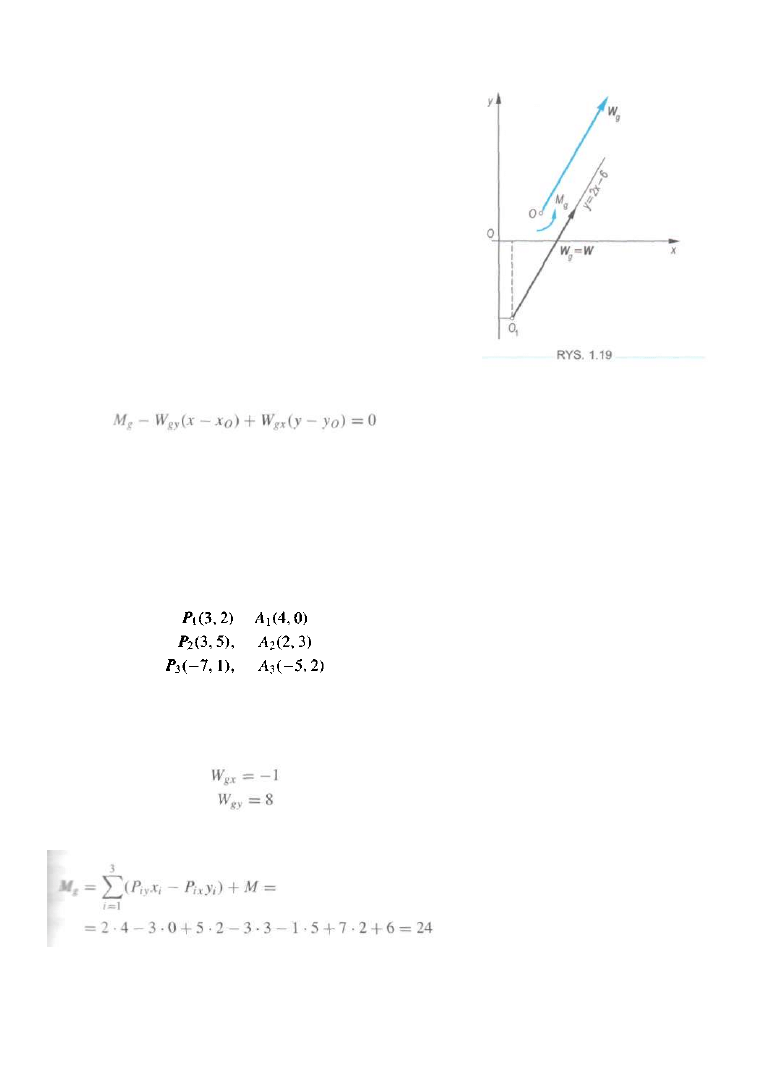
W celu lepszego zrozumienia rozwiązania przedstawiono

je na rys. 1.19. Układ czterech sił został tu zastąpiony wekto-

rem głównym o współrzędnych 3 i 6 oraz momentem głów-

nym o wartości 9. Okazuje się, że gdy wektor główny i mo-

ment główny są różne od zera, wówczas można układ zreduko-

wać do wypadkowej. Wiadomo, że wypadkowa jest to jedna

siła równoważna danemu układowi sił. Wypadkowa W bę-

dzie równa wektorowi głównemu, lecz jej punkt zaczepienia

musi leżeć na odpowiedniej prostej. Wyznaczymy równanie

tej prostej. Zredukujemy jeszcze raz cały układ sił do bie-

guna O

1

o współrzędnych (x, y). Oczywiście możemy do tego

bieguna zredukować równoważny układ W

g

, M

g

.

Otrzymamy

W

g1

= W

g

oraz M

g1

= M

g

- W

gy

{x - x

0

) + W

gx

(y - y

0

).

Jeżeli współrzędne (x, y) dobierzemy tak, że M

g1

=

0, to

wektor główny będzie wypadkową. Stąd otrzymamy równanie

prostej, wzdłuż której działa wypadkowa

Dla naszego przykładu mamy 9 — 6(x - 2) + 3(y - 1) = 0 .

Wypadkowa układu sił leży na prostej y = 2x — 6.

Zredukować dany układ do początku układu współrzędnych,

a nastepnie do wypadkowej; moment M — 6 jest przyłożony

w punkcie A

4

(2.2).

PRZYKŁAD 1.18

ROZWIĄZANIE

współrzędne wektora głównego wynoszą

a moment główny jest równy

Równanie linii działania wypadkowej wyznaczamy na

podstawie równania

lub w postaci kierunkowej y = -8x + 24.

Na podstawie wykonanej redukcji możemy wyznaczyć

warunki równowagi dowolnego płaskiego układu sił. Układ

taki pozostanie w równowadze, jeżeli zarówno wektor główny,

jak i moment główny będą równe zeru. Stąd dostajemy trzy

niezależne warunki równowagi

Podane równania równowagi możemy zapisać w innej równo­

ważnej postaci

z zastrzeżeniem, że punkty A, B, C nie leżą na jednej prostej,

lub w postaci

gdzie ostatni warunek oznacza sumę rzutów sił na dowolną

prostą /, która nie jest prostopadła do prostej wyznaczonej

przez punkty A i B.

Dla układu sił równoległych jako przypadku szczegól­

nego możemy obrać układ współrzędnych tak, aby siły były

równoległe do osi y. Wówczas otrzymamy dwa niezależne

warunki równowagi w postaci

PRZYKŁAD 1.20

RYS. 1.21

i na podstawie

kąta wewnętrznego trójkąta mam;
poprzedniego związku

Blok A jest w równowadze pod działaniem reakcji R

A

oraz sił w lince działających wzdłuż AC i AB. Ponieważ sił)

w

lince są te same, więc prosta AK (linia działania R

A

)

jest

dwusieczną kąta CAB. Na podstawie własności dwusiecznj

Ponieważ

Na układ działają trzy siły P, Q oraz reakcja R

A

.

Zatem

reakcja R

A

jest pionowa i równa P+Q. Z warunku momentów

względem A dostajemy

Dwie kulki o ciężarach P i Q złączono nieważkim prętem

3C.

W punktach B i C przymocowano sznur BAC o długości

równej /, który przerzucono przez blok A. Znaleźć AB i AC

w

położeniu równowagi (rys. 1.21).

Po podzieleniu stronami przez 2y cos a otrzymamy

gdzie h — a

cos a — 2b sin a.

to wstawieniu do równania dostajemy

Na pręt działają siły P1, P2 i napięcie nici S, przy czym Pi =

= y2b, P

2

— y2a,

gdzie y — ciężar przypadający na jed­

nostkę długości pręta.

Z warunku równowagi momentów względem punktu B

d

ostajemy

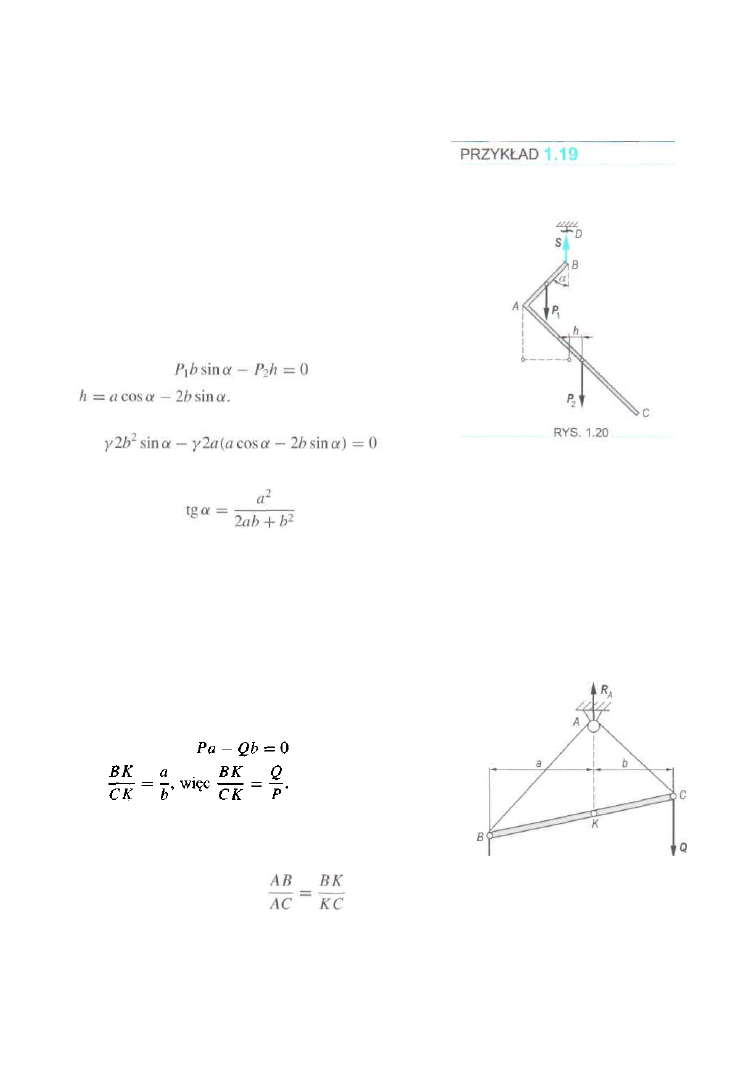
Jednorodny pręt zgięty w punkcie A pod kątem prostym jest

zawieszony na nici BD. Dane: AB — 2b, AC = 2a, a > b

rys. 1.20).

Znaleźć kąt a w położeniu równowagi.

1.4

Równowaga układu sił równoległych

ROZWIĄZANIE

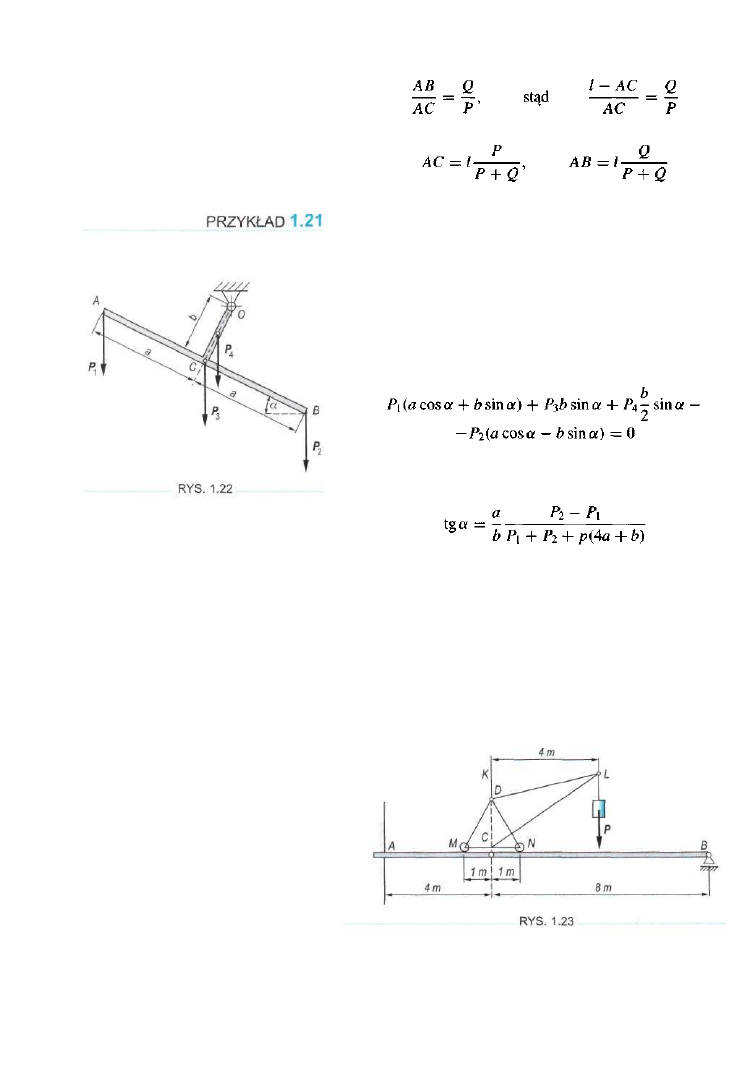
Pozioma belka przegubowa ACB ma koniec A zamocowań;

w ścianie, a koniec B oparty na przesuwnej podporze; w punk-

cie C znajduje się przegub. Belka jest obciążona dźwigiem

podnoszącym ciężar P = 1 kN. Przy wysunięciu ramienia

dźwigu na odległość KL = 4 m, środek ciężkości dźwigi

leży na pionowej CD. Ciężar dźwigu wynosi Q = 5 kN

Pomijając ciężar belki, wyznaczyć reakcje jej podpór. Rami

dźwigu leży w jednej płaszczyźnie z belką (rys. 1.23).

Po podstawieniu P3, = 4pa, PĄ = 2pb i podzieleniu stronami

przez cos a wyznaczamy

Dwa pręty AB i OC, których ciężar jednostki długości wynosi

2p są połączone prostopadle w punkcie C. W punktach A

i B zawieszono ciężarki P1 i P2 (P2 > P1). Wyznaczyć kąt

a

w położeniu równowagi (rys. 1.22).

ROZWIĄZANIE

Z warunku momentów względem punktu O otrzymamy rówj

nanie

zatem

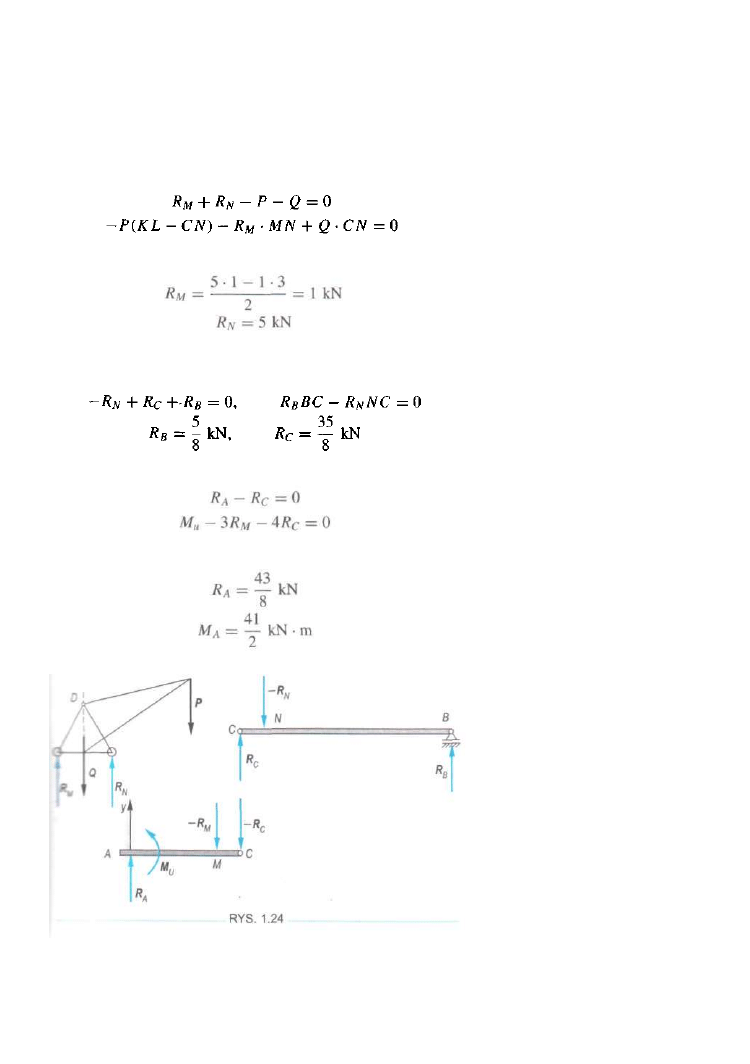
ROZWIĄZANIE

W tym przypadku rozbijamy układ złożony na trzy układy

proste (rys. 1.24). W pierwszej kolejności rozpatrzymy rów­

nowagę dźwigu. Dostajemy dwa równania równowagi w po­

staci

Stąd mamy

Belka BC będzie w równowadze, jeżeli reakcja Rc bę­

dzie pionowa. Stąd dostajemy

Warunki równowagi belki AC mają postać

Siad

stąd

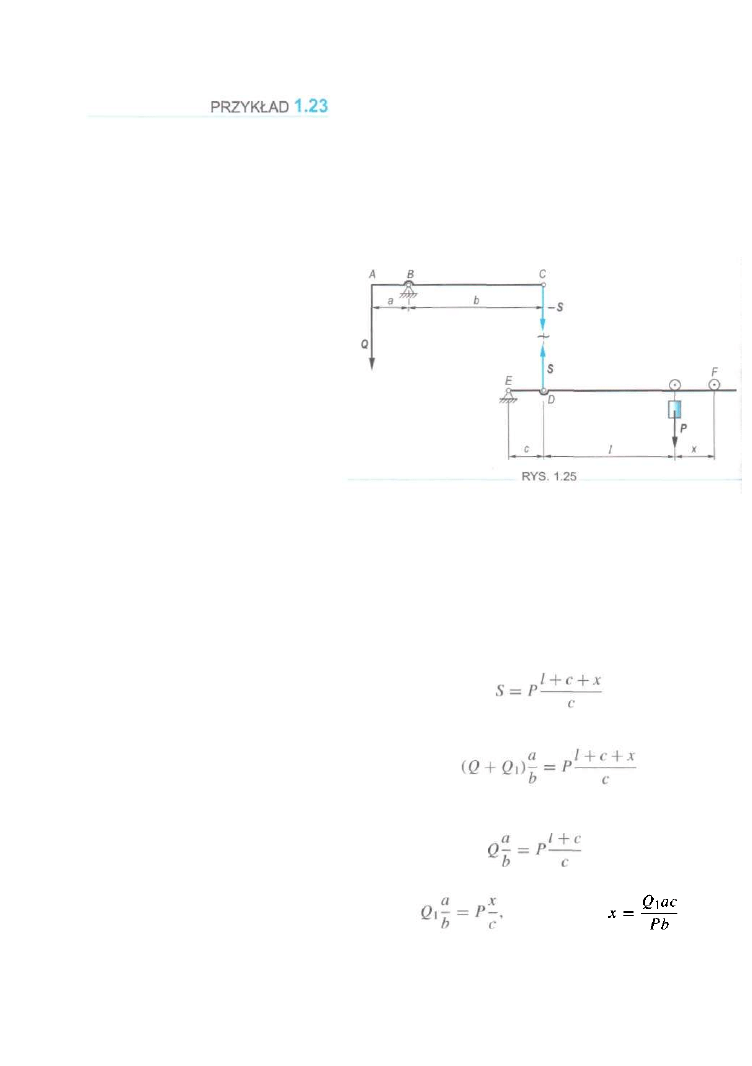
W celu zmierzenia dużych sił Q zbudowano układ dwóch

różnoramiennych dźwigni ABC i EDF, połączonych ze sobą

łącznikiem CD. W punktach B i E znajdują się nieruchome

podpory. Po dźwigni EDF może przesuwać się ciężar P. Siła

Q

przyłożona w punkcie A jest równoważona przez ten ciężar,

umieszczony w odległości / od punktu D. O jaką odległość x

należy przesunąć ciężar P, jeżeli do siły Q dodamy siłę Q1,

(rys. 1.25)?

ROZWIĄZANIE

Rozdzielmy myślowo pręt CD. Otrzymamy w ten sposób dwa

układy proste. Dla pierwszego układu z warunku równowag

w postaci sumy momentów względem punktu B uzyskujemy

a

siłę w pręcie CD równą S = (Q + Q\)-. Podobnie z wa-

b

runku momentów względem punktu E dla układu drugiego

dostajemy

Z porównania tych związków otrzymamy

Z warunków zadania wynika, że siła Q była zrównov

żona siłą P przyłożoną w odległości / od punktu D. Wted
dostajemy zależność . Po uwzględnieniu ostat-
niego związku możemy napisać