Metody rozwiązywania zadań

tekstowych

w edukacji

wczesnoszkolnej

Metoda analityczna - redukcyjna

• Polega na dokładnej analizie zadania –

znalezieniu w pierwszej kolejności
niewiadomej, a potem, cofając się do
treści zadania, ustaleniu, co trzeba
wiedzieć, aby znaleźć odpowiedź i czy te
informacje są zawarte w treści zadania.

• Następnie należy opisać dostrzeżone

zależności w postaci związków
matematycznych i wykonać
zaplanowane obliczenia.

W sklepie było 300 jajek w pudełkach po 12
jajek
w każdym. Po zamknięciu sklepu pozostało 9
pudełek
Ile pudełek z jajkami sprzedano w ciągu dnia?

• W zadaniu musimy ustalić,

ile pudełek

jajek sprzedano w ciągu dnia.

Jest to

nasza niewiadoma.

• Co trzeba wiedzieć, aby odpowiedzieć na

pytanie główne zadania?

Ile pudełek było w sklepie na początku i ile
zostało?

Trzeba zatem ustalić odpowiednie liczby.

Czy są w zadaniu dane wystarczające
do znalezienia odpowiedzi?

• Czy wiemy, ile było pudełek przed

rozpoczęciem sprzedaży?

• Nie, ale potrafimy to obliczyć. Trzeba podzielić

liczbę, które były na początku sprzedaży

w sklepie, przez liczbę jajek mieszczących się

w jednym pudełku, czyli:

300 : 12 = 25

• Od uzyskanego wyniku wystarczy teraz odjąć

liczbę pudełek, które pozostały w sklepie:

25 – 9 = 16

• Sprzedano 16 pudełek jajek.

Po przeprowadzeniu rozumowania można,

zapisać planowane działania w tzw. jednym

zapisie:

300: 12 – 9 =

• Zatem, najpierw patrzymy na pytanie,

potem sprawdzamy, czy dane

wystarczą do rozwiązania i ustalamy

drogę postępowania.

• A jeśli brakuje danych? Trzeba je

zdobyć z innych źródeł. Bardzo

pomocne są odpowiednie pytania

pomocnicze, które warto wcześniej

przygotować.

• Tok przyjętego postępowania można

przedstawić w postaci schematu

zawierającego stawiane pytania.

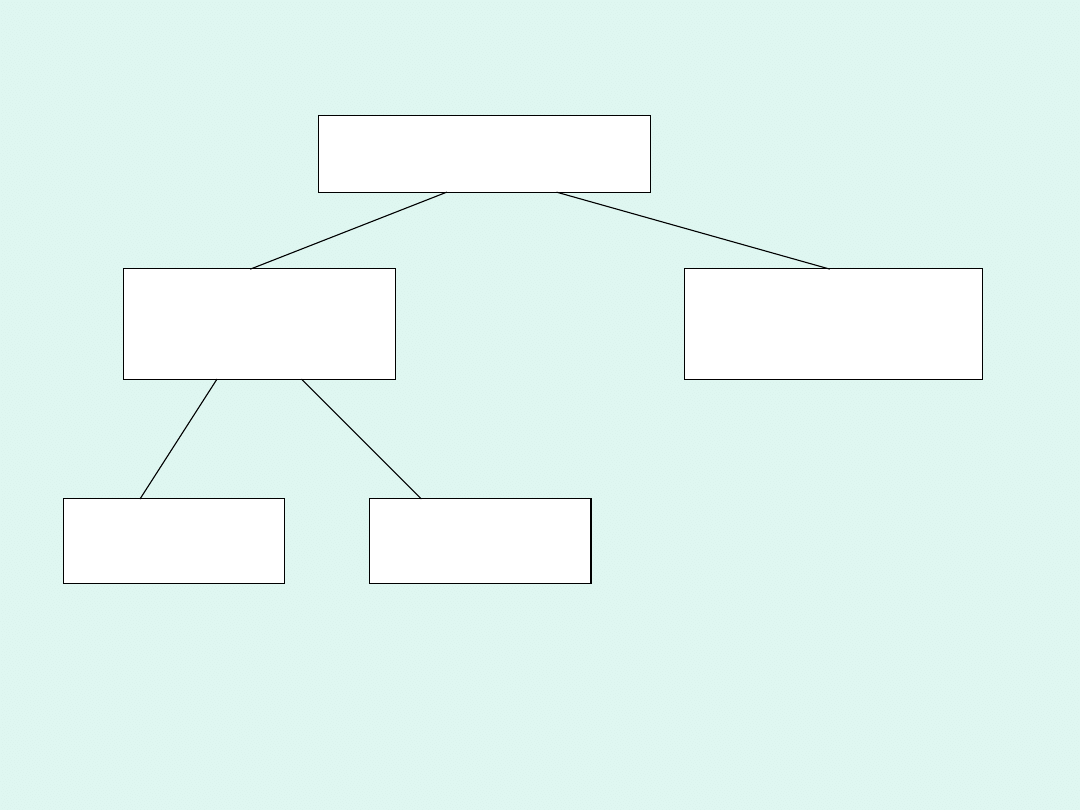
Ile pudełek jajek sprzedano w
ciągu dnia?

Ile pudełek było w sklepie na
poczatku?

Ile pudełek było
w sklepie na
początku?

Ile pudełek jajek
sprzedano w ciągu
dnia?

Ile pudełek jajek
pozostało po zamknięciu
sklepu?

Ile jajek było w
sklepie?

Ile jajek było w
każdym
pudełku?

Otrzymaliśmy drzewo z gałęziami (ramionami zwróconymi w dół).

Teraz trzeba ustalić działania między liczbami będącymi odpowiedziami
na pytania

w ramkach. Schemat zamienimy na typowe, znane dzieciom drzewko,
wystarczy odwrócić drzewko do postaci im znanej – ramionami do góry-
wpisując odpowiednie liczby.

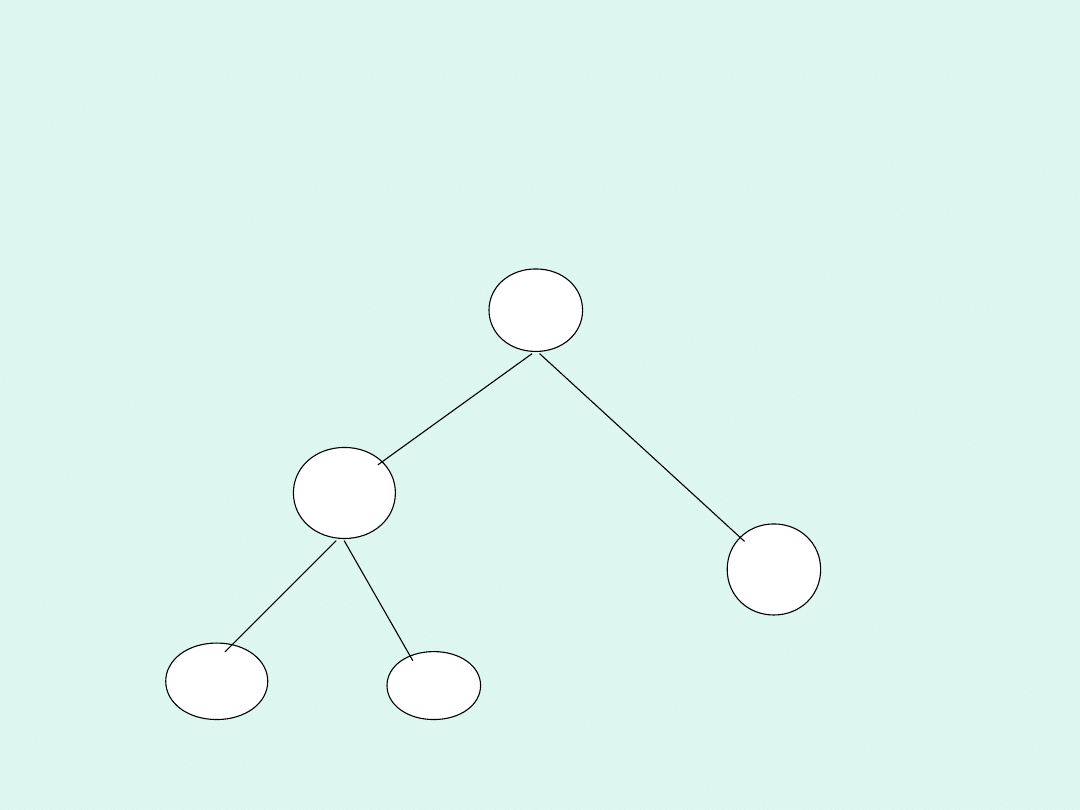
Takie postępowanie w fazie poznawania przez dziecko

metody rozwiązywania zadań z pewnością uświadomi

mu strukturę rozwiązania i pomoże przy rozwiązywaniu

zadań następnych.

-

:

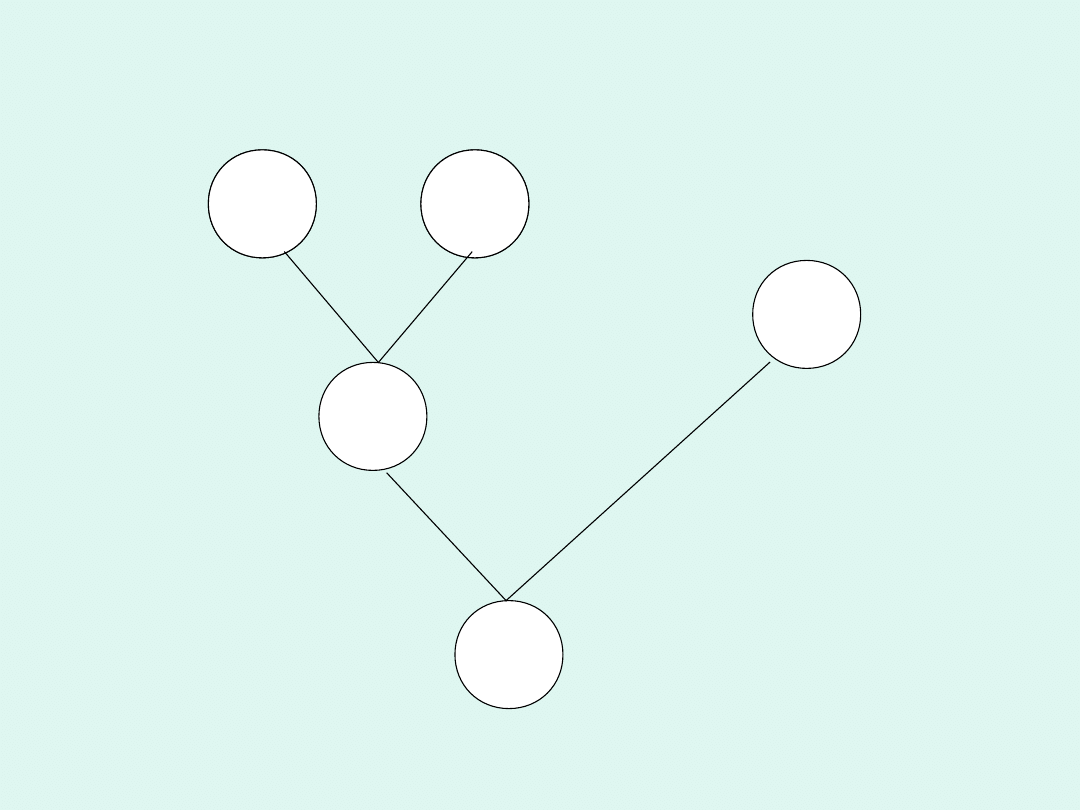
30
0

12

:

-

Metoda syntetyczna - dedukcyjna

• Polega na rozpoczynaniu od ogólnego spojrzenia na zadanie,

wyodrębnienie danych i przez wnioskowanie przechodzenie do szczegółów

– odkrycie niewiadomej

• Wiemy, że:

300 – tyle jajek było w sklepie
12 – po tyle jajek pakowano w pudełko
9 – tyle pudełek zostało w sklepie po zamknięciu

Czego można dowiedzieć się z tych danych,

o co można zapytać?

• ile jajek zostało po zamknięciu sklepu: 9 * 12

• ile pudełek z jajkami było w sklepie od początku:300 : 12

• ile jajek mieści się w 10 pudełkach: 10 * 12

• ile byłoby pudełek, gdyby jajka pakowano po 10 sztuk: 300 : 10

Takich pytań można postawić jeszcze dużo. Czy są takie, które

przybliżają nas do rozwiązania- znalezienie odpowiedzi na

pytania zawarte w zadaniu:

Ile pudełek z jajkami sprzedano w ciągu dnia?

• Skoro wiemy, ile jajek było na początku (300) i po

zakończeniu sprzedaży (9 * 12), to możemy łatwo
ustalić, ile jajek sprzedano w ciągu dnia: 300 – 9 * 12,
a otrzymany wynik dzieli się przez liczbę jajek w
pudełku, co daje informację o liczbie sprzedanych
pudełek z jajkami. Można to zapisać jako ciąg działań:

9 * 12 = 108
300 – 108 = 192

192 : 12 = 16

Uzyskaliśmy ten sam wynik, co w poprzednim

rozwiązaniu metodą analityczną, choć droga tym
razem była inna.

• Metoda syntetyczna wymaga od rozwiązującego

spojrzenia na dane w zadaniu i dostrzeganie
związków, zależności logicznie wypływające z
danych, nie zawsze dla dziecka oczywistych.
Wymaga od ucznia przewidywania możliwych do
wykonania operacji matematycznych, z których nie
wszystkie prowadzą do celu. Nie zawsze widać od
razu cel takiego postępowania, co dla dziecka
poznającego dopiero sztukę rozwiązywania zadań
nie zawsze jest w pełni zrozumiałe –

po co ja to

robię?.

Mimo, że metoda jest trudniejsza od

analitycznej,

rozwija umiejętność dostrzegania

zależności między danymi, stawiania pytań i
wnioskowania.

W tej metodzie również można

zastosować schemat graficzny ukazujący kolejność
postępowania.

Metoda kruszenia zadań

• Strategia

„kruszenia”

zadań jest jedną

z nowoczesnych metod rozwiązywania zadań tekstowych w
klasach I-III, a jednocześnie rozwijania aktywności twórczej

w matematyce wywodzącej się z założenia:

tworzenie nowych obiektów jest możliwe dzięki kruszeniu

istniejących.

Metodę te opracowała Jadwiga Hanisz
Metoda kruszenia polega na modyfikowaniu tzw. zadania

bazowego zwiększaniu lub zmniejszaniu liczb danych
i ich wartości, zastępowaniu danych innymi, rezygnacji
z niektórych danych, zmiany miejsca danych, a także
przekształcaniu zadania, jego odwracaniu, wprowadzaniu
nowych związków i zależności, uszczegóławianiu lub
uogólnianiu zadania.

Metodę kruszenia można stosować w

różnych wersjach.
Tym samym ma ogromne walory kształcące.

Wszystko zaczyna się od zadania bazowego

Jest to zadanie, najczęściej złożone, otwarte,

niestandardowe i nie ma nigdy pytania.

Tematyka zadań powinna być bliska

zainteresowaniom uczniów i łączyć się z

przeżyciami dzieci, a dane powinny dość

precyzyjnie odzwierciedlać rzeczywistość.

„Kruszenie” wymaga postawienia pytania

mającego związek z danymi- zbudowanie
zadania- i rozwiązaniu tego zadania.
Na początku pytanie może zaproponować
nauczyciel, a później uczniowie tworzą własne,
bardziej lub mniej związane z zadaniem bazowym.

Kruszenie zadań tekstowych, to:

• modyfikacja danych,
• zwiększenie lub zmniejszenie liczby danych i

ich wartości,

• zastępowanie danych innymi,
• zmiana miejsca danych,
• przekształcanie, odwracanie zadania,
• wprowadzanie nowych związków i zależności,
• uszczegóławianie lub uogólnianie zadania

itp.

• Uczniowie układają nie całe zadania, ale pytania do

zadań tekstowych. Jednakże, zanim uczeń postawi
pytanie, musi w myśli ułożyć zadanie, ustalić
właściwy związek miedzy danymi liczbowymi,
dostrzec niewiadomą i ustalić jej związek z danymi i
sformułować pytanie – problem który trzeba
przedstawić kolegom. Uczniowie udzielając
odpowiedzi na postawione przez kolegów pytania,
też musza w myśli lub w mowie głośnej odtworzyć
treść zadania, zakończonego rozważanym
problemem oraz zapisać jego rozwiązanie w postaci
formuły matematycznej. Jest to więc pełny proces
układania i rozwiązywania zadań tekstowych.

• Metoda doskonale się nadaje do pracy zespołowej
i grupowej

Metoda kruszenia rozwija u uczniów:

• Płynność myślenia- uczeń nie poprzestaje na ułożeniu jednego

zadania

• Giętkość myślenia- przechodzi z jednego toru myślenia na inny
• Oryginalność myślenia – uczeń układa coraz wymyślniejsze

pytania

• Jest zatem okazją do rozwijania aktywności matematycznej

podczas rozwiązywania zadań tekstowych.

• Przykład zadania bazowego:

W sklepie Janek kupił 7 ołówków po 2 zł, a Kasia 5 zeszytów po 4

zł.

• Metodę kruszenia stosuje się w różnych

wersjach

Wersja I. O co można zapytać- układanie

pytań do zadania bazowego

Rozwiązanie prowadzi się w następujących fazach:

1. Prezentacja zadania bazowego
2. Układanie pytań szczegółowych do zadania

bazowego

3. Analiza, weryfikacja pytań- czy na poszczególne

pytania można znaleźć odpowiedź, korzystając

z danych w zadaniu

4. Wybór dowolnego pytania przez ucznia i

samodzielne ułożenie treści zadania o tej samej lub

innej tematyce

5. Samodzielne rozwiązanie tego zadania przez ucznia

i zapis odpowiedzi

Wersja II. Co można obliczyć?

1. Prezentacja zadania bazowego
2. Układanie i zapisywanie na tablicy przez

uczniów wszelkich możliwych działań na liczbach
występujących w zadaniu bazowym i ich
obliczanie

3. Analiza działań, układanie do nich pytań i ich

zapis obok oraz wycieranie działań źle ułożonych

4. Wybór dowolnego działania i pytania, ułożenie

do nich samodzielnie nowego zadania o tej
samej lub innej tematyce

5. Samodzielne rozwiązanie tego zadania w

zeszycie i zapis odpowiedzi

Wersja III. Jak to przedstawić?

Obmyślanie zadań szczegółowych do zadania bazowego

i przedstawianie ich w formie zakodowanej

Wymaga dostrzeżenie w zadaniu bazowym

fragmentów, które można ze sobą powiązać i
utworzyć nowe zadania, a następnie przedstawienie
ich w zakodowanej formie (np. na osi liczbowej,
drzewku, grafie, za pomocą rysunku), a następnie
próby określenia ilustracji

Można zilustrować każdą część zadania oddzielnie, np.

ilustracja części o tulipanach i pytania wynikające
z ilustracji

Po ułożeniu pytań, dalszy ciąg postępowania jest

analogiczny jak poprzednio

Wersja IV. Co by było, gdyby…?

• „

Zabawa” z zadaniem bazowym, w którym można zmieniać dane

i układać nowe zadania, na zasadzie co by było gdyby?

Nowe zadania są zapisywane, a potem uczniowie próbują je

rozwiązywać

W sklepie było 50 kg owoców. W jednej skrzynce było 20 kg jabłek. W

drugiej 15 kg gruszek, a w trzeciej były śliwki

Można zmieniać dane w zadaniu. W początkowej fazie zmiana powinna

dotyczyć jednej wielkości, potem przy większym zaawansowaniu

uczniów w rozwiązywaniu zadań, zmiana może dotyczyć kilku wielkości.

Uczniowie wprowadzają zmiany na zasadzie: co by było, gdyby:

Jabłek było 10 kg? Wszystkich owoców było 40 kg?
Gruszek było dwa razy więcej niż jabłek? Śliwek było o 15 kg mniej niż

jabłek?

W ten sposób powstają nowe sytuacje zadaniowe, do których trzeba

ułożyć pytania, a następnie rozwiązać otrzymane zadania

Wersja V. dokładanie danych

•

Wersja ta polega na układaniu wszelkich możliwych
pytań do zadania bazowego, ale z prawem do
dokładania bądź zmieniania danych

W sklepie Janek kupił 7 ołówków po 2 zł, a Kasia 5

zeszytów po 4 zł. Jakie powstaną nowe zadania, jeśli
dołożymy do zadania nowe dane?

A.

Dzieci miały razem 40 zł.

B.

Janek miał 10 zł, a Kasia 25 zł

Przykładowe pytania do sytuacji w punkcie A
Czy wystarczy im pieniędzy na zakupy?
Ile otrzymają reszty?
Ile ołówków mogą kupić za wszystkie pieniądze?
Ile zeszytów mogą kupić za wszystkie pieniądze?