ROZWIĄZYWANIE

ROZWIĄZYWANIE

ZADAŃ TEKSTOWYCH

ZADAŃ TEKSTOWYCH

ZA POMOCĄ RÓWNAŃ

ZA POMOCĄ RÓWNAŃ

na poziomie klasy 6

Maciek zebrał o 14 grzybów więcej niż Adrian,
a razem mają 96 grzybów. Ile grzybów zebrał Adrian?

Etap 1. Analiza treści zadania – dane

zapisujemy

następująco;

a) niewiadomą,
b) co oznaczają poszczególne liczby w

zadaniu.

Etap 2. Układamy równanie.

Etap 3. Rozwiązujemy równanie.

Etap 4. Sprawdzamy rozwiązania.

Etap 5. Zapisujemy odpowiedź.

Maciek zebrał o 14 grzybów więcej niż Adrian
a razem mają 96 grzybów. Ile grzybów zebrał Adrian?

a) ustalamy niewiadomą z pytania
x – ilość grzybów zebranych przez Adriana

b) ustalamy co oznaczają poszczególne liczby w zadaniu?
14 – o tyle więcej grzybów zebrał Maćka
96 – ilość grzybów zebrana przez Adriana i

Maćka

Etap 1. - Analiza treści
zadania

Maciek zebrał o 14 grzybów więcej niż Adrian,
a razem mają 96 grzybów. Ile grzybów zebrał Adrian?

Zapisujemy dane:

x – ilość grzybów zebranych przez Adriana
x + 14 – ilość grzybów zebranych przez Maćka
96 – ilość grzybów zebrana przez Adriana i

Maćka

Etap 1. - Analiza treści
zadania

Etap 3. Rozwiązujemy
równanie.

L

=

P

x + (x + 14) = 96 opuszczamy nawias
x + x + 14 = 96 redukujemy wyrazy

podobne

2·x + 14 = 96
-14 -14 odejmujemy 14
2·x = 82
:2 :2 dzielimy przez 2

x = 41

Etap 4. Sprawdzenie
rozwiązania.

ilość grzybów Adrian

→ x

= 41

ilość grzybów

Maciek

→

x + 14 = 41 +

14=

55

razem →

41 +

55

= 96

Etap 5. Zapisujemy
odpowiedź.

Odp. Adrian zebrał 41 grzyby.

Maciek

Maciek

zebrał o 14 grzybów więcej niż Adrian,

zebrał o 14 grzybów więcej niż Adrian,

a razem mają 96 grzybów. Ile grzybów zebrał Adrian?

a razem mają 96 grzybów. Ile grzybów zebrał Adrian?

Dane:

x

- ilość grzybów Adriana

x

+ 14 – ilość grzybów Maćka

96 – grzyby Adriana i Maćka razem

Zapis w zeszycie.

Sprawdzenie:

Adrian – 41

Maciek – 41 + 14 = 55
Razem – 41 + 55 = 96

Odp.

Adrian zebrał 41

grzyby.

Rozwiązanie:

x + (x + 14) = 96
x + x + 14 = 96
2·x + 14 = 96
│-14
2·x = 82│:2
x = 41

Przykłady



z rozwiązaniami

Zad. 1. W trzech klasach szóstych jest razem

Zad. 1. W trzech klasach szóstych jest razem

64

64

uczniów. W klasie VI

uczniów. W klasie VI

a jest

a jest

24

24

uczniów,

uczniów,

a w klasie VI b jest

a w klasie VI b jest

tyle samo

tyle samo

uczniów co w klasie VI c.

uczniów co w klasie VI c.

Ilu uczniów liczy klasa VI b?

Ilu uczniów liczy klasa VI b?

Dane:

x – liczba uczniów klasy VIb
x – liczba uczniów klasy VIc
24 – liczba uczniów klasy VIa
64 – liczba uczniów w klasach szóstych

Rozwiązanie:

x + x + 24 = 64
2x + 24 = 64  - 24

2x = 40  : 2

x = 20

Sprawdzenie:

klasa VIa – 24 uczniów

klasa VIb – 20 uczniów
klasa VIc – 20 uczniów
razem VIa,b,c 64

Odp. Klasa VI b liczy 20 uczniów

.

Z

Z

ad. 2. Paulina ma

ad. 2. Paulina ma

trzy razy więcej

trzy razy więcej

widokówek niż Aleksandra a

widokówek niż Aleksandra a

razem mają

razem mają

72

72

widokówek. Ile widokówek ma Aleksandra?

widokówek. Ile widokówek ma Aleksandra?

Dane:

x – ilość widokówek Aleksandra

3x – ilość widokówek Paulina
72 – widokówek Aleksandra i Paulina

Rozwiązanie:

x + 3x = 72
4x = 72  : 4

x = 18

Sprawdzenie:
widokówki Aleksandry

– 18

widokówki Pauliny – 3·18 = 54

razem – 72

Odp. Aleksandra

ma 18 widokówek.

Zad. 3. Suma trzech kolejnych liczb naturalnych wynosi 252.

Zad. 3. Suma trzech kolejnych liczb naturalnych wynosi 252.

Jakie to liczby?

Jakie to liczby?

Dane:

x – pierwsza liczba naturalna
x + 1 – następna liczba naturalna
x + 2 – kolejna liczba naturalna

Rozwiązanie:

x + (x + 1) + (x + 2) = 252
x + x + 1 + x + 2 = 252
3x + 3 = 252  - 3

3x = 249  : 3

x = 83

Sprawdzenie:

pierwsza liczba naturalna - 83

następna liczba naturalna - 83 + 1 = 84
kolejna liczba naturalna - 83 + 2 =85
suma - 252

Odp.

Szukane liczby to 83, 84, 85.

Zad. 4. Suma trzech kolejnych liczb parzystych wynosi 270.
Jakie to liczby?

Dane:

2x – pierwsza liczba parzysta
2x + 2 – następna liczba parzysta
2x + 4 – kolejna liczba parzysta

Rozwiązanie:

2x + (2x + 2) + (2x + 4) = 270
2x + 2x + 2 + 2x + 4 = 270
6x + 6 = 270  - 6

6x = 264  : 6

x = 44

Sprawdzenie:

pierwsza liczba parzysta - 2* 44 = 88

następna liczba parzysta - 88 + 2 = 90
kolejna liczba parzysta - 88 + 4 = 92
suma - 270

Odp.

Szukane liczby to 88, 90, 92.

Zad. 5. Pani Sabina pobrał a ze swojego konta 6000 zł. Kasjerka
wypłaciła tę kwotę w
banknotach o nominałach 200 zł i 50 zł.
Banknotów dwustuzłotowych było o 10 więcej niż
pięćdziesięciozłotowych. Ile banknotów otrzymała Pani Sabina?

Dane:

x – ilość banknotów 50 złotowych
50 zł · x – kwota wypłacona w banknotach 50 złotowych
x + 10 – ilość banknotów 200 złotowych
200 zł ·(x + 10) – kwota wypłacona w banknotach 200 złotowych
12000 zł – cała kwota pobrana z banku przez pania Sabinę

Rozwiązanie:

50x + 200 · (x + 10) = 6000
50x + 200x + 2000 = 6000
250x + 2000 = 6000  - 2000

250x = 4000  : 250

x = 16

Sprawdzenie:

ilość banknotów 50 złotowych – 16 szt  kwota (50

· 16) = 800 zł
ilość banknotów 200 złotowych – 16 + 10 = 26 szt  kwota (200

· 26) = 5200 zł
razem ilość banknotów 42 szt razem
kwota 6000 zł

Odp.

Pani Sabina otrzymała 42 banknoty.

Zad. 6. Cztery cegły i 12kg pierza waży tyle samo co 8 cegieł i 4 kg
żelaza.
Ile waży cegła?

Dane:

x kg – waga 1 cegły
12 kg – waga pierza
24 kg – waga żelaza

Rozwiązanie:

cztery cegły i 12 kg pierza = 8 cegieł i 4 kg żelaza.
4x + 12 = 8x + 4 /-8x
-4x + 12 = 4  - 12

- 4x = - 8  : (- 2)

x = 2

Sprawdzenie:

L strona równania  4 · 2 kg + 12 kg = 8 kg + 12 kg = 20 kg

P strona równania  8 · 2 kg + 4 kg = 16 kg + 4 kg = 20 kg

L = P

Odp.

Cegła waży 2 kg.

Zad. 7. Damian ma książki na dwóch pólkach. Na górnej ma 2 razy
więcej
książek niż na dolnej. Gdyby z górnej półki przełożył na dolną 7
książek,
wówczas na obu półkach miałby taką samą ich ilość. Ile książek ma
Damian?

Dane:

x – ilość książek na dolnej półce
2x – ilość książek na górnej półce
k – ilość wszystkich książek

Rozwiązanie:

górna półka



dolna półka

2x > x
górna półka – 7

=

dolna półka + 7

2x - 7 = x + 7  - x

x - 7 = 7  + 7

x = 14

Sprawdzenie:

L strona równania  2 · 14 -7 = 28 - 7 = 21

P strona równania  14 + 7 = 21

L = P
k = 2 · 14 + 14 = 28 + 14 = 42

Odp. Damian

ma 42 książki.

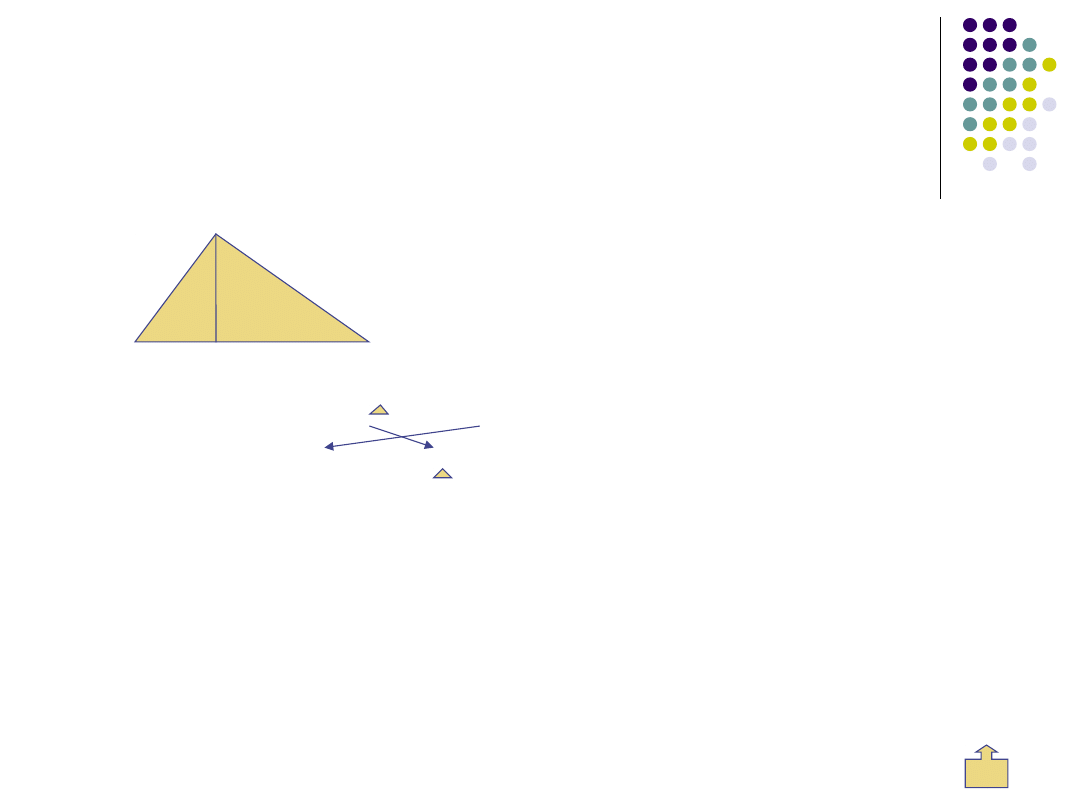
Zad. 8. Pole trójkąta jest równe 20 cm2. Jeden z boków tego trójkąta
ma długość 16 cm.
Oblicz długość wysokości opuszczonej na ten bok.

Dane:

Rozwiązanie:

P =

1

/

2

· a · h zamieniamy strony

równania

1

/

2

· a · h = P

1

/

2

· 12 · h = 24

6

· h = 24  : 6

h = 4

Sprawdzenie:

L = 20

P =

1

/

2

· 12· 4 = 6 · 4 = 24

L = P

Odp.

Wysokość trójkąta ma 4 cm.

a = 12
cm

h
=?

P=24

cm

2

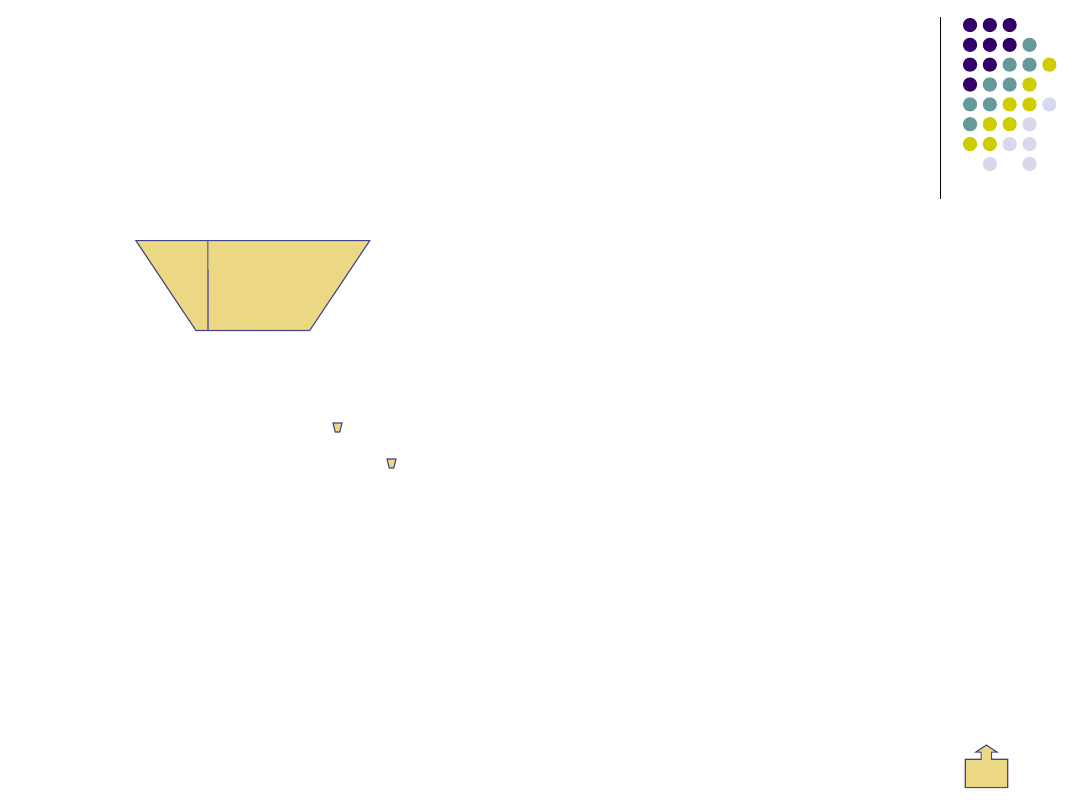
Zad. 9. Podstawy trapezu o polu 48 cm

2

mają długości 5 cm i 7 cm.

Jaką wysokość ma trapez?

Dane:

Rozwiązanie:

P =

1

/

2

(a + b)h

1

/

2

·(a + b) · h = P

1

/

2

·(4 + 8) · h = 48

1

/

2

·

12 · h = 48

6 · h = 48  : 6

h = 8

Sprawdzenie:

L = 48

P =

1

/

2

·(4 + 8) · 8 =

1

/

2

·

12 · 8 = 6 · 8 = 48

L = P

Odp.

Trapez ma wysokość 8 cm..

a = 4
cm

b = 8 cm

h =?

P=48

cm

2