„Matematyka jest

delikatnym kwiatem, który
rośnie nie na każdej glebie

i zakwita nie wiadomo

kiedy i jak..”

Jean Fabre

WYKORZYSTANIE RÓWNAŃ

DO ROZWIĄZYWANIA ZADAŃ

TEKSTOWYCH – ROZTWORY

Solanki, syropy i inne roztwory
potrafią przyprawić o ból głowy.
Chemia

to

nie

jedyny

przedmiot

na

którym

przychodzi się z nimi zmierzyć,
często

na

matematyce

pojawiają się zadania tekstowe
dotyczące

roztworów.

Na

szczęście w większości zadania
tego

typu

rozwiązuje

się

stosując podobne algorytmy.

CO NALEŻY ZROBIĆ ABY

ROZWIĄZAĆ ZADANIE

TEKSTOWE.

1. Przeczytaj uważnie treść zadania

2. Oznacz niewiadomą w zadaniu

3. Przeanalizuj treść zadania

4. Ułóż równanie

5. Rozwiąż równanie
6. Sprawdź poprawność rozwiązania i jego

zgodność z treścią zadania

7. Sformułuj odpowiedź

ROZTWÓR.

Roztwór to mieszanina rozpuszczalnika
(najczęściej wody) i substancji rozpuszczanej.
Mówimy, że roztwór jest czteroprocentowy,
gdy masa substancji rozpuszczonej stanowi
4% masy całego roztworu.
Stężenie

procentowe

roztworu

można

obliczyć według wzoru:

p – stężenie procentowe roztworu

s – masa substancji rozpuszczonej

r – masa roztworu (r = masa rozpuszczalnika

+ s)

PRZYKŁADOWE ZADANIA.

ZADANIE 1.
W 3 l wody rozpuszczono 2 kg soli. Jakie jest
stężenie procentowe tak otrzymanej solanki?
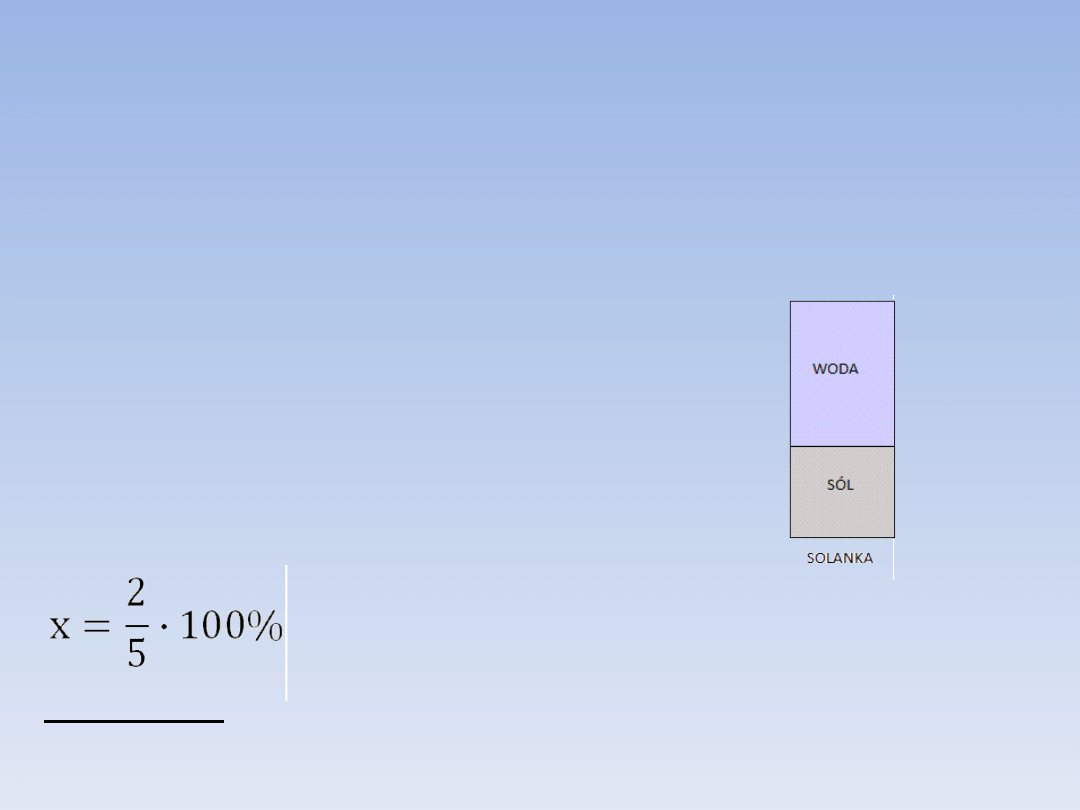
Analiza zadania:
x – stężenie procentowe solanki
3 kg – masa wody
2 kg – masa soli
3 kg + 2 kg = 5 kg – masa roztworu
Rozwiązanie (korzystamy ze wzoru):

x = 40%
Odpowiedź: Stężenie tej solanki wynosi 40%.

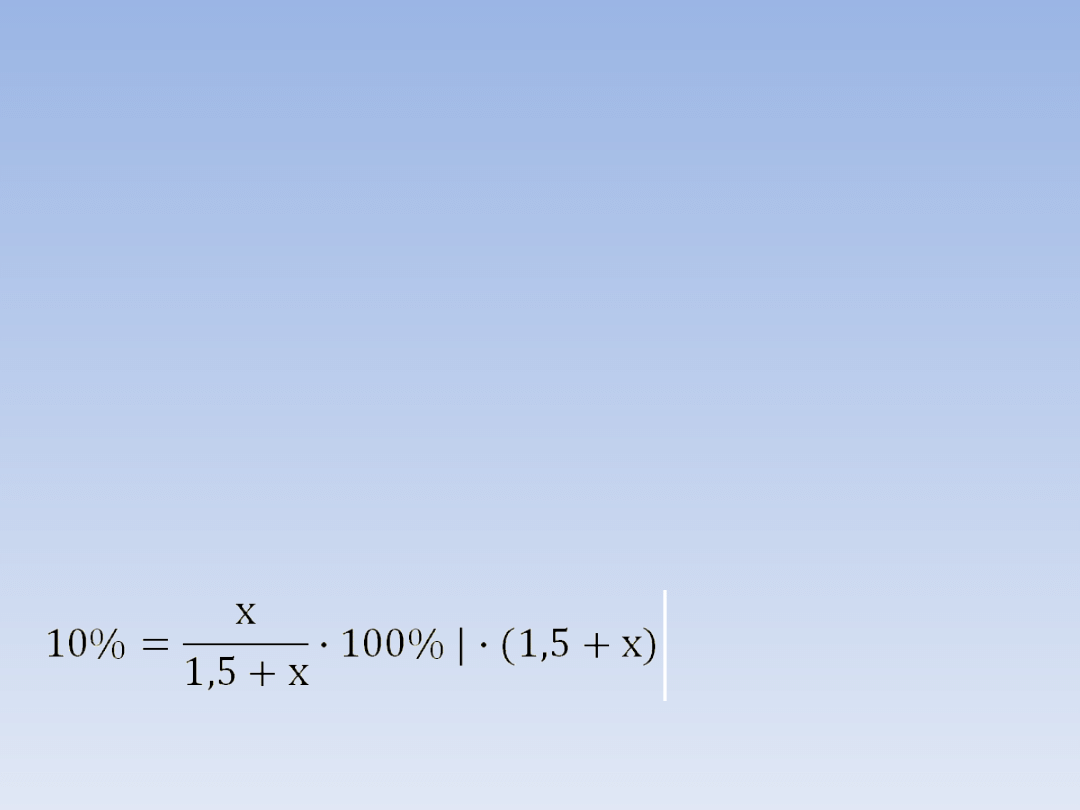
PRZYKŁADOWE ZADANIA.

ZADANIE 2.
Ile soli należy wsypać do 1,5 l wody aby
otrzymać roztwór dziesięcioprocentowy?
Analiza zadania:
x – masa soli, którą trzeba wsypać
1,5 kg – masa wody
10% - stężenie roztworu
(1,5 + x) kg – masa roztworu
Rozwiązanie (korzystamy ze wzoru):

10% ∙ (1,5 + x) = x ∙ 100% | : 100%

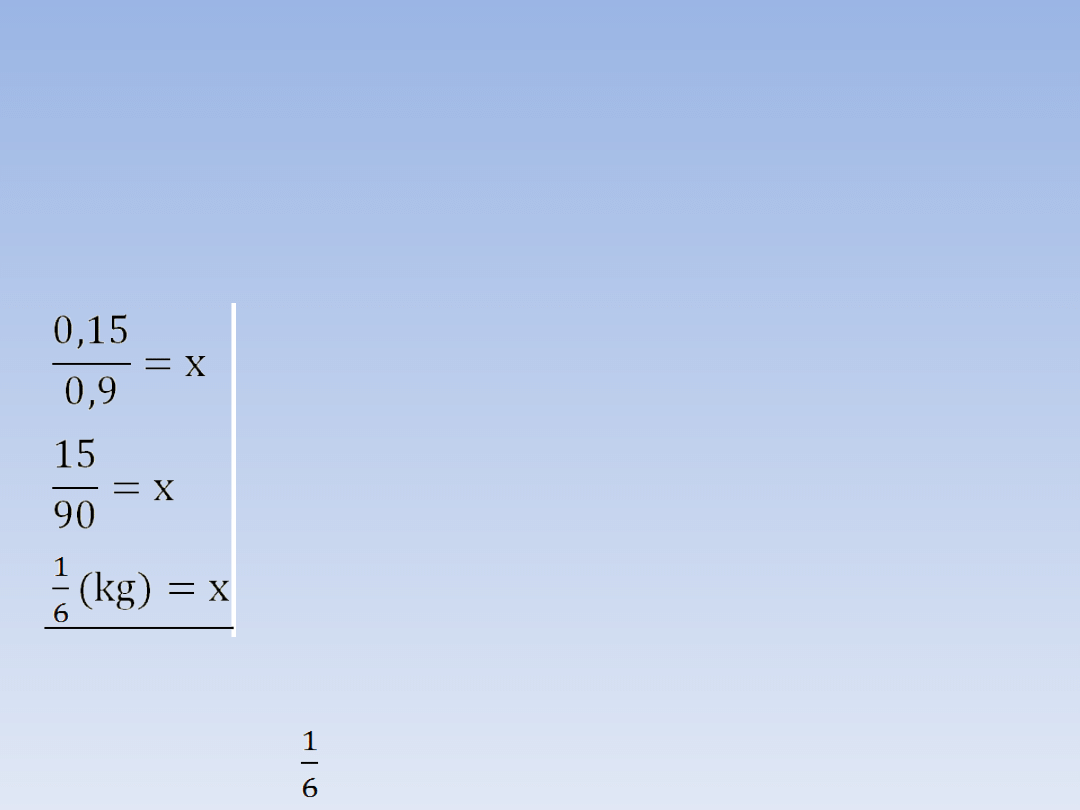
PRZYKŁADOWE ZADANIA.

ZADANIE 2 – ciąg dalszy.
0,1 ∙ (1,5 + x) = x
0,15 + 0,1x = x | - 0,1x
0,15 = 0,9x | :0,9

Odpowiedź:

Aby

otrzymać

roztwór

dziesięcioprocentowy należy wsypać kg
soli.

PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Ile wody należy dolać do 20 kg solanki
pięcioprocentowej, aby otrzymać solankę
czteroprocentową?
Analiza zadania:
x – masa wody, którą należy dolać
20 kg – masa „starego” roztworu
5% - stężenie „starego” roztworu
0,05 ∙ 20 kg – masa soli w „starym”
roztworze
(20 + x) kg – masa „nowego” roztwory
4% - stężenie „nowego” roztworu
0,04 ∙ (20 + x) kg – masa soli w „nowym”
roztworze

PRZYKŁADOWE ZADANIA.

ZADANIE 3 – ciąg dalszy.

Zauważmy, że w nowym roztworze zmienia
się tylko masa wody, masa soli pozostaje bez
zmian, na tej podstawie możemy zbudować
równanie:
0,04 ∙ (20 + x) = 0,05 ∙ 20
0,8 + 0,04x = 1

PRZYKŁADOWE ZADANIA.

ZADANIE 3 – ciąg dalszy.
Rozwiązanie równania:
0,8 + 0,04x = 1 | - 0,8

od obu stron równania

odejmuję 0,8

0,04x = 0,2 | :0,04

obie strony równania dzielę przez

0,04

x = 5 (kg)
Dla uproszczenia podczas rozwiązywania
równania nie zapisywaliśmy jednostek,
dlatego przy rozwiązaniu jednostka jest
zapisania w nawiasie ().
5 kg wody to oczywiście 5 l wody.
Odpowiedź: Aby otrzymać solankę
czteroprocentową należy dolać 5 l wody.

PRZYKŁADOWE ZADANIA.

ZADANIE 4.
Ile soli należy dosypać do 5 kg solanki
pięcioprocentowej

aby

otrzymać

solankę

dziesięcioprocentową?

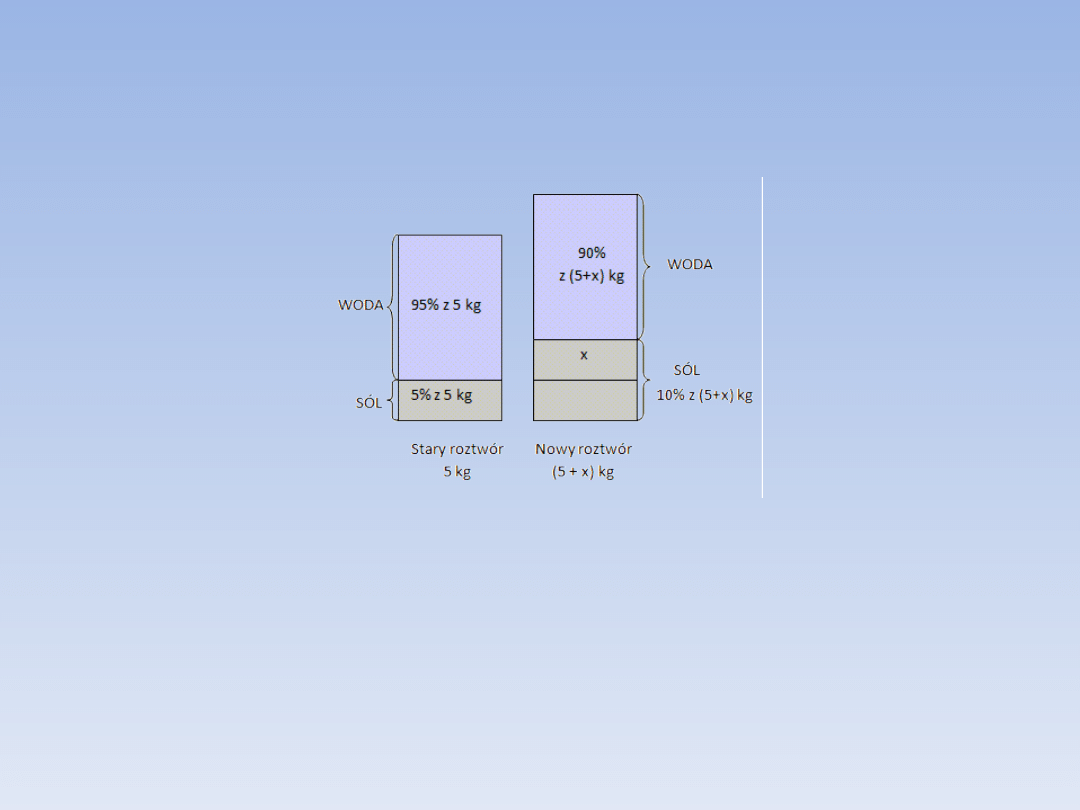
Analiza zadania:
x – masa soli, którą trzeba dosypać
5 kg – masa starego roztworu
5% - stężenie starego roztworu
0,05 ∙ 5kg – masa soli w starym roztworze
(5 + x) kg – masa nowego roztworu
10% - stężenie nowego roztworu
0,1 ∙ (5 + x) kg – masa soli w nowym roztworze

PRZYKŁADOWE ZADANIA.

ZADANIE 4 – ciąg dalszy.

Masa soli w starym roztworze jest o x kg
mniejsza od masy soli w nowym roztworze,
na tej podstawie tworzymy równanie:
0,05 ∙ 5 + x = 0,1(5 + x)
0,25 + x = 0,5 + 0,1x

PRZYKŁADOWE ZADANIA.

Zadanie 4 – ciąg dalszy.
Rozwiązanie równania:
0,25 + x = 0,5 + 0,1x
x – 0,1x = 0,5 - 0,25
0,9x = 0,25 | : 0,9

przenoszę niewiadome na
lewą, a liczby na prawą stronę
równania

Odpowiedź: Należy dosypać
kg soli, czyli około 28 dag.

PRZYKŁADOWE ZADANIA.

ZADANIE 5.
Do piętnastoprocentowego syropu dolano 10 kg

wody i otrzymano syrop dziesięcioprocentowy.
Jaka jest całkowita masa otrzymanego syropu?

x – masa nowego syropu
(x – 10) kg – masa starego syropu
15% - stężenie starego syropu
0,15 ∙ (x – 10) kg - masa cukru w starym

syropie

10% - stężenie nowego syropu
0,1x – masa cukru w nowym syropie.
Zmieniła się tylko ilość wody, więc możemy

porównać masę cukru w obu syropach.

PRZYKŁADOWE ZADANIA.

ZADANIE 5 – ciąg dalszy.
Ułożenie równania:
0,15 ∙ (x – 10) = 0,1x
0,15x – 1,5 = 0,1x
Rozwiązanie równania:
0,15x – 1,5 = 0,1x
0,15x – 0,1x = 1,5
0,05x = 1,5 | :0,05
x = 30 (kg)
Odpowiedź: Całkowita masa nowego syropu

wynosi 30 kg.

przenoszę niewiadome na
lewą, a liczby na prawą stronę
równania

PRZYKŁADOWE ZADANIA.

ZADANIE 6.
Z 15 kg syropu jednoprocentowego odparowano
wodę i otrzymano syrop półtoraprocentowy. Ile
wody odparowano?
Analiza zadania:
x – masa odparowanej wody
15 kg – masa starego syropu
1% - stężenie starego syropu
0,01 ∙ 15 kg – ilość cukru w starym syropie
(15 – x) kg – masa nowego syropu
1,5% - stężenie nowego syropu
0,015 ∙ (15 – x) kg – masa cukru w nowym
syropie

PRZYKŁADOWE ZADANIA.

ZADANIE 6 – ciąg dalszy.
Podobnie jak poprzednio porównujemy masę
substancji rozpuszczonej, bo ta się nie
zmieniła:
0,01 ∙ 15 = 0,015 ∙ (15 – x)
0,15 = 0,225 – 0,015x
Rozwiązanie równania:
0,015x = 0,225 – 0,15
0,015x = 0,075 | : 0,015
x = 5 (kg)
Odpowiedź: Odparowano 5 kg wody.

PRZYKŁADOWE ZADANIA.

ZADANIE 7.
Ile

kilogramów

roztworu

czterdziestoprocentowego należy zmieszać z 2
kilogramami

roztworu

trzydziestoprocentowego,

aby

otrzymać

roztwór trzydziestopięcioprocentowy?
Analiza zadania:
x – masa roztworu 40% którą należy dolać
0,4 ∙ x – masa substancji rozpuszczonej w
roztworze 40%
0,3 ∙ 2 kg – masa substancji rozpuszczonej w
roztworze

30%

0,35 ∙ (x + 2) kg – masa substancji
rozpuszczonej w

roztworze

35%

PRZYKŁADOWE ZADANIA.

ZADANIE 7 – ciąg dalszy.
Masa substancji rozpuszczonej w roztworze,
który mamy otrzymać, stanowi sumę mas
substancji rozpuszczonych z obu
zmieszanych roztworów, możemy zatem
zapisać następującą równość:
0,4x + 0,3 ∙ 2 = 0,35 ∙ (x + 2)
0,4x + 0,6 = 0,35x + 0,7
Rozwiązujemy równanie:
0,4x – 0,35x = 0,7 – 0,6
0,05x = 0,1 | :0,05
x = 2 (kg)

PRZYKŁADOWE ZADANIA.

ZADANIE 7 – ciąg dalszy.
Odpowiedź: Należy wziąć dwa kilogramy
roztworu czterdziestoprocentowego.

Powyższe

zadania

są

standardowymi

zadaniami

tekstowymi

dotyczącymi

roztworów. W oparciu o nie można
rozwiązywać podobne zadania – najczęściej
zmieniają się wyłącznie dane liczbowe.