19.03.2015 r.

Laboratorium 2

Twierdzenie o próbkowaniu i najważniejsze wnioski:

Sygnał zwany grzebieniem Diraca ma postać:

Imiona, nazwiska:
Grupa:

Zadanie 1: Wnioski z twierdzenia o próbkowaniu (zad. do rozwiązania na kartce)

Dany jest sygnał

).

12

sin(

)

2

sin(

)

(

t

t

t

s









Został spróbkowany z częstotliwością 4 Hz.

Jakie częstotliwości będzie zawierać widmo spróbkowanego sygnału?

Odpowiedź i uzasadnienie:

Zadanie 2: Próbkowanie w Matlabie

Utwórz sygnał y o dobranej przez siebie częstotliwości, dt=0.001, N=1000. Będziemy go
traktować jako symulację sygnału analogowego. Dobierz częstotliwość próbkowania sygnału y
i wykonaj próbkowanie, wynik zapisz w wektorze ys, takim, że:

Wyświetl obydwa sygnały na jednym wykresie.

Kod:

Wykresy:

Wygeneruj na jednym wykresie widmo obydwu sygnałów, używając polecenia fftshift:

plot(fs, Ts*fftshift(abs(fft( blackman(N)'.*ys))),

'r'

); hold on;

plot(fs, fftshift(abs(fft( blackman(N).*y))),

'b'

);

Wykresy:

Jaka relacja łączy widmo sygnału spróbkowanego i oryginalnego?

Odpowiedź:

Wypróbuj kilka częstotliwości próbkowania - większych i mniejszych od częstotliwości
wynikającej z twierdzenia o próbkowaniu.

Wykresy:

Komentarz:

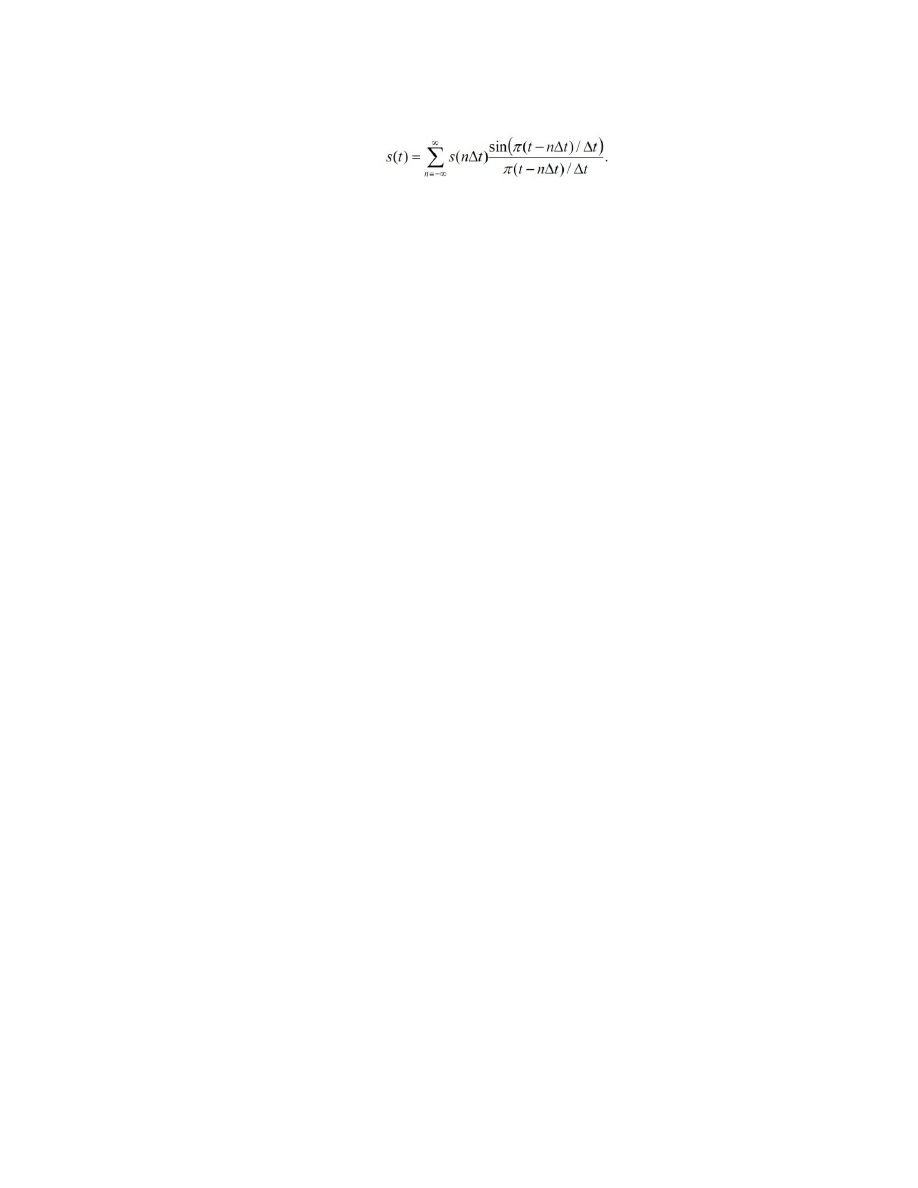
Zadanie 3: Odtwarzanie z próbek

Uzupełnij kod z zadania 2 o rekonstrukcję z próbek przy pomocy równania:

Aby odtworzyć sygnał y, trzeba zsumować przesunięte funkcje sinc, przeskalowane przez
wartości próbek. Można to zrobić np. budując macierz zawierającą w kolumnach przesunięte w
czasie wartości sinc i mnożąc tą macierz przez wektor próbek.

Kod:

Wypróbuj kilka częstotliwości próbkowania. Na czym polega zjawisko aliasingu w dziedzinie
czasu i w dziedzine częstotliwości?

Odpowiedź zilustrowana odpowiednimi wykresami: