Im
ię
i
n
az
w
is
ko
Li
cz
b
a
p
u
n
k
tó
w
:
N
r
in
d
e
k
su
n
r
p
y
tan
ia
1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
o
d
p
o
w
ie
d
ź
p
u
n
k
ty
1
.
O
u
kł
a
d
zi
e
o
t
ra
n
sm
it
a
n
cj
i
G
(s
)=k
/[
s(
s+5
)]
o
b
ję
ty
m
j
e
d
n
o
st
ko
w
y
m
s
p
rz
ę
że
n
ie
m
z
w
ro
tn
y
m
,
p
o
b
u
d
zo
n
y
m
s
ko
ki
e
m
j
e
d
n
o
st
ko
w
y
m
,
m
o
że
m
y
p
o
w
ie
d
zi
e
ć,
ż
e
a
.
w
s
tan
ie
u
stal
o
n
y
m
u
ch
y
b
s
te
ro
w
an
ia
je
st
z
e
ro
w
y
b
.
w
s
tan
ie
u
stal
o
n
ym
u
ch
y
b
s
te
ro
w
an
ia
je
st
w
ię
k
szy
o
d
z
e
ra
c.
w
s
tan
ie
u
stal
o
n
ym
u
ch
y
b
s
te
ro
w
an
ia
je
st
ty
m
w
ię
k
sz
y
,
im
w
ię
k
sz
e
j
e
st
w
zm
o
cn
ie
n
ie
k
d
.
u
k
ład
j
e
st
n
ie
st
ab
il
n
y
,
w
ię
c
stan
u
stal
o
n
y
n
ie
w
y
stą
p
i
2
.
T
ra
n
sm
it
a
n
cj
ą
s
ta
cj
o
n
a
rn
e
g
o
,
li
n
io
w
e
g
o
u
k
ła
d
u
p
rz
y
cz
y
n
o
w
e
g
o
j
e
st
a
.
sto
su
n
e
k
tr
an
sf
o
rm
at
y
L
ap
lac
e
’a
sy
g
n
ał
u
w
y
jś
ci
o
w
e
g
o
d
o
t
ran
sf
o
rm
at
y
s
y
g
n
a
łu
w
e
jś
ci
o
w
e
g
o
p
rz
y
zał
o
że
n
iu
ze
ro
w
e
j
w
ar
to
śc
i
p
o
czą
tk
o
w
e
j
sy
g
n
ał
u
n
a
w
y
jś
ci
u
u
kł
ad
u
b
.
o
d
w
ro
tn
a
tr
an
sf
o
rm
at
a
L
a
p
lac
e
’a
o
d
p
o
w
ie
d
zi
s
ko
ko
w
e
j
u
k
ład
u
c.
o
d
w
ro
tn
a
tr
an
sf
o
rm
at
a
L
a
p
lac
e
’a
o
d
p
o
w
ie
d
zi
i
m
p
u
ls
o
w
e
j
u
k
ład
u
d
.
tr
an
sm
it
an
cj
a
m
o
że
b
y
ć
zd
e
fi
n
io
w
an
a
j
e
d
y
n
ie
d
la
u
k
ła
d
ó
w
n
ie
li
n
io
w
y
ch
3
.
Li
n
io
w
y
u
k
ła
d
s
ta
cj
o
n
a
rn
y
o
2
w
e
jś
ci
a
ch
i
3
w
y
jś
ci
a
ch
m
o
żn
a
o
p
is
a
ć
za
p
o
m
o
cą
m
a
ci
e
rz
y
a
.
d
w
ó
ch
tr
an
sm
itan
cj
i
b
.
tr
ze
ch
t
ran
sm
itan
cj
i
c.
sz
e
śc
iu
t
ran
sm
itan
cj
i
d
.
tr
an
sm
it
an
cj
a
d
o
ty
czy
t
y
lk
o
u
k
ład
ó
w
o
j
e
d
n
y
m
w
y
jś
ci
u
,
tak
i
u
k
ład
m
o
żn
a
o
p
is
ać
je
d
y
n
ie
za
p
o
m
o
cą
ró
w
n
ań
s
tan
u
4
.
P
o
je
m
n
o
ść
c
ie
p
ln
a
c
ia
ła
i
n
fo
rm
u
je
n
a
s
o
a
.
o
b
ję
to
śc
i c
iał
a
w
d
an
e
j
te
m
p
e
ratu
rz
e
b
.
il
o
śc
i
ci
e
p
ła,
k
tó
rą
n
a
le
ży
d
o
star
cz
y
ć
d
o
c
ia
ła,
ab
y
o
g
rz
ać
j
e
o
j
e
d
n
o
st
k
ę
te
m
p
e
ra
tu
ry
c.
il
o
śc
i
ci
e
p
ła,
k
tó
rą
n
a
le
ży
d
o
star
cz
y
ć
d
o
j
e
d
n
e
g
o
k
il
o
g
ram
a
ci
ał
a,
ab
y
o
g
rz
ać
j
e
o
je
d
n
o
st
k
ę
t
e
m
p
e
ratu
ry
d
.
e
n
e
rg
ii
,
jak
a
d
o
star
czo
n
a
d
o
c
ia
ła
sp
o
w
o
d
u
je
z
w
ię
k
sze
n
ie
t
e
m
p
e
ra
tu
ry
1
k
g
c
ia
ła
o
1
K
5
.
M
e
to
d
a
l
in
e
a
ry
za
cj
i
u
k
ła
d
u
s
ta
cj
o
n
a
rn
e
g
o
w
d
o
w
o
ln
y
m
p
u
n
kc
ie
x
0
m
o
że
b
y
ć
za
st
o
so
w
a
n
a
d
la
u
k
ła
d
u
a
.
z
re
g
u
lato
re
m
p
rz
e
k
aź
n
ik
o
w
y
m
b
.
z
te
rm
o
stat
e
m
z
h
is
te
re
zą
c.
o
p
is
an
e
g
o
r
ó
w
n
an
ie
m
:
y
=
7
e
x+1
(
y
-
s
y
g
n
ał
w
y
jś
ci
o
w
y
,
x
–
s
y
g
n
ał
w
e
jś
ci
o
w
y
)
d
.
o
p
is
an
e
g
o
r
ó
w
n
an
ie
m
:
y
=|
x|
(
y
-
s
y
g
n
ał
w
y
jś
ci
o
w
y
,
x
–
s
y
g
n
ał
w
e
jś
ci
o
w
y
)
6
.
O
d
p
o
w
ie
d
zi
ą
w
s
ta
n
ie
u
st
a
lo
n
y
m
,
st
a
cj
o
n
a
rn
e
g
o
,
li
n
io
w
e
g
o
u
kł
a
d
u
d
y
n
a
m
ic
zn
e
g
o
n
a
p
o
b
u
d
ze
n
ie
s
in
u
so
id
a
ln
e
j
e
st
z
a
w
sz
e
a
.
sy
g
n
ał
s
in
u
so
id
al
n
y
o
t
e
j
sa
m
e
j
am
p
li
tu
d
zi
e
c
o
s
y
g
n
ał
w
e
jś
ci
o
w
y
le
cz
in
n
e
j
faz
ie
b
.
sy
g
n
ał
s
in
u
so
id
al
n
y
o
t
e
j
sa
m
e
j
am
p
li
tu
d
zi
e
c
o
s
y
g
n
ał
w
e
jś
ci
o
w
y
o
raz
t
e
j
sa
m
e
j
fa
zi
e
c.
sy
g
n
ał
s
in
u
so
id
al
n
y
o
t
e
j
sa
m
e
j
p
u
ls
a
cj
i
i
faz
ie
c
o
s
y
g
n
a
ł
w
e
jś
ci
o
w
y
d
.
sy
g
n
ał
s
in
u
so
id
al
n
y
o
a
m
p
li
tu
d
zi
e
i
f
az
ie
z
al
e
żn
e
j
o
d
tr
an
sm
itan
cj
i w
id
m
o
w
e
j
u
k
ła
d
u
7
.
O
u
kł
a
d
zi
e
l
in
io
w
y
m
m
ó
w
im
y
,
że
j
e
st
t
o
ta
ln
ie
s
ta
b
il
n
y
g
d
y
:
a
.
je
g
o
o
d
p
o
w
ie
d
ź
n
a
d
o
w
o
ln
y
s
y
g
n
a
ł
o
o
g
ran
ic
zo
n
e
j
w
a
rto
śc
i j
e
st
r
ó
w
n
ie
ż
o
g
ran
ic
zo
n
a
b
.
w
szy
st
k
ie
w
y
stę
p
u
jąc
e
w
n
im
s
y
g
n
ał
y
są
o
g
ran
ic
zo
n
e
,
je
śl
i
sy
g
n
ał
y
w
e
jś
ci
o
w
e
s
ą
o
g
ran
ic
zo
n
e
c.
b
ie
g
u
n
y
j
e
g
o
t
ran
sm
itan
cj
i z
n
a
jd
u
ją
si
ę
w
le
w
e
j,
o
tw
ar
te
j
p
ó
łp
łas
zc
zy
źn
ie
d
.
w
szy
st
k
ie
w
sp
ó
łc
zy
n
n
ik
i w
ie
lo
m
ian
u
m
ian
o
w
n
ik
a
je
g
o
t
ran
sm
itan
cj
i m
a
ją
te
n
s
a
m
zn
ak
8
.
W
y
st
ą
p
ie
n
ie
w
ie
rs
za
s
a
m
y
ch
z
e
r
w
t
a
b
li
cy
R
o
u
th
a
-H
u
rw
it
za
ś
w
ia
d
cz
y
o
t
y
m
,
że
a
.
tr
an
sm
it
an
cj
a
u
k
ład
u
p
o
si
a
d
a
ze
ra
n
a
o
si
u
ro
jo
n
e
j
b
.
n
as
tąp
ił
a
ko
m
p
e
n
sac
ja
ze
r
tr
an
sm
it
an
cj
i
u
k
ład
u
z
b
ie
g
u
n
am
i
c.
o
s
tab
il
n
o
śc
i
u
kł
ad
u
d
e
cy
d
u
ją
m
ie
js
ca
ze
ro
w
e
w
ie
lo
m
ian
u
p
o
m
o
cn
ic
ze
g
o
d
.
w
ie
lo
m
ian
p
o
m
o
cn
ic
zy
p
o
si
ad
a
m
ie
js
ca
ze
ro
w
e
n
a
o
si
u
ro
jo
n
e
j
9
.
O
s
zy
b
ko
śc
i
n
a
ra
st
a
n
ia
o
d
p
o
w
ie
d
zi
j
e
d
n
o
st
ko
w
e
j
u
k
ła
d
u
I
I
rz
ę
d
u
o
b
ie
g
u
n
a
ch
z
e
sp
o
lo
n
y
ch
sp
rz
ę
żo
n
y
ch
d
e
cy
d
u
je
a
.
czę
ść
r
ze
czy
w
is
ta
b
ie
g
u
n
ó
w
u
k
ład
u
b
.
czę
ść
u
ro
jo
n
a
b
ie
g
u
n
ó
w
u
kł
ad
u
c.
m
o
d
u
ł
b
ie
g
u
n
ó
w
u
k
ład
u
d
.
ar
g
u
m
e
n
t
b
ie
g
u
n
ó
w
u
k
ład
u
1
0
.
C
zę
ść
li
n
ii
p
ie
rw
ia
st
ko
w
y
ch
d
ą
ży
d
o
a
sy
m
p
to
t
d
la
w
zm
o
cn
ie
n
ia
d
ą
żą
ce
g
o
d
o
n
ie
sko
ń
cz
o
n
o
śc
i
g
d
y
a
.
li
czb
a
b
ie
g
u
n
ó
w
j
e
st
w
ię
k
sza
o
d
l
ic
zb
y
ze
r
b
.
li
czb
a
b
ie
g
u
n
ó
w
j
e
st
r
ó
w
n
a
li
czb
ie
ze
r
c.
u
k
ład
j
e
st
n
ie
st
ab
il
n
y
d
.
is
tn
ie
je
tak
a
w
ar
to
ść
w
zm
o
cn
ie
n
ia,
że
w
tab
li
cy
R
o
u
th
a
w
ie
lo
m
ian
u
u
k
ład
u
zam
k
n
ię
te
g
o
w
y
stąp
i
rzą
d
s
am
yc
h
z
e
r
1
1
.
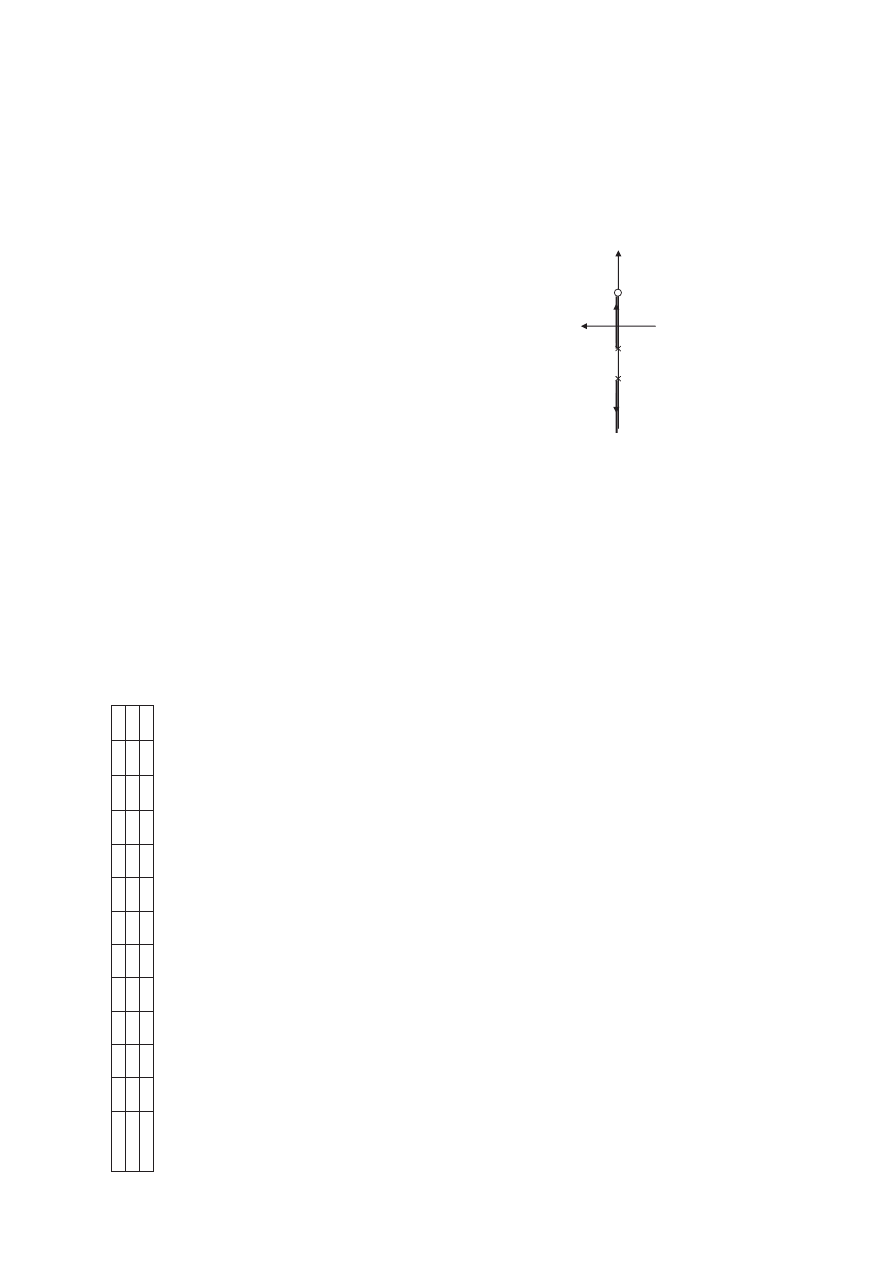
N
a
ry
su
n
ku
p
rz
e
d
st
a
w
io
n
o
li
n
ie
p
ie
rw
ia
st
ko
w
e
p
e
w
n
e
g
o
u
kł
a
d
u
.
M
o
że
m
y
o
n
im
p
o
w
ie
d
zi
e
ć,
ż
e
:
a
.
u
k
ład
t
e
n
j
e
st
s
tab
il
n
y
d
la
d
o
w
o
ln
e
g
o
k
b
.
w
u
k
ład
zi
e
t
ym
n
ie
w
y
stąp
ią
p
rz
e
re
g
u
lo
w
an
ia
c.
w
raz
ze
w
zr
o
st
e
m
w
zm
o
cn
ie
n
ia
ro
śn
ie
s
zy
b
ko
ść
u
k
ład
u
d
.
d
la
w
ar
to
śc
i
w
zm
o
cn
ie
n
ia
d
ąż
ąc
y
ch
d
o
n
ie
sk
o
ń
czo
n
o
śc
i
o
d
p
o
w
ie
d
ź
im
p
u
ls
o
w
a
u
k
ład
u
m
a
c
h
ar
ak
te
r
n
ar
as
ta
jąc
y
ch
d
rg
ań
1
2
.
C
zy
n
n
ik
(0
.1
s+1
)
zn
a
jd
u
ją
cy
s
ię
w
m
ia
n
o
w
n
iku
p
e
w
n
e
j
tr
a
n
sm
it
a
n
cj
i
n
a
a
sy
m
p
to
ty
cz
n
y
ch
ch
a
ra
kt
e
ry
st
y
ka
ch
c
zę
st
o
tl
iw
o
śc
io
w
y
ch
B
o
d
e
g
o
d
la
p
u
ls
a
cj
i
ω
>
1
0
0
se
k
-1
w
p
ro
w
a
d
zi
a
.
p
rz
e
su
n
ię
ci
e
c
h
a
ra
k
te
ry
st
yk
i
faz
o
w
e
j
o
-
9
0
°
b
.
p
rz
e
su
n
ię
ci
e
c
h
a
ra
k
te
ry
st
y
k
i
faz
o
w
e
j
o
-
4
5
°
c.
w
zr
o
st
w
zm
o
cn
ie
n
ia
z
sz
y
b
k
o
śc
ią
2
0
d
B/
d
e
k
d
.
sp
a
d
e
k
w
zm
o
cn
ie
n
ia
o
3
d
B
Im
R
e