1

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Organizacja i Architektura

Komputerów

Pamięć cache

2

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

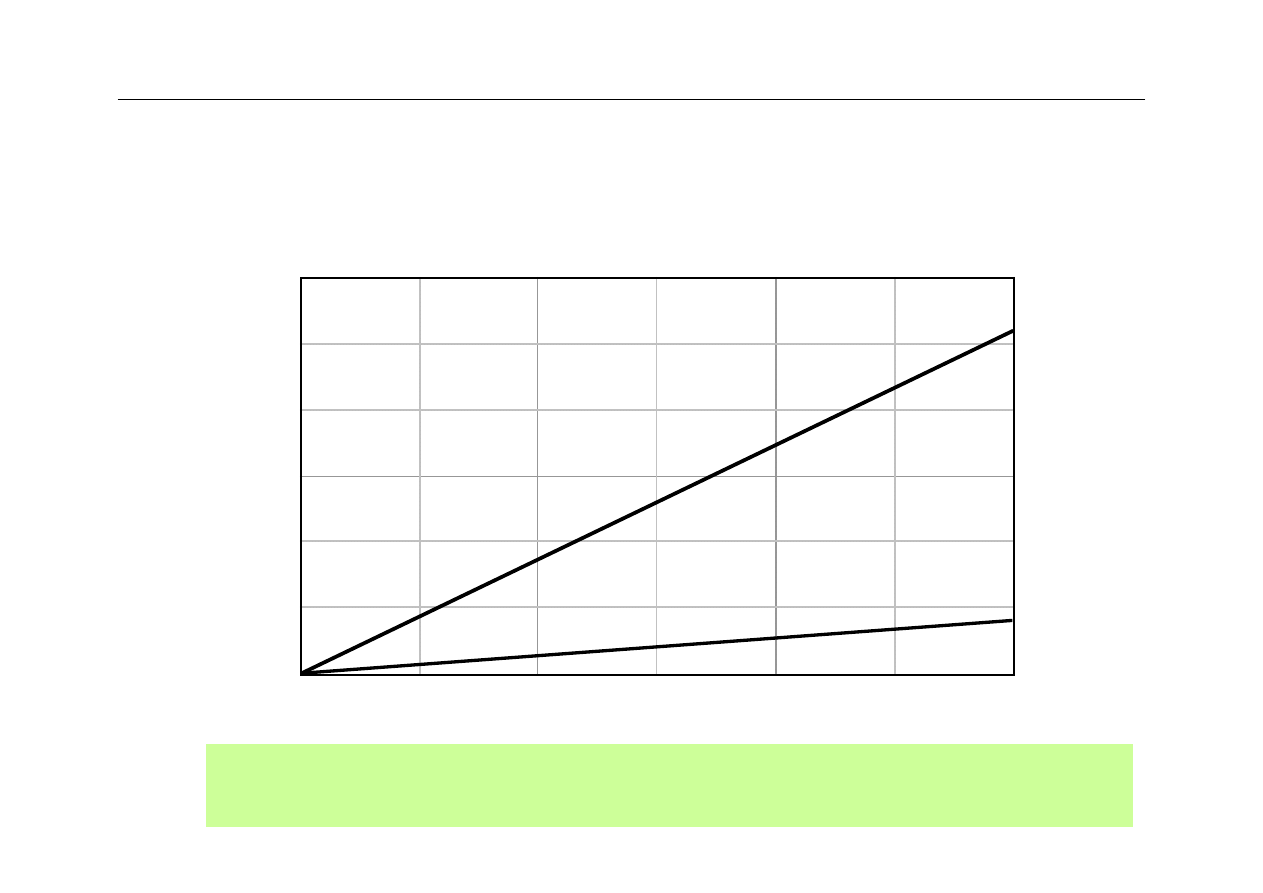
Wydajność: CPU i pamięć

Memory density and capacity have grown along with the CPU
power and complexity, but memory speed has not kept pace.

1990

1980 2000

2010

1

10

10

R

e

la

ti

ve

per

for

m

a

nc

e

Calendar year

Processor

Memory

3

6

3

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

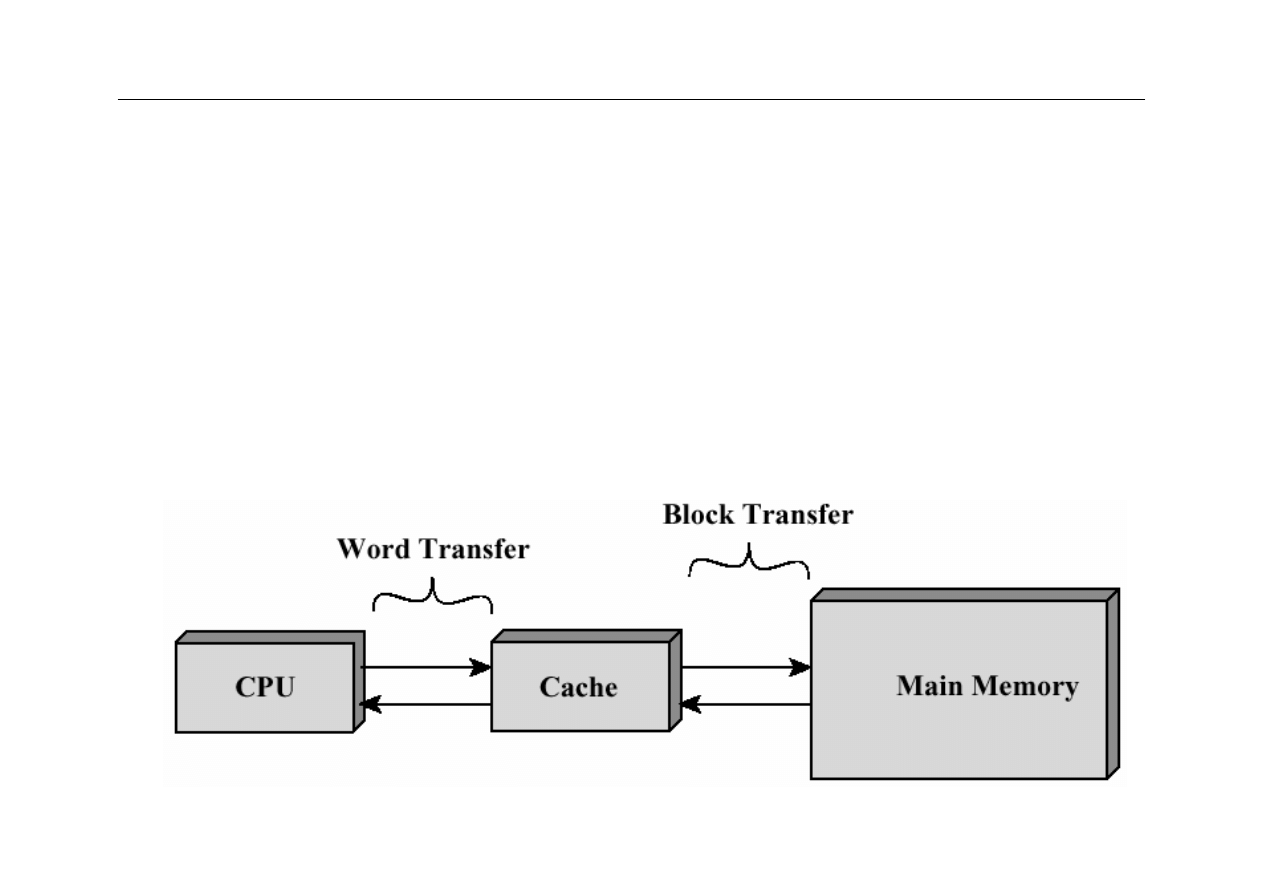
Pamięć cache – koncepcja

z

niewielka, ale szybka pamięć RAM

z

umieszczona między CPU a pamięcią główną
(operacyjną)

z

może być umieszczona w jednym układzie scalonym z
CPU lub poza CPU

4

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

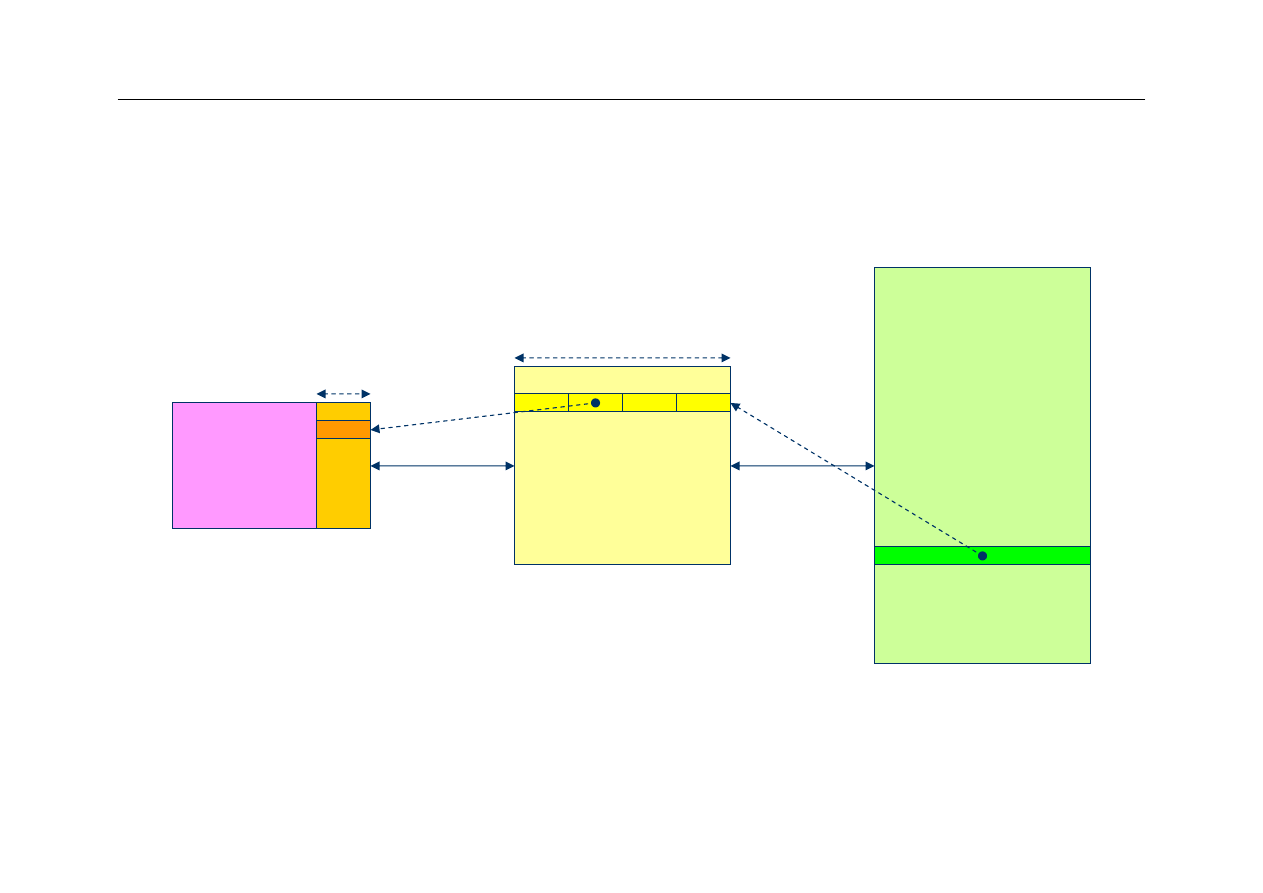
Pamięć cache – koncepcja

CPU

Cache

(fast)

memory

Main

(slow)

memory

Reg

file

Cache is transparent to user;
transfers occur automatically

Line

Word

5

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

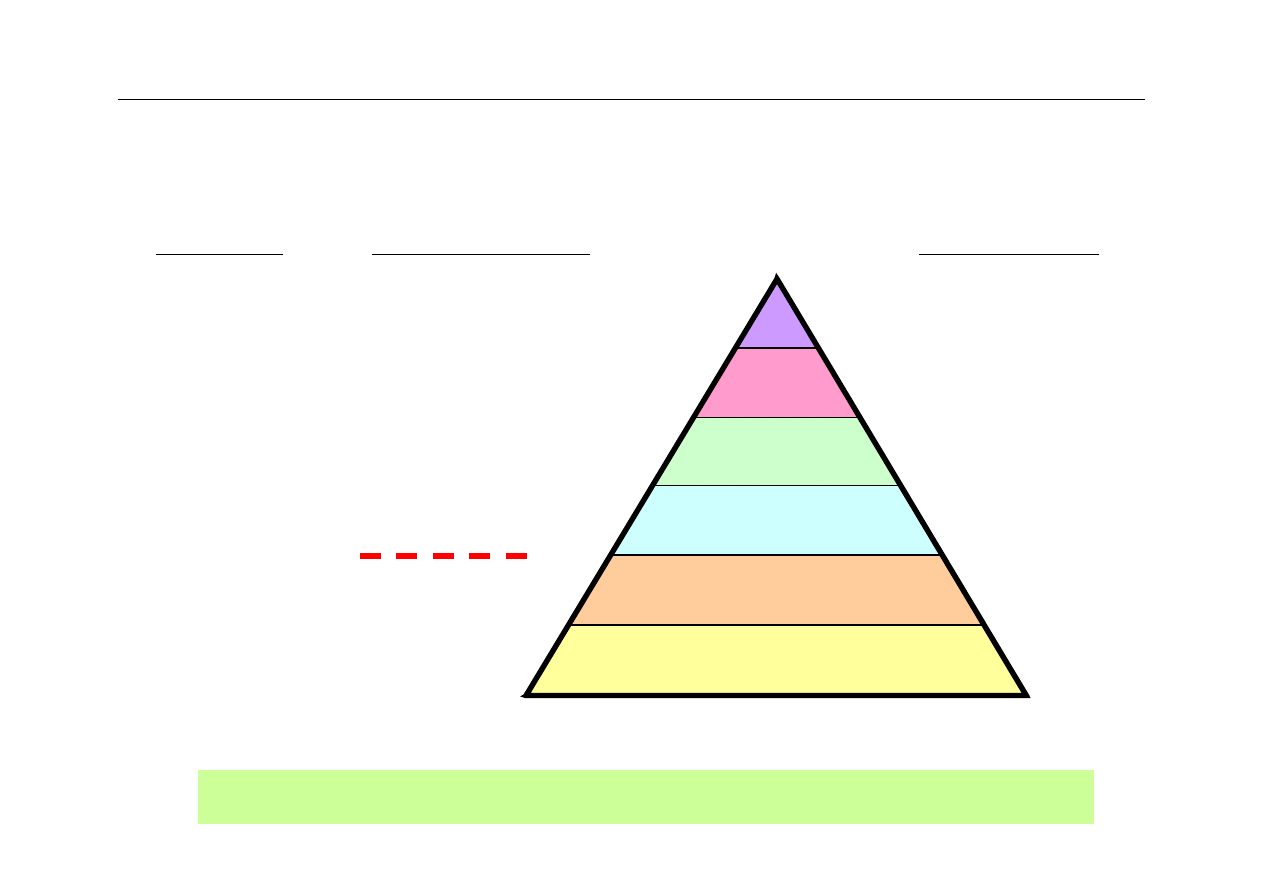
Hierarchiczny system pamięci

Tertiary

Secondary

Main

Cache 2

Cache 1

Reg’s

$Millions

$100s Ks

$10s Ks

$1000s

$10s

$1s

Cost per GB

Access latency

Capacity

TBs

10s GB

100s MB

MBs

10s KB

100s B

min+

10s ms

100s ns

10s ns

a few ns

ns

Speed

gap

Names and key characteristics of levels in a memory hierarchy.

6

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

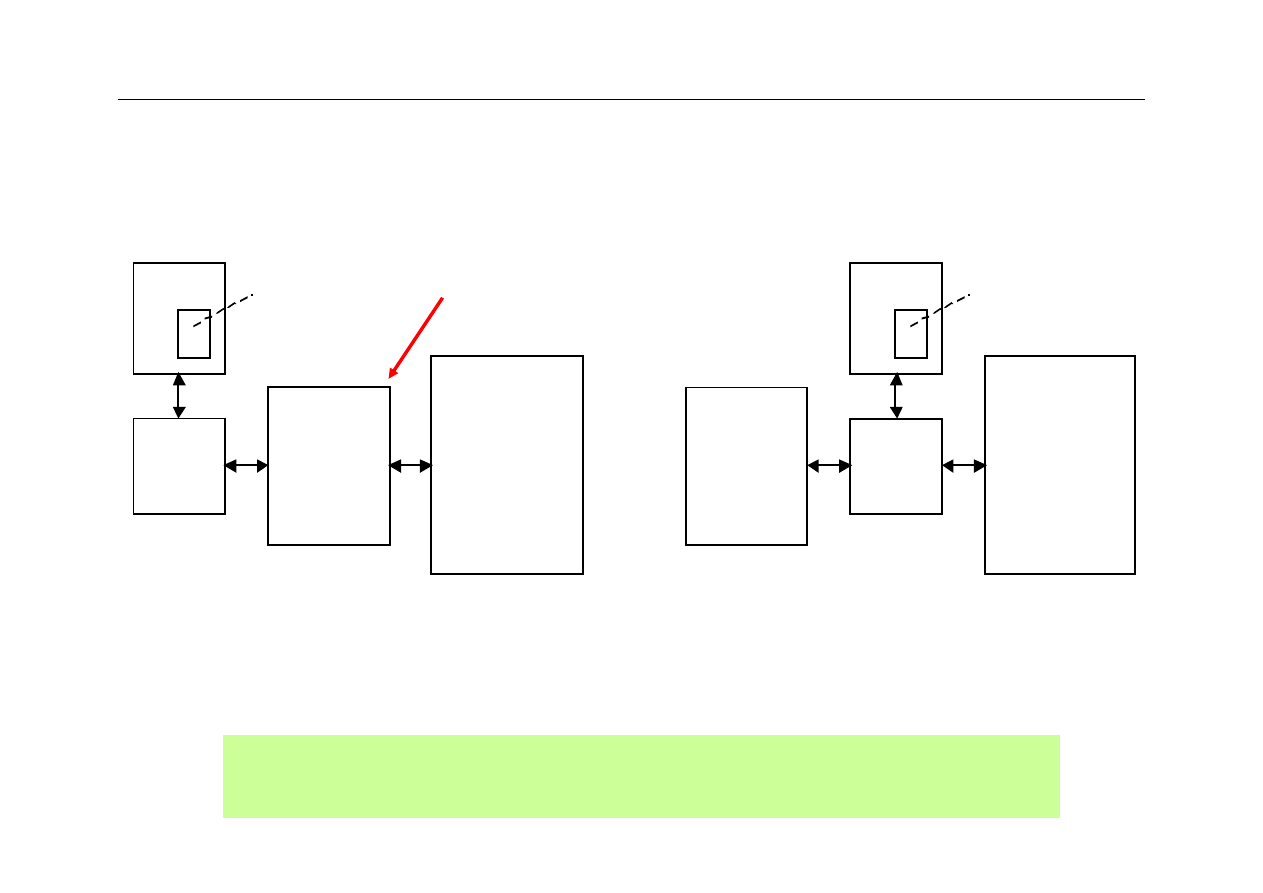
Połączenie CPU z cache

Level-2

cache

Main

memory

CPU

CPU

registers

Level-1

cache

Level-2

cache

Main

memory

CPU

CPU

registers

Level-1

cache

(a) Level 2 between level 1 and main

(b) Level 2 connected to “backside” bus

Cleaner and
easier to analyze

Cache memories act as intermediaries between the superfast
processor and the much slower main memory.

7

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Działanie pamięci cache

z

CPU żąda odczytu pamięci

z

sprawdza się, czy potrzebne dane znajdują się

w cache

z

jeśli tak, następuje szybki odczyt z cache

z

jeśli nie, przesyła się potrzebny blok danych z

pamięci głównej do cache

z

następnie żądane dane są przesyłane do CPU

z

pamięć cache jest wyposażona w znaczniki

(tags) pozwalające ustalić, które bloki pamięci

głównej są aktualnie dostępne w pamięci cache

8

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Zasady lokalności

z

Lokalność w sensie czasu:

jeśli CPU odwołuje się

do określonej komórki pamięci, jest
prawdopodobne, że w najbliższej przyszłości
nastąpi kolejne odwołanie do tej komórki

z

Lokalność w sensie przestrzeni adresowej:

jeśli

CPU odwołuje się do określonej komórki pamięci,
jest prawdopodobne, że w najbliższej przyszłości
nastąpi odwołanie do sąsiednich komórek pamięci

9

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Terminologia

z

cache hit

(trafienie): sytuacja, gdy żądana

informacja znajduje się w pamięci cache

wyższego poziomu

z

cache miss

(chybienie, brak trafienia): sytuacja,

gdy żądanej informacji nie ma w pamięci cache

wyższego poziomu

z

line, slot

(linijka, wiersz, blok): najmniejsza

porcja (kwant) informacji przesyłanej między

pamięcią cache, a pamięcią wyższego poziomu.

Najczęściej stosuje się linijki o wielkości 32

bajtów

10

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Terminologia

cd.

z

hit rate

(współczynnik trafień): stosunek liczby

trafień do łącznej liczby odwołań do pamięci

z

miss rate

(współczynnik chybień): 1 – hit rate

z

hit time

(czas dostępu przy trafieniu): czas

dostępu do żądanej informacji w sytuacji gdy

wystąpiło trafienie. Czas ten składa się z dwóch

elementów:

–

czasu potrzebnego do ustalenia, czy żądana

informacja jest w pamięci cache

–

czasu potrzebnego do przesłania informacji z

pamięci cache do procesora

11

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Terminologia

cd.

z

miss penalty

(kara za chybienie): czas potrzebny

na wymianę wybranej linijki w pamięci cache i
zastąpienie jej taką linijką z pamięci głównej,
która zawiera żądaną informację

z

czas

hit time

jest znacznie krótszy od czasu

miss penalty

(w przeciwnym przypadku

stosowanie pamięci cache nie miałoby sensu!)

12

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Problemy

z

W jaki sposób ustalić, czy żądana informacja znajduje
się w pamięci cache?

z

Jeśli już ustalimy, że potrzebna informacja jest w
pamięci cache, w jaki sposób znaleźć ją w tej pamięci
(jaki jest jej adres?)

z

Jeśli informacji nie ma w pamięci cache, to do jakiej
linijki ją wpisać z pamięci głównej?

z

Jeśli cache jest pełna, to według jakiego kryterium
usuwać linijki aby zwolnić miejsce na linijki sprowadzane
z pamięci głównej?

z

W jaki sposób inicjować zawartość pamięci cache?

13

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Odwzorowanie bezpośrednie

z

direct-mapped cache

z

każdy blok (linijka) w pamięci głównej jest
odwzorowywana (przyporządkowana) tylko
jednej linijce w pamięci cache

z

ponieważ cache jest znacznie mniejsza od
pamięci głównej, wiele różnych linijek pamięci
głównej jest odwzorowanych na tą samą linijkę
w cache

14

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Funkcja odwzorowująca

z

Najprostsza metoda odwzorowania polega na
wykorzystaniu najmniej znaczących bitów
adresu

z

Na przykład, wszystkie linijki w pamięci głównej,
których adresy kończą się sekwencją 000 będą
odwzorowane na tą samą linijkę w pamięci
cache

z

Powyższa metoda wymaga, by rozmiar pamięci
cache (wyrażony w linijkach) był potęgą liczby 2

15

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

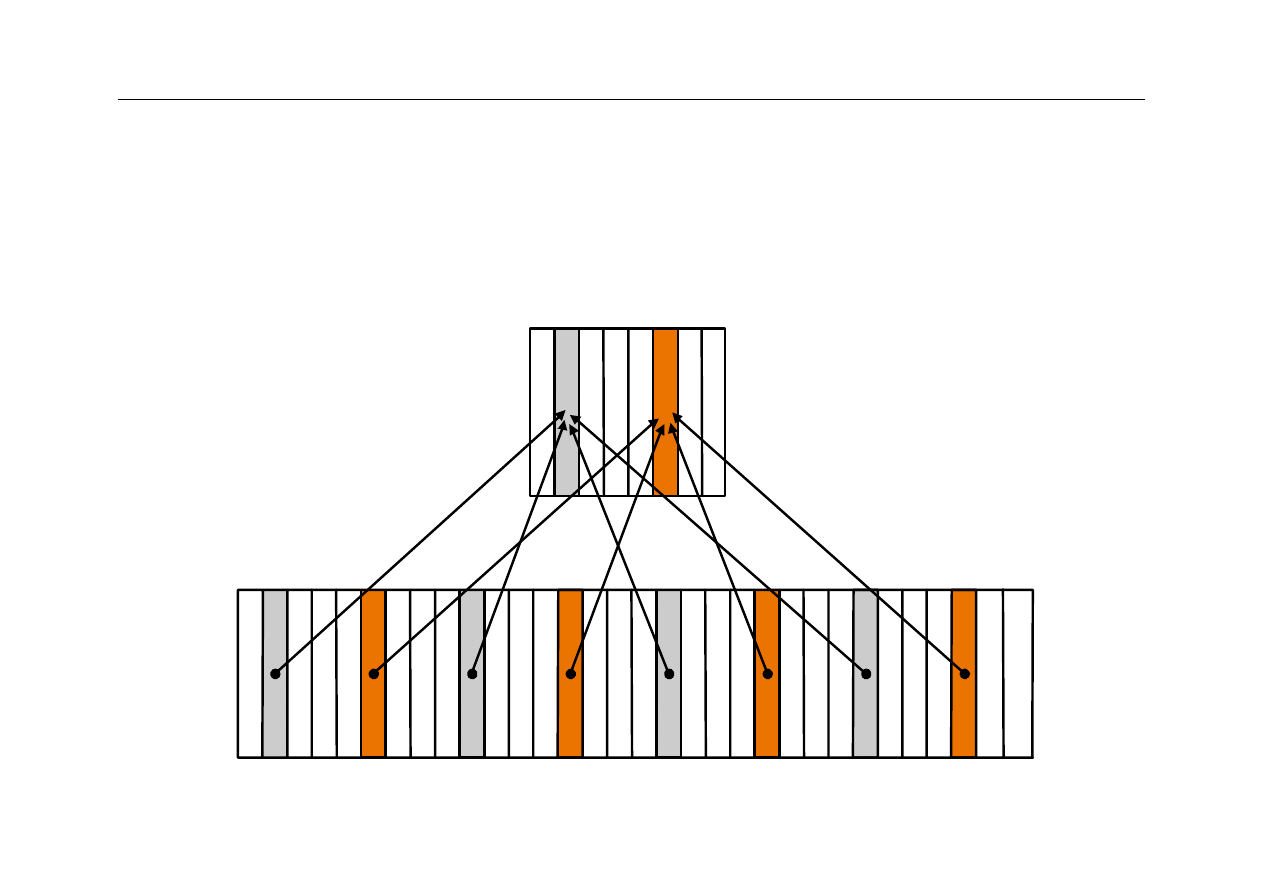
Odwzorowanie bezpośrednie

00001

00101

01001

01101

10001

10101

11001

11101

00

0

Cache

Memory

00

1

010

01

1

10

0

10

1

11

0

111

16

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Co znajduje się w linijce 000?

z

Wciąż nie wiemy, która linijka z pamięci głównej (z wielu

możliwych) znajduje się aktualnie w konkretnej linijce

pamięci cache

z

Musimy zatem zapamiętać adres linijki przechowywanej

aktualnie w linijkach pamięci cache

z

Nie trzeba zapamiętywać całego adresu linijki, wystarczy

zapamiętać tylko tę jego część, która nie została

wykorzystana przy odwzorowaniu

z

Tę część adresu nazywa się znacznikiem (tag)

z

Znacznik związany z każdą linijką pamięci cache

pozwala określić, która linijka z pamięci głównej jest

aktualnie zapisana w danej linijce cache

17

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Znaczniki – ilustracja

Pamięć główna

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

1100

1101

1110

1111

Znaczniki

Dane

18

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Inicjalizacja cache

z

Początkowo pamięć cache jest pusta

–

wszystkie bity w pamięci cache (włącznie z bitami
znaczników) mają losowe wartości

z

Po pewnym czasie pracy systemu pewna część
znaczników ma określoną wartość, jednak
pozostałe są nadal wielkościami losowymi

z

Jak ustalić, które linijki zawierają rzeczywiste
dane, a które nie zostały jeszcze zapisane?

19

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Bit ważności

(valid bit)

z

Należy dodać przy każdej linijce pamięci cache
dodatkowy bit, który wskazuje, czy linijka zawiera ważne
dane, czy też jej zawartość jest przypadkowa

z

Na początku pracy systemu bity ważności są zerowane,
co oznacza, że pamięć cache nie zawiera ważnych
danych

z

Przy odwołaniach CPU do pamięci, w trakcie
sprawdzania czy potrzebne dane są w cache należy
ignorować linijki z bitem ważności równym 0

z

Przy zapisie danych z pamięci głównej do pamięci cache
należy ustawić bit ważności linijki

20

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Rewizyta w cache

Memory

Valid

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

1100

1101

1110

1111

Tags

Data

21

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

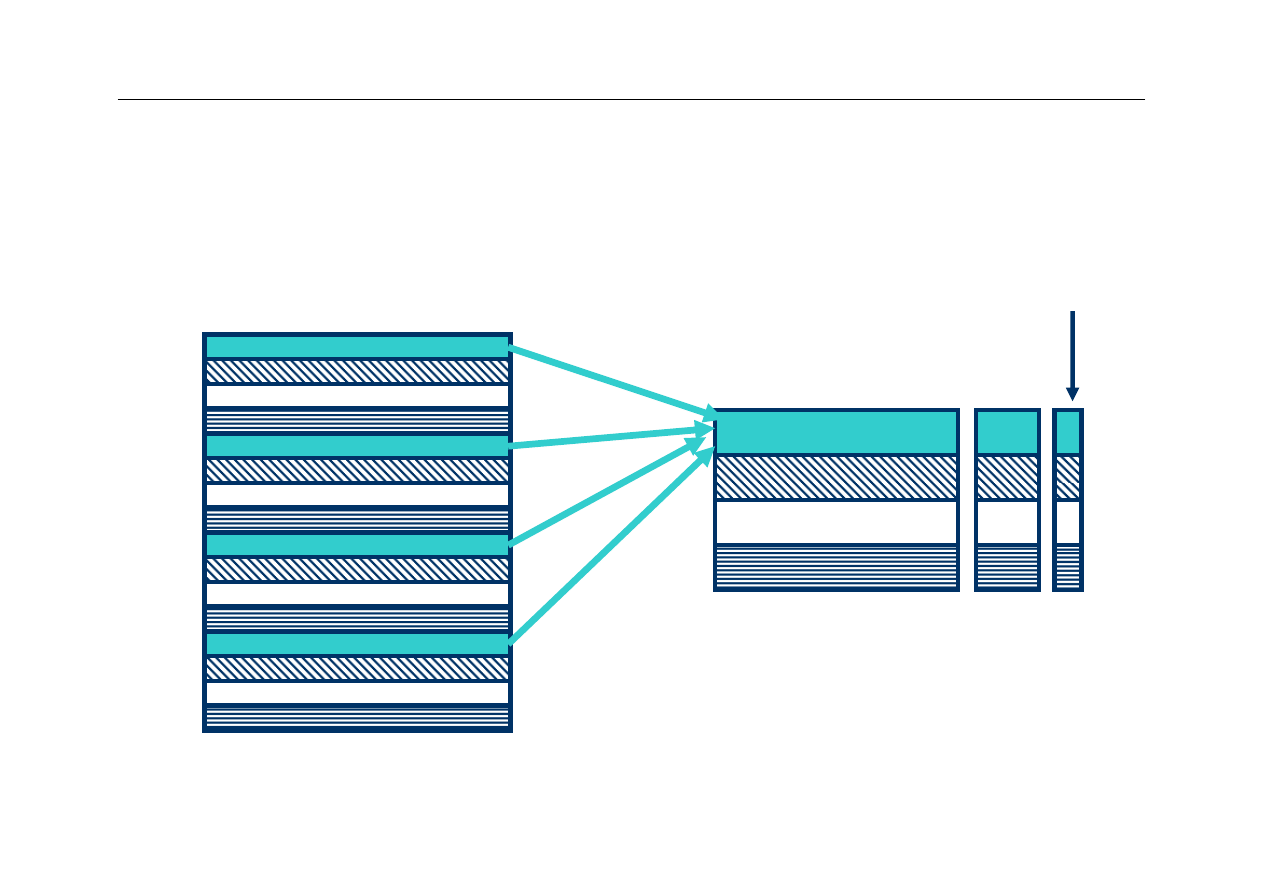
Prosta symulacja cache

z

Użyjemy prostej struktury z pamięcią cache L1
zbudowaną tylko z czterech linijek, podobną do
opisanej wcześniej

z

Założymy, że na początku bity ważności zostały
wyzerowane

22

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

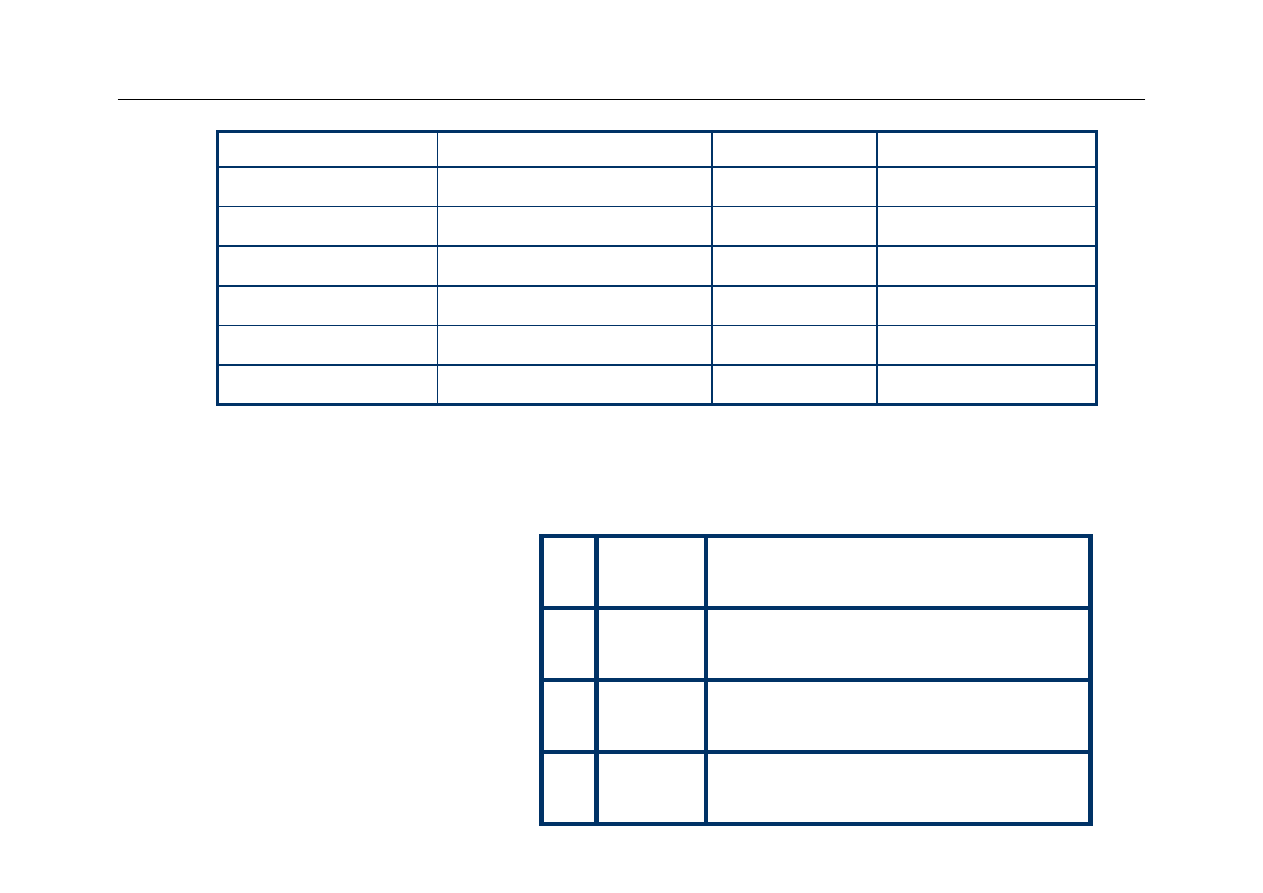
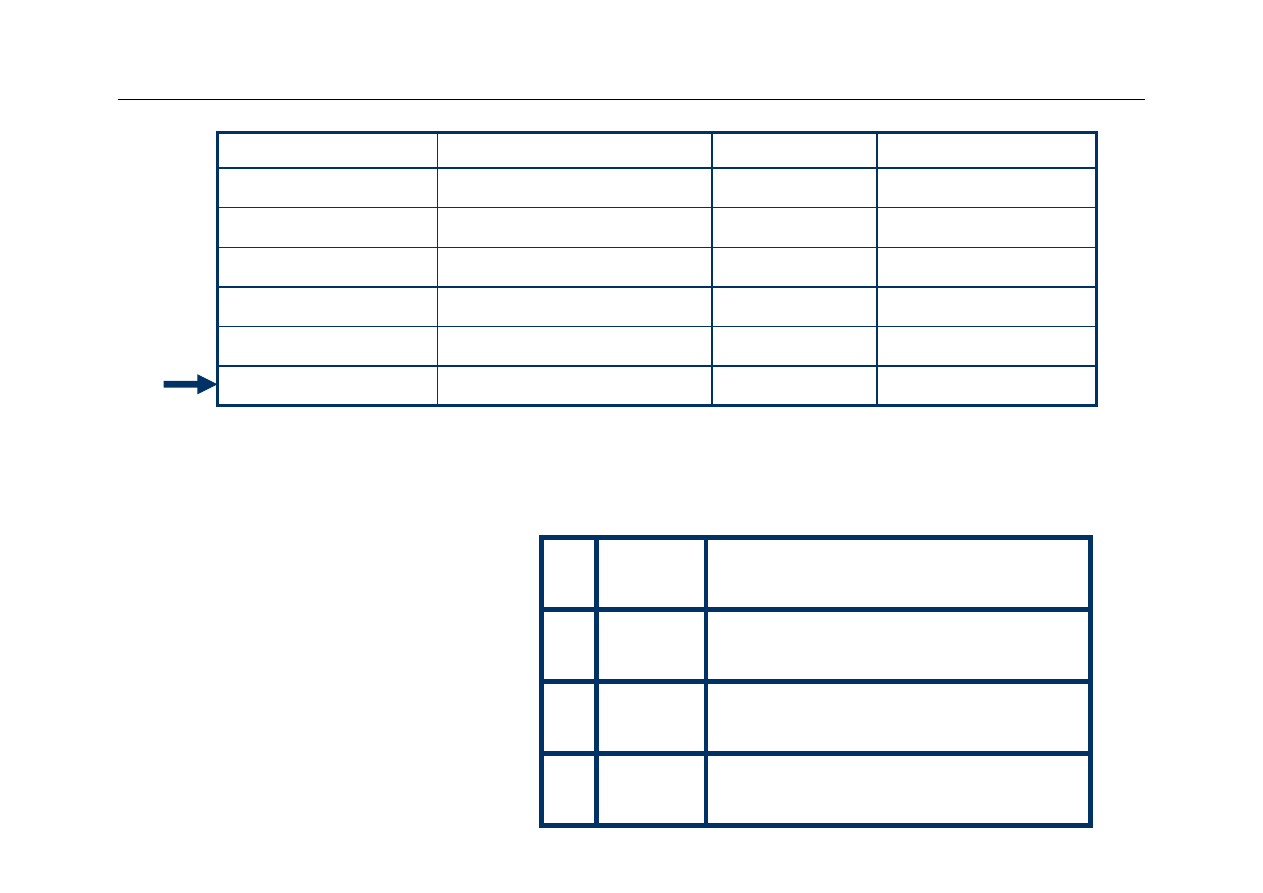
Założenie: sekwencja odwołań CPU

do pamięci

Adres

Adres binarny

Linijka

hit / miss

3

0011

11 (3)

8

1000

00 (0)

miss

2

0010

10 (2)

miss

4

0100

00 (0)

miss

3

0011

11 (3)

hit

00 (0)

miss

8

1000

miss

23

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Address

Binary Address

Slot

hit or miss

3

0011

11 (3)

8

1000

00 (0)

miss

2

0010

10 (2)

miss

4

0100

00 (0)

miss

3

0011

11 (3)

hit

00 (0)

miss

8

1000

miss

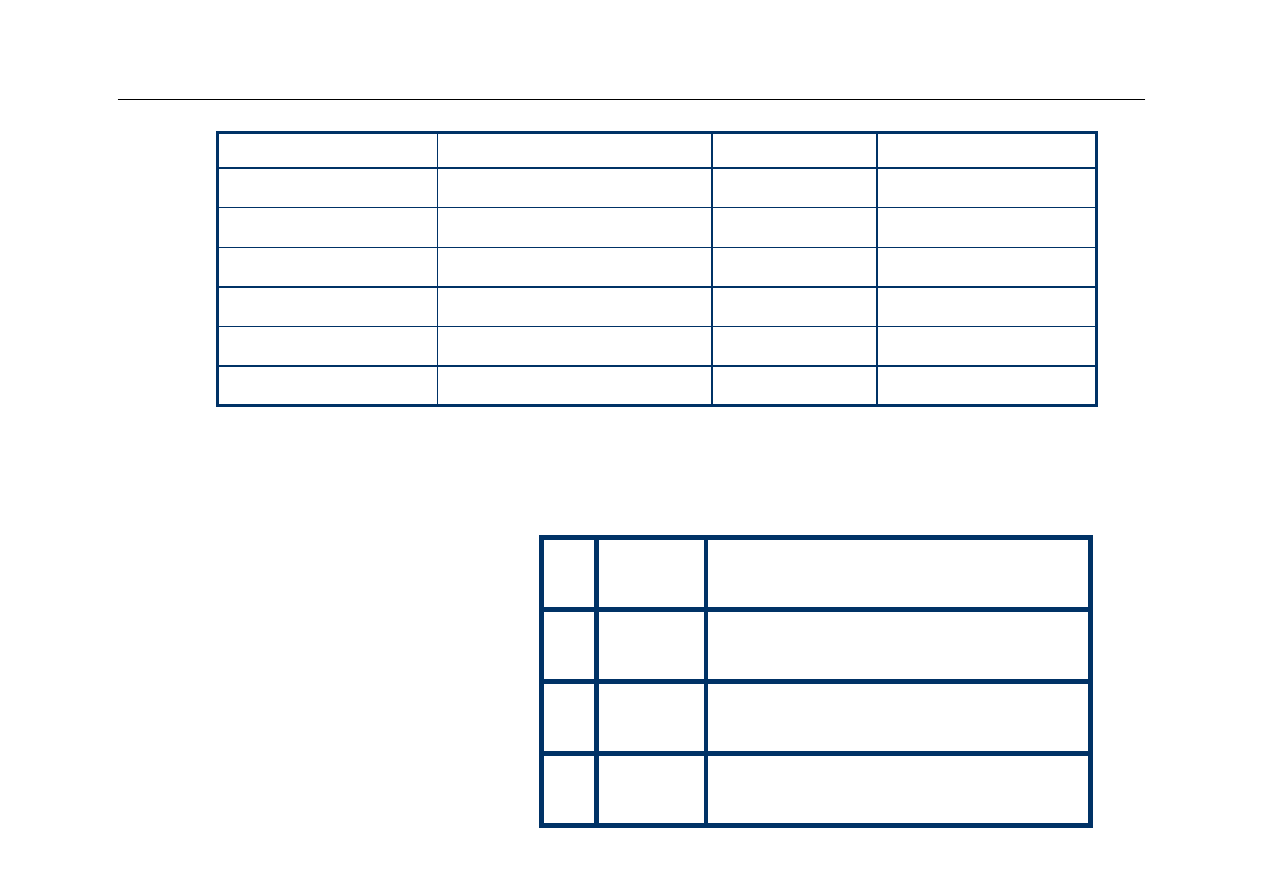
Slot

Tag

Data

V

00

01

10

11

24

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Address

Binary Address

Slot

hit or miss

3

0011

11 (3)

8

1000

00 (0)

miss

2

0010

10 (2)

miss

4

0100

00 (0)

miss

3

0011

11 (3)

hit

00 (0)

miss

8

1000

miss

Slot

Tag

Data

V

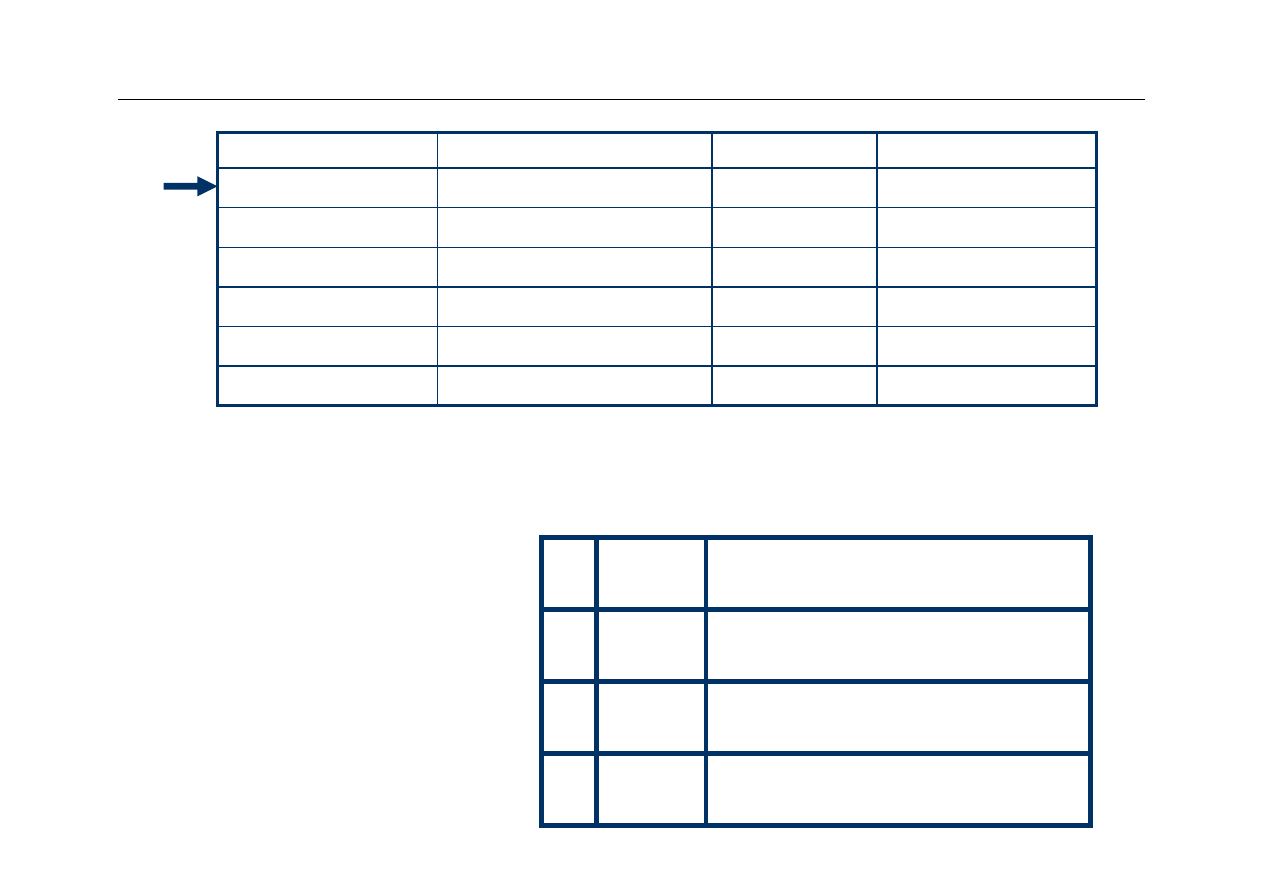
Inicjalizacja

bitów

ważności

00

01

10

11

0

0

0

0

25

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Address

Binary Address

Slot

hit or miss

3

00

11

11

(3)

8

1000

00 (0)

miss

2

0010

10 (2)

miss

4

0100

00 (0)

miss

3

0011

11 (3)

hit

00 (0)

miss

8

1000

miss

Slot

Tag

Data

V

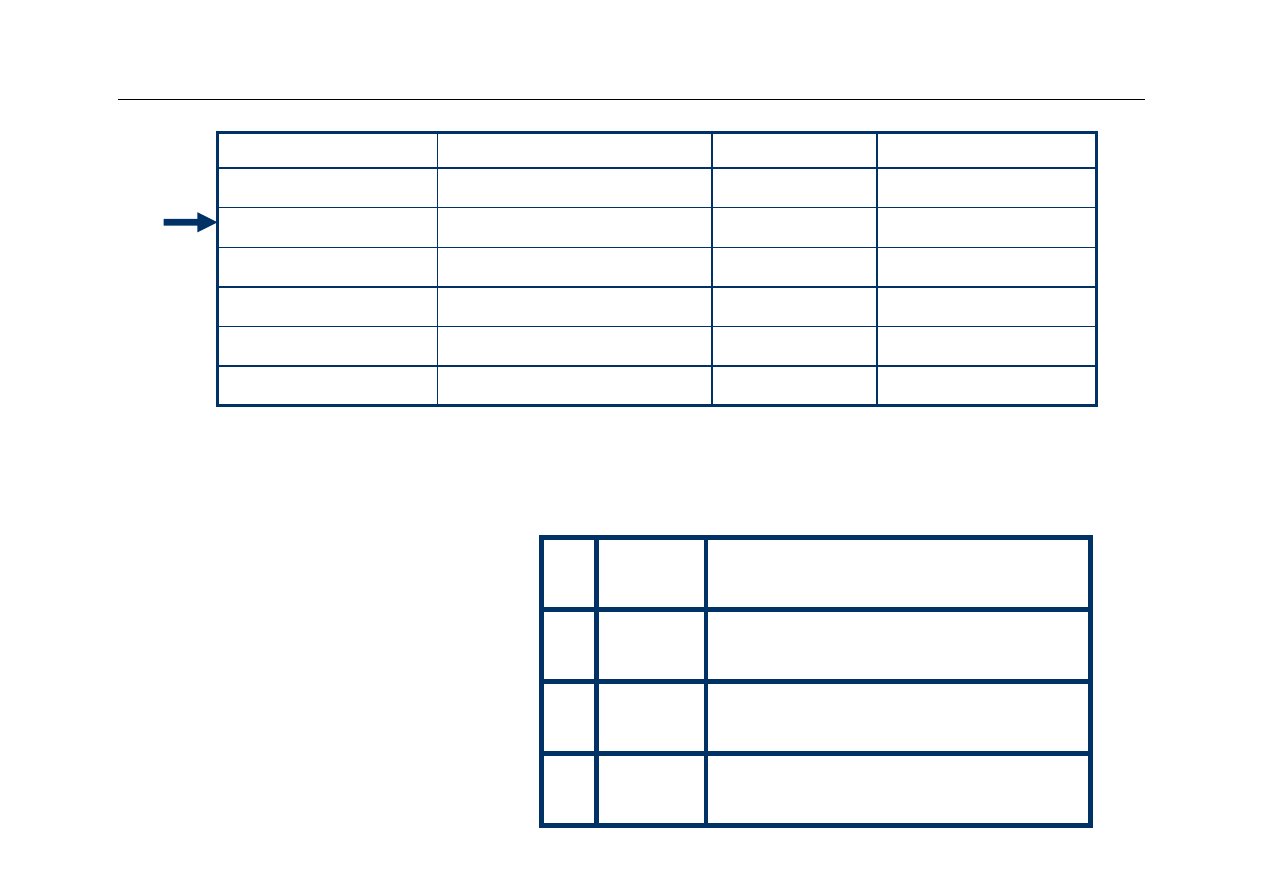
First Access

00

01

10

11

0

0

0

1

00

Mem[3]

26

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Address

Binary Address

Slot

hit or miss

3

0011

11 (3)

8

10

00

00

(0)

miss

2

0010

10 (2)

miss

4

0100

00 (0)

miss

3

0011

11 (3)

hit

00 (0)

miss

8

1000

miss

Slot

Tag

Data

V

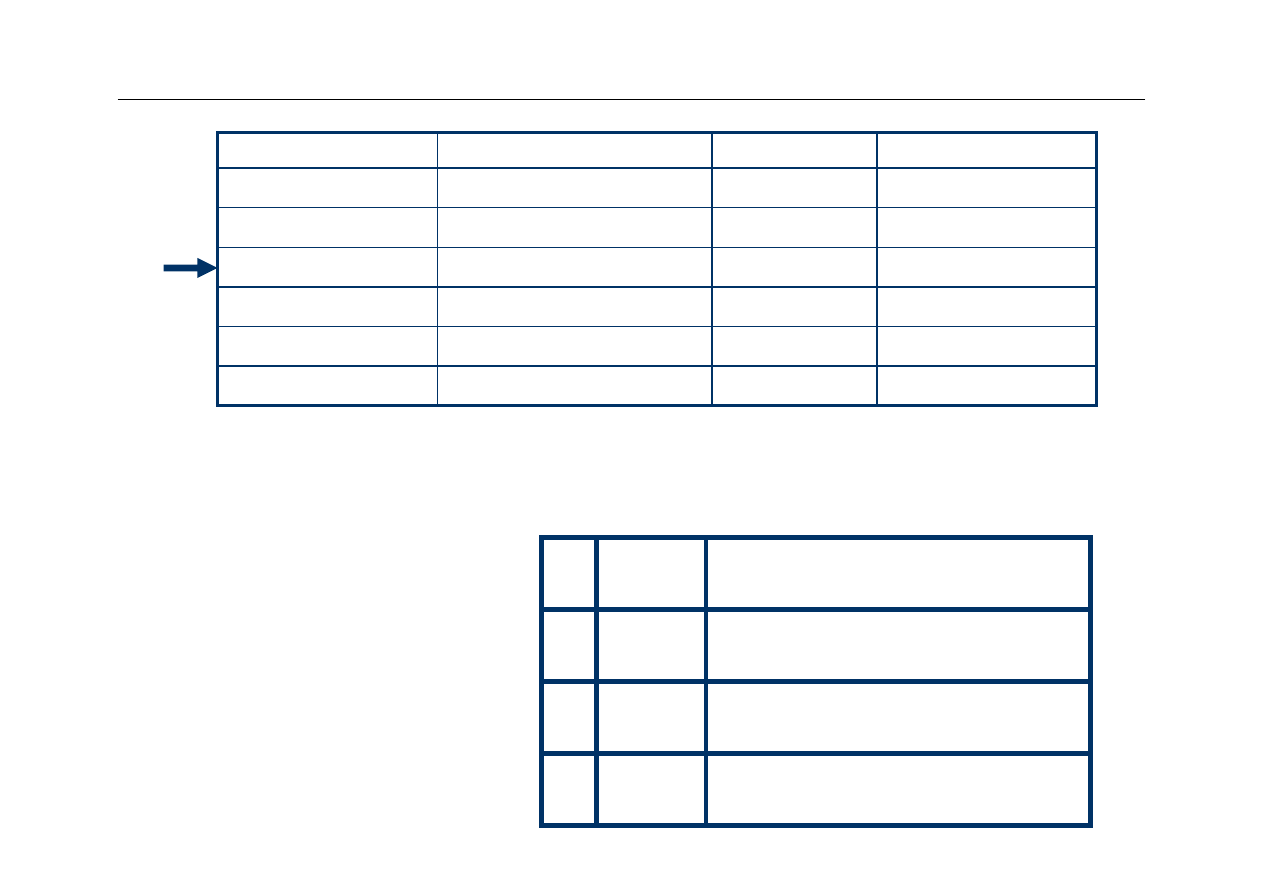
2nd Access

00

01

10

11

1

0

0

1

00 Mem[3]

10

Mem[8]

27

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Address

Binary Address

Slot

hit or miss

3

0011

11 (3)

8

1000

00 (0)

miss

2

0010

10 (2)

miss

4

0100

00 (0)

miss

3

00

11

11

(3)

hit

00 (0)

miss

8

1000

miss

Slot

Tag

Data

V

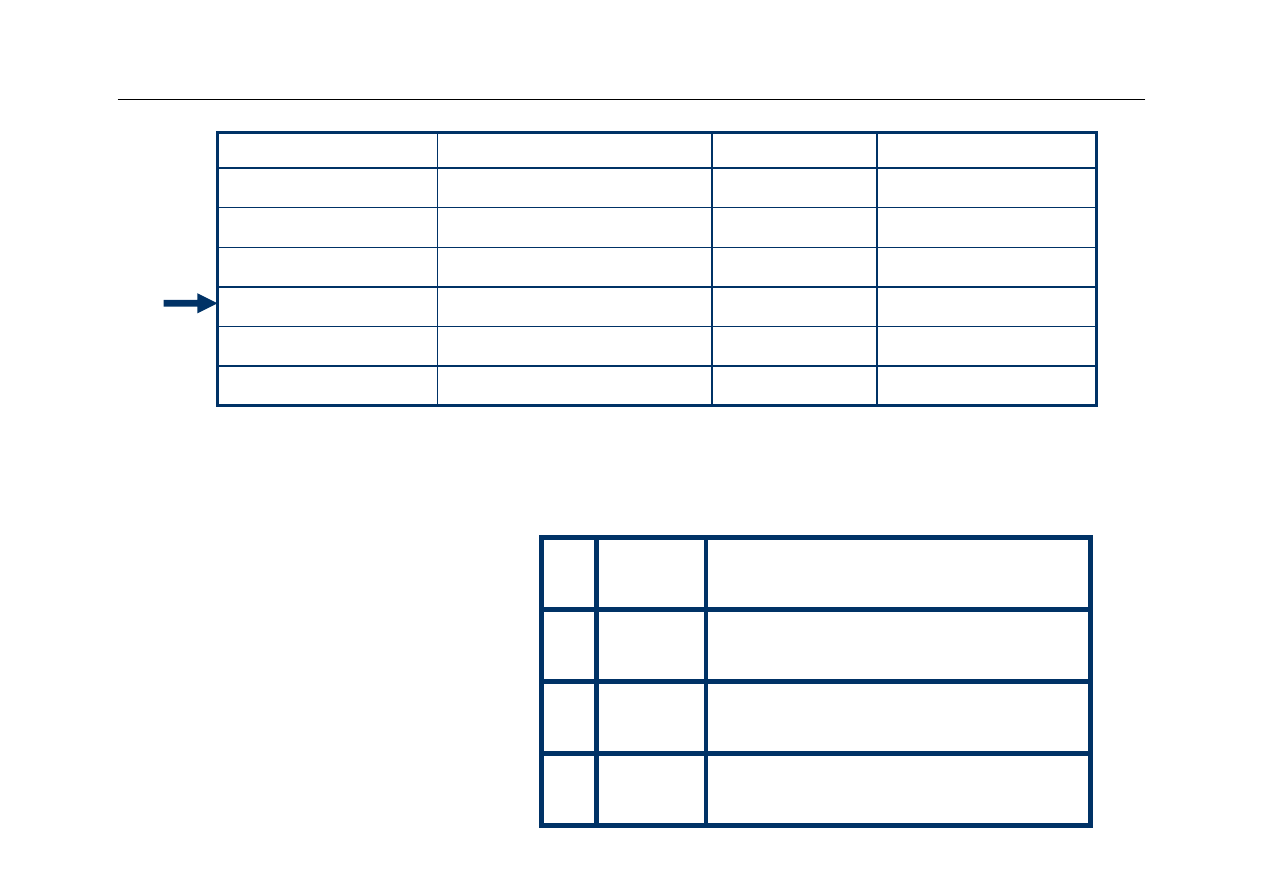
3rd Access

00

01

10

11

1

0

0

1

00

Mem[3]

10 Mem[8]

28

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Address

Binary Address

Slot

hit or miss

3

0011

11 (3)

8

1000

00 (0)

miss

2

00

10

10

(2)

miss

4

0100

00 (0)

miss

3

0011

11 (3)

hit

00 (0)

miss

8

1000

miss

Slot

Tag

Data

V

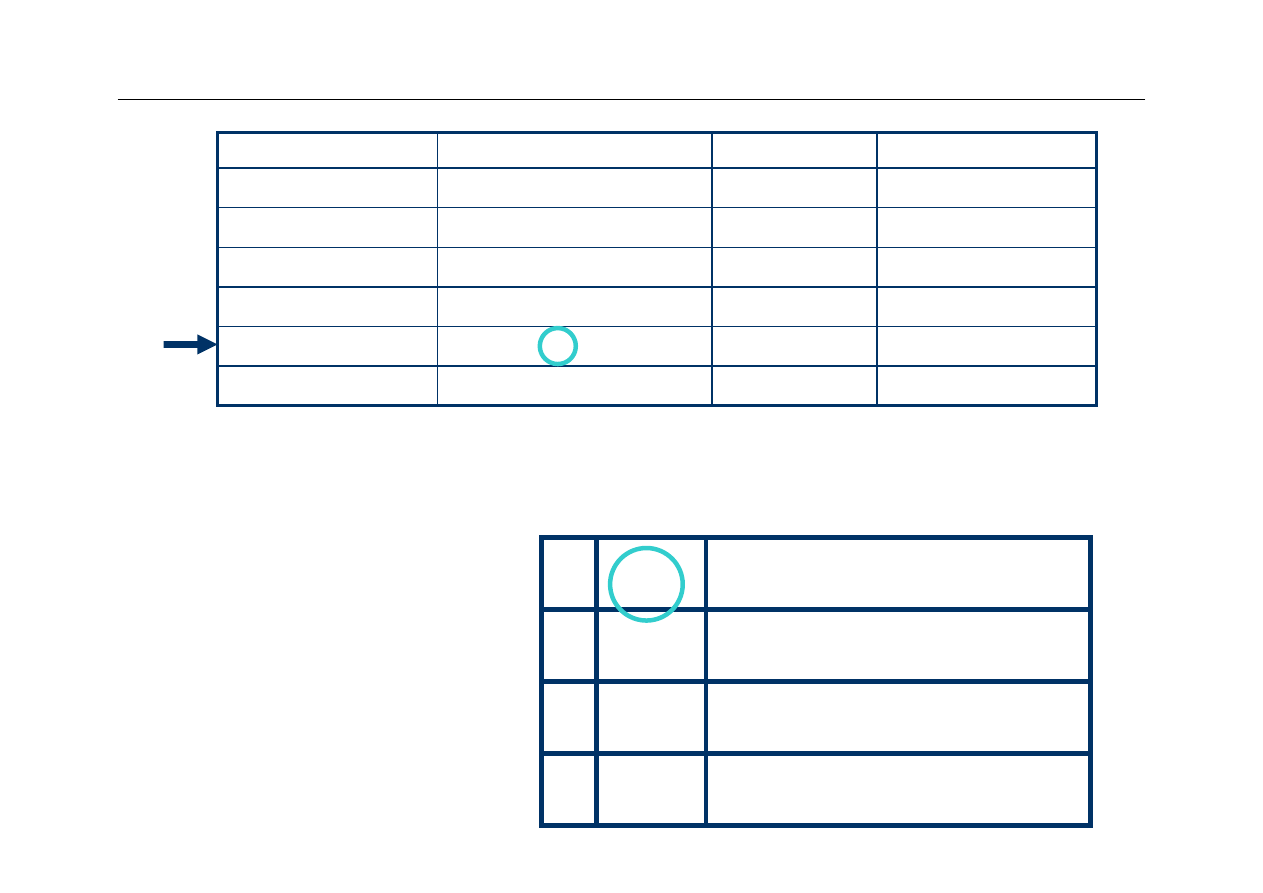
4th Access

00

01

10

11

1

0

1

1

00 Mem[3]

10 Mem[8]

00

Mem[2]

29

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Address

Binary Address

Slot

hit or miss

3

0011

11 (3)

8

1000

00 (0)

miss

2

0010

10 (2)

miss

4

01

00

00

(0)

miss

3

0011

11 (3)

hit

00 (0)

miss

8

1000

miss

Tag

V

Data

Slot

00

01

10

11

1

0

1

1

00 Mem[3]

10

Mem[8]

00 Mem[2]

01

Mem[4]

5th Access

30

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Address

Binary Address

Slot

hit or miss

3

0011

11 (3)

8

1000

00 (0)

miss

2

0010

10 (2)

miss

4

0100

00 (0)

miss

3

0011

11 (3)

hit

00

(0)

miss

8

10

00

miss

Slot

Tag

Data

V

6th Access

01

Mem[4]

00

01

10

11

1

0

1

1

00 Mem[3]

00 Mem[2]

10

Mem[8]

31

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Problem

z

Założenia projektowe:

–

32-bitowe adresy (2

32

bajtów w pamięci głównej, 2

30

słów

4-bajtowych)

–

64 KB cache (16 K słów). Każda linijka przechowuje 1 słowo

–

Odwzorowanie bezpośrednie (Direct Mapped Cache)

z

Ile bitów będzie miał każdy znacznik?

z

Ile różnych linijek z pamięci głównej będzie
odwzorowanych na tę samą linijkę w pamięci cache?

z

Ile bitów będzie zajmować łącznie kompletna linijka w
pamięci cache? (data + tag + valid).

32

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Rozwiązanie

z

Pamięć zawiera 2

30

słów

z

Cache zawiera 16K = 2

14

linijek (słów).

z

Każda linijka może przechowywać jedną z 2

30

/2

14

=

2

16

linijek pamięci głównej, stąd znacznik musi mieć

16 bitów

z

2

16

linijek w pamięci głównej ma łączną pojemność

równą 64K linijek – taki obszar jest
przyporządkowany każdej linijce w pamięci cache

z

Łączna pojemność pamięci cache wyrażona w bitach
wynosi 2

14

x (32+16+1) = 49 x 16K = 784 Kb

(98 KB!)

33

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Problem z zapisem

z

Write through

– zapis jednoczesny: dane są

zapisywane jednocześnie do cache i pamięci głównej.

–

Zaleta:

zapewnienie stałej aktualności danych w pamięci

głównej (memory consistency)

–

Wada:

duży przepływ danych do pamięci

z

Write back

– zapis opóźniony: aktualizuje się tylko

pamięć cache. Fakt ten odnotowuje się w specjalnym
dodatkowym bicie (dirty, updated). Przy usuwaniu
linijki z cache następuje sprawdzenie bitu i
ewentualna aktualizacja linijki w pamięci głównej.

–

Zaleta:

mniejszy przepływ danych do pamięci

–

Wada:

problemy ze spójnością danych w pamięci

34

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

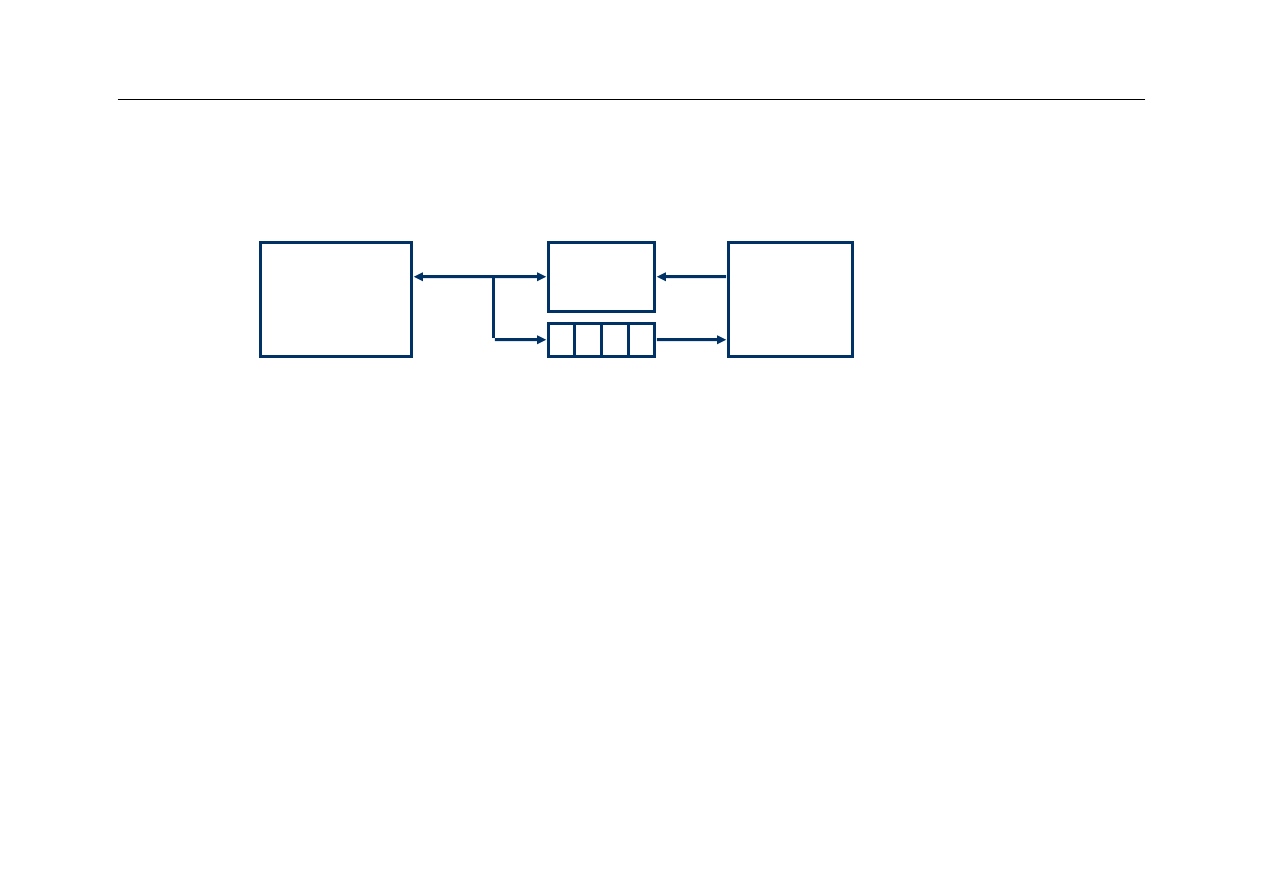
Zapis jednoczesny

(write through)

Procesor

Cache

Write Buffer

DRAM

z

W metodzie

write through

procesor zapisuje dane

jednocześnie do cache i do pamięci głównej

–

w zapisie do pamięci głównej pośredniczy bufor

–

przepisywanie danych z bufora do pamięci głównej obsługuje
specjalizowany kontroler

z

Bufor jest niewielką pamięcią FIFO (first-in-first-out)

–

typowo zawiera 4 pozycje

–

metoda działa dobrze, jeśli czestość operacji zapisu jest
znacznie mniejsza od 1 / DRAM write cycle

35

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Projekt cache - przykład

z

Założenia projektowe:

–

4 słowa w linijce

z

do przeprowadzenia odwzorowania pamięci używamy
adresów linijek

z

adres linijek jest określany jako adres/4.

z

przy odwołaniu ze strony CPU potrzebne jest pojedyncze
słowo, a nie cała linijka (można wykorzystać multiplekser
sterowany dwoma najmniej znaczącymi bitami adresu)

–

Cache 64KB

z

16 Bajtów w linijce

z

4K linijek

36

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

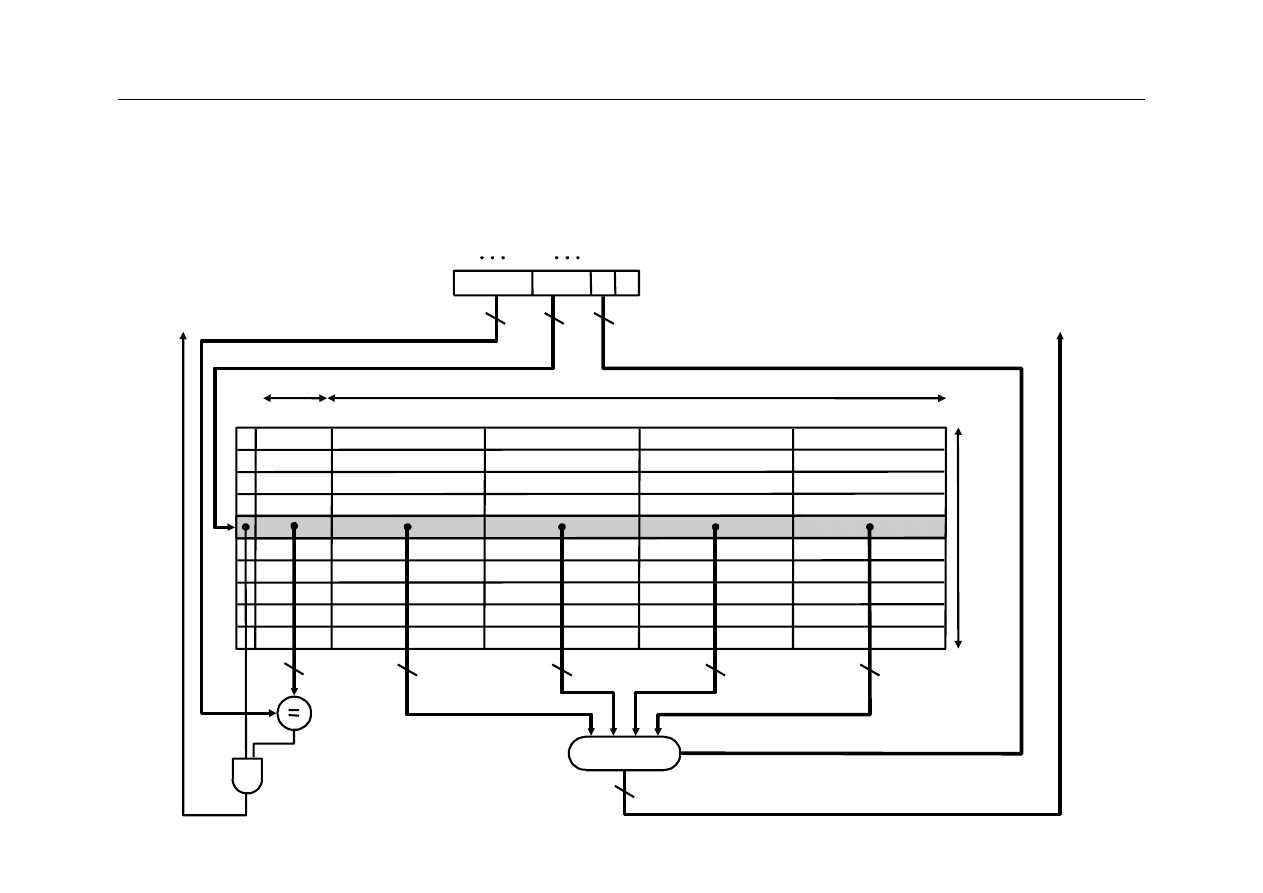
Projekt cache - rozwiązanie

Address (showing bit positions)

16

12

Byte

offset

V

Tag

Data

Hit

Data

16

32

4K
entries

16 bits

128 bits

Mux

32

32

32

2

32

Block offset

Index

Tag

31

16 15

4 3 2 1 0

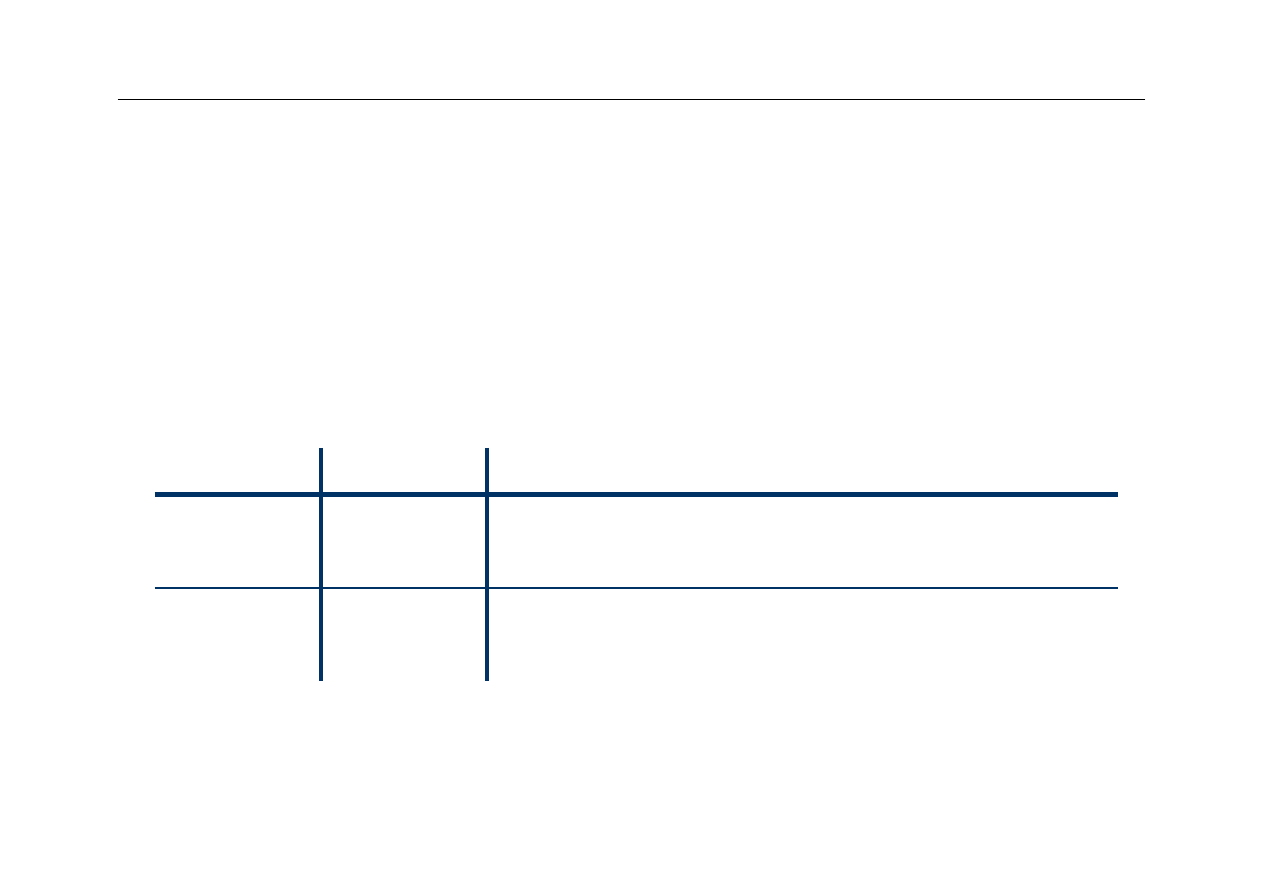
37

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wielkość linijki a wydajność

Przykład: DecStation 3100 cache z linijką

o rozmiarze 1 lub 4 słów

Rozmiar

Miss Rate

Program

gcc

1

6.1%

2.1%

5.4%

spice

1

1.2%

1.3%

1.2%

gcc

spice

4

2.0%

1.7%

1.9%

linijki

Instrukcje

Dane

Instr. + Dane

4

0.3%

0.6%

0.4%

38

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

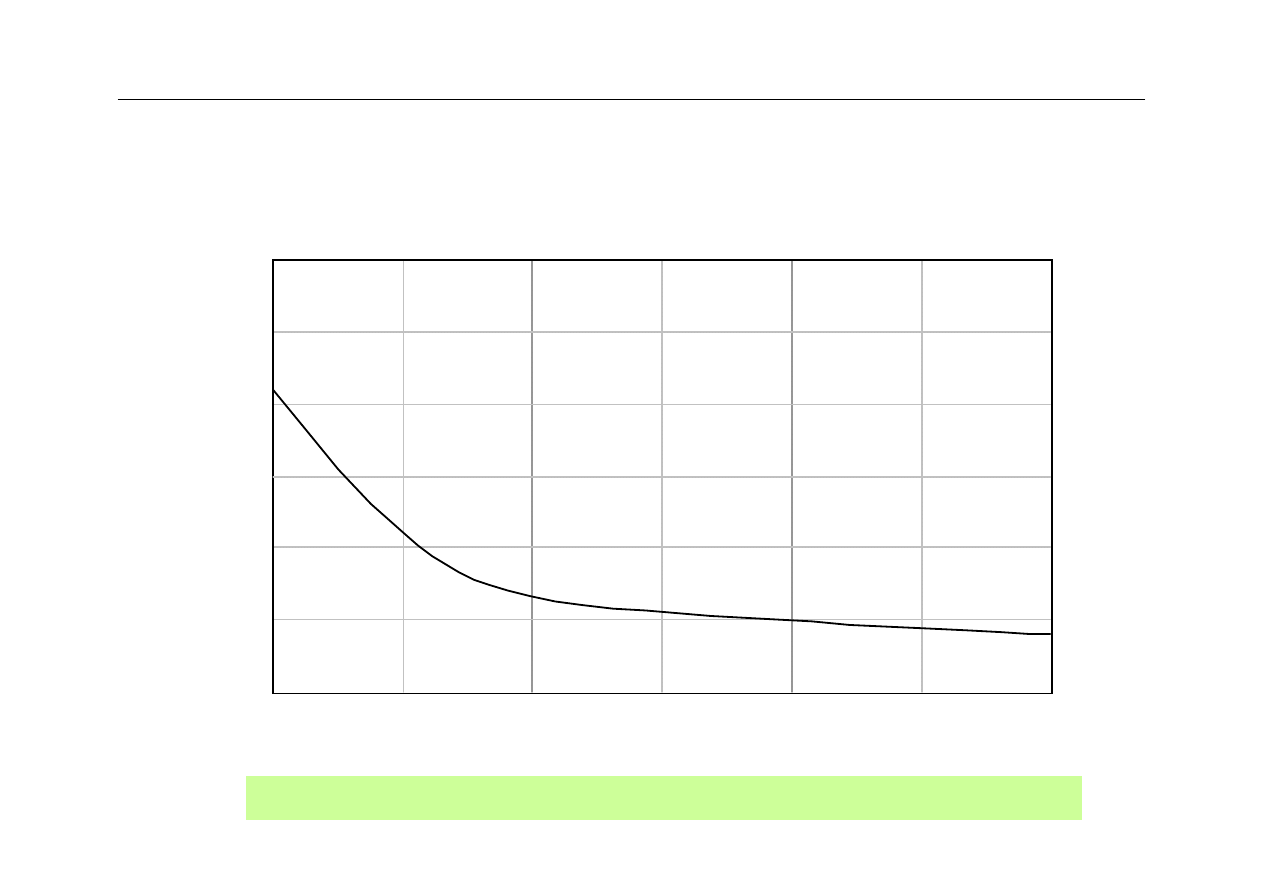
Czy duża linijka jest lepsza?

z

Zwiększanie rozmiaru linijki (przy ustalonym rozmiarze
pamięci cache) oznacza, że liczba linijek
przechowywanych w pamięci jest mniejsza

–

konkurencja o miejsce w pamięci cache jest większa

–

parametr miss rate wzrasta

z

Proszę rozważyć skrajny przypadek, gdy cała pamięć
cache tworzy jedną dużą linijkę!

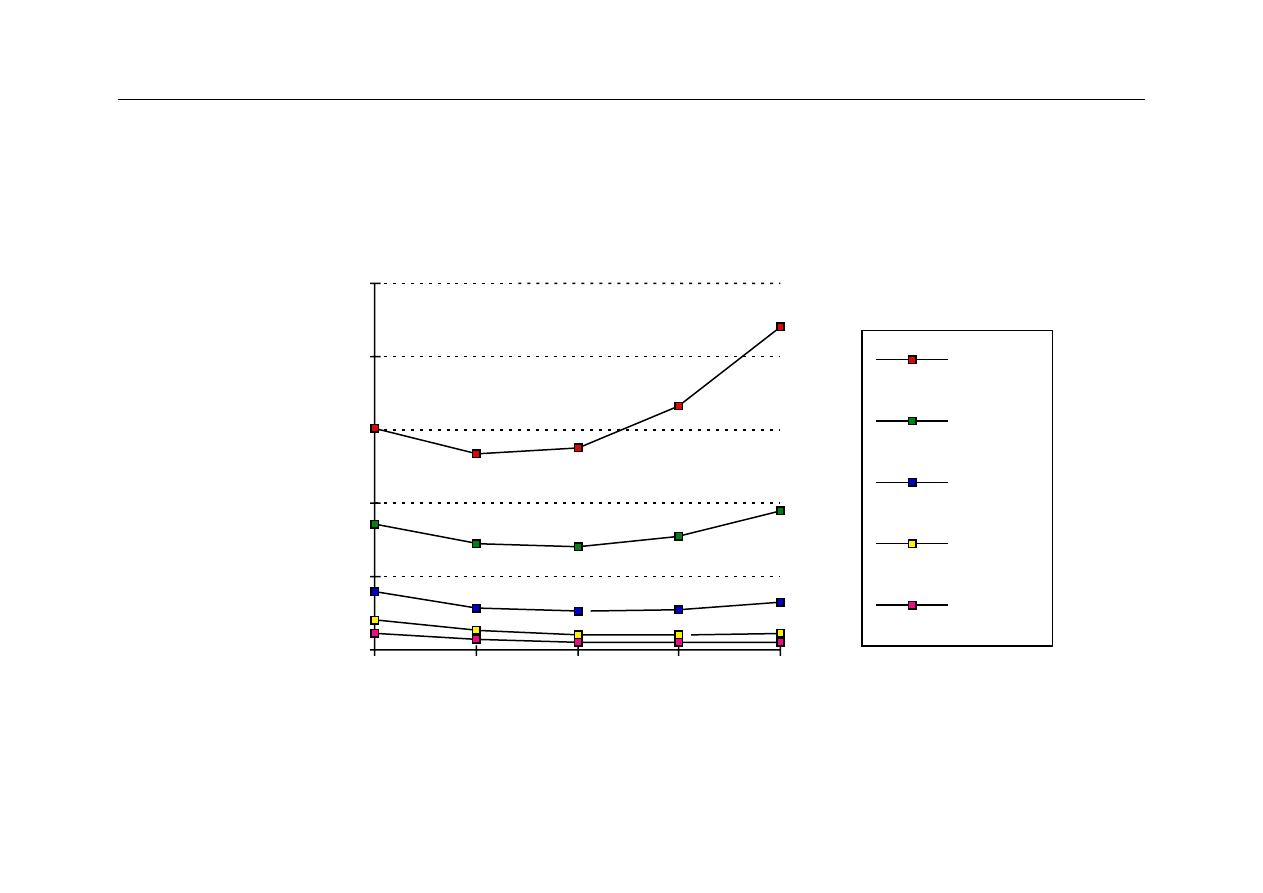
39

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Rozmiar linijki a miss rate

Rozmiar cache (bajty)

Miss
Rate

0%

5%

10%

15%

20%

25%

16

32

64

128

256

1K

4K

16K

64K

256K

Rozmiar linijki (bajty)

40

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Rozmiar linijki a miss penalty

z

Im większy jest rozmiar linijki, tym więcej czasu potrzeba na

przesłanie linijki między pamięcią główną a pamięcią cache

z

W przypadku chybienia czas sprowadzenia linijki wzrasta

(parametr miss penalty ma większą wartość)

z

Można budować pamięci zapewniające transfer wielu bajtów w

jednym cyklu odczytu, ale tylko dla niewielkiej liczby bajtów

(typowo 4)

z

Przykład: hipotetyczne parametry dostępu do pamięci głównej:

–

1 cykl CPU na wysłanie adresu

–

15 cykli na inicjację każdego dostępu

–

1 cykl na transmisję każdego słowa

z

Parametr miss penalty dla linijki złożonej z 4 słów:

1 + 4x15 + 4x1 = 65 cykli.

41

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wydajność cache

z

Średni czas dostępu do pamięci
AMAT –

average memory access time

AMAT = Hit time + Miss rate x Miss penalty

z

Poprawa wydajności pamięci cache polega na
skróceniu czasu AMAT przez:

1.

ograniczenie chybień (zmniejszenie miss rate,
zwiększenie hit rate)

2.

zmniejszenie miss penalty

3.

zmniejszenie hit time

42

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wydajność cache

z

Wydajność cache zależy głównie od dwóch czynników

:

–

miss rate

z

Zależy od organizacji procesora (hardware) i od

przetwarzanego programu (miss rate może się zmieniać).

–

miss penalty

z

Zależy tylko od organizacji komputera (organizacji pamięci

i czasu dostępu do pamięci)

z

Jeśli podwoimy częstotliwość zegara nie zmienimy

żadnego z tych parametrów (czas dostępu do pamięci

pozostanie taki sam)

z

Dlatego parametr speedup wzrośnie mniej niż

dwukrotnie

43

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wydajność cache - przykład

z

Załóżmy, że w pamięci cache z odwzorowaniem

bezpośrednim co 64 element pamięci jest

odwzorowany w tej samej linijce. Rozważmy

program:

for (i=0;i<10000;i++) {

a[i] = a[i] + a[i+64] + a[i+128];

a[i+64] = a[i+64] + a[i+128];

}

z

a[i]

,

a[i+64]

i a[i+128] używają tej samej linijki

z

Pamięć cache jest w powyższym przykładzie

bezużyteczna

44

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Jak zmniejszyć miss rate?

z

Oczywiście zwiększenie pamięci cache
spowoduje ograniczenie chybień, czyli
zmniejszenie parametru miss rate

z

Można też zmniejszyć miss rate ograniczając
konkurencję przy obsadzie linijek pamięci cache

–

Trzeba pozwolić linijkom z pamięci głównej na
rezydowanie w dowolnej linijce pamięci cache

45

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

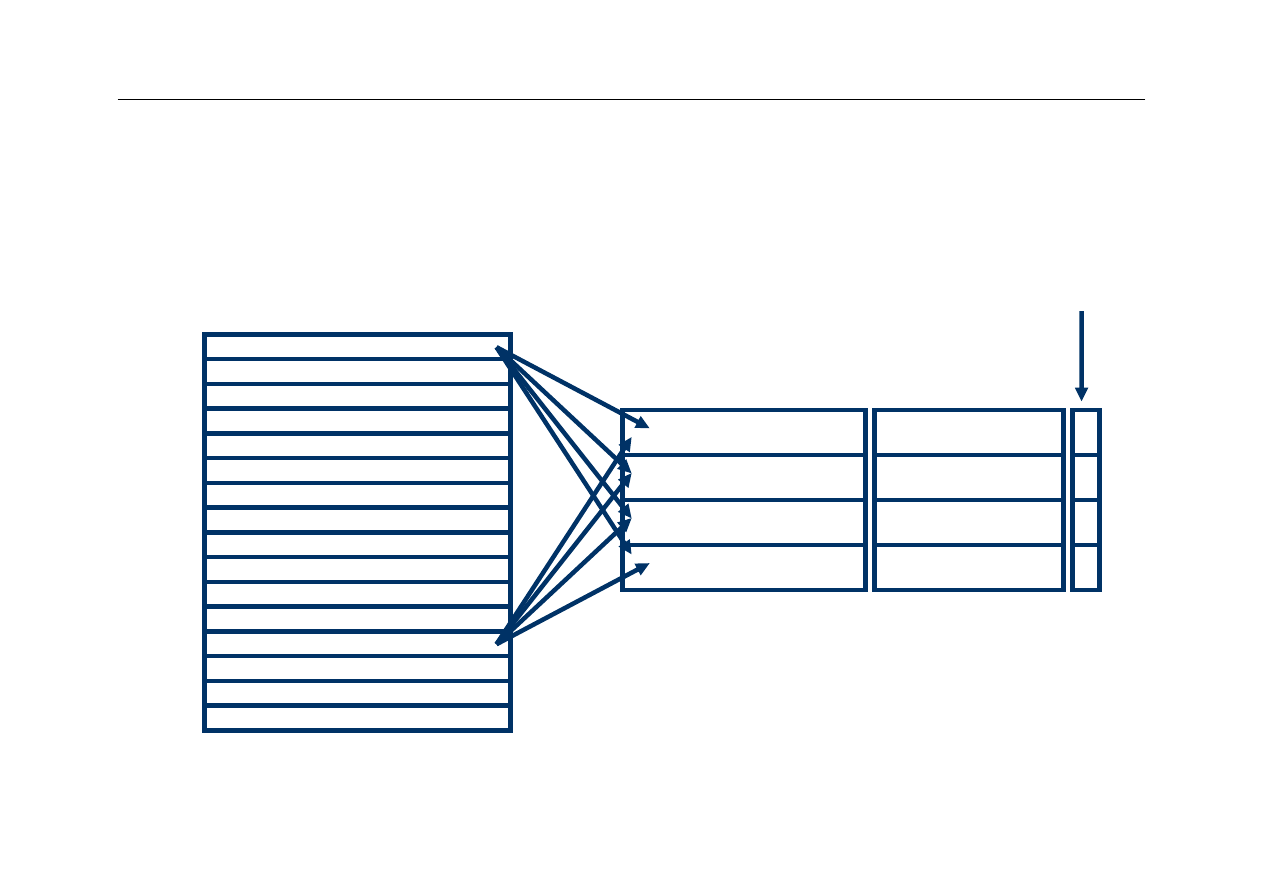
Odwzorowanie skojarzeniowe

z

Fully associative mapping

z

Zamiast odwzorowania bezpośredniego zezwalamy na
lokację linijek w

dowolnym miejscu pamięci cache

z

Teraz sprawdzenie czy dane są w pamięci cache jest
trudniejsze i zajmie więcej czasu (parametr hit time
wzrośnie)

z

Potrzebne są dodatkowe rozwiązania sprzętowe
(komparator dla każdej linijki pamięci cache)

z

Każdy znacznik jest teraz kompletnym adresem linijki w
pamięci głównej

46

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Odwzorowanie skojarzeniowe

Bit

ważności

Pamięć

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

1100

1101

1110

1111

Znaczniki

Dane

47

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Rozwiązanie kompromisowe

z

Odwzorowanie skojarzeniowe jest bardziej

elastyczne, dlatego parametr

miss rate

ma

mniejszą wartość

z

Odwzorowanie bezpośrednie jest prostsze

sprzętowo, czyli tańsze w implementacji

–

Ponadto lokalizacja danych w pamięci cache jest

szybsza (parametr

hit time

ma mniejszą wartość)

z

Szukamy kompromisu między miss rate a hit
time

.

z

Rozwiązanie pośrednie: odwzorowanie

sekcyjno-skojarzeniowe (

set associative

)

48

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Set Associative Mapping

z

Każda linijka z pamięci głównej może być

ulokowana w pewnym dozwolonym podzbiorze

linijek pamięci cache

z

Pojęcie

n-way set associative mapping

(odwzorowanie n-drożne sekcyjno-

skojarzeniowe) oznacza, że istnieje n miejsc

(linijek) w pamięci cache, do których może trafić

dana linijka z pamięci głównej placed.

z

Pamięć cache jest zatem podzielona na pewną

liczbę podzbiorów linijek, z których każdy

zawiera n linijek

49

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

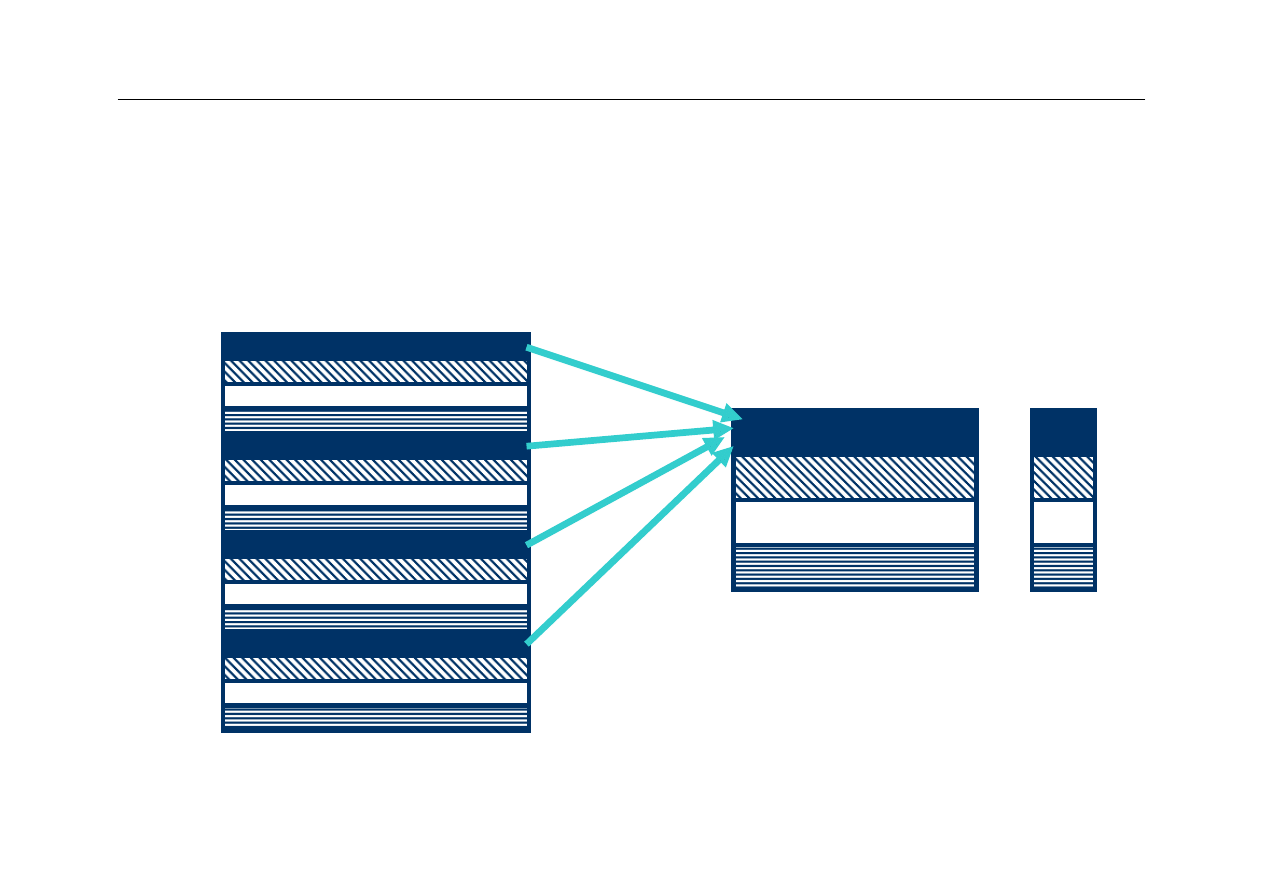
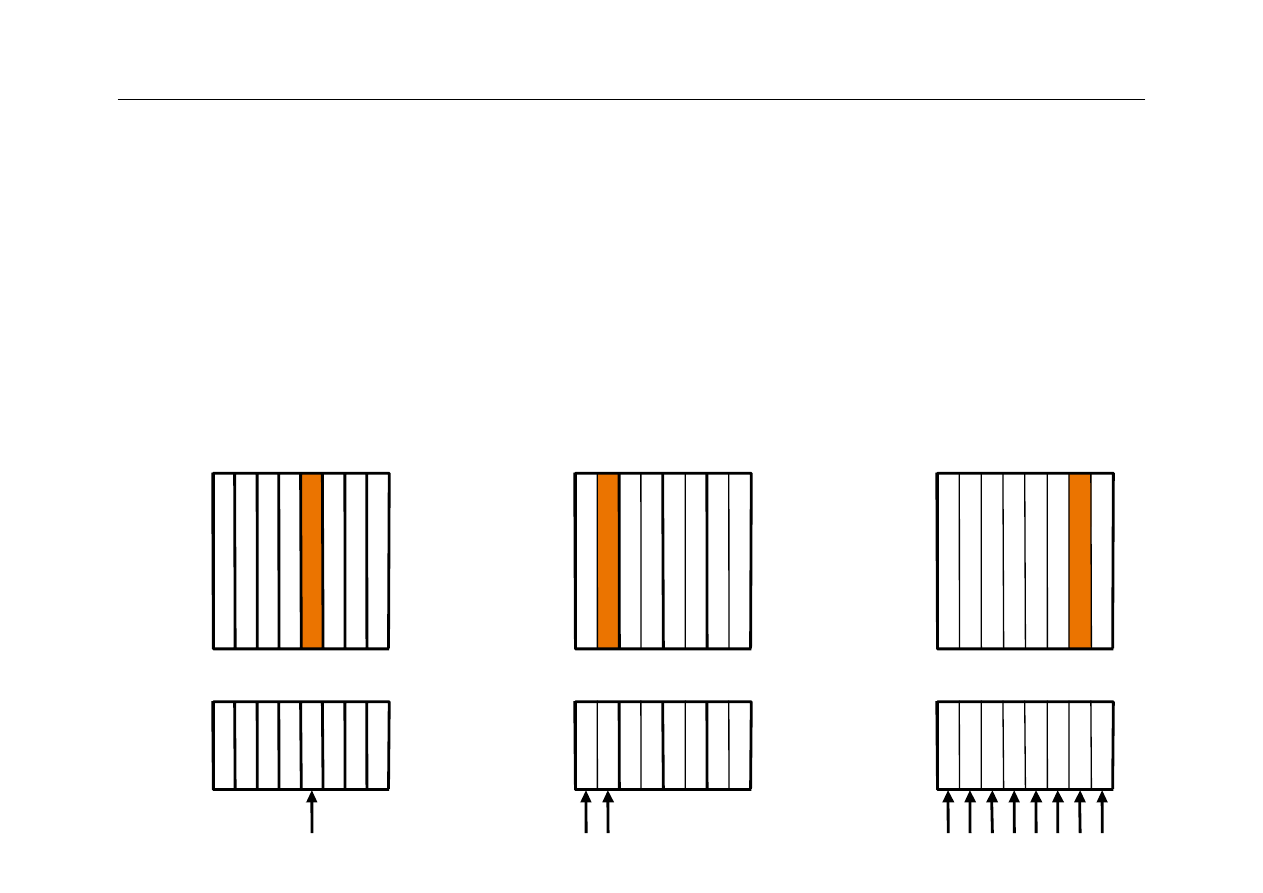
Porównanie odwzorowań

Przykład: cache składa się z 8 linijek, rozpatrujemy lokalizację
linijki z pamięci głównej o adresie 12

Linijka 12 może się
znaleźć w jednej z dwóch
linijek zbioru 0

Linijka 12 może się znaleźć
w dowolnej linijce cache

Linijka 12 może się
znaleźć tylko w linijce 4

1
2

Tag

Data

Block # 0 1 2 3 4 5 6 7

Search

Direct mapped

1
2

Tag

Data

Set #

0

1

2

3

Search

Set associative

1
2

Tag

Data

Search

Fully associative

50

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wydajność a n-drożność cache

Performance improvement of caches with increased associativity.

4-way

Direct 16-way

64-way

0

0.1

0.3

Mi

ss

ra

te

Associativity

0.2

2-way 8-way 32-way

51

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Odwzorowanie n-drożne

z

Odwzorowanie bezpośrednie jest szczególnym
przypadkiem n-drożnego odwzorowania sekcyjno-
skojarzeniowego przy n = 1 (1 linijka w zbiorze)

z

Odwzorowanie skojarzeniowe jest szczególnym
przypadkiem n-drożnego odwzorowania sekcyjno-
skojarzeniowego przy n równym liczbie linijek w pamięci
cache

z

Poprzedni przykład pokazuje, że odwzorowanie
4-drożne może nie dawać zauważalnej poprawy
wydajności cache w porównaniu z odwzorowaniem
2-drożnym.

52

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Algorytm wymiany linijek

z

W metodzie odwzorowania bezpośredniego nie
mamy wyboru przy zastępowaniu linijek –
problem strategii wymiany linijek nie istnieje

z

W metodzie odwzorowania sekcyjno-
skojarzeniowego należy określić strategię
wyboru linijek, które mają być usunięte przy
wprowadzaniu do cache nowych linijek

53

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Algorytm LRU

z

LRU

:

Least recently used

.

–

system zarządzania pamięcią cache rejestruje

historię każdej linijki

–

jeśli trzeba wprowadzić do cache nową linijkę, a w

dopuszczalnym zbiorze linijek nie ma wolnego

miejsca, usuwana jest najstarsza linijka.

–

przy każdym dostępie do linijki (hit) wiek linijki jest

ustawiany na 0

–

przy każdym dostępie do linijki wiek wszystkich

pozostałych linijek w danym zbiorze linijek jest

zwiększany o 1

54

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Implementacja LRU

z

Realizacja algorytmu LRU jest wykonywana sprzętowo

z

Obsługa LRU w pamięciach 2-drożnych jest łatwa –
wystarczy tylko 1 bit aby zapamiętać, która linijka (z
dwóch) w zbiorze jest starsza

z

Algorytm LRU w pamięciach 4-drożnych jest znacznie
bardziej złożony, ale stosowany w praktyce

z

W przypadku pamięci 8-drożnych sprzętowa realizacja
LRU staje się kosztowna i skomplikowana. W praktyce
używa się prostszego algorytmu aproksymującego
działanie LRU

55

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wielopoziomowa pamięć cache

z

Wielkość pamięci cache wbudowanej do procesora jest
ograniczona ze względów technologicznych

z

Ekonomicznym rozwiązaniem jest zastosowanie
zewnętrznej pamięci cache L2

z

Zwykle zewnętrzna pamięć cache jest szybką pamięcią
SRAM (czas miss penalty jest znacznie mniejszy niż w
przypadku pamięci głównej)

z

Dodanie pamięci cache L2 wpływa na projekt pamięci
cache L1 – dąży się do tego, by parametr hit time dla
pamięci L1 był jak najmniejszy

56

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wspólna a rozdzielona cache

z

We wspólnej pamięci cache dane i instrukcje są przechowywane

razem (architektura von Neumanna)

z

W rozdzielonej pamięci cache dane i instrukcje są przechowywane w

osobnych pamięciach (architektura harwardzka)

z

Dlaczego pamięć cache przechowująca instrukcje ma znacznie

mniejszy współczynnik miss rate?

Size

Instruction Cache Data Cache

Unified Cache

1 KB

3.06%

24.61%

13.34%

2 KB

2.26%

20.57%

9.78%

4 KB

1.78%

15.94%

7.24%

8 KB

1.10%

10.19%

4.57%

16 KB

0.64%

6.47%

2.87%

32 KB

0.39%

4.82%

2.48%

64 KB

0.15%

3.77%

1.35%

128 KB

0.02%

2.88%

0.95%

57

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wspólna a rozdzielona cache

z

Które rozwiązanie zapewnia krótszy czas dostępu
AMAT?

–

pamięć rozdzielona: 16 KB instrukcje + 16 KB dane

–

pamięć wspólna: 32 KB instrukcje + dane

z

Założenia:

–

należy użyć danych statystycznych dotyczących miss rate z
poprzedniego slajdu

–

zakładamy, że 75% dostępów do pamięci dotyczy odczytu
instrukcji, a 25% dostępów dotyczy danych

–

miss penalty

= 50 cykli

–

hit time

= 1 cykl

–

operacje odczytu i zapisu zajmują dodatkowo 1 cykl, ponieważ
jest tylko jeden port dla instrukcji i danych

58

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Wspólna a rozdzielona cache

AMAT = %instr x (instr hit time + instr miss rate x instr miss penalty) +

%data x (data hit time + data miss rate x data miss penalty)

Dla rozdzielonej pamięci cache:

AMAT = 75% x (1 + 0.64%x 50) + 25% x (1 + 6.47% x 50) =

2.05

Dla wspólnej pamięci cache:

AMAT = 75% x (1 + 2.48%x 50) + 25% x (1 + 2.48% x 50) =

2.24

W rozważanym przykładzie lepszą wydajność (krótszy czas dostępu

AMAT) zapewnia rozdzielona pamięć cache

59

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

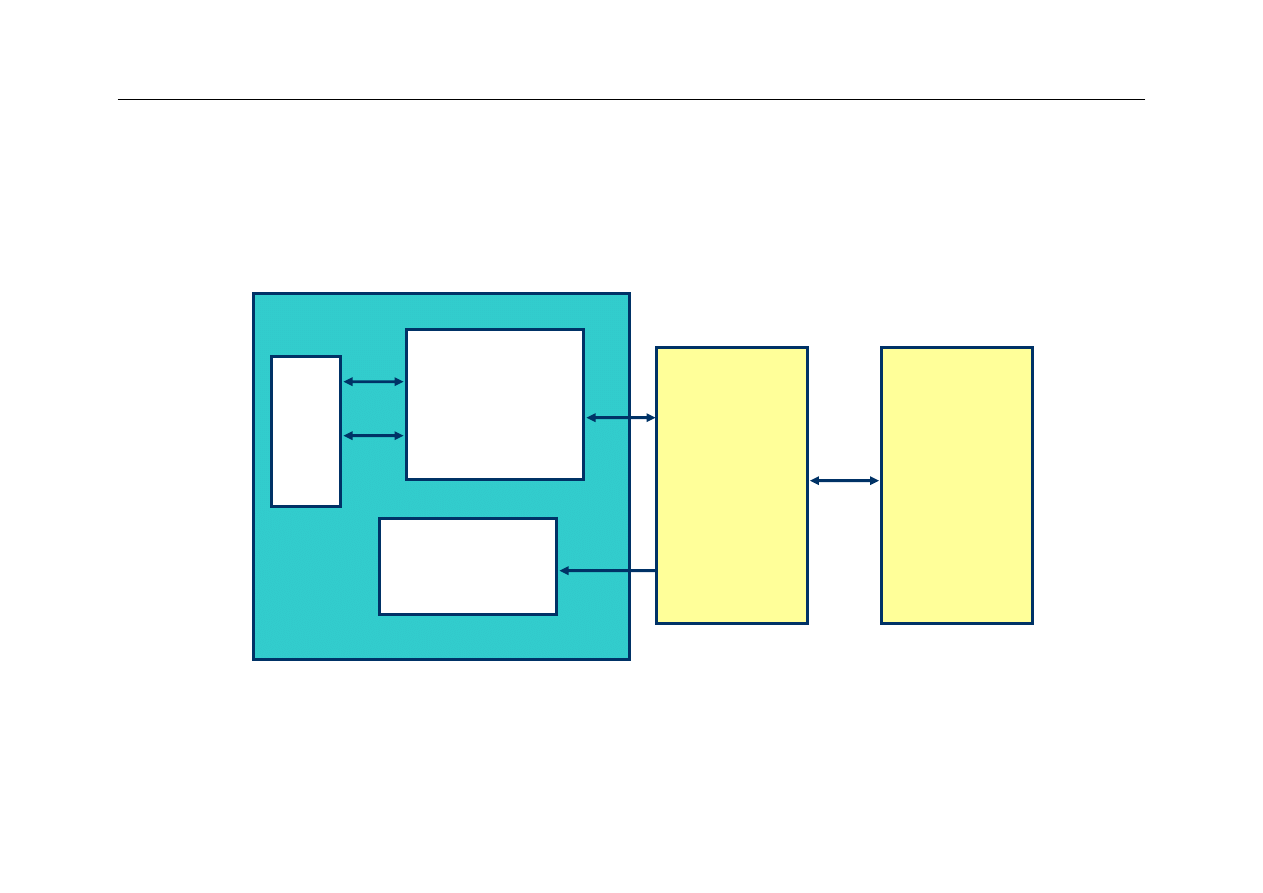
Przykład – cache w Pentium

Processor Chip

L1 Data

1 cycle latency

16KB

4-way assoc

Write-through

32B lines

L1 Instruction

16KB, 4-way

32B lines

Regs.

L2 Unified

128KB--2 MB

4-way assoc

Write-back

32B lines

Main

Memory

Up to 4GB

60

Wyższa Szkoła Informatyki Stosowanej i Zarządzania

Podsumowanie

z

Zasada lokalności

z

Hierarchiczny system pamięci

z

Koncepcja budowy i działania pamięci cache

z

Metody odwzorowania pamięci głównej i pamięci cache

–

odwzorowanie bezpośrednie (mapowanie bezpośrednie)

–

odwzorowanie asocjacyjne (pełna asocjacja)

–

częściowa asocjacja

z

Zapis danych i problem spójności zawartości pamięci

z

Wydajność pamięci cache, metody optymalizacji,

ograniczenia

z

Wymiana linijek w pamięci cache - algorytm LRU

z

Przykłady organizacji i architektury pamięci cache

z

Wspólna a rozdzielona pamięć cache