35. Zasada nieoznaczoności Heisenberga
Podejście podstawowe
Zasada nieoznaczoności - ogólny postulat mechaniki kwantowej głoszący, że nie wszystkie
wielkości z układu kwantowego mogą mieć jednocześnie dobrze określoną wartość.
Nie możemy na raz dokładnie zmierzyć:
–
położenia i pędu:
x p
ℏ
2
–
dwóch składowych momentu pędu:
L
i
L
j
ℏ
2
∣
〈 L
k
〉
∣
–
energii i czasu:
E t
ℏ
2
Nie jest tak, że pomiar np. położenia powoduje „zniszczenie”pędu. Zasadę nieoznaczoności należy
interpretować raczej w taki sposób, że niepewność pomiarowa jednej z wielkości rośnie, jeśli
niepewność drugiej będziemy zmniejszać, tzn. jeżeli bardzo dokładnie zmierzymy położenie, to
pomiar pędu będzie obarczony dużą niedokładnością, ale nie zmieni to samego pędu.
Wnioski z zasady nieoznaczoności
–
Ponieważ nie jest możliwe jednoczesne dokładne zmierzenie położenia i pędu, to model atomu
Bohra nie ma sensu. Zamiast o orbitach elektronów możemy mówić o chmurach elektronowych.
–
Z nieoznaczoności energii i czasu wynika, że próżni mogą powstawać cząstki na czas tym
krótszy im większa jest ich energia.
–
Z powyższego wynika tzw. parowanie czarnych dziur (promieniowanie Hawkinga)
Oczywiście z zasady nieoznaczoności może wynikać dużo innych faktów.
Podejście rozszerzone
Zasada nieoznaczoności jest konsekwencją braku komutacji operatorów.
Komutator dwóch operatorów A i B – wielkość oznaczana [A,B], której wartość równa jest różnicy
ilorazów prawostronnego i lewostronnego tych operatorów
[A,B] ═ AB − BA
Komutator jest miarą nieprzemienności operatorów.
Jeżeli komutator operatorów jest równy zero, mówimy, że operatory te komutują ze sobą.
1
Obserwabla – operator hermitowski (samosprzężony) reprezentujący mierzalną wielkość fizyczną.
Wartość średnia obserwabli:
〈 A〉=〈
∣
A
∣
〉=
∫
−∞
∞
∗
r Ardr
3
Wariancja – klasyczna miara zmienności. Wariancja zmiennej losowej X jest równa
2
X =E X
2
−
[
E
X
]
2
, gdzie E(X) – wartość oczekiwana. Pierwiastek kwadratowy z
wariancji to odchylenie standardowe.
Nieoznaczoność położenie-pęd
Operator położenia (wzdłuż osi x):
x= x
Operator pędu (x-owa składowa):
p
x
=−i ℏ ∂
∂ x
[ x , p
x
]=i ℏ
Zasada nieoznaczoności dla położenia i pędu:
2
x
2
p
x
ℏ
2
4
Nieoznaczoność składowych momentu pędu
Operator momentu pędu:
L=r×p
Składowe operatora:
L
x
=−i ℏ
y ∂
∂ z
−z ∂
∂ y
L
y
=−i ℏ
z ∂
∂ x
−x ∂
∂ z
L
z
=−i ℏ
x ∂
∂ y
− y ∂
∂ x
komutatory:
[ L
x
,
L
y
]=i ℏ L
z
[ L
x
,
L
z
]=−i ℏ L
y
[ L
y
,
L
z
]=i ℏ L
x
2
Ogólna postać zasady nieoznaczoności
Jeżeli w danym stanie kwantowym
∣
〉
wektory
A
∣
〉
i B
∣
〉
są prawidłowo
określonymi wektorami stanu, to
2
A
2
B
1
4
∣
〈
∣
[ A , B]
∣
〉
∣
2
gdzie
A , B
są dowolnymi obserwablami, natomiast
2
oznacza wariancję
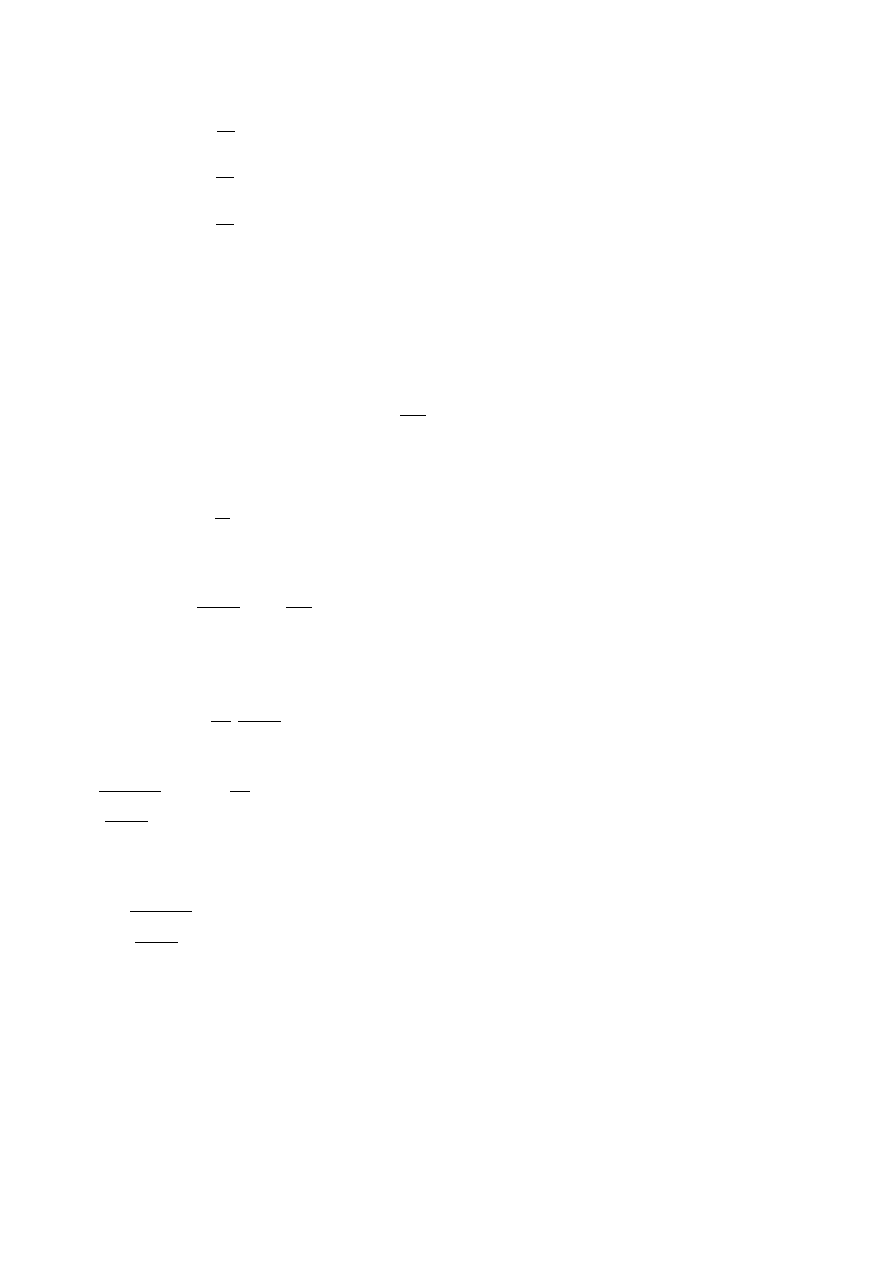
Zasady nieoznaczoności dla składowych momentu pędu:
2
L
x
2
L
y
ℏ
2
4
∣
〈 L
z
〉
∣
2
2
L
x
2
L
z
ℏ
2
4
∣
〈 L
y
〉
∣
2
2
L
y
2
L
z
ℏ
2
4
∣
〈L
x
〉
∣
2
Zasada nieoznaczoności energia-pęd
W mechanice kwantowej nie jest zdefiniowany operator czasu, dlatego ta zasada nieoznaczoności
nie jest tak rozumiana jak poprzednie i jest w inny sposób wyprowadzana.
Operatorem energii jest hamiltonian:
H = p
2
2m
V r , t
Weźmy zasadę nieoznaczoności dla dowolnej obserwabli, która nie zależy jawnie od czasu i
hamiltonianu
2
A
2
H
1
4
∣
〈
∣
[ A , H ]
∣
〉
∣
2
Skorzystajmy z równania:
〈
[ A , H ]
〉
=i ℏ
d
〈 A〉
dt
−i ℏ
〈
∂ A
∂t
〉
Ponieważ A nie zależy jawnie od czasu, drugi człon po prawej stronie jest zerowy.
Po podstawieniu:
2
A
2
H
ℏ
2
4
∣
d
〈 A〉
dt
∣
2
2
A
∣
d
〈 A〉
dt
∣
2
2
H
ℏ
2
4
Oznaczmy:
2
=
2
A
∣
d
〈 A〉
dt
∣
2
τ możemy interpretować jako czas trwania fluktuacji. Jest to czas potrzebny aby zmiany wartości
oczekiwanej A (mianownik) były porównywalne z jej odchyleniem standardowym (licznik).
3