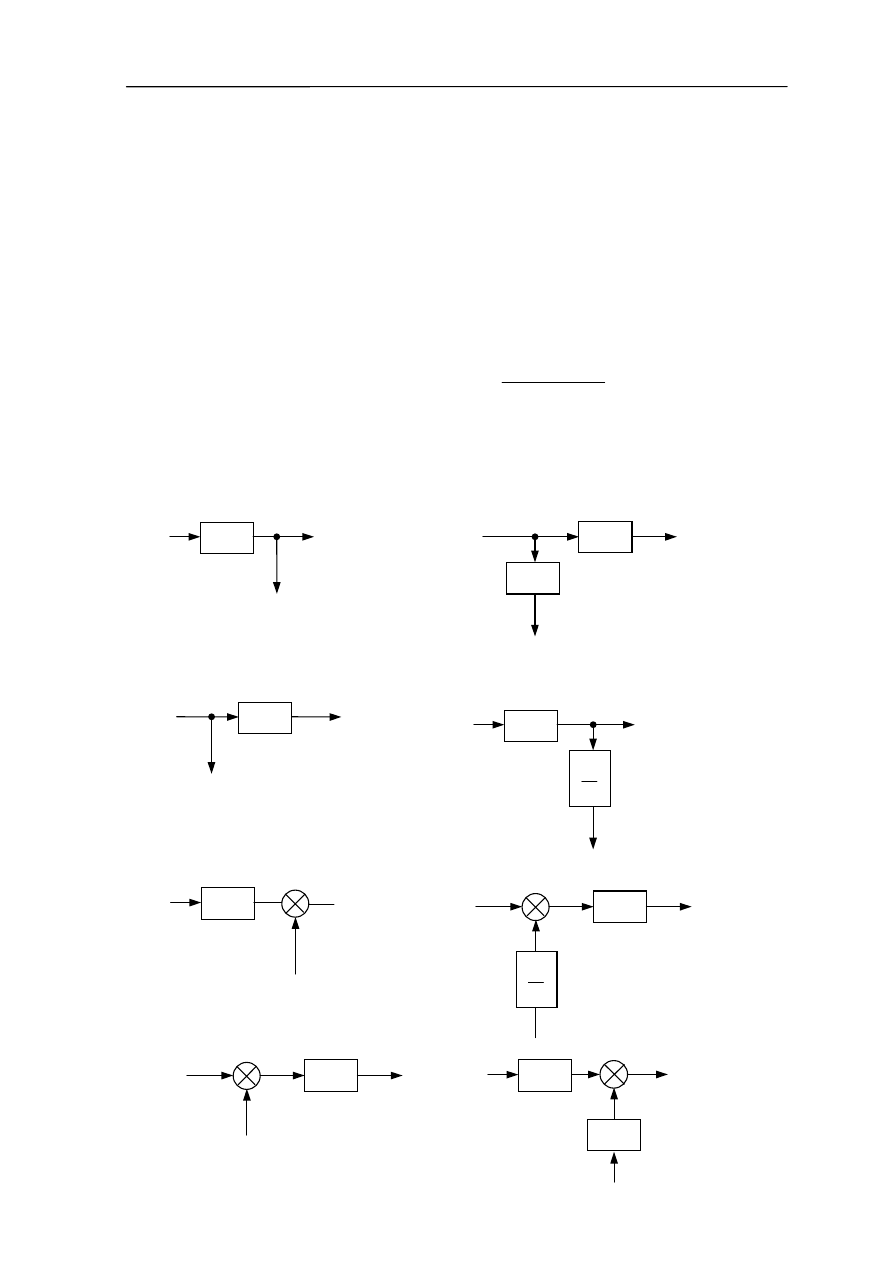
4. Przekształcenia schematów blokowych

42

4. PRZEKSZTAŁCENIA SCHEMATÓW BLOKOWYCH

Każdy z wyżej wymienionych modeli matematycznych można przedstawić jako blok,

czyli „czarną skrzynkę” z jednym wejściem i jednym wyjściem. W przypadku złożonych
systemów zestawy tych bloków tworzą skomplikowane struktury, dlatego do ich
uproszczenia stosuje się odpowiednie przekształcenia.

W praktyce stosuje się następujące połączenia bloków:

a) Połączenie szeregowe

∏

=

=

n

i

i

s

G

s

G

1

)

(

)

(

b) Połączenie równoległe

∑

=

=

n

i

i

s

G

s

G

1

)

(

)

(

c) Połączenie ze sprzężeniem zwrotnym

)

(

)

(

1

)

(

)

(

0

0

s

H

s

G

s

G

s

G

±

=

Na rysunku 4.1. przedstawiono podstawowe przekształcenia:

a) przesunięcie węzłów zaczepowych przed blok

b) przesunięcie węzłów zaczepowych za blok

c) przesunięcie węzłów sumujących przed blok

d) przesunięcie węzłów sumujących za blok

G

x

y

y

G

x

y

y

G

G

x

y

x

G

x

y

x

G

1

G

x

1

y

x

2

-

G

y

x

2

x

1

-

G

y

G

1

x

2

x

1

-

G

x

1

y

x

2

G

-

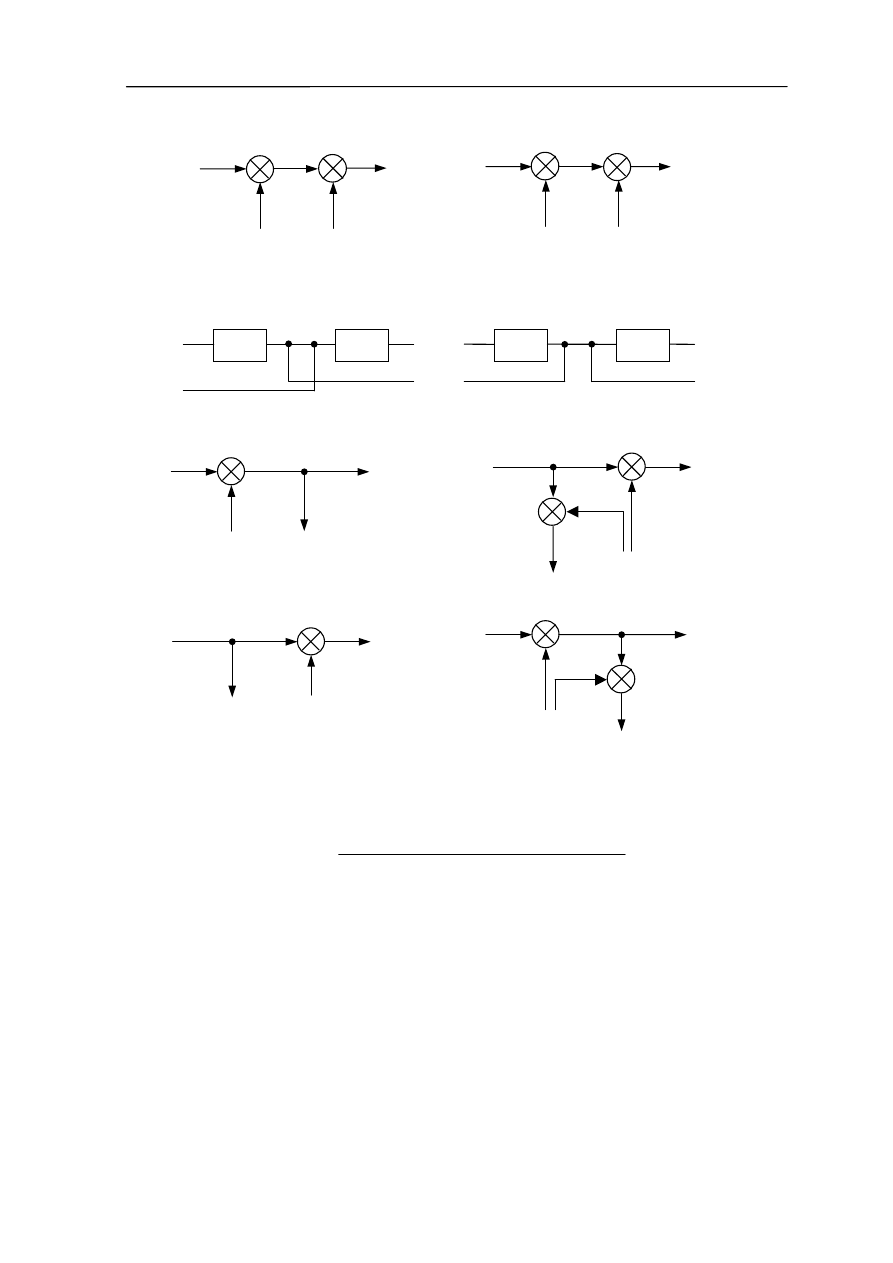
4. Przekształcenia schematów blokowych

43

e) zmiana położenia węzłów sumujących

f) zmiana położenia węzłów zaczepowych

g) przesunięcie węzła zaczepowego przed węzeł sumujący

h) przesunięcie węzła sumującego przed węzeł zaczepowy

Rys. 4.1

W układzie gdzie łatwo wyznaczyć tor główny można stosować mnemotechniczną

metodę oczkową. Jeżeli mamy n torów sprzężeń zwrotnych to

( )

∑

+

=

n

oczek

h

zamknietyc

cji

Transmitan

otwartego

toru

cja

Transmitan

s

G

1

1

Oczka należy brać takie aby był ten sam kierunek przepływu sygnałów.
Ustalenie znaku w mianowniku: obchodząc oczko będziemy mieli parzystą ilość węzłów
sumacyjnych (odwzorowujących znak) z ujemnym sprzężeniem zwrotnym to iloczyn
transmitancji dla danego oczka ma znak „ - ”, a przy nieparzystej ilości węzłów ma znak
„+”.

y=x

1

-x

2

+x

3

y

x

2

x

1

-

x

3

+

x

1

-x

2

y=x

1

+x

3

-x

2

y

x

2

x

1

-

x

3

+

x

1

+x

3

G

1

x

1

y

1

G

2

y

1

y

1

y

2

G

1

x

1

y

1

G

2

y

1

y

1

y

2

y

x

2

x

1

-

y

y

x

2

x

1

-

y

-

y

x

2

x

1

-

x

1

y

+

x

2

x

1

-

x

1

4. Przekształcenia schematów blokowych

44

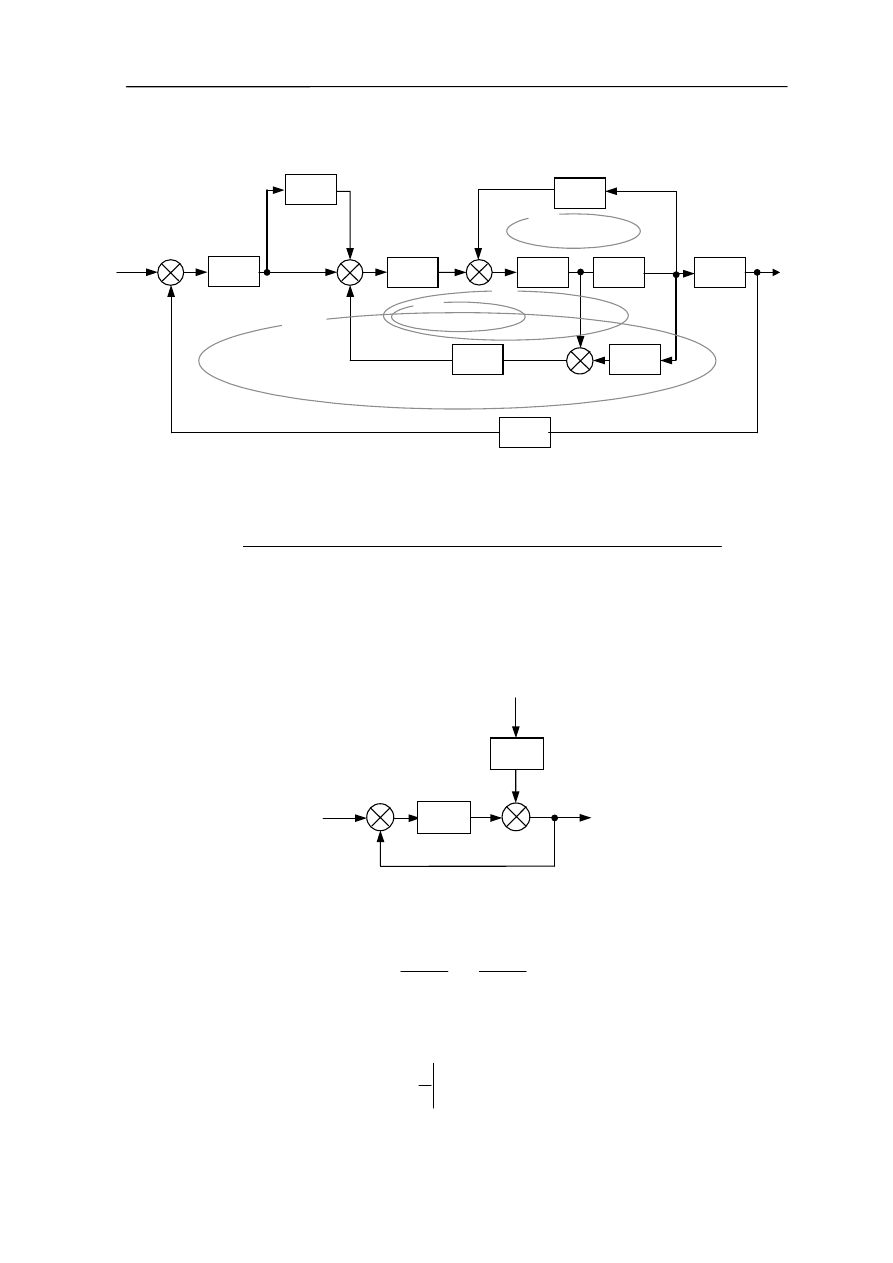
Przykład 4.1
Wyznaczyć transmitancję wypadkową układu z rysunku 4.2.

Rys. 4.2

( )

(

)

(

)

!

!

!

!

"

!

!

!

!

#

$

!

! "

!

! #

$

!

"

!#

$

!

"

!#

$

4

0

6

5

4

3

2

1

3

3

2

5

4

3

2

2

4

3

1

1

5

4

6

5

4

3

2

1

1

1

1

oczko

oczko

oczko

oczko

H

G

G

G

G

G

G

H

H

G

G

G

H

G

G

H

G

G

G

G

G

G

G

G

s

G

+

+

+

+

+

+

=

Przykład 4.2
Wyznaczyć transmitancję: układu otwartego, układu otwartego w funkcji wymuszenia
f=f(y), układu zamkniętego, układu zamkniętego w funkcji wymuszenia f=f(y) oraz układu
zamkniętego przyjmując uchyb regulacji za sygnał wyjściowy.

Rys. 4.3

f

G

G

x

G

G

y

o

z

o

o

+

+

+

=

1

1

Transmitancje:
a) układu otwartego

o

f

G

y

=

=

0

ε

G

1

(s)

G

3

(s)

G

4

(s)

G

5

(s)

G

6

(s)

X(s)

G

2

(s)

H

1

(s)

H

2

(s)

H

3

(s)

H

0

(s)

Y(s)

1

2

3

4

-

-

-

+

G

z

y

x

f

ε

G

o

-

+

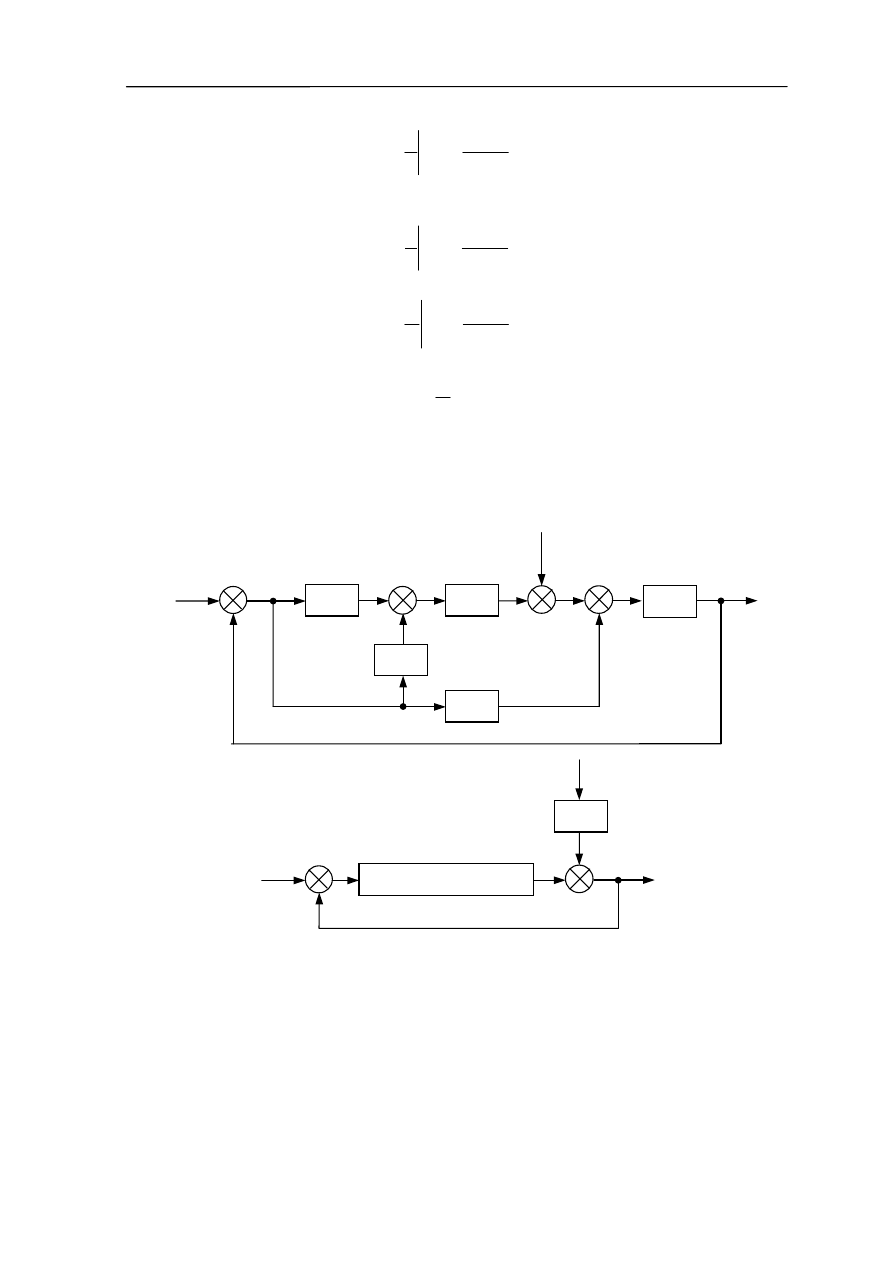
4. Przekształcenia schematów blokowych

45

b) układu zamkniętego

o

o

f

G

G

x

y

+

=

=

1

0

c) uchybowa

o

f

G

x

+

=

=

1

1

0

ε

d) zakłóceniowa

o

z

x

G

G

f

y

+

=

=

1

0

e) układu otwartego dla zakłócenia f.

y

f

=G

z

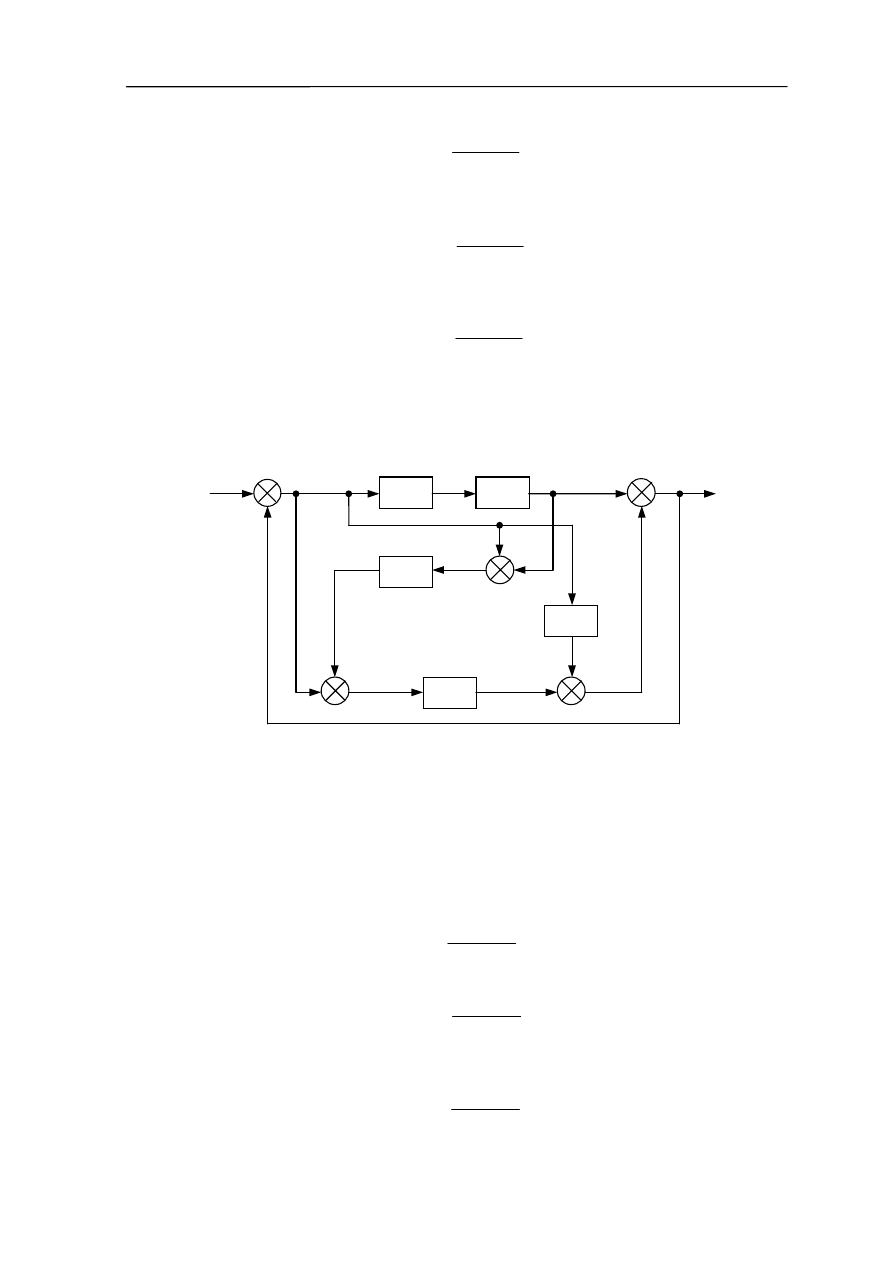
Przykład 4.3.
Wyznaczyć transmitancję układu otwartego, układu otwartego w funkcji wymuszenia
f=f(y), układu zamkniętego, układu zamkniętego w funkcji wymuszenia f=f(y) oraz układu
zamkniętego przyjmując uchyb regulacji za sygnał wyjściowy.

Rys. 4.4

Transmitancje mają postać:
a) układu otwartego

( ) (

)

[

]

5

3

4

2

1

G

G

G

G

G

s

G

O

+

+

=

b) układu otwartego w funkcji wymuszenia f=f(y)

( )

5

G

s

G

Of

=

G

1

G

5

G

3

G

4

G

2

y

x

ε

1

f

ε

2

ε

-

+

+

+

[(G

1

+G

2

)G

4

+G

3

]G

5

G

5

y

x

f

ε

-

+

4. Przekształcenia schematów blokowych

46

c) układu zamkniętego

( )

( )

( )

s

G

s

G

s

G

O

O

z

+

=

1

d) układu zamkniętego w funkcji wymuszenia f=f(y)

( )

( )

s

G

G

s

G

O

f

z

+

=

1

5

e) układu zamkniętego przyjmując uchyb regulacji za sygnał wyjściowy (transmitancja

uchybowa)

( )

( )

s

G

s

G

O

z

+

=

1

1

ε

Przykład 4.4
Wyznaczyć transmitancję: układu otwartego, układu otwartego w funkcji wymuszenia
f=f(y), układu zamkniętego, układu zamkniętego w funkcji wymuszenia f=f(y) oraz układu
zamkniętego przyjmując uchyb regulacji za sygnał wyjściowy.

Rys. 4.5

Transmitancje mają postać:
a) układu otwartego

( )

[

]

5

4

3

2

1

2

1

1

G

G

G

G

G

G

G

s

G

O

+

+

+

=

b) układu otwartego w funkcji wymuszenia f=f(y)

( )

4

3

G

G

s

G

Of

=

c) układu zamkniętego

( )

( )

( )

s

G

s

G

s

G

O

O

+

=

1

d) układu zamkniętego w funkcji wymuszenia f=f(y)

( )

( )

s

G

G

G

s

G

O

f

+

=

1

4

3

e) układu zamkniętego przyjmując uchyb regulacji za sygnał wyjściowy (transmitancja

uchybowa)

( )

( )

s

G

s

G

O

+

=

1

1

ε

G

1

G

5

G

3

G

4

G

2

y

x

ε

f

-

+

+

+