Rozdziaª 1

Schematy blokowe ukªadów automatyki

Autorzy:

Marcin Stachura

1.1 Algebra schematów blokowych

1.1.1 Zasady przeksztaªcania schematów blokowych

W celu uproszczenia wypadkowej transmitancji operatorowej regulatora, obiektu regulacji

lub caªego ukªadu regulacji w przypadku, gdy skªada si¦ on z kilku elementów ró»nie

poª¡czonych, nale»y wyprowadzi¢ zale»no±ci na transmitancj¦ wypadkow¡. Ka»dy ukªad

regulacji, niezale»nie od tego czy jest bardziej lub niej zªo»ony, mo»na rozªo»y¢ na cz¦±ci

skªadaj¡ce si¦ z elementów poª¡czonych szeregowo, równolegle, w ukªadzie ze sprz¦»eniem

zwrotnym i równolegle z oddzielnymi wej±ciami lub wyj±ciami.
Zasady przeksztaªcania schematów blokowych w celu ich uproszczenia i okre±lenia trans-

mitancji ukªadu nazywane s¡ algebr¡ schematów blokowych. W tablicy

1.1

,

1.2

przedstawiono zestawienie zasadniczych przykªadów takich przeksztaªce«. Ich znajomo±¢

wystarcza do okre±lenia transmitancji dowolnie zªo»onego ukªadu.
Transmitancj¦ wypadkow¡ du»ej liczby elementów ró»nie poª¡czonych znajduje si¦, w

prostszych przypadkach, drog¡ rozªo»enia ukªadu na cz¦±ci proste. Jednak»e ta metoda

wymaga du»ej przejrzysto±ci schematu blokowego, co przy bardziej zªo»onych ukªadach

regulacji mo»e powodowa¢ pewne trudno±ci. Dlatego w takich przypadkach najlepiej jest

post¦powa¢ nast¦puj¡co:

1. Dla ka»dego punktu w¦zªowego , do którego dochodzi kilka sygnaªów zestawia

si¦, zgodnie z zasad¡ superpozycji, równanie i z otrzymanego w ten sposób ukªadu

równa« wyznacza si¦ szukan¡ transmitancj¦.

2. W ka»dym punkcie w¦zªowym wszystkie sygnaªy odchodz¡ce s¡ wzajemnie sobie

równe i jednocze±nie ka»dy z tych sygnaªów odchodz¡cych równa si¦ sumie wszyst-

kich sygnaªów przychodz¡cych.

1

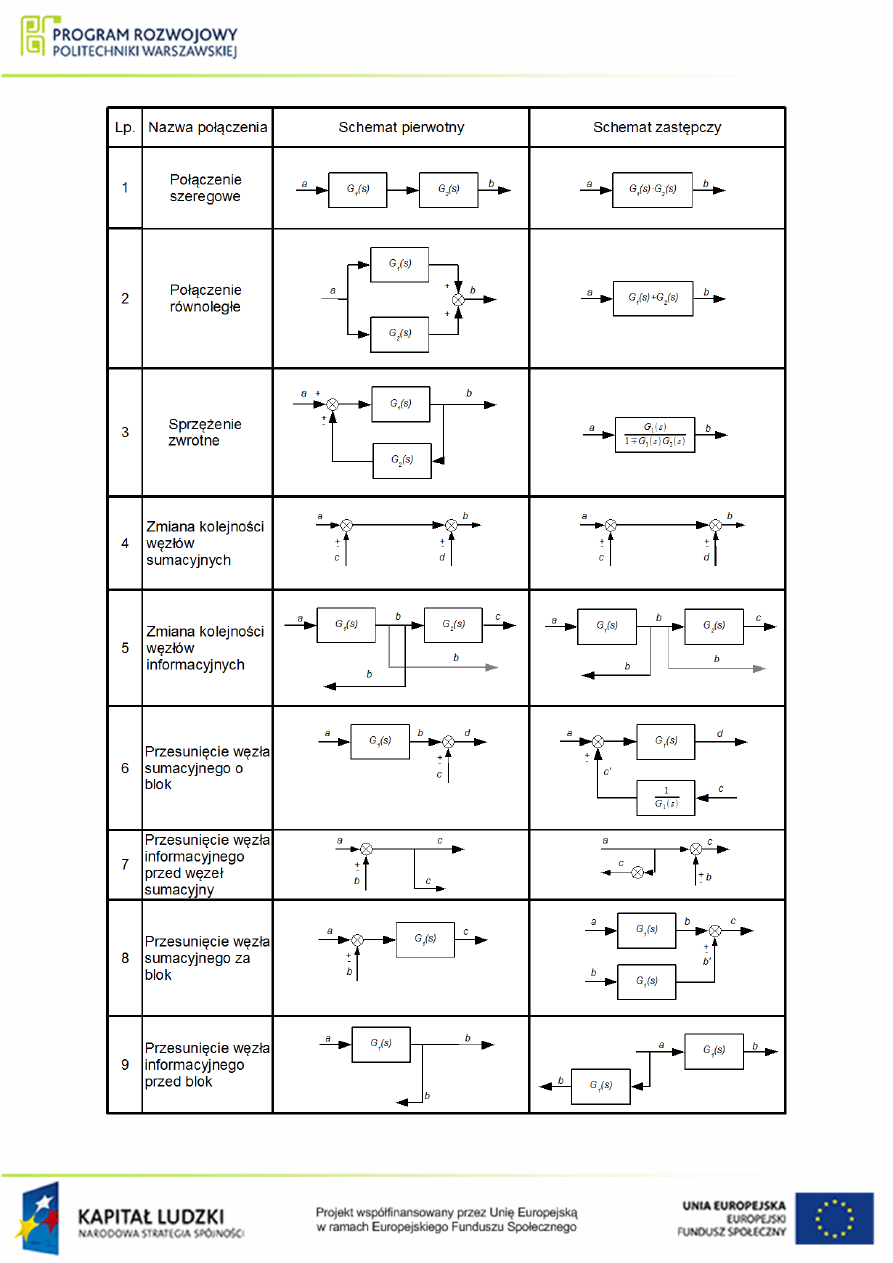
Rysunek 1.1 Tablica podstawowych przeksztaªce« schematów blokowych, cze±¢ a.

2

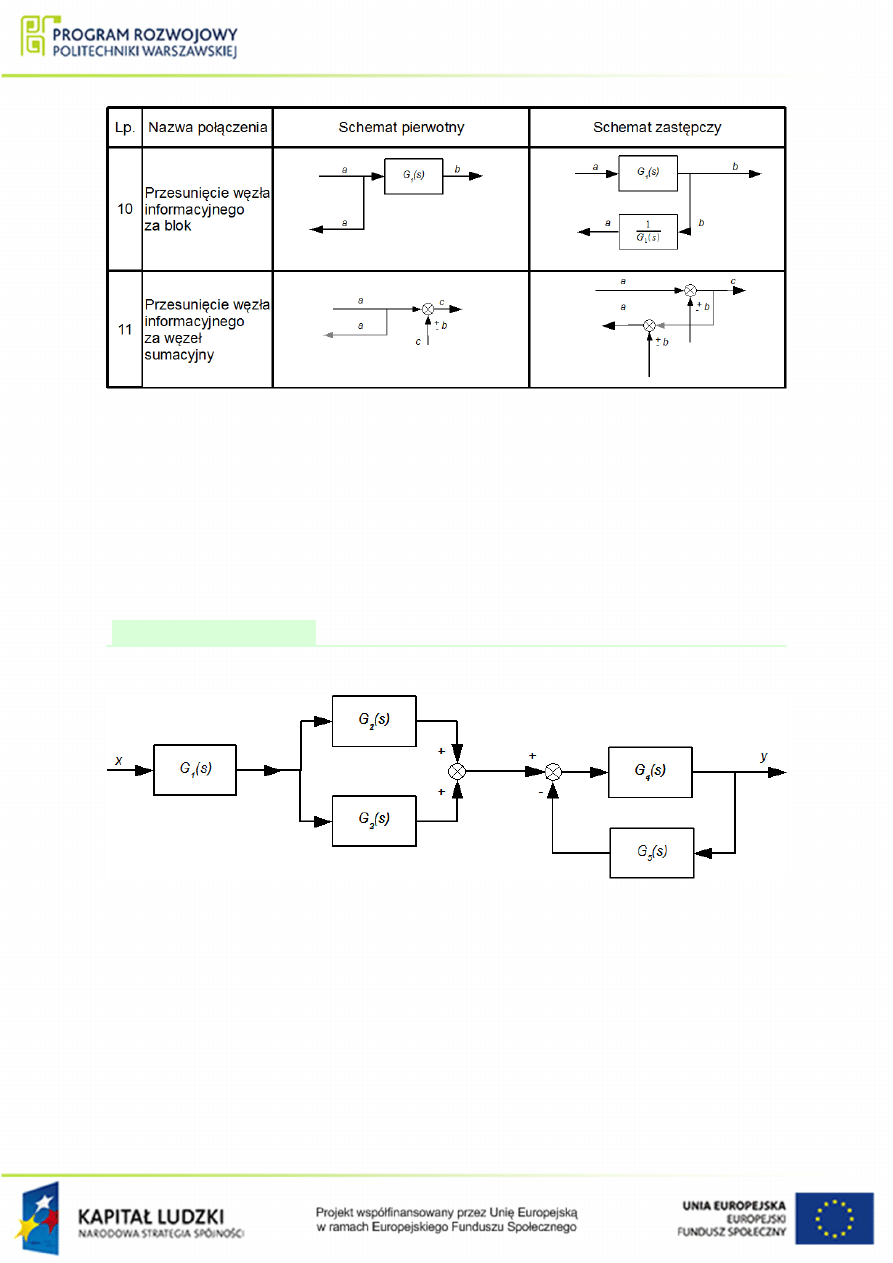
Rysunek 1.2 Tablica podstawowych przeksztaªce« schematów blokowych, cze±¢ b.

W przypadkach zªo»onych, gdy transmitancj¦ ukªadu wyra»a si¦ jako funkcj¦ transmi-

tancji jego elementów wprowadza si¦ uproszczone oznaczenie transmitancji, np. zamiast
G

x

(s)

piszemy po prostu G

x

.

1.1.2 Przykªady zada«

Przykªad 1.1

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.1

.

Rysunek 1.3 Ukªad poª¡cze« elementów do przykªadu

1.1

Rozwi¡zanie:
Šatwo zauwa»y¢, korzystaj¡c z tablicy

1.1

, »e w prosty sposób mo»na wyznaczy¢ dwie

transmitancje zast¦pcze Z

1

, Z

2

transmitancji G

2

, G

3

(poz. 2. poª¡czenie równolegªe) oraz

G

4

, G

5

(poz. 3. sprz¦»enie zwrotne) (rys

1.4

):

3

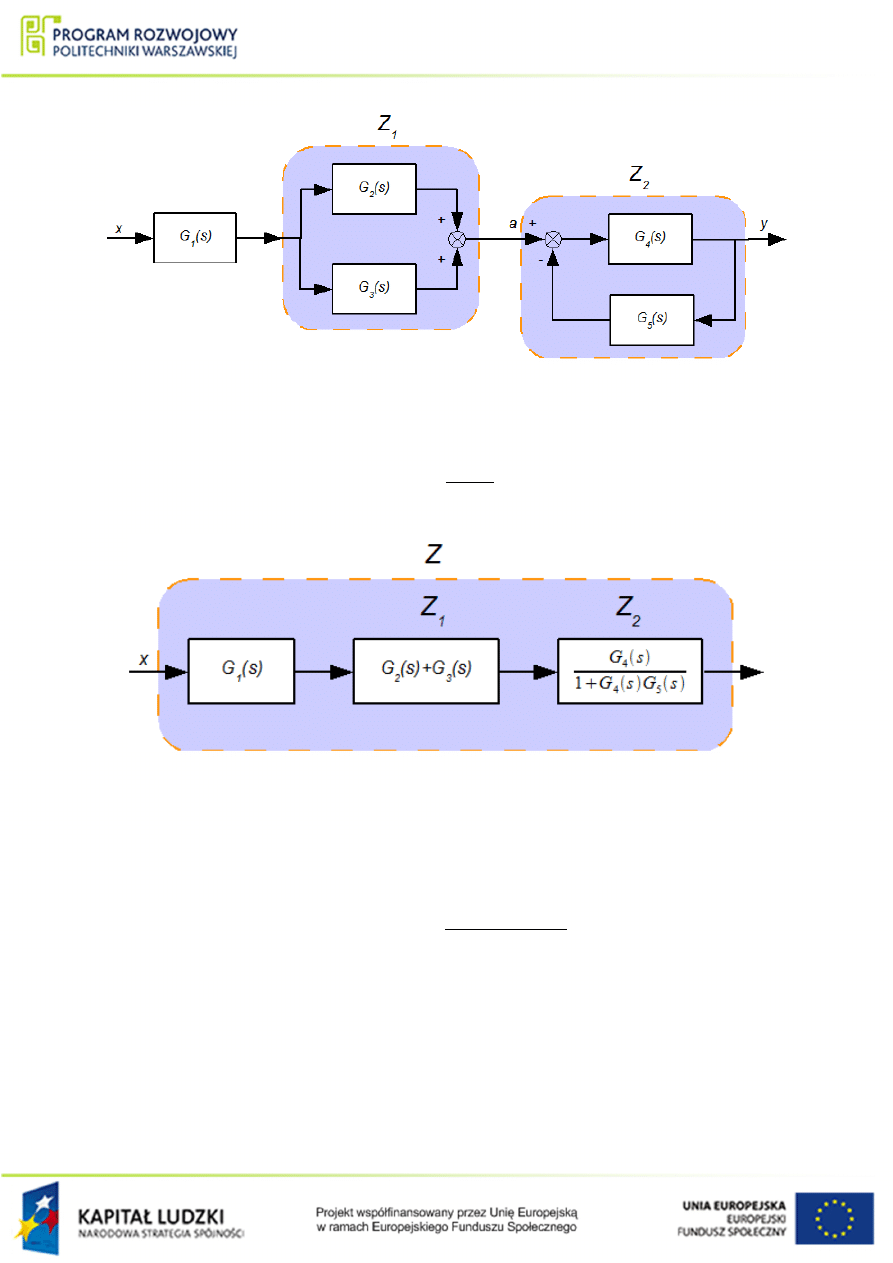
Rysunek 1.4 Wyznaczanie transmitancji zast¦pczych dla elementów o

transmitancjach G

2

, G

3

oraz G

4

, G

5

.

Przy czym Z

1

= G

2

+ G

3

, natomiast Z

2

=

G

4

1+G

4

G

5

. Wyj±ciowy ukªad mo»na wi¦c przed-

stawi¢ nast¦puj¡co:

Rysunek 1.5 Zmodykowany ukªad poª¡cze« dla przykªadu

1.1

Nast¦pnie wyznaczana jest transmitancja zast¦pcza caªego ukªadu wyj±ciowego Z(z ta-

blicy

1.1

. poz. 1, poª¡czenie szeregowe, rys.

1.1

), która wynosi¢ b¦dzie:

Z = G

1

Z

1

Z

2

=

G

1

G

4

(G

2

+ G

3

)

1 + G

4

G

5

(1.1)

4

Przykªad 1.2

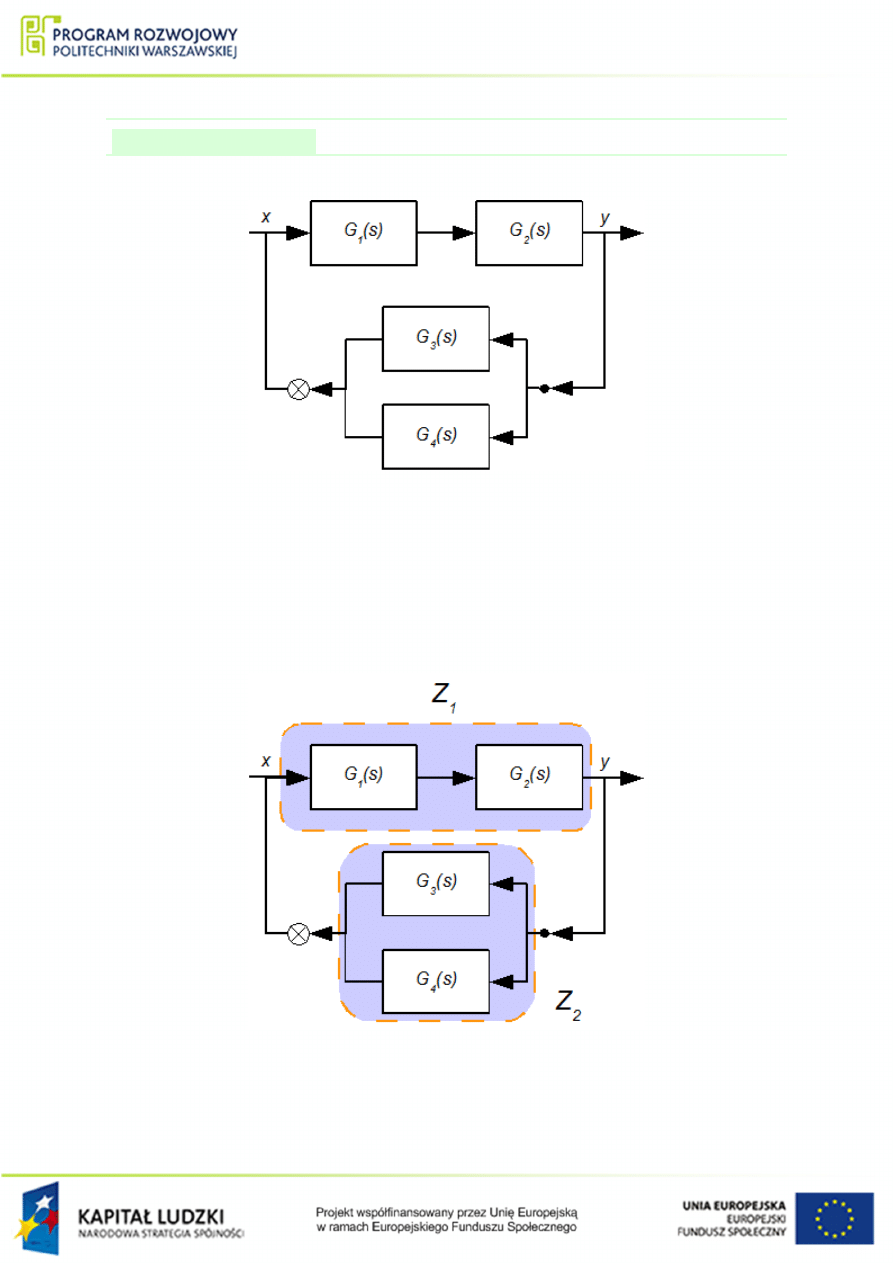
Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.6

.

Rysunek 1.6 Ukªad poª¡cze« elementów do przykªadu

1.2

.

Rozwi¡zanie:
Podobnie jak w poprzednim przykªadzie (przykªad

1.1

) wyznaczamy dwie transmitancje

zast¦pcze Z

1

, Z

2

transmitancji G

1

, G

2

(poz. 1. poª¡czenie szeregowe) oraz G

3

, G

4

(poz. 3.

poª¡czenie równolegªe) (rys.

1.7

):

Rysunek 1.7 Wyznaczanie transmitancji zast¦pczych dla elementów o

transmitancjach G

1

, G

2

oraz G

3

, G

4

.

Przy czym Z

1

= G

2

G

3

, natomiast Z

2

= G

3

+G

4

. Wyj±ciowy ukªad mo»na wi¦c przedstawi¢

5

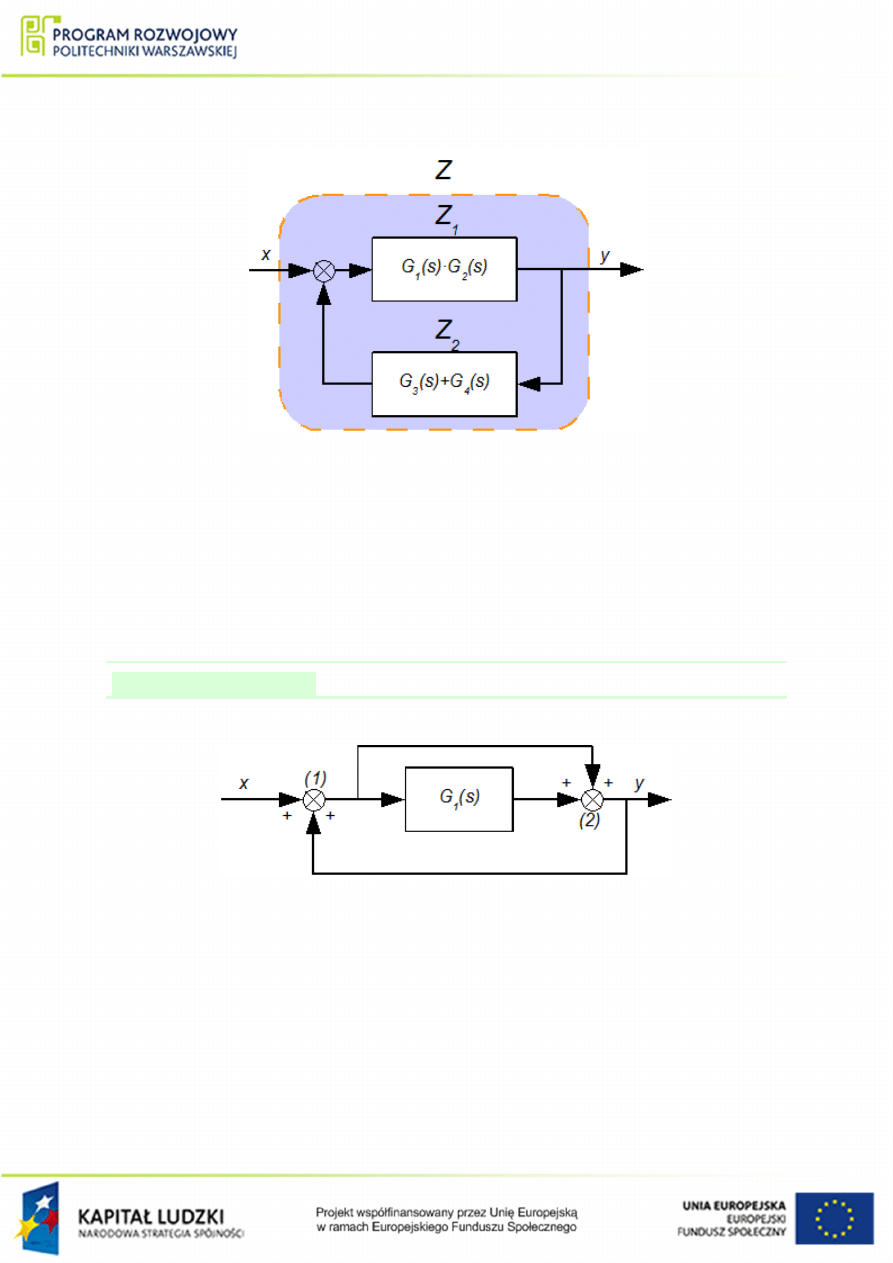
nast¦puj¡co:

Rysunek 1.8 Zmodykowany ukªad poª¡cze« dla przykªadu

1.2

.

Nast¦pnie wyznaczana jest transmitancja zast¦pcza caªego ukªadu wyj±ciowego Z(z ta-

blicy

1.1

. poz. 3, sprz¦»enie zwrotne, rys.

1.8

), która wynosi¢ b¦dzie:

(1.2)

Przykªad 1.3

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.9

.

Rysunek 1.9 Ukªad poª¡cze« elementów do przykªadu

1.3

.

Rozwi¡zanie:
W pierwszej kolejno±ci nale»y przenie±¢ w¦zeª sumacyjny (1) za czªon o transmitancji
G

1

(zgodnie z tablic¡

1.1

. poz. 8, przesuni¦cie w¦zªa sumacyjnego za blok), otrzymuj¡c

schemat jak na rys.

1.10

:

6

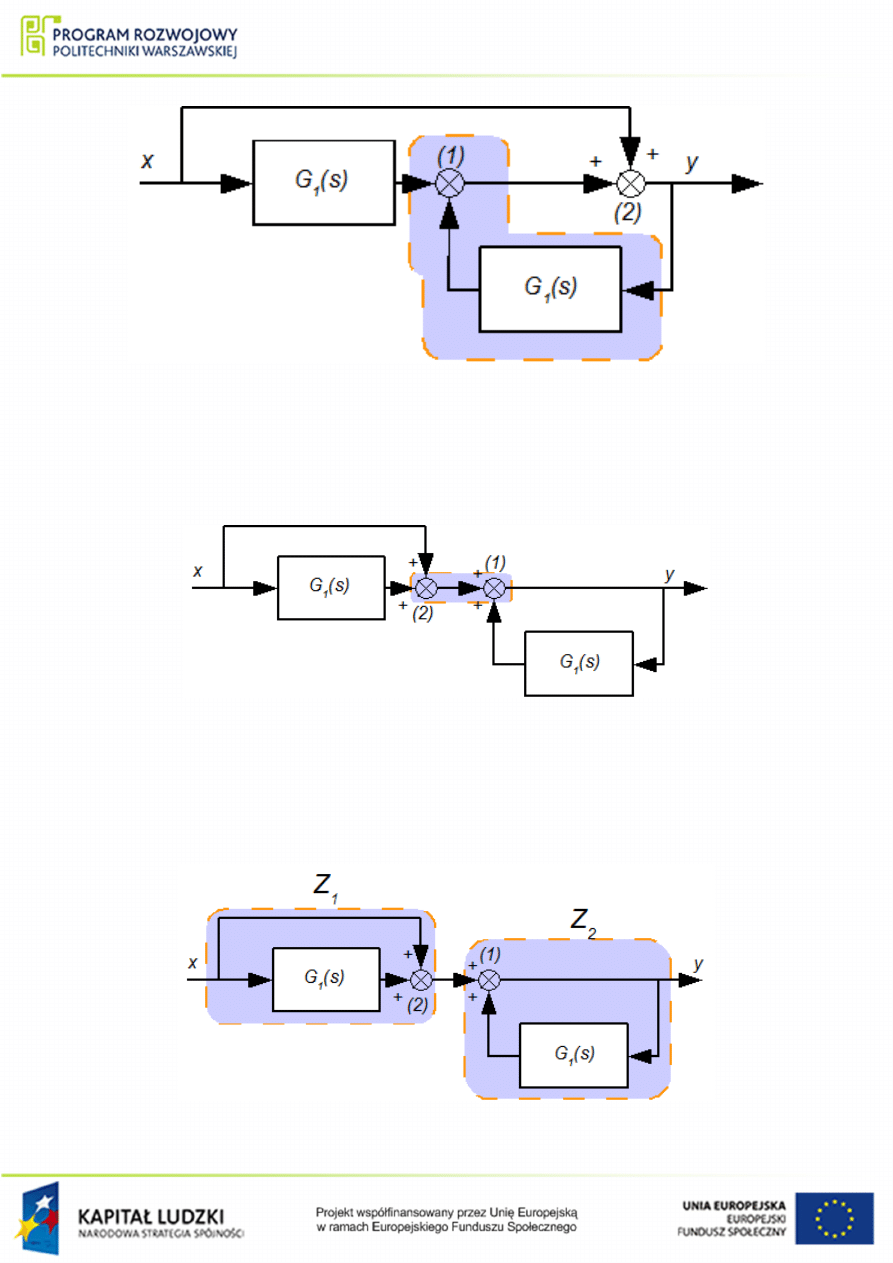
Rysunek 1.10 Zmodykowany ukªad poª¡cze« dla przykªadu

1.3

.

Nast¦pnie nale»y przestawi¢ kolejno±¢ w¦zªów sumacyjnych (1) oraz (2) (zgodnie z tablic¡

1.1

. poz. 4, zmiana kolejno±ci w¦zªów sumacyjnych), otrzymuj¡c schemat jak na rys.

1.11

:

Rysunek 1.11 Zmodykowany ukªad poª¡cze« dla przykªadu

1.3

.

Dzi¦ki zamianie w¦zªów sumacyjnych mo»na upro±ci¢ uzyskany schemat do dwóch trans-

mitancji zast¦pczych Z

1,

Z

2

, a nast¦pnie wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu (rys.

1.12

)

Rysunek 1.12 Zmodykowany ukªad poª¡cze« dla przykªadu

1.3

.

7

Transmitancja zast¦pcza b¦dzie miaªa posta¢:

Z = Z

1

Z

2

= (G

1

+ 1)

1

(1 − G

1

)

=

1 + G

1

1 − G

1

(1.3)

Przykªad 1.4

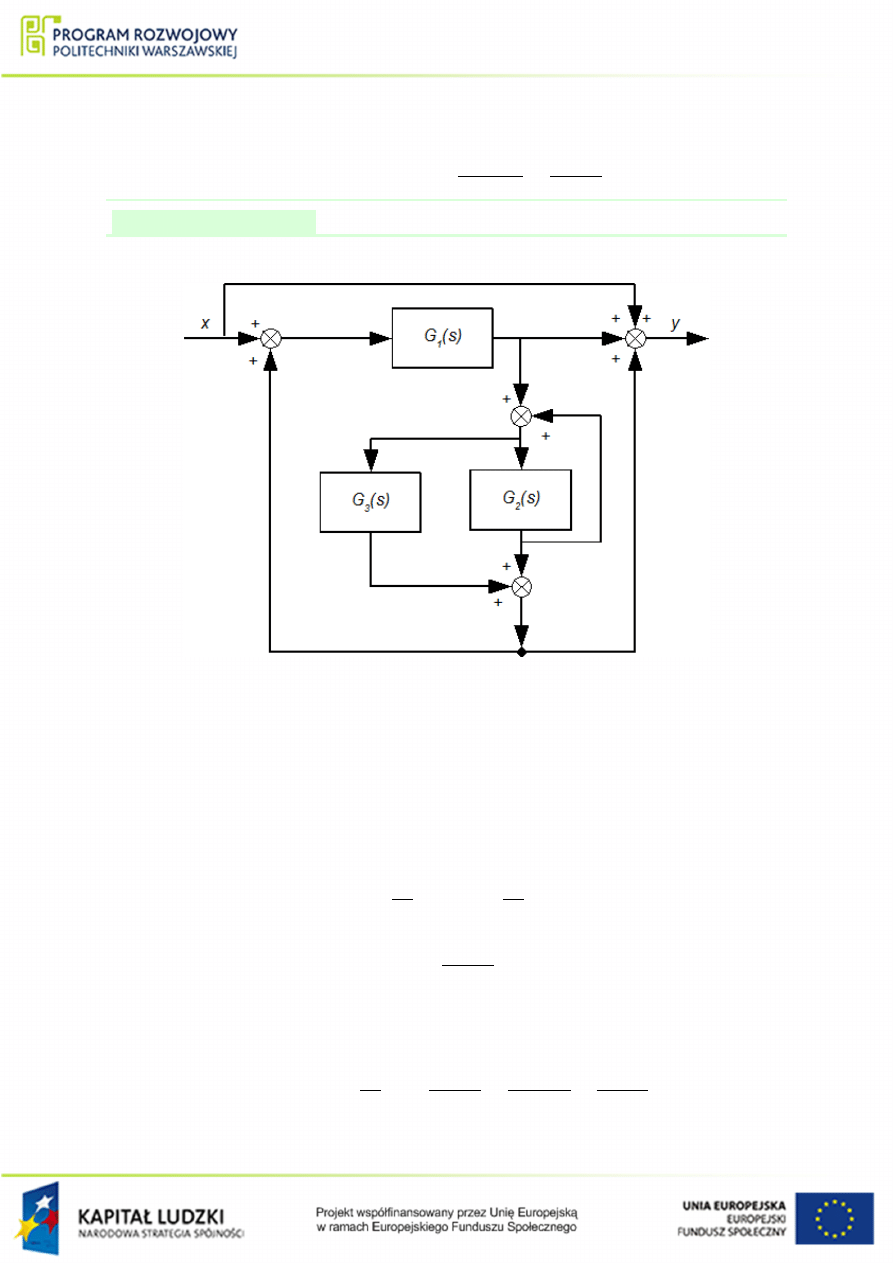
Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.4

.

Rysunek 1.13 Ukªad poª¡cze« elementów do przykªadu

1.4

W zadaniu tym, na pocz¡tek nale»y przesun¡¢ w¦zeª informacyjny przy transmitancji G

3

za blok o transmitancji G

2

(zgodnie z tablic¡

1.1

poz. 10, przesuni¦cie w¦zªa informacyj-

nego za blok) rys.

1.4

A. Nast¦pnie wyznaczane s¡ dwie transmitancje zast¦pcze Z

1,

Z

2

dla elementów zaznaczonych na rys.

1.4

B. Wynosz¡ one odpowiednio (sprz¦»enie zwrotne

oraz poª¡czenie szeregowe patrz j.w.):

Z

1

=

1

G

2

G

3

+ 1 =

G

3

G

2

+ 1

(1.4)

Z

2

=

G

2

1 + G

2

(1.5)

Uzyskano w ten sposób ukªad poª¡cze« jak na rys.

1.15

A, transmitancja zast¦pcza Z

3

wynosi:

Z

3

= Z

1

Z

2

=

G

3

G

2

+ 1

G

2

1 + G

2

=

G

3

G

2

G

2

2

+ G

2

+

G

2

1 + G

2

(1.6)

8

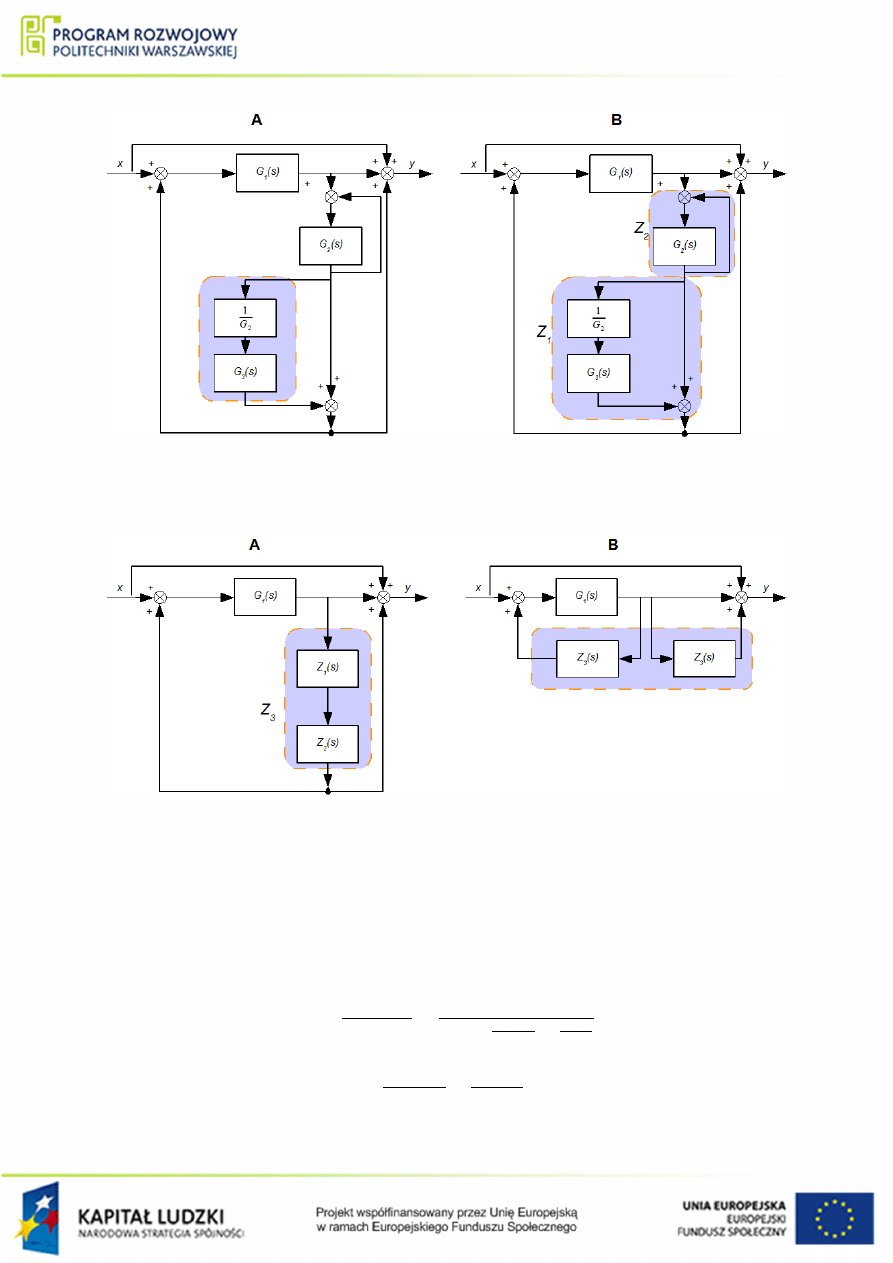
Rysunek 1.14 Zmodykowany ukªad poª¡cze« elementów do przykªadu

1.4

Rysunek 1.15 Zmodykowany ukªad poª¡cze« elementów do przykªadu

1.4

. Krok

drugi.

Nast¦pnie dzielimy w¦zeª informacyjny transmitancji Z

3

na dwie cz¦±ci (rys.

1.15

B).

W kolejnym kroku przesuwamy w¦zeª sumacyjny oraz wyznaczamy dwie transmitancje

zast¦pcze Z

4

, Z

5

(rys.

1.16

A), które wynosz¡ odpowiednio:

Z

4

=

G

1

1 + G

1

Z

3

=

G

1

1 + G

1

G

3

G

2

G

2
2

+G

2

+

G

2

1+G

2

(1.7)

Z

5

=

G

3

G

2

G

2

2

+ G

2

+

G

2

1 + G

2

+ 1

(1.8)

9

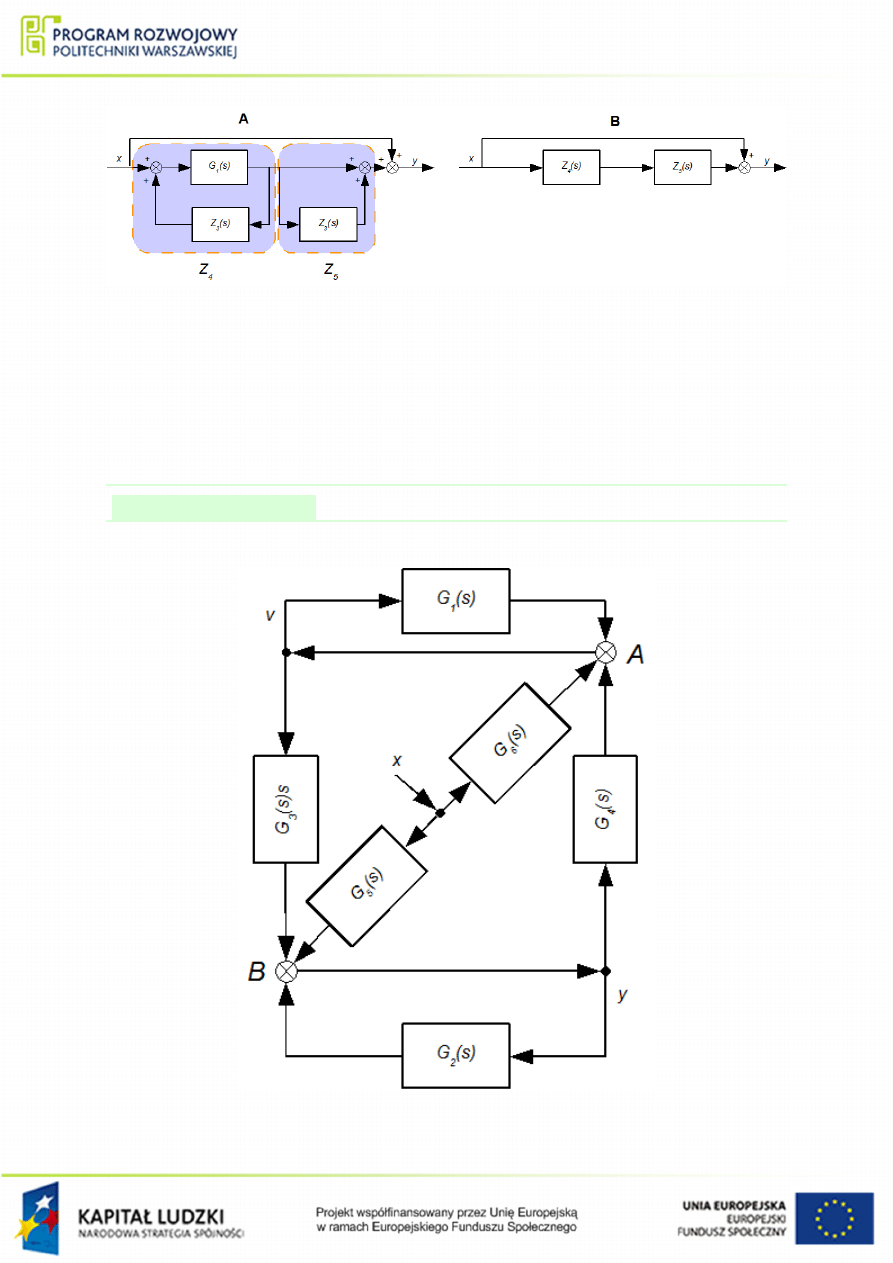
Rysunek 1.16 Zmodykowany ukªad poª¡cze« elementów do przykªadu

1.4

. Krok

trzeci.

Ostatecznie transmitancja zast¦pcza Z caªego ukªadu wynosi (rys.

1.16

B):

Z = (Z

4

Z

5

) + 1

(1.9)

Przykªad 1.5

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.17

.

Rysunek 1.17 Ukªad poª¡cze« elementów do przykªadu

1.5

.

10

Wskazówka: W podanym przykªadzie pro±ciej jest wyznaczy¢ równania dla w¦zªów

sumacyjnych A i B i analitycznie wyznaczy¢ poszukiwan¡ transmitancj¦ zast¦pcz¡.

W odniesieniu do w¦zªa sumacyjnego A sªuszne jest równanie:

v = vG

1

+ xG

6

+ yG

4

(1.10)

a w odniesieniu do w¦zªa sumacyjnego B równanie:

y = yG

2

+ xG

5

+ vG

3

(1.11)

Ruguj¡c z powy»szych równa« zmienn¡ v otrzymuje si¦:

y

x

=

G

6

(1 − G

2

) + G

4

G

5

(1 − G

1

) (1 − G

2

) − G

3

G

4

(1.12)

Co jest szukan¡ transmitancj¡ zast¦pcz¡.

11

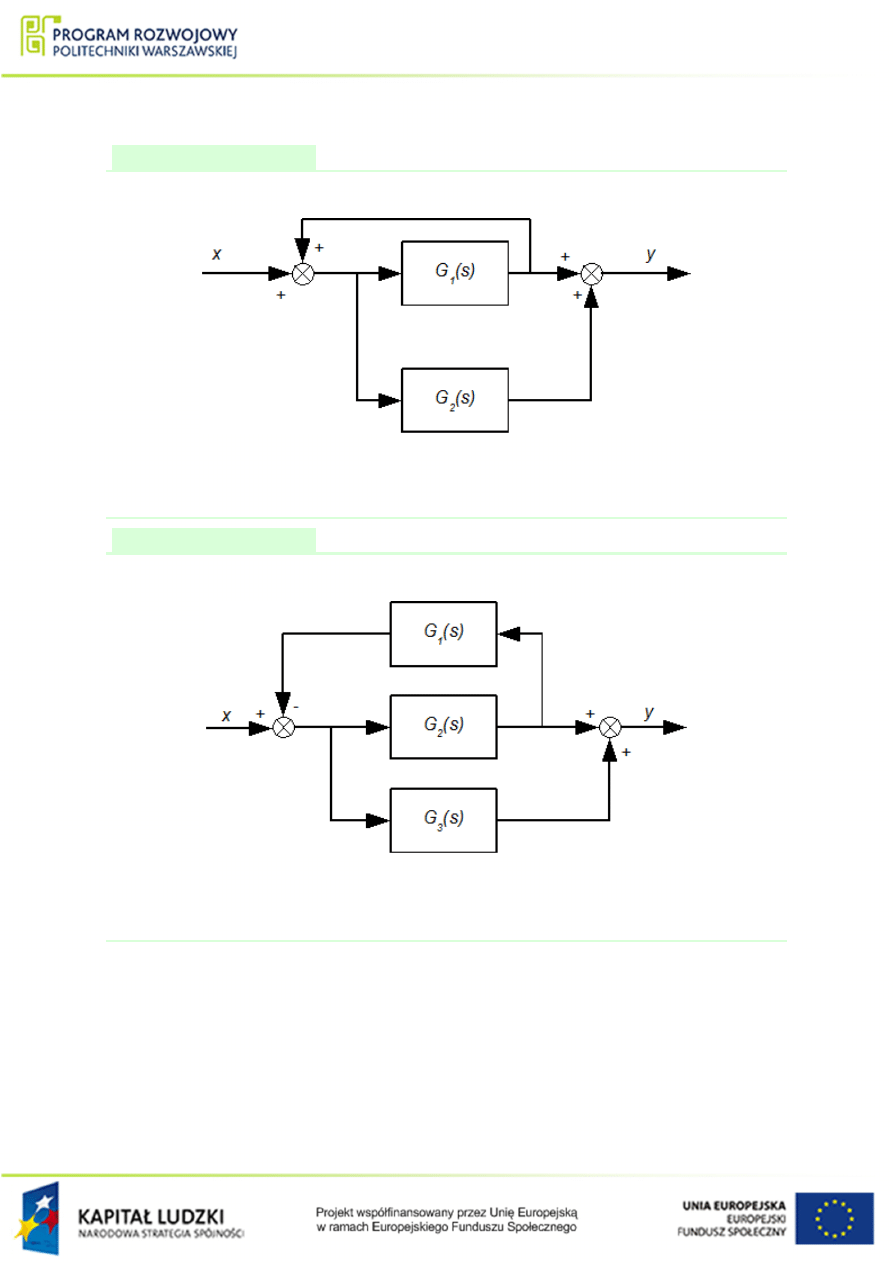
1.1.3 Zadania do samodzielnego rozwi¡zania

Przykªad 1.6

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.6

Rysunek 1.18 Ukªad poª¡cze« elementów do przykªadu

1.6

Przykªad 1.7

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.19

.

Rysunek 1.19 Schemat poª¡cze« elementów do przykªadu

1.7

.

12

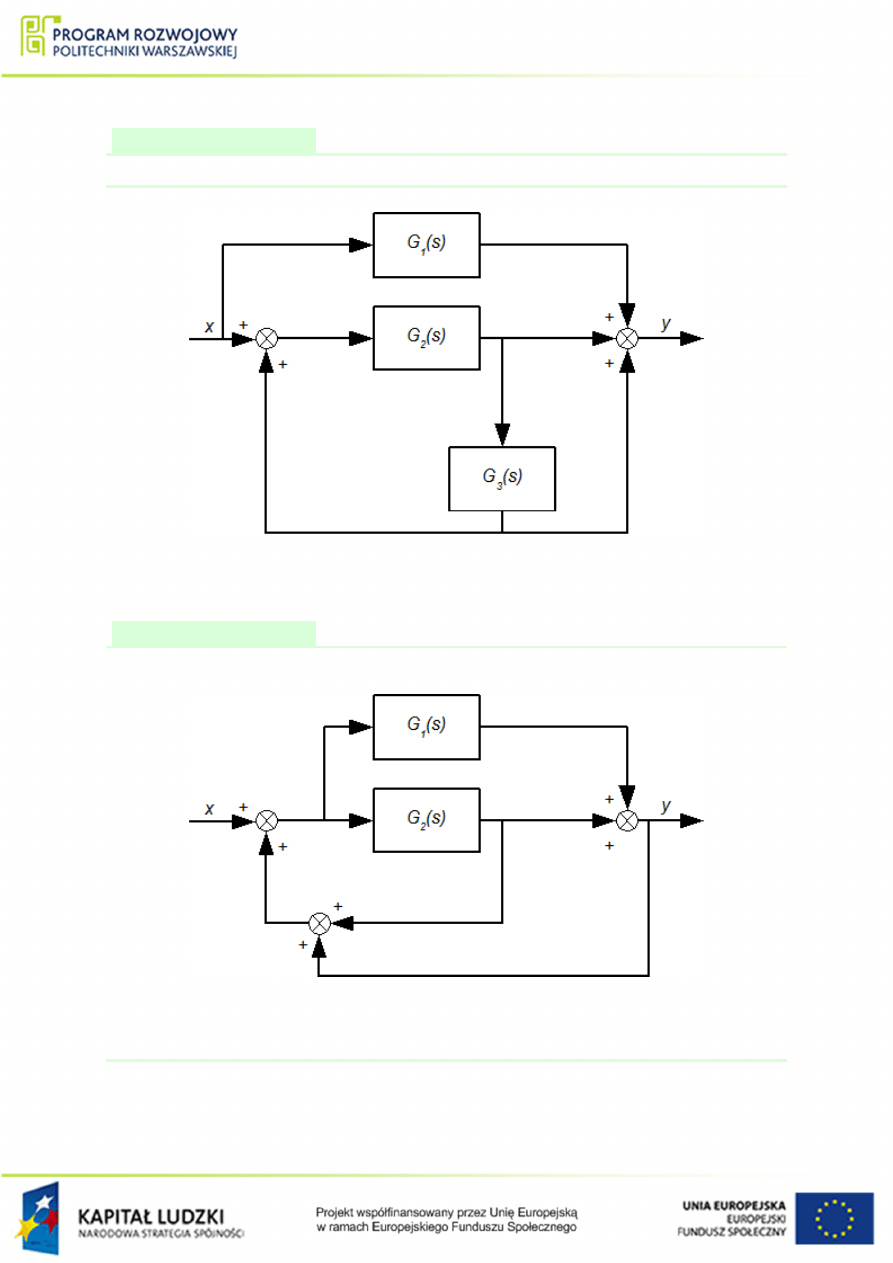
Przykªad 1.8

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.20

Rysunek 1.20 Schemat poª¡cze« elementów do przykªadu

1.8

.

Przykªad 1.9

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.9

Rysunek 1.21 Schemat poª¡cze« elementów do przykªadu

1.9

13

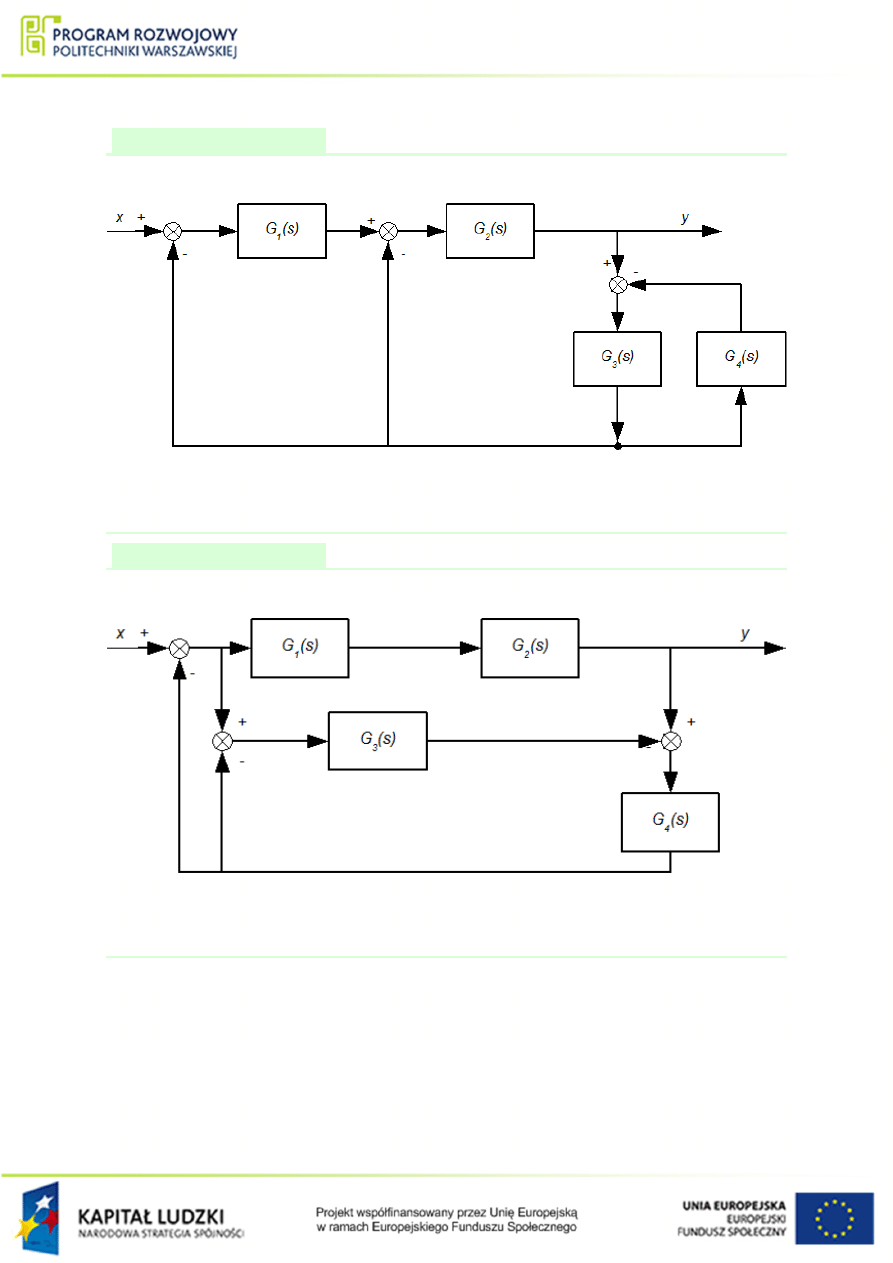
Przykªad 1.10

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.10

Rysunek 1.22 Schemat poª¡cze« elementów do przykªadu

1.10

Przykªad 1.11

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.11

Rysunek 1.23 Schemat poª¡cze« elementów do przykªadu

1.11

14

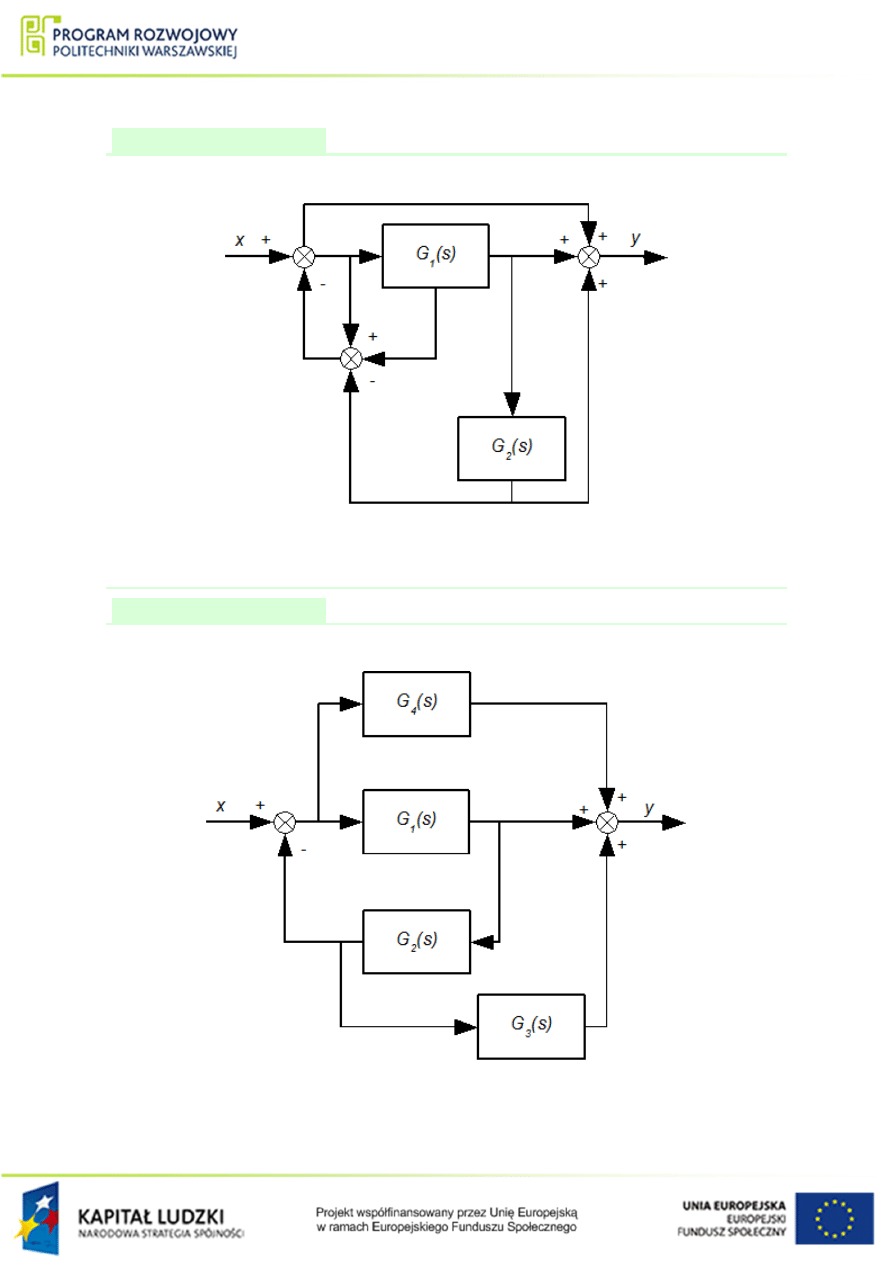
Przykªad 1.12

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.12

Rysunek 1.24 Schemat poª¡cze« elementów do przykªadu

1.12

Przykªad 1.13

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.13

Rysunek 1.25 Schemat poª¡cze« elementów do przykªadu

1.13

15

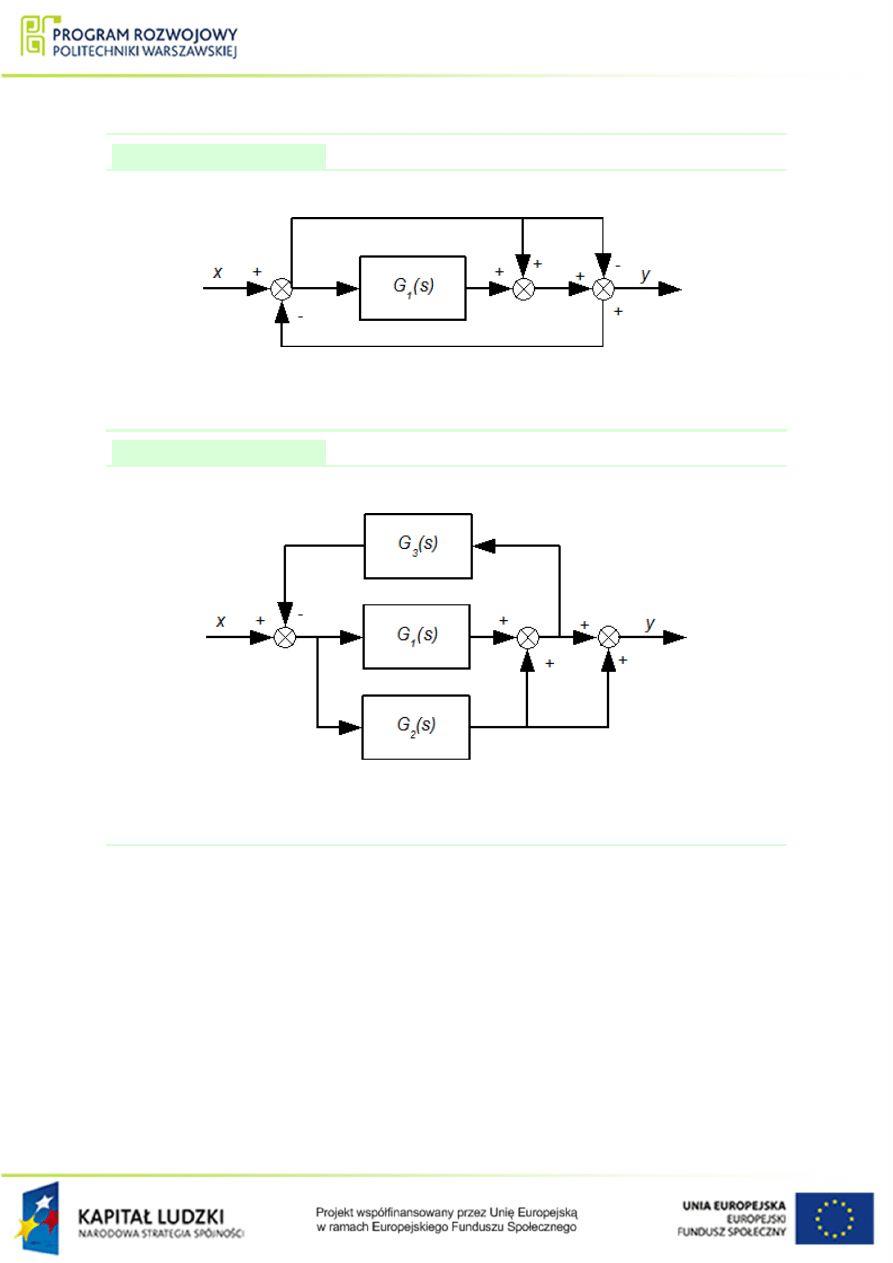
Przykªad 1.14

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.14

Rysunek 1.26 Schemat poª¡cze« elementów do przykªadu

1.14

Przykªad 1.15

Wyznaczy¢ transmitancj¦ zast¦pcz¡ ukªadu przedstawionego na rys.

1.15

Rysunek 1.27 Schemat poª¡cze« elementów do przykªadu

1.15

16

1.2 Schematy blokowe ukªadów automatyki

Analizuj¡c ukªady automatyki pro±ciej jest wykorzystywa¢ schematy blokowe ni» schematy

technologiczne. Utworzenie schematu blokowego, skªadaj¡cego si¦ z szeregu transmitancji

operatorowych wymaga opisania poszczególnych zespoªów technologicznych odpowiednimi

równaniami, a nast¦pnie wyznaczenia na tej podstawie transmitancji operatorowych. Wy-

znaczone transmitancje ukªadane s¡ nast¦pnie w schemat blokowy, na podstawie, którego

mo»na wyznaczy¢ transmitancj¦ zast¦pcz¡ caªego ukªadu.

1.2.1 Przykªady zada«

Przykªad 1.16

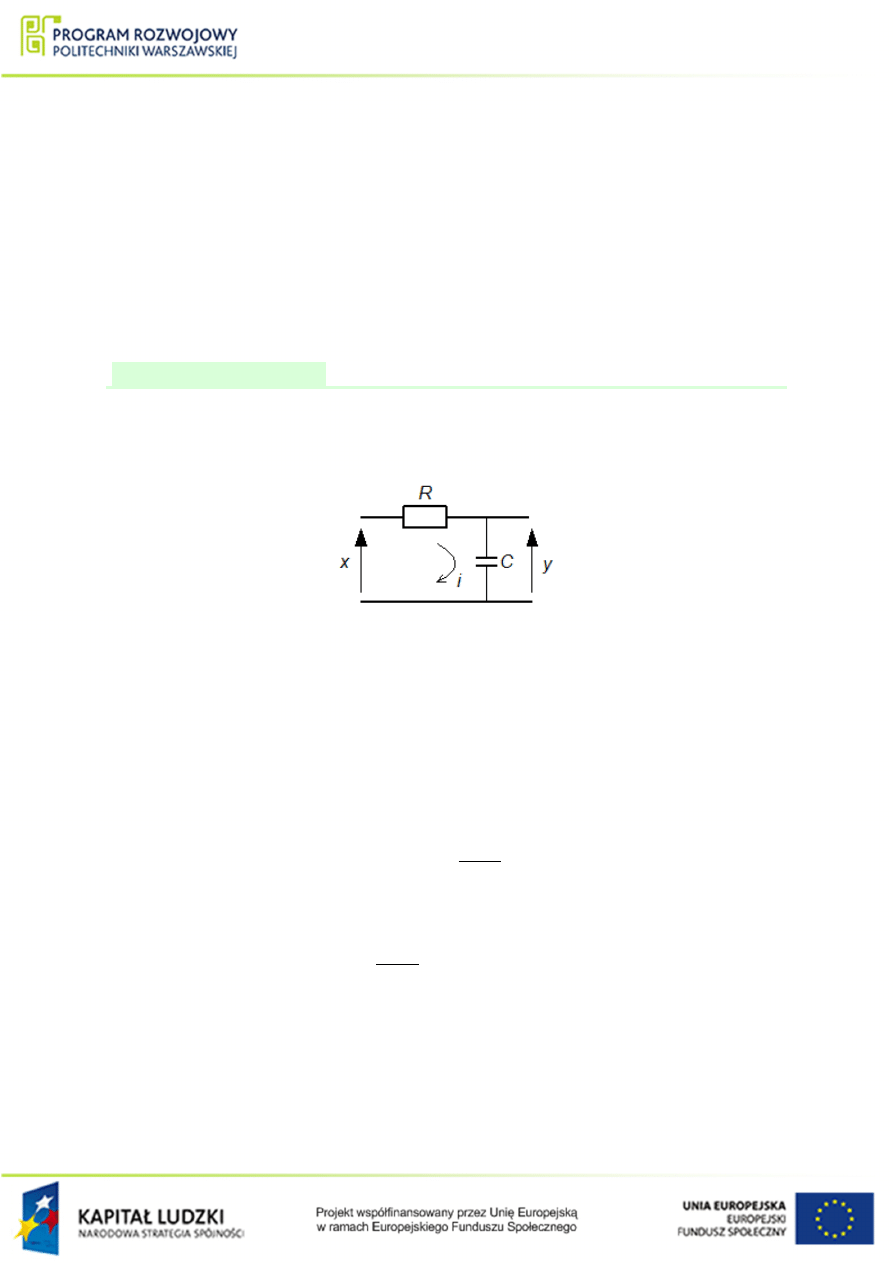
Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu elektrycznego przed-

stawionego na rys.

1.16

. Wymuszeniem jest napi¦cie x, natomiast wyj±ciem obiektu na-

pi¦cie oznaczone jako y.

Rysunek 1.28 Schemat prostego ukªadu elektrycznego do przykªadu

1.16

Napi¦cie x mo»na okre±li¢ jako:

x (t) = Ri (t) + y (t)

(1.13)

przy czym:

i (t) = C

dy (t)

dt

(1.14)

Z zale»no±ci (

1.13

), (

1.14

) mo»na wyznaczy¢ równanie ró»niczkowe ukªadu:

T

dy (t)

dt

+ y (t) = x (t)

(1.15)

gdzie:

T = RC

(1.16)

Dziaªaj¡c na równanie (

1.15

) transformat¡ Laplace'a otrzymujemy:

T sy (s) + y (s) = x (s) ⇒ y (s) (Ts + 1) = x (s)

(1.17)

17

Transmitancja ukªadu wynosi wi¦c:

G (s) =

y (s)

x (s)

=

1

Ts + 1

(1.18)

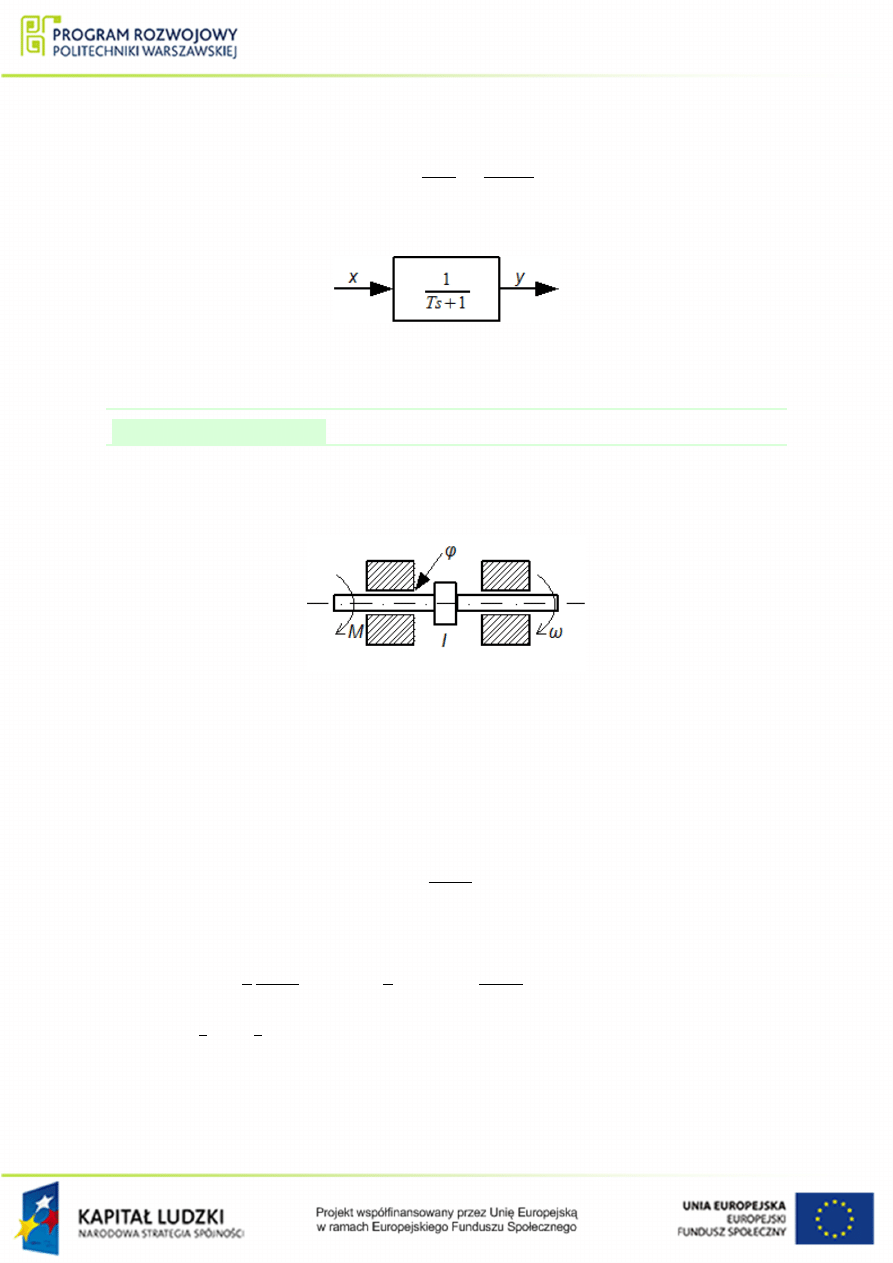
A jego schemat blokowy mo»na przedstawi¢ nast¦puj¡co:

Rysunek 1.29 Schemat blokowy ukªadu z rys.

1.16

.

Przykªad 1.17

Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu mechanicznego przed-

stawionego na rys.

1.30

. Wymuszeniem jest moment obrotowy M przyªo»ony do waªu

wyj±ciem pr¦dko±¢ k¡towa ω.

Rysunek 1.30 Schemat prostego ukªadu mechanicznego do przykªadu

1.17

.

Gdzie: M - moment obrotowy, φ - wspóªczynnik tarcia lepkiego, I- moment bezwªadno±ci,
ω

- pr¦dko±¢ k¡towa.

Z II zasady dynamiki Newtona dla ruchu obrotowego mo»na napisa¢, »e:

M (t) = I

dω (t)

dt

+ φω (t)

(1.19)

A nast¦pnie, »e:

I

φ

dω (t)

dt

+ ω (t) =

1

φ

M (t) ⇒ T

dω (t)

dt

+ ω (t) = kM (t)

(1.20)

Gdzie :T =

I

φ

, k =

1

φ

.

Dziaªaj¡c na równanie (

1.20

) transformat¡ Laplace'a otrzymujemy:

T sω (s) + ω (s) = kM (s) ⇒ ω (s) (Ts + 1) = kM (s)

(1.21)

18

Transmitancja ukªadu wynosi wi¦c:

G (s) =

ω (s)

M (s)

=

k

Ts + 1

(1.22)

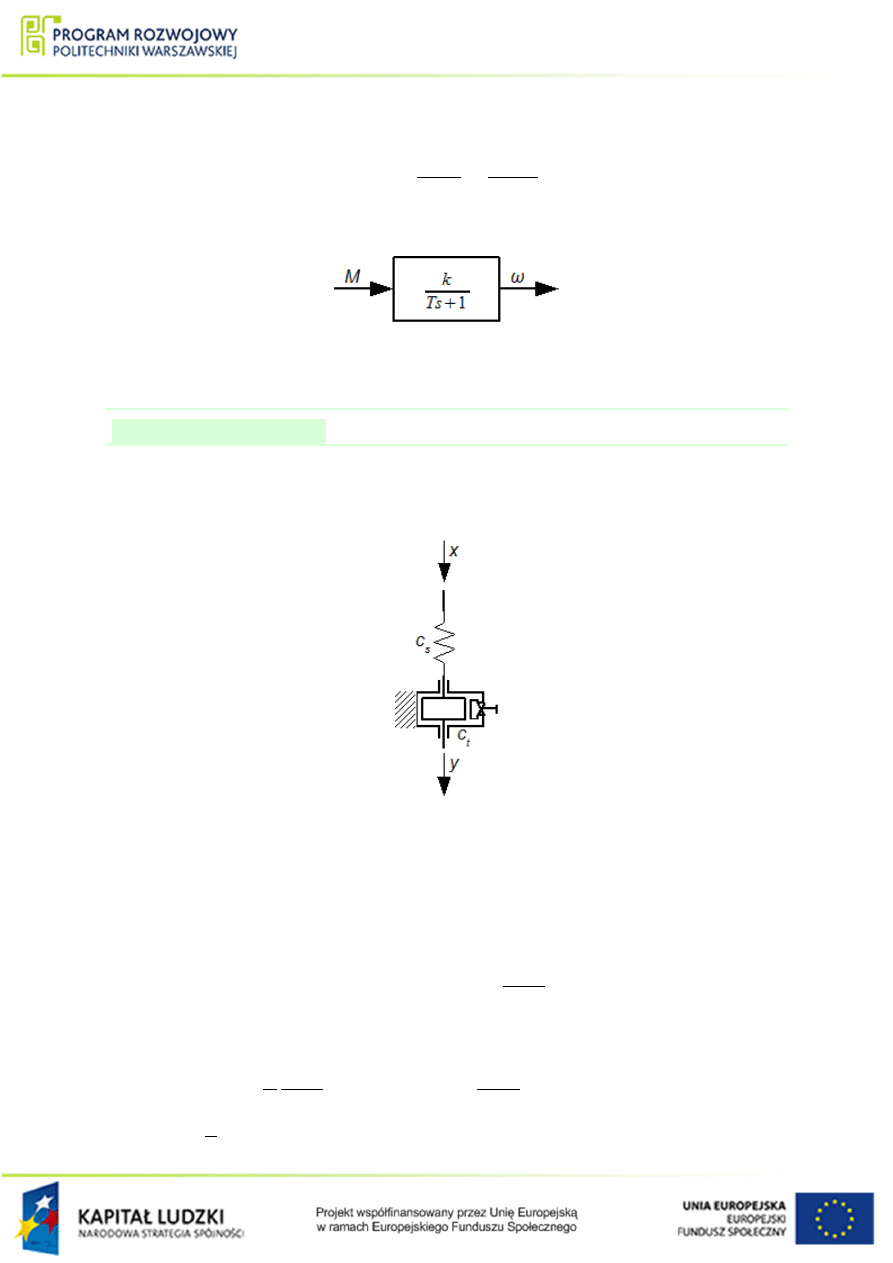
A jego schemat blokowy mo»na przedstawi¢ nast¦puj¡co:

Rysunek 1.31 Schemat blokowy ukªadu z rys.

1.30

.

Przykªad 1.18

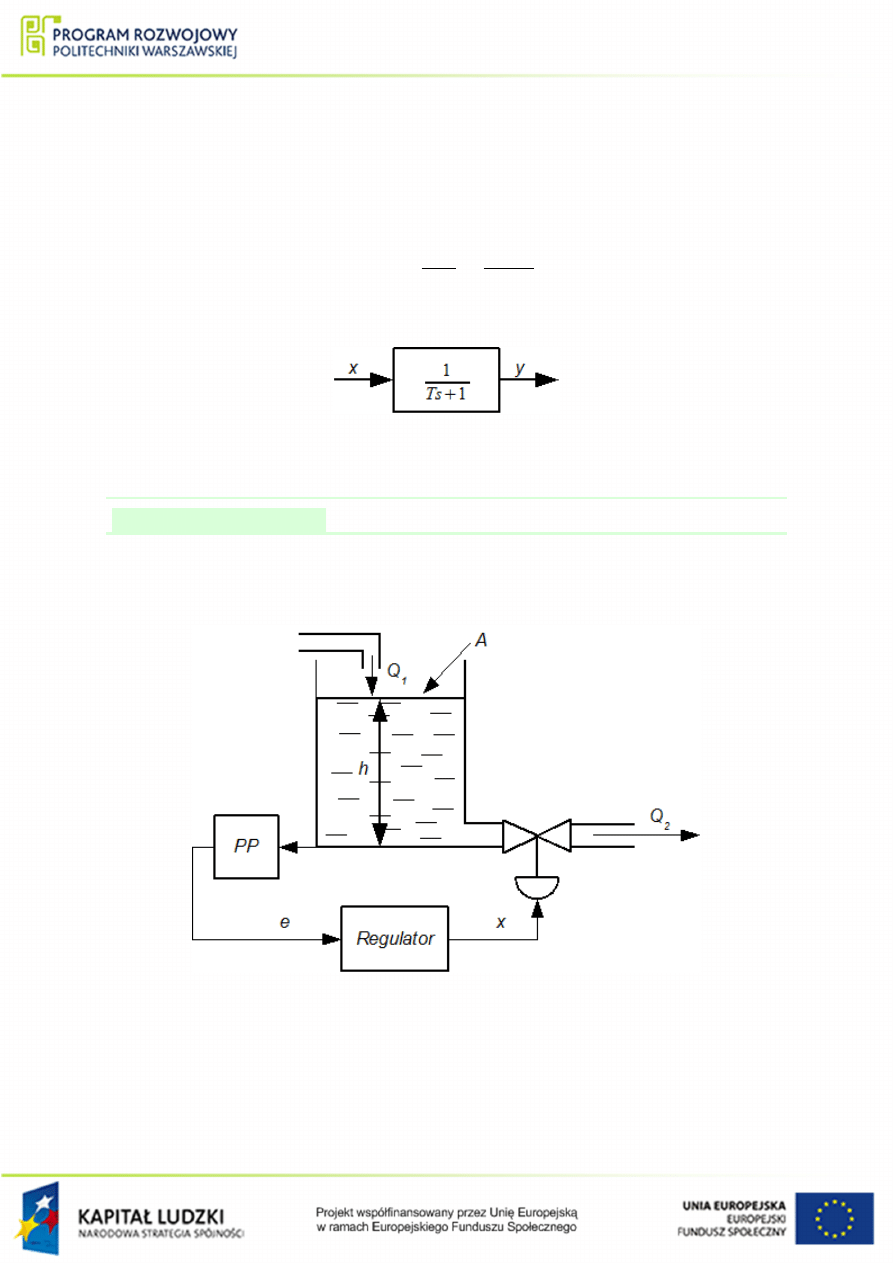
Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu mechanicznego przed-

stawionego na rys.

1.32

. Wymuszeniem jest przesuni¦cie x natomiast wyj±ciem przesu-

ni¦cie y.

Rysunek 1.32 Schemat prostego ukªadu mechanicznego do przykªadu

1.19

.

Gdzie: c

s

- staªa spr¦»ysto±ci spr¦»yny, c

t

- staªa tªumienia tªumika pneumatycznego.

Równanie siª przedstawionego ukªadu wygl¡da nast¦puj¡co:

(x (t) − y (t)) c

s

= c

t

dy (t)

dt

(1.23)

Z równania (

1.23

) mamy:

c

t

c

s

dy (t)

dt

+ y (t) = x (t) ⇒ T

dy (t)

dt

+ y (t) = x (t)

(1.24)

Gdzie: T =

c

t

c

s

.

19

Dziaªaj¡c na równanie (

1.24

) transformat¡ Laplace'a otrzymujemy:

Tsy (s) + y (s) = x (s) ⇒ y (s) (Ts + 1) = x (s)

(1.25)

Transmitancja ukªadu wynosi wi¦c:

G (s) =

y (s)

x (s)

=

1

Ts + 1

(1.26)

A jego schemat blokowy mo»na przedstawi¢ nast¦puj¡co:

Rysunek 1.33 Schemat blokowy ukªadu z rys.

1.32

Przykªad 1.19

Przykªad ten zostaª zaczerpni¦ty z [?] . Narysowa¢ schemat blokowy oraz wyznaczy¢

transmitancj¦ ukªadu przedstawionego na rys.

1.34

. Wymuszeniem jest nat¦»enie prze-

pªywu cieczy Q

1

a wyj±ciem poziom cieczy w zbiorniku h.

Rysunek 1.34 Schemat ukªadu regulacji automatycznej dla przykªadu

1.48

.

Charakterystyka przetwornika pomiarowego (element oznaczony jako PP , na rys.

1.34

)

wygl¡da nast¦puj¡co:

20

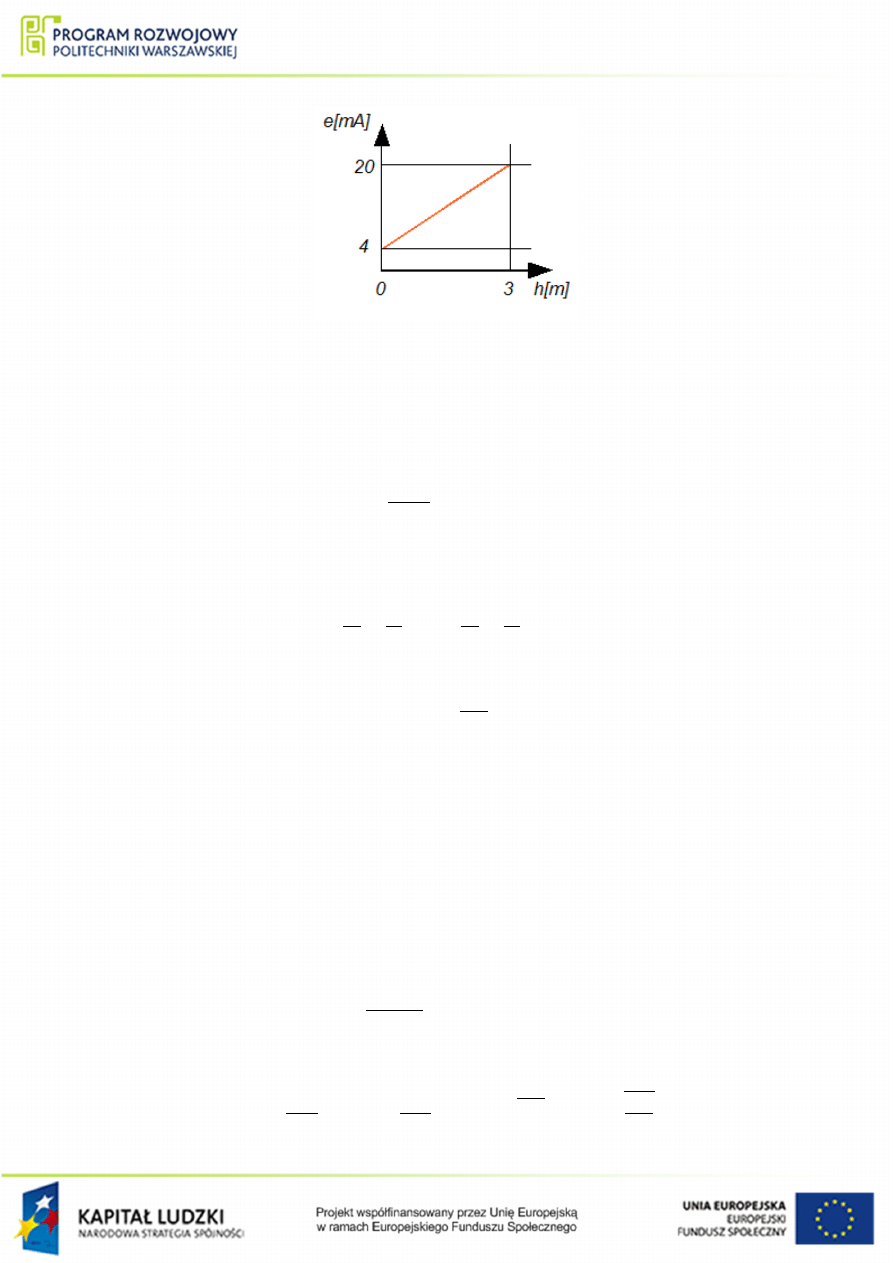
Rysunek 1.35 Charakterystyka przetwornika pomiarowego dla przykªadu

1.19

.

W pierwszej kolejno±ci wyznaczona zostanie transmitancja obiektu regulacji. W stanach

nieustalonych zmiany poziomu cieczy w zbiorniku mo»na opisa¢ za pomoc¡ zale»no±ci:

A

dh (t)

dt

= Q

1

− Q

2

(1.27)

Nat¦»enie przepªywu Q

2

mo»na obliczy¢ z równania Bernoulli'ego dla poziomu lustra

cieczy (1) oraz wypªywu ze zbiornika (2) mo»na zapisa¢ nast¦puj¡co:

v

2

1

2g

+

p

1

γ

+ h =

v

2

2

2g

+

p

2

γ

+ 0

(1.28)

Przyjmuj¡c v

1

= 0

oraz p

1

= p

2

otrzymuje si¦:

v

2

=

q

2gh

(1.29)

Na podstawie równania ci¡gªo±ci przepªywu tzn.:

Q

2

= f v

2

(1.30)

gdzie f - pole przekroju kanaªu zaworu.
Nast¦pnie nale»y zlinearyzowa¢ przedstawione równanie w wybranym punkcie pracy, ozna-

czonym h

n

, Q

1n

, f

n

. W otoczeniu wybranego punktu pracy przyrosty zmiennych h oraz Q

2

zast¦puje si¦ ich liniowymi aproksymacjami. Dla odró»nienia zapisu wszystkie przyrosty

oznaczane s¡ wi¦c poprzez dodanie symbolu ∆:

A

d∆h (t)

dt

= ∆Q

1

− ∆Q

2

(1.31)

Przyrost ∆Q

2

zast¡piony zostaje ró»niczk¡ zupeªn¡:

∆Q

2

=

∂Q

2

∂f

!

n

∆f +

∂Q

2

∂h

!

n

∆h =

q

2gh∆f + f

n

s

g

2h

n

∆h

(1.32)

21

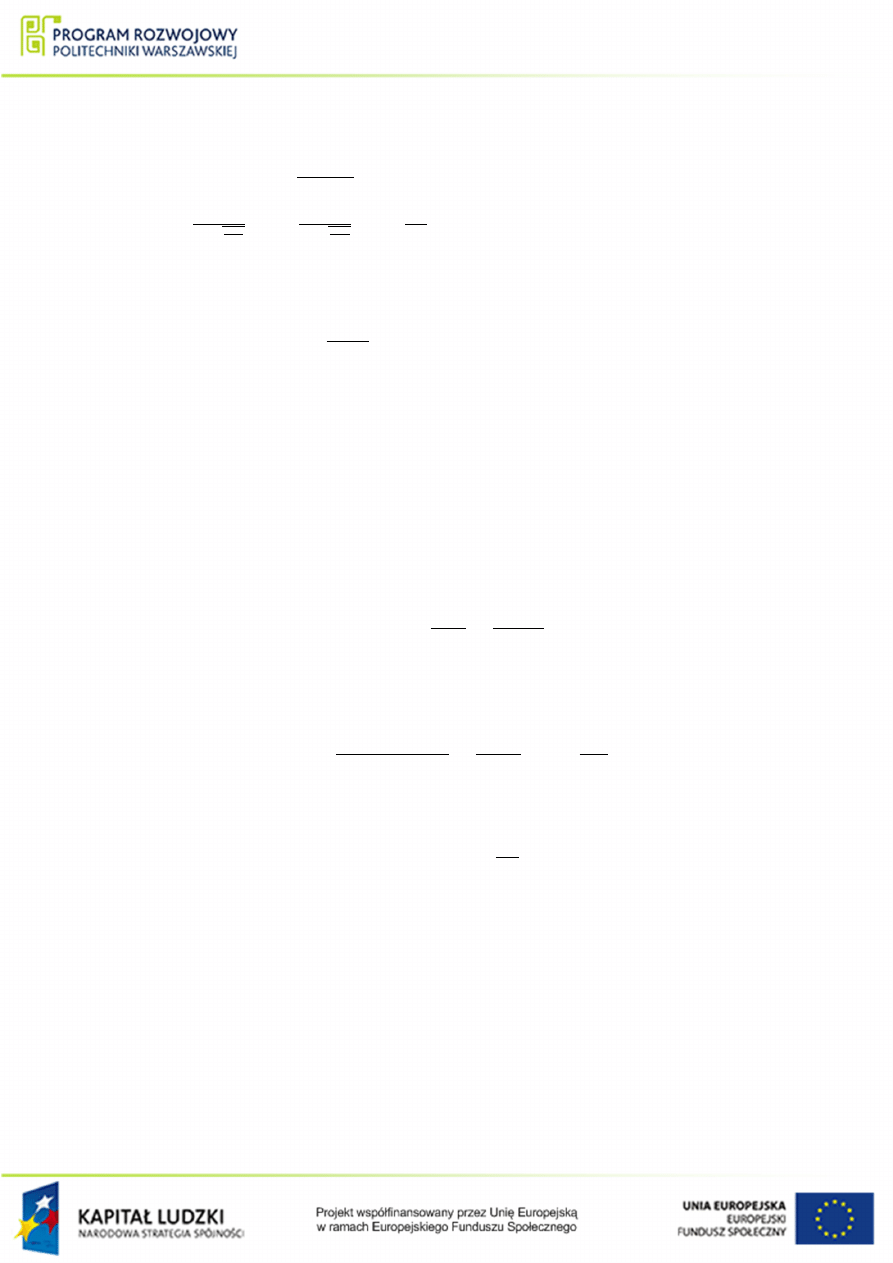
Zale»no±¢ (

1.31

) mo»na wi¦c zapisa¢ jako:

T

d∆h (t)

dt

+ ∆h (t) = k

1

∆Q

1

(t) − k

2

∆f (t)

(1.33)

Gdzie:T =

A

f

n

√

g

2hn

, k

1

=

1

f

n

√

g

2hn

, k

2

=

2h

n

f

n

Znak ∆ mo»e by¢ pomini¦ty, przy jednoczesnym uwzgl¦dnieniu »e w zale»no±ci (

1.31

)

wyst¦puj¡ przyrosty poszczególnych warto±ci.

T

dh (t)

dt

+ h (t) = k

1

Q

1

(t) − k

2

f (t)

(1.34)

Dziaªaj¡c na zale»no±¢ (

1.34

) transformat¡ Laplace'a otrzymujemy:

T sh (s) + h (s) = k

1

Q

1

(s) − k

2

f (s) ⇒ h (s) (T s + 1) = k

1

Q

1

(s) − k

2

f (s)

(1.35)

Oznaczaj¡c

v (s) = k

1

Q

1

(s) − k

2

f (s)

(1.36)

Mo»na wyznaczy¢ transmitancj¦ obiektu regulacji:

G

OB

(s) =

h (s)

v (s)

=

1

T s + 1

(1.37)

Przetwornik pomiarowy mo»na opisa¢ jako obiekt bezinercyjny ze wzmocnieniem. Wzmoc-

nienie przetwornika mo»na odczyta¢ z jego charakterystyki (rys.

1.35

).

k

PP

=

wy

max

− wy

min

we

max

− we

min

=

16

mA

3

m

= 5.33

mA

m

(1.38)

Jako regulator przyjmijmy regulator typu PI o transmitancji:

G

R

(s) = k

p

1 +

1

T

i

s

(1.39)

Wyj±ciem z regulatora jest sygnaª pr¡dowy o zakresie 4 20 mA, który podawany jest na

ustawnik pozycyjny, który mo»na zamodelowa¢ jako element bezinercyjny o wzmocnieniu
k

f

Wynikowe pole przekroju otwarcia zaworu wynosi¢ wi¦c b¦dzie:

f = k

f

x

(1.40)

Wykorzystuj¡c zale»no±ci (

1.36

) (

1.37

) (

1.38

) (

1.39

) (

1.40

) mo»na narysowa¢ schemat

blokowy ukªadu regulacji automatycznej, przedstawionego na rys.

1.34

22

Rysunek 1.36 [Tu wpisz Podpis rysunku. Uwaga: (1) Jedynie dla rysunków

osadzonych w rozdziaªach. W pozostaªych dokumentach element ten mo»na usun¡¢

zostanie on zignorowany.]

gdzie: 1 graczna reprezentacja zale»no±ci (

1.36

), 2 graczna reprezentacja zale»no±ci

(

1.37

) , 3 graczna reprezentacja zale»no±ci (

1.38

), 4 graczna reprezentacja zale»no±ci

(

1.39

), 5 - graczna reprezentacja zale»no±ci (

1.40

).

Transmitancja zast¦pcza ukªadu wynosi zatem:

G (s) =

h (s)

Q

1

(s)

= k

1

1

T s+1

1 +

1

T s+1

k

PP

k

f

k

2

k

p

T

i

s+1

T

i

s

=

k

1

T

i

s

(T s + 1) T

i

s + k

PP

k

f

k

2

k

p

(T

i

s + 1)

(1.41)

Przykªad 1.20

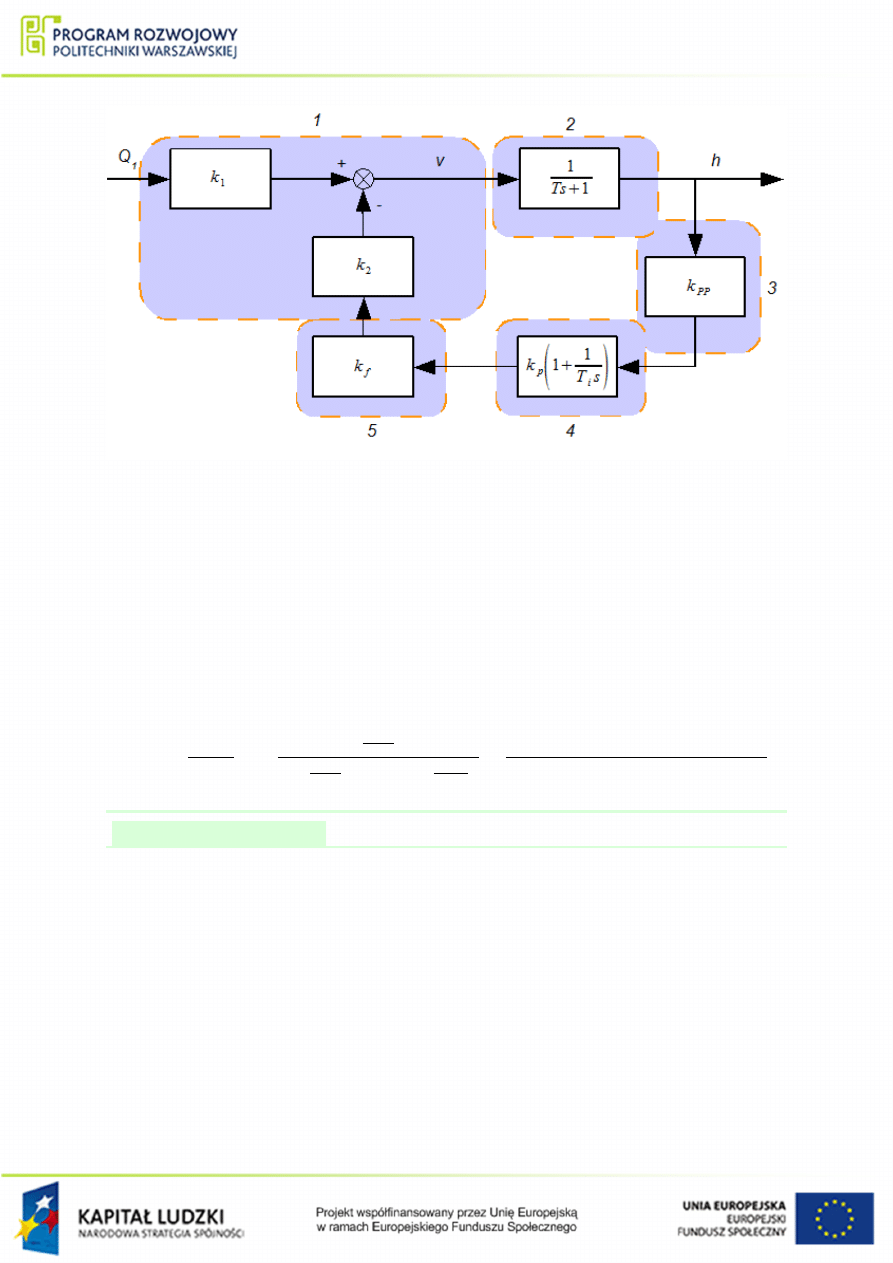
Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu mechanicznego przed-

stawionego na rys.

1.37

. Wymuszeniem jest przesuni¦cie x, natomiast wyj±ciem przesu-

ni¦cie y. Ci±nienia p

1

, p

2

s¡ staªe.

23

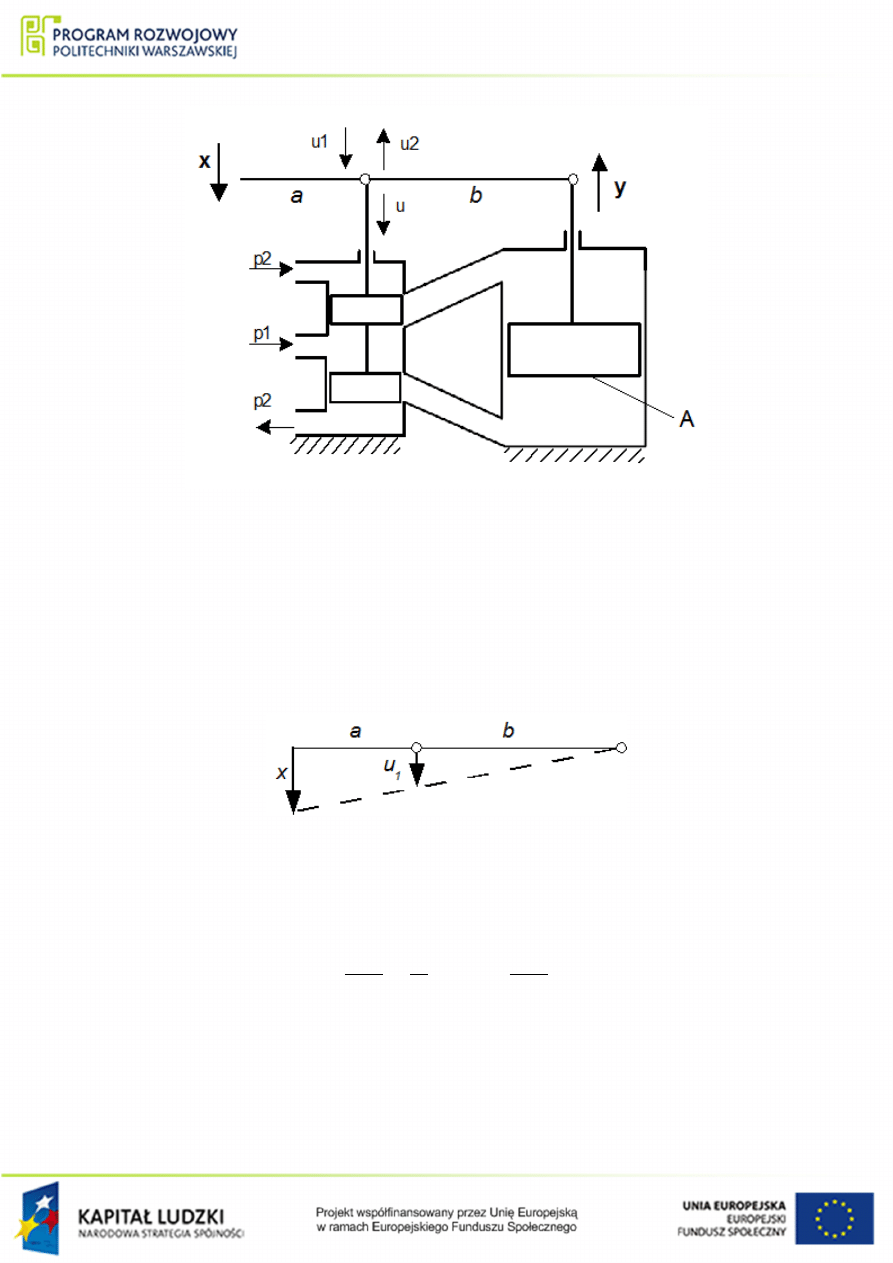
Rysunek 1.37 Schemat ukªadu mechanicznego do przykªadu

1.20

.

Zauwa»my »e przesuni¦cie u mo»na zapisa¢ jako sum¦ przesuni¦¢ u

1

oraz u

2

:

u = u

1

− u

2

(1.42)

Przesuni¦cie u

1

mo»na wyznaczy¢, unieruchamiaj¡c punkt d¹wigni dla przesuni¦cia y:

Rysunek 1.38 Sposób wyznaczenia przesuni¦cia u

1

:

Šatwo mo»na zauwa»y¢ (rys.

1.38

), »e:

x

a + b

=

u

1

b

⇒ u

1

= x

b

a + b

(1.43)

Podobnie, u

2

mo»na wyznaczy¢, unieruchamiaj¡c punkt d¹wigni dla przesuni¦cia x:

24

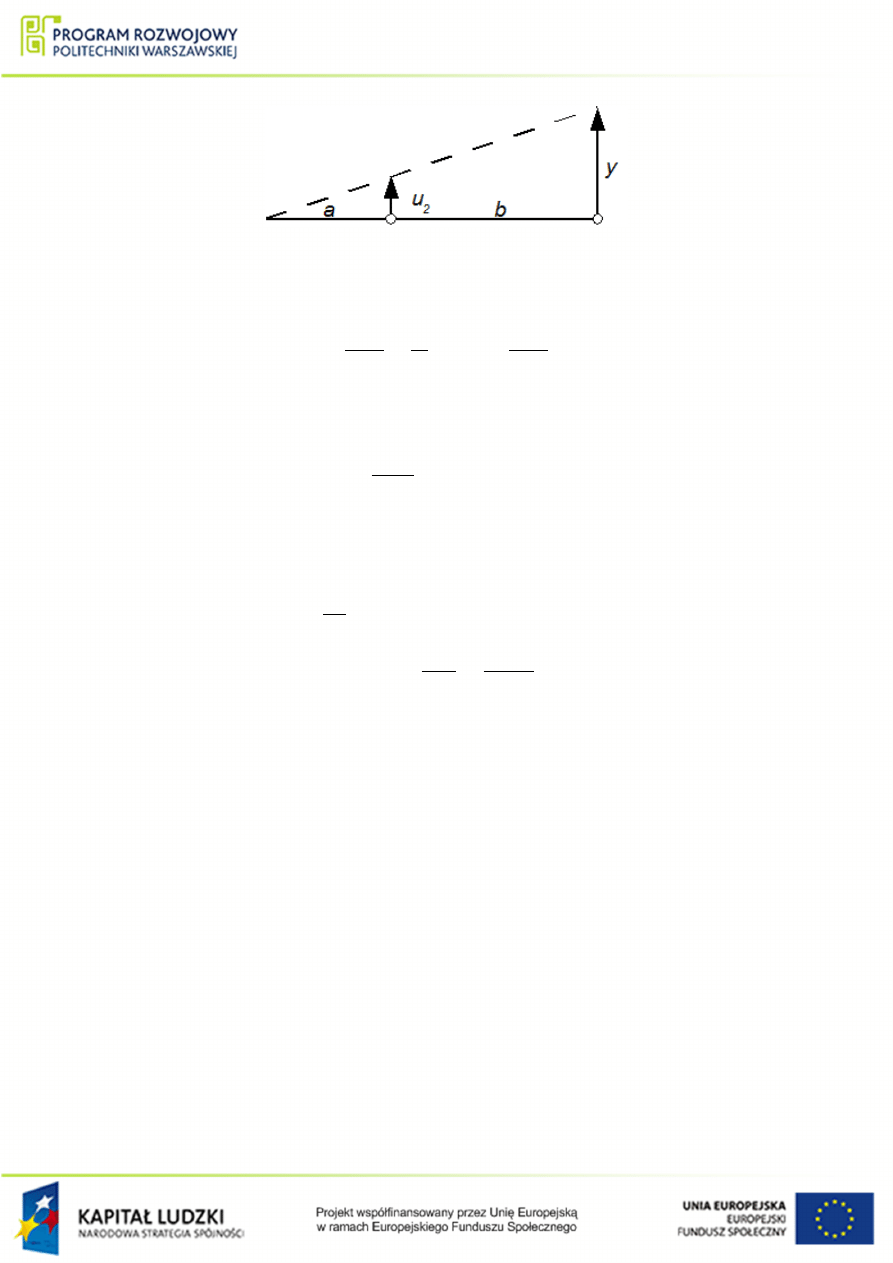
Rysunek 1.39 Sposób wyznaczenia przesuni¦cia u

2

:

y

a + b

=

u

2

a

⇒ u

2

= y

a

a + b

(1.44)

Nast¦pnie, zauwa»my, »e dla staªych ci±nie« p

1

, p

2

, element zaznaczony na rys.

1.40

mo»na

opisa¢ nast¦puj¡ca zale»no±ci¡:

T

dy (t)

dt

+ y (t) = ku (t)

(1.45)

Dziaªaj¡c na zale»no±¢ (

1.45

) transformat¡ Laplace'a otrzymujemy:

T sy (s) + y (s) = ku (s) ⇒ y (s) (Ts + 1) = ku (s)

(1.46)

St¡d transmitancja G (s) =

y(s)
u(s)

wynosi:

G (s) =

y (s)

u (s)

=

k

Ts + 1

(1.47)

Gdzie dla staªych ci±nie« p

1

, p

2

, T, k˜ (p

1

, p

2,

A)

25

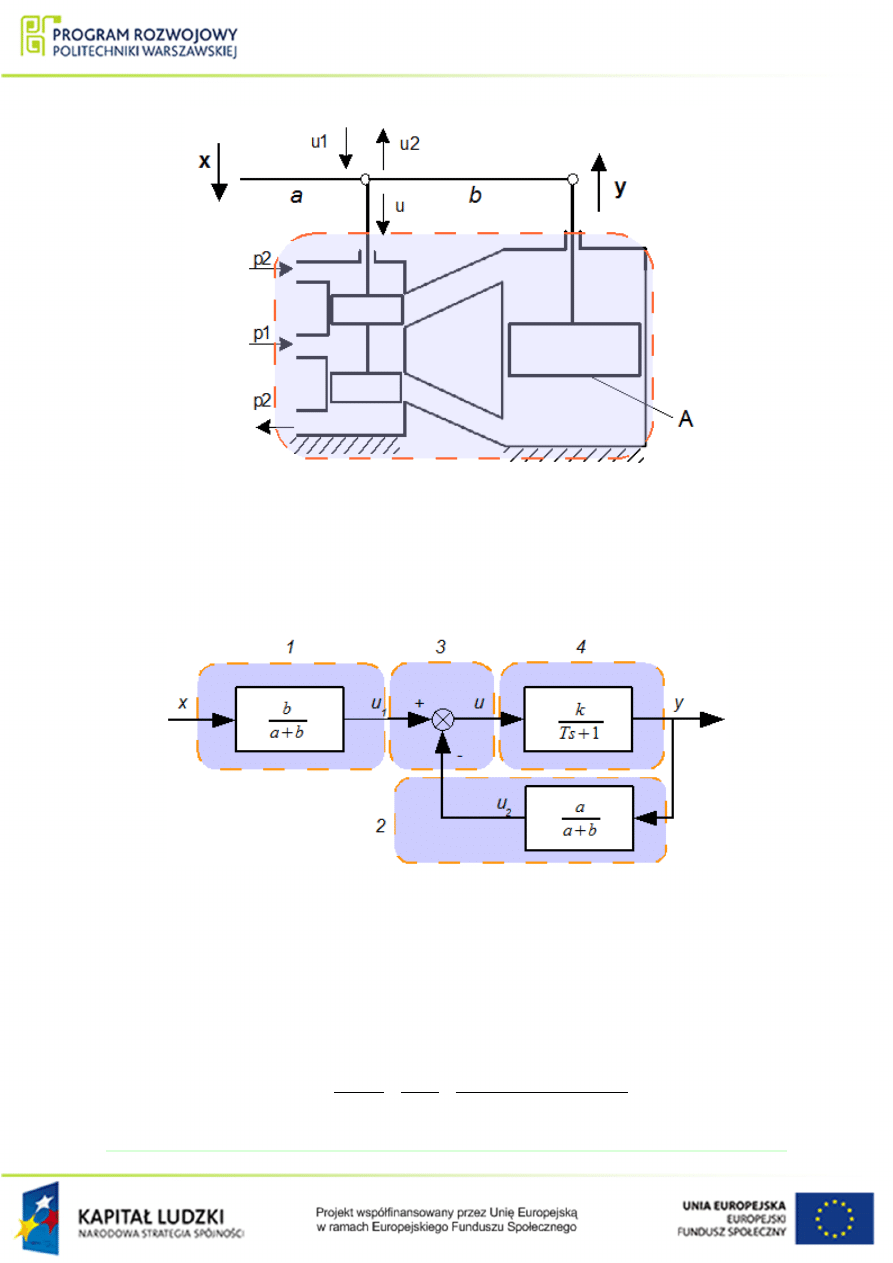
Rysunek 1.40 Wyznaczanie transmitancji zast¦pczej ukªadu elementów dla

przykªadu

1.20

.

Schemat blokowy ukªadu elementów z rys.

1.37

mo»na wi¦c przedstawi¢ nast¦puj¡co:

Rysunek 1.41 Schemat blokowy elementów z rys.

1.37

.

gdzie: 1 graczna reprezentacja zale»no±ci (

1.43

), 2 graczna reprezentacja zale»no±ci

(

1.44

) , 3 graczna reprezentacja zale»no±ci (

1.42

), 4 graczna reprezentacja zale»no±ci

(

1.46

).

Transmitancja zast¦pcza ukªadu przedstawionego na rys.

1.41

wynosi:

G

z

(s) =

k

Ts + 1

·

b

a + b

·

(Ts + 1) (a + b) + u · a

(Ts + 1) (a + b)

(1.48)

Oznaczenia j.w.

26

1.2.2 Zadania do samodzielnego rozwi¡zania

Przykªad 1.21

Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu mechanicznego przed-

stawionego na rys.

1.42

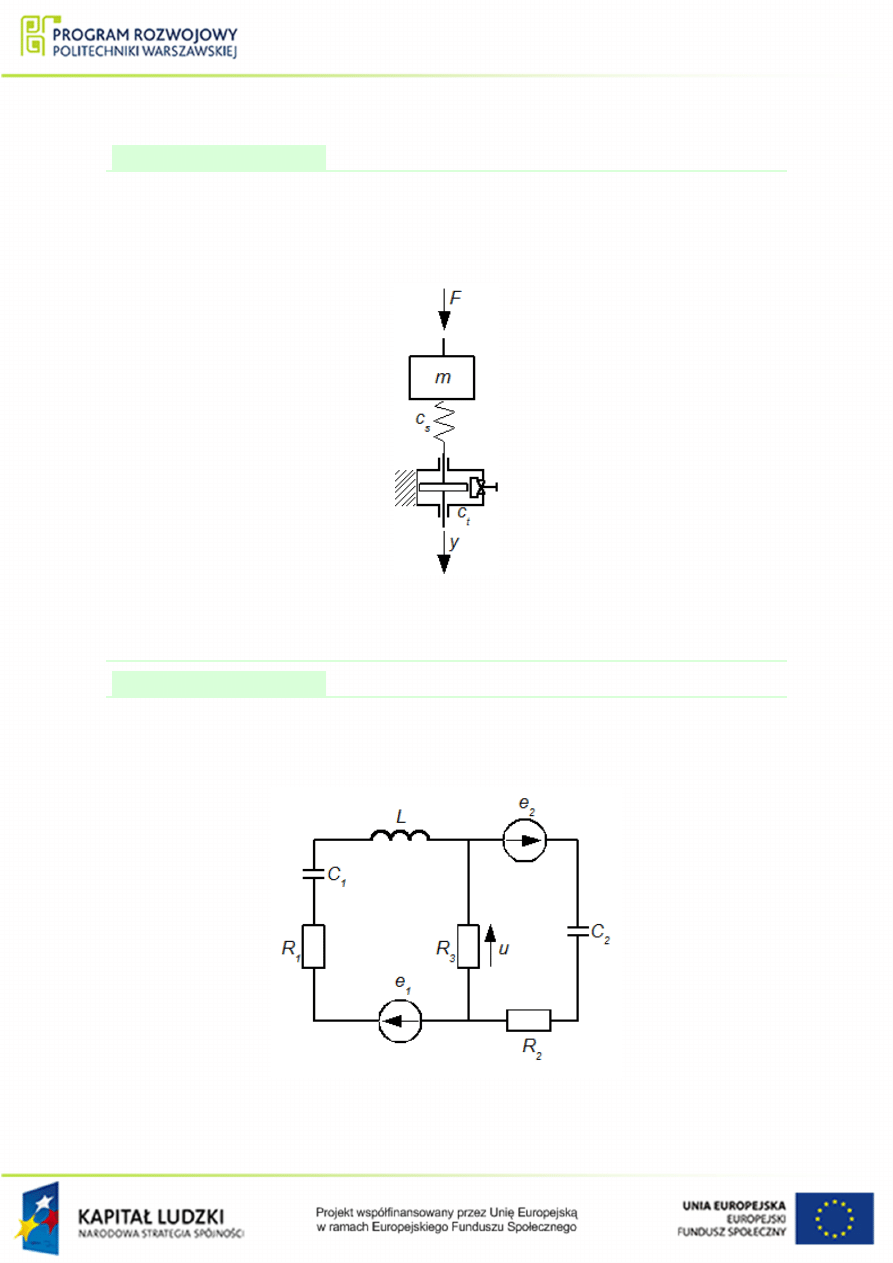
. Wymuszeniem jest siªa F, natomiast wyj±ciem przesuni¦cie y.

Mas¦ elementów oznaczono jako m, staª¡ spr¦»ysto±ci spr¦»yny jako c

s

, natomiast wspóª-

czynnik tªumienia jako c

t

.

Rysunek 1.42 Schemat mechaniczny do przykªadu

1.21

.

Przykªad 1.22

Narysowa¢ schemat blokowy ukªadu elektrycznego przedstawionego na rys.

1.43

. Wymu-

szeniami s¡ napi¦cia ¹ródªowe e

1

oraz e

2

, natomiast wyj±ciem napi¦cie u na rezystancji

R

3

.

Rysunek 1.43 Schemat elektryczny do przykªadu

1.22

.

27

Przykªad 1.23

Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu mechanicznego przed-

stawionego na rys.

1.44

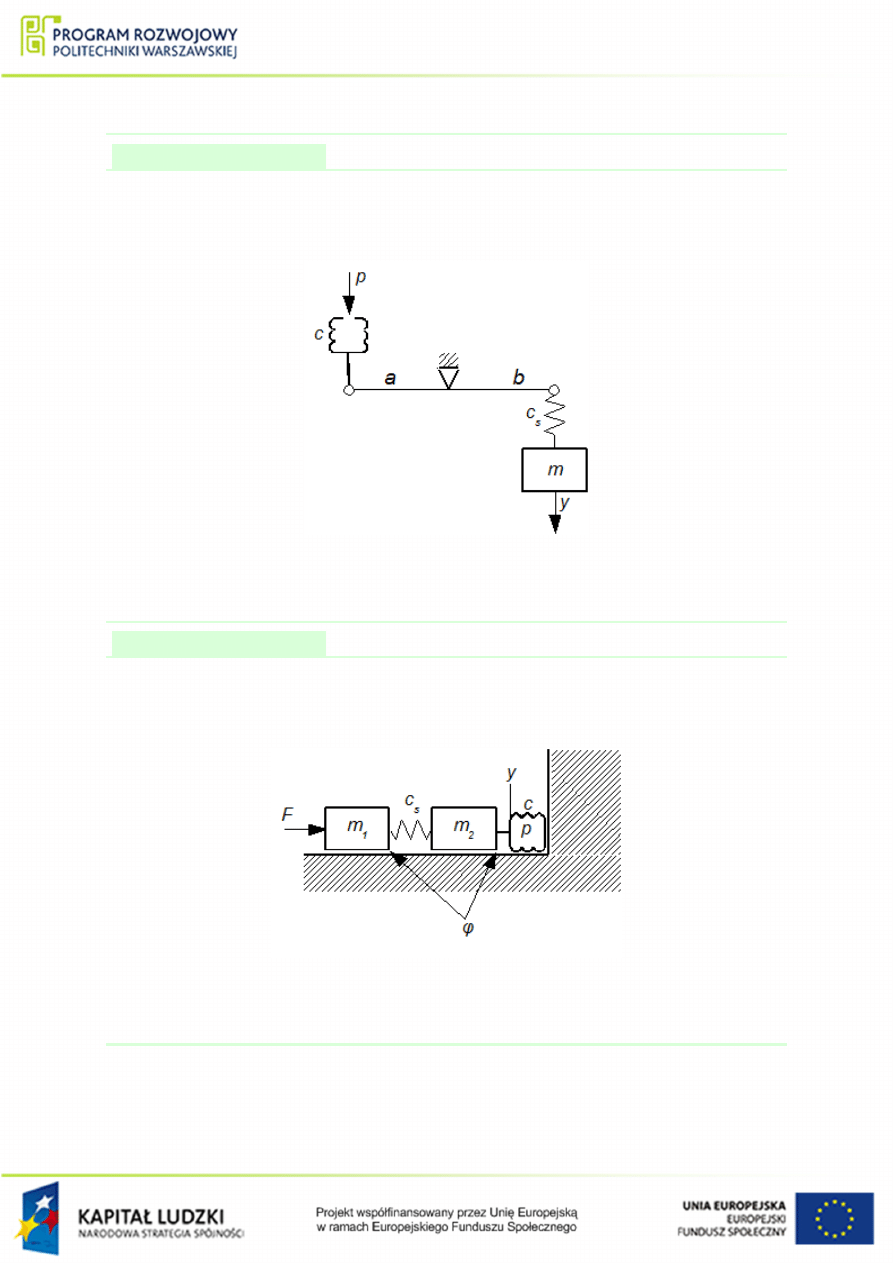
. Wymuszeniem jest ci±nienie p, natomiast wyj±ciem przesuni¦cie

y.

Rysunek 1.44 Schemat mechaniczny do przykªadu

1.23

.

Przykªad 1.24

Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu mechanicznego przed-

stawionego na rys.

1.45

. Wymuszeniem jest siªa F, natomiast wyj±ciem przesuni¦cie

y.

Rysunek 1.45 Schemat mechaniczny do przykªadu

1.24

.

28

Przykªad 1.25

Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu przedstawionego na

rys.

1.46

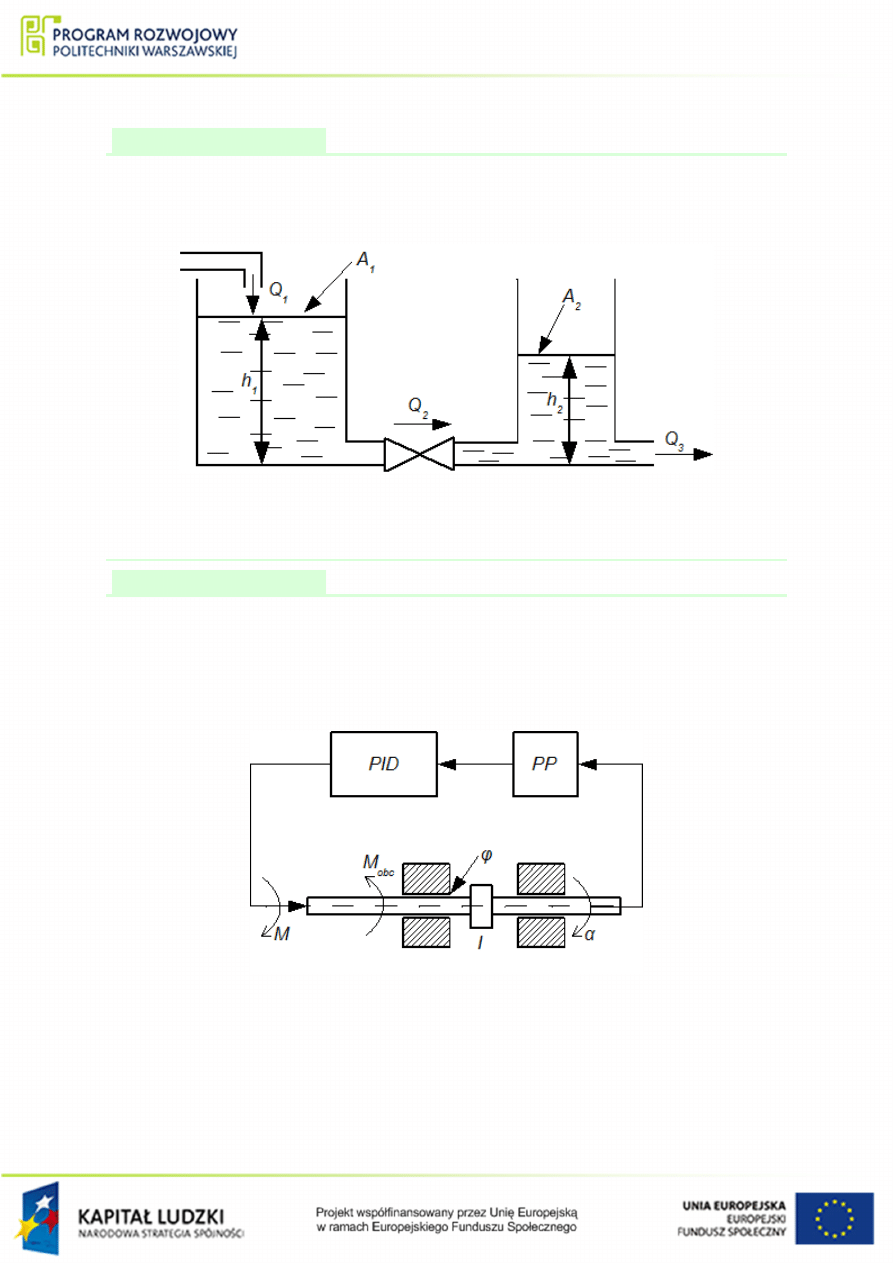
. Wymuszeniem jest nat¦»enie przepªywu Q

1

, natomiast wyj±ciem poziom cieczy

h

2

.

Rysunek 1.46 Schemat ukªadu elementów do przykªadu

1.25

.

Przykªad 1.26

Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ ukªadu regulacji przedsta-

wionego na rys.

1.47

. Wyj±ciem ukªadu jest k¡t obrotu waªu α. Regulator PID dziaªa

(poprzez pomini¦ty element wykonawczy) na waª momentem obrotowym M. Na ukªad

dziaªaj¡ zakªócenia pod postaci¡ momentu obci¡»enia M

obc

. Charakterystyka przetwor-

nika pomiarowego (PP) zostaªa przedstawiona na rys.

1.48

.

Rysunek 1.47 Schemat ukªadu regulacji do przykªadu

1.26

.

29

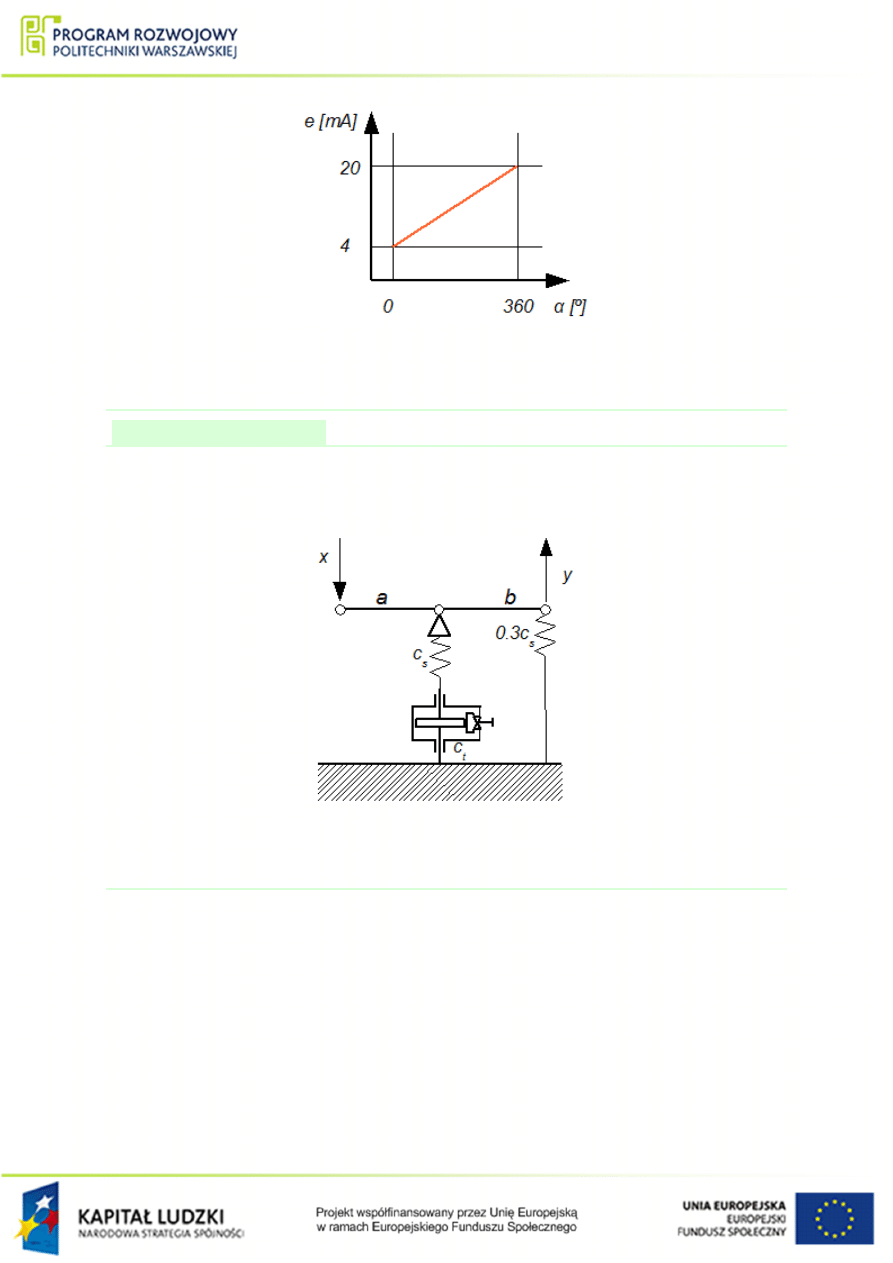
Rysunek 1.48 Charakterystyka przetwornika pomiarowego do przykªadu

1.26

.

Przykªad 1.27

Narysowa¢ achemat blokowy, oraz wyznaczy¢ transmitancj¦ zast¦pcza ukªadu elementów

przedstawionych na rys.

1.49

. Wymuszeniem jest przesuni¦cie x, natomiast wyj±ciem

przesuni¦cie y.

Rysunek 1.49 Schemat ukªadu do przykªadu

1.27

.

30

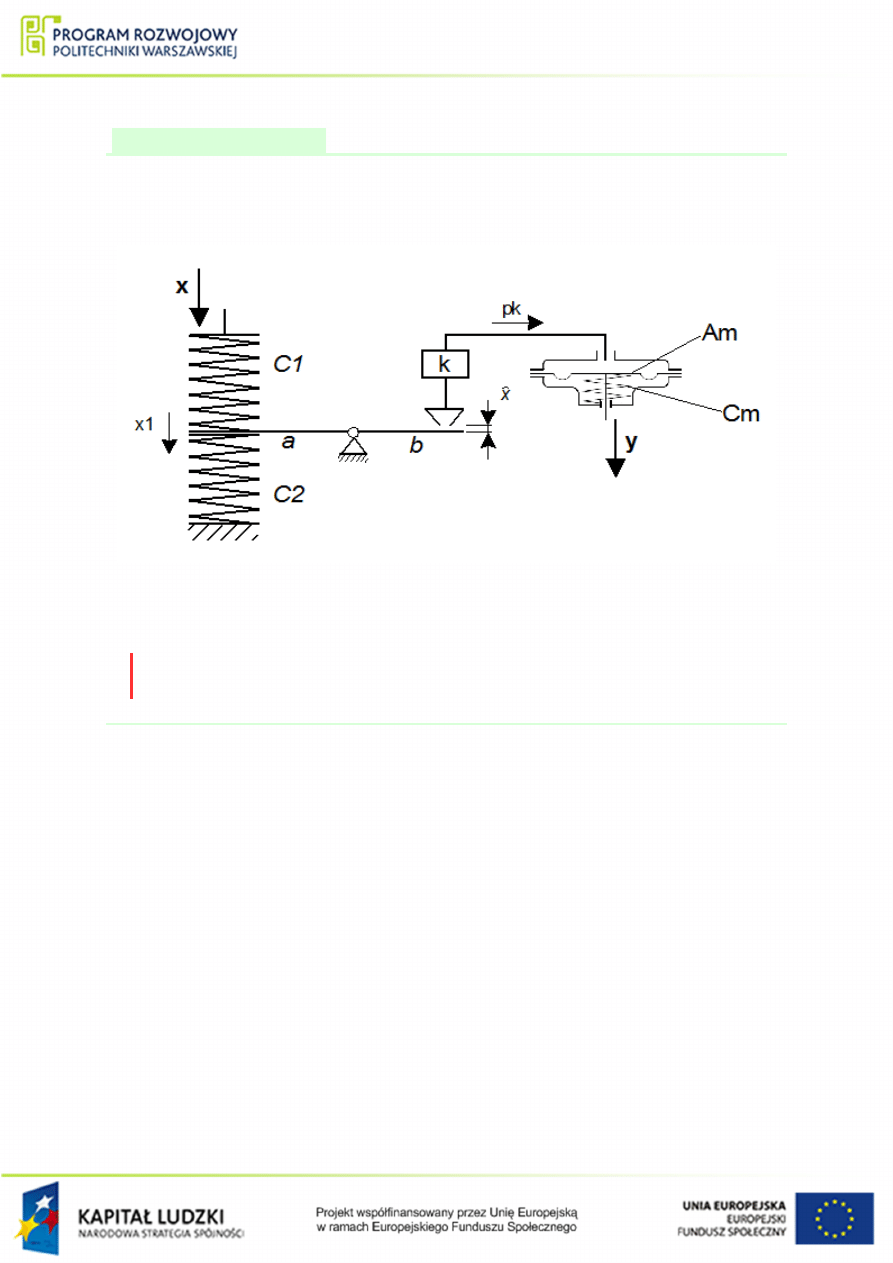
Przykªad 1.28

Narysowa¢ achemat blokowy, oraz wyznaczy¢ transmitancj¦ zast¦pcza ukªadu elemen-

tów przedstawionych na rys.

1.50

. Wymuszeniem jest przesuni¦cie x, natomiast wyj±ciem

przesuni¦cie y.

Rysunek 1.50 Schemat ukªadu do przykªadu

1.28

.

Wskazówka: Ci±nienie p

k

= k

ˆ

x

31

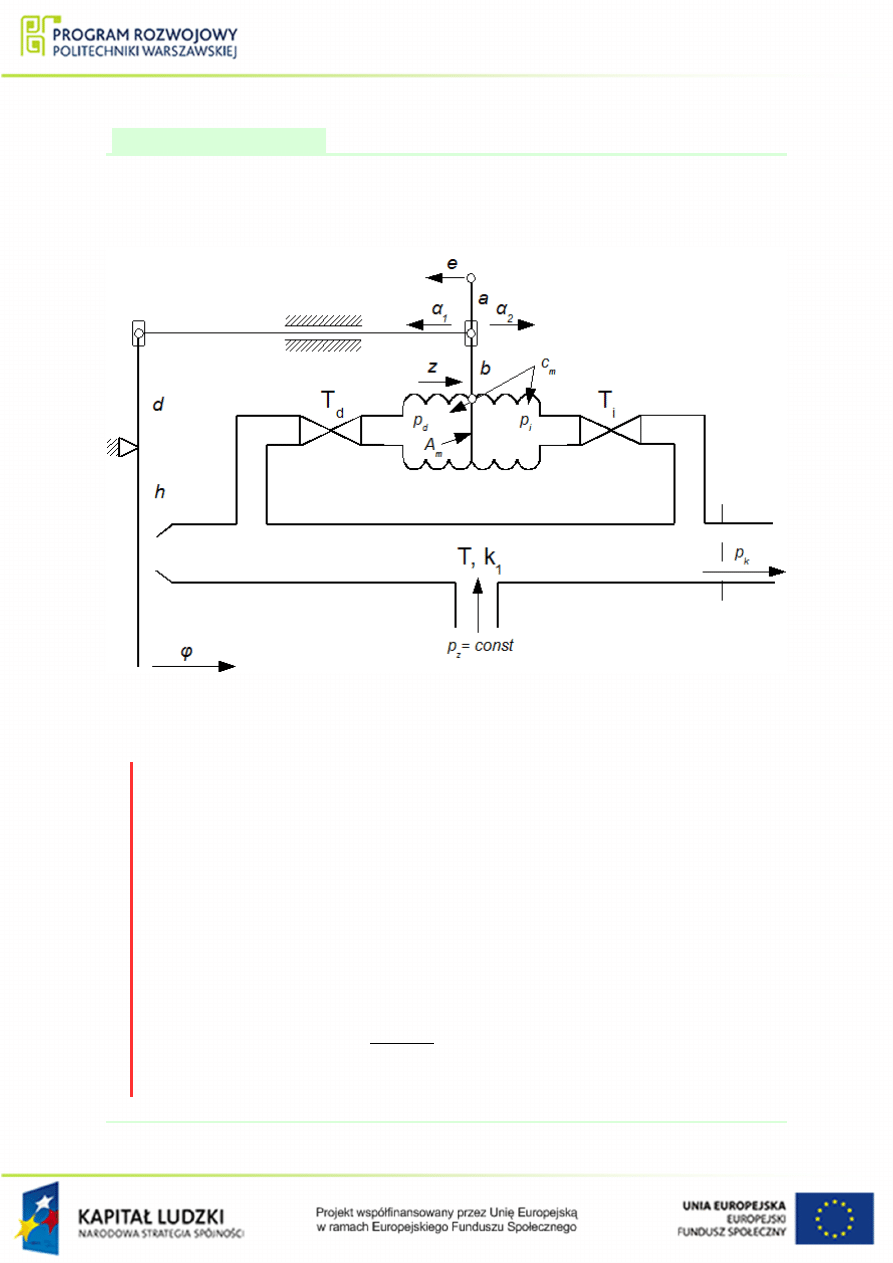
Przykªad 1.29

Narysowa¢ schemat blokowy oraz wyznaczy¢ transmitancj¦ pneumatycznego regulatora

PID, przedstawionego na rys.

1.51

. Wymuszeniem jest odchyªka regulacji e, wyj±ciem

ci±nienie p

k

.

Rysunek 1.51 Schemat pneumatycznego regulatora PID, do przykªadu

1.29

.

Wskazówka: W przedstawionym regulatorze wyró»ni¢ mo»na nast¦puj¡ce podze-

spoªy:

•

kaskada steruj¡ca o staªej czasowej T i wspóªczynniku wzmocnienia k

1

•

dwie kaskady elastyczne zamkni¦te o staªych czasowych T

d

oraz T

i

•

ukªad d¹wigni o ramionach a, b, d, h

Równianie kaskady steruj¡cej ma posta¢:

T

d∆p

k

(t)

dt

+ ∆p

k

(t) = k

1

φ (t)

(1.49)

32

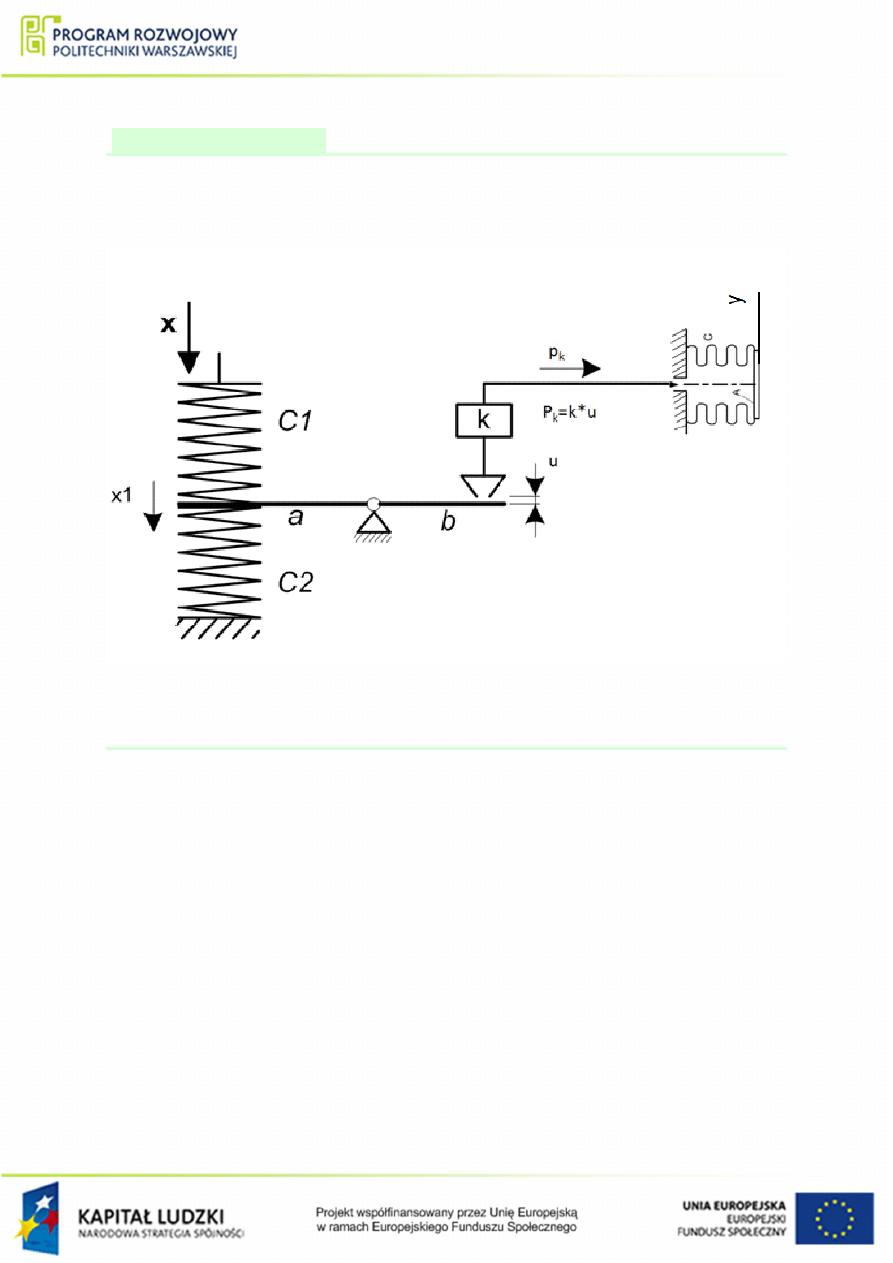
Przykªad 1.30

Narysowa¢ achemat blokowy, oraz wyznaczy¢ transmitancj¦ zast¦pcza ukªadu elementów

przedstawionych na rys.

1.52

. Wymuszeniem jest przesuni¦cie x, natomiast wyj±ciem

przesuni¦cie y.

Rysunek 1.52 Schemat ukªadu do przykªadu

1.30

.

33