Giełda Papierów Wartościowych w Warszawie

1

Błażej Wajszczuk Paweł Mielnicki

Kontrakty terminowe

na obligacje skarbowe

Giełda Papierów Wartościowych w Warszawie

2

Spis treści

Rozdział 1. Podstawowe elementy charakterystyki obligacji

3

1.1.

Definicja 3

1.2.

Czas do wykupu

4

1.3.

Kupon i odsetki

5

1.4.

Wycena obligacji i ich rentowność 6

1.5.

Krzywa dochodowości 8

1.6.

Miary ryzyka obligacji

9

Rozdział 2. Wprowadzenie do kontraktów terminowych na obligacje

15

2.1.

Definicja 15

2.2.

Nabycie/wystawienie kontraktu

15

2.3.

Specyfikacja kontraktu

16

2.4.

System depozytów zabezpieczających 18

2.5.

Koszty utrzymywania pozycji (Cost of carry)

19

2.6.

Współczynnik konwersji

21

2.7.

Obligacja najtańsza w dostawie (Cheapest to Deliver – CTD)

22

2.8.

Wycena kontraktu

24

Rozdział 3. Przykłady wykorzystania kontraktów

25

3.1.

Pozycja długa / krótka

26

3.2.

Strategie spreadowe

28

3.3.

Transakcje zabezpieczające 30

3.4.

Perfect hedge

31

3.5.

Ryzyko bazy

32

3.6.

Wyznaczanie współczynników zabezpieczenia

34

Rozdział 4. Arbitraż cash and carry (basis trading)

37

Literatura

40

Giełda Papierów Wartościowych w Warszawie

3

Rozdział 1. Podstawowe elementy charakterystyki obligacji

1.1 Definicja

Obligacje są jednym z podstawowych instrumentów rynku kapitałowego. Geneza ich

powstania wiąże się ściśle z chęcią firm do poszukiwania źródeł pozyskiwania kapitału

innych niż kredyt bankowy. Z punktu widzenia emitenta, a tak będziemy nazywać

sprzedającego obligacje, emisja obligacji na rynku kapitałowym ma wiele przewag wobec

zaciągnięcia kredytu bankowego. Jedną z podstawowych jest możliwość dotarcia do wielu

podmiotów dysponujących kapitałem jednocześnie. Widać więc, że firma nie musi ograniczać

się do jednego banku oraz jego indywidualnej oceny zasadności udzielenia kredytu. Zalety

pozyskiwania kapitału poprzez rynek finansowy dostrzegły także rządy wielu państw.

Obecnie rynki obligacji zdominowane są przez obligacje rządowe. Dzieje się tak z

kilku powodów. Po pierwsze zadłużenie kraju jest z reguły bardzo duże, jeżeli porównać je do

całości rynku. Powoduje to, że dług ten charakteryzuje się największą płynnością. Po drugie

zakłada się, że obligacje emitowane przez państwo są instrumentami pozbawionymi ryzyka

1

.

Nie oznacza to, że automatycznie stają są najefektywniejszą formą lokaty kapitału, ale

gwarantuje, że zainwestowany kapitał na pewno wróci do inwestora. Oczywiście w oczach

inwestora dług rządu amerykańskiego jest dużo bezpieczniejszy niż dług rządu polskiego.

Inaczej mówiąc ryzyko, że rząd amerykański nie wykupi swoich obligacji jest dużo mniejsze.

Z drugiej jednak strony, zwrot z inwestycji w obligacje polskie będzie większy niż zwrot z

inwestycji w obligacje amerykańskie. Dzieje się tak dlatego, że na rynkach kapitałowych

istnieje konkurencja o kapitał. Z uwagi na fakt, że Polska posiada niższy rating kredytowy

2

musi proponować inwestorom wyższe stopy zwrotu z obligacji. Oznacza to, że albo musi

sprzedawać dług taniej, albo musi proponować inwestorom wyższe kupony (odsetki).

Niezależnie więc od wybranego sposobu proponuje inwestorom wyższą stopę zwrotu.

Obligacją będziemy nazywać papier wartościowy przynoszący okresowe dochody

swojemu posiadaczowi o pierwotnym terminie wykupu powyżej jednego roku. Dla

dopełnienia informacji warto powiedzieć, że mimo iż na rynku polskim są emitowane papiery

generujące tylko jeden przepływ w dacie zapadalności, tzw. obligacje zerokuponowe, nie są

1

Z punktu widzenia inwestorów krajowych.

2

Rating kredytowy to ocena nadana przez niezależna agencję ratingową, określająca ryzyko inwestycji w dane

aktywo finansowe.

Giełda Papierów Wartościowych w Warszawie

4

one jednak brane pod uwagę przy obrocie kontraktami terminowymi i dlatego nie znalazły się

w tak ujętej definicji.

1.2 Czas do wykupu

Czas do wykupu jest to czas jaki pozostaje do wykupu obligacji przez jej emitenta.

Przykładowo więc dla obligacji o symbolu DS0509 datą wykupu będzie 24 maja 2009 roku

3

.

Tego dnia Skarb Państwa reprezentowany przez Ministra Finansów wykupi obligację od ich

posiadaczy po cenie nominalnej oraz wypłaci ostatni należący się kupon.

Obecnie Skarb Państwa emituje obligacje o zapadalności 2, 5, 10 i 20 lat zazwyczaj w

czasie comiesięcznych aukcji. Oczywiście rzadko zdarza się, aby w dacie emisji obligacje

dokładnie odpowiadały zapadalności na przykład pięciu lat. Zamiast tego obligacje jednej

serii oferowane są inwestorom na wielu aukcjach i przetargach zamiany

4

. Ostatecznie więc

inwestor może kupić obligację o zapadalności 4,5 roku wciąż jednak kupując 5-letni

benchmark, czyli obligację najpłynniejszą i najbardziej zbliżoną zapadalnością do 5 lat. Warto

przy tym zaznaczyć, że kryterium płynności jest w tym przypadku zdecydowanie ważniejsze,

a obligacje o większej płynności to takie, których po prostu wyemitowano więcej. Te właśnie

cieszą się największym zainteresowaniem inwestorów.

Ministerstwo Finansów odpowiada na takie zainteresowanie rynku sprzedając

obligacje o zapadalnościach 2, 5, 10 i 20 lat. W każdym momencie są więc na rynku cztery

podstawowe benchmarki odpowiadające tym terminom do zapadalności. Obligacje te cieszą

się największym zainteresowaniem inwestorów i de facto decydują o wycenie pozostałych

obligacji znajdujących się na krzywej dochodowości

5

.

W specyfikacji kontraktu zapisano, iż kontrakt terminowy opiewa na obligacje o

terminie wykupu nie krótszym niż 2 lata i dziewięć miesięcy i nie dłuższym niż 5 lat i sześć

miesięcy, licząc od dnia wykonania kontraktu. Widać więc, że z upływem czasu i emisją

kolejnych serii obligacji będzie zmieniał się skład obligacji spełniających ten wymóg.

Obligacja, która dziś jest obligacją 20-letnią za 15 lat będzie spełniać warunki kontraktu

będąc wtedy jednocześnie najprawdopodobniej 5-letnim benchmarkiem.

3

Dokładny dzień wykupu podawany jest w liście emisyjnym każdej obligacji, znajdującym się na stronie

Ministerstwa Finansów (

www.mf.gov.pl

)

4

Przetargi zamiany, ogłaszane przez Ministerstwo Finansów, sprowadzają się do zamiany obligacji, którym

zbliża się moment wykupu na obligacje o długich okresach zapadalności.

5

Patrz rozdział o krzywej dochodowości.

Giełda Papierów Wartościowych w Warszawie

5

1.3 Kupon i odsetki

Jak już wiadomo z definicji, mówimy tutaj o papierach wypłacających okresowo

dywidendy pieniężne ich posiadaczom. Płatności te będziemy nazywać kuponami. Obligacje

stanowiące aktywo bazowe kontraktów terminowych, wypłacają kupony raz do roku.

Przykładowo więc obligacja DS0509 będzie wypłacać kupon co roku 24 maja przy czym

ostatnia płatność będzie miała miejsce 24 maja 2009 r.

Obliczenie

wysokości kuponu nie jest trudne. Wystarczy tylko przemnożyć nominał

obligacji przez wysokość kuponu, aby w ten sposób uzyskać kwotę płatności kuponowej.

Czyli dla obligacji wypłacającej roczny kupon w wysokości 6% będzie to kwota 6 złotych,

licząc od 100 złotych wartości nominalnej.

Dla dalszych rozważań należy wprowadzić dwa dodatkowe pojęcia: cenę czystą i

cenę brudną obligacji. Kiedy kupujemy nową serię obligacji, która do tej pory nie była

przedmiotem obrotu na rynku, płacimy tylko cenę wynikającą z rentowności obligacji.

Podobnie się stanie, gdy kupimy obligacje na początku nowego okresu odsetkowego.

Zapłacimy wtedy tylko cenę czystą obligacji, czyli cenę bez narosłych odsetek.

Co jednak, gdy inwestor nabywa obligacje w trakcie okresu kuponowego?

Sprzedający musi dostać wynagrodzenie za to, że był posiadaczem obligacji przez pewien

okres. Innymi słowy należy mu się pewna cześć płatności kuponowej, czyli narosłe do dnia

sprzedaży odsetki. Narosłe odsetki obliczymy za pomocą następującej formuły:

y

d

y

C

AI

−

×

=

gdzie:

C - wysokość kuponu

y - aktualna liczba dni pomiędzy dwiema datami wypłaty rocznych odsetek

d - aktualna liczba dni pomiędzy dniem rozliczenia dostawy, a dniem wypłaty odsetek

(kuponu) następującym po dniu dostawy,

Ogólny wniosek jest więc taki, że cena czysta wraz z należnymi odsetkami da cenę

brudną obligacji czyli tę, którą inwestor musi zapłacić, aby wejść w posiadanie obligacji.

Oczywiście w dacie płatności kuponu posiadający obligację otrzyma cały kupon, ale

faktycznie jego dochód stanowi tylko ta część, która należy mu się z faktu posiadania

Giełda Papierów Wartościowych w Warszawie

6

obligacji przez określoną liczbę dni. Jeżeli inwestor posiadałby na przykład daną obligację w

portfelu tylko przez 7 dni to otrzyma on odsetki dokładnie za tyle dni.

Emitowane przez Skarb Państwa obligacje mają konwencję naliczania odsetek na

bazie act/act. Oznacza to, że do naliczania odsetek wykorzystuje się faktyczną ilość dni w

okresie odsetkowym i dzieli przez faktyczną ilość dni w danym roku odsetkowym.

Przykład nr 1

Rozpatrzmy zakup obligacji DS0509 w dniu 2 listopada 2004 r. Okres odsetkowy ma 365 dni

a do daty płatności kolejnego kuponu pozostają 203 dni. Kupon wynosi 6%. Podstawiając do

wzoru otrzymamy:

663

,

2

365

203

365

6

=

−

×

=

AI

Jeśli więc cena czysta tej obligacji wynosi 96,00 to po dodaniu odsetek nabywca zapłaci

98,663 złotego za każde 100 złotych nominału.

1.4 Wycena obligacji i ich rentowność

Wartość obligacji to zdyskontowana na dziś wartość bieżąca wszystkich płatności

kuponowych, jak również wartość bieżąca raty kapitałowej. Suma tych wartości daje cenę

obligacji. Zależność tę można opisać następującym wzorem:

n

n

i

i

r

r

C

PV

)

1

(

100

)

1

(

0

+

+

+

=

∑

=

gdzie:

r – rentowność obligacji

n - liczba lat pozostałych do wykupu papieru wartościowego.

C – roczny kupon przypadający na 100 PLN nominału obligacji.

PV - bieżąca wartość obligacji.

Stopa procentowa wykorzystana w powyższym równaniu jest stopą dochodowości

obligacji do wykupu (YTM – yield to maturity ). Tak więc gdybyśmy znali cenę obligacji to

przekształcając to równanie względem „r” otrzymalibyśmy stopę dochodowości danej

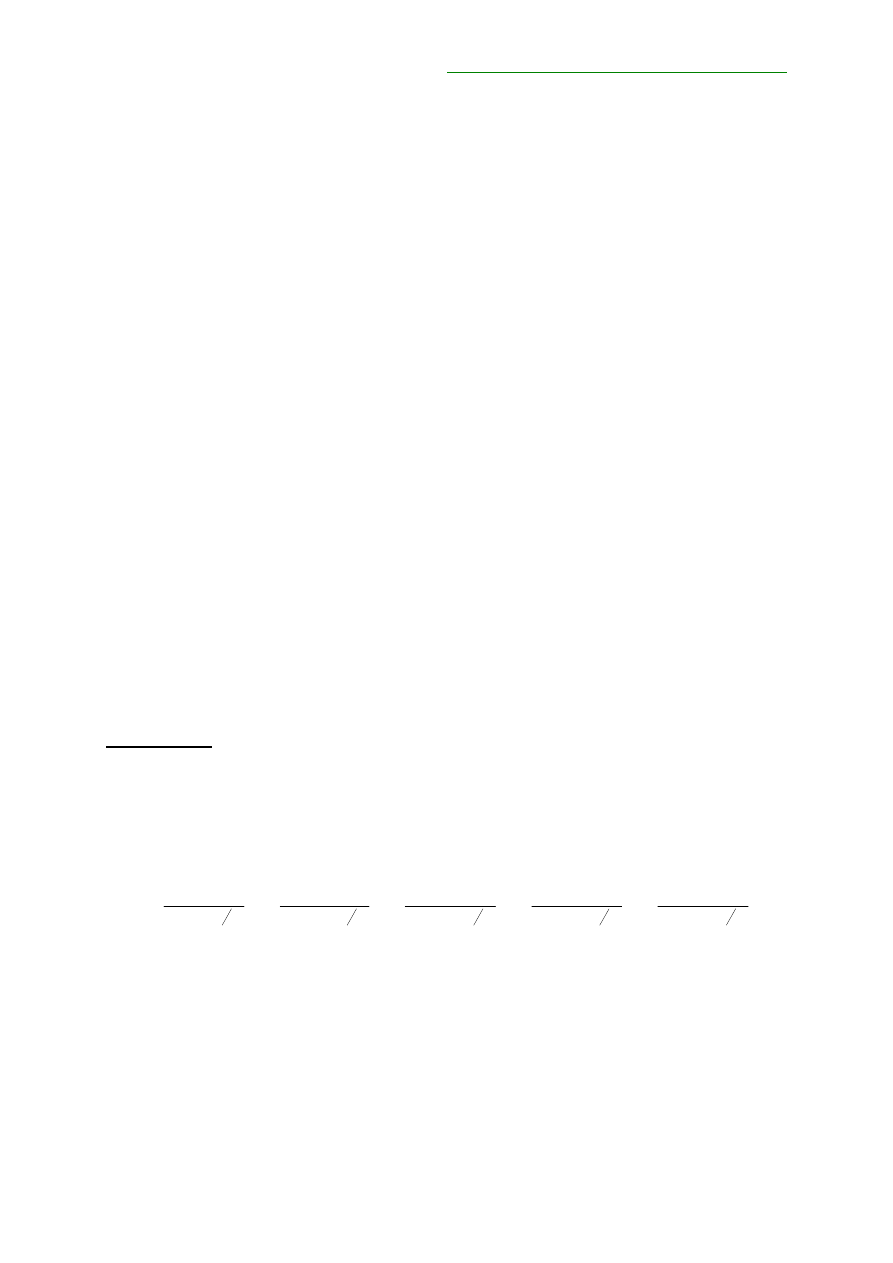
Giełda Papierów Wartościowych w Warszawie

7

obligacji. W praktyce takie obliczenia były bardzo żmudne z uwagi na dużą liczbę

pierwiastków równania i dlatego do obliczenia rentowości warto skorzystać z formuły „szukaj

wyniku” aplikacji Microsoft Excel lub wykorzystać jedną z gotowych funkcji tego programu.

Stopa

dochodowości do wykupu jest najczęściej wykorzystywaną miarą

dochodowości obligacji. Zakłada ona, że obligacja jest trzymana w portfelu inwestora do

wykupu, a odsetki są reinwestowane po tej właśnie stopie. To ostatnie założenie można

podważyć, gdyż właściwie nie zdarza się, aby reinwestycja była dokonywana po tej samej

stopie przez cały okres trwania inwestycji. Teoretycznie można wyliczyć terminowe stopy

forward-forward

6

, aby w ten sposób określać przyszłą stopę reinwestycji odsetek, w praktyce

jednak stopa YTM jest najpowszechniej stosowaną miarą dochodowości obligacji.

Z

zależności ceny i rentowności wynika kilka ciekawych wniosków. Z równania

widać, że gdyby powiększyć mianownik, czyli de facto zwiększyć rentowność obligacji to

cena obligacji spadnie. Jest to niezwykle ważna zależność, z której wynika, że cena obligacji

jest odwrotnie skorelowana z jej rentowością. Kolejny istotny wniosek, który płynie z analizy

równania to fakt, iż gdyby rentowność obligacji wyniosła dokładnie tyle co kupon, to wartość

obligacji równałaby się jej wartości nominalnej. W sytuacji, gdy rentowność obligacji jest

mniejsza niż wartość kuponu, wówczas cena obligacji kształtuje się powyżej ceny

nominalnej. Dlatego też dla nowych serii obligacji wysokość kuponu jest dobierana tak, aby

cena obligacji wynosiła dokładnie tyle lub trochę mniej niż jej wartość nominalna.

Przykład nr 2

Wykorzystajmy obligacje DS0509 po raz drugi. Tym razem policzymy cenę obligacji

na dzień 2 listopada 2004 r zakładając 7% rentowność tego papieru. Nasze obliczenia będą

przedstawiały się następująco:

(

)

(

)

(

)

(

)

(

)

82

,

98

%)

7

1

(

106

%)

7

1

(

6

%)

7

1

(

6

%)

7

1

(

6

%)

7

1

(

6

365

203

4

365

203

3

365

203

2

365

203

1

365

203

=

+

+

+

+

+

+

+

+

+

=

+

+

+

+

PV

Od obliczonej w ten sposób ceny należy odjąć narosłe odsetki do dnia 2 listopada.

Wielkość tę obliczyliśmy już w poprzednim podrozdziale. Cena czysta będzie więc wynosiła

96,16 złotego. Obliczenie można sprawdzić wstawiając te dane do formuły „Yield” w arkuszu

Microsoft Excel.

Giełda Papierów Wartościowych w Warszawie

8

1.5 Krzywa dochodowości

Na wielu rynkach, w tym także na rynku polskim, w obrocie znajduje się

równocześnie wiele serii obligacji. Każda z nich charakteryzuje się innym czasem do wykupu

i nierzadko rentownością. Jeśli zestawić te dwie informacje na jednym rysunku to otrzymamy

krzywą, która będzie opisywać zależność okresu do zapadalności i rentowności - otrzymaną

krzywą będzie tzw.krzywą dochodowości.

Jest

bardzo

ważne, aby przy konstrukcji konkretnej krzywej wykorzystywać obligacje

tej samej klasy, czyli emisje pochodzące od jednego emitenta. Zalecenie to można pominąć

gdy budujemy krzywą dla obligacji korporacyjnych. Trudno przecież wymagać, żeby

pojedyncza korporacja emitowała obligacje pokrywające całą krzywą. W przypadku jednak

obligacji rządowych zaleca się wykorzystywanie obligacji o tym samym ratingu

7

pochodzących od tego samego emitenta i denominowanych w tej samej walucie.

Krzywa

dochodowości jest jednym z ważniejszych narzędzi do analizy rynku

obligacji. Rentowności obligacji rządowych od tych o najkrótszym okresie zapadalności do

tych najdłuższych, wyznaczają poziom rentowności dla wszystkich innych instrumentów

dłużnych na rynku. Krzywa jest więc wykorzystywana do wyceny zarówno obligacji

będących w obrocie, jak i nowo emitowanych. Na podstawie krzywej można także wyliczyć

przyszłe terminowe stopy procentowe i dzięki temu prognozować przyszłe zmiany stóp

procentowych na rynku.

Krzywa wskazuje także w prosty sposób, w których miejscach obligacje generują

najwyższy zwrot. Wyceniając obligacje przy pomocy krzywej można także dowiedzieć się,

która obligacja jest tania lub droga w porównaniu do krzywej. Innymi słowy krzywa pozwala

znaleźć obligacje z jakiś powodów źle wycenione przez rynek, a więc te, które powinny

zostać sprzedane lub kupione w formie transakcji bezpośredniej, ewentualnie wykorzystane

do skonstruowania innej strategii.

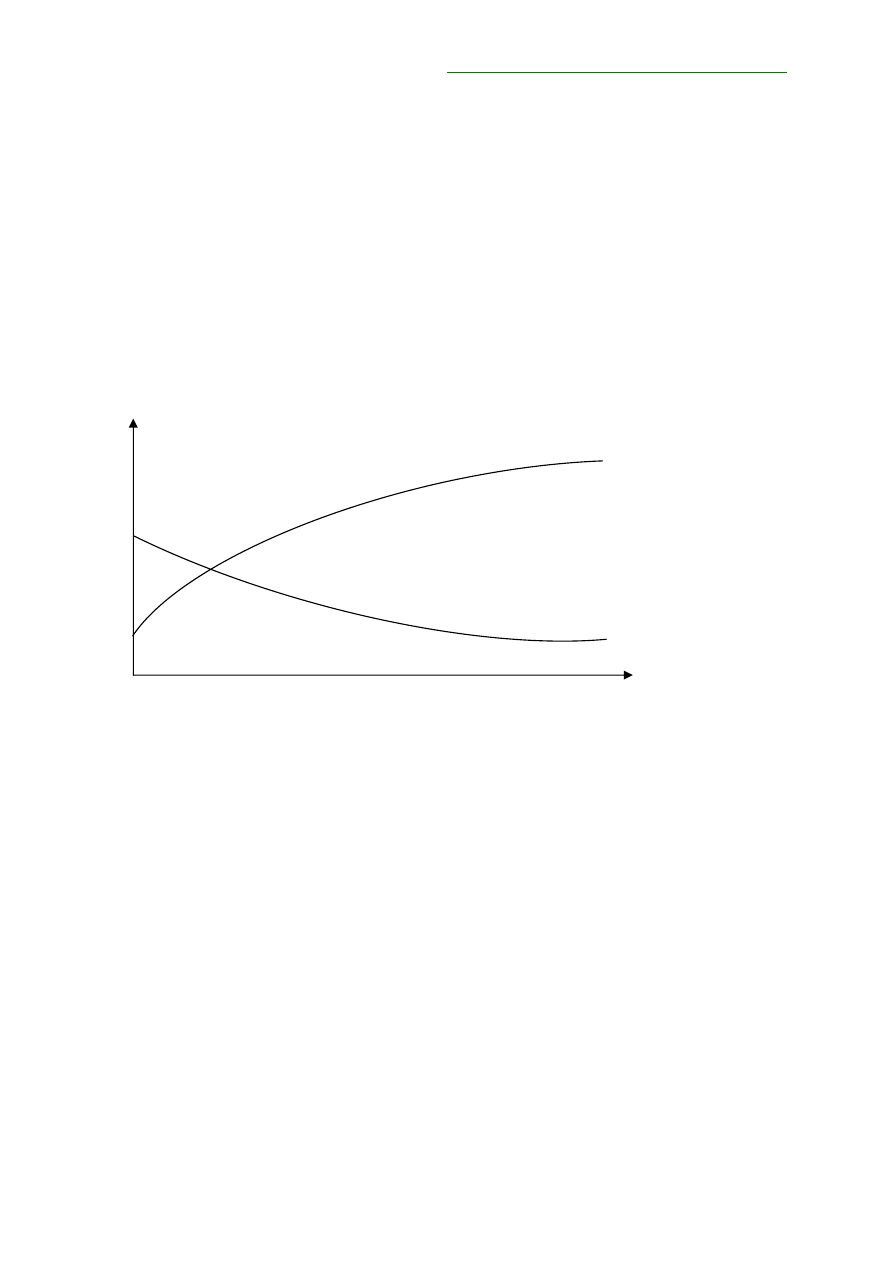
Generalnie

można wyróżnić dwa rodzaje krzywych: rosnące i malejące tak jak zostało

to przedstawione na rysunku poniżej. Krzywe oczywiście nie zawsze mają tak gładki

przebieg. Często w określonych przedziałach czasowych krzywa jest rosnąca, a później - w

6

Stopa forward-forward (terminowa) to teoretyczna stopa procentowa obowiązująca przez dany okres w

przyszłości. Przykładowo może to być roczna stopa procentowa obowiązująca za rok. Stopy te wyliczane są z
bieżących krzywych dochodowości.

7

System ratingów kredytowych jest bardzo ważnym elementem oceny ryzyka inwestycji w obligacje. Im

wyższy rating tym mniejsze prawdopodobieństwo nie wykupienia obligacji przez emitenta.

Giełda Papierów Wartościowych w Warszawie

9

innych - malejąca. Wpływ na to mają oczekiwania rynku co do kształtowania się przyszłych

stóp procentowych. Decyzje Rady Polityki Pieniężnej, dane makroekonomiczne lub inne

wydarzenia ze świata biznesu i polityki silnie oddziaływają na krzywą, ukazując zmiany

nastrojów inwestorów. Często także różnice w płynności poszczególnych serii decydują o

wyglądzie krzywej. Mniej płynne obligacje z reguły dużo silniej reagują na zmiany krzywej

dochodowości. Dzieje się tak ponieważ nie zawsze jest wystarczająca ilość chętnych do

kupna/sprzedaży obligacji co powoduje, iż obligacje takie często nienaturalnie zmieniają

kształt krzywej.

Rysunek nr 1. Przykładowe krzywe dochodowości dla obligacji

Niezależnie jednak od kształtu krzywej nie powinno się podważać jej fundamentów. Z

krzywą się po prostu nie dyskutuje. Czasem jej kształt może nam się wydawać co najmniej

dziwny lub bezzasadny, pamiętać jednak należy o tym, że to siły rynku nadały taki, a nie inny

wygląd krzywej i wszystkie instrumenty muszą być wyceniane według takiej właśnie

krzywej. Gdyby jednak inwestor był pewien, że rynek źle wycenia przyszłe ruchy stóp

procentowych i krzywa zmieni w niedługim czasie swój wygląd, to może otworzyć pozycję w

obligacjach lub kontraktach futures licząc, że jego prognozy sprawdzą się i osiągnie zysk.

Wciąż jednak będzie zawierał transakcje po cenach wynikających z bieżącej krzywej.

1.6 Miary ryzyka obligacji

W części poświęconej wycenie obligacji wspomniane zostało, że zależność ceny i

rentowności jest odwrotna; tzn. wraz ze wzrostem rentowności spada cena. Zależność ta nie

r

t

Krzywa rosnąca

Krzywa malejąca

Giełda Papierów Wartościowych w Warszawie

10

jest jednak liniowa. Oznacza to, że wzrostowi rentowności nie towarzyszy proporcjonalny

spadek ceny. Jak widać na załączonym rysunku relacja ta przybiera formę krzywej.

Rysunek nr 2. Zależność zmiany ceny obligacji od zmiany rentowności (YTM).

Krzywa ta jest ewidentnie wypukła i stąd nazwa zależności cena/rentowność –

convexity ( wypukłość ). Cechą szczególną wszystkich obligacji jest fakt, iż w przypadku

takiej samej zmiany rentowności (spadek, wzrost np. o 1punkt procentowy) wzrost ceny

obligacji, spowodowany spadkiem rentowności jest większy niż spadek ceny obligacji

wywołany wzrostem rentowności. Jest to ważna informacja dla posiadającego obligacje, gdyż

zarobi on więcej niż straci na takiej samej zmianie rentowności. Istnieje także inna ważna

zależność, o której warto pamiętać dokonując inwestycji w obligacje. Te instrumenty, które

posiadają wyższe kupony cechują się niższą zmiennością ceny niż obligacje z niskimi

kuponami. Inwestując w dłużne papiery wartościowe o długich terminach zapadalności

warto pamiętać, że takie obligacje charakteryzują się większą zmiennością ceny. Dlatego jeśli

oczekujemy spadków stóp procentowych warto jest posiadać w portfelu obligacje

długoterminowe, gdyż wzrost ceny będzie większy. Oczywiście w sytuacji, gdy mamy do

czynienia z zacieśnianiem polityki pieniężnej straty posiadaczy obligacji długoterminowych

są proporcjonalnie większe.

W tym miejscu należy uwzględnić pojęcie duration. Gdybyśmy posiadali w portfelu

dwie obligacje z takimi samymi datami zapadalności, ale różnymi kuponami to

stwierdzilibyśmy, że wyżej oprocentowana obligacja przynosi większość swojej rentowności

w postaci kuponów. Ponadto obligacja z wyższym kuponem zapewnia szybszy zwrot

zainwestowanych środków, będąc jednocześnie mniej wrażliwą na zmiany stóp

procentowych.

Widać więc, że kryterium zapadalności obligacji nie jest najlepszym odzwierciedleniem

ryzyka, jakie niesie inwestycja w kuponowe papiery skarbowe. Zamiast tego można policzyć

średni czas do terminu wystąpienia każdego przepływu pieniężnego ważonego za pomocą

cena

YTM

Giełda Papierów Wartościowych w Warszawie

11

jego wielkości. Gdy teraz zamienimy nominalne wartości przepływów i przyjmiemy zamiast

tego ich wartość teraźniejszą, to obliczymy w ten sposób duration obligacji. Wzór przyjmie

więc następującą postać:

(

)

PV

k

t

PVC

D

×

×

=

∑

gdzie:

PVC – wartość bieżąca kuponu

t - czas do wystąpienia przepływu

k - ilość płatności w roku ( dla rynku polskiego wartość zawsze równa 1)

PV - cena obligacji.

Warto

podsumować kilka zależności, o których powiedzieliśmy wcześniej. Po

pierwsze, przy innych czynnikach niezmiennych, im dłuższy jest okres do wykupu obligacji

tym większa wrażliwość obligacji na zmianę ceny. Po drugie, przy innych czynnikach

niezmiennych, im dłuższy jest okres do wykupu obligacji tym większe jest duration. Po

trzecie, zakładając niezmienność innych czynników, im niższy jest kupon obligacji tym

większa wrażliwość na zmianę ceny. Ponieważ wyprowadzając wzór na duration

zauważyliśmy, że mniejsze płatności kuponowe implikują wyższy wskaźnik duration,

możemy wykorzystać duration do mierzenia zmienności cen obligacji. W tym celu

wykorzystamy poniższy wzór:

100

1

1

×

∆

×

×

+

−

=

∆

Y

D

r

PV

gdzie:

∆PV – procentowa zmiana ceny

∆Y - zmiana rentowności

D

r

×

+

−

1

1

- zmodyfikowane duration (MD)

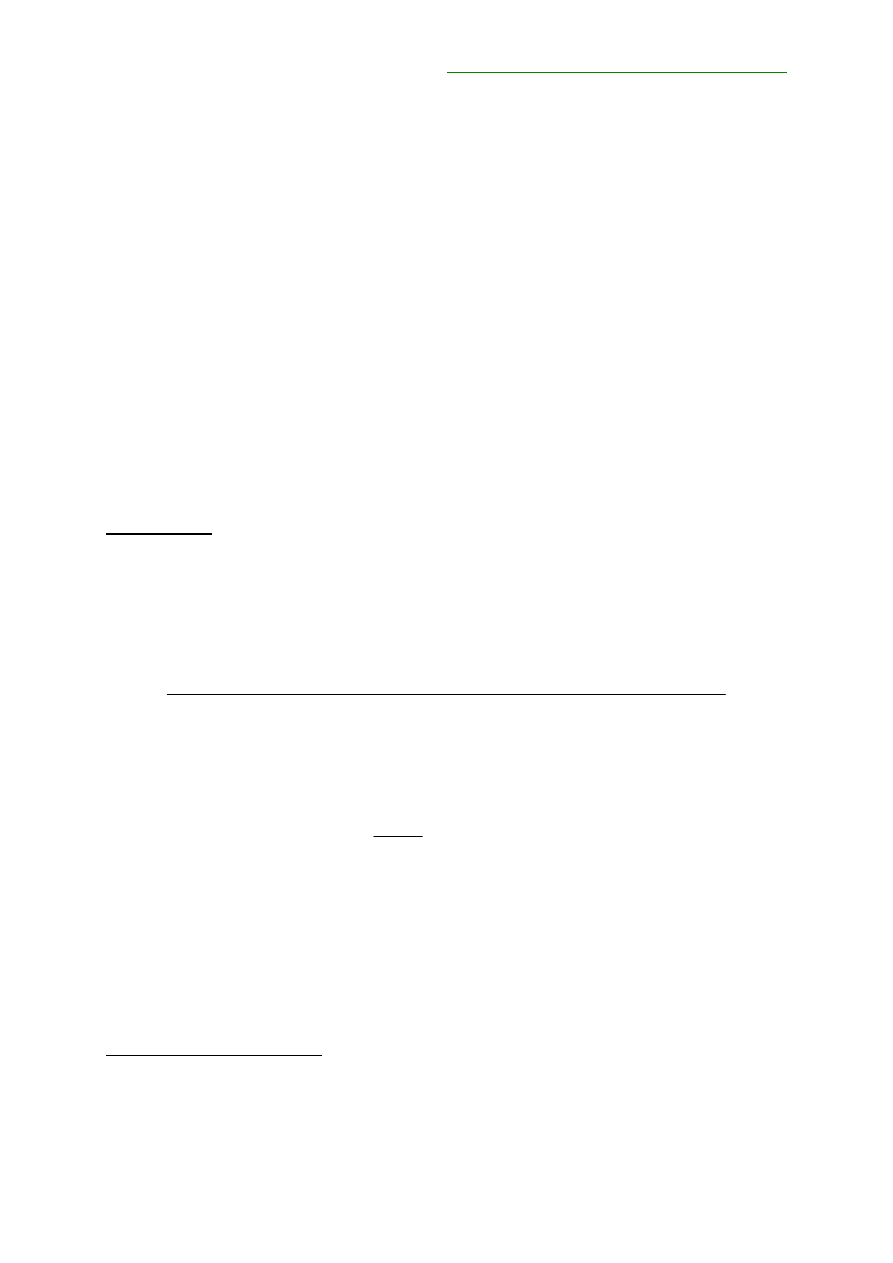
Giełda Papierów Wartościowych w Warszawie

12

Wprowadzone w tym wzorze pojęcie zmodyfikowanej duracji jest niczym innym niż

współczynnikiem wrażliwości łączącym zmianę ceny z ujemną zmianą stopy dochodowości.

Na tej podstawie można przedstawić kolejną miarę obrazującą wrażliwość zmiany wartości na

zmianę stopy dochodowości. Wartość punktu bazowego czyli BPV (basis point value), a o

nim tu mowa, odpowiada na pytanie, o ile zmieni się wartość naszej pozycji po przesunięciu

się stopy dochodowości o jeden punkt bazowy

8

. Wzór będzie się przedstawiał następująco:

PV

MD

BPV

×

×

=

0001

,

0

Miara ta jest powszechnie używana do zabezpieczania pozycji w obligacjach przy pomocy

instrumentów pochodnych w tym także kontraktów terminowych.

Przykład nr 3

Spróbujmy wykorzystać opisane powyżej informacje do porównania dwóch różnych

obligacji: omawianej już wcześniej obligacji DS0509 oraz obligacji PS0608

9

. Obliczenia

przeprowadzimy na dzień 2 listopada 2004 r. Duration obligacji DS0509 będzie wynosiło

10

:

008

,

4

82

,

98

57

,

4

88

,

77

57

,

3

72

,

4

57

,

2

05

,

5

57

,

1

4

,

5

57

,

0

78

,

5

=

×

+

×

+

×

+

×

+

×

=

D

Procentowa zmiana ceny przy wzroście rentowności o 0,1% wyniesie:

=

×

×

+

−

=

∆

100

%

1

,

0

%

7

1

008

,

4

PV

-0,37%,

a BPV dla pozycji o wartości 10 mln:

3746

ln

10

0001

,

0

75

,

3

=

×

×

=

m

BPV

8

1b.p. = 1 punkt procentowy / 100

9

Obligacja PS0608 posiada termin wykupu 24 czerwca 2008, oraz kupon 5,75%.

10

Każdy z elementów w liczniku równania to wartość bieżąca kuponu przemnożona przez czas pozostały do

jego wystąpienia.. Obliczenia dla pierwszej płatności kuponowej zostaną więc policzone w następujący
sposób:

365

/

203

*

6

*

365

/

203

%)^

7

1

/(

1

57

,

0

*

78

,

5

+

=

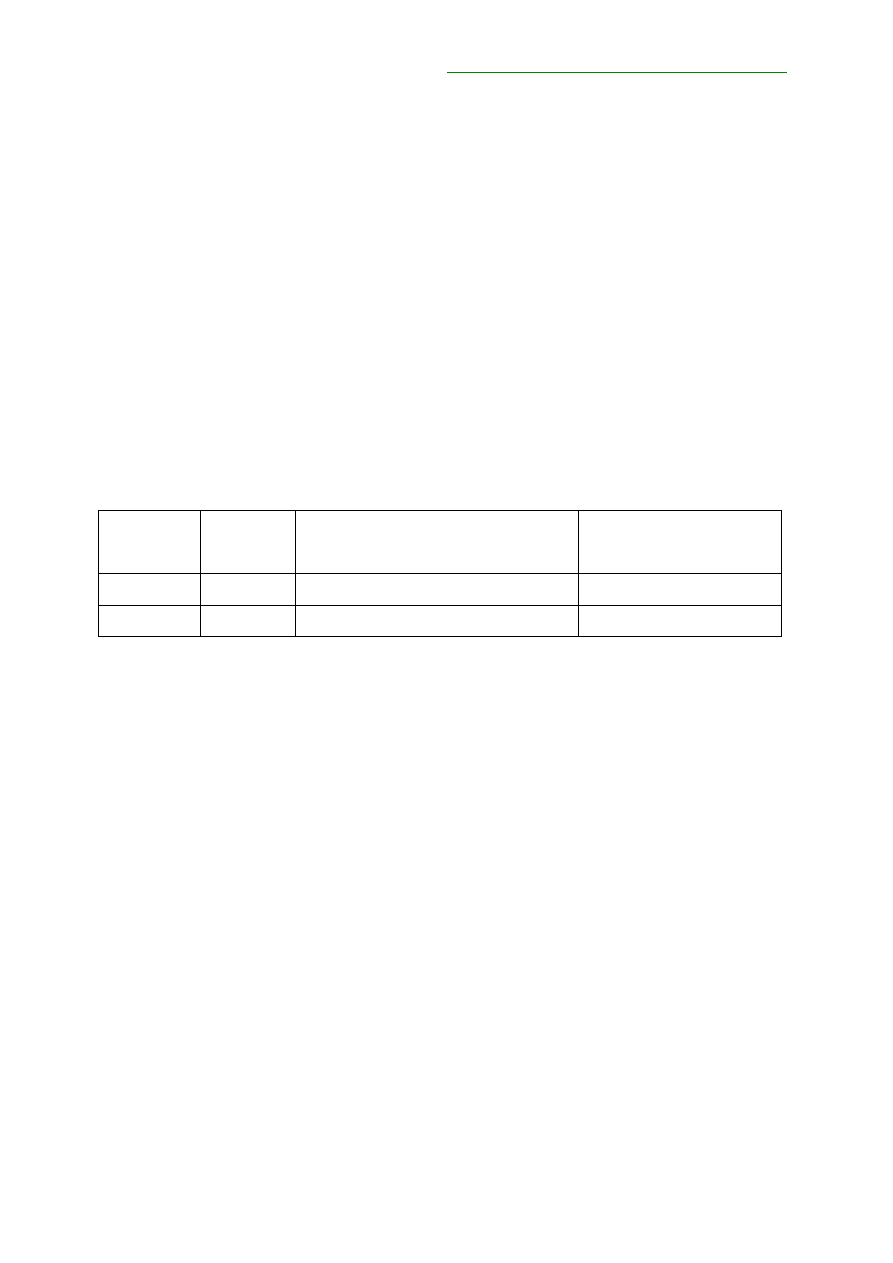
Giełda Papierów Wartościowych w Warszawie

13

Podsumowując obliczenia możemy powiedzieć, że obligacja DS0509 ma duration równe 4

lata, co powoduje, że wzrost rentowności o 0,1% spowoduje spadek ceny o 0,37%.

Jednocześnie na pozycji wartej 10 mln przy zmianie rentowności o 1 b.p. stracimy lub

zyskamy 3746 złotych.

Dla obligacji PS0608 parametry te kształtują się następująco: duration 3.45 roku, spadek ceny

po wzroście rentowności o 0,1% wynosi 0,31%, a BPV dla pozycji 10 mln wynosi 3117

złotych. Widać więc, że ta obligacja z krótszym okresem do wykupu cechuje się mniejszą

wrażliwością ceny na zmianę rentowności.

Tabela nr 1 Podsumowanie przykładu nr 3.

Obligacja Duration Procentowa zmiana ceny przy

zmianie rentowności o 0,1% (∆PV)

BPV dla pozycji o

wartości 10 mln zł (w zł)

DS0509 4,008

-0,37

%

3746

PS0608 3,45

-0,31

%

3117

Przedstawione miary ryzyka dość dobrze opisują zmiany wartości obligacji przy

małych ruchach krzywej dochodowości. Duration jest jednak liniową miarą zmiany ceny, a

na samym początku powiedzieliśmy, że zależność cena/rentowność jest nieliniowa i przy

dużych spadkach rentowności ceny obligacji wzrosną bardziej niż wynikałoby to z duration.

Z kolei duże wzrosty rentowności wprowadzą ceny na poziomy wyższe niż te, wyliczone przy

zastosowaniu duration. Jeśli zmodyfikujemy rysunek z początku rozdziału lepiej zobaczymy

tę zależność:

Giełda Papierów Wartościowych w Warszawie

14

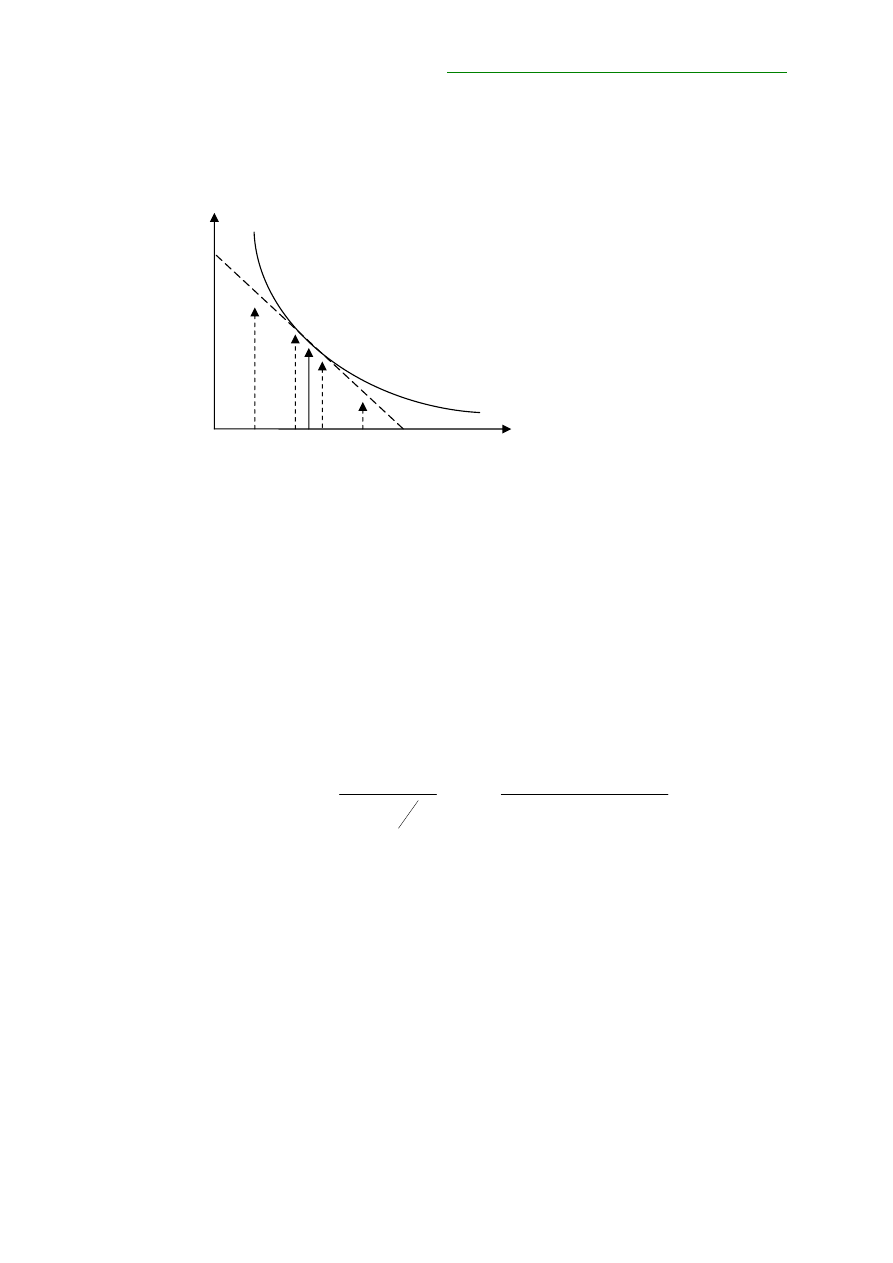
Rysunek 3. Przykładowe zmiany ceny obligacji pod wpływem zmian dochodowości.

Rysunek

pokazuje,

że dla małych zmian w dochodowości (na rysunku Y

1

i Y

2

)

wyliczenia przy wykorzystaniu duration są zgodne z rzeczywistym rozkładem ceny i

rentowności. Gdy jednak weźmiemy pod uwagę większe zmiany (na rysunku Y

3

i Y

4

) to

okaże się, że otrzymane wyniki nie pokrywają się z faktycznym rozkładem cena/ rentowność

obligacji. Współczynnikiem, który opisuje te zależności jest wspomniane już w tym rozdziale

wypukłość (convexity). Definiuje je poniższy wzór:

( )

[

]

( )

∑

=

×

×

+

×

×

+

=

n

PV

k

PVC

t

t

k

r

Convexity

1

1

2

2

1

1

1

gdzie:

PVC – wartość bieżąca kuponu

t - czas do wystąpienia przepływu

k - ilość płatności w roku ( dla rynku polskiego wartość zawsze równa 1)

PV - cena obligacji.

Procentowa zmiana wynikająca z wypukłości (convexity) obligacji będzie definiowana

następująco:

100

5

,

0

×

∆

×

×

=

∆

Y

Convexity

PV

cena

YTM

Y

1

Y Y

2

Y

3

Y

4

Giełda Papierów Wartościowych w Warszawie

15

Można zatem wykorzystać te wzory do policzenia zmiany ceny przy dużych ruchach krzywej

dochodowości.

Przykład nr 4

Wykorzystajmy jeszcze raz obligację DS0509. Po podstawieniu do wzoru otrzymamy

wypukłość (convexity) równe 18.74. Załóżmy teraz duży, 2 procentowy wzrost rentowności.

Procentowa zmiana ceny wyniesie 0,375%. Nie jest to oczywiście całkowita zmiana ceny

obligacji, ale tylko ta wynikająca z wypukłości obligacji. Prawdziwą zmianę ceny otrzymamy

sumując zmianę ceny wyliczoną za pomocą duration i tą wyliczoną z wypukłości. Tak więc

przy wzroście rentowności o 2% cena spadnie o 7,11% i wzrośnie o 7,86%, jeżeli założymy

2% spadek rentowności obligacji. Obligacja zachowuje się więc zgodnie z tym, co zostało

przedstawione z tym rozdziale. Porównywalna zmiana rentowności powoduje, że obligacja

mocniej zyskuje na cenie aniżeli traci.

Rozdział 2. Wprowadzenie do kontraktów terminowych na obligacje

2.1 Definicja

Kontrakt terminowy, będący przedmiotem obrotu na giełdzie jest bezwzględnym

zobowiązaniem do kupna lub do sprzedaży wystandaryzowanej liczby i jakości aktywów w

danym czasie w przyszłości.

Kontrakt terminowy na obligacje jest umową zawartą na giełdzie pomiędzy sprzedającym

obligacje skarbowe na dany termin a kupującym te obligacje na termin na warunkach

określonych przez Giełdę (patrz rozdział 2.3).

2.2 Nabycie/wystawienie kontraktu

Inwestor kupujący kontrakt terminowy na obligacje jest nabywcą kontraktu. Zajmuje on

pozycję długą w kontrakcie, zobowiązując się tym samym do kupna określonej ilości

instrumentu bazowego (obligacji skarbowych) po określonej cenie (ostatecznej cenie

rozliczeniowej obligacji) w danym dniu w przyszłości (w dniu wykonania kontraktu).

Inwestor sprzedający kontrakt terminowy na obligacje jest wystawcą kontraktu. Zajmuje on

pozycję krótką w kontrakcie, zobowiązując się tym samym do sprzedaży określonej wielkości

Giełda Papierów Wartościowych w Warszawie

16

instrumentu bazowego, jakim są obligacje skarbowe, po określonej cenie (ostatecznej cenie

rozliczeniowej obligacji) w danym dniu w przyszłości (w dniu wykonania kontraktu).

2.3 Specyfikacja kontraktu

ƒ

Nazwa skrócona kontraktu: FPS5kr

gdzie:

F - rodzaj instrumentu

PS5 – skrót nazwy instrumentu bazowego

k - kod określający miesiąc wykonania kontraktu (określony uchwałą Zarządu

Giełdy)

r - ostatnia cyfra roku wykonania.

ƒ

Kod kontraktu: Nadawany przez podmiot rozliczający zgodnie ze standardem ISIN

ƒ

Seria kontraktu: Określa grupę kontraktów terminowych charakteryzujących się w

szczególności tym samym instrumentem bazowym oraz tą samą datą wygaśnięcia.

ƒ

Instrument bazowy: Instrumentem bazowym kontraktu będącym przedmiotem

kontraktu jest hipotetyczna obligacja o zapadalności w momencie rozliczenia
kontraktu równej 5 lat, kuponie 6,00% i tej samej wiarygodności kredytowej co
obligacje Skarbu Państwa.

ƒ

Wartość nominalna kontraktu: 100 000 zł.

ƒ

Mnożnik: 1000 zł

ƒ

Jednostka notowania: Cena podawana jest w punktach procentowych za 100 zł

wartości nominalnej kontraktu

ƒ

Minimalny krok notowania: 0,01 punktu procentowego

ƒ

Wartość minimalnego kroku notowania: 10 zł.

ƒ

Miesiące wykonania: Dwa najbliższe miesiące z cyklu marzec, czerwiec, wrzesień,

grudzień

ƒ

Ostatni dzień obrotu: Dzień sesyjny przypadający w trzeci piątek miesiąca

wykonania. Jeżeli w tym dniu zgodnie z kalendarzem giełdy nie odbywa się sesja
wówczas jest to ostatni dzień sesyjny przypadający przed trzecim piątkiem miesiąca
wykonania. W sytuacjach szczególnych Giełda może określić inny ostatni dzień
obrotu, podając informację o tym do wiadomości uczestników rynku, co najmniej na 4
tygodnie wcześniej. W przypadku podjęcia przez Giełdę decyzji o zaprzestaniu
wprowadzania kolejnych serii kontraktów terminowych Giełda przekaże taką
informację do wiadomości uczestników rynku oraz powiadomi KPWiG

11

najpóźniej

na 3 tygodnie przed planowaną datą wprowadzenia kolejnej serii kontraktu.

ƒ

Dzień wygaśnięcia: Dzień ustalenia ostatecznego kursu rozliczeniowego kontraktu.

Ten sam dzień, co ostatni dzień obrotu

ƒ

Pierwszy dzień obrotu nowej serii: Pierwszy dzień sesyjny po dniu wygaśnięcia

poprzedniej serii kontraktów. W przypadku pierwszych serii kontraktów w danej
klasie określany jest przez Zarząd Giełdy i przekazywany do wiadomości uczestników
rynku najpóźniej na 7 dni przed rozpoczęciem obrotu

ƒ

Dzienny kurs rozliczeniowy kontraktu: Dzienny kurs rozliczeniowy kontraktu

określany jest po każdej sesji począwszy od dnia, w którym zawarto pierwszą
transakcję kontraktami danej serii z wyjątkiem ostatniego dnia obrotu. Za dzienny
kurs rozliczeniowy kontraktu uznaje się kurs zamknięcia kontraktów danej serii. Jeśli

11

Komisja Papierów Wartościowych i Giełd

Giełda Papierów Wartościowych w Warszawie

17

w czasie sesji nie określono kursu zamknięcia za dzienny kurs rozliczeniowy
kontraktu przyjmuje się ostatni kurs rozliczeniowy kontraktu.Jeśli jednak w arkuszu
zleceń na zamknięciu jest choć jedno zlecenie z limitem lepszym (kupna wyższym,
sprzedaży niższym) od kursu rozliczeniowego kontraktu określonego na w/w
warunkach i wprowadzone przynajmniej 5 minut przed końcem notowań, za kurs
rozliczeniowy kontraktu przyjmuje się limit najlepszego z tych zleceń. W przypadku
zleceń kupna jest to najwyższy limit zlecenia kupna przekraczający kurs określony na
w/w warunkach. I odwrotnie, w przypadku zleceń sprzedaży jest to najniższy limit
zlecenia sprzedaży poniżej kursu określonego na w/w warunkach. W sytuacjach
szczególnych, po konsultacji z KDPW

12

, Giełda ma prawo wyznaczyć kurs

rozliczeniowy kontraktu inny niż wyznaczony na warunkach określonych powyżej.

ƒ

Dzienna cena rozliczeniowa kontraktu: Dzienny kurs rozliczeniowy kontraktu

przemnożony przez mnożnik.

ƒ

Ostateczny kurs rozliczeniowy kontraktu: Określany w dniu wygaśnięcia kontraktu

jako ważona obrotami średnia arytmetyczna kursów wszystkich transakcji kontraktami
danej serii zawartych w ciągu ostatniej godziny notowań ciągłych i na zamknięcie
notowań ciągłych. W przypadku braku transakcji w ciągu ostatniej godziny notowań
ciągłych i na zamknięcie notowań ciągłych ostateczny kurs rozliczeniowy kontraktu
wyznaczony zostaje analogicznie jak dzienny kurs rozliczeniowy kontraktu.
Ostateczny kurs rozliczeniowy kontraktu służy do wyznaczenia ostatecznej ceny
rozliczeniowej obligacji w przypadku rozliczenia kontraktu przez dostawę obligacji
lub ostatecznej ceny rozliczenia pieniężnego w sytuacji rozliczenia pieniężnego
kontraktu.

ƒ

Ostateczna cena rozliczeniowa kontraktu: Ostateczny kurs rozliczeniowy kontraktu

przemnożony przez mnożnik

ƒ

Wykonanie kontraktu: Wykonanie kontraktu następuje przez dostawę obligacji na

zasadach określonych przez KDPW. Przedmiotem dostawy z tytułu realizacji
zobowiązań wynikających z tytułu jednego kontraktu terminowego mogą być
obligacje tylko jednej serii obligacji skarbowych zaliczonych do listy obligacji do
dostawy. W sytuacji szczególnej możliwe jest wykonanie kontraktu poprzez
rozliczenie pieniężne lub częściowe rozliczenie pieniężne na zasadach określonych
przez KDPW.

ƒ

Lista obligacji do dostawy: Lista obligacji mogących być przedmiotem dostawy jest

określana przed pierwszym dniem obrotu danej serii kontraktu przez KDPW w
porozumieniu z Giełdą i publikowana. Zawiera ona dla każdej serii obligacji
współczynnik konwersji i kwotę narosłych odsetek na dzień dostawy obligacji. KDPW
w porozumieniu z Giełdą i Ministrem Finansów może rozszerzyć listę obligacji po
wprowadzeniu nowych obligacji do obrotu, jeżeli obligacje te spełniają ww. kryteria.
Rozszerzenie listy obligacji może nastąpić nie później niż w ostatnim dniu roboczym
miesiąca poprzedzającego miesiąc, w którym następuje wykonanie danej serii
kontraktu. Z listy nie można usunąć serii obligacji już do niej zaliczonej.

ƒ

Dzień wykonania kontraktu: Dniem wykonania kontraktu danej serii przez dostawę

obligacji jest czwarty dzień roboczy następujący po ostatnim dniu obrotu. Wykonanie
kontraktu przez dostawę obligacji następuje w oparciu o ostateczną cenę
rozliczeniową obligacji. W sytuacji szczególnej, w przypadku rozliczenia pieniężnego
kontraktu, dniem wykonania jest trzeci dzień roboczy następujący po ostatnim dniu
obrotu. Rozliczenie pieniężne kontraktu następuje w oparciu o ostateczną cenę
rozliczenia pieniężnego kontraktu.

12

Krajowy Depozyt Papierów Wartościowych

Giełda Papierów Wartościowych w Warszawie

18

ƒ

Ostateczna cena rozliczeniowa obligacji: Ostateczna cena rozliczeniowa obligacji

jest wyznaczana dla każdej serii obligacji mogących być przedmiotem dostawy w
oparciu o ostateczny kurs rozliczeniowy kontraktu, wartość narosłych odsetek i
odpowiedni współczynnik konwersji danej serii obligacji.

Wartość ostatecznej ceny rozliczeniowej jest podawana z dokładnością do jednego

grosza. Ostateczna cena rozliczeniowa obligacji dla danej serii wyliczana jest zgodnie
z następującą formułą:

i

i

i

AI

1000

OKR

100

CF

OCR

+

×













×

=

gdzie:
OCR

i

– ostateczna cena rozliczeniowa obligacji odpowiadająca „i”-tej serii,

CF

i

– współczynnik konwersji odpowiadający ”i”-tej serii obligacji,

OKR– ostateczny kurs rozliczeniowy kontraktu,

AI

i

– iloczyn narosłych odsetek od „i”-tej serii obligacji i liczby 100.

Jeżeli dzień przyznania prawa do odsetek przypada w okresie od T do T+3 (gdzie T

est ostatnim dniem obrotu danej serii kontraktów) lub wcześniej to odsetki te nie są

uwzględniane.

Współczynnik konwersji dla danej serii obligacji obliczany jest według formuły

przedstawionej w rozdziale 2.6.

Narosłe odsetki naliczane są zgodnie z tabelą odsetkową, publikowaną przez

Ministerstwo Finansów na dzień rozliczenia kontraktu

ƒ

Ostateczna cena rozliczenia pieniężnego kontraktu: Cena, w oparciu o którą nastąpi

rozliczenie pieniężnie kontraktu w sytuacji wyjątkowej. Cena wyznaczana jest na
zasadach określonych przez KDPW

ƒ

Wstępny depozyt zabezpieczający wnoszony przez inwestora: Minimalna

wysokość jest określona przez KDPW.Podmiot prowadzący rachunek inwestora może
określić wyższy poziom depozytu zabezpieczającego wnoszonego przez inwestora.

ƒ

Sytuacje szczególne: Sytuacje szczególne występują w przypadku, gdy spełnienie

świadczenia poprzez dostawę fizyczną byłoby połączone z nadmiernymi trudnościami
z przyczyn niezależnych od stron transakcji. Za sytuację szczególną należy rozumieć
między innymi przypadek, w którym wartość wszystkich otwartych pozycji w danej
serii kontraktów terminowych w ostatnim dniu obrotu przekroczy 20% wartości emisji
obligacji, które wchodzą w skład listy obligacji do dostawy. W przypadkach
szczególnych Zarząd Giełdy określa zasady postępowania i niezwłocznie podaje je do
publicznej wiadomości

2.4 System depozytów zabezpieczających

13

System depozytów zabezpieczających ma za zadanie gwarantowanie rozliczeń

transakcji zawartych na kontraktach terminowych na obligacje. Nad jego prawidłowym

funkcjonowaniem czuwa KDPW.

13

Szczegółowe informacje nt. systemu depozytów zabezpieczających zamieszczono w pkt 4. „Warunków obrotu

dla programu kontraktów terminowych na obligacje skarbowe…”. Tekst warunków obrotu jest dostępny na
stronie internetowej Giełdy.

Giełda Papierów Wartościowych w Warszawie

19

Elementami systemu gwarantowania rozliczeń są między innymi następujące elementy:

1. Właściwy depozyt zabezpieczający

2. Wstępny depozyt zabezpieczający

3. Właściwy depozyt zabezpieczający dostawę

Właściwy depozyt zabezpieczający

jest wnoszony przez uczestników rozliczających i ma na

celu zabezpieczenie ryzyka jednodniowej zmiany ceny. Jest on naliczany codziennie po

zakończeniu sesji, osobno na każdy portfel, przy czym uwzględniona zostaje korelacja w

obrębie portfela. Może on być częściowo wniesiony w formie papierów wartościowych (do

wysokości 60% depozytu). Dochody z zarządzania właściwym depozytem zabezpieczającym

są przekazywane uczestnikom rozliczającym co kwartał. Wysokość właściwego depozytu

zabezpieczającego obliczana jest wg następującej formuły:

%

poziomDZ

mnoznik

kurs

WDZ

×

×

=

gdzie:

WDZ

–

właściwy depozyt zabezpieczający

kurs – kurs rozliczeniowy kontraktu

mnożnik – mnożnik kontraktu w wysokości 1000 zł

poziom DZ% - poziom depozytu zabezpieczającego wyrażony w procentach (2%)

Wstępny depozyt zabezpieczający

jest wnoszony przez inwestora do uczestnika

rozliczającego w momencie składania zlecenia. Jego wartość minimalną ogłasza KDPW,

natomiast uczestnik rozliczający może żądać wyższego poziomu wstępnego depozytu

zabezpieczającego. Inwestor jest zobowiązany do utrzymywania depozytu na poziomie

zabezpieczającym zawarte przez niego transakcje, przy czym wysokość utrzymywanego

depozytu nie może być niższa od wielkości właściwego depozytu zabezpieczającego

wyliczonego przez KDPW dla portfela transakcji. W przypadku wystąpienia niekorzystnej

zmiany ceny, lub zmiany składu portfela, które spowodują, że wielkość utrzymywanego

depozytu spadnie poniżej aktualnej wartości właściwego depozytu zabezpieczającego,

inwestor ma obowiązek uzupełnić brakującą część depozytu tj. do wysokości ustalonej przez

Giełda Papierów Wartościowych w Warszawie

20

uczestnika rozliczającego w umowie prowadzenia rachunku, jednak nie mniejszej niż 140%

wartości aktualnego właściwego depozytu zabezpieczającego.

Właściwy depozyt zabezpieczający dostawę

stanowi część właściwego depozytu

zabezpieczającego. Pobierany jest w celu zabezpieczenia ryzyka związanego z kontraktami,

które już wygasły, ale nie zostały jeszcze wykonane (depozyt 4-dniowy). Naliczany jest on

codzienne dla każdego kontraktu będącego w okresie dostawy. W przypadku pozycji krótkiej,

właściwy depozyt zabezpieczający dostawę jest naliczany do dnia przelewu obligacji na konto

dostawy. Z kolei posiadaczom pozycji długich jest on zwracany po rozliczeniu kontraktu

terminowego.

Wysokość właściwego depozytu zabezpieczającego dostawę obliczana jest wg następującej

formuły:

DD

%

poziomDZ

mnoznik

kurs

WDZD

×

×

×

=

gdzie:

WDZD - właściwy depozyt zabezpieczający dostawę

kurs – kurs rozliczeniowy kontraktu

mnożnik – mnożnik kontraktu w wysokości 1000 zł

poziom DZ% - poziom depozytu zabezpieczającego wyrażony w procentach (2%)

DD – liczba dni pozostająca do dnia dostawy

Rozrachunki polegające na ustaleniu zobowiązań i należności inwestorów z tytułu zawarcia

transakcji na rynku terminowym, w tym wynikające z obowiązku utrzymywania depozytów

zabezpieczających, dokonywane są codziennie na koniec dnia, na podstawie dziennych cen

rozliczeniowych lub ostatecznej ceny rozliczeniowej. Redukują one w ten sposób ryzyko

rynkowe do ryzyka jednodniowego.

2.5 Koszty utrzymywania pozycji (Cost of carry)

Posiadanie obligacji w portfelu, a także ich brak wiążą się z możliwością osiągania

dodatkowych przychodów lub ponoszenia kosztów. Inwestor posiadający długą pozycję w

Giełda Papierów Wartościowych w Warszawie

21

obligacjach może ją finansować dokonując transakcji repo

14

na rynku pieniężnym. Przy

rosnącej krzywej osiągnie on dodatkowy zysk, gdyż kupi obligację z wyższą rentownością

finansując ją po niższej stopie procentowej. W takim wypadku powiemy o pozytywnym lub

dodatnim carry. Gdyby jednak krzywa miała ujemne nachylenie to koszt finansowania

pozycji byłby wyższy niż dochód osiągany z tytułu trzymania obligacji. Mamy wtedy do

czynienia z negatywnym carry.

2.6 Współczynnik konwersji

Specyfika kontraktów terminowych na obligacje powoduje, iż posiadacz zajmujący

pozycję krótką ma możliwość dostarczenia dowolnej obligacji o terminie nie krótszym niż 2

lata i dziewięć miesięcy i nie dłuższym niż 5 lat i sześć miesięcy. Biorąc pod uwagę, że w tak

zdefiniowanym koszyku znajduje się kilka możliwych do dostarczenia serii obligacji,

niezbędne jest określenie, jaką cenę za te obligacje otrzyma inwestor zajmujący pozycję

krótką. Ceny obliczane są za pomocą współczynnika konwersji, który wyznaczany jest wg

następującej formuły:

y

d

y

C

PV

r

CF

y

d

−

×

−

×

+

=

−

)

1

(

gdzie:

n

n

n

n

i

i

r

r

r

C

C

r

r

C

PV

)

1

(

100

)

1

(

1

1

)

1

(

100

)

1

(

1

0

+

+













+

−

×

+

=

+

+

+

×

=

∑

=

gdzie:

CF – współczynnik konwersji

r – stopa procentowa służąca do wyznaczenia współczynnika konwersji równa 6% w

skali roku

n - liczba lat pozostałych do wykupu papieru wartościowego licząc od daty płatności

kuponu następującego po dniu dostawy. Jeżeli dzień przyznania prawa do odsetek

wypada w okresie od dnia T do dnia T+3 lub wcześniej i kupon jest wypłacany po

dniu rozliczenia dostawy, to nie jest on uwzględniany przy wyznaczaniu wartości „n”.

14

Transakcja polegająca na udzieleniu kredytu pod zastaw papierów wartościowych np. obligacji

Giełda Papierów Wartościowych w Warszawie

22

C– roczny kupon przypadający na 100 PLN nominału obligacji. Jeżeli dzień ustalenia

prawa do odsetek od obligacji wypada w okresie od dnia T do dnia T+3 to ta płatność

nie jest uwzględniana

y - aktualna liczba dni pomiędzy dwiema datami wypłaty rocznych odsetek

uwzględniająca dzień dostawy (365 lub 366 dni)

d - aktualna liczba dni pomiędzy dniem rozliczenia dostawy (T+4) a dniem wypłaty

odsetek (kuponu) następującym po dniu dostawy,

PV - bieżąca wartość 100 PLN wartości nominału obligacji zdyskontowana stopą r na

dzień wypłaty kuponu

Wartości, które przybiera współczynnik konwersji, zależą od kuponu przyjętej do

obliczeń obligacji. W związku z powyższym można wyróżnić trzy przedziały liczbowe, w

których będzie oscylował współczynnik konwersji:

•

dla obligacji z kuponem większym niż 6% współczynnik konwersji będzie większy od

100,

•

w przypadku obligacji z kuponem mniejszym niż 6% (przykładowo obligacja PS0608)

współczynnik konwersji będzie przybierał wartości mniejsze od 100,

•

dla obligacji z kuponem równym 6%, jak na przykład DS0509, DS1109,

współczynnik konwersji będzie oscylował wokół jedności.

Dobrze jest znać zasady liczenia tego współczynnika, jednakże niekoniecznie trzeba

przeprowadzać tak żmudne wyliczenia, gdyż wartości te będą publikowane przez KDPW

przed pierwszym dniem obrotu danej serii kontraktów terminowych na obligacje i podawane

z dokładnością do sześciu miejsc po przecinku. Wartość współczynnika konwersji będzie

odpowiadać 100 PLN wartości nominalnej obligacji.

2.7 Obligacja najtańsza w dostawie (Cheapest to Deliver – CTD)

Kalkulacja obligacji CTD jest kolejną implikacją faktu, iż zajmujący krótką pozycję

inwestor może dostarczyć dowolną obligację z koszyka. Jest oczywistym, iż będzie się on

starał dostarczyć taką obligację, której koszt zakupu będzie jak najmniejszy. Do wyliczenia

obligacji CTD stosuje się tzw. bazę brutto. Ta obligacja, dla której wartość bazy będzie

najmniejsza jest obligacją CTD. Kalkulację bazy przeprowadza się według następującej

formuły:

Giełda Papierów Wartościowych w Warszawie

23

100

100

×













×

−

=

b

F

CF

S

BASIS

gdzie:

BASIS – baza brutto

S – cena spot obligacji

F

b

– bieżąca cena kontraktu terminowego

CF – współczynnik konwersji

Rachunek taki należy przeprowadzić dla wszystkich serii obligacji dostępnych do

dostawy. Kalkulacja bazy jest procesem ciągłym, ponieważ kształt krzywej dochodowości

zmienia się cały czas pod wpływem zmian oczekiwań uczestników rynku co do kształtowania

się przyszłych poziomów stóp procentowych, wskaźników ekonomicznych i innych ważnych

dla rynku wydarzeń. Należy przy tym podkreślić, że rzadko mamy do czynienia z

przesunięciami równoległymi krzywej. Częściej mają miejsce zmiany nachylenia krzywej w

jej poszczególnych segmentach. Wpływa to w istotny sposób na wycenę obligacji i tym

samym może powodować zmianę serii obligacji, która w danym momencie będzie najtańsza

w dostawie. Monitorowanie obligacji CTD jest także ważne z innego powodu. Wraz z

zapadaniem kolejnych serii kontraktów zmieniać się będzie skład koszyka obligacji

możliwych do dostarczenia, co może sprawić, że konieczne będzie wybranie nowej obligacji

będącej najtańszą w dostawie.

Przykład nr 5

Spróbujmy porównać bazę dla dwóch różnych obligacji DS0509 i PS0608. Mamy dane

współczynniki konwersji 99,96 dla DS0509 i 99,18 dla obligacji PS0608. Ceny tych obligacji

na dzień 2 listopada 2004 kształtują się odpowiednio 96,16 i 96,05. Załóżmy, że przykładowy

kurs terminowy dla grudniowych kontraktów wynosi 96,25. Po podstawieniu do wzoru

otrzymamy wysokość bazy: – 5,15 dla obligacji DS0509 i 58 dla obligacji PS0608. Jeśli

mielibyśmy rozstrzygać tylko na podstawie tylko dwóch obligacji uznalibyśmy, że DS0509

jest obligacją najtańszą w dostawie.

Giełda Papierów Wartościowych w Warszawie

24

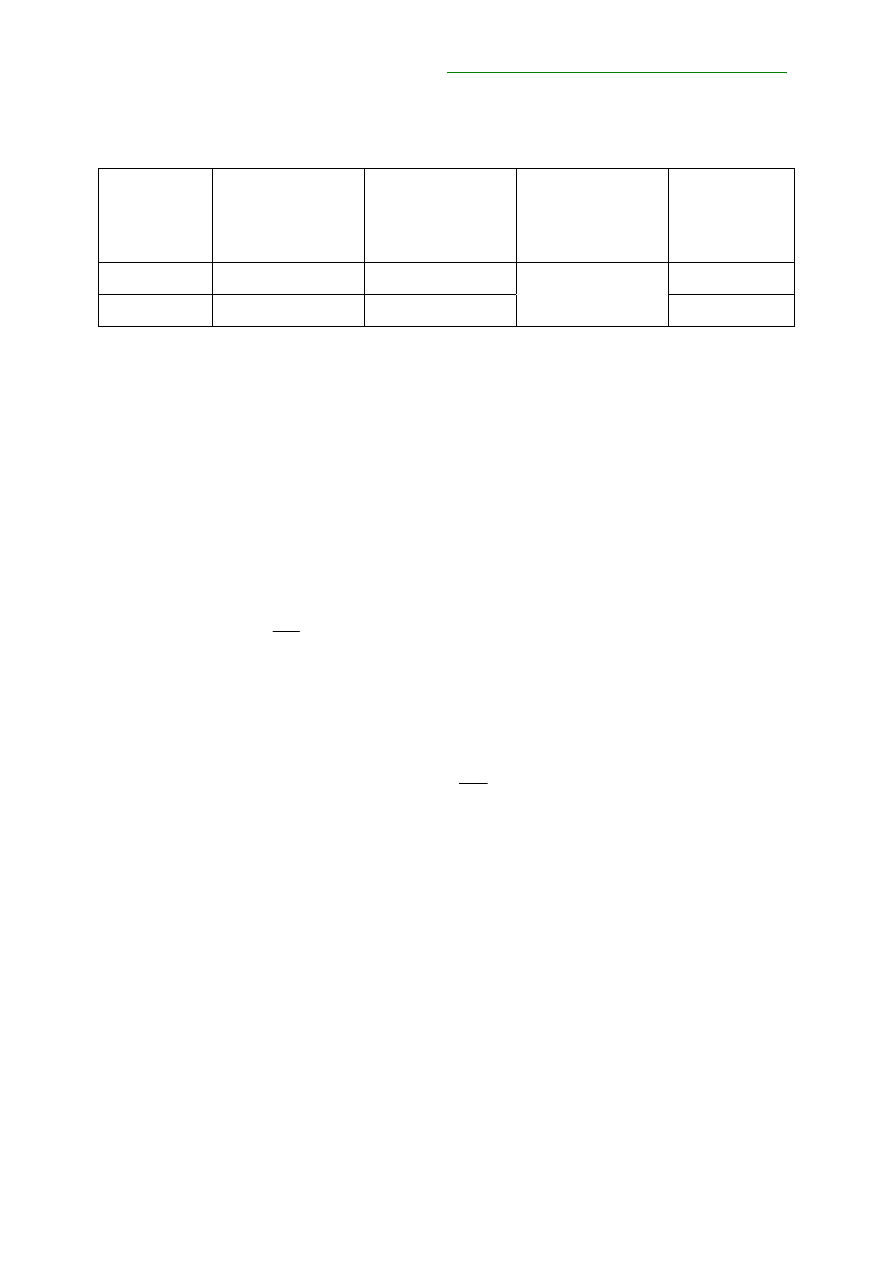
Tabela nr 2. Podsumowanie przykładu.

Obligacje Wartość

współczynnika

konwersji (CF)

Przykładowe ceny

obligacji 2.11.2004

(czyste)

Przykładowy kurs

kontraktu

terminowego

Baza dla

obligacji

DS0509 99,96

96,16

-5,15

PS0608 99,18

96,05

96,25

58

2.8 Wycena kontraktu

Dokładne obliczanie ceny terminowej jest utrudnione z uwagi na dowolność wyboru

serii obligacji będących przedmiotem dostawy. Zakłada się jednak, że cena terminowa

kontraktu powinna być jak najbardziej zbliżona do ceny terminowej obligacji CTD.

Teoretyczną cenę kontraktu opisuje wzór:

CF

P

F

t

=

gdzie:

(

)

t

t

AI

t

r

AI

S

P

−













×

+

×

+

=

365

1

gdzie:

F – teoretyczna cena kontraktu terminowego

CF – współczynnik konwersji

S – cena spot obligacji

AI – odsetki naliczone na początku transakcji

AI

t

– odsetki naliczone na końcu transakcji

r - stopa procentowa

t - czas pozostający do końca trwania kontraktu

Giełda Papierów Wartościowych w Warszawie

25

Wartość P

t

jest to po prostu wartość przyszła obligacji wyrażona poprzez jej cenę czystą (bez

narosłych odsetek). Z uwagi na to, że kontrakt wystawiany jest na standardowe obligacje o

kuponie 6%, konieczne jest wykorzystanie współczynnika konwersji, aby otrzymać

ekwiwalent interesującej nas obligacji.

W powyższym wzorze istotną kwestią jest dobranie przez inwestora właściwej stopy

procentowej. Teoretycznie powinna być to stopa procentowa wolna od ryzyka, jednakże

instytucje finansowe dla dokładniejszego obliczenia ceny kontraktu przyjmują za wartość „r”

stopę, po której są w stanie pożyczyć i ulokować środki pozyskane na zakup lub ze sprzedaży

obligacji. Wynikiem obliczeń powinien być zatem wolny od arbitrażu

15

przedział wahań

Przykład nr 6

Wykorzystajmy raz jeszcze obligację DS0509 do obliczania ceny teoretycznej hipotetycznego

grudniowego kontraktu. Dysponujemy następującym danymi:

• data rozliczenia kontraktu 23 grudnia,
• data wyznaczenia ceny teoretycznej 2 listopada.
• liczba dni od daty rozliczenia do daty płatności kuponowej upłynie więc 152 dni,
• czas trwania transakcji to 51 dni.
• Cena obligacji wynosi 96,16
• współczynnik konwersji wynoszący 99,96,
• stopa procentowa na poziomie 6,5%.

Z

przykładu w rozdziale pierwszym wiemy, że brudna cena obligacji na 2 listopada

wynosi 98,82.. Cenę terminową policzymy w następujący sposób:

(

)

22

,

96

5

,

3

365

51

%

5

,

6

1

82

,

98

=

−

×

+

×

=

t

P

Po podzieleniu przez współczynnik konwersji otrzymamy cenę 96,25, Jest to cena teoretyczna

kontraktu opiewającego na tą obligacje.

Rozdział 3. Przykłady wykorzystania kontraktów

Odkąd 22 sierpnia 1977, na giełdzie Chicago Board of Trade rozpoczęto handel

kontraktami terminowymi na amerykańskie obligacje skarbowe, rynek futures na papiery

rządowe przeżywa na świecie stały i szybki rozwój. Nadszedł również czas na giełdę

warszawską. Istnieje niepowtarzalna okazja skorzystania także w Polsce z szeregu różnych

Giełda Papierów Wartościowych w Warszawie

26

korzyści, jakie niesie za sobą inwestowanie w kontrakty terminowe, których nie posiadają

instrumenty bilansowe takie jak: obligacje skarbu państwa, bony skarbowe czy akcje

przedsiębiorstw.

Wachlarz

zastosowań kontraktów terminowych jest bardzo szeroki, od transakcji

spekulacyjnych począwszy, poprzez różnego rodzaju zabezpieczenia aktywów finansowych

przed ryzykiem stóp procentowych (np. zabezpieczenie posiadanego portfela obligacji ze

stałym kuponem przed spadkiem cen), na transakcjach arbitrażowych

16

skończywszy.

Podstawową korzyścią, jaką niesie ze sobą inwestycja w kontrakty terminowe, jest możliwość

gry na wzrost stóp procentowych bez ponoszenia takich kosztów, jak w przypadku

wykorzystania podobnej strategii na rynku kasowym obligacji.

3.1 Pozycja długa/krótka

Otwarcie pozycji długiej polega na zakupie kontraktów terminowych na obligacjach.

Występuje wtedy przewaga należności związanych z nabyciem kontraktów nad

zobowiązaniami. Operację taką dokonujemy w przypadku, gdy oczekujemy w najbliższej

przyszłości spadku stóp procentowych. Ekonomicznie jest to równoznaczne z zakupem

papierów rządowych, w oczekiwaniu na wzrost ich cen. Należy zwrócić uwagę, że kupno

kontraktu stwarza możliwość osiągnięcia identycznych zysków co w przypadku zakupu

obligacji, lecz przy znacznie mniejszym zaangażowaniu kapitałowym.

Otwarcie pozycji krótkiej w kontraktach terminowych polega na ich sprzedaży.

Występuje wtedy przewaga zobowiązań nad należnościami. Jest to równoznaczne ze

sprzedażą obligacji. Jednak w przypadku aktywa bilansowego, jakim jest np. papier

skarbowy, sprzedaż wymusza posiadanie go na rachunku. Oczywiście obligację można

pożyczyć, jednak zazwyczaj operacja taka, jeśli dla danego inwestora jest w ogóle możliwa,

niesie ze sobą pewien koszt, tym wyższy, im dłuższy jest okres inwestycji. Sprzedaż,

kontraktu (otwarcie pozycji krótkiej), podobnie jak w przypadku pozycji długiej, niesie ze

sobą jedynie koszt finansowania depozytu zabezpieczającego

17

.

15

Zagadnienie arbitrażu jest omówione w rozdziale 3.

16

Operacja arbitrażowa polega na wykorzystaniu różnic w kwotowaniu dwóch instrumentów o tym samym lub

zbliżonym profilu ryzyka w tym samym momencie i czasie na dwóch różnych rynkach. Dzięki nim zysk
arbitrażysty pozbawiony jest ryzyka związanego z upływem czasu. Jedynie ponosi on ryzyko rozliczenia
transakcji przez kontrahenta, które przy obecnym poziomie rozwoju instytucji clearingowych, można przyjąć za
nieznaczące.

17

Np. odsetki od kredytu przeznaczonego na depozyt zabezpieczający.

Giełda Papierów Wartościowych w Warszawie

27

W przypadku wystandaryzowanych instrumentów, jakimi są kontrakty terminowe,

zawarcie przeciwnego kontraktu na te same obligacje, w tej samej ilości i o tym samym

terminie wygaśnięcia, zamyka pozycję długą lub krótką. Nie zawarcie transakcji przeciwnej

skutkuje koniecznością - w dniu wygaśnięcia kontraktu - nabycia (dla pozycji długiej) lub

sprzedaży (przy pozycji krótkiej) odpowiedniej ilości obligacji skarbowych (CTD).

Przykład nr 7.

Poniżej przeanalizujemy jednocześnie otwarcie długiej/krótkiej pozycji poprzez

nabycie/sprzedaż kontraktów terminowych:

Parametry transakcji:

• Nominał jednego kontraktu: 100 000 PLN
• Mnożnik : 1000
• Poziom depozytu zabezpieczającego określony procentowo: 2% wartości kontraktu
• Liczba nabytych/sprzedanych kontraktów: 20
• Liczba dni posiadanej pozycji długiej/krótkiej: 15
• Cena kupna/sprzedaży kontraktu terminowego przy otwarciu pozycji: 97,05
• Cena zamknięcia pozycji długiej/krótkiej: 97,45
• Koszt finansowania otwartej pozycji w okresie jej „życia”: 6% p.a.

(np. koszt zaciągniętego kredytu na depozyt zabezpieczający kontrakt terminowy.)

• Oprocentowanie depozytu zabezpieczającego (przychód ze środków pozostających w

depozycie)

18

: 5% p.a.

• Średnia cena kontraktu w okresie jego utrzymania: 97,25

Wartość transakcji otwarcia pozycji długiej/krótkiej:

liczba kontraktów x cena otwarcia x mnożnik = 20 x 97,05 x 1000 = 1 941 000 PLN

Depozyt zabezpieczający składany w momencie otwarcia pozycji:

liczba kontraktów x cena otwarcia x mnożnik x poziom depozytu zabezp. =

20 x 97,05 x 1000 x 2% = 38 820 PLN

Średnia wartość depozytu zabezpieczającego w okresie „życia” otwartej pozycji:

18

Depozyt zabezpieczający złożony w Krajowym Depozycie Papierów Wartościowych stanowi środki, które są

reinwestowane na rynku pieniężnym w depozyty krótkoterminowe (zazwyczaj na okres 1 lub 2 tygodni) bądź w
bony skarbowe z krótkim terminem zapadalności. Uzyskane w ten sposób odsetki, pomniejszone o marżę

Giełda Papierów Wartościowych w Warszawie

28

20 x 97,25 x 1000 x 2% = 38 900 PLN

Koszt finansowania depozytu zabezpieczającego pozycji długiej/krótkiej:

Średnia wartość zaangażowania

19

x koszt finansowania x liczba dni /365 =

38 900 x 6% x 15 / 365 = 95,92 PLN

Przychód od depozytu zabezpieczającego pozycji długiej/krótkiej:

Średnia wartość depozytu x oprocentowanie odsetek x liczba dni /365 =

38 900 PLN x 5% x 15 / 365 = 79,93 PLN

Wartość transakcji zamknięcia pozycji długiej/krótkiej:

liczba kontraktów x cena zamknięcia x mnożnik= 20 x 97,45 x 1000 = 1 949 000 PLN

Wynik transakcji dla inwestora, który otworzył pozycję długą o następnie ją zamknął

(zysk):

wartość zamknięcia – wartość otwarcia – koszt finansowy + przychód od depozytu

zabezpieczającego = 1 949 000 – 1 941 000 – 95,92 + 79,93 = 7 984,01 PLN

Wynik transakcji dla inwestora, który otworzył pozycję krótką a następnie ją zamknął

(strata):

wartość otwarcia - wartość zamknięcia – koszt finansowy + przychód od depozytu

zabezpieczającego = 1 941 000 – 1 949 000 – 95,92 + 79,93 = - 8 015,99 PLN

Podsumowując, należy stwierdzić, że inwestor, który otworzył długą pozycję a następnie ją

zamknął zarobił prawie 8 tys. zł, natomiast inwestor, który otworzył krótką pozycję a

następnie ją zamknął stracił nieco więcej niż 8 tys. zł.

Należy przy tym zwrócić uwagę, że funkcjonuje zasada równania do rynku, czyli

codziennego rozliczania kwot zysków/strat dla stron transakcji w oparciu o kursy

transakcyjne oraz dzienne kursy rozliczeniowe. W ten sposób ryzyko rynkowe ograniczone

jest do ryzyka jednodniowego, zaś wynik z transakcji jest odzwierciedlany na bieżąco w

postaci faktycznych przepływów pieniężnych.

3.2 Strategie spreadowe

Idea tego typu strategii zakłada zwrot dla inwestora w postaci marży, wynikającej z

różnicy w dochodowościach, pomiędzy co najmniej dwiema, wchodzącymi w skład strategii,

pozycjami długą i krótką. Dodatkowo poszczególne transakcje są tak dobrane, aby ryzyko

operacyjną, (pobieranej od inwestorów w wysokości około 0,5% p.a.) są okresowo wypłacane posiadaczom za
okres ich utrzymania.

Giełda Papierów Wartościowych w Warszawie

29

związane z inwestycją było ograniczone do konkretnego scenariusza zachowania się rynku. I

tak, można grać na zmiany nachylenia kąta krzywej dochodowości, czyli np. wzrost

rentowności obligacji 2-letnich i spadek rentowności 5-letnich

(zakup obligacji 5-letnich i sprzedaż odpowiedniej ilości kontraktów, dla których aktywem

bazowym jest koszyk obligacji 2-letnich). Można grać na zawężenie się, na skutek

oczekiwanego wejścia Polski do strefy EURO, różnicy oprocentowania polskich i

niemieckich (lub wyemitowanych przez inny kraj ze strefy EURO) obligacji skarbowych

(kupno obligacji polskich i sprzedaż odpowiedniej ilości kontraktów, dla których aktywem

bazowym jest koszyk obligacji niemieckich

20

). Można wreszcie grać na różnicy

dochodowości kilku różnych instrumentów, wynikającej z odmiennej ich charakterystyki.

Mogą to być dwie (lub więcej) serie kontraktów terminowych o różnych terminach

wygaśnięcia, ale opartych na tym samym koszyku obligacji, bądź też opartych na różnych

koszykach instrumentów bazowych.

Oczywiście zawsze możemy zakładać, że np. zmiana rentowności na krzywej

dochodowości, dotyczyć będzie tylko pewnych określonych jej obszarów, np. wzrost w ciągu

roku dochodowości instrumentów od 3-letnich do 7-letnich, a spadek dochodowości

wszystkich innych, tj. krótszych i dłuższych. Do utworzenia jednak strategii inwestycyjnej,

która przynosiłaby profit inwestorowi w przypadku zrealizowania się takiego scenariusza,

konieczne byłoby zastosowanie większej ilości instrumentów, o różnych terminach

zapadalności i różnych duration.

Przykład nr 8.

Transakcja spreadowa: jednoczesne otwarcie pozycji długiej w kontrakcie czerwcowym i

krótkiej pozycji w kontrakcie marcowym

21

Parametry transakcji:

Otwarcie pozycji

• Liczba otwieranych kontraktów marcowych i czerwcowych: po 50 w każdej serii
• Cena sprzedaży kontraktu marcowego przy otwarciu pozycji: 97,05

19

Średnia wartość zaangażowania to środki przeznaczone na pokrycie depozytu zabezpieczającego w wysokości

depozytu wstępnego

20

W przypadku, gdy inwestor ma dostęp do rynku, na którym handlowane są takie kontrakty.

21

Jest to tzw. kupno spreadu, czyli długa pozycja w kontrakcie z dłuższym terminem wygaśnięcia i krótka

pozycja w kontrakcie z krótszym terminem wygaśnięcia. Przy kalkulacji wyniku pomijamy koszt finansowania i
przychód z tytułu utrzymywania depozytów zabezpieczających. Stanowią one wartości nieznaczne w
porównaniu z właściwym wynikiem na transakcji spreadowej. Kalkulacja wyników z tytułu utrzymywania
depozytów zabezpieczających została omówiona w poprzednim przykładzie.

Giełda Papierów Wartościowych w Warszawie

30

• Cena kupna kontraktu czerwcowego przy otwarciu pozycji: 97,75
• Spread kupna = 97,75 – 97,05 = 0,70

Zamknięcie pozycji

• Cena kupna kontraktu marcowego przy zamknięciu pozycji: 96,95
• Cena sprzedaży kontraktu czerwcowego przy zamknięciu pozycji: 98,05
• Spread sprzedaży = 98,05 – 96,95 = 1,10

Kalkulacja wyniku transakcji spreadowej

22

.

liczba sztuk x (spread sprzedaży–spread kupna) x 1000=50x(1,10–0,70)x1000 = 20 000 PLN

Tabela nr 2 Podsumowanie przykładu.

Seria marcowa

Seria czerwcowa

Kurs po którym została otwarta

pozycja (sprzedaż serii marcowej,

zakup czerwcowej)

97,05 97,75

Kurs po którym została zamknięta

pozycja (zakup serii marcowej,

sprzedaż czerwcowej)

96,95 98,05

Wynik na poszczególnych seriach (na

1 kontrakcie)

Zysk 10 bp na serii

Zysk 30 bp na serii

Wynik sumaryczny na strategii(na 1

kontrakcie)

Zysk 40 bp

Łączny wynik finansowy na całej

strategii

40 bp * 50 kontraktów * 1000 = 20 000 zł

3.3 Transakcje zabezpieczające

Drugim, po spekulacji, zastosowaniem kontraktów terminowych na obligacjach, jest

możliwość wykorzystywania ich do zabezpieczania portfeli instrumentów dłużnych przede

wszystkim przed ryzykiem stóp procentowych. Większość obligacji dostępnych w Polsce i na

22

Bez kosztu finansowania i przychodu odsetkowego dla depozytów zabezpieczających.

Giełda Papierów Wartościowych w Warszawie

31

świecie posiada stały, niezmienny w czasie kupon

23

. Taka konstrukcja powoduje określone

konsekwencje dla ich posiadaczy w postaci ryzyka spadku wartości rynkowej na skutek

wzrostu stóp procentowych. Tym bardziej jest to dotkliwe, im dłuższe jest duration obligacji.

Jeśli więc skład portfela papierów wartościowych jest optymalny (z punktu widzenia ich

posiadacza) pod względem ryzyka kredytowego, a jednocześnie obawiamy się, że nastąpi w

najbliższej przyszłości wzrost rynkowych stóp procentowych, najwłaściwszym

postępowaniem byłoby jego czasowe zabezpieczenie, a nie odsprzedaż. W drugim przypadku

dużo wyższe byłyby koszty, związane z ponownym odtworzeniem portfela papierów

wartościowych (co wynika z istnienia często dużej różnicy pomiędzy ceną rynkową kupna i

sprzedaży danej emisji papierów wartościowych, zwłaszcza, gdy ich ilość jest niewielka), niż

zakup i późniejsza odsprzedaż kontraktów zabezpieczających. Zabezpieczenia portfela można

dokonywać na wiele różnych sposobów

24

. Jednak ze względu na dostępność instrumentu dla

większości inwestorów, kontrakty terminowe pozwalają na niemal natychmiastowe zarówno

zabezpieczenie, jak i odbezpieczenie portfela papierów wartościowych.

Mechanizm

działania takiego zabezpieczenia jest podobny do transakcji spreadowych.

Różnica polega przede wszystkim na celu zawarcia takiej operacji oraz dążeniu do

najlepszego dopasowania instrumentów zabezpieczanego oraz zabezpieczającego, pod

względem wrażliwości na zmiany stóp procentowych. Innymi słowy przy dopasowywaniu

obu instrumentów dąży się do tego, aby każda zmiana rynkowych stóp procentowych nie

powodowała zmiany wartości rynkowej łącznego portfela obligacji i zabezpieczających je

kontraktów terminowych. Oczywiście, gdy inwestor oceni, że ryzyko niekorzystnego dla

portfela kształtowania się rynkowych stóp procentowych wystarczająco spadło, może

zrezygnować z zabezpieczenia poprzez zamknięcie pozycji w kontraktach terminowych.

3.4 Perfect hedge

Perfect hedge oznacza zabezpieczenie, zapewniające maksymalnie możliwe

uniewrażliwienie na zmiany wartości rynkowej posiadanego portfela instrumentów

finansowych. Całkowite zabezpieczenie portfela nie jest możliwe z kilku powodów:

23

Dotyczy to zarówno obligacji rządowych jak i korporacyjnych.

24

Poprzez kontrakty terminowe (futures), transakcje swapowe stóp procentowych IRS, opcje na stopę

procentową CAP, FLOOR, COLLAR, czy też otwierając krótkie pozycje w obligacjach. Ze względu na dużą
płynność i niskie koszty, najwygodniejsze są do tego swapy stóp procentowych, jednak dotyczy to operacji o
dużych nominałach tj. od kilku milionów wzwyż, co stanowi znaczącą barierę dla wielu inwestorów.

Giełda Papierów Wartościowych w Warszawie

32

• Wartość otwartej pozycji w kontraktach jest równa sumie wystandaryzowanych wartości

wszystkich zawartych kontraktów. Dlatego, gdyby okazało się, że pełne zabezpieczenie

portfela nastąpiłoby np. po nabyciu 7,5 kontraktów , inwestor mógłby jedynie zawrzeć 7

bądź 8 kontraktów, powodując lekkie niedopasowanie pozycji zabezpieczającej i

zabezpieczanej.

• Każdy kontrakt terminowy na obligacje zbudowany jest na ściśle określonym koszyku

papierów wartościowych o zbliżonych terminach zapadalności. Zmiany wartości

kontraktu zazwyczaj różnią się od zmian wartości poszczególnych obligacji wchodzących

w skład koszyka, gdyż zmiana wartości pojedynczego papieru tylko w części (z pewną

określoną w definicji kontraktu wagą) wpływa na zmianę wartości całego koszyka.

• Portfel obligacji może posiadać odmienne od kontraktu terminowego zmodyfikowane

duration. W skrócie oznacza to, że portfel obligacji i kontrakt mogą być wrażliwe na

zmiany stóp procentowych, umiejscowionych w dwóch różnych punktach krzywej

dochodowości. Przy zmianie kąta nachylenia tej krzywej, wartości rynkowe pozycji

zabezpieczanej i zabezpieczającej mogą się wówczas zmieniać w różny sposób.

• Najczęściej termin wygaśnięcia kontraktów różni się od daty, do której zamierzamy

zabezpieczyć posiadany portfel obligacji. Wówczas może zaistnieć konieczność rolowania

kontraktów na kolejną serię. Skutkuje to poniesieniem dodatkowych kosztów

transakcyjnych.

• Występuje ryzyko bazy.

Przykład nr 9. Perfect hedge

Transakcja zabezpieczana:

1. Zakup obligacji DS0509 o nominale 10 mln PLN (10 000 sztuk).

2. BPV obligacji wynosi 3 970 PLN

25

.

Transakcja zabezpieczająca:

1. Sprzedaż kontraktów marcowych na obligacje, w liczbie sztuk dobranej tak, aby BPV

kontraktów było najbardziej zbliżone do BPV pozycji w obligacjach DS0509 (czyli

zbliżony do wartości 3 970 PLN).

Przy tak skonstruowanym zabezpieczeniu długiej pozycji w obligacjach, zmiana rynkowych

stóp procentowych powoduje taką samą co do wartości lecz z przeciwnym znakiem, zmianę

25

Przy zmianie rynkowych stóp procentowych o 1 punkt bazowy wartość pozycji nominału 10 mln złotych

obligacji DS0509 ulegnie zmianie o 3 970 PLN.

Giełda Papierów Wartościowych w Warszawie

33

w pozycji zabezpieczanej i zabezpieczającej, co powoduje, że łączny wynik operacji

oscylować będzie wokół zera.

3.5

Ryzyko bazy

Bazą obligacji nazywamy różnicę pomiędzy czystą ceną rynkową obligacji za 100

PLN ich wartości nominalnej, a iloczynem współczynnika konwersji dla danej obligacji i ceną

kontraktu terminowego, płaconą za 100 PLN.

Baza obligacji = (S – F x CF/100) x 100

gdzie:

S – cena rynkowa obligacji ( za 100 PLN wartości nominalnej)

F – cena kontraktu terminowego ( za 100 PLN wartości nominalnej), w którego

koszyku znajduje się dana obligacja

CF- współczynnik konwersji danej obligacji

Ryzyko bazy to ryzyko zmiany jej wartości, wynikające z różnego kształtowania się w

czasie ceny kontraktu i ceny obligacji i niezmienności współczynnika konwersji.

Posiadacz kontraktów na obligacje może zamienić je na odpowiednią ilość obligacji CTD w

terminie jego wykonania. Zmiany wartości kontraktu odzwierciedlają zmiany wartości

obligacji aktualnie będącej CTD dla danego kontraktu. Jednak dany kontrakt może stanowić

podstawę zabezpieczenia dla innej obligacji, nie należącej nawet do jego koszyka. Mając do

czynienia z dwiema różnymi obligacjami, istnieje pewne ryzyko, że z upływem czasu, ich

wartości rynkowe będą podlegać innym zmianom.

Ponadto

nabywając kontrakt terminowy stajemy się posiadaczem obligacji CTD w

późniejszym terminie niż kupując obligację na rynku kasowym. W okresie pomiędzy tymi

dwiema datami posiadamy wolne środki, które możemy ulokować w depozycie lub innym

aktywie. Inwestycja ta przyniesie nam dodatkowy profit w postaci odsetek, które możemy

zaliczyć do wyniku. Stąd inny jest koszt finansowania obligacji kupionej na rynku kasowym a

inny obligacji otrzymanej z tytułu wygaśnięcia posiadanego przez nas kontraktu, gdyż zakup

każdej z nich realizowany jest w innym czasie. Z tego powodu wynik finansowy na tych

dwóch pozycjach może być inny.

Giełda Papierów Wartościowych w Warszawie

34

Wszystkie

omówione

powyżej czynniki determinują brak możliwości pełnego

zabezpieczenia portfela obligacji kontraktami terminowymi. Pozostaje więc perfect hedge.

Czasem jednak nie chcemy całkowicie wyeliminować, a jedynie ograniczyć ryzyko związane

z posiadanym portfelem obligacji. Częściowe jego zabezpieczenie – cross hedge- może być

czasem konieczne ze względu na zbliżanie się do granicy pewnych limitów

ostrożnościowych

26

, narzucanych zarządzającym portfelami instrumentów finansowych.

Częściej jednak wynika z chęci pozostawienia przez inwestora pozycji spekulacyjnej w

obligacjach niezabezpieczonych kontraktami, która może przynieść dodatkowy zysk.

3.6 Wyznaczanie współczynników zabezpieczenia

Współczynnik zabezpieczenia to liczba kontraktów terminowych danej serii,

niezbędna do zabezpieczenia określonego portfela obligacji. Aby uzyskać tzw. perfect hedge,

czyli najlepsze możliwe zabezpieczenie papierów wartościowych w portfelu, szukamy

optymalnego współczynnika zabezpieczenia stosując jedną z kilku metod lub ich kombinację.

Do podstawowych metod należą:

1. Metoda wartości nominalnej

Jest to najprostsza z metod wyznaczania współczynnika zabezpieczenia, czyli liczby

kontraktów niezbędnych do zabezpieczenia portfela papierów wartościowych.

Wartość tę wyznacza się z wzoru:

o

terminoweg

kontraktu

Nominał

obligacji

portfela

Nominał

enia

zabezpiecz

ik

Wspólczynn

=

gdzie: Nominał portfela obligacji równy jest sumie nominałów wszystkich papierów

wartościowych, wchodzących w jego skład,

Nominał kontraktu terminowego

– w przypadku kontraktu terminowego na obligacje:

100 000 PLN.

26

Limity ostrożnościowe określają maksymalne poziomy zaangażowania bądź ryzyka, związanego z

posiadanym portfelem instrumentów finansowych.

Giełda Papierów Wartościowych w Warszawie

35

Przykład nr 10.

Wyznaczymy współczynnik zabezpieczenia dla pozycji w obligacjach PS0608 o nominale

25 mln PLN:

kontaktów

250

PLN

tys

100

PLN

ln

m

25

enia

zabezpiecz

ik

Wspólczynn

=

=

Aby zabezpieczyć taką pozycję należy sprzedaż 250 kontraktów.

Aktywami bazowymi ww. kontraktów są obligacje o najbardziej zbliżonym terminie

zapadalności. Np. mając w portfelu obligacje 4-, 5- i 6-letnie, zabezpieczamy je kontraktami

na obligacje 5-letnie. Oczywiście stosując tę metodę musimy zdawać sobie sprawę z

odmiennej wrażliwości na ryzyko stóp procentowych przy identycznym nominale pozycji

zabezpieczanej i zabezpieczającej. Dlatego ryzyko bazy jest stosunkowo wysokie (w

porównaniu z innymi metodami).

W kolejnych dwóch metodach przyjmuje się założenie, że współczynnik

zabezpieczenia (liczbę kontraktów zabezpieczających dany portfel) oblicza się dzieląc zmianę

wartości portfela obligacji przy określonej zmianie rynkowych stóp procentowych, przez

zmianę wartości jednego kontraktu przy identycznej zmianie stóp.

2. Metoda zmodyfikowanego duration

Zmodyfikowane duration (MD) instrumentu finansowego jest miarą jego wrażliwości

na zmiany stóp procentowych, oznaczającą procentową zmianę jego ceny przy zmianie

dochodowości o 1 punkt procentowy. W metodzie tej współczynnik zabezpieczenia wyznacza

się z wzoru:

10000

x

S

MD

CF

S

MD

enia

zabezpiecz

ik

Wspólczynn

CTD

CTD

CTD

obligacji

portfela

obligacji

portfela

×

×

×

=

gdzie:

MD portfela obligacji –zmodyfikowane duration całego portfela obligacji

S portfela obligacji – wartość rynkowa portfela obligacji

CF

CTD

–współczynnik konwersji obligacji CTD.

MD

CTD

– zmodyfikowane duration obligacji CTD

S

CTD

– wartość rynkowa 1 sztuki obligacji CTD (cena dirty price)

Giełda Papierów Wartościowych w Warszawie

36

Współczynnik zabezpieczenia, czyli liczbę kontraktów, które należy sprzedać lub kupić

zaokrągla się do najbliższej liczby całkowitej.

Przykład nr 11.

Inwestor posiada portfel obligacji PS0507 o nominale 15 mln PLN. Na dzień 18 listopada

2004 r.:

MD portfela obligacji wynosi 2,115,

S portfela obligacji = 16 266 759 PLN (dla ceny czystej równej 104,02)

CF

CTD =

100 (przykładowo, gdy np. obligacją CTD dla kontraktu jest DS0509)

MD

CTD

=MD

DS0509

=3,967

Niech S

CTD

= 999,16

kontraktów

87

10000

x

16

,

999

967

,

3

100

16266759

115

,

2

enia

zabezpiecz

ik

Wspólczynn

=

×

×

×

=

Przy zastosowaniu tej metody otrzymujemy zabezpieczony portfel papierów

wartościowych o całkowitym zmodyfikowanym duration równym 0. W rzeczywistości jednak

nie oznacza to, że takie dobranie liczby kontraktów zabezpieczających zabezpieczy nam w

całości portfel obligacji przed ryzykiem stóp procentowych, gdyż z upływem czasu ponowne

wyznaczenie z powyższego wzoru współczynnika zabezpieczenia, może wskazać na inną jego

wartość.

3. Metoda wrażliwości (BPV)

BPV instrumentu finansowego jest podobnie jak zmodyfikowane duration, miarą jego

wrażliwości na zmiany stóp procentowych, lecz wyrażoną wartościowo. Oznacza ona zmianę

wartości rynkowej danej pozycji przy równoległym przesunięciu krzywej dochodowości o

1 punkt bazowy.

Metoda BPV pozwala wyliczyć współczynnik zabezpieczenia w taki sposób, aby zmiana

rynkowych stóp procentowych o 1 punkt bazowy spowodowała identyczną co do wartości

(lecz z przeciwnymi znakami) zmianę pozycji zabezpieczającej i zabezpieczanej.

Współczynnik zabezpieczenia wylicza się poprzez podzielenie BPV portfela obligacji

przez BPV kontraktu terminowego lub w inny sposób - dzieląc BPV portfela obligacji przez

BPV obligacji CTD wyznaczonego dla kontraktu zabezpieczającego.

Giełda Papierów Wartościowych w Warszawie

37

10000

x

BPV

CF

BPV

enia

zabezpiecz

ik

Wspólczynn

CTD

CTD

obligacji

portfela

×

=

gdzie:

BPV portfela obligacji –wartość punktu bazowego BPV całego portfela obligacji

BPV

CTD

– wartość punktu bazowego BPV 1 sztuki obligacji CTD.

CF

CTD

–współczynnik konwersji obligacji CTD.

(DS0509 - obligacja CTD dla kontraktu)

Przykład nr 12.

Niech inwestor posiada portfel złożony z obligacji DS0509 o nominale 10 mln PLN oraz

obligacji PS0608 o nominale 20 mln PLN.

BPV portfela obligacji = BPV

10mlnDS0509

+ BPV

20mlnPS0608

=

3 712 PLN + 6 082 PLN = 9 794 PLN

Niech CF

CTD =

100 (przykładowo, gdy np. obligacją CTD dla kontraktu jest DS0509)

BPV

CTD

=0,3712 dla 1 sztuki

kontrakty

264

10000

x

PLN

3712

,

0

100

PLN

9794

enia

zabezpiecz

ik

Wspólczynn

=

×

=

Zastosowanie którejkolwiek z wyżej wymienionych metod do wyliczenia współczynnika

zabezpieczenia nie daje gwarancji pełnego zabezpieczenia portfela papierów wartościowych,

gdyż musiałyby być spełnione pewne warunki, które w rzeczywistości nie występują. Np. w

metodzie wrażliwości (BPV) przyjmuje się założenie o równoległym przesunięciu krzywej

dochodowości.

W praktyce portfel obligacji zabezpiecza się kilkoma różnymi seriami kontraktów

terminowych. Dzięki temu, istnieje możliwość uzyskania dosyć precyzyjnego zabezpieczenia,

poprzez dopasowanie zarówno BPV jak i zmodyfikowanego duration portfela obligacji i

zabezpieczających je kontraktów.

4 Arbitraż cash and carry (basis trading)

27

27

Wymienione strategie arbitrażu cash & carry, zaczerpnięte zostały z książki The Treasury Bond Basis-An

In-Depth Analysis for Hedgers, Speculators and Arbitrageurs, autorzy: Galen D.Burghardt, Terrence M.Belton,
Morton Lane i Jon Papa.

Giełda Papierów Wartościowych w Warszawie

38

Arbitraż ten polega na otwarciu przeciwstawnych i wzajemnie się zamykających pozycji

na dwóch różnych rynkach w tym samym momencie w czasie. Inwestor wykorzystuje

sytuację, w której dwa instrumenty o zbliżonej charakterystyce są odmiennie wyceniane,

dając możliwość uzyskania zysku bez ponoszenia ryzyka stóp procentowych

28

. W niniejszym

punkcie omówione zostaną podstawowe strategie arbitrażu cash & carry:

a) Sprzedaż drogiej bazy (selling expensive basis).

Strategia ta polega na sprzedaży obligacji CTD z jednoczesnym otwarciem długiej pozycji

w odpowiednim kontrakcie terminowym. Krótka pozycja w papierze wartościowym pociąga

za sobą konieczność zawarcia transakcji BuySellBack (BSB)

29

, czyli de facto pożyczenia

papieru na przewidywany okres trwania arbitrażu. Powstaje więc dodatkowy koszt z

transakcji BSB

30

, który należy uwzględnić przy kalkulacji wyniku arbitrażu.

Jeśli dana obligacja pozostaje CTD aż do wygaśnięcia kontraktu, wówczas jej baza dąży do 0

(w dacie dostarczenia obligacji po wygaśnięciu kontraktu). Na dochód z transakcji składa się

wynik osiągnięty z wielkości sprzedanej bazy pomniejszony o koszt sfinansowania krótkiej

pozycji obligacji CTD.

b) Sprzedaż bazy obligacji, która nie jest CTD (Selling the Basis of Non-Cheap Bonds).

W strategii tej następuje sprzedaż obligacji nie będącej CTD. Zazwyczaj wykorzystuje się

obligację benchmarkową, najbardziej płynną lub ostatnio wyemitowaną, która przez to

charakteryzuje się wyższą ceną rynkową niż pozostałe papiery z koszyka danego kontraktu.

Baza tej obligacji, nie będącej CTD, nie musi dążyć do 0. Zależy ona od spreadu pomiędzy jej

stopą zwrotu, a stopą zwrotu obligacji CTD. Wynik na tym arbitrażu, podobnie jak w punkcie

a) zależy od wielkości sprzedanej bazy pomniejszonej o koszt sfinansowania krótkiej pozycji

obligacji.

28

W rzeczywistości istnieje pewne ryzyko, związane z niemożliwością całkowitego dopasowania pozycji

zabezpieczającej i zabezpieczanej, pod względem wrażliwości na zmiany stóp procentowych, kursów
walutowych bądź innych parametrów rynkowych.

29

Nie zawsze transakcja BSB jest dostępna dla inwestorów. Z tego powodu kupno taniej bazy jest strategią

bardziej powszechną.

30

W transakcji BSB w zamian za pożyczone obligacje, składany jest u kontrahenta transakcji depozyt równy

wartości rynkowej pożyczonej obligacji. Oprocentowanie takiego depozytu (przychód) jest zazwyczaj niższe od
rynkowych stawek depozytów na dany termin, a więc od stawek, po których w najlepszym razie transakcja ta
mogłaby być sfinansowania. Dodatkowy koszt z BSB to różnica pomiędzy stopą BSB a stopą, po której
transakcja była sfinansowana.

Giełda Papierów Wartościowych w Warszawie

39

c) Kupno taniej bazy (Buying Cheap Basis)

Strategia ta polega na zakupie obligacji z jednoczesnym otwarciem krótkiej pozycji w

odpowiednim kontrakcie terminowym. Nie niesie ona ze sobą kosztu finansowania krótkiej

pozycji w obligacjach.

d) Spread kalendarzowy (calendar spread)

Polega on na kupnie kontraktu z jednoczesną odsprzedażą kontraktu o innym terminie

wygaśnięcia, ale zbudowanym na tym samym koszyku obligacji. Strategia ta stosowana jest

wówczas, gdy – zdaniem inwestora - rynkowy spread pomiędzy cenami obu kontraktów

nadmiernie wzrósł ponad przeciętny poziom lub nadmiernie spadł poniżej przeciętnego

poziomu i jest duże prawdopodobieństwo, że spread ten wróci do poziomu przeciętniego.

Przykład nr 13. Kupno bazy

Inwestor kupuje obligacje DS0509 o wartości nominalnej 10 mln PLN po cenie 96,16.

Niech DS0509 jest obligacją CTD i jednocześnie CF

CTD

= 99,96. Jednocześnie otwiera krótką

pozycję w 100 grudniowych kontraktach na obligacje po cenie 96,25. Data waluty zakupu

obligacji oraz otwarcia pozycji w kontraktach: 2 listopada 2004 r.

Wartość kupna obligacji: 10.000 sztuk x (96,16% x 1000 + odsetki 26,63) = 9.882.300

PLN.

W momencie otwarcia pozycji na rynku kasowym i rynku terminowym, inwestor kupił bazę:

15

,

5

100

96

,

99

x

25

,

96

16

,

96

Baza

−

=













−

=

Pozycja utrzymywana jest przez 1 miesiąc.

Parametry zamknięcia pozycji:

Data waluty: 2 grudnia 2004 r.

Cena sprzedaży obligacji: 96,66

Cena zamknięcia pozycji poprzez zakup kontraktu: 96,55

Koszt finansowania otwartych pozycji: 7% p.a.

Giełda Papierów Wartościowych w Warszawie

40

W momencie zamykania pozycji na rynku kasowym i rynku terminowym, inwestor sprzedaje

bazę:

862

,

14

100

96

,

99

x

55

,

96

66

,

96

Baza

=













−

=

Na

łączny wynik z transakcji składają się następujące elementy:

PLN

000

.

50

100

16

,

96

66

,

96

x

PLN

ln

m

10

h

obligacjac

na

Wynik

=













−

=

PLN

000

.

30

100

55

,

96

25

,

96

x

PLN

000

.

100

x

.

szt

100

h

kontraktac

na

Wynik

−

=

−

=

PLN

07

,

857

.

56

365

dni

30

x

%

7

x

PLN

300

.

882

.

9

ia

finansowan

Koszt

−

=

=

Łączny wynik z transakcji = 50.000 –30.000+49.300-56.857,07 = 12.442,93 PLN

W przypadku transakcji polegającej na sprzedaży bazy, inwestor liczy, że przez okres

utrzymywania otwartej pozycji w obligacjach i w kontraktach, zmniejszenie wartości bazy

przyniesie mu zysk

Literatura:

• Binkowski P., Beeck, H. Innowacje bankowe. Instrumenty terminowego rynku

finansowego, Poltext, Warszawa 1998

• Burghardt G,.Belton T.M , Lane M, Papa J The Treasury Bond Basis-An In-Depth

Analysis for Hedgers, Speculators and Arbitrageurs, - IRWIN Professional Publishing,

Chicago 1994

• Fabozzi F. Rynki Obligacji – Analiza i Strategie, WIG-PRESS, Warszawa 2000
• Hull J., Kontrakty terminowe i opcje: wprowadzenie, WIG-PRESS, Warszawa 1999

Giełda Papierów Wartościowych w Warszawie

41

• Hedging i nowoczesne usługi finansowe, praca zbiorowa pod redakcją naukową Mariana

Biegańskiego i Alfreda Janca, Akademia Ekonomiczna w Poznaniu, Poznań 2001

• Holliwell J, Ryzyko finansowe. Metody identyfikacji i zarządzania ryzykiem finansowym,

LIBER, Warszawa 2001

• Jajuga K., Jajuga T., Inwestycje. Instrumenty finansowe. Ryzyko finansowe. Inżynieria

finansowa, Wydawnictwo Naukowe PWN, Warszawa 1999

• Marciniak Z., Zarządzanie wartością i ryzykiem przy wykorzystaniu instrumentów

pochodnych, SGH, Warszawa 2001

• REUTERS Instrumenty pochodne -wprowadzenie, Dom wydawniczy ABC, Kraków2001
• REUTERS, Rynek walutowy i pieniężny – wprowadzenie, Dom Wydawniczy ABC,

Kraków 2001

• Smithson Ch.W., Zarządzanie ryzykiem finansowym: instrumenty pochodne, inżynieria

finansowa i maksymalizacja wartości, Dom Wydawniczy ABC, Kraków 2000

• Steiner R., Kalkulacje finansowe, Dom Wydawniczy ABC, Warszawa 2000
• Tarczyński, W., Zwolankowski M., Inżynieria finansowa, Placet, Warszawa 1999