
Politechnika Śląska
Gliwice, 2006/2007
Wydział: Automatyki, Elektroniki i Informatyki
Semestr: 6 (letni)
Kierunek: Automatyka i robotyka
Podstawy Automatyki
– laboratorium
Ćw 7. Korekcja liniowych układów regulacji.
Data ćwiczeń laboratoryjnych:
25.04.2007
Grupa: 1
Sekcja: 3
Skład osobowy sekcji:
Zięba Andrzej
Bojko Marcin
Pawliczek Krystian
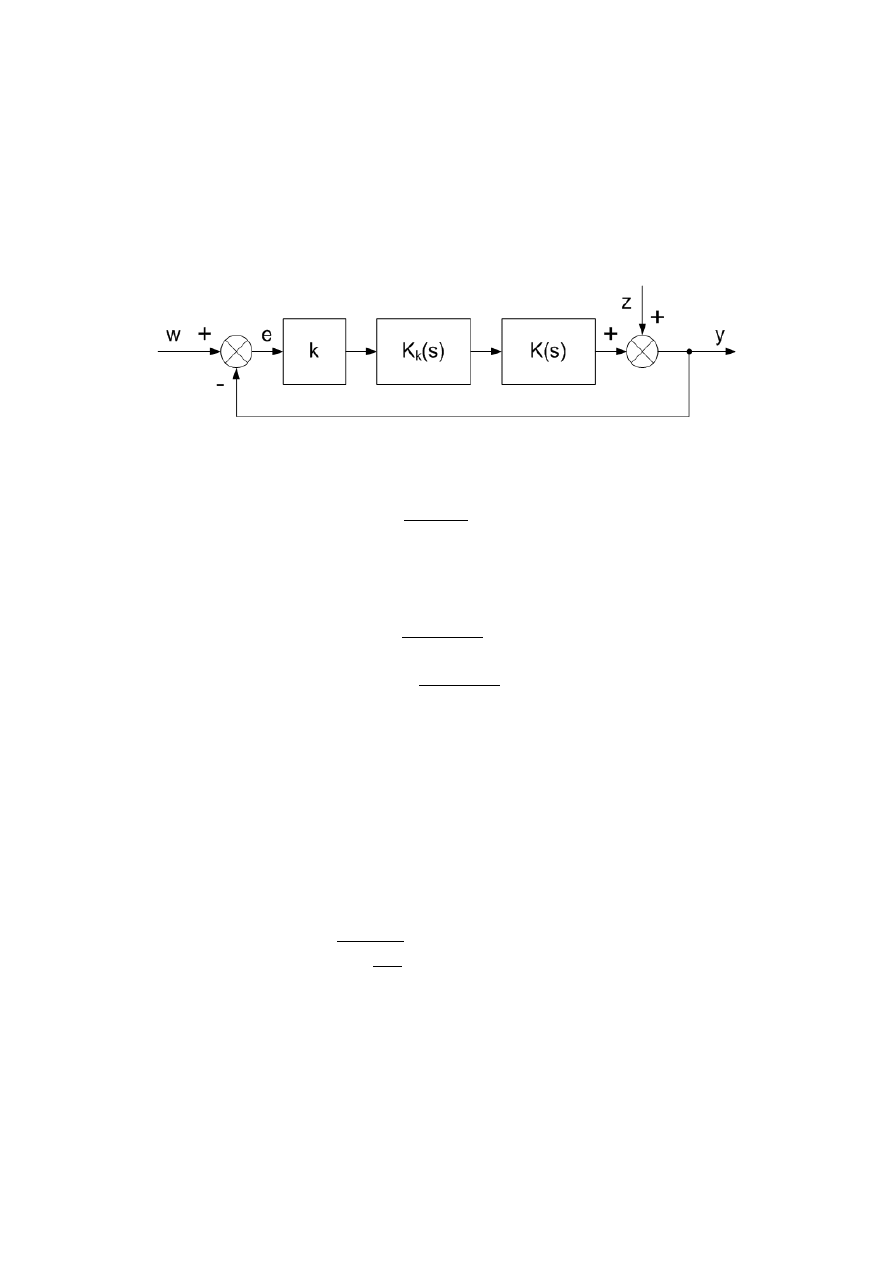
1. Cel ćwiczenia:
Celem ćwiczenia było przyswojenie sobie procedur strojenia korektorów i analiza pracy
układu z korektorem i bez niego – czyli analiza wpływu różnego typu korektorów na jakość
regulacji w układzie zamkniętym.
2. Program ćwiczenia:
Dany jest układ regulacji jak na rysunku 1.
Rysunek 1. Struktura układu regulacji.
K
k
(s) – transmitancja korektora
K(s) – transmitancja obiektu
k – wzmocnienie
W trakcie ćwiczenia należy przeprowadzić syntezę układu z korektorem PI oraz PD, w którym obiektem
regulowanym jest inercja rzędu trzeciego:
K s=
1
1sT
3
,gdzie T = 3,5. Porównanie jakości działania układu
będzie się opierało na analizie następujących wskaźników:
a) wartość zapasu fazy;
b) wartość zapasu amplitudy;
c) wartość uchybu w stanie ustalonym;
d) postać wskaźnika regulacji
q =
∣
1
1K j
∣
;
e) postać wskaźnika nadążania
M =
∣
K j
1 K j
∣
;
f)
wartość przeregulowania;
g) wartość czasu regulacji;
Przebieg ćwiczenia:
A. Układ bez korektora (K
k
(s) = 1):
1. Wykreślić charakterystykę Nyquista obiektu K(s). Określić warunki stabilności układu zamkniętego
korzystając z kryterium Nyquista. Wyznaczyć parametry k
gr
, ω
gr
.
2. Dobrać wzmocnienie k tak, aby zapas amplitudy ΔK = 2 (ΔL = 6,02 dB).
3. Wykreślić charakterystykę Nyquista dla układu.
4. Wykreślić odpowiedź skokową układu zamkniętego.
5. Wykreślić przebieg czasowy uchybu regulacji.
6. Wykreślić przebieg wskaźników nadążania M(ω) i regulacji q(ω).
B. Układ z korektorem PD
K
k
s =
1sT
PD
1s
T
PD
:
1. Zakładając α = 4 wyznaczyć stałą czasową korektora T
PD
zgodnie z procedurą strojenia.
2. Dla rozpatrywanego układu korekcyjnego wyznaczyć wzmocnienie graniczne k
gr
. Dobrać wartość
wzmocnienia korygującego k tak, aby zapas amplitudy ΔK = 2.
3. Wykreślić charakterystykę Nyquista dla układu i porównać ją z charakterystyką układu bez korektora.
4. Wykreślić odpowiedź skokową i porównać ją z odpowiedzią układu bez korektora.
5. Wykreślić przebieg czasowy uchybu regulacji i porównać z przebiegiem tej wielkości dla układu bez
korektora.
6. Wykreślić przebieg wskaźników nadążania M(ω) i regulacji q(ω) i porównać je z odpowiednimi
wskaźnikami układu bez korektora.
7. Ocenić działanie korektora PD.
C. Układ z korektorem PI
K
k
s=
1sT
PI
1sT
PI
:
1. Zakładając α = 4 wyznaczyć stałą czasową korektora T
PI
zgodnie z procedurą strojenia.
2. Dla rozpatrywanego układu korekcyjnego wyznaczyć wzmocnienie graniczne k
gr
. Dobrać wartość
wzmocnienia korygującego k tak, aby zapas amplitudy ΔK = 2.
3. Wykreślić charakterystykę Nyquista dla układu i porównać ją z charakterystyką układu bez korektora.
4. Wykreślić odpowiedź skokową i porównać ją z odpowiedzią układu bez korektora.
5. Wykreślić przebieg czasowy uchybu regulacji i porównać z przebiegiem tej wielkości dla układu bez
korektora.
6. Wykreślić przebieg wskaźników nadążania M(ω) i regulacji q(ω) i porównać je z odpowiednimi
wskaźnikami układu bez korektora.
7. Ocenić działanie korektora PI.
D. Porównać działanie korektora PI i PD. Zwróć uwagę na potrzebne wzmocnienie korygujące.
3. Realizacja zadań:
Ad A. Analiza układu bez korektora.
Ad A.1.
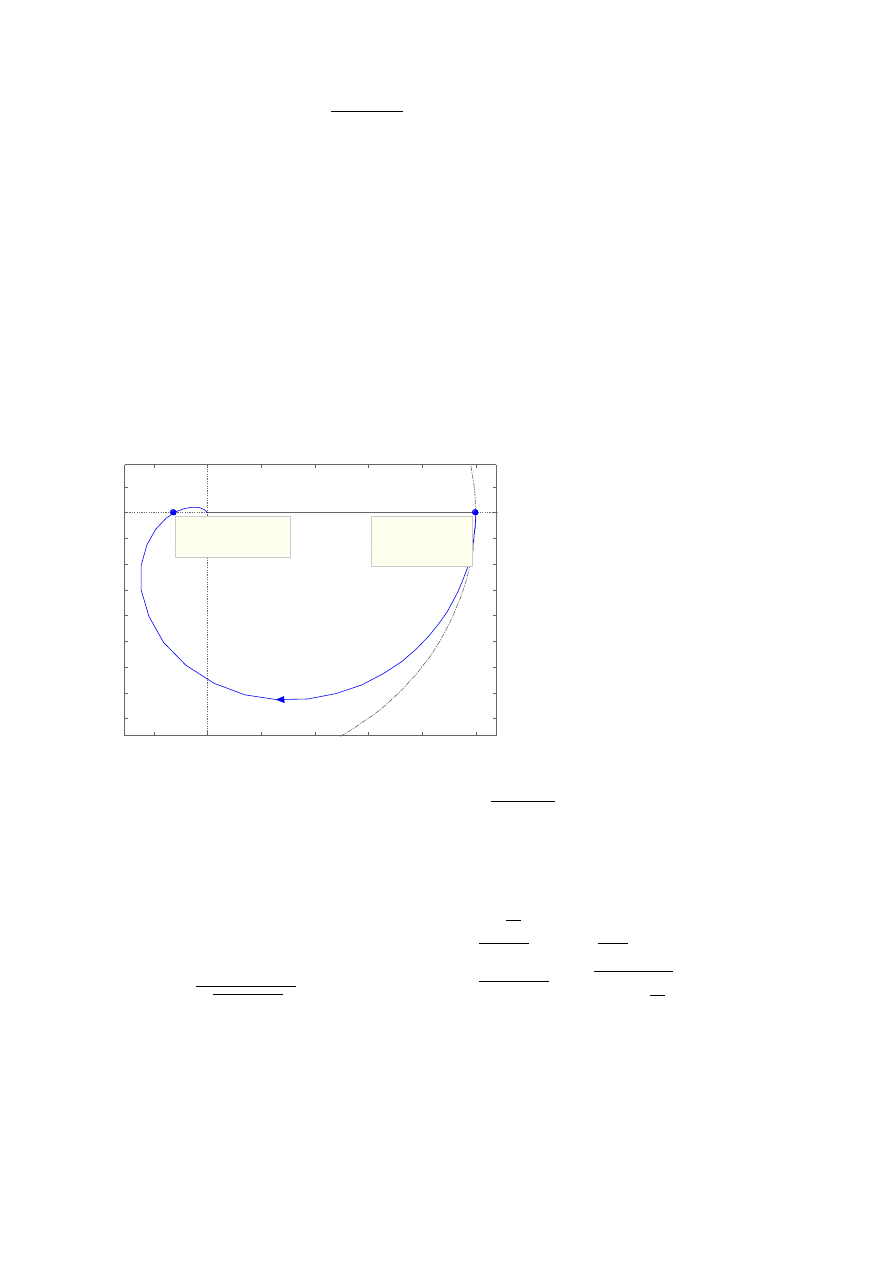
Rysunek 2. Charakterystyka Nyquista dla obiektu K(s).
Można odczytać:
ΔL = 18.1 dB
Δφ = 180
o
Rozpatrujemy transmitancje układu otwartego: K s=
k
1sT
3
, gdzie T = 3,5.
Korzystając z obliczeniowego kryterium Nyquista (charakterystyka układu otwartego
jest regularna) określamy warunki stabilności układu zamkniętego i wyznaczamy parametry
graniczne: k
gr
i ω
gr
.
gr
=−
3 arctg
gr
T =−
gr
=
tg
3
T
≈
0,4949
rad
s
K
gr
=
k
1
gr
2
T
2
3
1
k
1
gr
2
T
2
3
=
1tg
2
3
3
=
8
k
gr
=
8
Warunek stabilności układu zamkniętego: k k
gr
=
8
Ad A.2.
Aby zapas amplitudy wynosił ΔK = 2, należy dobrać wartość wzmocnienia k jako połowę
wartości k
gr
. Czyli k = 4.
- 0 . 2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
- 0 . 8
- 0 . 7
- 0 . 6
- 0 . 5
- 0 . 4
- 0 . 3
- 0 . 2
- 0 . 1
0
0 . 1
S y s t e m : K
G a i n M a r g i n ( d B ) : 1 8 . 1
A t f r e q u e n c y ( r a d / s e c ) : 0 . 4 9 5
C l o s e d L o o p S t a b l e ? Y e s
S y s t e m : K
P h a s e M a r g i n ( d e g ) : - 1 8 0
D e l a y M a r g i n ( s e c ) : In f
A t fr e q u e n c y ( r a d / s e c ) : 0
C l o s e d L o o p S t a b l e ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is

Ad A.3.
Rysunek 3. Charakterystyka Nyquista dla obiektu k·K(s).
Można odczytać:
ΔL = 6.02 dB
ΔK = 2
Δφ = 27,1
o
Ad A.4.
Rysunek 4. Odpowiedź skokowa układu zamkniętego.
Można odczytać:
y
ust
= 0.8
y
p
= 0.43 (53,75 %)
t
r
(przy Δ = 0.01) = 67,6 s
Ad A.5.
Rysunek 5. Przebieg czasowy uchybu regulacji.
Można odczytać:
e
ust
= 0.2
- 1
- 0 . 5
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
4
- 2 . 5
- 2
- 1 . 5
- 1
- 0 . 5
0
S y s t e m : K 1
P h a s e M a r g i n ( d e g ) : 2 7 . 1
D e l a y M a r g i n ( s e c ) : 1 . 3 4
A t f r e q u e n c y ( r a d / s e c ) : 0 . 3 5 2
C l o s e d L o o p S t a b l e ? Y e s
S y s t e m : K 1
G a i n M a r g i n ( d B ) : 6 . 0 2
A t f r e q u e n c y ( r a d / s e c ) : 0 . 4 9 5
C l o s e d L o o p S t a b l e ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
1 0 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
S y s t e m : u n t i t l e d 1
T i m e ( s e c ) : 9 . 5 7
A m p l i t u d e : 1 . 2 3
S y s t e m : u n t i t l e d 1
T i m e ( s e c ) : 6 7 . 6
A m p l i t u d e : 0 . 7 9
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
1 0 0
- 0 . 4
- 0 . 2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
Ad A.6.
Rysunek 6. Przebiegi wskaźników częstotliwościowych.
Można odczytać:
M
max
= 2.41
ω
Mrez
= 0.388 rad/s
φ
max
= 2.98
ω
φrez
= 0.411 rad/s
Ad B. Analiza układu z korektorem PD.
Na zamieszczonych przebiegach i charakterystykach kolorem niebieskim oznaczone są
te dotyczące układu z korektorem, natomiast na zielono te dotyczące układu bez korektora (w
celach porównawczych).
Ad B.1. Wyznaczenie nastaw korektora dla α = 4;
Na podstawie charakterystyki Nyquista korektora PD:
K max
=
max
K
=
K
∗
=
arcsin
−
1
1
, gdzie :
∗
=
T
PD
K max
≈
0,6435 rad
Na podstawie charakterystyki Nyquista obiektu wyznaczyć pulsację ω
x
:
x
=−−
K max
x
=
tg
K max
3
T
≈
0,8947
rad
s
Obliczyć wartość stałej czasowej T
PD
tak, aby dla otrzymanej wcześniej pulsacji ω
x
kąt
przesunięcia fazowego korektora był największy (ω
*
= ω
x
):
x
=
T
PD
T
PD
=
x
≈
2,2354 s
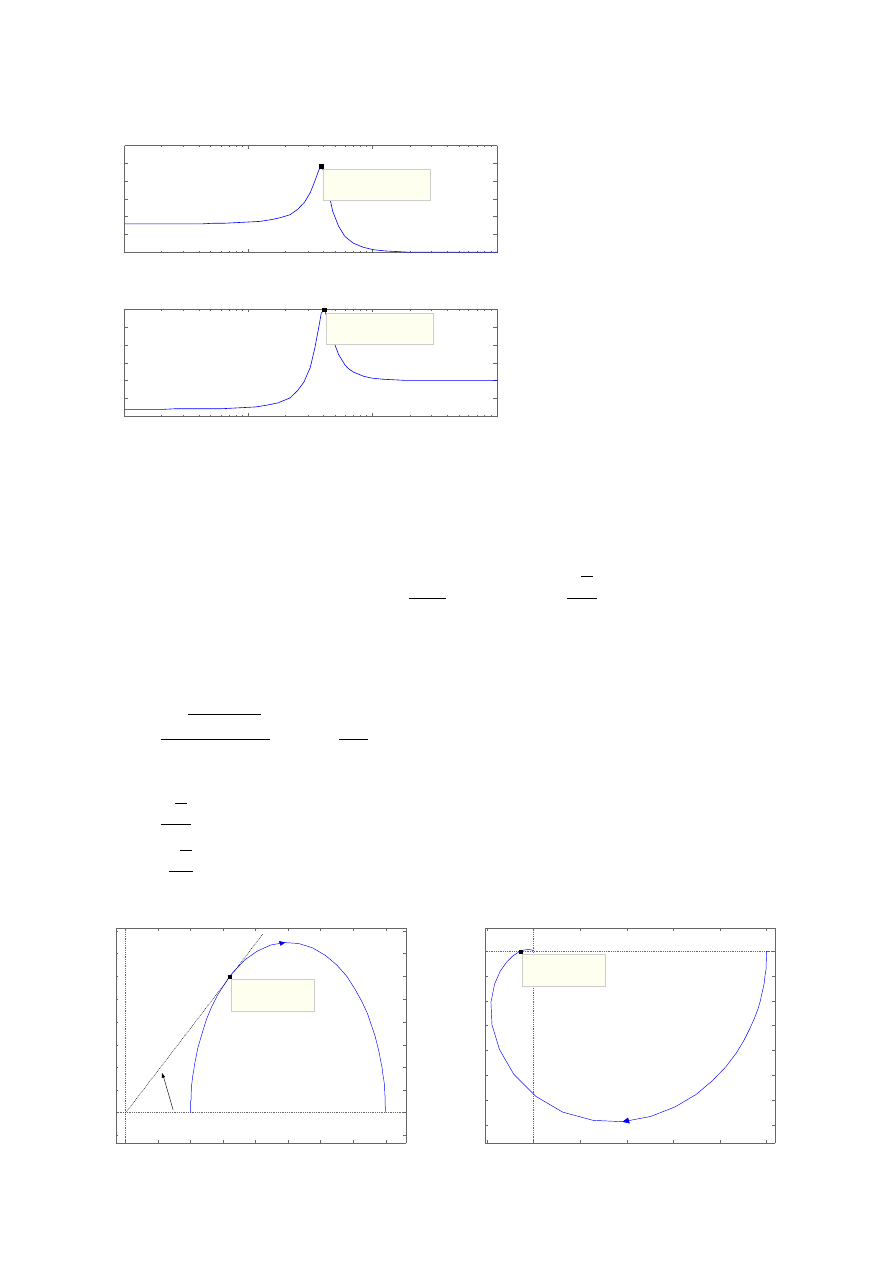
Rysunek 7. Charakterystyka Nyquista korektora.
Rysunek 8. Charakterystyka Nyquista obiektu z korektorem.
1 0
- 2
1 0
- 1
1 0
0
1 0
1
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : u n t i t l e d 1
F r e q u e n c y ( r a d / s e c ) : 0 . 3 8 8
M a g n i t u d e ( a b s ) : 2 . 4 1
1 0
- 2
1 0
- 1
1 0
0
1 0
1
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : u n t i t l e d 1
F r e q u e n c y ( r a d / s e c ) : 0 . 4 1 1
M a g n i t u d e ( a b s ) : 2 . 9 8
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
4
- 0 . 2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 . 6
S y s t e m : K _ P D
R e a l : 1 . 6
I m a g : 1 . 2
F r e q u e n c y ( r a d / s e c ) : 0 . 8 9 5
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
φ
K m a x
- 0 . 2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
- 0 . 7
- 0 . 6
- 0 . 5
- 0 . 4
- 0 . 3
- 0 . 2
- 0 . 1
0
S y s t e m : u n t i t l e d 1
R e a l : - 0 . 0 5 7 2
I m a g : - 0 . 0 0 0 7 7 3
F r e q u e n c y ( r a d / s e c ) : 0 . 8 9 5
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
Jak widać na rysunku 7, dla wyznaczonej wartości pulsacji ω
x
kąt przesunięcia
fazowego jest największy i wynosi φ
K max
. Natomiast zaznaczony punkt na rysunku 8 (dla
wyznaczonej wartości pulsacji ω
x
) leży niemalże na osi liczb rzeczywistych. Punkt ten leżałby
dokładnie na osi liczb rzeczywistych, gdyby nie wpływ błędów zaokrągleń.
Ad B.2.
Do wyznaczenia wzmocnienia granicznego k
gr
przyjęto pulsację graniczną równą ω
x
.
Następnie wzmocnienie graniczne wyznaczone z wykorzystaniem polecenia „solve” w środowisku
Matlab, z następujących zależności:
K s=
k 1sT
PD
1sT
3
1s
T
PD
gdzie: T = 3,5 s; T
PD
= 2,2354 s; α = 4
K
gr
=
k
1
gr
2
T
PD
2
1
gr
2
T
2
3
1
gr
2
T
PD
2
2
1
k
gr
=
1
gr
2
T
2
3
1
gr
2
T
PD
2
2
1
gr
2
T
PD
2
≈
17,76
Aby zapas amplitudy wynosił ΔK = 2, należy dobrać wartość wzmocnienia k jako połowę
wartości k
gr
. Czyli k = 8,88.
Ad B.3.
Rysunek 9. Charakterystyka Nyquista układu otartego.
Można odczytać:
ΔL = 6.02 dB
ΔK = 2
Δφ = 17,9
o
- 1
0
1
2
3
4
5
6
7
8
9
- 7
- 6
- 5
- 4
- 3
- 2
- 1
0
1
S y s t e m : u n t i t l e d 1
P h a s e M a r g i n ( d e g ) : 1 7 . 9
D e l a y M a r g i n ( s e c ) : 0 . 4 9
A t fr e q u e n c y ( r a d / s e c ) : 0 . 6 3 6
C l o s e d L o o p S t a b l e ? Y e s
S y s t e m : u n t i t l e d 1
G a i n M a r g i n ( d B ) : 6 . 0 2
A t fr e q u e n c y ( r a d / s e c ) : 0 . 8 9 5
C l o s e d L o o p S t a b l e ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
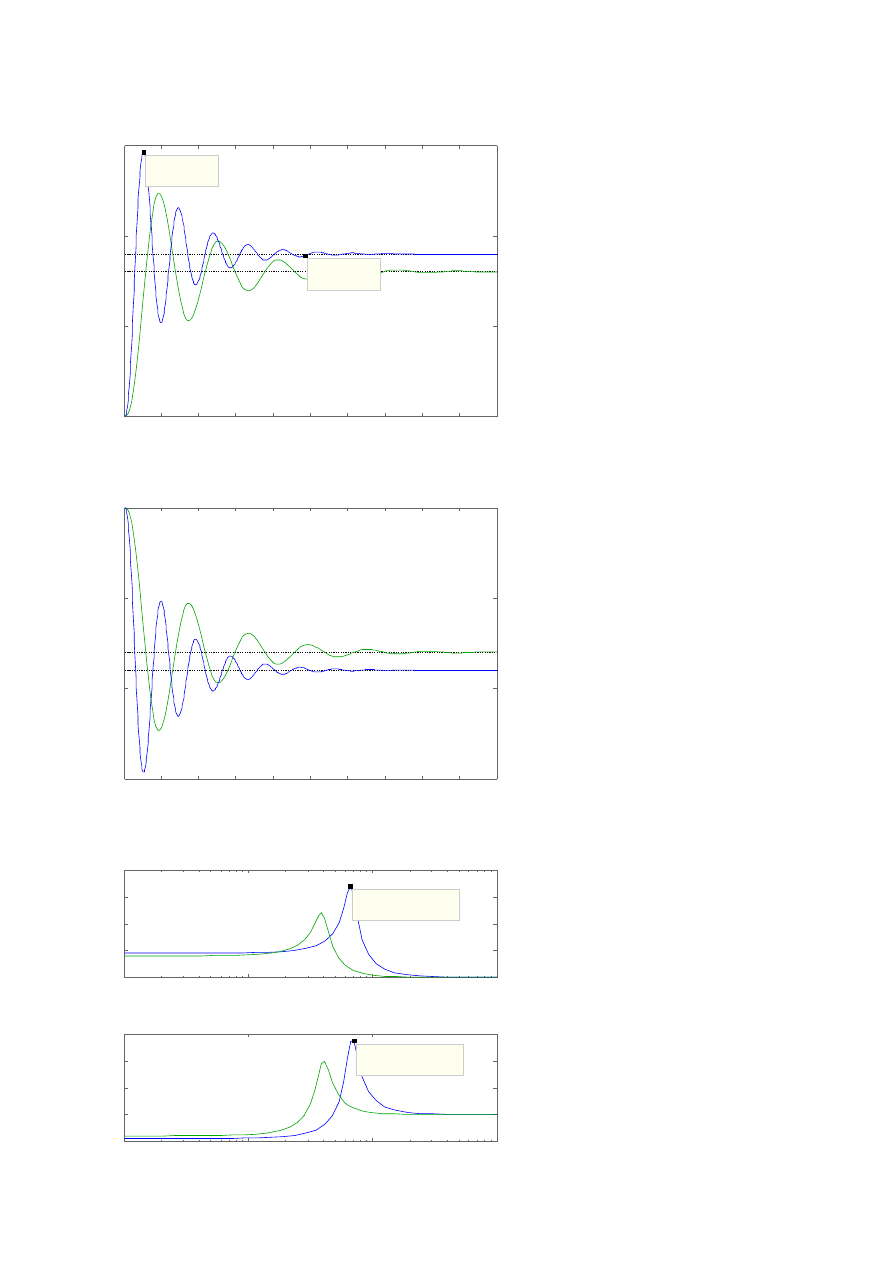
Ad B.4.
Rysunek 10. Odpowiedź skokowa układu zamkniętego.
Można odczytać:
y
ust
= 0.899
y
p
= 0.561 (62,40 %)
t
r
(przy Δ = 0.01) = 48,6 s
Ad B.5.
Rysunek 11. Przebieg czasowy uchybu regulacji.
Można odczytać:
e
ust
= 0.101
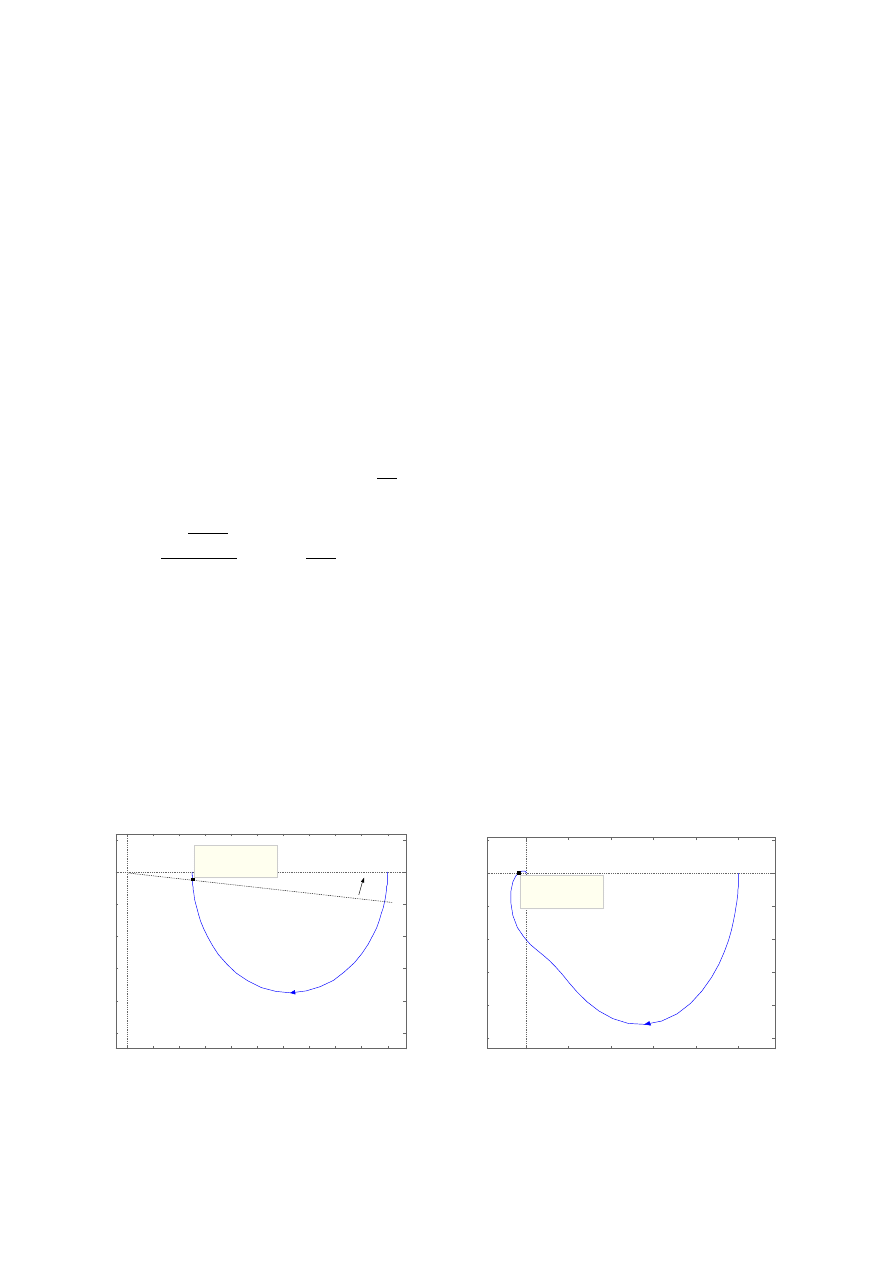
Ad B.6.
Rysunek 12. Przebiegi wskaźników częstotliwościowych.
Można odczytać:
M
max
= 3.39
ω
Mrez
= 0.667 rad/s
φ
max
= 3.75
ω
φrez
= 0.706 rad/s
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
1 0 0
0
0 . 5
1
1 . 5
S y s t e m : u n t i t l e d 1
T i m e ( s e c ) : 5 . 1 9
A m p l i t u d e : 1 . 4 6
S y s t e m : u n t i t l e d 1
T i m e ( s e c ) : 4 8 . 6
A m p l i t u d e : 0 . 8 8 9
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
1 0 0
- 0 . 5
0
0 . 5
1
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
1 0
- 2
1 0
- 1
1 0
0
1 0
1
0
1
2
3
4
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : u n t i t l e d 1
F r e q u e n c y ( r a d / s e c ) : 0 . 6 6 7
M a g n i t u d e ( a b s ) : 3 . 3 9
1 0
- 2
1 0
- 1
1 0
0
1 0
1
0
1
2
3
4
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : u n t i t l e d 1
F r e q u e n c y ( r a d / s e c ) : 0 . 7 0 6
M a g n i t u d e ( a b s ) : 3 . 7 5
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
Ad B.7. Ocena działania korektora (utrzymywany jest stały zapas modułu ΔK = 2).
Po dołączeniu korektora:
●
maleje zapas fazy;
●
maleje uchyb w stanie ustalonym;
●
rośnie wartość przeregulowania;
●
maleje czas regulacji;
●
rosną maksymalne wartości wskaźników częstotliwościowych;
●
rosną częstotliwości rezonansowe wskaźników częstotliwościowych;
●
zwiększa się zdolność nadążania w paśmie podrezonansowym;
●
zwiększa się zdolność tłumienia zakłóceń w pasmie podrezonansowym;
Ad C. Analiza układu z korektorem PI.
Na zamieszczonych przebiegach i charakterystykach kolorem niebieskim oznaczone są
te dotyczące układu z korektorem, natomiast na zielono te dotyczące układu bez korektora (w
celach porównawczych).
Ad C.1. Wyznaczenie nastaw korektora dla α = 4;
Za pomocą charakterystyki Nyquista obiektu wyznaczyć częstotliwość ω
x
:
x
=−
, gdzie : =5
o
=
36
rad
x
=
tg
−
3
T
≈
0,4632
rad
s
Wykorzystując charakterystykę Nyquista elementu korekcyjnego określić wartość stałej
czasowej T
PI
tak, aby dla otrzymanej wyżej pulsacji ω
x
kąt przesunięcia fazowego korektora
wynosił
K
x
=− . Wykorzystano polecenie „solve”.
K
x
=
arctg
x
T
PI
−
arctg
x
T
PI
=−
T
PI
≈
0,6318 lub 18,4440
Wybieramy większą wartość stałej czasowej ponieważ dla tej mniejszej wartości, kąt
przesunięcia fazowego dla pulsacji ω
x
będzie również równy -π/36 ale jego usytuowanie przypada
na nieinteresujący nas punkt charakterystyki Nyquista korektora. Czyli T
PI
≈
18,4440 .
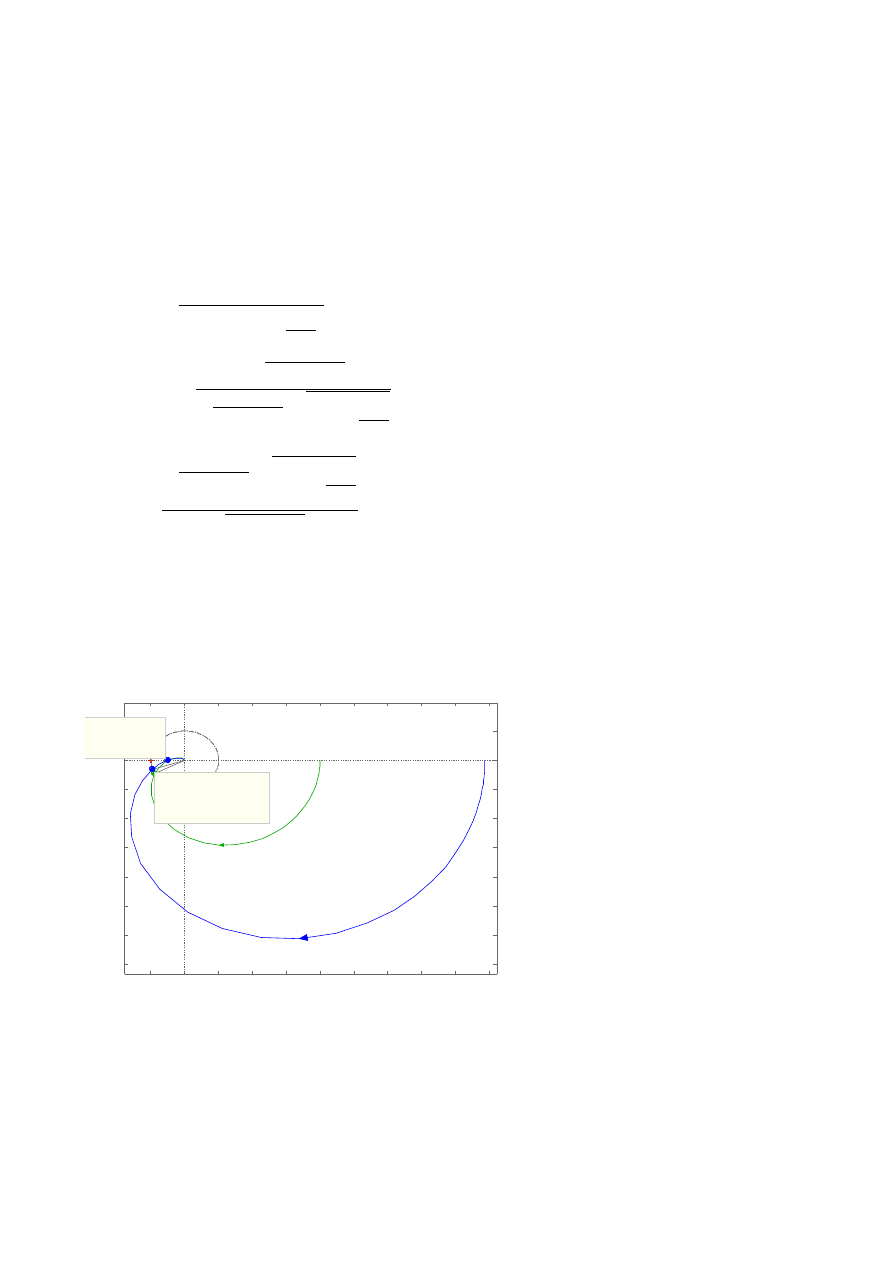
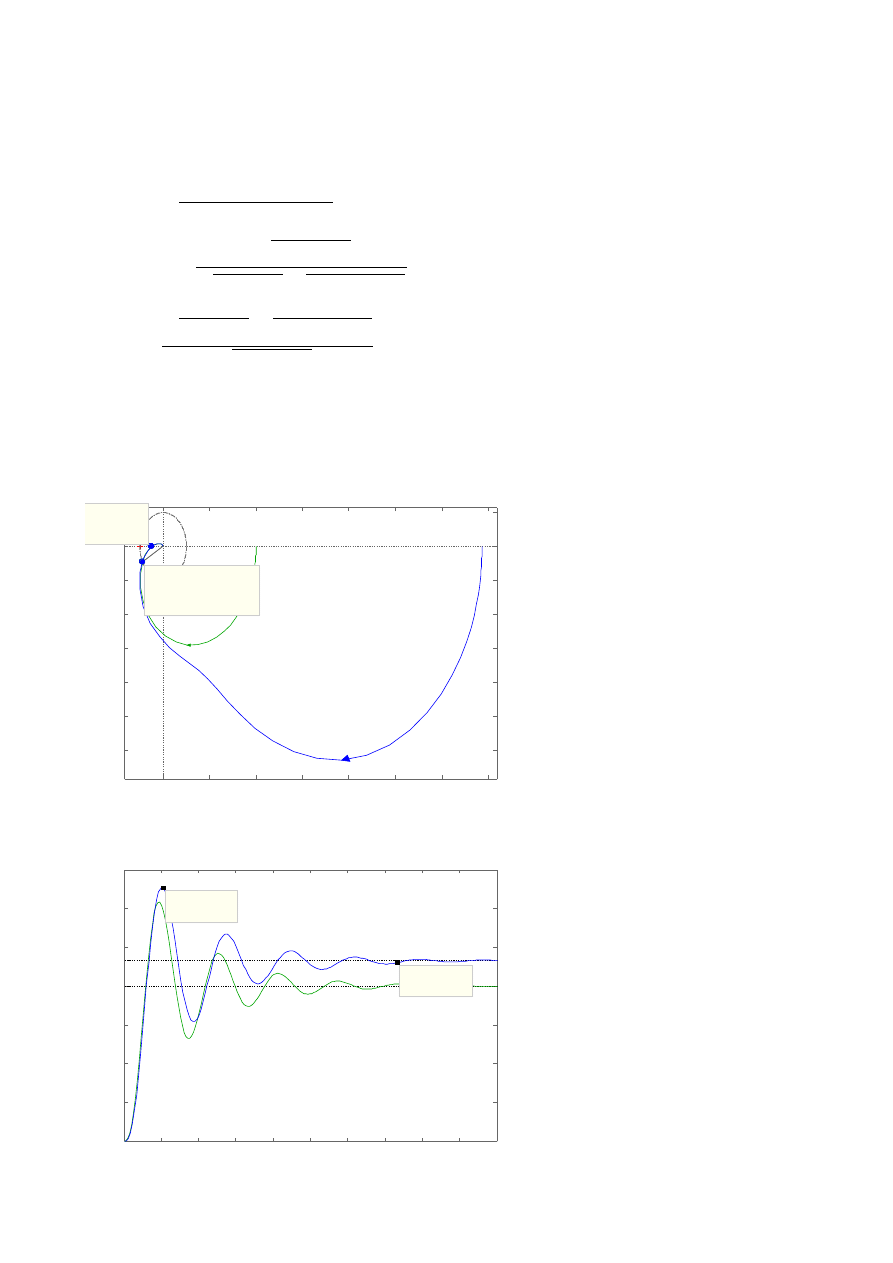
Rysunek 13. Charakterystyka Nyquista korektora.
Rysunek 14. Charakterystyka Nyquista obiektu z korektorem.
Jak widać na rysunku 13, dla wyznaczonej wartości pulsacji ω
x
kąt przesunięcia
fazowego jest największy i wynosi około 5
o
. Natomiast zaznaczony punkt na rysunku 14 (dla
wyznaczonej wartości pulsacji ω
x
) leży niemalże na osi liczb rzeczywistych. Punkt ten leżałby
dokładnie na osi liczb rzeczywistych, gdyby nie wpływ błędów zaokrągleń.
0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 7
0 . 8
0 . 9
1
- 0 . 5
- 0 . 4
- 0 . 3
- 0 . 2
- 0 . 1
0
0 . 1
S y s t e m : K _ P I
R e a l : 0 . 2 5 1
I m a g : - 0 . 0 2 2 1
F r e q u e n c y ( r a d / s e c ) : 0 . 4 6 3
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
φ
K
(
ω
x
)
≈
- 5
o
0
0 . 2
0 . 4
0 . 6
0 . 8
1
- 0 . 5
- 0 . 4
- 0 . 3
- 0 . 2
- 0 . 1
0
0 . 1
S y s t e m : u n t i t l e d 1
R e a l : - 0 . 0 3 6 8
I m a g : - 0 . 0 0 0 8 2 7
F r e q u e n c y ( r a d / s e c ) : 0 . 4 6 3
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
Ad C.2.
Do wyznaczenia wzmocnienia granicznego k
gr
przyjęto pulsację graniczną równą ω
x
.
Następnie wzmocnienie graniczne wyznaczone z wykorzystaniem polecenia „solve” w środowisku
Matlab, z następujących zależności:
K s=
k 1sT
PD
1sT
3
1s T
PD
gdzie: T = 3,5 s; T
PD
= 18,4440 s; α = 4
K
gr
=
k
1
gr
2
T
PD
2
1
gr
2
T
2
3
1
gr
2
T
PD
2
2
1
k
gr
=
1
gr
2
T
2
3
1
gr
2
T
PD
2
2
1
gr
2
T
PD
2
≈
27,47
Aby zapas amplitudy wynosił ΔK = 2, należy dobrać wartość wzmocnienia k jako połowę
wartości k
gr
. Czyli k = 13,735.
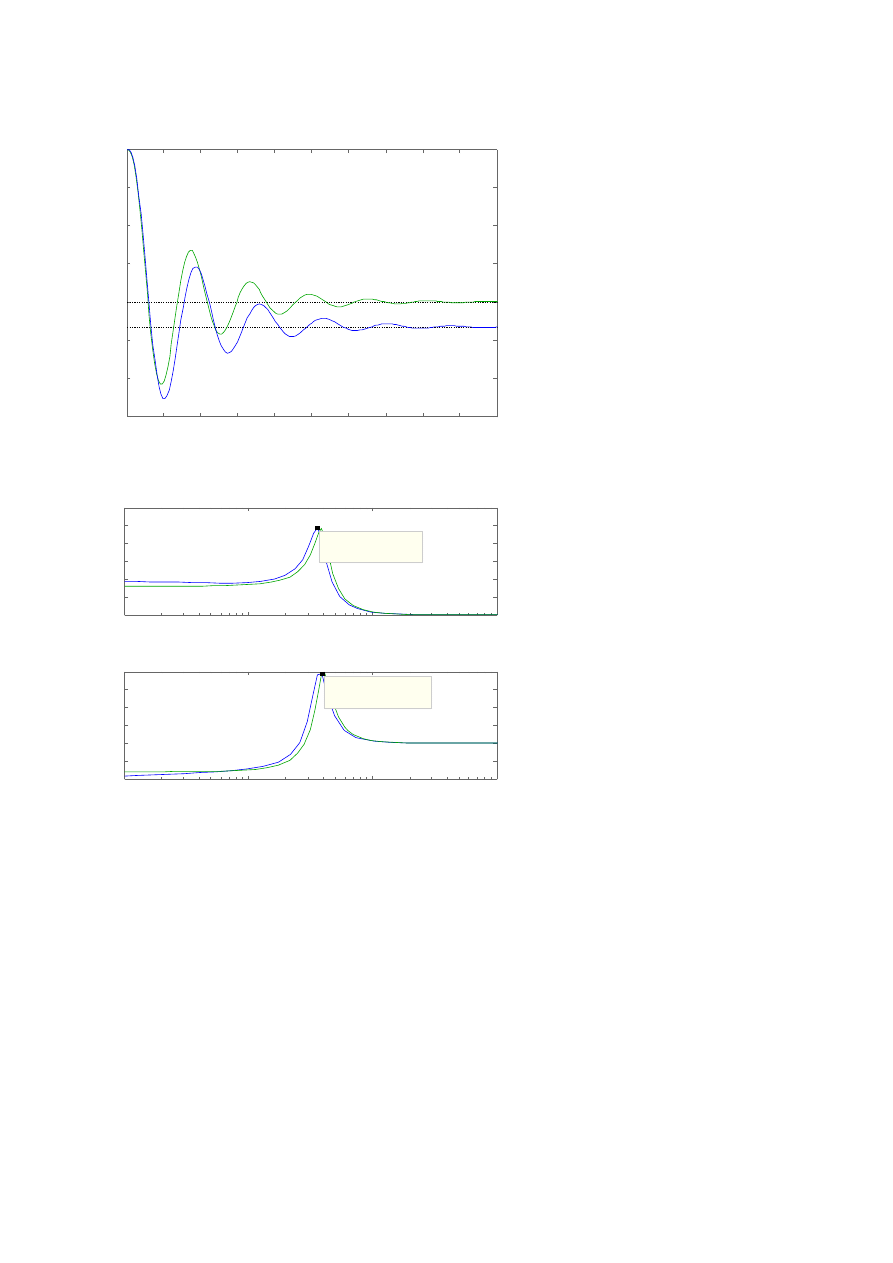
Ad C.3.
Rysunek 15. Charakterystyka Nyquista układu otartego.
Można odczytać:
ΔL = 6.02 dB
ΔK = 2
Δφ = 26,8
o
Ad C.4.
Rysunek 16. Odpowiedź skokowa układu zamkniętego.
Można odczytać:
y
ust
= 0.932
y
p
= 0.378 (40,56 %)
t
r
(przy Δ = 0.01) = 73,4 s
0
2
4
6
8
1 0
1 2
1 4
- 6
- 5
- 4
- 3
- 2
- 1
0
1
S y s t e m : u n t i t l e d 1
G a i n M a r g i n ( d B ) : 6 . 0 2
A t f r e q u e n c y ( r a d / s e c ) : 0 . 4 6 3
C l o s e d L o o p S t a b l e ? Y e s
S y s t e m : u n t i t l e d 1
P h a s e M a r g i n ( d e g ) : 2 6 . 8
D e l a y M a r g i n ( s e c ) : 1 . 4 4
A t fr e q u e n c y ( r a d / s e c ) : 0 . 3 2 5
C l o s e d L o o p S t a b l e ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
1 0 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
S y s t e m : u n t i t l e d 1
T i m e ( s e c ) : 1 0 . 3
A m p l i t u d e : 1 . 3 1
S y s t e m : u n t i t l e d 1
T i m e ( s e c ) : 7 3 . 4
A m p l i t u d e : 0 . 9 2 2
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
Ad C.5.
Rysunek 17. Przebieg czasowy uchybu regulacji.
Można odczytać:
e
ust
= 0.068
Ad C.6.
Rysunek 18. Przebiegi wskaźników częstotliwościowych.
Można odczytać:
M
max
= 2.43
ω
Mrez
= 0.360 rad/s
φ
max
= 2.94
ω
φrez
= 0.389 rad/s
Ad C.7. Ocena działania korektora (utrzymywany jest stały zapas modułu ΔK = 2).
Po dołączeniu korektora:
●
maleje zapas fazy (nieznacznie);
●
maleje uchyb w stanie ustalonym;
●
maleje wartość przeregulowania;
●
rośnie czas regulacji;
●
maksymalne wartości wskaźników częstotliwościowych nie zmieniają się znacząco;
●
częstotliwości rezonansowe wskaźników częstotliwościowych nie zmieniają się znacząco;
●
zwiększa się zdolność nadążania w paśmie podrezonansowym;
●
zwiększa się zdolność tłumienia zakłóceń w pasmie podrezonansowym;
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
1 0 0
- 0 . 4
- 0 . 2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
1 0
- 2
1 0
- 1
1 0
0
1 0
1
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : u n t i t l e d 1
F r e q u e n c y ( r a d / s e c ) : 0 . 3 6
M a g n i t u d e ( a b s ) : 2 . 4 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : u n t i t l e d 1
F r e q u e n c y ( r a d / s e c ) : 0 . 3 8 9
M a g n i t u d e ( a b s ) : 2 . 9 4
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
Ad D. Porównanie działania korektorów PI i PD:
Tabela 1. Zestawienie wyników w celu porównania działania korektorów:
Układ:
ΔK Δφ
[
o
]
y
ust
e
ust
y
p
[%]
t
r
[s]
(Δ=0.01)
M
max
ω
Mmax
[rad/s]
φ
max
ω
φmax
[rad/s]
Bez korektora:
2
27,1 0,800 0,200 53,75
67,6
2,41
0,388
2,98
0,411
Z korektorem PD:
2
17,9 0,899 0,101 62,40
48,6
3,39
0,667
3,75
0,706
Z korektorem PI:
2
26,8 0,932 0,068 40,56
73,4
2,43
0,360
2,94
0,389
Porównanie działania korektorów dla zadanego obiektu regulacji (nastawa wzmocnienia
korygującego dobrana tak aby zapas amplitudy wynosił 2):
●
Zastosowanie obu korektorów powoduje zmniejszenie zapasu fazy w porównaniu do układu
bez korektora. Jednakże dla zastosowanego korektora PI zapas ten maleje nieznacznie co
jest niewątpliwą zaletą stosowania tego korektora.
●
Zastosowanie obu typów korektorów zmniejsza wartość uchybu regulacji w stanie
ustalonym. W przypadku zastosowanego korektora PI wartość uchybu w stanie ustalonym
jest najmniejsza co jest niewątpliwą zaletą stosowania tego korektora.
●
Zastosowanie korektora PI zmniejsza wartość przeregulowania – duża zaleta szczególnie w
układach, które na przykład zasilają jakiś obiekt i mogło by dojść do jego uszkodzenia na
skutek zbyt wysokiej amplitudy sterującej. Zastosowanie korektora PD zwiększa wartość
przeregulowania co często bywa niepożądane.
●
Niewątpliwą zaletą zastosowania korektora PD jest zmniejszenie czasu regulacji.
Zastosowanie korektora PI zwiększa ten czas.
●
Zaletą stosowania korektora PD jest zwiększenie zakresu przedziału podrezonansowego dla
obu wskaźników częstotliwościowych, ale niestety rosną wartości pików rezonansowych.
Zastosowanie korektora PI zmniejsza nieco zakres przedziału podrezonansowego, co często
bywa niepożądane, szczególnie przy tłumieniu zakłóceń o wyższych częstotliwościach.
Natomiast nieznacznie maleją wartości maksymalne wskaźników częstotliwościowych.
Odnośnie wzmocnienia korygującego i współczynnika α:
●
Większe tłumienie procesów przejściowych można uzyskać zwiększając wzmocnienie.
Korektor PI umożliwia niemalże alfa-krotne zwiększenie wzmocnienia granicznego przy
niewielkim zmniejszeniu pasma podrezonansowego. Dlatego zmieniając wartość
wzmocnienia korygującego można wymusić lepsze tłumienie procesów przejściowych, w
zależności od interesujących nas kryteriów jakości regulacji.
●
Zastosowanie korektora PD pozwala znacznie zwiększyć częstotliwość drgań własnych na
granicy stabilności (częstotliwość ta rośnie ze wzrostem wartości maksymalnego kąta
fazowego korektora, czyli ze wzrostem współczynnika α). Zapewniając odpowiednie
tłumienie procesów przejściowych (odpowiednią wartość wzmocnienia korygującego),
spowoduje szybsze tłumienie procesów przejściowych, czyli zwiększy się szybkość
regulacji.
4. Wnioski końcowe:
●
Korektory PD stosujemy wszędzie tam, gdzie zależy nam na zwiększeniu czasu regulacji i
pasma nadążania.
●
Korektory PI stosujemy wszędzie tam, gdzie zależy nam na niższej wartości uchybu
regulacji w stanie ustalonym i większym tłumieniu procesów przejściowych.
●
Zalety korektora PD i PI łączy w sobie korektor PID, który stosowany jest w układach o
złych parametrach regulacji i wymagana jest ich znaczna poprawa.
●
Nastawa wzmocnienia korygującego na odpowiedniej wartości jest niezbędna, ponieważ
zapewnia ona spełnienie zamierzonych celów stosowania korektora.
●
Parametry korektorów poprawiają się ze wzrostem parametru α w rozsądnych granicach.
Document Outline
Wyszukiwarka
Podobne podstrony:
Ćw 7 Korekcja liniowych układów regulacji
Korekcja liniowych układów regulacji
Korekcja liniowych układów regulacji, Elektrotechnika, SEM4, ARA ćwiczenia
Korekcja liniowych układów regulacji
Korekcja liniowych układów regulacji
cw 7?danie ukladow regulacji dwupolozeniowej
08 Ocena jakości liniowych układów regulacji
cw 7?danie ukladow regulacji dwupolozeniowej
08 Ocena jakości liniowych układów regulacji
ćw 7 Badanie układów regulacji dwupołożeniowej
cw 7 Badanie ukladow regulacji dwupolozeniowej
8 ocena jakości układów regulacji
Metoda projektowania układów regulacji za pomocą linii pierwiastkowych
cw 7 porownanie metod sterowania i regulacji
Lab 6 Drgania Swobodne Liniowych Układów Dyskretnych
korektywa teoria opracowanie pytan, Fizjoterapia, ćw. korekcyjne
Ćw.3-Obwody liniowe prądu stałego, sem2
konspekt cw 3 1 programowanie liniowe
więcej podobnych podstron