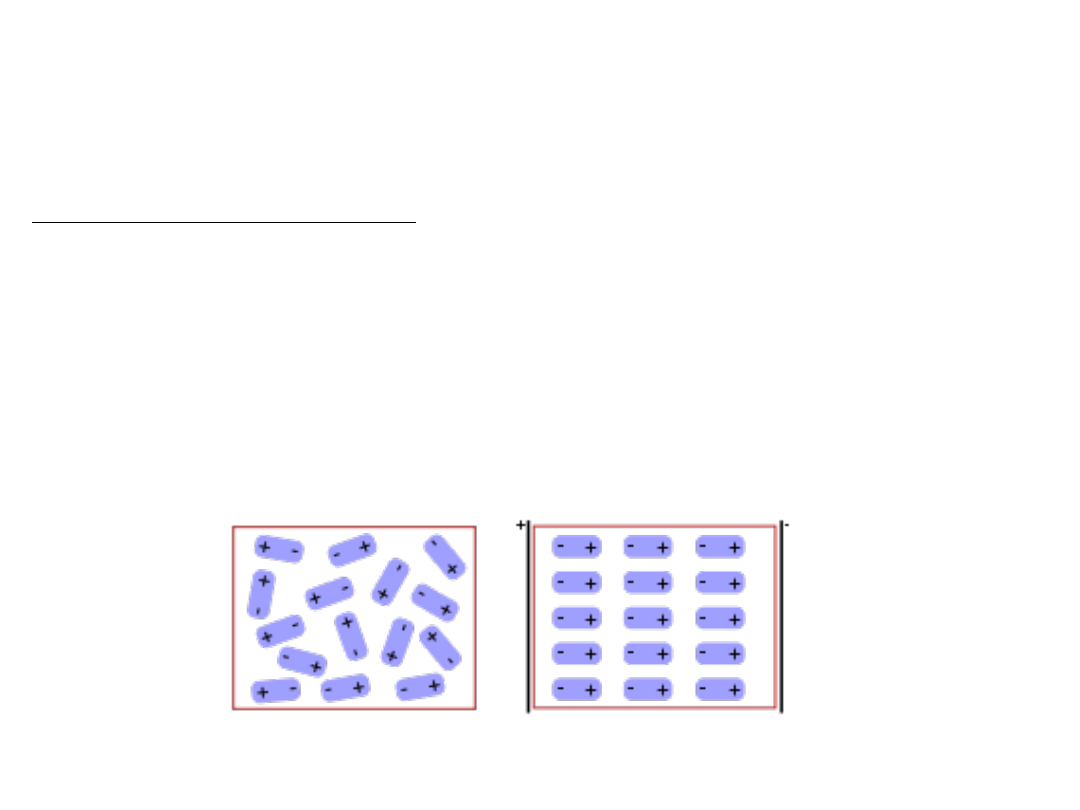
Wprowadzenie dielektryku pomiędzy okładki kondensatora powoduje osłabienie natężenia

pola elektrycznego między płytkami, na których nagromadzony jest dany ładunek. Przyczyną

zmniejszenia natężenia jest polaryzacja dielektryka.

Mechanizm polaryzacji dielektryka:

Jeżeli kondensator naładowany jest do odpowiedniego potencjału i na okładkach znajdują

się ładunki +q i –q, to ładunki na okładkach kondensatora zakłócają równowagę elektryczną

w dielektryku, indukując w nim ładunki przeciwnego znaku. Efekt ten opisuje się poprzez

polaryzację (P)

, czyli sumaryczny moment dipolowy indukowany w jednostkowej objętości

dielektryka.

-

Dipole indukowane

w spolaryzowanym dielektryku

Efekt indukowanego momentu dipolowego w cząsteczce jest proporcjonalny do

natężenia pola działającego na cząsteczkę (E

1

):

oraz

Gdzie:



- współczynnik proporcjonalności - polaryzowalność, skłonność konfiguracji

elektronowej cząsteczki do ulegania deformacji pod wpływem pola elektrycznego

Miarą wpływu przyłożonego pola na polaryzację cząsteczki jest jej

polaryzowalność

,

liczbowo równa momentowi dipolowemu wzbudzonemu przez pole elektryczne o

natężeniu jednostkowym.

1

E

ind

ind









1

E

n

P

ind

















3

4

2

'

1

'

A

m

N

d

M

P











Polaryzowalność cząsteczki (



), polaryzację molową (P) czy moment dipolowy cząsteczki

(



) można obliczyć na podstawie pomiarów stałej dielektrycznej:

Równanie

CLAUSIUSA - MOSOTTIEGO

M – masa cząsteczkowa

d - gęstość związku

N

A

– liczba Avogadro

k – stała Boltzamanna





























kT

N

M

d

P

A

m

3

3

4

2

'

1

'

2











Równanie

DEBYE’A

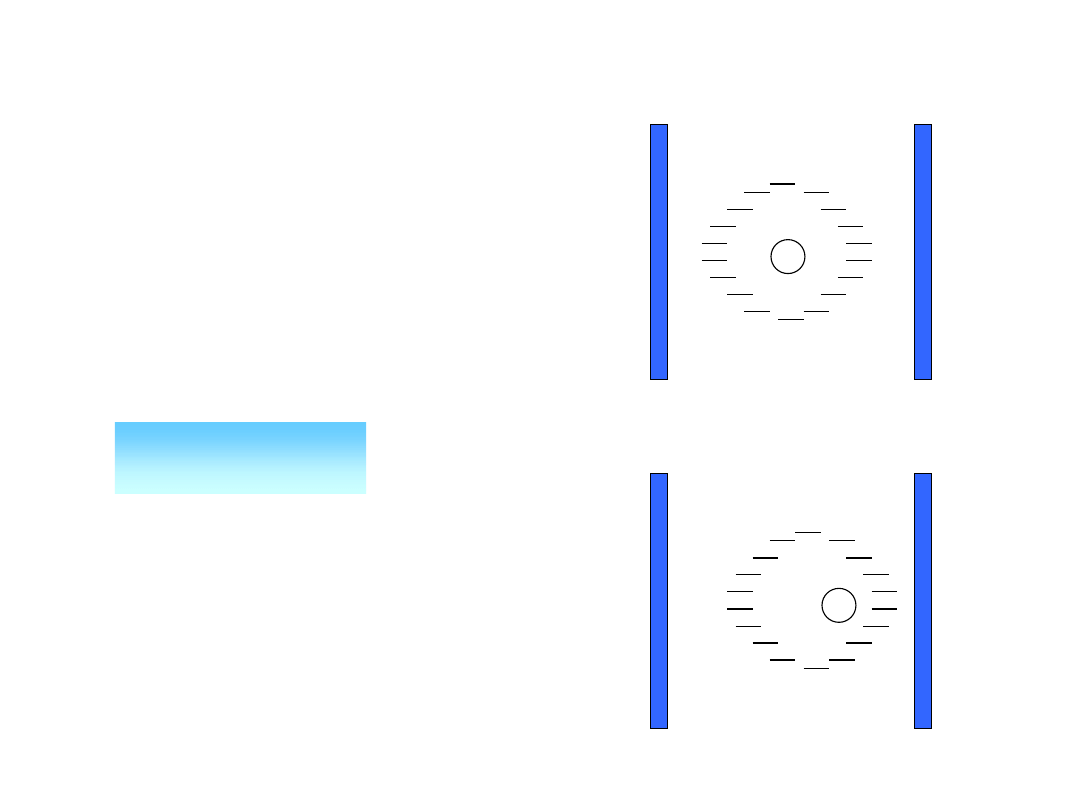
Polaryzacja elektronowa (P

el

)

Wynika z zaburzenia rozkładu gęstości

elektronowej wokół jąder atomowych. Pod

wpływem pola elektrycznego indukowany

jest w każdym atomie moment dipolowy,

proporcjonalny do natężenia pola:



- polaryzowalność (ma wymiar objętości,

jest rzędu 10

-24

cm

3

,

tzn. objętości kuli o promieniu

orbity elektronowej).

E

el

ind









+

+

+

+

+

+

+

-

-

-

-

-

-

-

+

+

nieobecne pole

pole elektryczne

Zjawiska zachodzące podczas

polaryzacji elektronowej

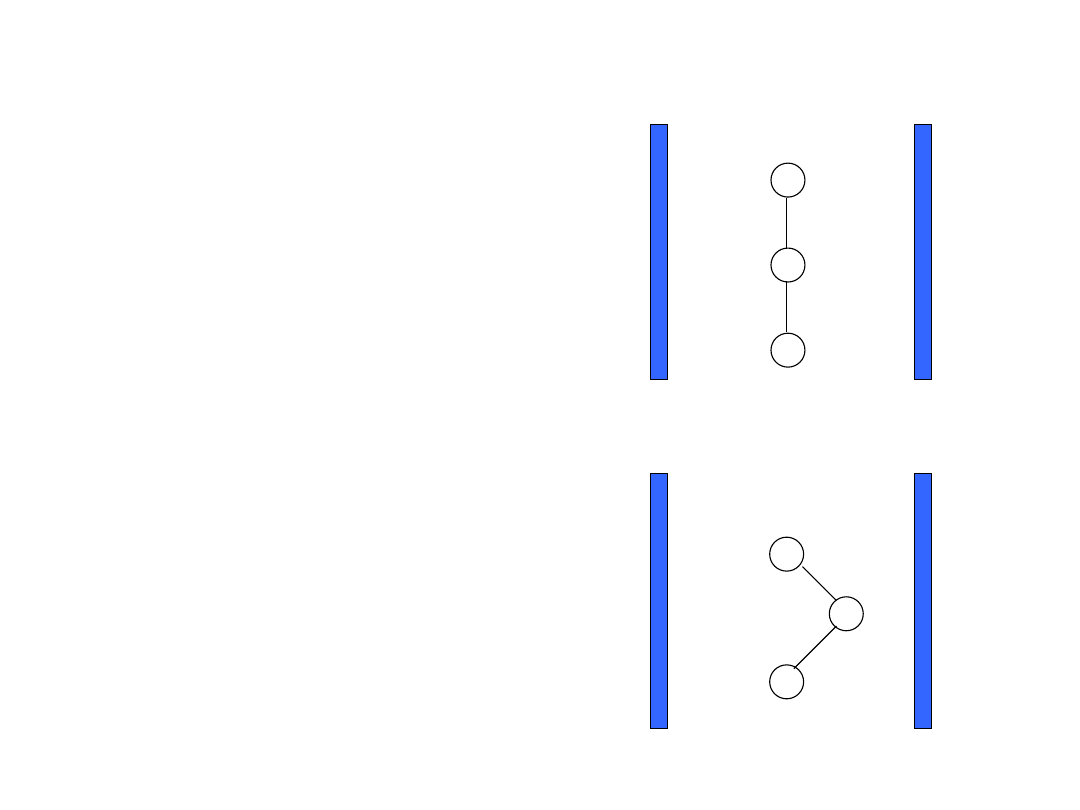
Polaryzacja atomowa (P

at

)

Jest

rezultatem

zmiany

geometrii

cząsteczek,

a

więc

odległości

międzyatomowych

oraz

kątów

walencyjnych. Polaryzacja atomowa jest

znaczna w przypadku związków o

charakterze jonowym lub zawierających

silne polarne grupy, łatwo deformujące

się pod wpływem pola. Moment

indukowany,

wskutek

polaryzacji

atomowej, również jest proporcjonalny

do natężenia pola.

+

+

+

+

+

+

+

-

-

-

-

-

-

-

nieobecne pole

pole elektryczne

Zjawiska zachodzące podczas

polaryzacji atomowej

-

+

-

+

-

-

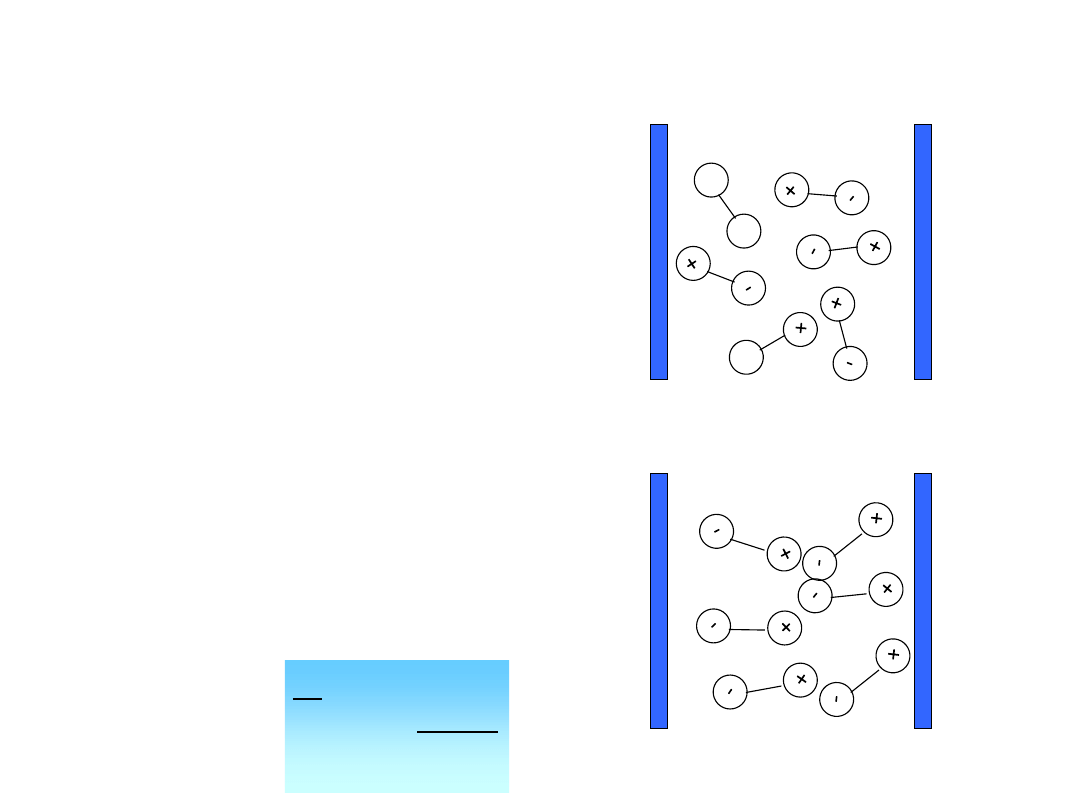
Polaryzacja dipolowa (orientacji) (P

or

)

Występuje w przypadku związków, których

cząsteczki maja trwałe momenty dipolowe.

Pod wpływem pola elektrycznego dochodzi

do orientowania się trwałych dipoli

względem kierunku pola i uzyskuje się stan

statystycznego uporządkowania.

Średnia polaryzowalność dipolowa zależy od

trwałych momentów dipolowych oraz od

temperatury, która niekorzystnie wpływa na

stan uporządkowania:

kT

dip

3

2







+

+

+

+

+

+

+

-

-

-

-

-

-

-

nieobecne pole

pole elektryczne

Zjawiska zachodzące podczas

polaryzacji dipolowej

-

+

-

Polaryzacja indukowana (P

ind

)

Każdy dielektryk, nawet taki, którego cząsteczki nie są dipolami, ulega wpływowi

zewnętrznego pola elektrycznego. Efekt ten nazwany jest polaryzacją indukowaną i można

go rozłożyć na dwie składowe:

- polaryzację elektronową (P

el

) wywołaną zaburzeniem przez zewnętrzne pole chmury

elektronowej w cząsteczkach dielektryka;

- polaryzacja atomową (P

at

) wywołaną przesunięciem jąder atomowych jednych w

stosunku do drugich (zmiana geometrii cząsteczki)

ind

A

at

el

ind

N

P

P

P





0

3







d

M

kT

N

P

P

P

ind

A

or

ind

c





























2

1

3

3

2

0











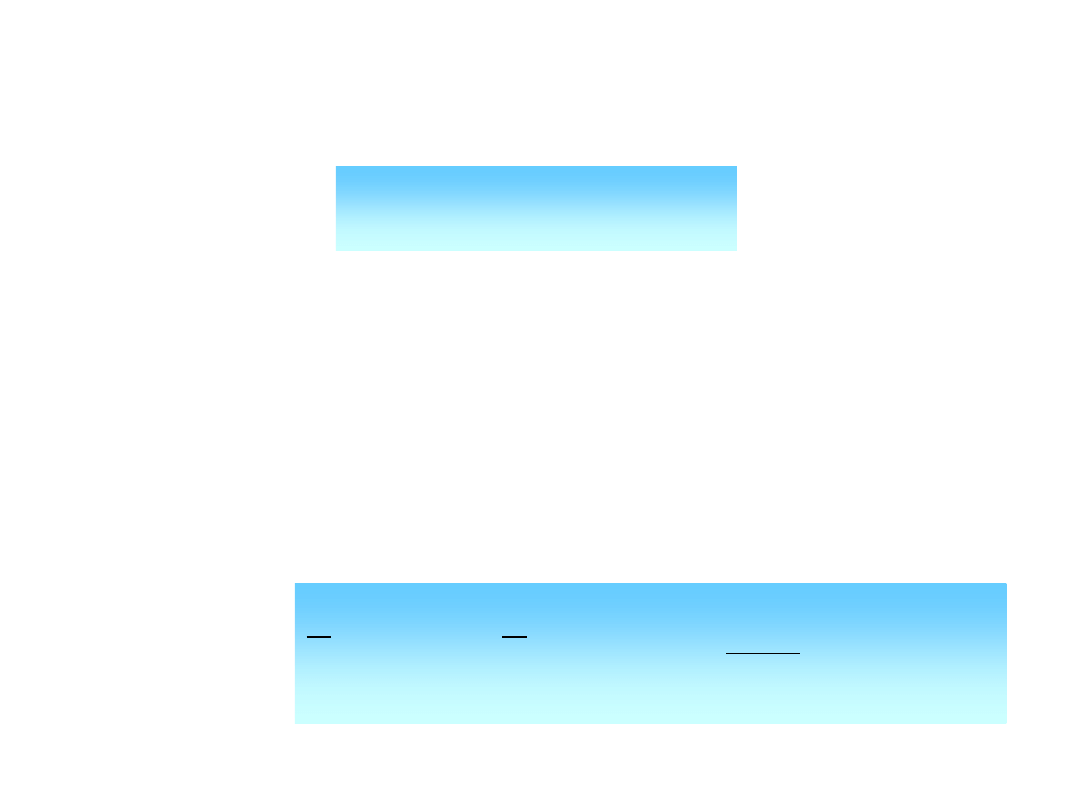
POLARYZOWALNOŚĆ

Polaryzowalność ogólna (całkowita) równa jest sumie wszystkich trzech składowych

dip

at

el















Polaryzowalność ogólna jest związana z mierzalną, makroskopową właściwością
substancji – przenikalnością dielektryczną



.

Natomiast jeżeli w polu elektrycznym znajduje się cząsteczka polarna o trwałym

momencie dipolowym, to ulega ona zarówno polaryzacji dipolowej, jak i indukowanej.

Średni całkowity moment elektryczny takiej cząsteczki jest sumą obu polaryzacji:

1

1

2

3

E

E

kT

ind

or

ind

c





































gdzie: całkowita polaryzowalność cząsteczki



=



ind

+



or

Wyznaczanie refrakcji molowej

Badając zjawisko załamania światła można wyciągnąć pewne wnioski odnośnie struktury

cząsteczek ośrodka przezroczystego na które pada światło. Promień świetlny przechodząc

z ośrodka, w którym ma prędkość c

1

do ośrodka, w którym ma prędkość c

2

, ulega na

powierzchni granicznej częściowemu odbiciu i załamaniu. W wyniku tego zjawiska

promień zmienia swój pierwotny kierunek, przy czym, zgodnie z

prawem Snelliusa

,

stosunek sinusa kąta padania do sinusa kąta załamania jest dla danej pary ośrodków

wielkością stałą, zwaną współczynnikiem załamania światła, równą stosunkowi prędkości

światła w obydwu ośrodkach.

2

1

sin

sin

c

c

n











- kąt padania,



- kąt załamania, c

1

, c

2

– prędkość światła w ośrodku 1 i 2

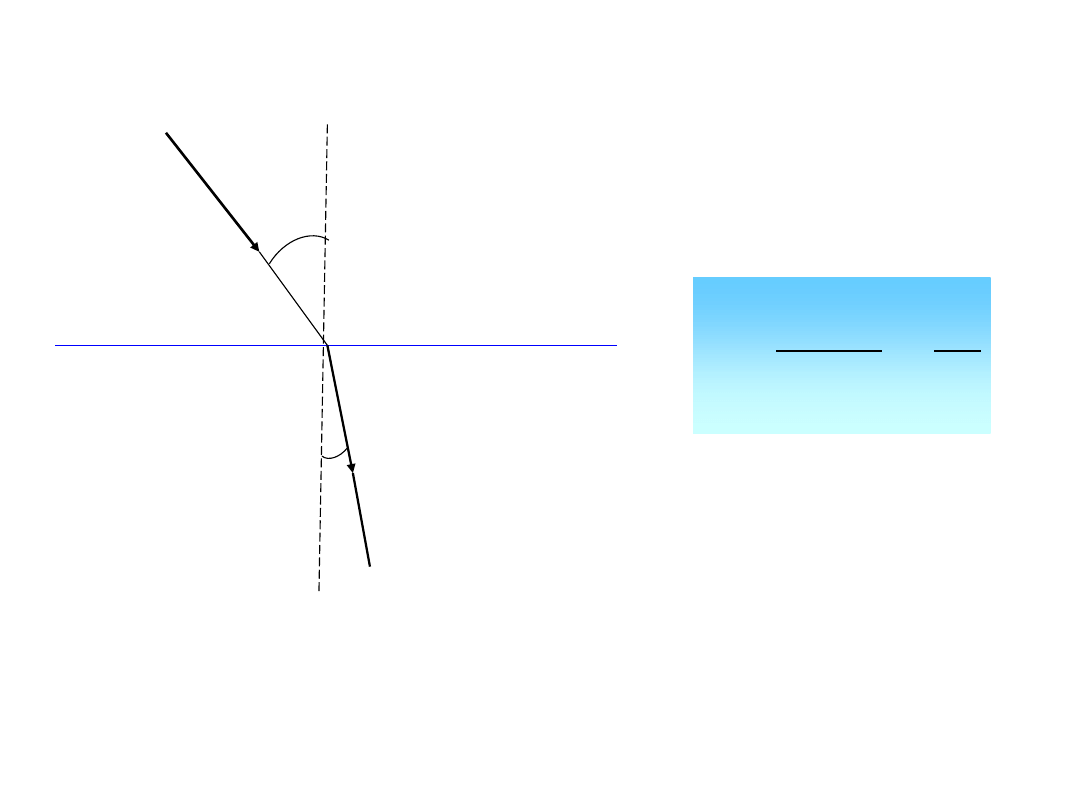
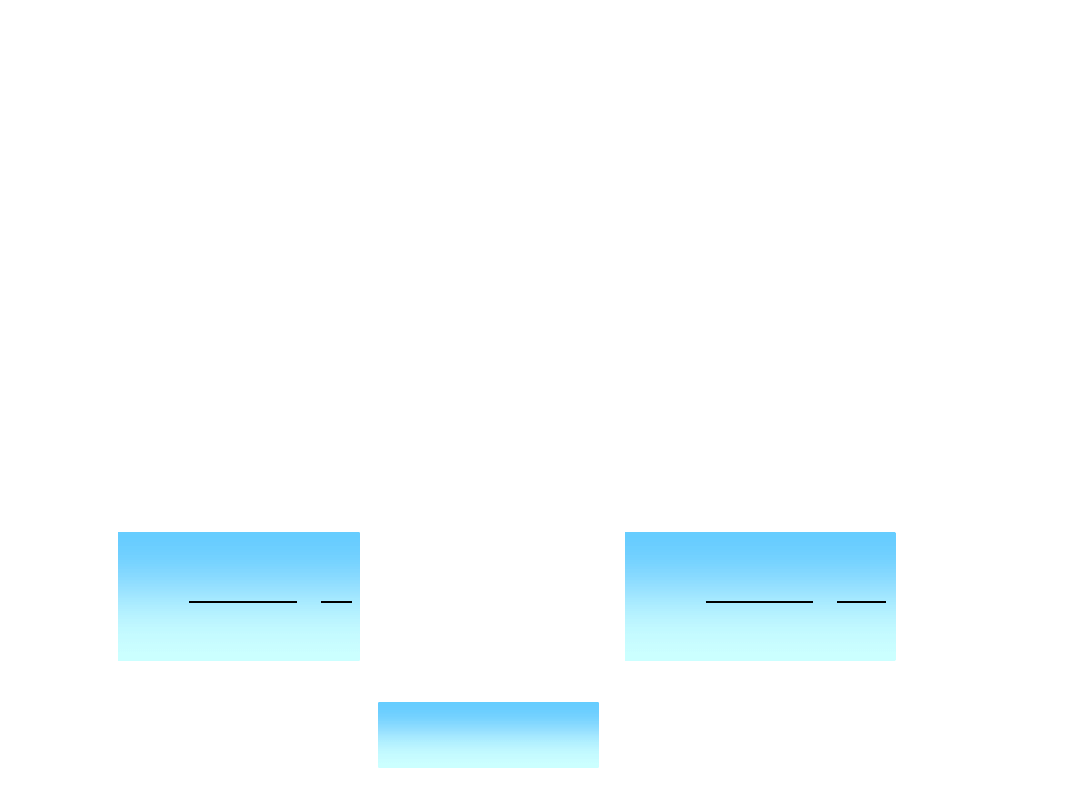
Załamanie światła

Ośrodek 1

Ośrodek 2





2

1

sin

sin

c

c

n









Jeżeli załamanie światła następuje w ten sposób, że kąt



jest mniejszy od kąta



, to

ośrodek 2 nosi nazwę optycznie gęstszego niż ośrodek 1.
Jeżeli kąt



jest większy od kąta



, to ośrodek 2 jest ośrodkiem optycznie rzadszy niż

ośrodek 1.
Próżnia jest ośrodkiem optycznie najrzadszym – największa prędkość.

GRANICA FAZ

Współczynnik załamania światła wyznaczony względem próżni nazywa się bezwzględnym

współczynnikiem załamania (N), który oznacza się z reguły tylko dla gazów.

Dla cieczy i ciał stałych wyznacza się zwykle współczynnik załamania (n) względem

powietrza, ponieważ różnica pomiędzy wartościami N i n jest niewielka (ok. 0,03%)

Badania współczynnika załamania znajdują zastosowanie m.in. przy określaniu budowy

związków chemicznych, wykorzystując równania Lorentza i Lorenza na refrakcję właściwą

i molową:

d

M

n

n

R









2

1

2

2

d

n

n

r

1

2

1

2

2









M

r

R





Refrakcja molowa ma wymiar objętości molowej, a jej jednostką jest jednostka objętości

molowej, a więc m

3

/mol lub cm

3

/mol (współczynnik załamania światła jest wielkością

niemianowaną).

Refrakcja molowa określa objętość, którą rzeczywiście zajmują w przestrzeni cząsteczki 1

mola substancji (jest mniejsza od objętości molowej).

Refrakcja molowa jest wielkością charakterystyczną i stałą dla danego związku

chemicznego, niezależną od temperatury i ciśnienia, natomiast zależną od długości fali

światła. W przypadku stosowania linii żółtego światła sodowego oznacza się ją symbolem

R

D

.

Refrakcja molowa jest

wielkością

addytywną

– może być rozłożona na stałe udziały

atomowe (suma refrakcji atomów R

a

) i udziały wiązań (suma refrakcji wiązań R

w

) z

uwzględnieniem poprawek, wynikających ze szczególnej struktury elektronowej (np.

układy z elektronami



, które wykazują zwykle podwyższoną podatność do polaryzacji, a

także pewne zdeformowane układy atomowe).













i

w

i

i

a

i

R

n

R

n

R

n

i

– oznacza liczbę określonych atomów i wiązań w cząsteczce

Korzystając z powyższego równania można obliczyć refrakcję molową związku, gdy znana
jest jego budowa. Wielkość tę można wyznaczyć również doświadczalnie, mierząc w
określonej temperaturze współczynnik załamania światła i gęstość oraz wyznaczając masę
molową danego związku. Porównując wyniki otrzymane teoretycznie i eksperymentalnie
dla kilku możliwych struktur badanego połączenia, można określić, która z nich jest
właściwa.

Refrakcja molowa mieszaniny (roztworu) wykazuje również właściwości addytywne i równa

się sumie udziałów refrakcji molowych poszczególnych składników mieszaniny.

Dla roztworu dwuskładnikowego wielkość tą można wyrazić wzorem:

2

2

1

1

R

x

R

x

R

mieszaniny





x

1

,x

2

– ułamki molowe substancji 1 i 2; R

1

, R

2

– refrakcje molowe czystych substancji 1 i 2.

Doświadczalną wartość refrakcji molowej roztworu dwuskładnikowego wyznacza się na

podstawie równania:

mieszaniny

mieszaniny

mieszaniny

mieszaniny

d

M

x

M

x

n

n

R

2

2

1

1

2

2

2

1















Pomiar współczynnika załamania światła

Przyrządy stosowane do pomiaru współczynnika załamania światła noszą nazwę

refraktometrów. Zasada ich działania polega na tym, że jeżeli promień świetlny

przechodząc z ośrodka optycznie rzadszego do gęstszego pada na powierzchnię graniczną

pod kątem 90

0

, to załamanie następuje pod kątem



g

, który nazywa się katem granicznym.

Obserwacja promienia załamanego pozwala zauważyć, że w tych warunkach pole widzenia

jest podzielone na 2 ostro od siebie oddzielone części: jasną i ciemną. W tej sytuacji, tzn.

dla kąta padania



=90

0

g

g

n





sin

1

sin

90

sin

0





Pomiaru współczynnika załamania światła dokonuje się poprzez zmierzenie wartości

kąta granicznego w refraktometrze.

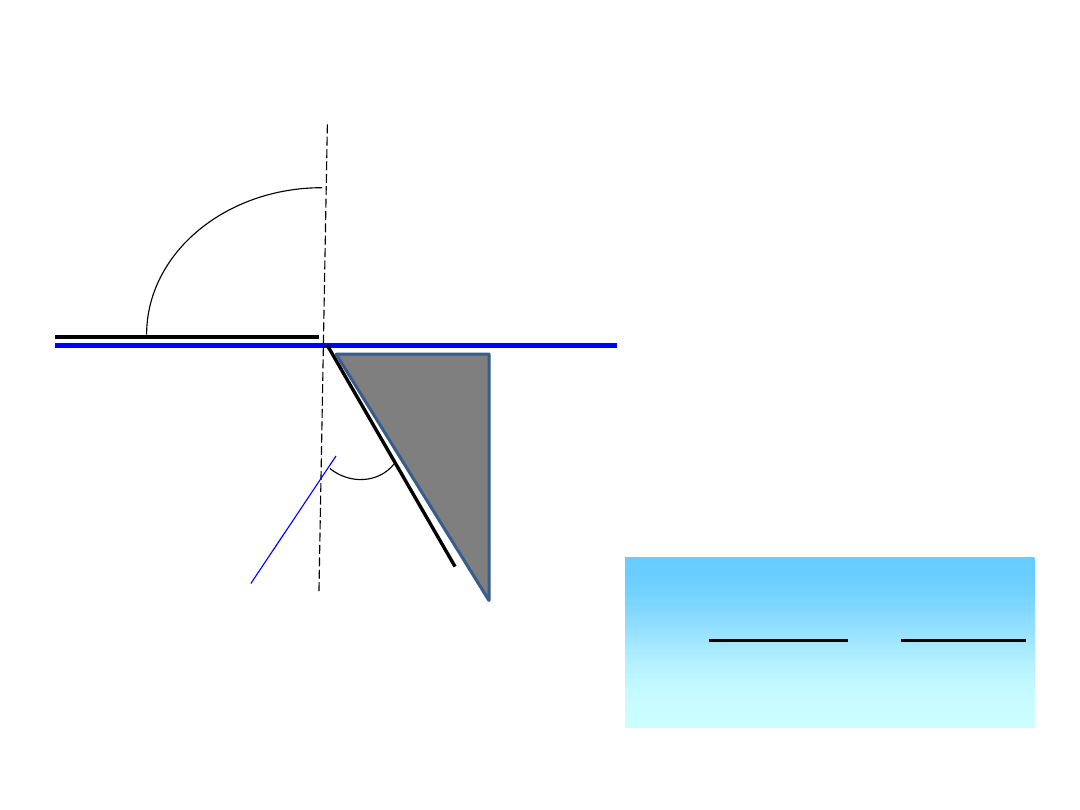
Kąt graniczny i zasada działania refraktometru

GRANICA FAZ

Ośrodek
optycznie
rzadszy

Pole
jasne

90

0



g

Ośrodek
optycznie
gęstszy

Pole ciemne

Kąt
graniczny

g

g

n





sin

1

sin

90

sin

0





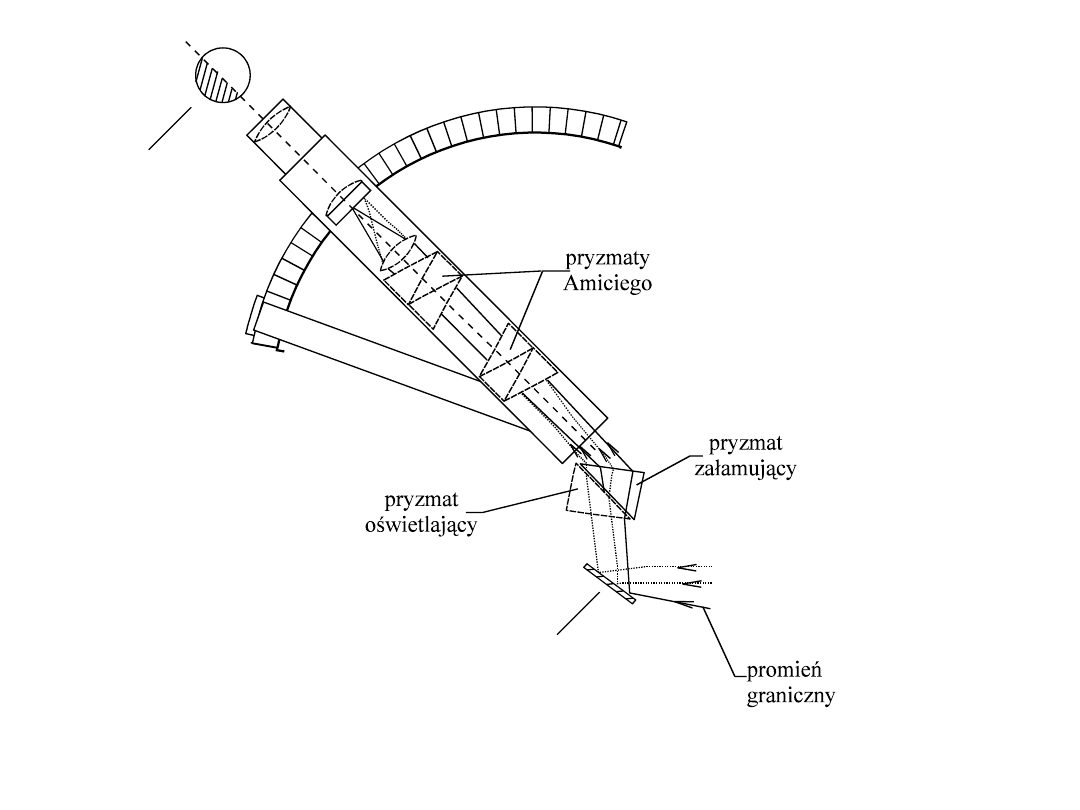
Refraktometr Abbego

lusterko

okular

Zasada działania refraktometru Abbego

Cienką warstwę badanej cieczy umieszcza się pomiędzy dwoma pryzmatami wykonanymi

ze szkła charakteryzującego się dużym współczynnikiem załamania. Promienie świetlne

(monochromatyczne) odbite od lusterka przechodzą do pryzmatu oświetlającego o

matowej powierzchni wewnętrznej, załamują się w nim i pod różnymi kątami padają na

badaną substancję. Następnie po przejściu przez warstwę substancji trafiają pod kątem

90

0

na pryzmat załamujący, w którym załamują się pod kątem granicznym, przez co pole

widzenia w okularze jest częściowo jasne a częściowo ciemne. Wszystkie promienie, które

padają pod kątem większym niż kąt graniczny zostają całkowicie odbite i nie przedostają

się do drugiego pryzmatu. Ustawiając lunetkę tak, aby granica cienia była w środku pola

widzenia (umożliwiają to dwie cienkie skrzyżowane nici „pajęcze”), można na

odpowiedniej skali odczytać współczynnik załamania światła badanej cieczy za pomocą

lunetki.

Wbudowany w refraktometr zespół pryzmatów Amiciego powoduje odchylanie

wszystkich promieni o długości fal innych niż żółta linia światła sodowego.

Wyznaczanie momentu dipolowego i polaryzowalności cząsteczki

Stałą dielektryczną materiału mierzy się umieszczając go między okładkami kondensatora –

w przypadku cieczy wypełnia się nią naczynie, w którym zanurza się płytki kondensatora.

Kondensator włącza się następnie w jedno ramię mostka elektrycznego, np. mostka

Wheatstone’a do pomiaru oporów i równoważy się pojemność badanego kondensatora za

pomocą regulowanego kondensatora porównawczego, nie zawierającego dielektryka

między okładkami. Pojemność kondensatora porównawczego można obliczyć na podstawie

jego

geometrii.

Tą metodą wyznacza się pojemność kondensatora badanego, z dielektrykiem i bez

dielektryka, oraz określa się stała dielektryczną badanego materiału. Do pomiarów stosuje

się prąd zmienny o częstotliwości ok. 1 MHz.

Gdy badany związek jest ciekły lub stały, pomiarom poddaje się jego roztwory

w nieaktywnych rozpuszczalnikach niepolarnych, np. w CCl

4

lub benzenie.

Równanie Debye’a zakłada niezależne zachowanie się cząsteczek polarnych. Cząsteczki

dipolowe silnie oddziałują na siebie wzajemnie; najbardziej uzasadnione jest więc

stosowanie równania Debye’a do rozcieńczonych roztworów związków polarnych w

niepolarnych rozpuszczalnikach.

Pomiar stałej dielektrycznej i zastosowanie równania Debye’a nie umożliwia

bezpośredniego wyznaczenia oddzielnie



i



.





























kT

N

M

d

P

A

m

3

3

4

2

1

2











Równanie

DEBYE’A

Istnieją dwie zasadnicze metody uzyskiwania tych dwóch wielkości.

T

k

N

N

d

M

P

A

A

1

3

3

4

3

4

2

1

2







































Pierwsza metoda polega na pomiarze



i d jako funkcji temperatury i wykorzystaniu

otrzymanych danych do graficznego przedstawienia jako funkcji 1/T.

d

M







2

1





Y

X

a

b

=

+

Na podstawie równania Debye’a można oczekiwać, że zależność ta będzie prostoliniowa (jest

ona spełniona przez chlorowcowodory). Na podstawie nachylenia prostej można wyznaczyć

moment dipolowy, a z przecięcia się prostej z osią Y polaryzowalność. Metoda ta jest dość

prosta i zawodzi jedynie w przypadku, gdy cząsteczki są w różnym stopniu zasocjowane w

różnych temperaturach lub gdy konfiguracja cząsteczki zmienia się z temperaturą.

Druga metoda, umożliwiająca wyznaczenie polaryzowalności w polaryzacji molowej (P), oparta

jest na zależności między stałą dielektryczną a współczynnikiem załamania, wynikającej z

elektromagnetycznej teorii promieniowania Maxwella. Użyte do pomiaru współczynnika

załamania promieniowanie widzialne związane jest z polem elektrycznym o tak dużej

częstotliwości (ok. 10

15

Hz), że orientacja cząsteczek nie nadąża za zmianami pola. Stąd nie

odgrywają tutaj roli dipole trwałe, lecz jedynie polaryzacja cząsteczek.

Z teorii Maxwella wynika, że w przypadku substancji zbudowanych z cząsteczek nie mających

trwałych momentów dipolowych:

n

2

=



gdzie: n – współczynnik załamania światła

Wynika z tego, że nawet gdy cząsteczki dielektryka mają momenty dipolowe, można obliczyć

udział polaryzowalności w całkowitej polaryzacji molowej (P) za pomocą wzoru:

Pomiary współczynnika załamania umożliwiają więc określenie wartości



, którą łącznie z

danymi dotyczącymi stałej dielektrycznej można wykorzystać do wyznaczenia momentu

dipolowego cząsteczki (



).





3

4

2

1

2

2

















A

N

d

M

n

n

P

Uproszczoną metodę wyznaczenia momentu dipolowego czystych cieczy polarnych

zaproponował Onsager:



 







2

2

2

2

0

2

2

2

9



















n

d

M

n

n

N

kT

A











Równanie to wynika z przybliżonego założenia, że cząsteczka badanej cieczy jest dipolem

znajdującym się w sferycznej jamie. Z takich dipoli składa się cały rozpuszczalnik.

W celu obliczenia momentu dipolowego należy wykonać pomiary:

1) gęstości (piknometr)

2) współczynnika załamania światła (refraktometr Abbego)

3) względnej przenikalności elektrycznej badanych cieczy (metoda mostkowa –

uniwersalny mostek RLC)

w temperaturze otoczenia.