Ć w i c z e n i e 27

WYZNACZANIE ELEKTRONOWEJ

POLARYZOWALNOŚCI CZĄSTECZKI WODY

27.1 Wstęp teoretyczny

Zjawisko polaryzacji dielektryków wymaga zdefiniowania pojęcia dipola elektrycznego.
Dipolem elektrycznym nazywamy układ dwóch jednakowych ładunków elektrycznych o przeciw-
nych znakach umieszczonych w pewnej odległości od siebie. Rozpatrzmy przypadek dwóch punk-
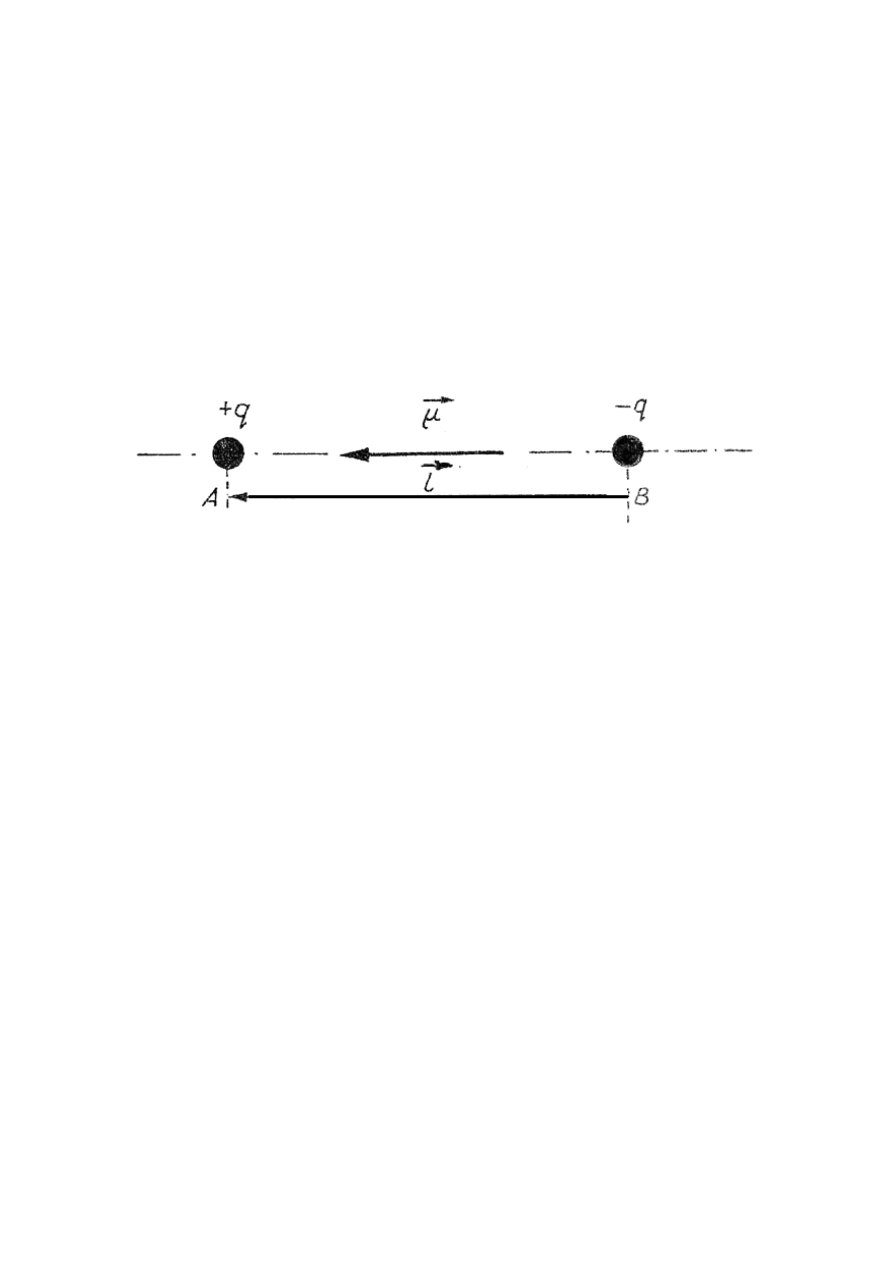
towych jednakowych, różnoimiennych ładunków elektrycznych (rys.27.1).

Rys.27.1. Dipol

Punkt A, w którym skupiony jest ładunek dodatni dipola nazywamy jego biegunem dodatnim, a
punkt B – biegunem ujemnym. Prostą łączącą bieguny dipola, nazywamy jego osią. Podstawową
wielkością charakteryzującą dipol elektryczny jest moment dipolowy

µ

r , określony jako wektor

skierowany od ładunku ujemnego do dodatniego i liczbowo równy iloczynowi bezwzględnej
wartości naboju jednego z biegunów dipola q i odległości między ładunkami l:

l

q

r

r =

µ

(27.1)

Wektor nazywamy ramieniem dipola. Zwyczajową jednostką momentu dipolowego jest debye
(D) [czyt. debaj], a w układzie SI wprowadzono jednostkę kulombometr ( 1D = 3,334 10

l

r

-30

C m).

Pojęcie dipola można również stosować do układów złożonych z więcej niż dwóch ładunków, pod
warunkiem, że suma algebraiczna wszystkich ładunków układu równa się zeru i że środki rozkła-
du gęstości ładunków obu znaków nie pokrywają się. Środek rozkładu gęstości ładunków danego
znaku przyjmujemy wówczas za odpowiedni biegun dipola, a suma ładunków danego znaku – za
ładunek tego bieguna. Takimi złożonymi układami są cząsteczki chemiczne w stanie obojętnym
(tzn. niezjonizowane). Jeśli więc środek ciężkości ładunków jąder atomowych nie pokrywa się ze
środkiem ciężkości ładunków powłok elektronowych, wówczas cząsteczka jest w myśl powyższej
definicji dipolem. Moment dipolowy cząsteczki chemicznej zależy od wielkości spolaryzowania
poszczególnych jej wiązań (tylko wiązania H – H, O – O, C – C itp. są niespolaryzowane) oraz od
jej przestrzennej struktury (wzajemnego przestrzennego rozmieszczenia poszczególnych wiązań),
co przedstawia tabela 27.1.
Cząsteczka wody jest dipolem, ponieważ nie ma struktury liniowej, lecz kątową (rys.27.2). Przy-
pisuje się jej promień równy 0,138 nm.

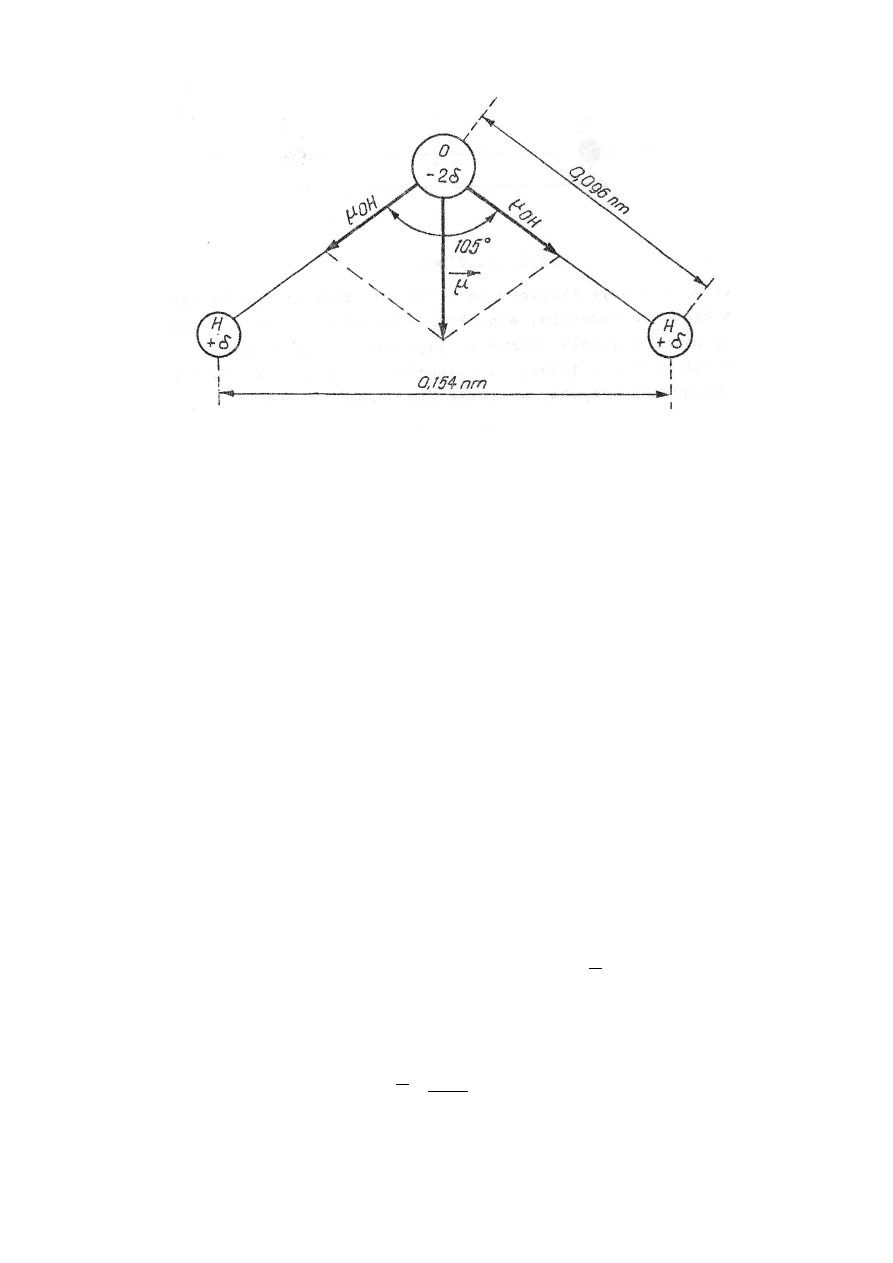
Rys.27.2. Struktura cząsteczki wody. Moment dipolowy cząsteczki jest sumą geometrycz-

ną momentów dipolowych poszczególnych par atomów O – H

Jak wynika z tabeli 27.1, cząsteczki niektórych dielektryków nie posiadają momentu dipolowego.
Nazywamy je niespolaryzowanymi. Aby zaobserwować zjawisko polaryzacji dielektryka należy
go wprowadzić w obręb pola elektrycznego (np. między okładki naładowanego kondensatora).
W ogólnym przypadku mogą wówczas zachodzić trzy mechanizmy indukowania (wywoływania)
momentu dipolowego w wybranej objętości dielektryka:
1. Jeżeli cząsteczka jest dipolem elektrycznym, wówczas w polu elektrycznym na jej biegun

dodatni działa siła kulombowska skierowana wzdłuż przechodzącej przez dany punkt linii sił
w stronę jej zwrotu, zaś na biegun ujemny – siła o zwrocie przeciwnym (rys.27.3a). Zatem na
dipol działa para sił, która stara się go ustawić tak, by skierował swą oś wzdłuż linii sił, tj.
w pozycji charakteryzującej się minimum energii potencjalnej. Zjawisko to nazywamy pola-
ryzacją skierowaną.
Jeżeli dielektryk o cząsteczkach spolaryzowanych nie przebywa w zewnętrznym polu elek-
trycznym, to w wyniku nieuporządkowanego ruch cieplnego cząsteczek wektory ich momen-
tów dipolowych wykazują chaotyczną orientację, w wyniku, której suma wektorowa momen-
tów dipolowych wszystkich cząsteczek zawartych w dowolnej objętości dielektryka równa się
zeru. Natomiast w obecności zewnętrznego pola elektrycznego dążą one do zajęcia położenia,
w którym wektory momentów dipolowych (

µ

r ) są zgodne z kierunkiem wektora natężenia

pola

E

r

.

Ruch cieplny cząsteczek (rosnący z temperaturą) przeszkadza w pełnym uporządkowaniu ich
położeń. W eksperymencie możemy, więc tylko mówić o średniej wartości rzutu momentu
dipolowego jednej cząsteczki na kierunek natężenia pola ( ) jako miary zaistaniałego
uporządkowania położeń cząsteczek.

m

Wyraźny obraz polaryzacji skierowanej i jej ujęcie ilościowe podaje teoria Deby’a. godnie
z nią słuszny jest związek:

T

k

E

m

3

2

µ

=

(27.2)

gdzie: k – stała Boltzmanna, T – temperatura w skali bezwzględnej, E – natężenie pola elek-
trycznego,

µ - moment dipolowy.

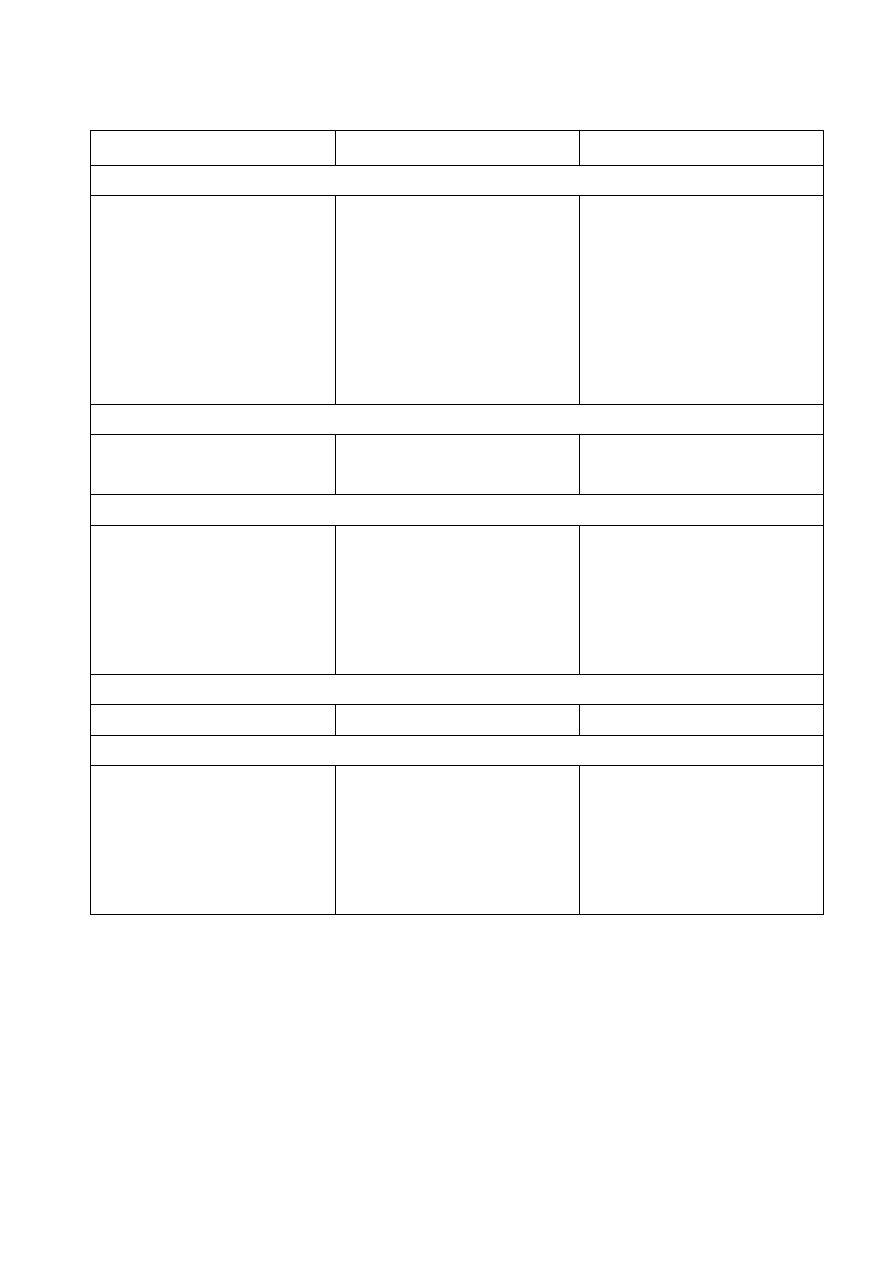
T a b e l a 27.1

Momenty dipolowe niektórych cząsteczek chemicznych

Wzór cząsteczki

µ

r [D]

Struktura

cząsteczki dwuatomowe

CO

HCl

HBr

NaJ

KCl

KJ

H

2

,O

2

,N

2

0,11
1,04
0,79

4,9
6,8
6,8

0

liniowa
liniowa
liniowa
liniowa
liniowa
liniowa
liniowa

cząsteczki trójatomowe

CO

2

,CS

2

,HgCl

2

,BeBr

2

H

2

O

0

1,87

liniowa

kątowa

cząsteczki czteroatomowe

NH

3

PH

3

AsH

3

BCl

3

, BF

3

, BBr

3

H

2

O

2

1,46
0,55
0,15

0

2,13

czworościenna
czworościenna
czworościenna

płaska

zwichrowana

cząsteczki pięcioatomowe

CH

4

, CCl

4

, SiH

4

, SiCl

4

0 tetraedryczna

cząsteczki bardziej złożone

CH

3

OH

C

2

H

5

OH i dalsze homologi

węglowodory

chlorobenzen

parachlorotoluen

1,69

1,6

0

1,55

1,9

2. Zewnętrzne pole elektryczne działające na atomy powoduje deformację ich powłok elektro-

nowych. Działanie pola elektrycznego powoduje deformację kształtu ujemnie naładowanej
powłoki elektronowej w ten sposób, że środek gęstości rozkładu ładunku ujemnego tej po-
włoki przesuwa się przeciwnie do zwrotu wektora natężenia zewnętrznego pola elektrycz-
nego. Towarzyszy temu przesunięcie jądra zgodnie ze zwrotem wektora natężenia pola.
Zjawisko to nazywamy polaryzacją elektronową ( rys.27.3.b).
Rozsunięcie ładunków przeciwnych znaków wytwarza w każdej cząsteczce dipol. Po usu-
nięciu pola zewnętrznego deformacja znika i cząsteczki tracą swoją biegunowość. Takie di-
pole istniejące tylko w zewnętrznym polu nazywamy indukowanymi. Są one wzbudzane
zawsze w kierunku linii sił zewnętrznego pola elektrycznego bez względu na temperaturę
dielektryka i związany z nią ruch cieplny.

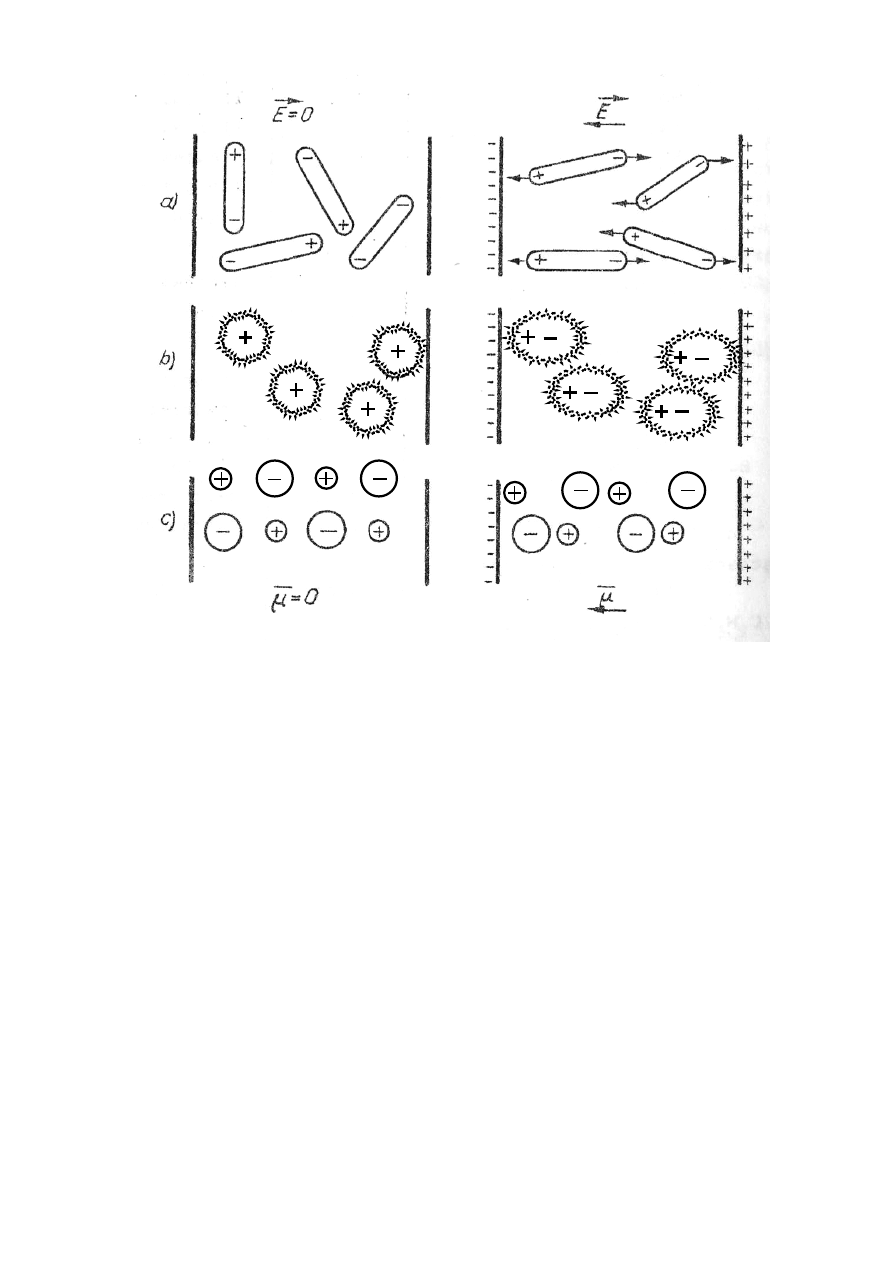
Rys.27.3. Zjawisko polaryzacji: a skierowanej – zaznaczono siły kulombowskie działające

na dipole, b) elektronowej, c) jonowej

3. Atomy lub grupy polarne cząsteczki pod wpływem zewnętrznego pola ulegają przesunię-

ciu lub obrotowi. Zjawisko to nazywamy polaryzacją jonową, np. w dielektrykach krysta-
licznych odznaczających się jonową siatką krystaliczną ( jak NaCl, CaCl

2

) wszystkie jony

dodatnie przesuwają się wzdłuż linii sił pola w stronę ich zwrotu, natomiast wszystkie jony
ujemne – w stronę przeciwną ( rys.27.3c ).

Na wielkość całkowitej polaryzacji ośrodka ma wpływ suma trzech omówionych procesów, przy
czym zjawisko drugie i trzecie występuje w cząsteczkach wszystkich substancji, natomiast pierw-
sze – tylko w substancjach polarnych, tj. takich, których cząsteczki są trwałymi dipolami elek-
trycznymi. Widzimy więc, że we wszystkich zjawiskach polaryzacji dielektryka pod wpływem
pola elektrycznego powstaje moment dipolowy P w kierunku linii sił pola (zwany wektorem po-
laryzacji

). Jest on proporcjonalny do natężenia pola E. Możemy więc zapisać

P

= N

α E

( 27.3 )

Współczynnik proporcjonalności

α nazywamy polaryzowalnością danej substancji, a N jest licz-

bą dipoli znajdujących się w jednostce objętości. Wektor polaryzacji jest równy sumie wektorowej
elektrycznych momentów dipolowych atomów (cząsteczek) zawartych w jednostce objętości.

Uwzględniając mechanizmy indukowania polaryzacji ośrodka całkowita polaryzowalność (

α)

substancji jest sumą trzech polaryzowalności: skierowanej (

α

sk

), jonowej (

α

j

) i elektronowej (

α

e

)

α = α

sk

+

α

j

+

α

e

( 27.4)

Równanie Clausiusa–Mosottiego określa związek pomiędzy polaryzowalnością i stałą dielek-
tryczną (

ε) substancji

α

N

π

3

4

ρ

M

2

ε

1

ε

A

=

+

−

(27.5)

gdzie: M – masa cząsteczkowa substancji,

ρ - gęstość substancji, N

A

- liczba Avogadra.

Jest ono bardzo ważne, gdyż jest związkiem mikroskopowej wielkości fizycznej (jaką jest

α) z

wielkością makroskopową (

ε). Wielkości fizyczne mikroskopowe opisujące mikroświat nie dają

się bezpośrednio zmierzyć. Równanie Clausiusa-Mosottiego pozwala na podstawie pomiarów
przenikalności dielektrycznej (

ε) wyznaczyć polaryzowalność substancji (α).

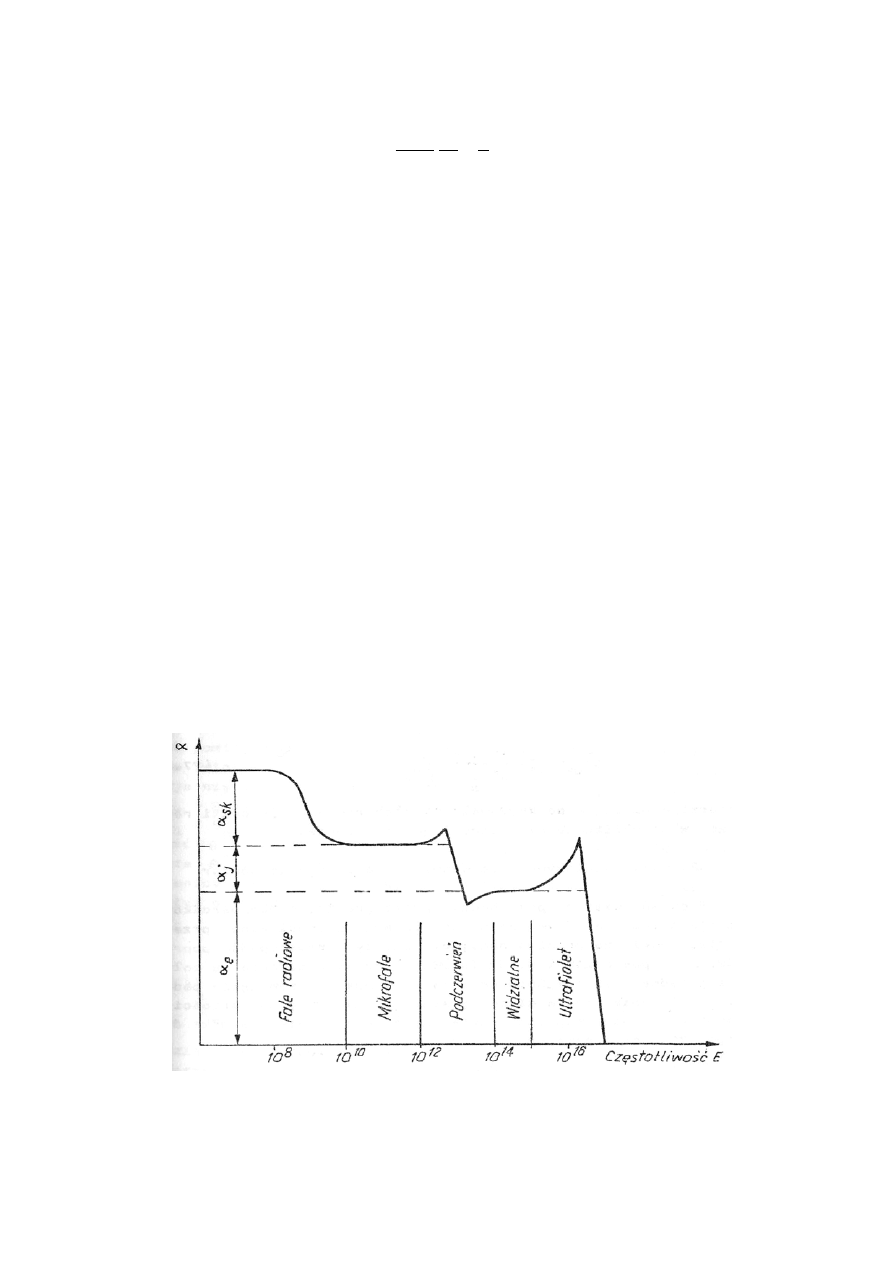
W ćwiczeniu wyznaczamy polaryzowalność elektronową wody. Jak więc wyodrębnić tę składową
od pozostałych składowych polaryzowalności? Metodą jest zastosowanie zmiennego pola elek-
trycznego i wykorzystanie zjawiska wygaszania polaryzacji skierowanej i jonowej przy dużych
częstotliwościach (rys.27.4).
Umieszczając cząsteczki dipolowe w polu elektrycznym o pewnej częstotliwości obserwujemy, że
dipole muszą mieć trochę czasu na zmianę orientacji w przestrzeni po zmianie kierunku pola na
przeciwny. Potrzebny jest czas, aby większość cząsteczek dokonała obrotu o 180

0

. Stopniowo

zwiększając częstotliwość pola elektrycznego dochodzimy w końcu do takiej częstotliwości, przy
której cząsteczki nie zdążą zareagować na zmiany pola zewnętrznego. W ten sposób przy często-
tliwościach mikrofalowych (10

10

– 10

12

Hz) zjawisko polaryzacji skierowanej zostanie wyelimi-

nowane. W tych warunkach cząsteczki badanej substancji będą mogły wykazywać tylko polary-
zowalność jonową i elektronową. W analogiczny sposób można wyeliminować z polaryzowalno-
ści całkowitej także udział składowej jonowej, gdyż ona również wiąże się z pewnym przesunię-
ciem mas. Przy optycznej częstotliwości pola elektrycznego w cząsteczkach badanej substancji
zachodzi już tylko polaryzacja elektronowa.
Z powyższych rozważań wynika następujący praktyczny wniosek. W celu wyznaczenia polary-
zowalności elektronowej cząsteczek wody należy umieścić je w polu elektrycznym o optycznej
częstotliwości ( 10

14

- 10

15

Hz). A więc wystarczy oświetlić je widzialną falą elektromagnetyczną,

gdyż ona zawiera w sobie wymagane zmienne pole elektryczne.

Rys 27.4. Zależność polaryzowalności od częstotliwości zmiennego pola elektrycznego.

Jeżeli ośrodek nie jest ferromagnetyczny (przenikalność magnetyczna

≅ 1) jego współczynnik

załamania (n) wyraża się wzorem wynikającym z teorii Maxwella:

ε

n

=

2

n

ε

=

A więc:

(27.6)

Stosując równanie Clausiusa-Mosottiego tylko dla polaryzowalności elektronowej i uwzględniając
wzór (27.6) otrzymujemy wzór Lorentza-Lorenza:

e

A

2

α

N

π

3

ρ

2

n

=

+

2

4

M

1

n

−

(27.7

)

Widzimy, że w bardzo prosty sposób, bo dokonując pomiaru współczynnika załamania substancji
(u nas wody) można wyznaczyć jej polaryzowalność elektronową jako jedyną niewiadomą w
równaniu 27.7..
Z przekształcenia powyższej zależności otrzymujemy:

A

2

e

N

ρ

2

n

4

α

+

=

π

2

M

1

n

3

−

(27.8)

Z teorii wynika, że polaryzowalność elektronowa cząsteczki równa się w przybliżeniu sześcianowi
jej promienia.

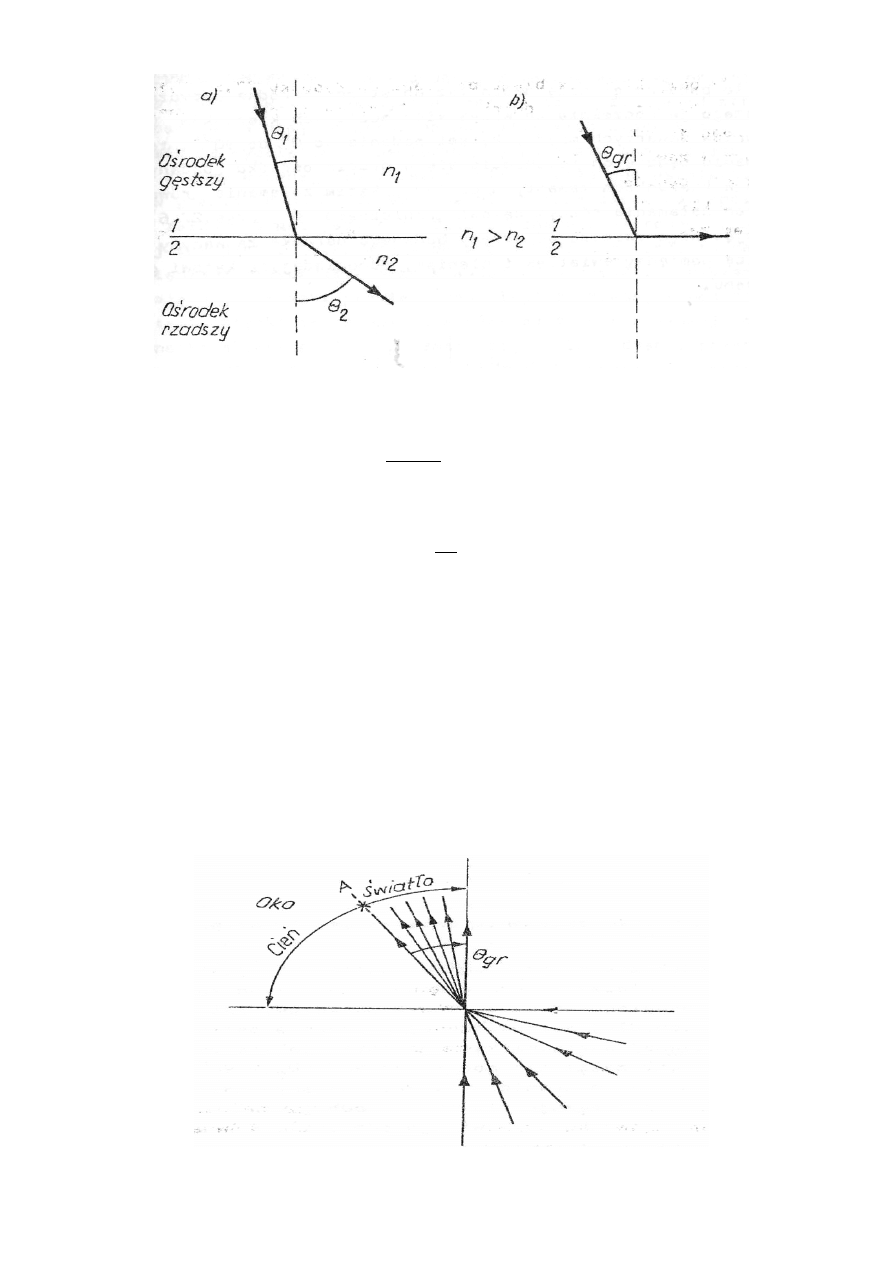
27.1.1. Współczynnik załamania światła i jego pomiar.

Promień świetlny przechodząc przez granicę dwóch ośrodków doznaje załamania. Prawo załama-
nia światła, sformułowane przez Fermiego mówi, że promień padający, odbity i prostopadła pro-
wadzona do powierzchni międzyfazowej w punkcie padania są położone w jednej płaszczyźnie
oraz że stosunek sinusów kątów padania i załamania jest wielkością stałą (niezależną od wartości
tych kątów) zwaną współczynnikiem załamania światła ośrodka drugiego względem pierwszego
(rys. 27.5a)

n

const

sin

2

Θ

sin

1

=

=

Θ

2

1

i

Θ

Θ

1

2

Θ

>

(

27.

9

)

gdzie:

– odpowiednio kąty padania i załamania, n – współczynnik załamania.

Jeżeli ośrodek, z którego biegnie światło (1) jest próżnią lub powietrzem, to mówimy o bez-
względnym współczynniku załamania światła dla drugiego ośrodka. W przypadku, gdy światło
załamuje się od prostopadłej poprowadzonej w punkcie padania (tzn.

Θ

), dla pewnej war-

tości kąta padania ( jak na rys. 27.5b)

Θ

1

o

90

2

=

Θ

gr

Θ

, otrzymamy załamanie pod kątem 90

0

(

).

Wartość

nazywamy kątem granicznym. Przy dalszym zwiększaniu kąta padania

światło

nie załamuje się już, lecz odbija całkowicie od granicy ośrodków ( zjawisko całkowitego we-
wnętrznego odbicia). Równanie (27.9) w tym przypadku przyjmuje postać

1

Θ

gr

Θ

=

optycznie

optycznie

Rys. 27.5. Zjawisko załamania światła (a) i kąt graniczny (b)

n

90

sin

sin

=

Θ

o

gr

(27.10)

czyli

2

1

1

2

n

n

,

n

n

n

sin

>

=

=

Θ

gr

(27.11)

gdzie n

1

, n

2

są bezwzględnymi współczynnikami załamania ośrodka pierwszego i drugiego.

Widać, zatem, że można wyznaczyć współczynnik załamania światła jakiegoś ciała mierząc war-
tość kąta granicznego

gr

Θ . Może być on łatwo zmierzony.

Odwróćmy kierunek biegu promieni na rysunku 27.5. Jeżeli światło pada na granicę dwóch faz od
strony ośrodka optycznie rzadszego jednocześnie ze wszystkich możliwych kierunków ( tzn. kie-
runków zawartych między kątami padania od 0

0

do 90

0

), to po załamaniu będzie on rozchodzić się

w drugim ośrodku (badanym) tylko w kierunkach zawartych pomiędzy kątem załamania równym
0

0

, a kątem załamania równym kątowi granicznemu

gr

Θ (rys.27.6). Obserwując, więc światło od

strony badanego ośrodka zauważymy ostrą granicę pomiędzy światłem i cieniem, odpowiadającą
kątowi granicznemu.

3 2

4

5

1

6

6

5

4

3

1

2

Rys.27.6. Kąt graniczny i zasada działania refraktometru Abbego

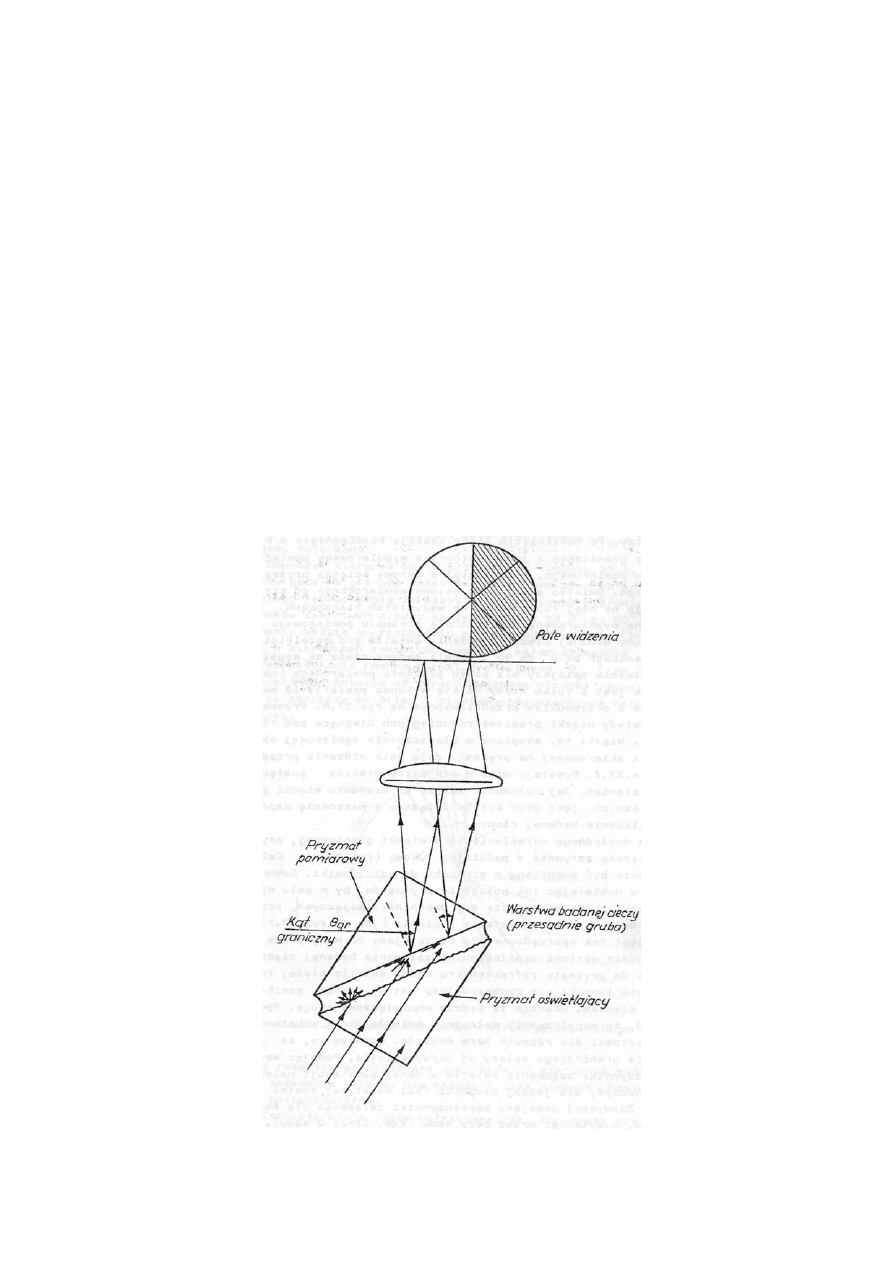
Na tej zasadzie są zbudowane przyrządy do mierzenia współczynników załamania światła dla cie-
czy i ciał stałych. Noszą one nazwę refraktometrów.
Istnieje wiele typów refraktometrów. Zapoznamy się z refraktometrem Abbego. Podstawową jego
częścią jest para pryzmatów (rys.27.7). Jeden nazywa się pryzmatem pomiarowym, a drugi oświe-
tlającym. Pomiędzy nie wprowadza się warstwę badanej cieczy. Warstewka cieczy graniczy z
jednej strony z wypolerowaną powierzchnią pryzmatu pomiarowego, a z drugiej z matową ścianką
pryzmatu oświetlającego. Światło padając na matową powierzchnię od strony szkła zostaje na niej
rozproszone we wszystkich kierunkach. Następnie to rozproszone światło pada na wypolerowaną
powierzchnię pryzmatu pomiarowego od strony badanej cieczy pod wszelkimi kątami w granicach
od 0

0

do 90

0

. Jeżeli badana ciecz ma współczynnik załamania mniejszy niż szkło pryzmatu pomia-

rowego, to mamy do czynienia z przypadkiem przedstawionym na rys.27.6. Pryzmat opuszczają
wiązki promieni równoległych biegnące pod różnymi kątami. Wiązki te są skupione w płaszczyź-
nie ogniskowej obiektywu lunetki (rys.27.7). Powstaje więc w nim ostra granica pomiędzy świa-
tłem a cieniem. Położenie tej granicy zależy od kierunku wiązki promieni granicznych, jest więc
ściśle związane z wartością współczynnika załamania badanej cieczy.
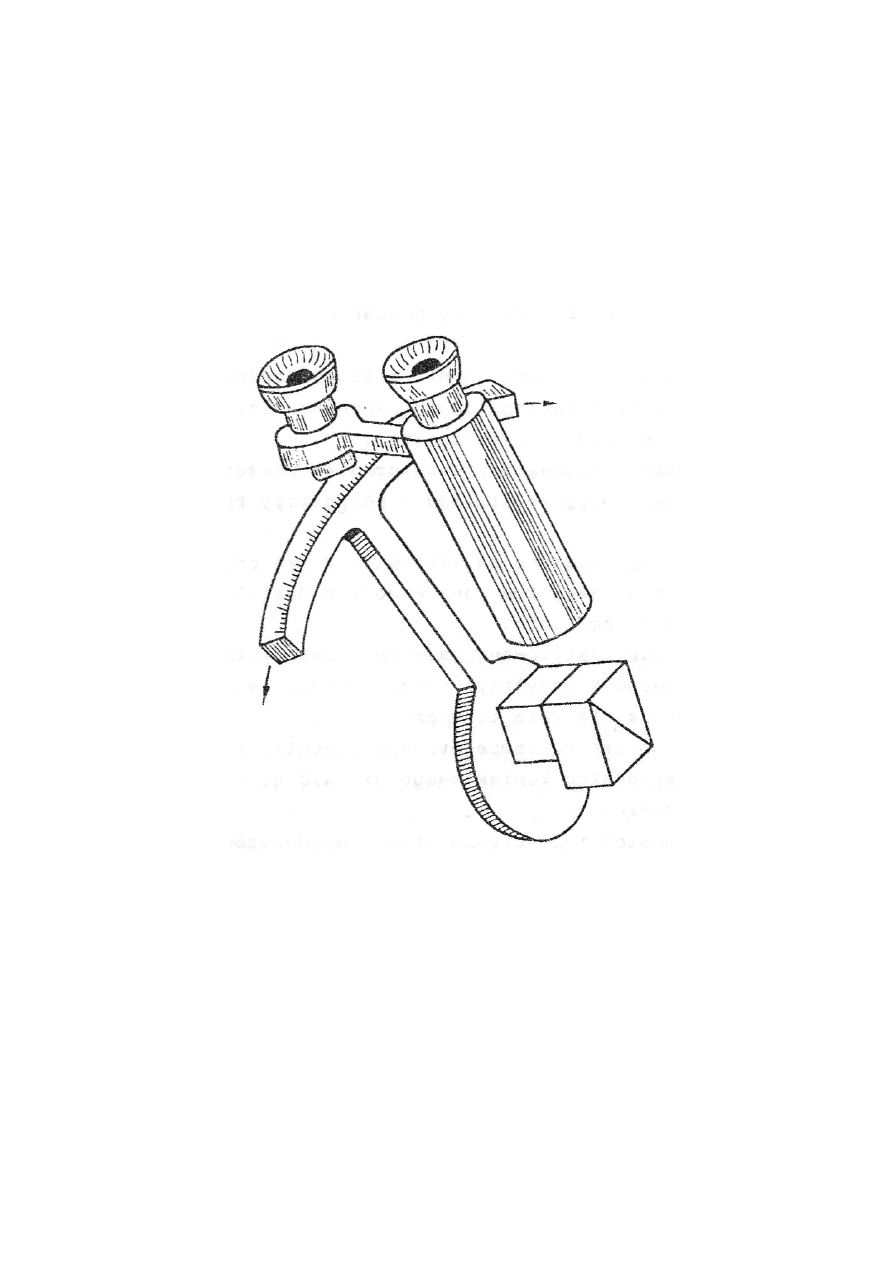
W celu dokładnego określenia kąta wiązki granicznej, pryzmaty są związane sztywnie z podziałką
łukową (rys.27.8). Cały ten układ może być pochylany w stosunku do osi lunetki. Dokonujemy
pomiaru dobierając tak położenie pryzmatów, by w polu widzenia lunetki punkt przecięcia się
dwóch nici przypadał dokładnie na granicy światła i cienia (jak na rys.27.7). Podziałka jest tak
sporządzona, że odczytujemy na niej przez lupę bezpośrednio wartość współczynnika załamania
badanej cieczy.

Rys. 27.7. Schemat refraktometru Abbego

Jeżeli do pryzmatu refraktometru wpada światło białe, to w polu widzenia lunetki nie zaobserwu-
jemy ostrej granicy pomiędzy światłem a cieniem. Granica ta będzie wtedy tęczową smugą. Po-
chodzi to stąd, że współczynnik załamania światła danej substancji ma różne wartości dla różnych
barw światła. Oznacza to, że i wartość kąta granicznego zależy od barwy światła. Podając wartość
współczynnika załamania światła w danej substancji należy zawsze zaznaczyć, dla jakiej długości
fali świetlnej został on zmierzony. Zazwyczaj podajemy współczynniki załamania dla światła żół-
tego, wysyłanego przez pary sodu (tzw. linia D sodu).
Refraktometr którym się posługujemy, jest zaopatrzony w tzw. urządzenie kompensujące, które
pozwala posługiwać się światłem białym do określenia współczynników załamania w świetle linii
D sodu.

Rys.27.8. Refraktometr Abbego

27.2. Opis układu pomiarowego

Układ pomiarowy stanowi refraktometr Abbego, którego układ termostatujący połączony jest
z układem pompującym ultratermostatu. Ponieważ w ćwiczeniu mierzymy zależności współczyn-
nika załamania wody od temperatury, więc metalowe oprawki pryzmatów muszą być termostato-
wane. Realizuje się to przepuszczając przez metalowe oprawki pryzmatów wodę termostatującą z
termostatu. Przy włączeniu do sieci zostaje uruchomiony silnik poruszający wewnątrz termostatu
mieszadełko, służące do wyrównania temperatury kąpieli, jednocześnie zostaje stworzona możli-
wość włączenia systemu podgrzewającego jego kąpiel. Do tego celu służy kontaktowy termometr
rtęciowy, zamocowany w otworze pokrywy. Podgrzewana woda tłoczona jest za pomocą pompki
poprzez węże do oprawki pryzmatów pomiarowych refraktometru.

U w a g a !

Temperatura wody w termostacie może się różnić od temperatury oprawki pryzmatów

- tę temperaturę mierzy oddzielny termometr.

Posługiwanie się termostatem jest opisane w ćwiczeniu 7 (pkt.7.2).

27.3. Przebieg pomiarów

1. Zaznajomić się z poszczególnymi częściami refraktometru (pryzmaty, lupa, podziałka współ-

czynnika załamania, lunetka, kompensator, zwierciadło oświetlające).

2. Zaznajomić się z budową i przeznaczeniem poszczególnych elementów termostatu (grzałki,

obwód chłodzący, termometr kontaktowy).

3. Ustawić przyrząd poziomo na statywie, zdjąć pryzmat oświetlający, przemyć go watą zmoczo-

ną w wodzie destylowanej i osuszyć bibułką do sączenia.

4. Wprowadzić wodę destylowaną na wypolerowaną płaszczyznę pryzmatu pomiarowego i przy-

łożyć pryzmat oświetlający. Podnieść refraktometr na statywie do oporu.

5. Odczytać z termometru temperaturę otoczenia. Kręcąc w lewo pokrętłem termometru kontak-

towego ustawić go poniżej temperatury otoczenia.

6. Włączyć termostat i po pięciu minutach odczytać temperaturę w komorze refraktometru Abbe-

go.

7. Dokonać pomiaru współczynnika załamania wody. W tym celu skierowujemy przyrząd do źró-

dła światła i nastawiamy zwierciadło oświetlające tak, by światło oświetlało pryzmaty od dołu.
Następnie za pomocą śruby znajdującej się po lewej stronie przyrządu zmieniamy pochylenie
pryzmatów aż do chwili, gdy w lunecie ukaże się granica, na ogół tęczowa, pomiędzy jasnym i
ciemnym polem. Teraz za pomocą śruby po prawej stronie przyrządu dobieramy takie położe-
nie pryzmatów kompensatora, by granica pomiędzy polami widzenia stała się ostra i bezbarw-
na. Sprowadzamy tę granicę do pokrycia się ze skrzyżowaniem nici pajęczych. Następnie za
pomocą lupy umieszczonej nad podziałką (najlepiej lewym okiem bez odrywania prawego od
lunetki) odczytujemy wartość współczynnika załamania z dokładnością do 4 miejsca dziesięt-
nego (ostatnie miejsce szacujemy). Czynność tę, jak w każdym pomiarze – powtarzamy wielo-
krotnie, nastawiając za każdym razem na nowo granicę światła i cienia w lunetce.

8. Ustawić termometr kontaktowy termostatu na 55

0

C i włączyć grzałkę.

9. Dokonać pomiaru współczynnika załamania wody co 5

0

C (tak jak w pkt.7), lecz jeden raz.

10. Po osiągnięciu temperatury 50

0

C wyłączyć grzałkę. Wskaźnik termometru kontaktowego

sprowadzić poniżej temperatury otoczenia. Odkręcić kran z wodą połączony z obwodem chło-
dzącym termostatu.

11. Wykonać pomiary współczynnika załamania wody w tych samych temperaturach, co w pkt.9.

Obniżając temperaturę od 50

0

C do temperatury pokojowej.

12. Oszacować graniczne błędy odczytu n (

∆n) oraz temperatury (∆T).

27.4. Opracowanie wyników pomiarów

1. Na podstawie wyników pomiarów wykreślić zależność n(T).
2. Korzystając ze wzoru (27.8) obliczyć polaryzowalność wody dla wybranych wartości

temperatury. Wartości gęstości wody w funkcji temperatury podane są w tablicy 5 na końcu
skryptu. Na podstawie tablicy, biorąc pod uwagę błąd wyznaczenia temperatury (

∆T),

oszacować graniczny błąd wyznaczenia gęstości wody (

∆ρ).

3. Korzystając z prawa przenoszenia błędów obliczyć względny błąd graniczny polaryzowalno-

ści

α

e

dla wybranej temperatury

ρ

∆ρ

)

1

(n

2)

(n

n

n

6

α

α

2

2

e

e

+

−

+

∆

⋅

=

∆

.

Obliczyć błąd graniczny bezwzględny

∆α

e

.

4. Dokonać oceny otrzymanych wyników. Czy polaryzowalność

α

e

zależy od temperatury?

27.5. Pytania kontrolne

1. Na czym polega zjawisko polaryzacji dielektrycznej?
2. Co nazywamy wektorem polaryzacji ośrodka?
3. Omówić mechanizm indukowania polaryzacji jonowej, elektronowej i skierowanej.
4. W jaki sposób można wyznaczyć polaryzowalność elektronową wody?
5. Omówić stosowaną metodę pomiaru współczynnika załamania n.

L i t e r a t u r a

[1] Basiński A., Bielowski A. i inni: Chemia fizyczna. PWN, Warszawa 1966.
[2] Kittel C.: Wstęp do fizyki ciała stałego. PWN, Warszawa 1974.
[3] Feynman R. P., Leighton R.S., Sunds M.: Feynmana wykłady z fizyki. PWN, Warszawa 1970.
[4] Chełkowski A.: Fizyka dielektryków. PWN, Warszawa 1972