Kujawsko-Pomorska Bydgoszcz, 27.03.2012

Szkoła Wyższa w Bydgoszczy

Wydział Techniczny

Kierunek Geodezja i Kartografia

Doświadczenie nr 2

Wyznaczenie współczynnika

załamania szkła i wody

Wykonał:

Adam Piasecki

Studia niestacjonarne

Rok II, grupa III

Geodezja i Kartografia

Część I WSTĘP TEORETYCZNY

Współczynnik załamania światła jest wielkością opisującą załamanie światła przy przejściu z jednego ośrodka do drugiego, a więc wielkość ta opisuje własności ośrodków.

Względny współczynnik załamania światła ośrodka drugiego względem pierwszego to stosunek sinusa kąta padania do sinusa kąta załamania jest wielkością równą stosunkowi szybkości światła w tych ośrodkach. Powyższe prawo zwane jest prawem Snelliusa i wiąże ze sobą kąt załamania z kątem padania, gdzie kątem załamania nazywamy kąt jaki tworzy promień załamany z normalna.

Promień padający, promień załamania i prosta normalna do powierzchni granicznej w punkcie przecięcia tej powierzchni leżą w jednej płaszczyźnie, a kąty spełniają zależność:

gdzie:

n₁ - współczynnik załamania w ośrodku 1

n₂ - współczynnik załamania w ośrodku 2

α - kąt padania (czyli kąt pomiędzy normalną do powierzchni padania, a kierunkiem wiązki padającej)

β - kąt załamania (czyli kąt pomiędzy normalną do powierzchni padania, a kierunkiem wiązki załamanej).

Względny współczynnik załamania ośrodka drugiego względem pierwszego jest równy stosunkowi bezwzględnych współczynników załamania tych dwóch ośrodków:

Bezwzględny współczynnik załamania światła określa się jako współczynnik załamania światła na granicy dowolnego ośrodka i próżni(v₁=c). Jest on związany z szybkością światła w tym ośrodku (v₂=v).

W związku z powyższymi informacjami prawo Snelliusa można zapisać za pomocą bezwzględnych współczynników załamania:

Współczynnik załamania zależy od długości fali, materiału i jego jakości wchodzącego w skład danego ośrodka. Współczynnik zależy również od gęstości, gdyż rośnie wraz z gęstością dla danego ośrodka, np. w atmosferze maleje wraz z wysokością. Zależność współczynnika załamania ośrodka od częstotliwości fali świetlnej nazywa się dyspersją. Skutkiem tego zjawiska jest załamanie się pod różnymi kątami wiązek światła o różnych barwach padających na granicę ośrodków.

Droga optyczna (L) to iloczyn drogi geometrycznej przebytej przez promień światła i bezwzględnych współczynnik załamania światła dla danego ośrodka. Droga biegu promieni świetlnych zależy od ośrodka, w którym biegnie promień. Mówi o tym zasada Fermata: promień biegnie od jednego punktu do drugiego po najkrótszej drodze optycznej, bowiem wówczas przebywa tą odległość w najkrótszym czasie. Okazuje się bowiem, że najkrótsza droga geometryczna nie jest wcale najszybsza. Drogę optyczną wyraża wzór:

l=n◦s

gdzie:

l - droga optyczna

S - rzeczywista droga przebyta przez światło (droga geometryczna),

n - bezwzględny współczynnik załamania światła ośrodka, w którym światło się rozchodzi.

Z definicji drogi optycznej wynika, że w próżni jest ona równa drodze geometrycznej. Często przyjmuje się w przybliżeniu, że podobnie jest w powietrzu, ze względu na to, że współczynnik załamania powietrza względem próżni jest bliski jedności.

Wyznaczenie wzoru roboczego:

Celem doświadczenia było wyznaczenie współczynnika załamania. W pierwszym etapie mierzono drogę optyczną identycznego dystansu (s) wypełnionego powietrzem oraz szkłem. Dokonano pięciu pomiarów w powietrzu. Następnie dokonano tego samego odcinka tak, aby promień lasera przechodził przez szkło.

W drugim etapie ustawiono dalmierz laserowy w takim miejscu, aby promień lasera przeszedł przez naczynie z wodą. Po pięciokrotnym pomierzeniu wielkości pomierzono ten sam odcinek przez pusty pojemnik pięć razy.

Wyznaczając współczynnik załamania światła dla szkła oraz wody na podstawie pomiarów drogi optycznej wyprowadzamy wzór roboczy. Wzorem wyjściowym jest wzór na drogę optyczną, który wyraża iloczyn współczynnika załamania oraz drogi geometrycznej.

W doświadczeniu dokonano pomiaru długości odcinka przy użyciu dalmierza laserowego w dwóch ośrodkach. Znając wzór na długość drogi optycznej otrzymujemy zależność:

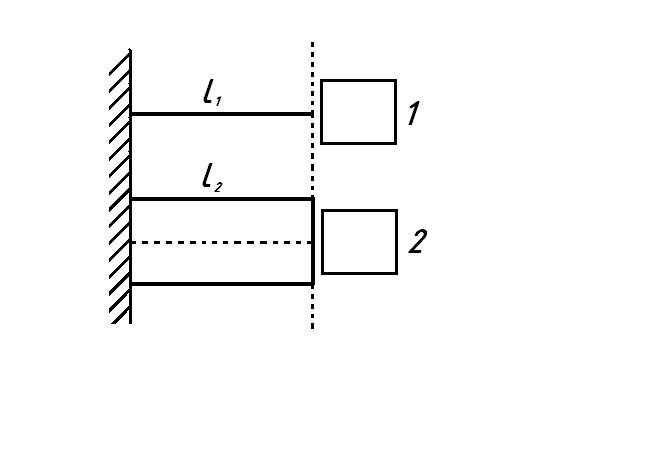
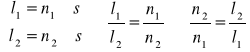
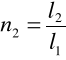
Wzór roboczy:

gdzie:

n₁ - bezwzględny współczynnik załamania w powietrzu

n₂ - bezwzględny współczynnik załamania dla wody

s - droga geometryczna (dystans mierzony np. linijką)

l₁ - droga optyczna przy pomiarze pierwszego ośrodka

l₂ - droga optyczna przy pomiarze drugiego ośrodka

Część II OPIS PRZEPROWADZONEGO DOŚWIADCZENIA, WYNIKI POMIARÓW, DOKŁADNOŚĆ UŻYTYCH PRZYRZĄDÓW

A) Wyznaczenie współczynnika załamania szkła:

Potrzebne przyrządy:

- Dalmierz LEICA DISTO^TM D2

- szklany walec

Opis przeprowadzonego doświadczenia dla wyznaczanie współczynnika załamania szkła:

1. Ustawić dalmierz w odległości odpowiadającej długości walca.

2. Dokonać pomiaru składającej się z 5 odczytów w jednej serii.

3. Przyłożyć szklany walec do ściany, a do walca dalmierz.

4. Dokonać pomiaru składającej się z 5 odczytów w jednej serii.

Tabela wyników pomiaru dla wyznaczanie współczynnika załamania szkła

Lp.	l1 [mm]	l2 [mm]
1	65	103
2	65	104
3	66	104
4	65	106
5	65	105

Pomiar drogi optycznej w powietrzu l₁

Pomiar drogi optycznej w szkle l₂

B) Wyznaczenie współczynnika załamania wody:

Potrzebne przyrządy:

- Dalmierz LEICA DISTO^TM D2

- rurka polarymetryczna

- woda

Opis przeprowadzonego doświadczenia:

1. Ustawić dalmierz w odległości odpowiadającej pustej rurki polarymetrycznej.

2. Dokonać pomiaru składającej się z 5 odczytów w jednej serii.

3. Napełnić rurkę polarymetryczną woda.

3. Przyłożyć rurkę polarymetryczną do ściany, a do rurki dalmierz.

4. Dokonać pomiaru składającej się z 5 odczytów w jednej serii.

Tabela wyników pomiaru

Lp.	l3 [mm]	l4 [mm]
1	162	218
2	158	218
3	163	217
4	162	218
5	163	218

Pomiar z użyciem pustej rurki polarymetrycznej l₃

Pomiar z użyciem wypełnionej wodą rurki polarymetrycznej l₄

Część III OBLICZENIE WYZNACZONEJ WIELKOŚCI

Obliczenie wyznaczonej wielkości:

A) Wyznaczanie współczynnika załamania dla szklanego walca

Lp.	l1 [mm]	l2 [mm]
1	65	103
2	65	104
3	66	104
4	65	106
5	65	105
śr.	65,2	104,4

Dokładność przyrządu: ΔX=1mm; λ=660nm

n1=1; t=22°C,

n_szkl.walca=104,4/65,2=1,6012269

B) Wyznaczanie współczynnika załamania dla wody

Lp.	l3 [mm]	l4 [mm]
1	162	218
2	158	218
3	163	217
4	162	218
5	163	218
śr.	161,6	217,8

Dokładność przyrządu: ΔX=1mm; λ=660nm

n1=1; t=22°C,

n_wody=217,8/161,6=1,3477722

Część IV SZACOWANIE NIEPEWNOŚCI POMIARU

1. dla szklanego walca

Lp.	l1 [mm]	l2 [mm]	lśr1-l1	lśr2-l2	(lśr1-l1)^2	(lśr2-l2)^2
1	65	103	0,2	1,4	0,04	1,96
2	65	104	0,2	0,4	0,04	0,16
3	66	104	-0,8	0,4	0,64	0,16
4	65	106	0,2	-1,6	0,04	2,56
5	65	105	0,2	-0,6	0,04	0,36
Śr	65,2	104,4	∑=0,0	∑=0,0	∑=0,80	∑=5,20

Obliczenie niepewności pomiarowej typu A i typu B

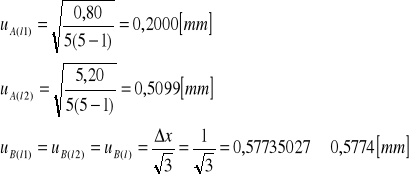
Obliczenie niepewności pomiarowej

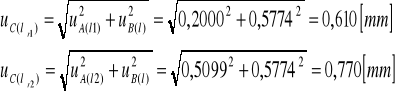
Obliczenie niepewności pomiarowej

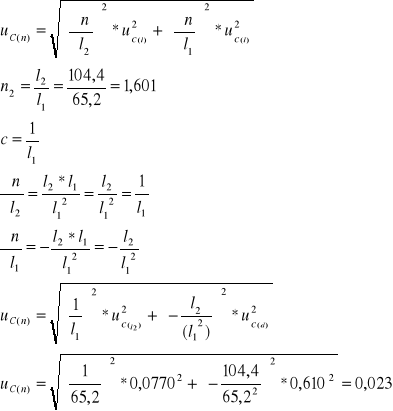
2. dla rurki z wodą

Lp.	l3 [mm]	l4 [mm]	lśr1-l1	lśr2-l2	(lśr1-l1)^2	(lśr2-l2)^2
1	162	218	-0,4	-0,2	0,16	0,04
2	158	218	3,6	-0,2	12,96	0,04
3	163	217	-1,4	0,8	1,96	0,64
4	162	218	-0,4	-0,2	0,16	0,04
5	163	218	-1,4	-0,2	1,96	0,04
Śr	161,6	217,8	∑=0,0	∑=0,0	∑=17,20	∑=0,80

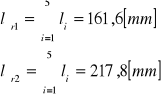
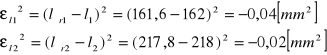
Obliczenie niepewności pomiarowej typu A i typu B

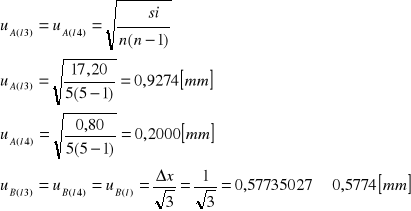
Obliczenie niepewności pomiarowej

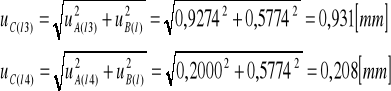
Obliczenie niepewności pomiarowej

Część V ZAPIS KOŃCOWY I WNIOSKI

Współczynnik załamania dla szklanego walca wyniósł 1,601
0,046, a dla rurki wypełnionej wodą 1,348
0,016.

Drogi optyczne są różne, ponieważ różne są współczynniki załamania.

7

c - prędkość światła w próżni

v - prędkość światła w ośrodku

n - bezwzględny współczynnik załamania

---