Politechnika Śląska w Gliwicach
Wydz. Mechaniczny-Technologiczny
Kierunek :Mechanika i budowa maszyn
SPRAWOZDANIE
Temat: Wyznaczanie współczynnika załamania szkła dla pryzmatu.
Wyznaczanie stałej siatki dyfrakcyjnej.
Pomiar długości fali światła laserowego.
Solich Jacek
Siwiec Jakub
Pańczak Mariusz
Grupa II
Sekcja III
WPROWADZENIE
Pryzmat.
Pryzmat jest przezroczystą bryłą ograniczoną dwiema przecinającymi się płaszczyznami. Prosta K, będąca śladem ich i przecięcia nazywamy krawędzią łamiącą, a kąt zawarty między płaszczyznami - kątem łamiącym. Płaszczyzna prostopadła do krawędzi łamiącej nazywa się przecięciem głównym.
Bezwzględny współczynnik załamania światła przez ośrodek określa stosunek prędkości światła w próżni c do prędkości fazowej światła w tym ośrodku v:
n=c/v
Natomiast względny współczynnik załamania światła na granicy dwóch ośrodków określa stosunek prędkości światła w ośrodku II do prędkości światła w ośrodku I:
n1,2=v2/v1=n1/n2
Prawo Snelliusa - prawo załamania
sin/sin=v1/v2=n
gdzie:
=ϕ/2 =(δmin+ϕ)/2
Ponieważ współczynnik załamania światła zależy od długości fali, więc dla promieni o różnych długościach fali uzyskamy różne kąty odchylenia dla tego samego kąta padania. Jest to wykorzystywane w spektometrii do rozszczepiania światła.
Zastosowanie pryzmatów:
Dwa pryzmaty o kącie łamiącym 90o dają peryskop stosowany w łodziach podwodnych, artylerii itp.(rys.a)
Pryzmaty PORRO odwracają bieg prmieni i są wykorzystywane w lornetkach (rys.b).
Odwrócenie wiązki bez zmiany kierunku biegu promieni realizują pryzmaty DOVEGO (rys.c)
Dyfrakcja światła.
Dyfrakcja (ugięcie) jest zespołem zjawisk związanych z odkształceniem fali podczas jej rozchodzenia się w ośrodkach niejednorodnych. Natomiast dla fali płaskiej dyfrakcją jest odkształcenie w ośrodku jednorodnym. Odkształcenie to charakteryzuje się powstawaniem nowych kierunków rozchodzenia się fal, nieprzewidzianych przez założenia geometrii optycznej, np. w przypadku przechodzenia fali przez szczelinę powinniśmy zaobserwować cień, jednakże na skutek dyfrakcji widać (pod pewnymi kątami) smugi jaśniejsze i ciemniejsze. Dyfrakcja występuje dla każdego rodzaju fali, ale wraz ze wzrostem częstotliwości fal można zobaczyć, że zjawisko dyfrakcji jest coraz słabsze.
Dyfrakcja została po raz pierwszy zauważona przez włoskiego uczonego Grimeldiego, ale dopiero Young wyjaśnił to zjawisko. Uczony ten do zasady Huygensa dodał założenie, iż wzdłuż czoła fali zachodzi poprzeczne przekazywanie amplitudy drgań. Wyjaśnia to obraz 10 rzędów nakładających się na siebie barwnych prążków powstałych przy przepuszczeniu np. światła lampy łukowej poprzez szczelinę. Ponadto według Younga powstawanie fal ugiętych ma znaczenie lokalne oraz zachodzi w okolicy granicy cienia za krawędzią przesłony lub w obszarze oświetlonym.
Siatka dyfrakcyjna.
Dyfrakcję można podzielić zależnie od odległości szczeliny od źródła lub szczeliny od ekranu. Jeśli jedna z tych odległości jest skończona to wtedy jest to tzw. dyfrakcja Fresnela. Natomiast jeśli obie odległości są bliskie nieskończoności to jest to tzw. dyfrakcja Fraunhofera. Efekty tej dyfrakcji można zaobserwować jedynie przy użyciu soczewki skupiającej ustawionej w odległości ogniskowej od ekranu, a to dlatego, że na szczelinę światło pada równolegle. Pierwszą siatkę dyfrakcyjną zbudował Fraunhofer w 1823r. Była ona zbudowana z drutów mosiężnych o średnicy 50 m naciągniętych na 2 śruby o skoku gwintu 150 m. Miała ona na 1 mm 7 drutów. Natomiast współczesne siatki dyfrakcyjne są wykonywane na kliszach fotograficznych z zastosowaniem techniki laserowej.
Niech na siatkę dyfrakcyjną pada prostopadle fala płaska o długości . Szerokość szczeliny wynosi a , a ich wzajemna odległość b.
Ugięte fale, jako spójne, interferują dając w pewnych kierunkach wzmocnienie natężenia, w innych zaś - osłabienie.
Wzmocnienie wystąpi, gdy różnica dróg optycznych jest wielokrotnością długości fali:
(a+b)·sin k·
Wielkość: d = a + b nazywa się stałą siatki dyfrakcyjnej, a k - rzędem prążka dyfrakcyjnego czyli:
d·sin = k·
Dla światła monochromatycznego obraz dyfrakcji składa się z szeregu jasnych prążków rozłożonych symetrycznie po obu stronach prążka zerowego, leżącego na przedłużeniu wiązki padającego światła. Zaś dla światła nie-monochromatycznego obrazem są prążki barwne, nakładające się częściowo w miarę wzrostu rzędu k.
Siatki dyfrakcyjne stosuje się w spektrografach do pomiaru długości fal. Miarą jakości siatki jest tzw. zdolność rozszczepiająca:
gdzie d jest najmniejszym przedziałem różnicy długości fali dającym się rozróżnić w k - tym prążku.
Światło laserowe.
Z elektrodynamiki kwantowej wiadomo, że naładowane cząstki emitują lub pochłaniają pojedyncze fotony. Np. elektron emituje foton przy przejściu ze stanu energetycznego wyższego na niższy. Zjawisko to nazywa się emisją spontaniczną. Jeśli natomiast substancję podda się promieniowaniu to elektrony tej substancji przejdą na wyższy poziom energetyczny. To zjawisko nazywa się absorpcją lub inaczej promieniowaniem optycznym. Zarówno emisji, jak i absorpcji towarzyszy tzw. promieniowanie wymuszone. Ma ono identyczne cechy jak absorpcja. Emitowane fotony mają tą samą energię, co fotony wymuszające i razem zwiększają amplitudę bez zmiany kierunku rozchodzenia, fazy oraz polaryzacji.
Emisję wymuszoną stosuje się w laserach oraz maserach. Trzeba tylko zwiększyć prawdopodobieństwo zaistnienia procesów emisji wymuszonej kosztem emisji spontanicznej oraz absorpcji oraz wytworzyć warunki do po-wstania drgań samowzbudnych. Do układu wprowadza się silne sprzężenie zwrotne, dzięki czemu część wypromieniowanej energii powraca i powoduje następne akty promieniowania wymuszonego.
Najpopularniejszymi laserami są lasery impulsowe, zbudowane na ciele stałym, lasery gazowe i lasery półprzewodnikowe.
Laser impulsowy składa się z substancji czynnej (Al2O3 z dodatkami Cr2O3-rubin, CaF2 , CaWO4 , YAG lub szkło optyczne) w postaci pręta z polerowanymi optycznie powierzchniami czołowymi, które spełniają rolę wkładu rezonatorów optycznych. Pręt ten znajduje się wewnątrz lampy błyskowej zasilanej z baterii kondensatorów. Podczas jednego aktu emitowana jest energia rzędu 100 J, co przy akcji 1 ms daje moc do kilkudziesięciu kW. W laserze o modulowanej dobroci rezonatora można otrzymać impulsy o mocy GW i czasie rzędu ns.
W laserze półprzewodnikowym głównym elementem czynnym jest dioda półprzewodnikowa z arsenku galu, arsenku indu lub fosforku indu. Rolę rezonatora optycznego pełnią ścianki zewnętrzne prostopadłe do złącza P-N. Jedna z tych ścianek pokryta jest dielektrykiem i całkowicie odbija światło. A przez drugą ściankę częściowo przepuszczalną wydostaje się promieniowanie laserowe na zewnątrz. Laser ten charakteryzuje się małym rozmiarem, dużą sprawnością (duża moc na jednostkę objętości) i prostotą konstrukcji.
Laser gazowy składa się z rury kwarcowej z gazem lub mieszaniną gazów pod obniżonym ciśnieniem oraz z pary płaskich zwierciadeł o nierówno-miernych powierzchniach porównywalnych z długością fali. Źródłem energii wzbudzenia atomów lub jonów może być generator wysokiej częstotliwości, generator mikrosekundowy, źródło prądu stałego lub generator ultradźwiękowy. W laserze helowoneonowym absorpcja polega na wzbudzaniu atomów neonu w efekcie zderzeń z elektronami lub na wymianie energii pomiędzy wzbudzonymi atomami helu i niewzbudzonymi atomami neonu. Następuje wtedy stan inwersji obsadzeń poziomów energetycznych, więc atomy neonu w wyniku emisji wymuszonej przechodzą w niższe stany energetyczne. Oprócz światła czerwonego o długości 632.8 nm można otrzymać promieniowanie podczerwone o długości fali 1150 nm i 3390 nm.
Wyznaczanie stałej siatki dyfrakcyjnej - opracowanie wyników pomiarów.
Obliczamy średnią arytmetyczną wartość dla rzędu n = 1 (na lewo i prawo):
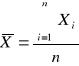
- wartość poprawna
1l = 6°34'
1p = 6°49'
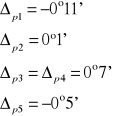
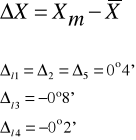
Obliczamy błąd bezwzględny:
Obliczamy błąd średni kwadratowy:
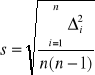
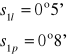
A więc można zapisać:
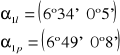
Obliczamy średnią arytmetyczną wartość dla rzędu n = 2 (na lewo i prawo):
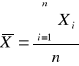
- wartość poprawna
2l = 13°16'
2p = 13°29'
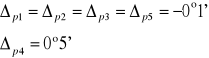
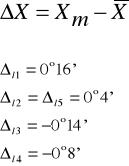
Obliczamy błąd bezwzględny:
Obliczamy błąd średni kwadratowy:
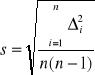
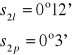
A więc można zapisać:
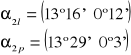
Obliczamy średnią arytmetyczną wartość dla rzędu n = 3 (na lewo i prawo):
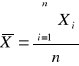
- wartość poprawna
2l = 20°12'
2p = 20°23'
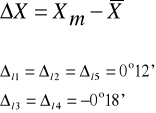
Obliczamy błąd bezwzględny:
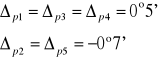
Obliczamy błąd średni kwadratowy:
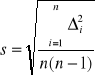
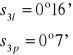
A więc można zapisać:
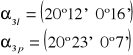
Zestawiając otrzymane wyniki w tabelce:
n = 1 |
n = 2 |
n = 3 |
|||
1l |
1p |
2l |
2p |
3l |
3p |
|
|
|
|
|
|
Obliczamy średnie wartości kątów ugięcia dla poszczególnych rzędów:
![]()
![]()
dla n = 1:
![]()
dla n = 2:
![]()
dla n = 3:
korzystając z metody pochodnej logarytmicznej wyznaczamy błąd bezwzględny:
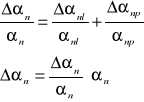
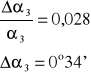
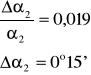
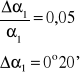
A więc średnią wartość kąta ugięcia można zapisać w postaci:
dla n = 1:
![]()
dla n = 2:
![]()
dla n = 3:
![]()
Obliczamy stałą siatki dyfrakcyjnej korzystając z obliczonych średnich wartości kątów ugięcia dla poszczególnych rzędów:
![]()
λ = 589,3 μm.
A następnie metodą pochodnej logarytmicznej obliczamy błąd bezwzględny:
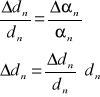
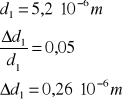
dla n = 1 :
a więc po odpowiednim zaokrągleniu wyznaczona stała siatki dyfrakcyjnej dla n = 1 wynosi:
![]()
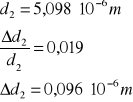
dla n = 2 :
![]()
a więc po odpowiednim zaokrągleniu wyznaczona stała siatki dyfrakcyjnej dla n = 2 wynosi:
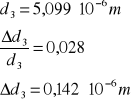
dla n = 3 :
![]()
a więc po odpowiednim zaokrągleniu wyznaczona stała siatki dyfrakcyjnej dla n = 3 wynosi:

Zestawiając otrzymane wyniki :
obliczamy średnią ważoną wartość stałej siatki dyfrakcyjnej:
wagę obliczmy ze wzoru:
Xi |
Xi |
Wi |
5.2·10-6 |
0.3·10-6 |
2,22 |
5.1·10-6 |
0.1·10-6 |
20,00 |
5.1·10-6 |
0.2·10-6 |
5,00 |
Średnia ważona:
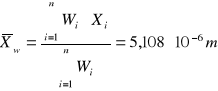
Błąd max. średniej ważonej:
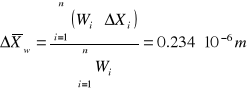
A więc ostatecznie średnia ważona wartość stałej siatki dyfrakcyjnej (po odpowiednim zaokrągleniu) wynosi:
![]()
Pomiar długości fali światła laserowego - opracowanie wyników pomiarów.
Tabela pomiarowa.
n |
x [mm] |
|
|
lewo |
prawo |
1 |
32,5 |
32 |
2 |
67 |
65 |
3 |
106 |
103 |
d = (5,1 ± 0,3)·10-6 m - stała siatki dyfrakcyjnej
l = 24 cm = 0,24 m - odległość siatki od ekranu
Obliczamy średnią odległość jasnych prążków dyfrakcyjnych od prążka zerowego dla poszczególnych rzędów:
![]()
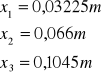
długość fali światła laserowego:
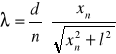
a następnie korzystając z metody pochodnej logarytmicznej obliczamy błąd bezwzględny wyznaczonej długości fali światła laserowego:
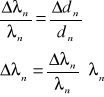
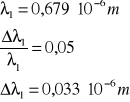
dla n = 1:
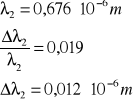
dla n = 2:
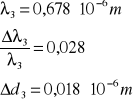
dla n = 3:

A więc wyznaczona długość fali światła laserowego (po odpowiednich zaokrągleniach) wynosi:
Obliczamy średnią wartość długości fali światła laserowego:
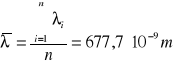
- wartość poprawna
Błąd bezwzględny:
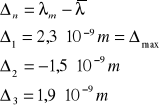
A więc ostatecznie wyznaczona długość fali światła laserowego lasera helowo-neonowego wynosi:
= (677,6 ± 2,3) nm
Wyznaczanie współczynnika załamania szkła dla pryzmatu - opracowanie wyników pomiarów.
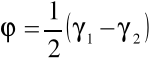
Obliczmy wartość kąta łamiącego pryzmatu wg wzoru:
Tabela pomiarowa 1
L.p. |
γ2 |
γ2 |
1 |
218,5 |
129 |
2 |
225,5 |
135,5 |
3 |
223,5 |
134 |
4 |
225,5 |
136 |
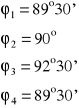
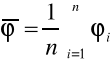
Obliczamy średnią wartość kąta łamiącego:
![]()
Obliczamy błąd średni kwadratowy wyznaczenia kąta łamiącego wg wzoru:
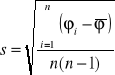
![]()
Ostatecznie wartość kąta łamiącego pryzmatu (po odpowiednich zaokrągleniach) wynosi:
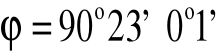
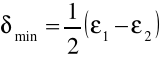
Obliczamy kąt minimalnego odchylenia stosując wzór:
Kąt zerowy = 180o 20'
L.p. |
1 |
2 |
1 |
210o |
146o30' |
2 |
213o |
149o30' |
3 |
222o30' |
159o |
4 |
211o30' |
148o |
5 |
209o |
145o |
6 |
208o |
144o30' |
7 |
221o30' |
158o |
8 |
209o30' |
146o30' |
9 |
206o30' |
143o |

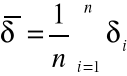
Obliczamy średnią wartość kąt minimalnego odchylenia:
![]()
Obliczamy błąd średni kwadratowy wyznaczenia kąta minimalnego odchylenia wg wzoru:
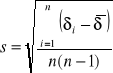
![]()
Ostatecznie wartość kąta minimalnego odchylenia (po odpowiednich zaokrągleniach) wynosi:
![]()
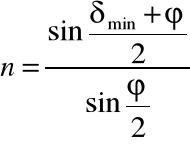
Obliczamy współczynnik załamania światła dla pryzmatu stosując wzór:
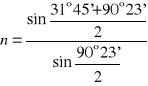
![]()
PODSUMOWANIE!!!
Stała siatki dyfrakcyjnej:
d = (5,1 ± 0,3).10-6 m = (5,1 ± 0,3) m
Długość fali światła laserowego:
= (677,6 ± 2,3) nm
Współczynnik załamania szkła w pryzmacie
n=1,23
17
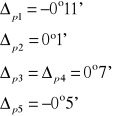
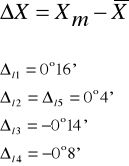
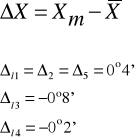
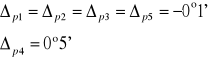
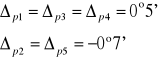
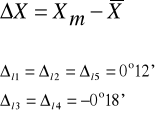
![]()
![]()
![]()
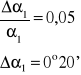
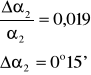
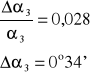
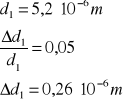
![]()
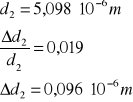
![]()
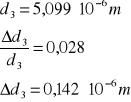
![]()
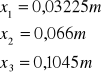

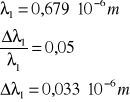
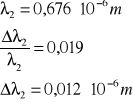
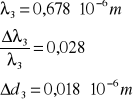

![]()
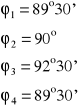
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
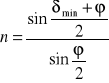
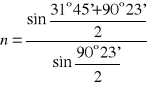
![]()
Wyszukiwarka
Podobne podstrony:
Wyznaczanie wspolczynnika zalamania szkla dla pryzmatu2
FIZYKA LABORATORIUM SPRAWOZDANIE Wyznaczanie współczynnika załamania szkła dla pryzmatu wers
Współczynnik załamania szkła, Ć 73B moje, Wyznacznie współczynnika załamania szkła metodą kąta najmn
76 WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA SZKŁA ZA POMOCĄ SPEKTROMETRU
,Laboratorium podstaw fizyki, Wyznaczanie współczynnika załamania szkła soczewki względem powietrza
Współczynnik załamania szkła, ĆW 73, WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA SZKŁA METODĄ KĄTA NAJMNIEJS
Współczynnik załamania szkła, ĆW 73, WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA SZKŁA METODĄ KĄTA NAJMNIEJS
FIZYKA LABORATORIUM SPRAWOZDANIE Wyznaczanie współczynnika załamania szkła
Doświadczenie nr 2 Wyznaczenie współczynnika załamania szkła i wody, Studia, Geodezja, III SEMESTR,
Współczynnik załamania szkła, Ć 73BN, Wyznacznie współczynnika załamania szkła metodą kąta najmniejs
76 - WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA SZKŁA ZA POMOCĄ SPEKTROMETRU, Materiały na studia, Fizyka
Wyznaczanie współczynnika załamania światła dla cieczy za pomocą refrakto metru?bego
76 - WYZNACZANIE WSPÓŁCZYNNIKA ZAŁAMANIA SZKŁA ZA POMOCĄ SPEKTROMETRU.x
Wyznaczanie współczynnika załamania światła metodą pryzmatu
308 Wyznaczanie współczynnika załamania światła dla cieczy za pomocą refraktometru Abbego
Wyznaczanie wspolczynnika zalamania swiatla w powietrzu, fff, dużo
Wyznaczanie współczynnika załamania światła metodą najmniejszego odchylenia w pryzmacie sprawkox
więcej podobnych podstron