Tablice

Tablice

Tablice

Tablice

Tablice

Tablice

K n

h

K n

h

Tablice

Tablice

K n

h

K n

h

Karnaugh

Karnaugh

Karnaugh

Karnaugh

6 marca 2011

Tablice Karnaugh

2

Tablice

Tablice Karnaugh

Karnaugh

Tablice

Tablice Karnaugh

Karnaugh

Tablice Karnaugh są graficzną reprezentacją tablic prawdy.

Tablice Karnaugh są graficzną reprezentacją tablic prawdy.

Każda kratka reprezentuje jeden minterm

Każda kratka reprezentuje jeden minterm

00

11

00

00

00

FF

xx

00

xx

11

xx

22

10

10

11

11

01

01

00

00

xx

22

xx

11

xx

00

00

11

00

00

00

11

11

11

00

00

22

00

00

11

00

m

m

00

m

m

11

00

44

11

66

00

22

11

00

00

xx

00

22

00

00

11

00

44

00

00

00

11

33

00

11

11

00

m

m

22

m

m

33

m

m

11

55

11

77

00

33

11

11

11

55

11

11

00

11

66

11

00

11

11

44

00

00

00

11

m

m

44

m

m

55

m

m

66

h

h

6 marca 2011

Tablice Karnaugh

3

77

11

11

11

11

m

m

66

m

m

77

Karnaugh Map

Karnaugh Map

Tablice

Tablice Karnaugh

Karnaugh

Tablice

Tablice Karnaugh

Karnaugh

Każde dwa sąsiednie pola różnią się między sobą tylko

Każde dwa sąsiednie pola różnią się między sobą tylko

jednym bitem. Dotyczy to również pól skrajnych

jednym bitem. Dotyczy to również pól skrajnych

(ostatnie pole

(ostatnie pole

j

ym

m. D y y

w

p

j y

j

ym

m. D y y

w

p

j y

(

p

(

p

różni się tylko jednym bitem od pierwszego pola w szeregu).

różni się tylko jednym bitem od pierwszego pola w szeregu).

10

10

11

11

01

01

00

00

xx

22

xx

11

00

44

11

66

00

22

11

00

00

10

10

11

11

01

01

00

00

22 11

xx

00

11

55

11

77

00

33

11

11

11

00

44

11

66

00

22

11

00

00

6 marca 2011

Tablice Karnaugh

4

55

77

33

11

Tablice

Tablice Karnaugh

Karnaugh

Tablice

Tablice Karnaugh

Karnaugh

Suma dwóch sąsiednich mintermów o tej samej wartości

Suma dwóch sąsiednich mintermów o tej samej wartości

logicznej może być uproszczona do jednego iloczynu

logicznej może być uproszczona do jednego iloczynu

xx

22

xx

11

logicznego, w którym wyeliminowana zostaje jedna

logicznego, w którym wyeliminowana zostaje jedna

zmienna.

zmienna.

00

44

11

66

00

22

11

00

00

10

10

11

11

01

01

00

00

xx

22

xx

11

xx

00

11

55

11

77

00

33

11

11

11

00

44

11

66

00

22

11

00

00

Biorąc mintermy z pierwszej kolumny otrzymamy zależność:

Biorąc mintermy z pierwszej kolumny otrzymamy zależność:

xx

22

’x

’x

11

’x

’x

00

’ +

’ + xx

22

’x

’x

11

’x

’x

00

== xx

22

’x

’x

11

’(x

’(x

00

’ +

’ + xx

00

) = x

) = x

22

’x

’x

11

’’

6 marca 2011

Tablice Karnaugh

5

22 11 00

22 11 00

22 11

((

00

00

))

22 11

Upraszczając wyrażenie można wyeliminować zmienną x

Upraszczając wyrażenie można wyeliminować zmienną x

00

..

Tablice

Tablice Karnaugh

Karnaugh

Tablice

Tablice Karnaugh

Karnaugh

Aby uprościć funkcję logiczną wykorzystując tablice Karnaugh,

Aby uprościć funkcję logiczną wykorzystując tablice Karnaugh,

należy pogrupować sąsiednie kratki zawierające wartości

należy pogrupować sąsiednie kratki zawierające wartości

logiczne 1

logiczne 1

10

10

11

11

01

01

00

00

xx

22

xx

11

logiczne 1.

logiczne 1.

Zadajemy sobie pytanie: Kiedy funkcja logiczna ma wartość 1?

Zadajemy sobie pytanie: Kiedy funkcja logiczna ma wartość 1?

00

11

00

11

00

10

10

11

11

01

01

00

00

xx

00

11

55

11

77

00

33

11

11

11

00

44

11

66

00

22

11

00

00

xx

22

xx

00

55

77

33

11

xx

22

’x

’x

11

’’

xx

22

xx

11

xx

22

xx

00

6 marca 2011

Tablice Karnaugh

6

22 11

22 11

F = x

F = x

11

’x

’x

22

’ + x

’ + x

11

xx

22

+ x

+ x

00

xx

22

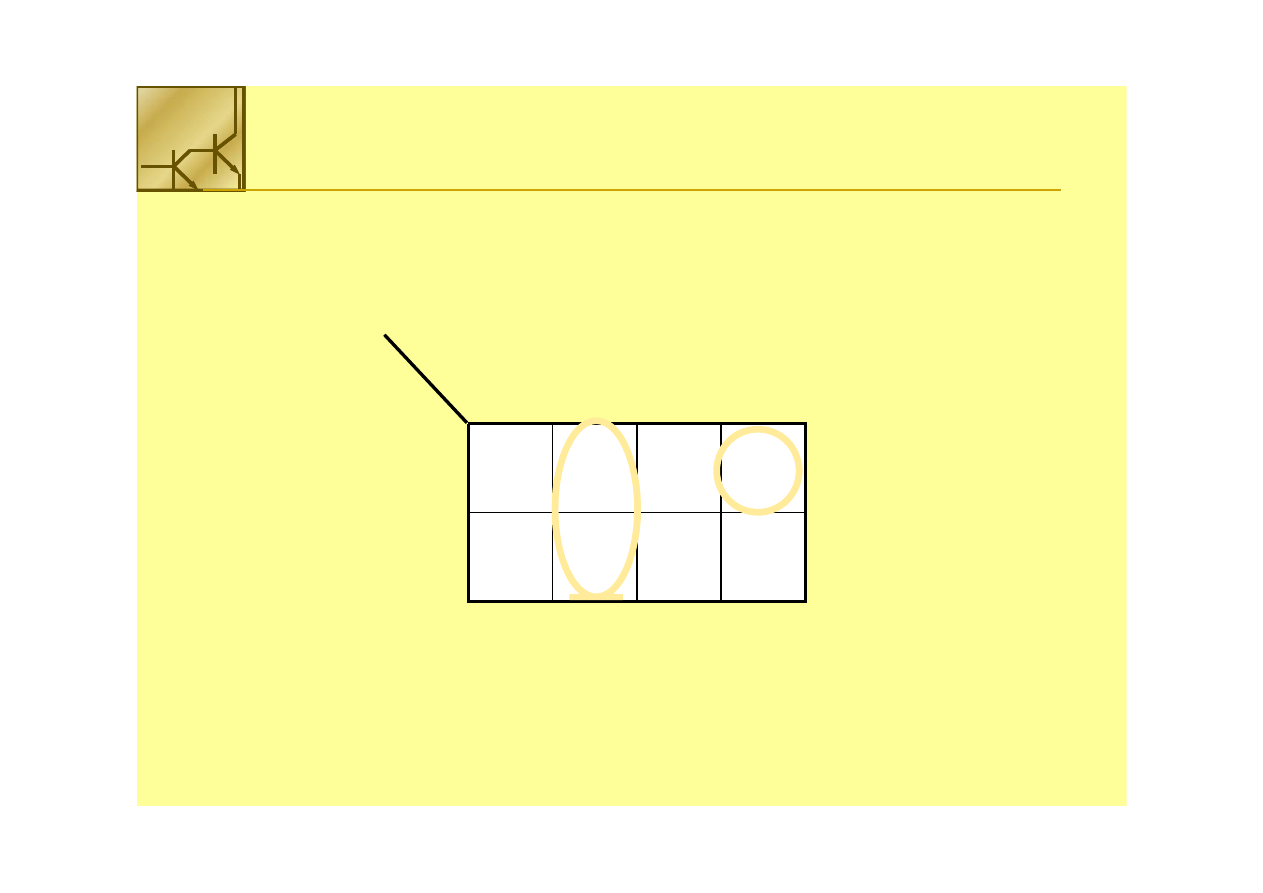
Tablice

Tablice Karnaugh

Karnaugh

Tablice

Tablice Karnaugh

Karnaugh

Można też zadać pytanie:

Można też zadać pytanie:

Kiedy funkcja logiczna ma wartość 0?

Kiedy funkcja logiczna ma wartość 0?

10

10

11

11

01

01

00

00

xx

22

xx

11

00

44

11

66

00

22

11

00

00

xx

00

11

55

11

77

00

33

11

11

11

xx

22

+

+ xx

11

’’ xx

00

+ x

+ x

11

+ x

+ x

22

’’

F =

F =

(x

(x +

+ xx’’ ) ) (x

(x + x

+ x + x

+ x ’)’)

6 marca 2011

Tablice Karnaugh

7

F =

F =

(x

(x

22

+

+ xx

11

) ) ⋅⋅ (x

(x

00

+ x

+ x

11

+ x

+ x

22

))

Zasady upraszczania tablic Karnaugh

Zasady upraszczania tablic Karnaugh

Zasady upraszczania tablic Karnaugh

Zasady upraszczania tablic Karnaugh

•• Grupujemy sąsiednie kwadraty zawierające 1 (0)

Grupujemy sąsiednie kwadraty zawierające 1 (0)..

•• Ilość zgrupowanych kwadratów musi być potęgą liczby dwa

Ilość zgrupowanych kwadratów musi być potęgą liczby dwa

np. 1, 2, 4, 8

np. 1, 2, 4, 8..

•• Staramy się grupować jak największą liczbą kwadratów

Staramy się grupować jak największą liczbą kwadratów..

•• W pierwszej kolejności grupujemy kwadraty, które mogą

W pierwszej kolejności grupujemy kwadraty, które mogą

znajdować się tylko w jednym kwadracie

znajdować się tylko w jednym kwadracie

•• Każda jedynka może być grupowana wielokrotnie

Każda jedynka może być grupowana wielokrotnie

l k

d k

l k

d k

6 marca 2011

Tablice Karnaugh

8

•• Jeżeli wszystkie jedynki zostały zgrupowane

Jeżeli wszystkie jedynki zostały zgrupowane –– uproszczenie

uproszczenie

tablicy jest zakończone

tablicy jest zakończone

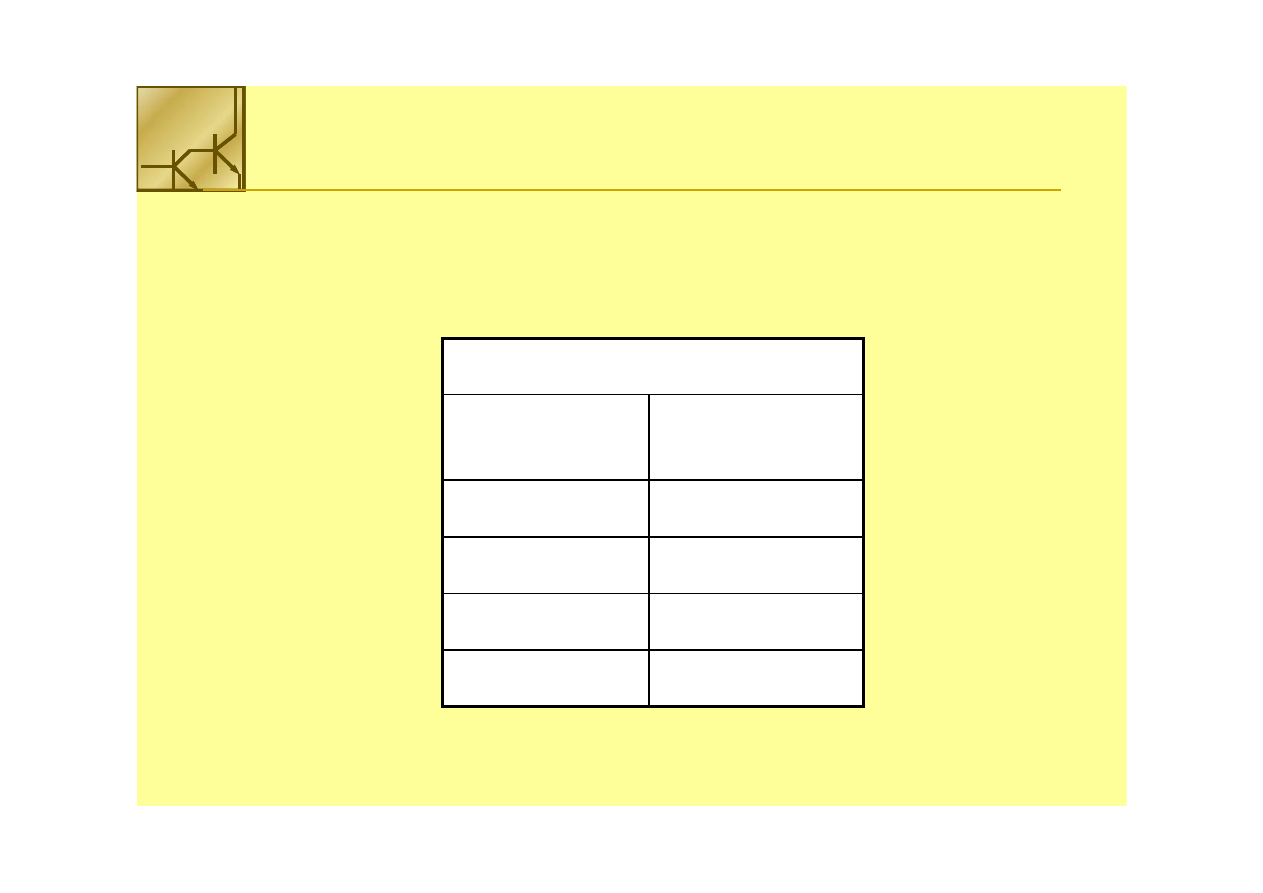
Tablice

Tablice Karnaugh

Karnaugh

Tablice

Tablice Karnaugh

Karnaugh

Liczba wyeliminowanych zmiennych w zależności od

Liczba wyeliminowanych zmiennych w zależności od

rozmiaru zaznaczonej grupy

rozmiaru zaznaczonej grupy

Tablica z 3 zmiennymi

Tablica z 3 zmiennymi

j g py

j g py

Ilość kwadratów w

Ilość kwadratów w

grupie

grupie

Liczba

Liczba

wyeliminowanych

wyeliminowanych

zmiennych

zmiennych

11

00

11

00

22

11

44

22

88

33

6 marca 2011

Tablice Karnaugh

9

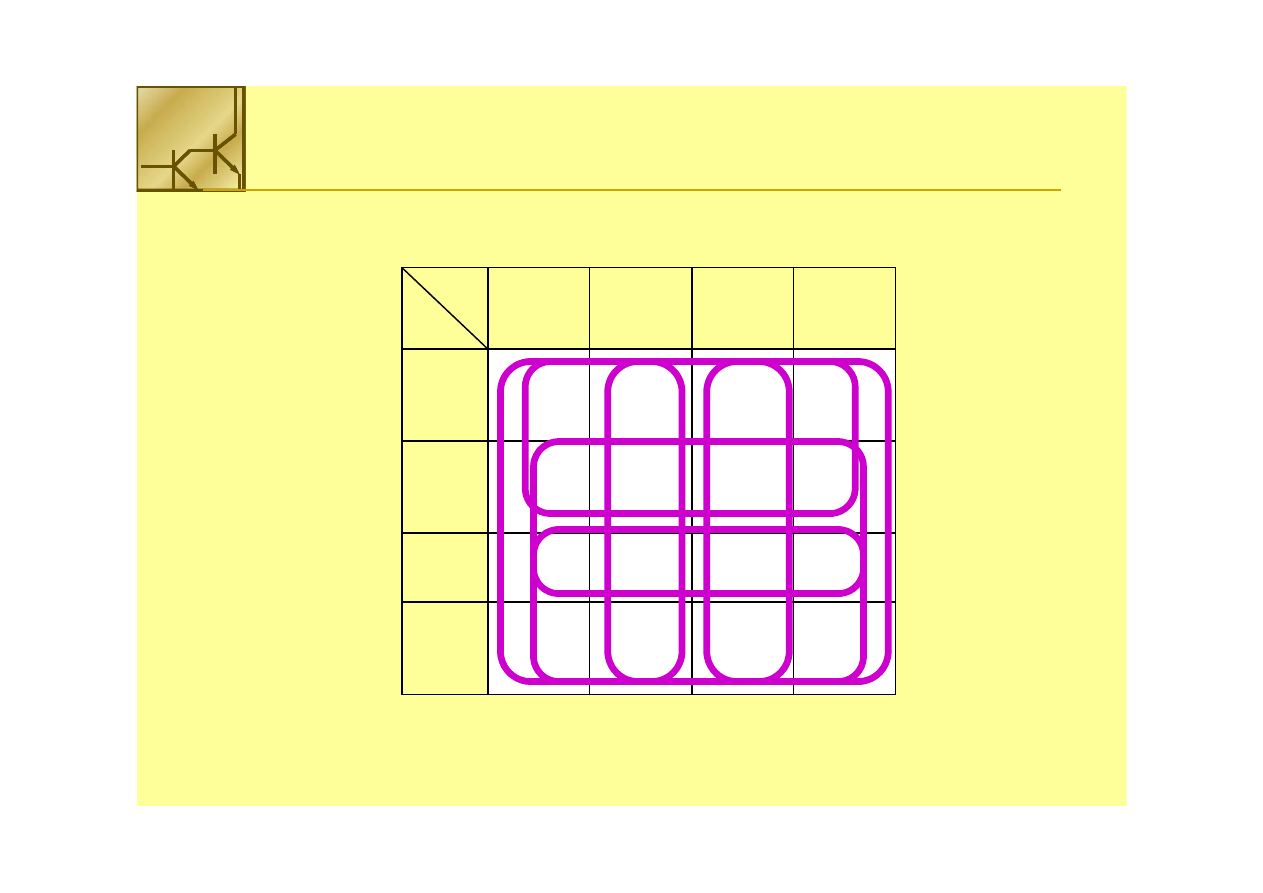
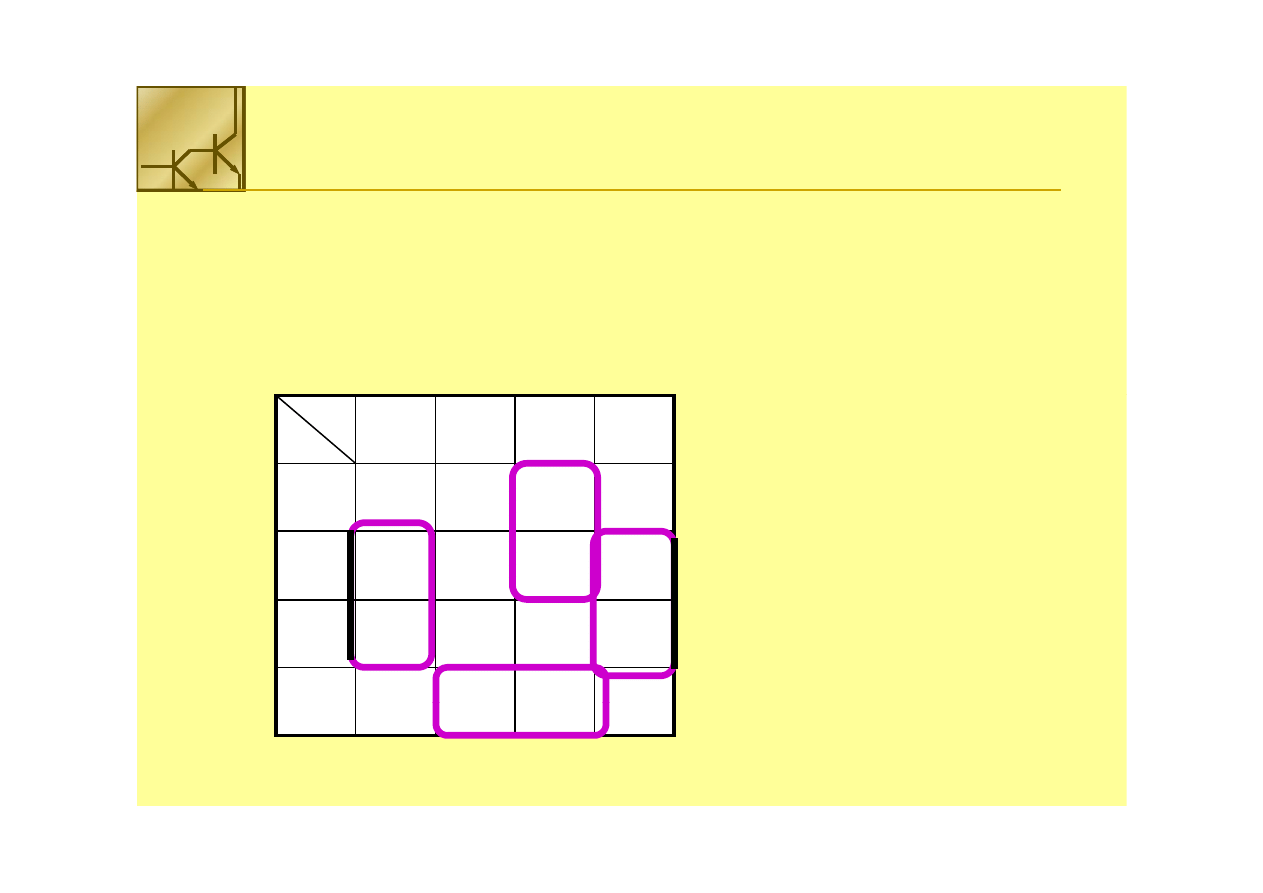
Grupowanie kwadratów

Grupowanie kwadratów

Grupowanie kwadratów

Grupowanie kwadratów

xx

33

xx

22

xx

33

xx

22

xx

11

xx

00

00

00

01

01

11

11

10

10

00

00

00

00

01

01

01

01

11

11

10

10

6 marca 2011

Tablice Karnaugh

10

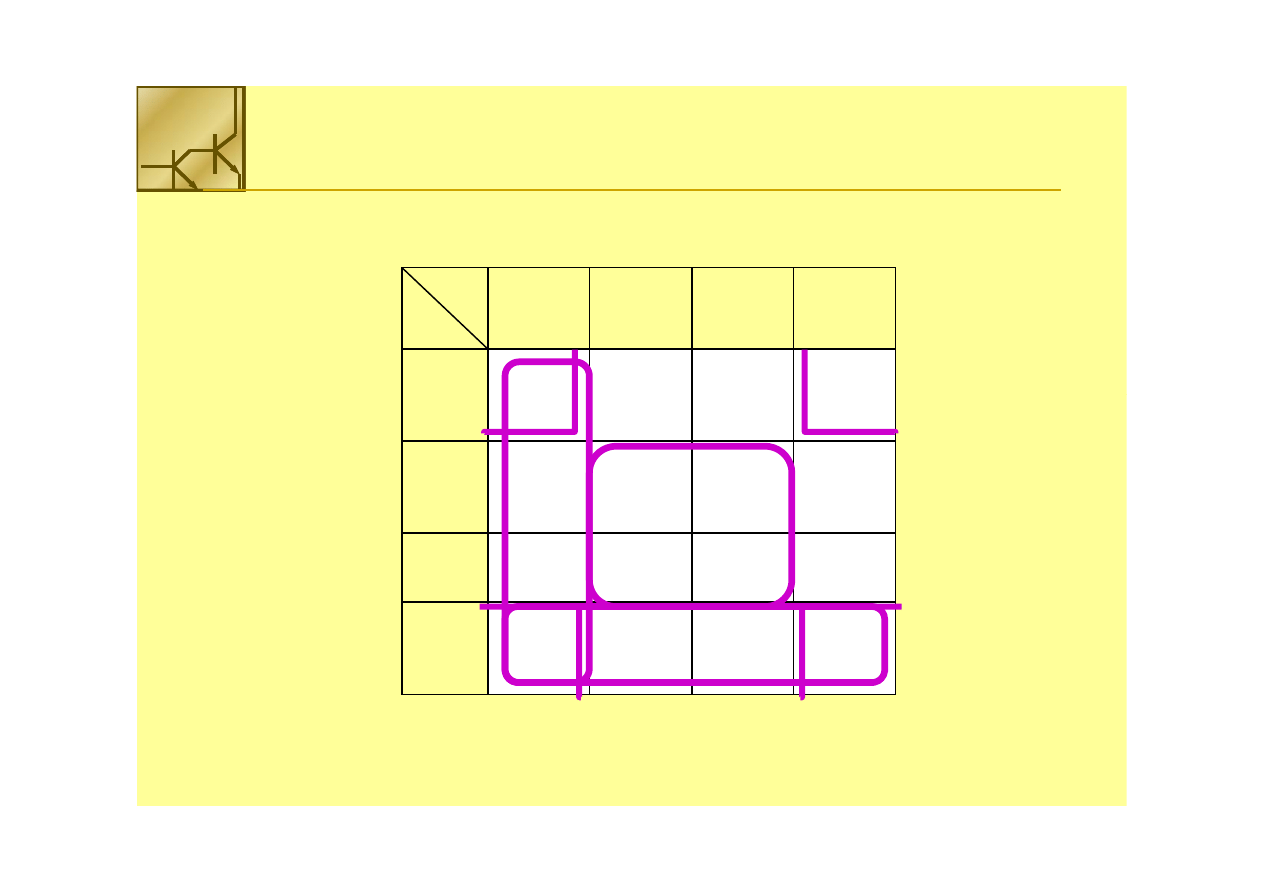
Grupowanie kwadratów

Grupowanie kwadratów

Grupowanie kwadratów

Grupowanie kwadratów

xx

33

xx

22

xx

33

xx

22

xx

11

xx

00

00

00

01

01

11

11

10

10

00

00

00

00

01

01

01

01

11

11

10

10

6 marca 2011

Tablice Karnaugh

11

Tablica Karnaugh z funkcji kanonicznej

Tablica Karnaugh z funkcji kanonicznej

Tablica Karnaugh z funkcji kanonicznej

Tablica Karnaugh z funkcji kanonicznej

Przykład uproszczenia wyrażenia przedstawionego w postaci

Przykład uproszczenia wyrażenia przedstawionego w postaci

kanonicznej

kanonicznej

(

)

(

)

FF= Σ

= Σ

(1,3,6,9,11,12,13,14)

(1,3,6,9,11,12,13,14)

F = x

F = x

00

xx

22

’

’

++

xx

33

xx

22

xx

11

xx

00

00

00

01

01

11

11

10

10

00

00

F x

F x

00

xx

22

+ x

+ x

00

’’

xx

11

xx

22

++

00 00 11 00

00

00

01

01

+ x

+ x

11

’’

xx

22

xx

33

00 00 11 00

11 00 11

11

0

4

12

8

1

5

13

9

11

11

10

10

11 00 00 11

00 11

11 00

3

7

15

11

6 marca 2011

Tablice Karnaugh

12

10

10

00 11

11 00

2

6

14

10

Warunek

Warunek Don’t

Don’t--Care

Care

Warunek

Warunek Don’t

Don’t--Care

Care

Dla niektórych funkcji niektóre kombinacje wejściowe są

Dla niektórych funkcji niektóre kombinacje wejściowe są

nieużywane, np. funkcja kodowania decymalnego BCD, gdzie

nieużywane, np. funkcja kodowania decymalnego BCD, gdzie

kodowane jest 10 cyfr na 16 możliwych kombinacji (4 bity).

kodowane jest 10 cyfr na 16 możliwych kombinacji (4 bity).

Minterm związany z nieużywaną kombinacja wejściową

Minterm związany z nieużywaną kombinacja wejściową

Minterm związany z nieużywaną kombinacja wejściową

Minterm związany z nieużywaną kombinacja wejściową

nazywa się

nazywa się “don’t

“don’t care

care conditions”

conditions”

Z t

i

Z t

i d ’t

d ’t

t bli K

h

ż

ś ić

t bli K

h

ż

ś ić

Zastosowanie

Zastosowanie don’t

don’t--care

care w tablicy Karnaugh może uprościć

w tablicy Karnaugh może uprościć

funkcje wyjściową

funkcje wyjściową

Don’t

Don’t--care

care jest zapisywane w tablicy jako

jest zapisywane w tablicy jako “X”

“X”

D

D

j

p yw

w

y j

j

p yw

w

y j

X

X

Warunek

Warunek

don’t

don’t--care

care może być traktowany jako zero lub

może być traktowany jako zero lub

jeden zależnie od potrzeby

jeden zależnie od potrzeby

6 marca 2011

Tablice Karnaugh

13

jeden, zależnie od potrzeby.

jeden, zależnie od potrzeby.

Warunek

Warunek Don’t

Don’t--Care

Care

Warunek

Warunek Don’t

Don’t--Care

Care

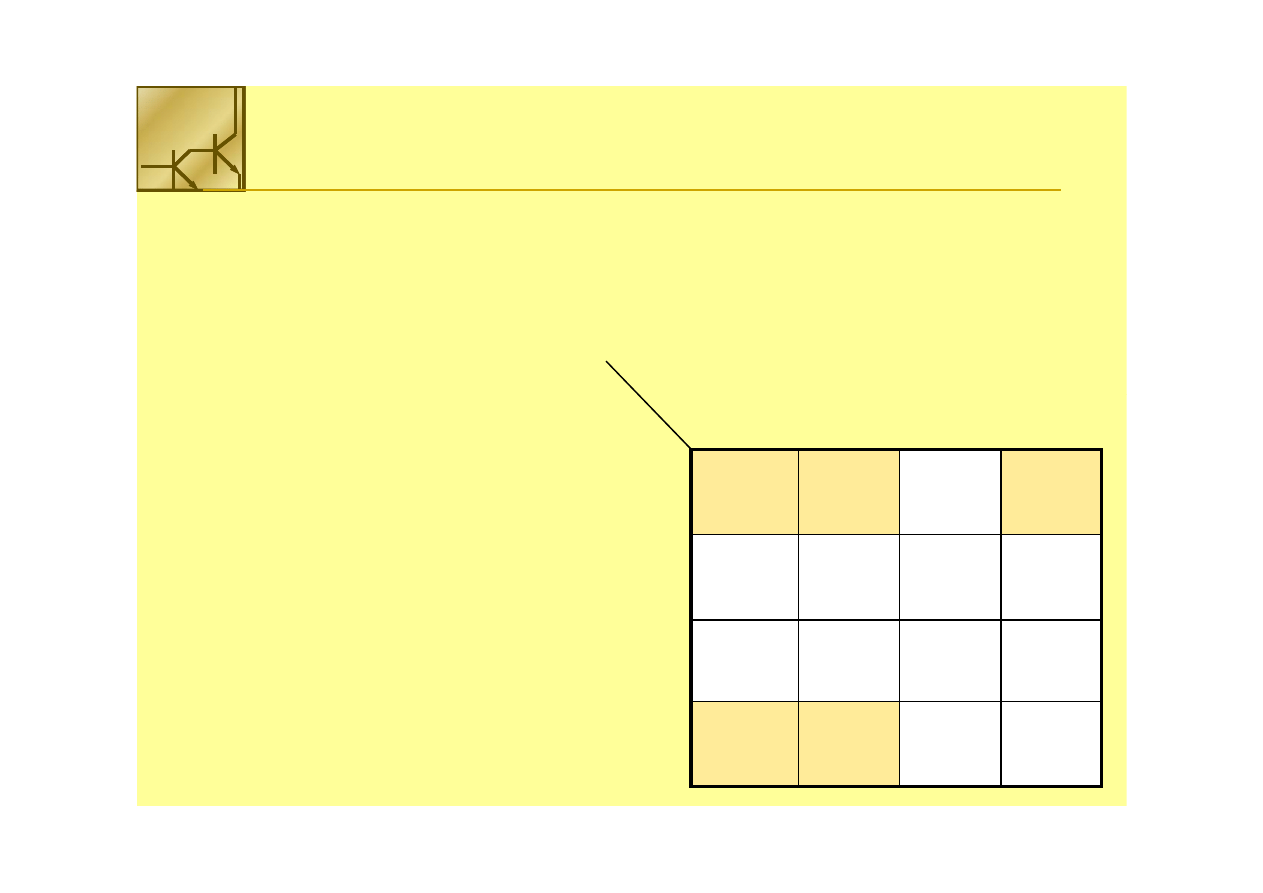
Zadanie:

Zadanie: Zdefiniować funkcję, która będzie zapalała diodę

Zdefiniować funkcję, która będzie zapalała diodę

LED przy liczbach parzystych:

LED przy liczbach parzystych:

F(

F(xx

33

,,xx

22

,,xx

11

,,xx

00

) = Σ(0, 2, 4, 6, 8)

) = Σ(0, 2, 4, 6, 8)

xx

33

xx

22

33 22

xx

11

xx

00

00

00

01

01

11

11

10

10

00

00

11

11

00

11

W kodzie BCD liczby binarne 10, 11, 12, 13, 14, and

00

00

01

01

00

44

12

12

88

11

55

13

13

99

11

11

00

11

00

00

00

00

15 są nieużywane, czylidon’t-care.

Rozwiązanie

Rozwiązanie

11

11

11

55

13

13

99

33

77

15

15

11

11

00

00

00

00

00

00

00

00

nie

nie względniające

względniające don’t

don’t care

care

F(

F(xx

33

,,xx

22

,,xx

11

,,xx

00

) =

) = xx

00

’’xx

33

’ +

’ + xx

00

’’xx

11

’’xx

22

’’

6 marca 2011

Tablice Karnaugh

14

10

10

22

66

14

14

10

10

11

11

00

00

Warunek

Warunek Don’t

Don’t--Care

Care

Warunek

Warunek Don’t

Don’t--Care

Care

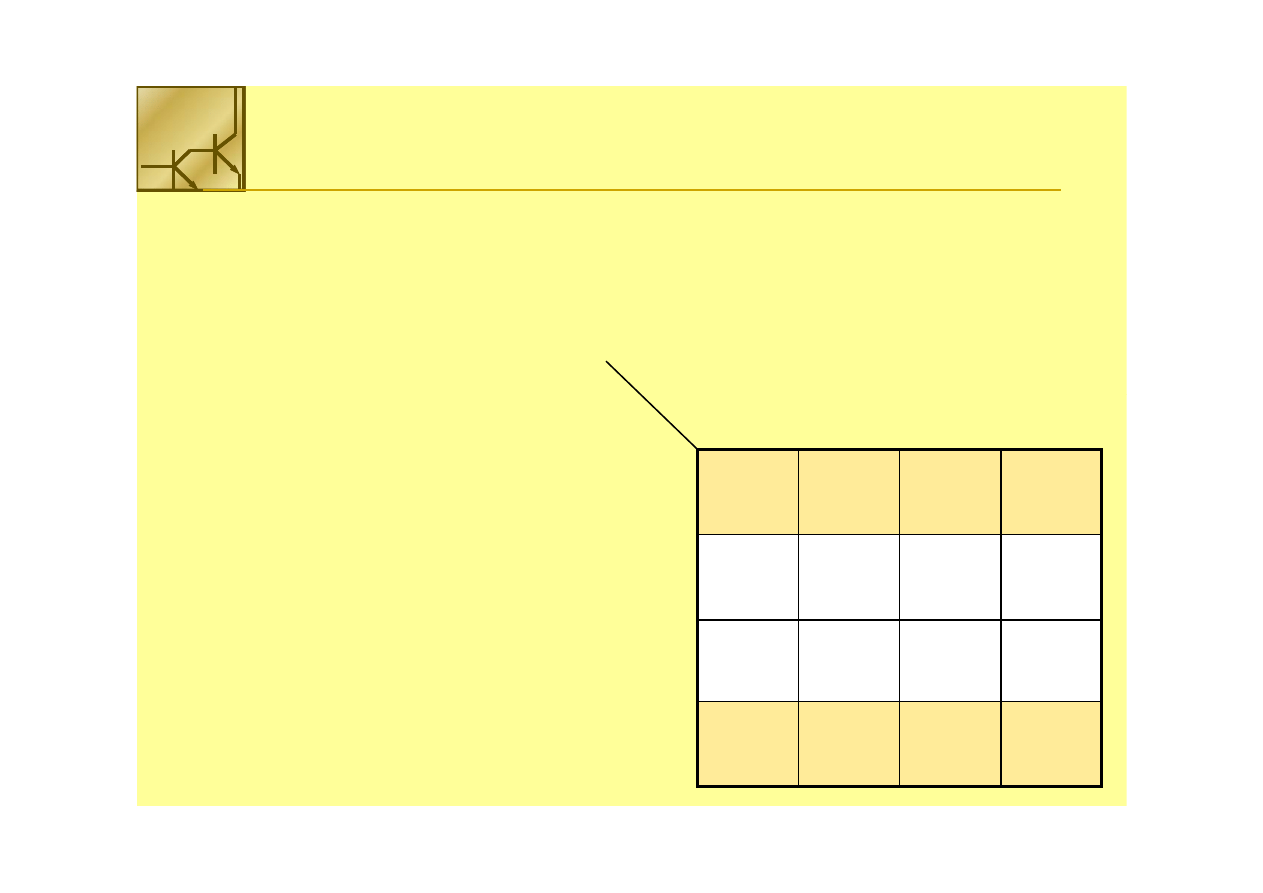
Zadanie:

Zadanie: Zdefiniować funkcję, która będzie zapalała diodę LED

Zdefiniować funkcję, która będzie zapalała diodę LED

przy liczbach parzystych:

przy liczbach parzystych:

F(

F(xx

33

,,xx

22

,,xx

11

,,xx

00

) = Σ(0, 2, 4, 6, 8)

) = Σ(0, 2, 4, 6, 8)

xx

33

xx

22

33 22

xx

11

xx

00

00

00

01

01

11

11

10

10

00

00

11

11

X

X

11

W kodzie BCD liczby binarne 10, 11, 12, 13,

00

00

01

01

00

44

12

12

88

11

55

13

13

99

X

X

00

00

X

X

00

14, and 15 są nieużywane, czylidon’t-care.

Rozwiązanie uwzględniające

Rozwiązanie uwzględniające

don’t

don’t care

care

11

11

11

55

13

13

99

33

77

15

15

11

11

00

00

X

X

X

X

don t

don t care

care

F(

F(xx

33

,,xx

22

,,xx

11

,,xx

00

) =

) = xx

00

’ ’

6 marca 2011

Tablice Karnaugh

15

10

10

22

66

14

14

10

10

11

11

X

X

X

X

Budowa układu logicznego

Budowa układu logicznego

Budowa układu logicznego

Budowa układu logicznego

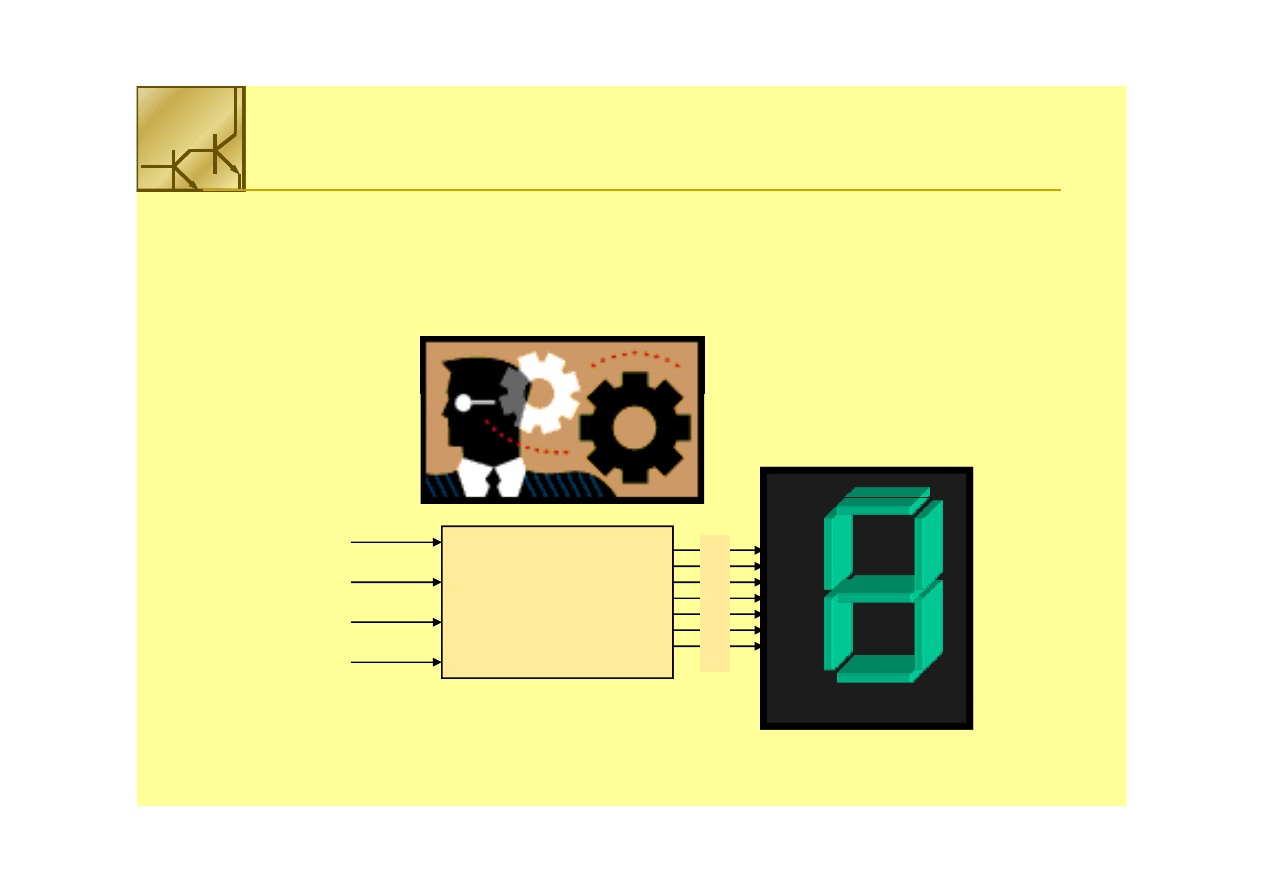
Zadanie:

Zadanie:

Zbudować układ logiczny sterownika do wyświetlacza 7

Zbudować układ logiczny sterownika do wyświetlacza 7--

segmentowego

segmentowego

aa

Decoder

Decoder

xx

00

xx

11

ff

gg

bb

aa

A

A

BB

CC

D

D

BCD to 7

BCD to 7 segm

segm

xx

22

xx

33

cc

dd

ee

D

D

EE

FF

G

G

6 marca 2011

Tablice Karnaugh

16

dd

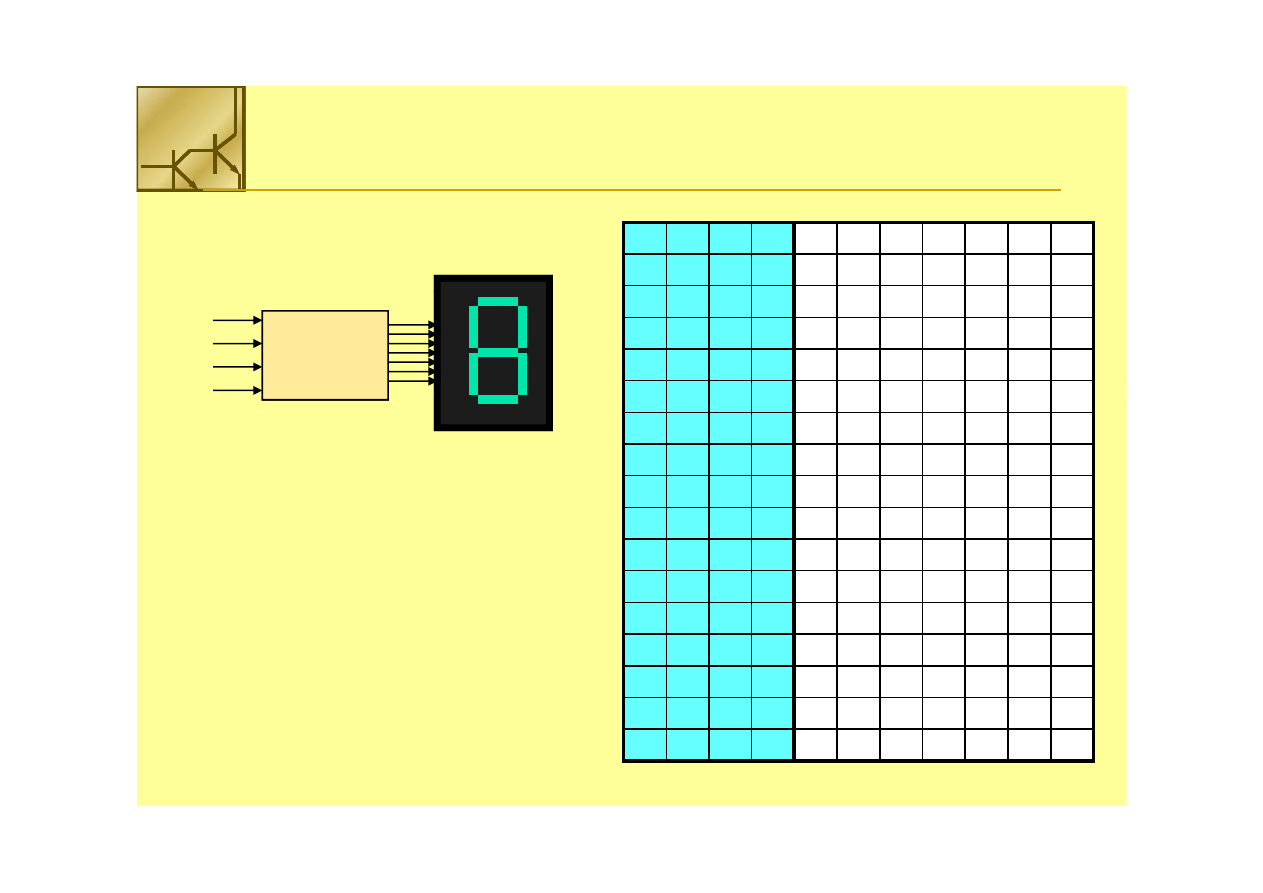
Budowa układu logicznego

Budowa układu logicznego

Budowa układu logicznego

Budowa układu logicznego

1. Zbuduj tablicę prawdy

1. Zbuduj tablicę prawdy

xx

33

xx

22

xx

11

xx

00

aa

bb

cc

dd

ee

ff

gg

00

00

00

00

11

11

11 11

11

11

00

Decoder

Decoder

BCD to 7 segm

BCD to 7 segm

xx

00

xx

11

xx

22

xx

33

bb

cc

ee

ff

aa

gg

00

00

00

11

00

00

11

00

00

00

11

11

00

11

00

00

00

11

11 00

00

00

00

11

11

00 11

11

00

11

11

11

11 11

00

00

11

00

11

11 00

00

11

11

11

11

11

11

11

11

00

11

11

11

11

11

11

00

dd

00

11

00

00

00

11

00

11

00

11

11

00

00

11

11

11

00

11

11 00

00

11

11

11

00

11 11

00

11

11

11

00

11 11

11

11

11

11

11

11 00

00

00

00

00

11

11

11

11

00

00

00

11

00

00

11

11

00

11

00

11

11

11 00

00

00

00

11

11

11 11

11

11

11

11

11

11 11

00

11

11

xx

xx

xx

xx

xx

xx

xx

11

00

11

11

11

11

00

00

11

11

00

11

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

6 marca 2011

Tablice Karnaugh

17

11

11

11

00

11

11

11

11

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

xx

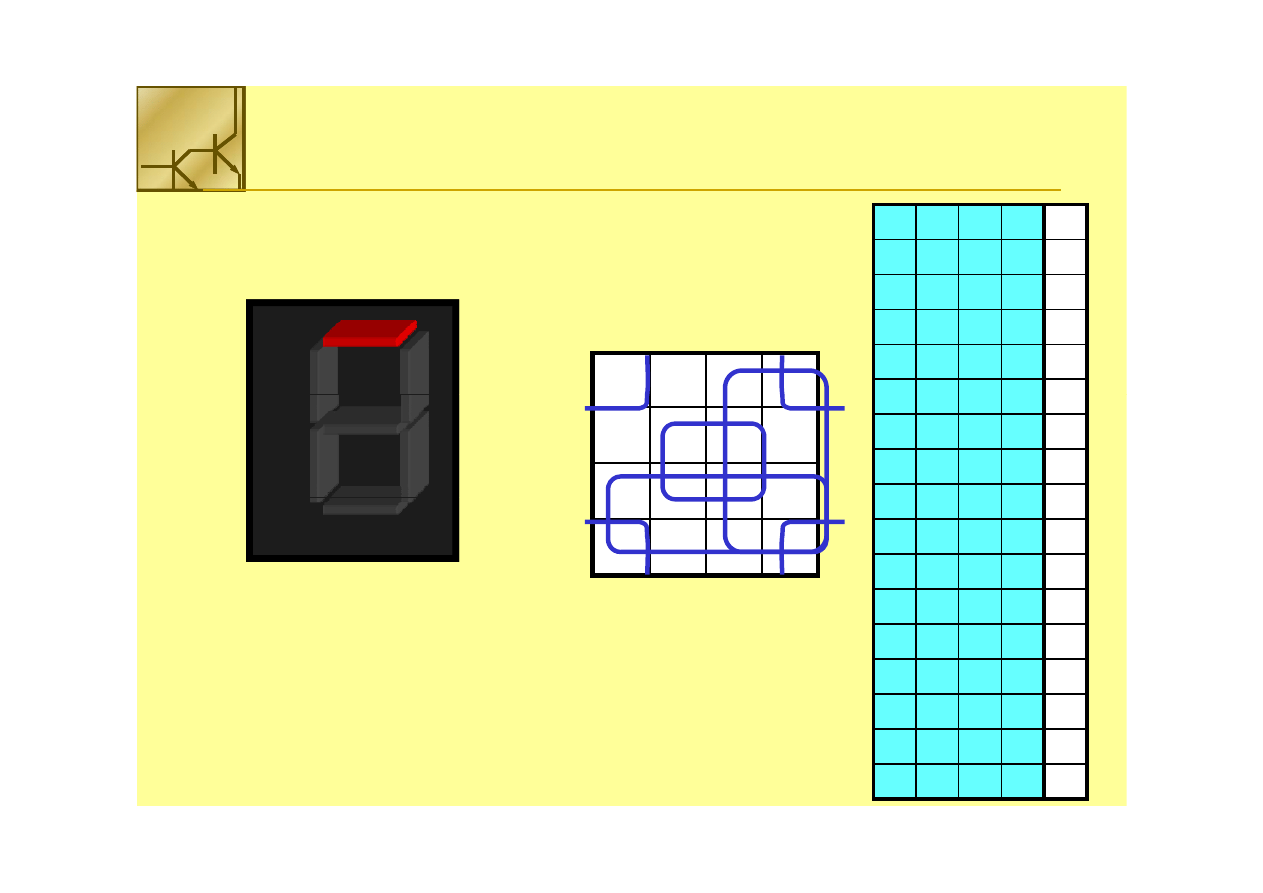
Budowa układu logicznego

Budowa układu logicznego

Budowa układu logicznego

Budowa układu logicznego

2. Utworzyć tablicę Karnaugh

2. Utworzyć tablicę Karnaugh

xx

33

xx

22

xx

11

xx

00

aa

00

00

00

00

00

00

00

11

11
00

00

00

00

11

00

00

11

00

00

00

11

11

00

11

00

00

ff

bb

aa

xx

33

xx

22

xx

11

xx

00

00

00 01

01 11

11 10

10

00

00

00

11
11
00

X

X

00

11

00

00

00

11

00

11

00

11

11

00

00

11

11

11

cc

ee

ff

gg

bb

01

01

11

11

00
11
11
11

X

X

X

X

X

X

X

X

00

11

11

11

11

00

00

00

11

00

00

11

11

00

11

00

dd

11

11

10

10

11

11

11

X

X

X

X

X

X

X

X

11

00

11

00

xx

11

00

11

11

xx

11

11

00

00

xx

11

11

00

00

a = x

a = x

11

+ x

+ x

33

+ x

+ x

00

xx

22

+ x’

+ x’

00

x’

x’

22

3. Zapisać funkcję logiczną

3. Zapisać funkcję logiczną

6 marca 2011

Tablice Karnaugh

18

11

11

00

00

xx

11

11

11

00

xx

11

11

11

11

xx

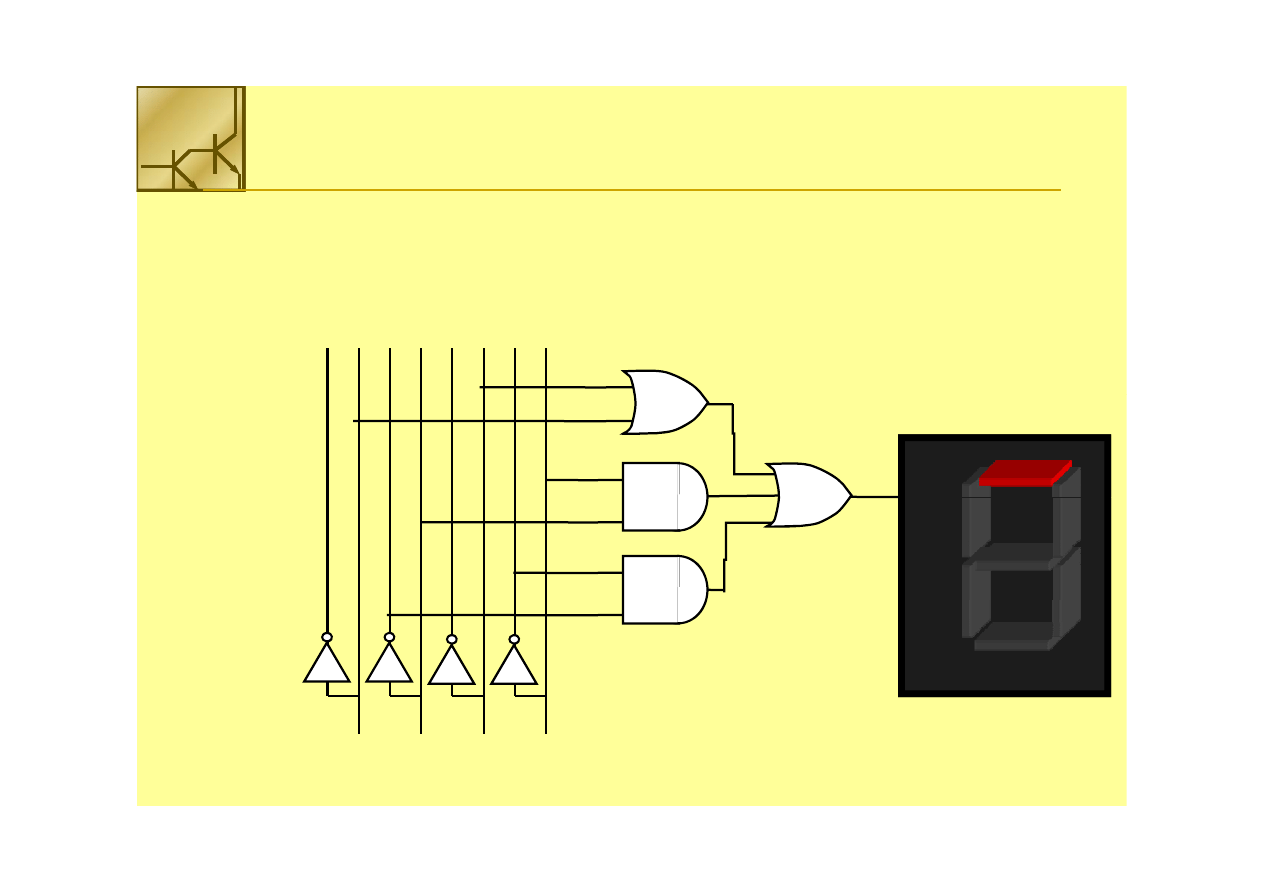
Budowa układu logicznego

Budowa układu logicznego

Budowa układu logicznego

Budowa układu logicznego

4.

4. Narysować schemat układu logicznego

Narysować schemat układu logicznego

a = (x

a = (x +x

+x ) + x

) + x xx + x’

+ x’ x’

x’

a = (x

a = (x

11

+x

+x

33

) + x

) + x

00

xx

22

+ x

+ x

00

xx

22

aa

ff

gg

bb

ee

cc

dd

6 marca 2011

Tablice Karnaugh

19

xx

3

3

xx

2

2

xx

11

xx

00