
24 kwietnia 2013
Wojciech Kucewicz
1

24 kwietnia 2013
Tablice Karnaugh
2
Tablice
Karnaugh
Tablice
Karnaugh
24 kwietnia 2013
Tablice Karnaugh
3
Tablice Karnaugh
Tablice Karnaugh
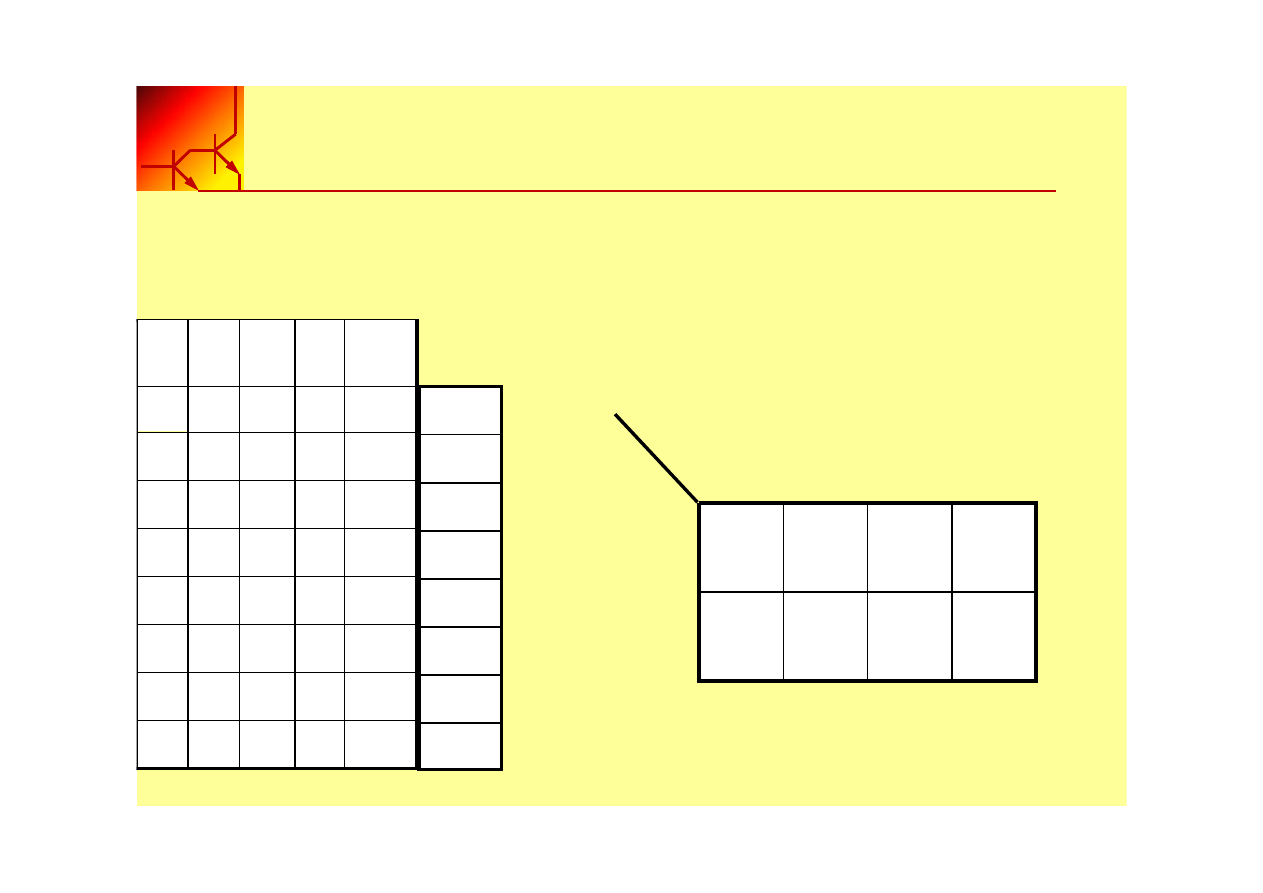
Tablice Karnaugh są graficzną reprezentacją tablic prawdy.
Każda kratka reprezentuje jeden minterm
1
5
1
7
0
3
1
1
1
0
4
1
6
0
2
1
0
0
10
11
01
00
x
2
x
1
x
0
5
1
1
0
1
6
1
0
1
1
7
1
1
1
1
0
1
0
0
0
1
1
1
0
0
2
0
0
1
0
4
0
0
0
1
3
0
1
1
0
F
x
0
x
1
x
2
m
0
m
1
m
2
m
3
m
4
m
5
m
6
m
7
Karnaugh Map
24 kwietnia 2013
Tablice Karnaugh
4
Tablice Karnaugh
Tablice Karnaugh
1
5
1
7
0
3
1
1
1
0
4
1
6
0
2
1
0
0
10
11
01
00
x
2
x
1
x
0
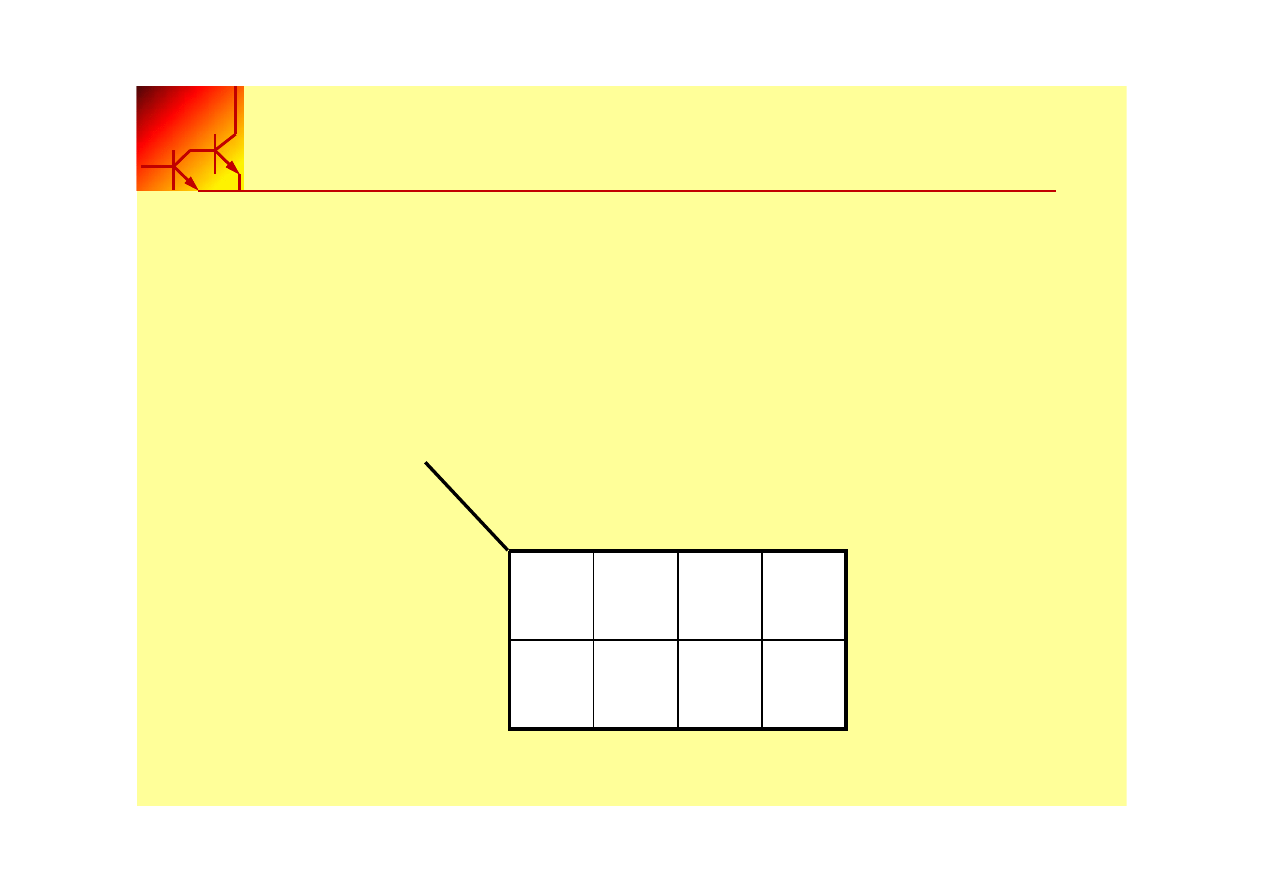
Każde dwa sąsiednie pola różnią się między sobą tylko
jednym bitem. Dotyczy to również pól skrajnych
(ostatnie pole
różni się tylko jednym bitem od pierwszego pola w szeregu).
24 kwietnia 2013
Tablice Karnaugh
5
Tablice Karnaugh
Tablice Karnaugh
1
5
1
7
0
3
1
1
1
0
4
1
6
0
2
1
0
0
10
11
01
00
x
2
x
1
x
0
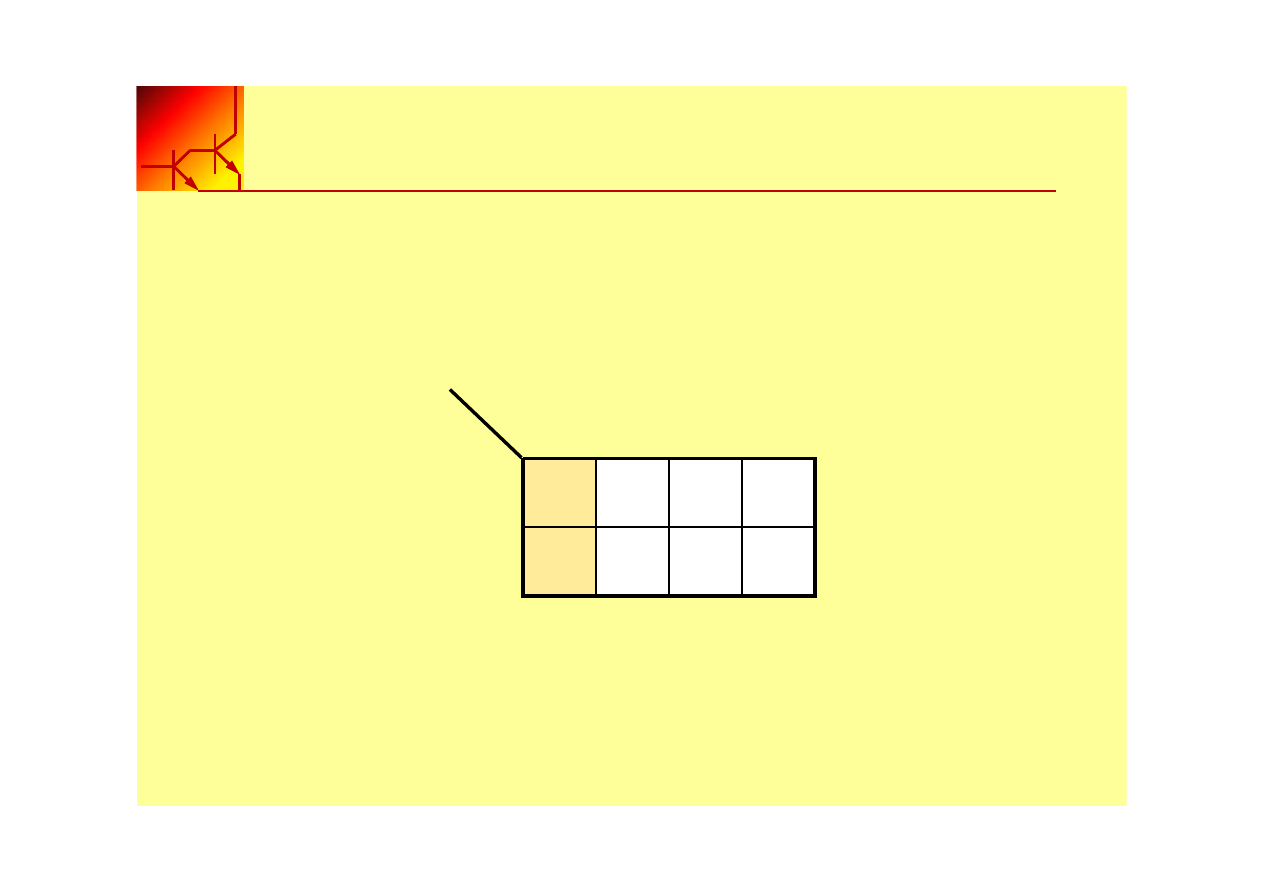
Suma dwóch sąsiednich mintermów o tej samej wartości logicznej może być
uproszczona do jednego iloczynu logicznego, w którym wyeliminowana zostaje
jedna zmienna.
Biorąc mintermy z pierwszej kolumny otrzymamy zależność:
x
2
’x
1
’x
0
’ + x
2
’x
1
’x
0
= x
2
’x
1
’(x
0
’ + x
0
) = x
2
’x
1
’
Upraszczając wyrażenie można wyeliminować zmienną x
0
.

24 kwietnia 2013
Tablice Karnaugh
6
Tablice Karnaugh
Tablice Karnaugh
1
5
1
7
0
3
1
1
1
0
4
1
6
0
2
1
0
0
10
11
01
00
x
2
x
1
x
0
x
2
’x
1
’
x
2
x
1
x
2
x
0
F = x
1
’x
2
’ + x
1
x
2
+ x
0
x
2
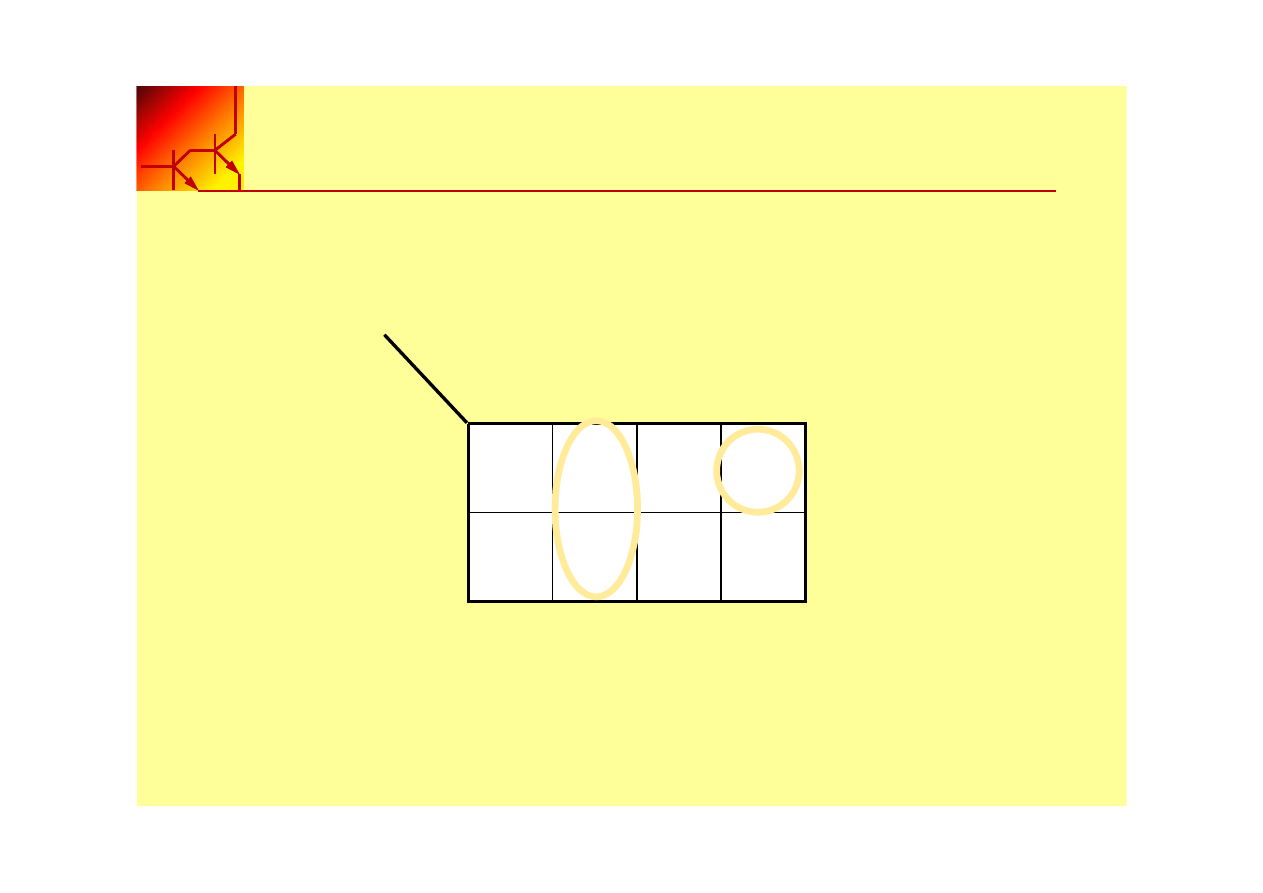
Aby uprościć funkcję logiczną wykorzystując tablice Karnaugh, należy
pogrupować sąsiednie kratki zawierające wartości logiczne 1.
Zadajemy sobie pytanie: Kiedy funkcja logiczna ma wartość 1?
24 kwietnia 2013
Tablice Karnaugh
7
Tablice Karnaugh
Tablice Karnaugh
1
5
1
7
0
3
1
1
1
0
4
1
6
0
2
1
0
0
10
11
01
00
x
2
x
1
x
0
x
2
+ x
1
’ x
0
+ x
1
+ x
2
’
F’ =
(x
2
+ x’
1
) (x
0
+ x
1
+ x
2
’)
Można też zadać pytanie:
Kiedy funkcja logiczna ma wartość 0?

24 kwietnia 2013
Tablice Karnaugh
8
Zasady upraszczania tablic Karnaugh
Zasady upraszczania tablic Karnaugh
• Grupujemy sąsiednie kwadraty zawierające 1 (0).
• Ilość zgrupowanych kwadratów musi być potęgą liczby dwa
np. 1, 2, 4, 8.
• Staramy się grupować jak największą liczbą kwadratów.
• W pierwszej kolejności grupujemy kwadraty, które mogą
znajdować się tylko w jednym kwadracie
• Każda jedynka może być grupowana wielokrotnie
• Jeżeli wszystkie jedynki zostały zgrupowane – uproszczenie
tablicy jest zakończone

24 kwietnia 2013
Tablice Karnaugh
9
Tablice Karnaugh
Tablice Karnaugh
Tablica z 3 zmiennymi
Ilość kwadratów w
grupie
Liczba
wyeliminowanych
zmiennych
1
0
2
1
4
2
8
3
Liczba wyeliminowanych zmiennych w zależności od
rozmiaru zaznaczonej grupy
24 kwietnia 2013
Tablice Karnaugh
10
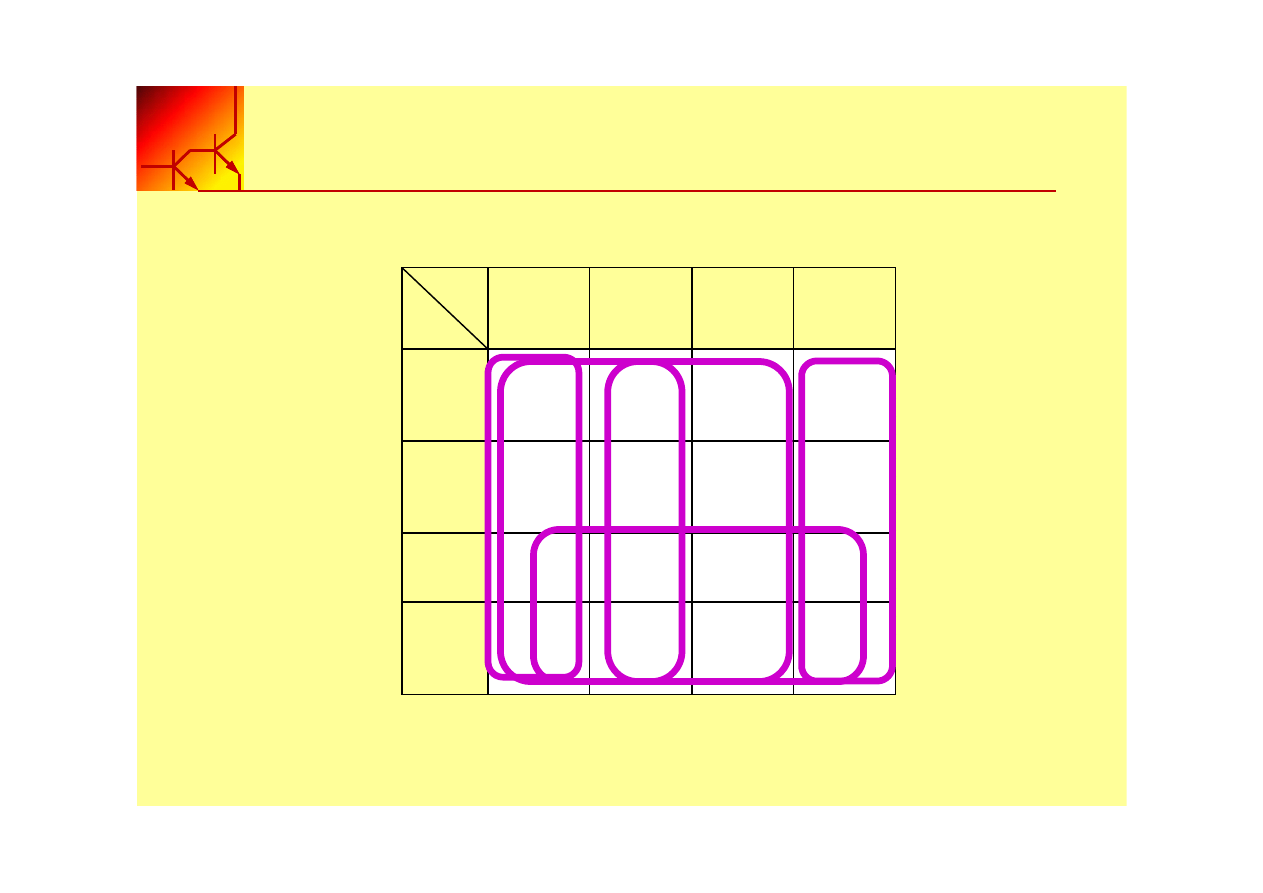
Grupowanie kwadratów
Grupowanie kwadratów
x
3
x
2
x
1
x
0
00
01
11
10
00
01
11
10
24 kwietnia 2013
Tablice Karnaugh
11
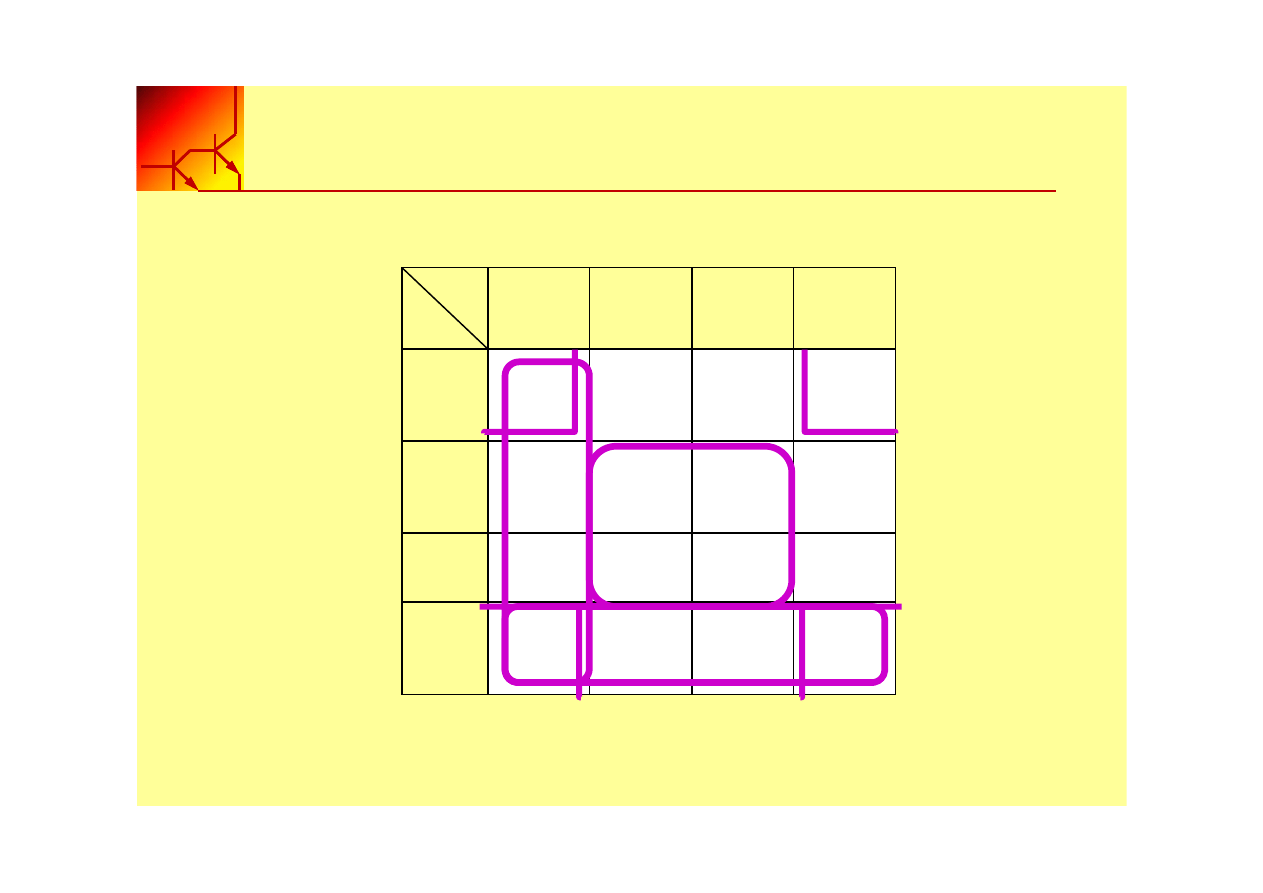
Grupowanie kwadratów
Grupowanie kwadratów
x
3
x
2
x
1
x
0
00
01
11
10
00
01
11
10
24 kwietnia 2013
Tablice Karnaugh
12
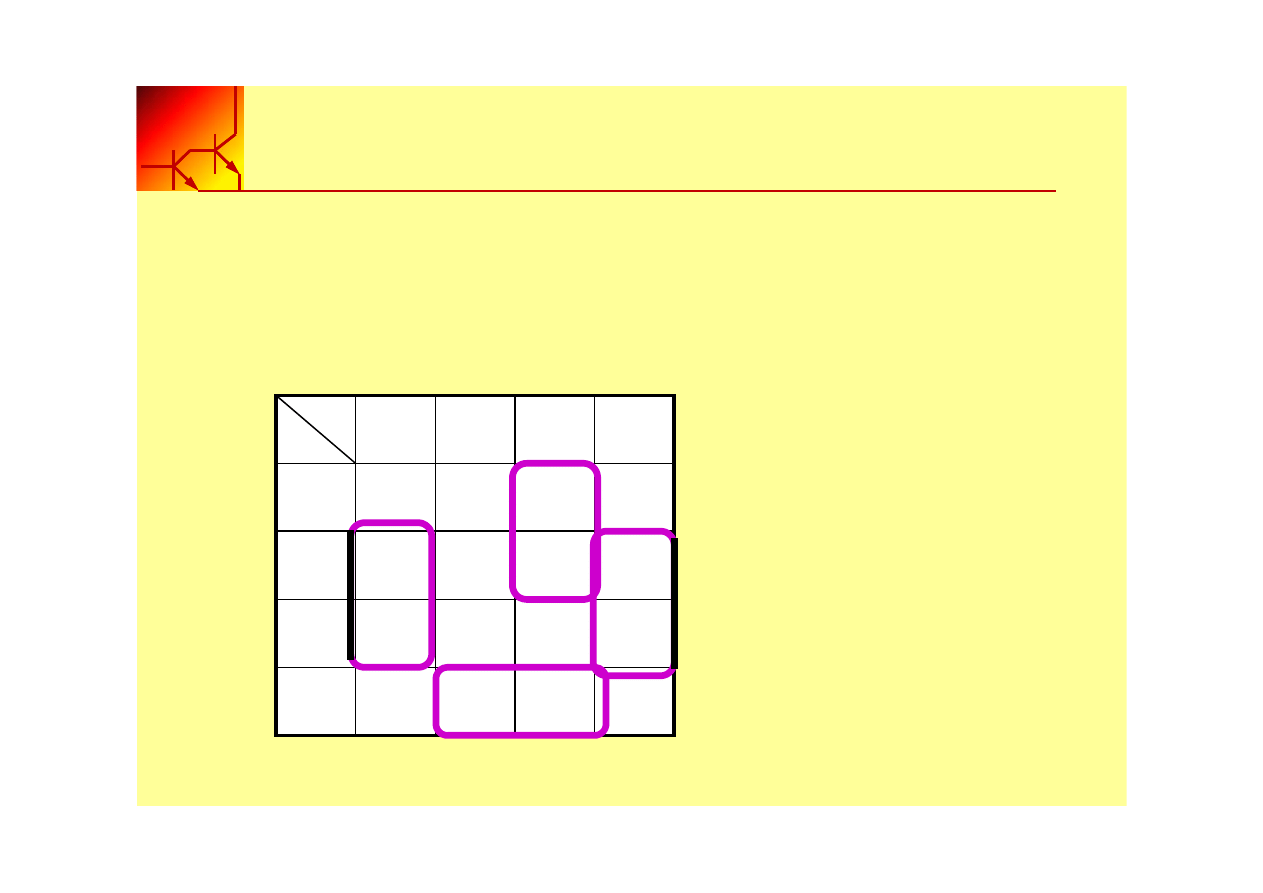
Tablica Karnaugh z funkcji kanonicznej
Tablica Karnaugh z funkcji kanonicznej
x
3
x
2
x
1
x
0
00
01
11
10
00
01
11
10
Przykład uproszczenia wyrażenia przedstawionego w postaci
kanonicznej
F(1,3,6,9,11,12,13,14)
F = x
0
x
2
’
+
+ x
0
’
x
1
x
2
+
+ x
1
’
x
2
x
3
0 0 1 0
1 0 1
1
1 0 0 1
0 1
1 0
0
4
12
8
1
5
13
9
3
7
15
11
2
6
14
10

24 kwietnia 2013
Tablice Karnaugh
13
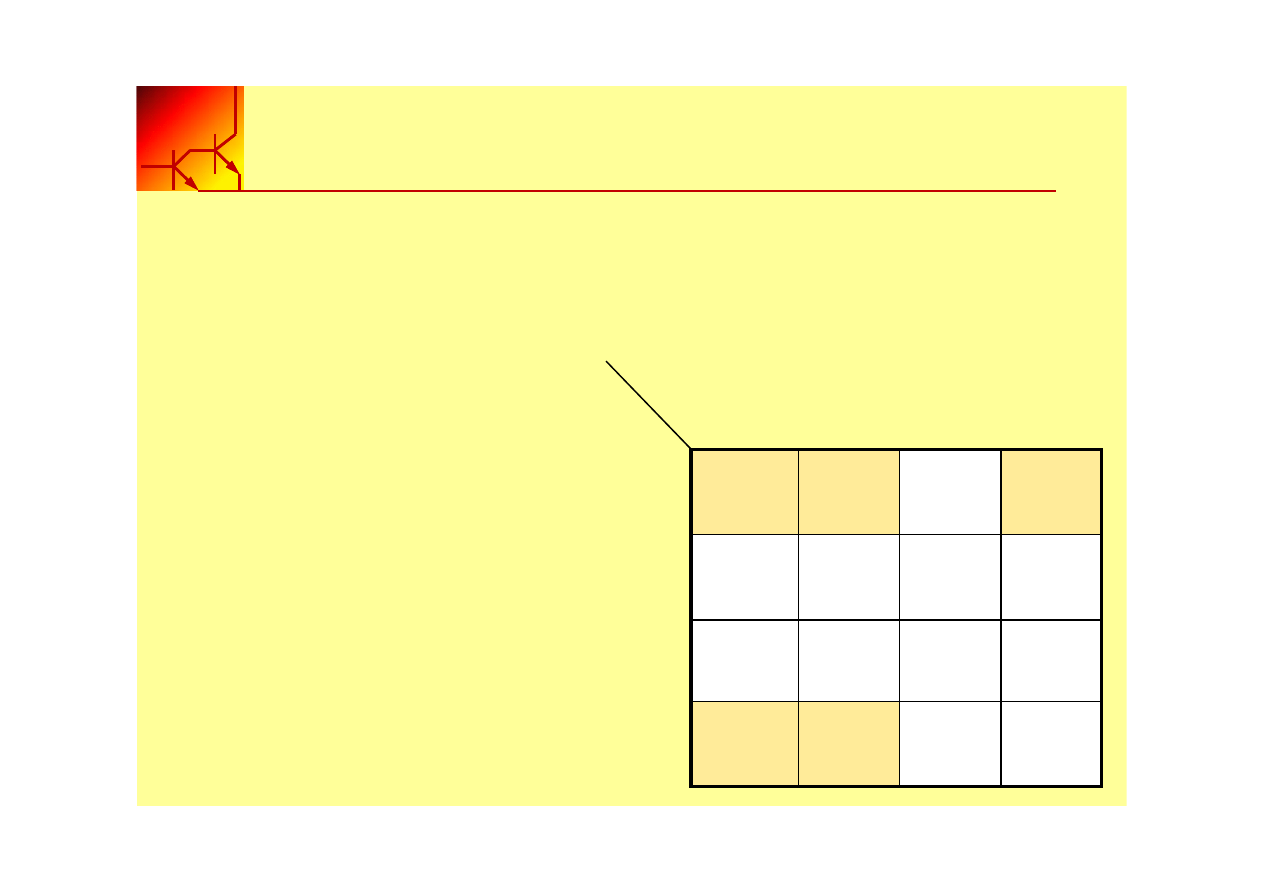
Warunek Don’t-Care
Warunek Don’t-Care
Dla niektórych funkcji niektóre kombinacje wejściowe są
nieużywane, np. funkcja kodowania decymalnego BCD, gdzie
kodowane jest 10 cyfr na 16 możliwych kombinacji (4 bity).
Minterm związany z nieużywaną kombinacja wejściową
nazywa się “don’t care conditions”
Zastosowanie don’t-care w tablicy Karnaugh może uprościć
funkcje wyjściową
Don’t-care jest zapisywane w tablicy jako “X”
Warunek
don’t-care może być traktowany jako zero lub
jeden, zależnie od potrzeby.
24 kwietnia 2013
Tablice Karnaugh
14
Warunek Don’t-Care
Warunek Don’t-Care
Przykład: Zdefiniować funkcję, która będzie zapalała diodę
LED przy liczbach parzystych:
F(x
3
,x
2
,x
1
,x
0
) = Σ(0, 2, 4, 6, 8)
x
3
x
2
x
1
x
0
00
01
11
10
00
01
11
10
0
4
12
8
1
5
13
9
3
7
15
11
2
6
14
10
1
1
0
1
0
0
0
0
0
0
0
0
1
1
0
0
W kodzie BCD liczby binarne 10, 11, 12,
13, 14 i 15 są nieużywane, czyli 0
Rozwiązanie
nie względniające don’t care
F(x
3
,x
2
,x
1
,x
0
) = x
0
’x
3
’ + x
0
’x
1
’x
2
’
24 kwietnia 2013
Tablice Karnaugh
15
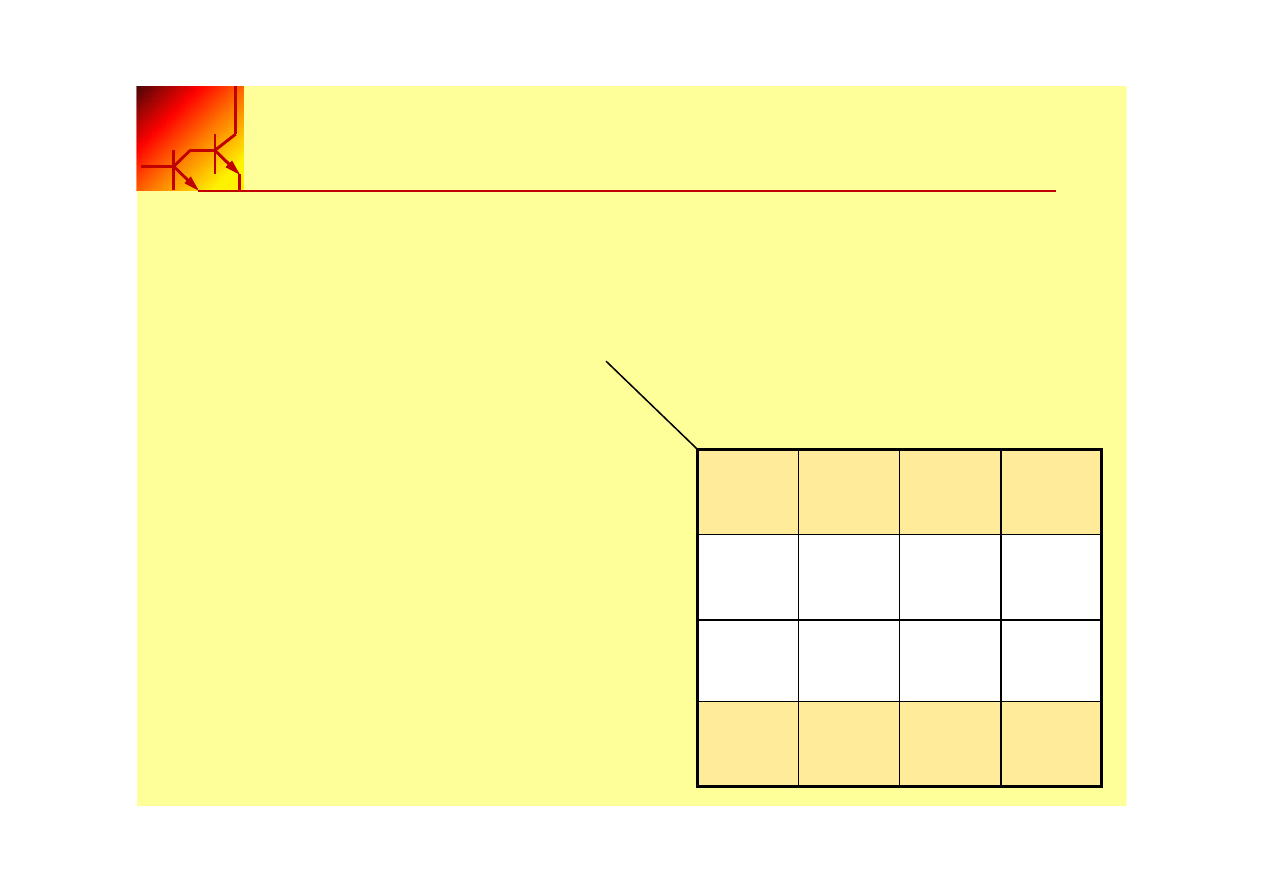
Warunek Don’t-Care
Warunek Don’t-Care
Przykład: Zdefiniować funkcję, która będzie zapalała diodę
LED przy liczbach parzystych:
F(x
3
,x
2
,x
1
,x
0
) = Σ(0, 2, 4, 6, 8)
x
3
x
2
x
1
x
0
00
01
11
10
00
01
11
10
0
4
12
8
1
5
13
9
3
7
15
11
2
6
14
10
1
1
X
1
0
0
X
0
0
0
X
X
1
1
X
X
W kodzie BCD liczby binarne 10, 11, 12, 13,
14, i 15 są nieużywane, czyli „don’t-care”.
Rozwiązanie uwzględniające
don’t care
F(x
3
,x
2
,x
1
,x
0
) = x
0
’
24 kwietnia 2013
Tablice Karnaugh
16
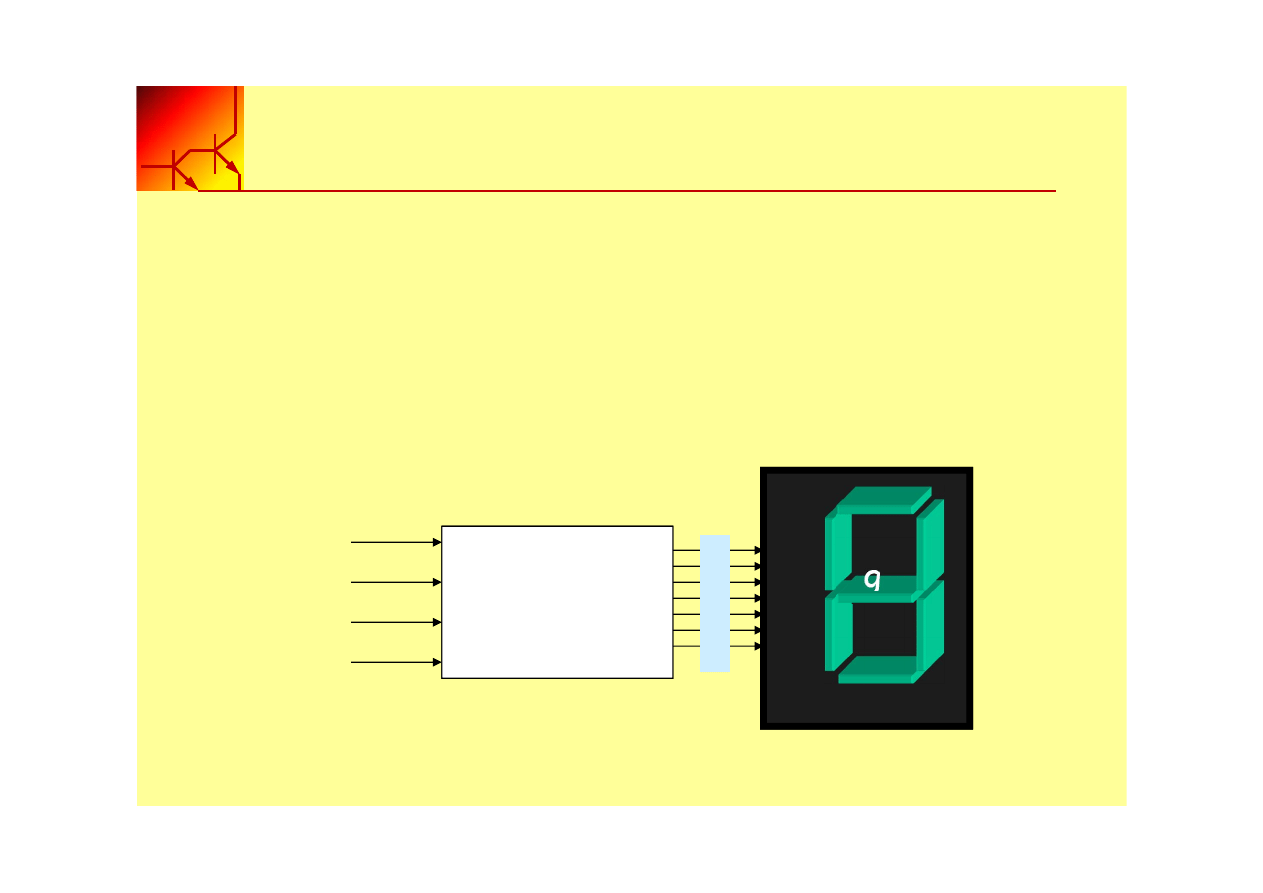
Budowa układu logicznego
Budowa układu logicznego
Przykład:
Zbudować układ logiczny sterownika do wyświetlacza 7-
segmentowego
Decoder
BCD to 7 segm
x
0
x
1
x
2
x
3
c
d
e
f
g
b
a
A
B
C
D
E
F
G
24 kwietnia 2013
Tablice Karnaugh
17
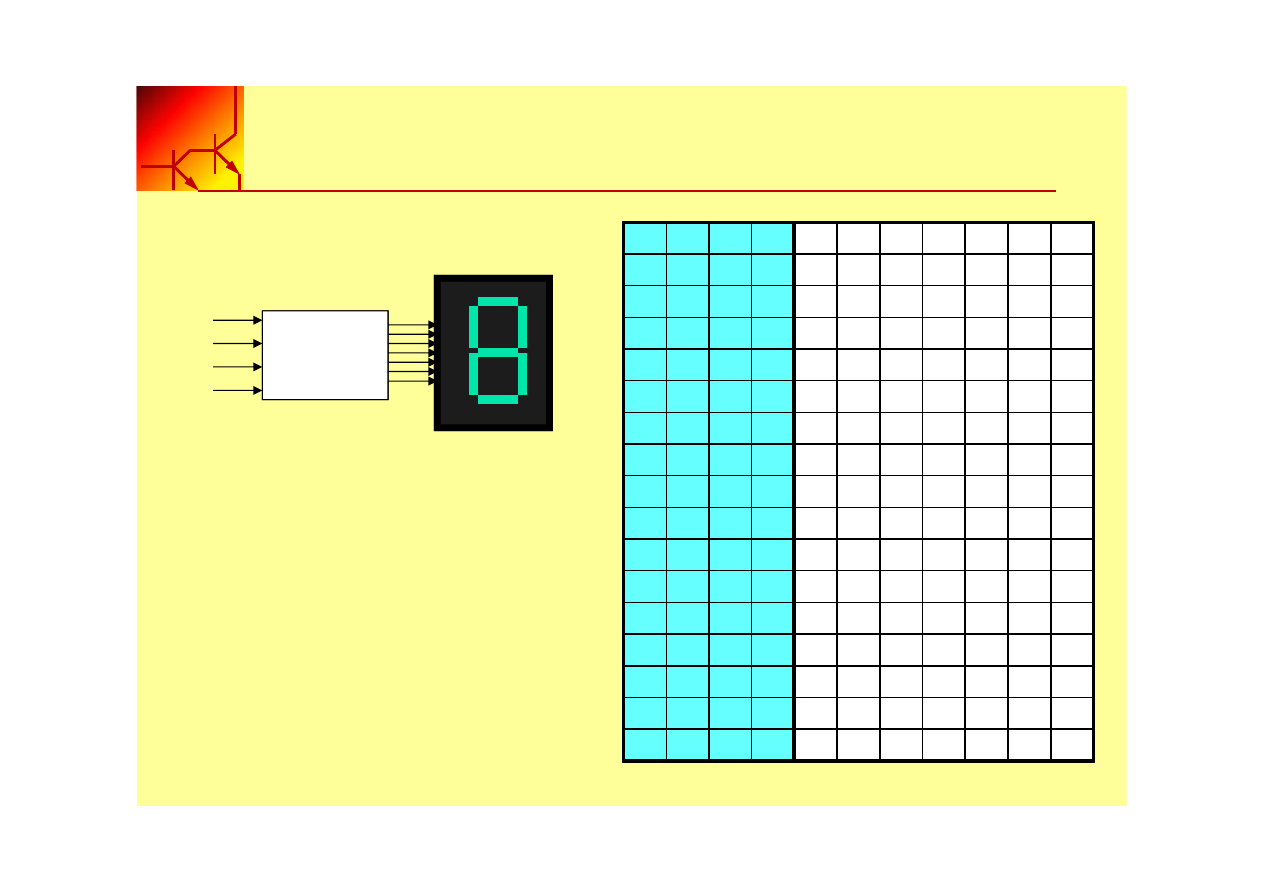
Budowa układu logicznego
Budowa układu logicznego
1
1
1
1
1
1
0
Decoder
BCD to 7 segm
x
0
x
1
x
2
x
3
b
c
d
e
f
a
g
1. Zbuduj tablicę prawdy
x
3
x
2
x
1
x
0
a
b
c
d
e
f
g
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
1
1
1 1
1
1
0
0
1
1 0
0
0
0
1
1
0 1
1
0
1
1
1
1 1
0
0
1
0
1
1 0
0
1
1
1
0
1 1
0
1
1
1
0
1 1
1
1
1
1
1
1 0
0
0
0
1
1
1 1
1
1
1
1
1
1 1
0
1
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
24 kwietnia 2013
Tablice Karnaugh
18
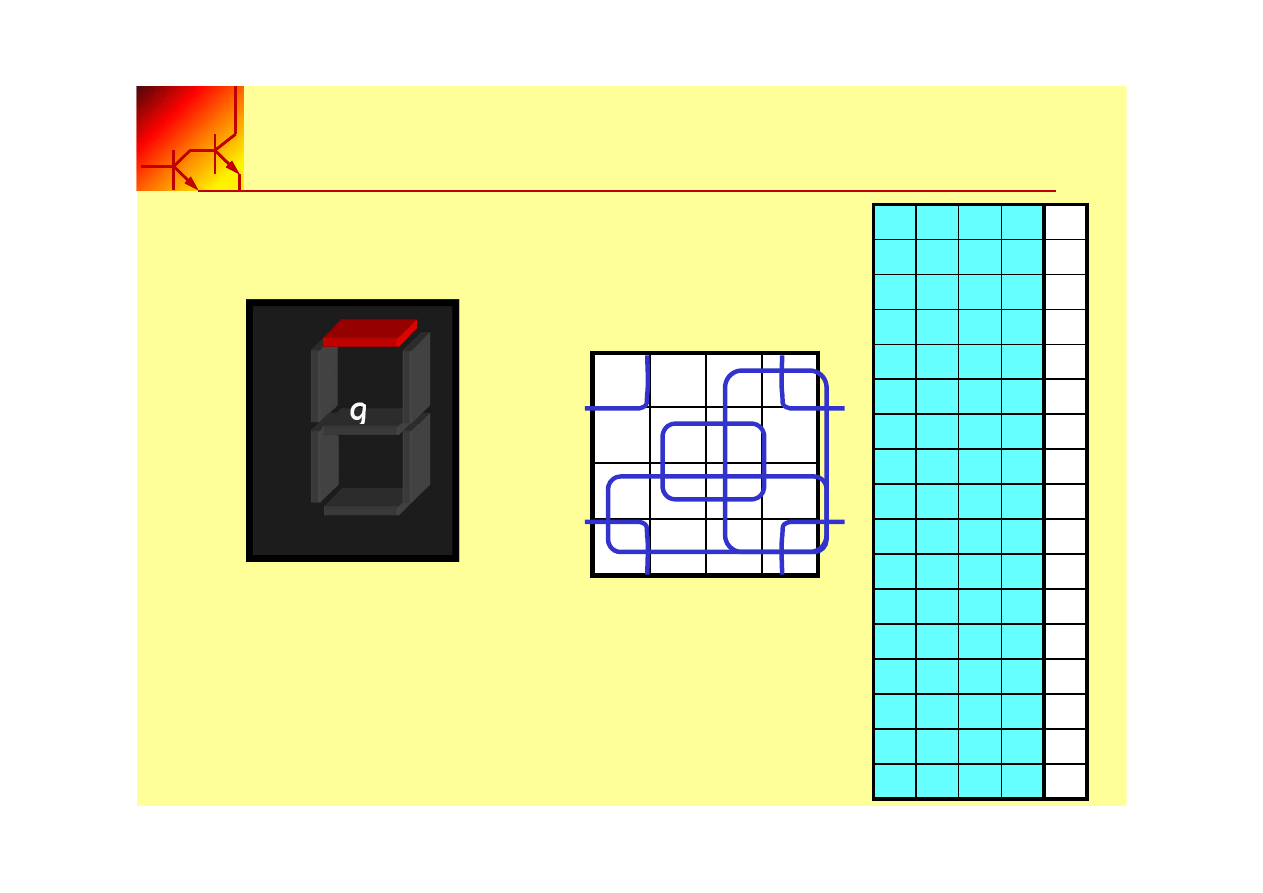
Budowa układu logicznego
Budowa układu logicznego
2. Utworzyć tablicę Karnaugh
x
3
x
2
x
1
x
0
a
0
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
x
1
0
1
1
x
1
1
0
0
x
1
1
0
0
x
1
1
1
0
x
1
1
1
1
x
c
d
e
f
g
b
a
x
3
x
2
x
1
x
0
00 01 11 10
00
01
11
10
1
0
1
1
0
1
1
1
1
1
X
X
X
X
X
X
a = x
1
+ x
3
+ x
0
x
2
+ x’
0
x’
2
3. Zapisać funkcję logiczną
24 kwietnia 2013
Tablice Karnaugh
19
Budowa układu logicznego
Budowa układu logicznego
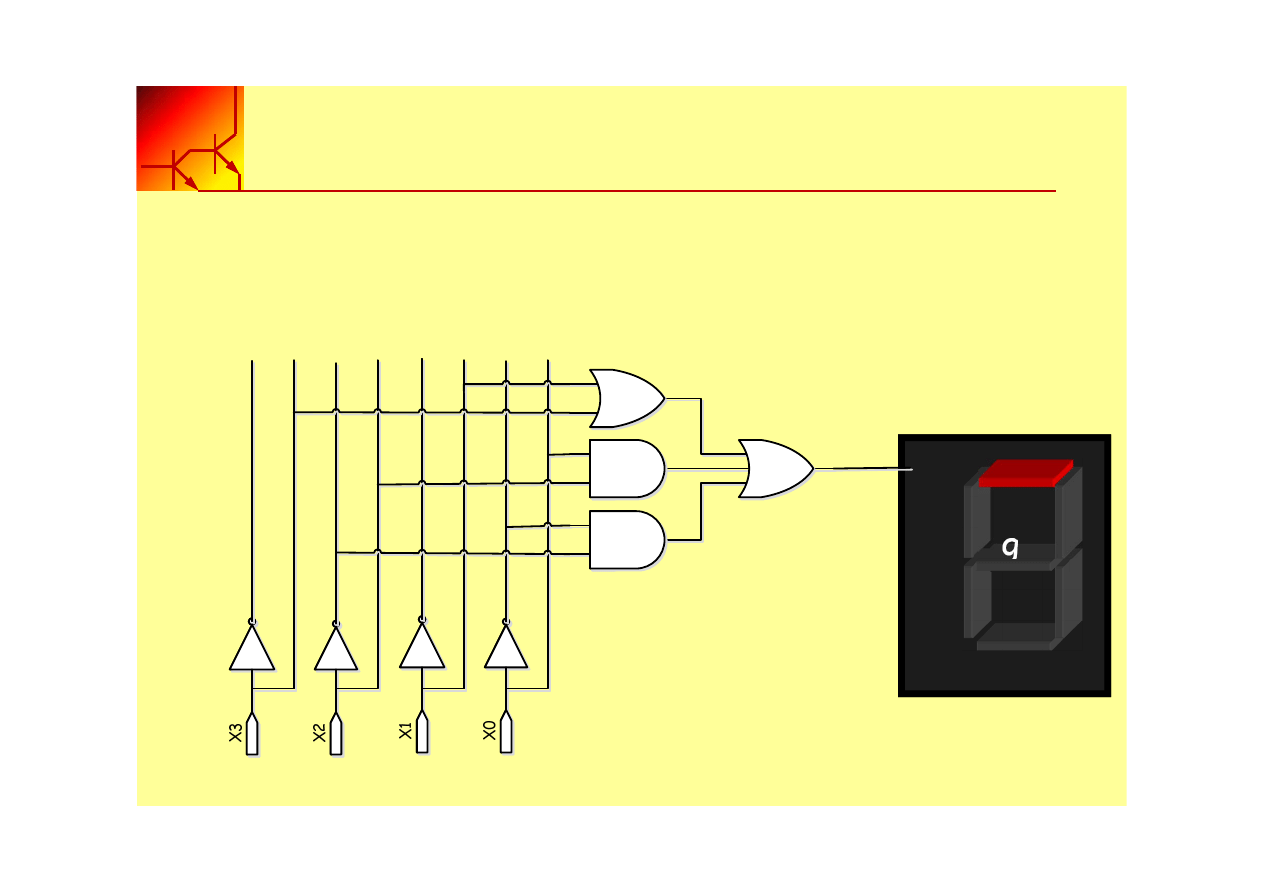
4. Narysować schemat układu logicznego
c
d
e
f
g
b
a
a = (x
1
+x
3
) + x
0
x
2
+ x’
0
x’
2
X1
X0
X3
X2
24 kwietnia 2013
Wojciech Kucewicz
20
Budowa układu logicznego
Budowa układu logicznego
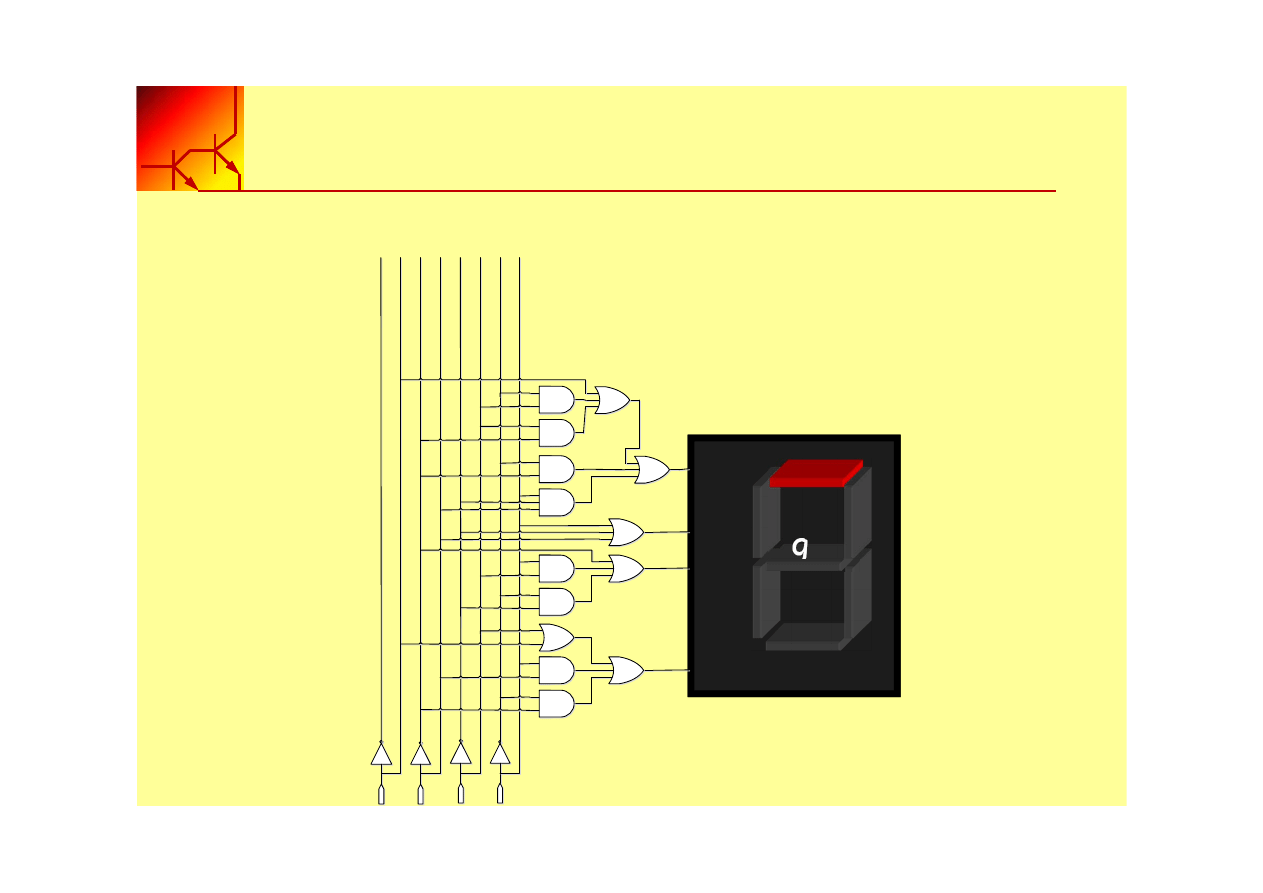
5. Dorysować schemat układu logicznego dla kolejnych diod
X1
X0
X3
X2
d
c
b
a
c
d
e
f
g
b
a
Wyszukiwarka
Podobne podstrony:
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
D20031152Lj id 130579 Nieznany
mechanika 3 id 290735 Nieznany
więcej podobnych podstron