
1
Metoda Gaussa-Seidla

2
A·x = b
x = G·x + c
A = A
L
+ A
D
+ A
U
=
0
.
.
.
.
.
0
.
0
0
.
0
0
2
1
21
n
n
L
a
a
a
A
=
nn
D
a
a
a
A
.
0
0
.
.
.
.
0
.
0
0
.
0
22
11
=
0
.
0
0
.
.
.
.
.
0
0
.
0
2
1
12
n
n
U
a
a
a
A
(A
L
+ A
D
+ A
U
)·x = b
(A
L
+ A
D
)·x = - A
U
·x + b
(A
L
+ A
D
)·x
(k+1)
= - A
U
·x
(k)
+ b k = 0, 1, …
,...
1
,
0
1
)
(
1
)
1
(
1
)
1
(
=
⋅
+
⋅
⋅
−
⋅
⋅
−
=
⋅
−
−
+
−
+
k
b
A
x
A
A
x
A
A
x
A
D
k
U
D
k
L
D
k
D
3
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
,...
1
,
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
,
1
1
1
,
2
2
1
,
1
1
1
,
33
3
,
33
3
,
4
33
34
1
,
2
33
32
1
,
1
33
31
1
,
3
22
2
,
22
2
,
3
22
23
1
,
1
22
21
1
,
2
11
1
,
11
1
,
3
11
13
,
2
11
12
1
,
1
=
+
⋅
−
−
⋅
−
⋅
−
=
+
⋅
−
−
⋅
−
⋅
−
⋅
−
=
+
⋅
−
−
⋅
−
⋅
−
=
+
⋅
−
−
⋅
−
⋅
−
=
+
−
−
+
+
+
+
+
+
+
+
+
k
a
b
x
a
a
x
a
a
x
a
a
x
a
b
x
a
a
x
a
a
x
a
a
x
a
a
x
a
b
x
a
a
x
a
a
x
a
a
x
a
b
x
a
a
x
a
a
x
a
a
x
nn
n
k
n
nn
nn
k
nn
n
k
nn
n
k
n
k
n
n
k
k
k
k
k
n
n
k
k
k
k
n
n
k
k
k
K
K
K
K
wektor c
n
,...,
,
i
a
b
c
ii
i
2
1
=
=
Macierz G

4
Zaczynamy obliczenia od przyj
ę
cia,
ż
e
c
x
=
)
0
(
Ko
ń
czymy obliczenia gdy
ε
<
−
+
)
(
)
1
(
k
k
x
x
Rozwi
ą
zanie
*
)
1
(
x
x
k
=
+

5
⋅⋅
⋅
⋅
⋅
⋅
⋅
⋅⋅
⋅
⋅⋅
⋅
=
nn
n
n
n
n
g
g
g
g
g
g
g
g
g
G
2
1
2
22
21
1
12
11
Warunki zbie
ż
no
ś
ci
n
,...,
,
i
g
n
,...,
,
j
g
n
j
ij
n
i
ij
2
1
1
2
1
1
1
1
=
<
=
<
∑
∑
=
=
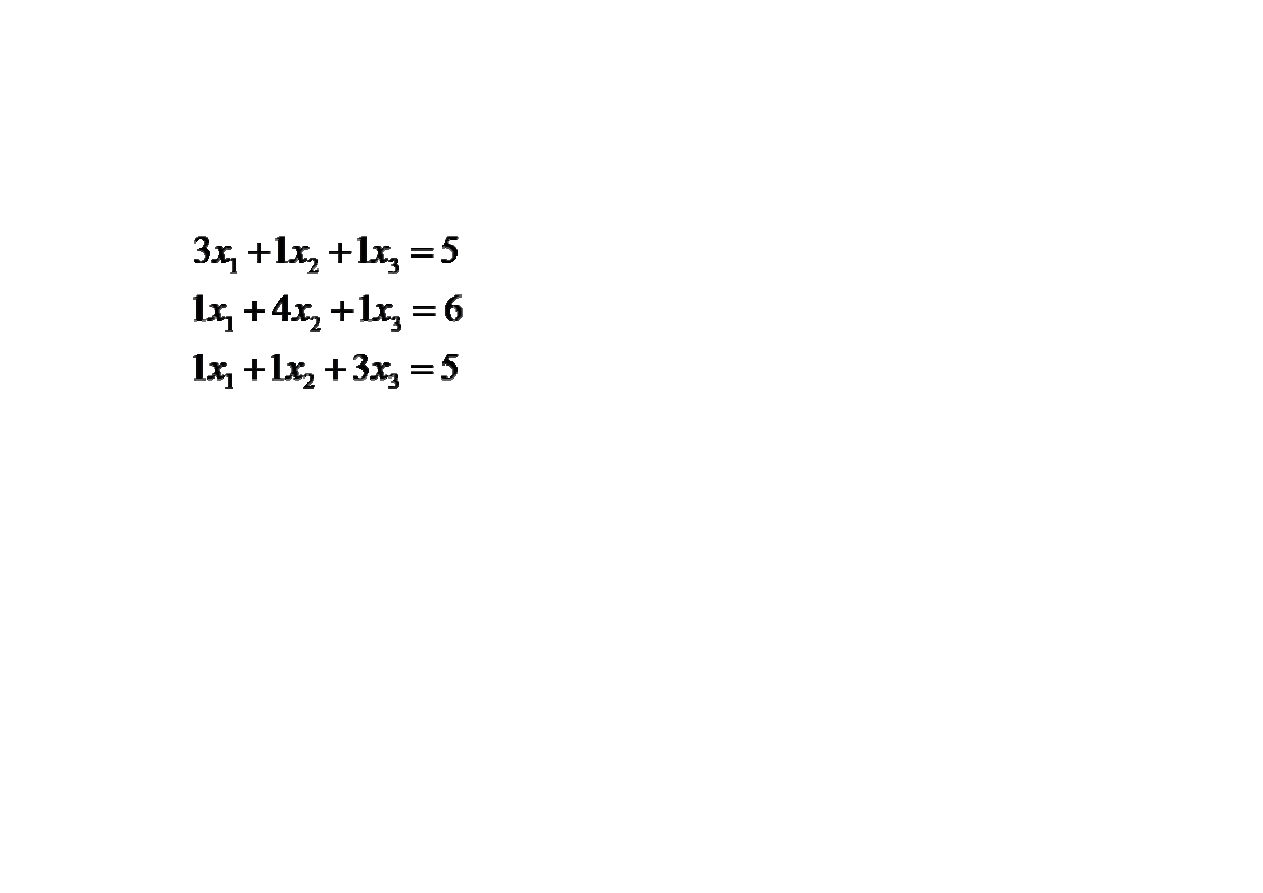
6
Przykład
Wyszukiwarka
Podobne podstrony:
Metoda Eliminacji Gaussa i Gaussa Seidla
Metoda Gaussa
METODA GAUSSA
Metoda Gaussa
Metoda Gaussa Seidela, GAUSSAID
6 Metoda Gaussa (1)
Projekt1 Meoda Gaussa seidlacka
Metoda Gaussa
Metoda Gausa Seidla MW
Metoda Gaussa Newtona przykład f Tornqvista
równań liniowych metoda Gaussa 06 2012
Metoda Gaussa obliczania rzędu macierzy
MOJE METODA GAUSSA SEIDELA
Rozwiązywanie równań metodą Gaussa
Metoda Gaussa powierzchnia
Metoda eliminacji Gaussa (1)
więcej podobnych podstron