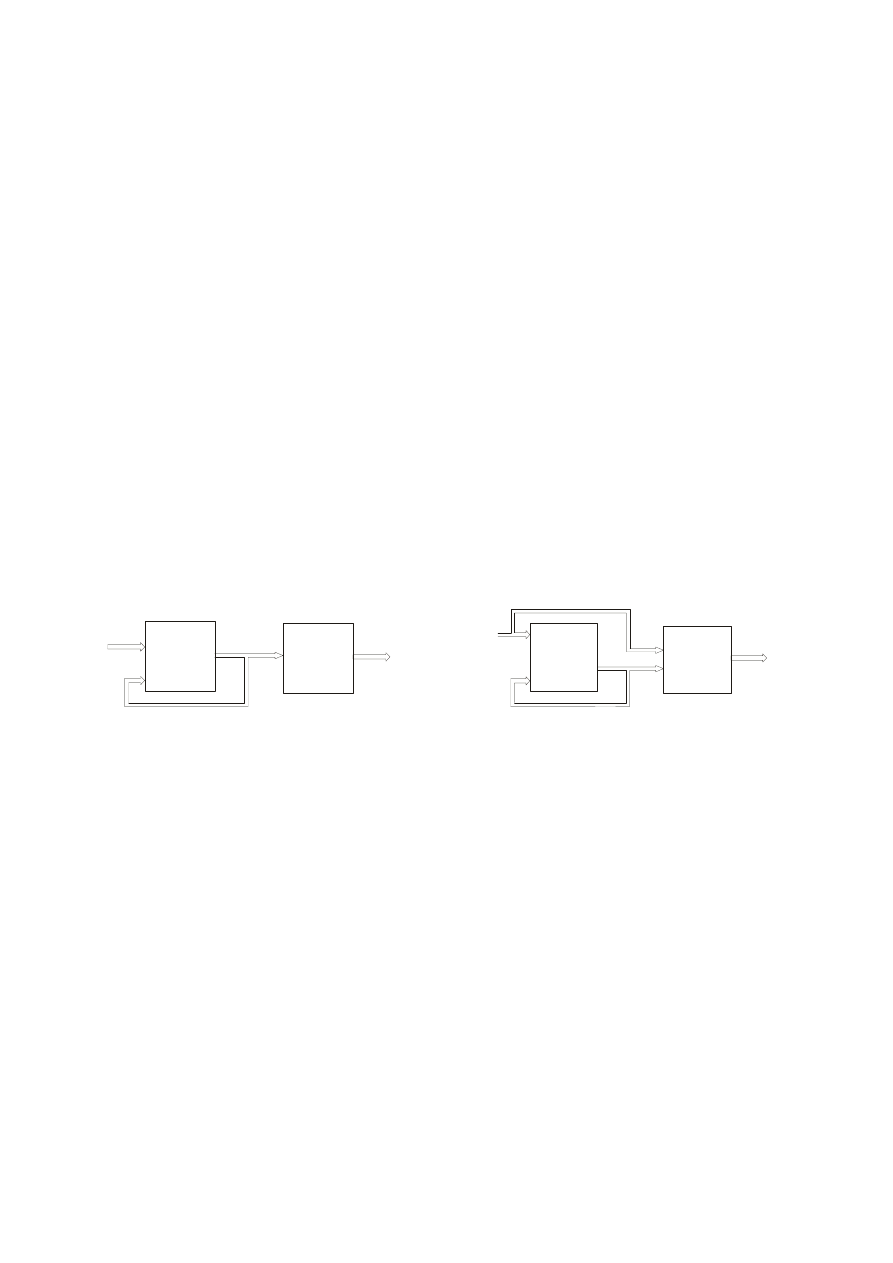
1

UKŁADY SEKWENCYJNE

1. Przerzutniki asynchroniczne i synchroniczne

2. Klasyfikacja układów sekwencyjnych

Układy sekwencyjne:

a) – układy procesowo zależne

- układy czasowo zależne

b) – układy Moore’a
- układy Mealy’ego
c) – układy asynchroniczne

- układy synchroniczne

d) – układy o programach liniowych

- układy o programach rozgałęzionych

e) - układy o działaniu cyklicznym

- układy acykliczne

f) – układy deterministyczne

- układy probabilistyczne













Schemat układu Moore’a

Schemat układu Mealy’ego

Funkcja przejść

Funkcja przejść

)

,

(

1

t

t

t

X

Q

Q







)

,

(

1

t

t

t

X

Q

Q







Funkcja wyjść

Funkcja wyjść

)

(

1

t

t

Q

Y





)

,

(

2

t

t

t

Q

X

Y





X

t

Q

t+1

Q

t

Y

t

X

t

Q

t+1

Q

t

2

3.

Synteza układów sekwencyjnych z elementów logicznych i
przerzutników

Ze względu na charakter zależności pomiędzy kolejnymi stanami sygnałów

oddziałujących na obiekt, można wyróżnić trzy typy procesów:

- w których określony jest czas trwania kolejnych faz procesu, a więc i czas trwania

kolejnych stanów sygnałów oddziałujących na obiekt,

- w których, czas trwania kolejnych faz procesu nie jest określony - rozpoczęcie

realizacji danej fazy uzależnione jest od zakończenia fazy poprzedniej,

- w których występują obydwa wymienione przypadki.

Układ przeznaczony do sterowania procesem pierwszego typu nazywa się układem

czasowo–zależnym. Układ taki nie ma sygnałów wejściowych, informujących o stanie
sterowania procesu. Układ czasowo-zależny realizować może tylko program liniowy. Układ
przeznaczony do sterowania procesem drugiego typu nazywa się procesowo-zależnym. Układ
sterowania procesami trzeciego typu jest rozwiązaniem pośrednim między układem czasowo
– zależnym a procesowo-zależnym.
Ogólnie w procesie syntezy układów sekwencyjnych można wyróżnić etapy:

- formalizacja założeń, czyli sformułowanie założeń w postaci umożliwiającej

tworzenie modelu matematycznego układu (w etapie tym wyodrębnia się stany
wewnętrzne, często w ilości większej niż jest to niezbędne, oraz przypisuje im stany
wyjść - przyjmuje się zatem model układu Moore’a. Najczęściej wyjściową formą
zapisu działania automatu jest pierwotna tablica przejść i wyjść, graf lub sieć działań,

- minimalizacja liczebności zbioru stanów wewnętrznych (w etapie tym podejmuje się

również decyzję o ewentualnej zmianie układu Moore'a na układ Mealy'ego, co
prowadzi do dalszego, zmniejszenia liczby stanów wewnętrznych),

- kodowanie, czyli przypisanie poszczególnym stanom wewnętrznym stanów sygnałów

pamięciowych,

- wyznaczanie funkcji wyjść,
- wyznaczanie funkcji przejść,
- sporządzenie schematów blokowych i montażowych,
- realizacja układu.

Przykład 1

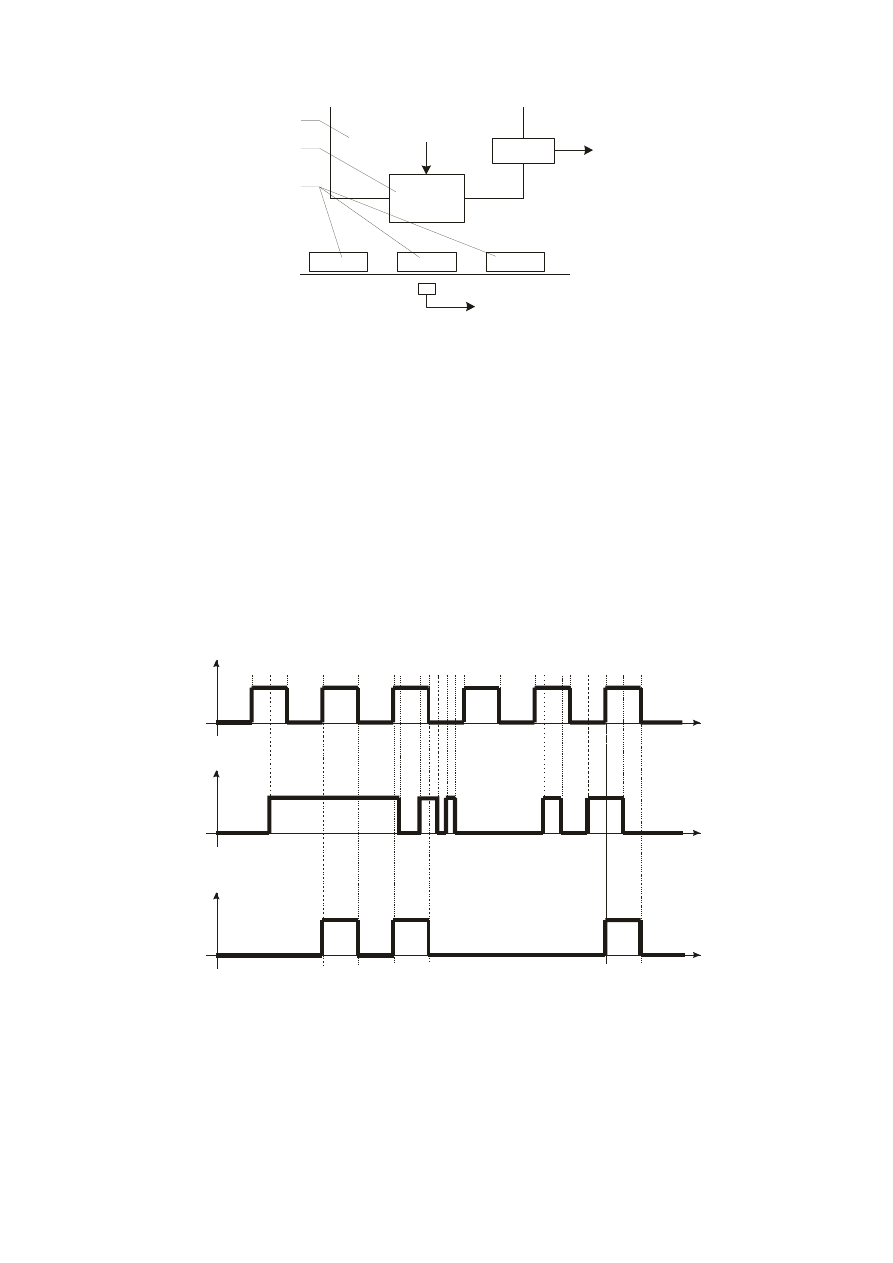
W wielogniazdowym automacie montażowo-pakującym (rys. 1) wyroby po

zmontowaniu gromadzone są w magazynie 1 i ładowane w kilku gniazdach do pojemników 3.
Do poszczególnych gniazd co pewien czas dostarczany jest pusty pojemnik 3, który pozostaje
w gnieździe przez okres wtedy tylko wystarczający do pełnego załadowania, kiedy ładowanie
rozpocznie się natychmiast po dostarczeniu pojemnika do gniazda. W okresach kiedy w
magazynie nie ma wystarczającej do pełnego załadowania kolejnego pojemnika ilości wy-
robów z magazynu do pojemnika nie powinno być uruchamiane. Z automatu wydalane są
wtedy puste pojemniki. Sortowanie pojemników na puste i pełne odbywa się poza automatem.

Urządzenie przekładające 2 włączane jest przez sygnał y=1. Urządzenie to powinno

być włączone na czas trwania sygnału x

1

=1, informującego o obecności pojemnika w

gnieździe, lecz tylko wtedy jeżeli w momencie pojawienia się stanu x

1

=1sygnał x

2

=1. Sygnał

x

2

=1 informuje o tym, że w magazynie znajduje cię wystarczająca do pełnego załadowania

kolejnego pojemnika ilość wyrobów.

Należy zaprojektować układ sterujący urządzeniem przekładającym 2. Zadaniem tego

układu jest zabezpieczenie przed możliwością częściowego zapełniania pojemników.

3

y

x

1

x

2

1

2

3

Rys. 1. Schemat do przykładu 1

Rozwiązanie

Projektowany układ ma jeden sygnał wyjściowy y (sterujący pracą urządzenia

przekładającego) oraz dwa sygnały wejściowe: x

1

i x

2

. Nie może to być układ kombinacyjny,

ponieważ dla x

1

=x

2

=1 zarówno może być y=0 (jeżeli stan x

1

=1 rozpoczął się gdy x

2

=0) jak i

y=1 (jeżeli stan x

1

=1 rozpoczął się gdy było x

2

=1). Jest to więc układ sekwencyjny. Ponieważ

zmiany stanu wyjść powinny zachodzić w momentach zmian stanów wejść, należy przyjąć, że
jest to układ asynchroniczny.

Dla układów o niewielkiej liczbie sygnałów wejściowych tablicę przejść i wyjść

tworzy się na podstawie przebiegów czasowych sygnałów. Ponieważ w trakcie pracy układu
wystąpić mogą różne sekwencje sygnałów wejściowych (nie ma określonego cyklu przebiegu
sygnałów – jest to więc układ o rozgałęzionym programie pracy), należy utworzyć
przykładowy przebieg czasowy sygnałów, starając się uwzględnić w nim wszystkie mogące
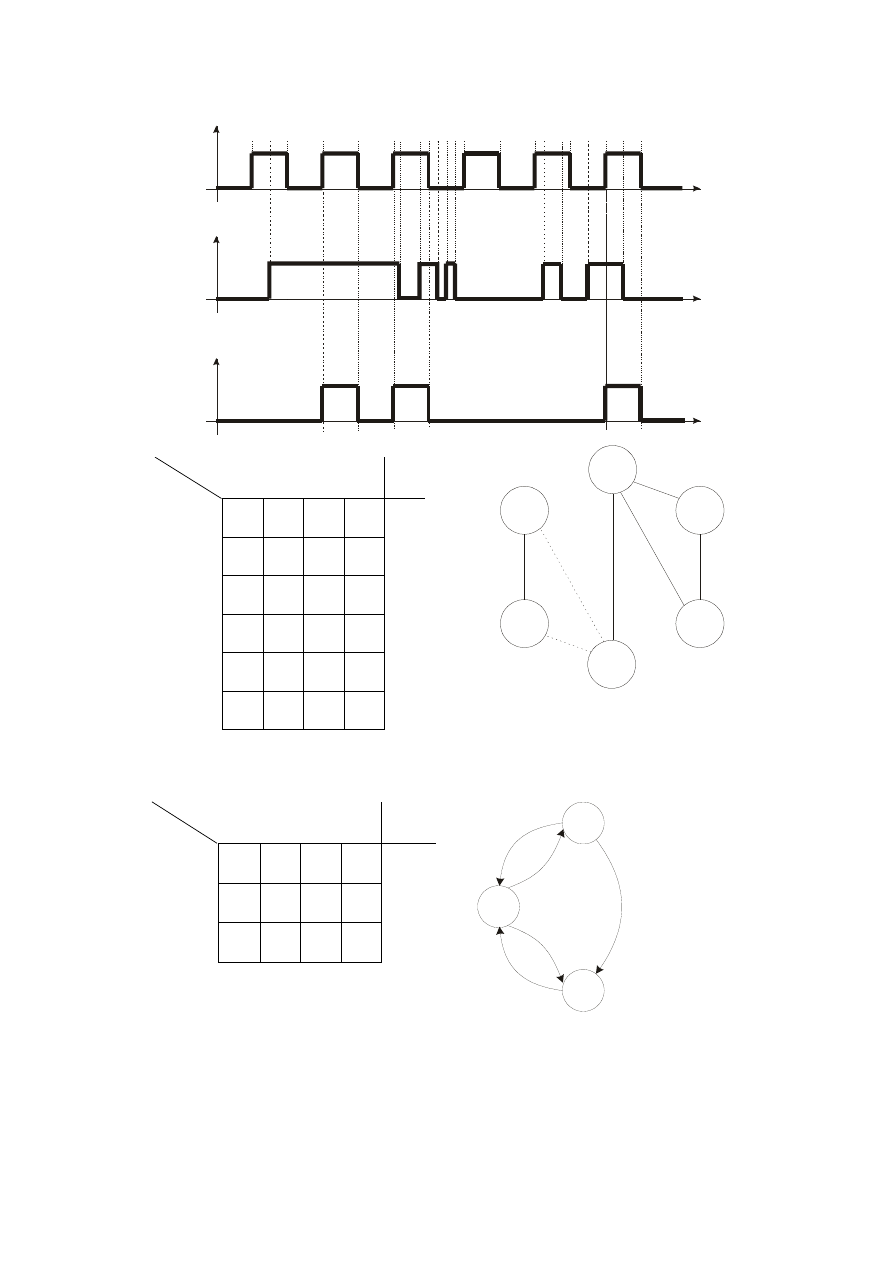
wystąpić podczas pracy sekwencje zmian. Przykład takiego przebiegu czasowego pokazano
na rys.

t

t

t

x

1

x

2

y

0

2

1

3

4

4

3

5 4 0

3

3

0 1

0 1 2 1 0 3 4 5

0

a)

4

t

t

t

x

1

x

2

y

0

2

1

3

4

4

3

5 4 0

3

3

0 1

0 1 2 1 0 3 4 5

0

0

1

2

3

4

5

Q

t+1

d)

e)

x

1

x

2

Q

t

00

01

11

10

y

0

1

2

Q

t+1

Rys. 2. Rysunek do przykładu 1: a) przebiegi czasowe sygnałów; b) pierwotna tablica przejść
i wyjść, c) wykres skracania, d) uproszczona (skrócona) tablica przejść i wyjść, e) wykres
przejść

x

1

x

2

Q

t

00

01

11

10

y

0

1

2

3

4

5

a)

b)

c)

1

2

0

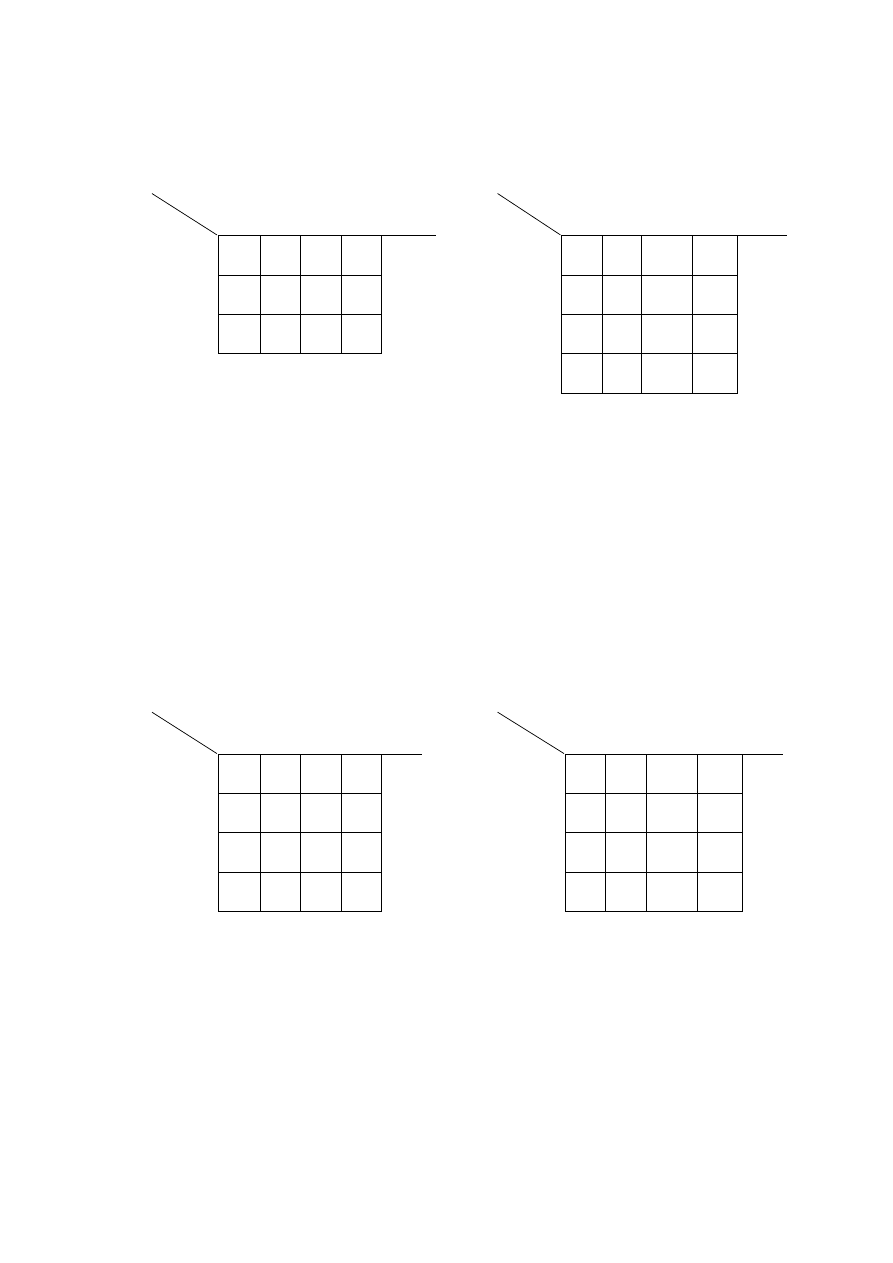
5

Wariant z przejściem cyklicznym

Tablica nie zakodowana

Tablica zakodowana

x

1

x

2

Q

t

00

01

11

10

y

0

1

2

Q

t+1

x

1

x

2

Q

1

Q

2

00

01

11

10

y

00

01

11

10

,

1

1



t

Q

1

2



t

Q

Funkcje przejść:




Fukcja wyjść:



Wariant z dodatkowym stanem wewnętrznym

Tablica nie zakodowana

Tablica zakodowana

x

1

x

2

Q

t

00

01

11

10

y

0

1

2

3

Q

t+1

x

1

x

2

Q

1

Q

2

00

01

11

10

y

00

01

11

10

,

1

1



t

Q

1

2



t

Q

Funkcje przejść:




Fukcja wyjść:

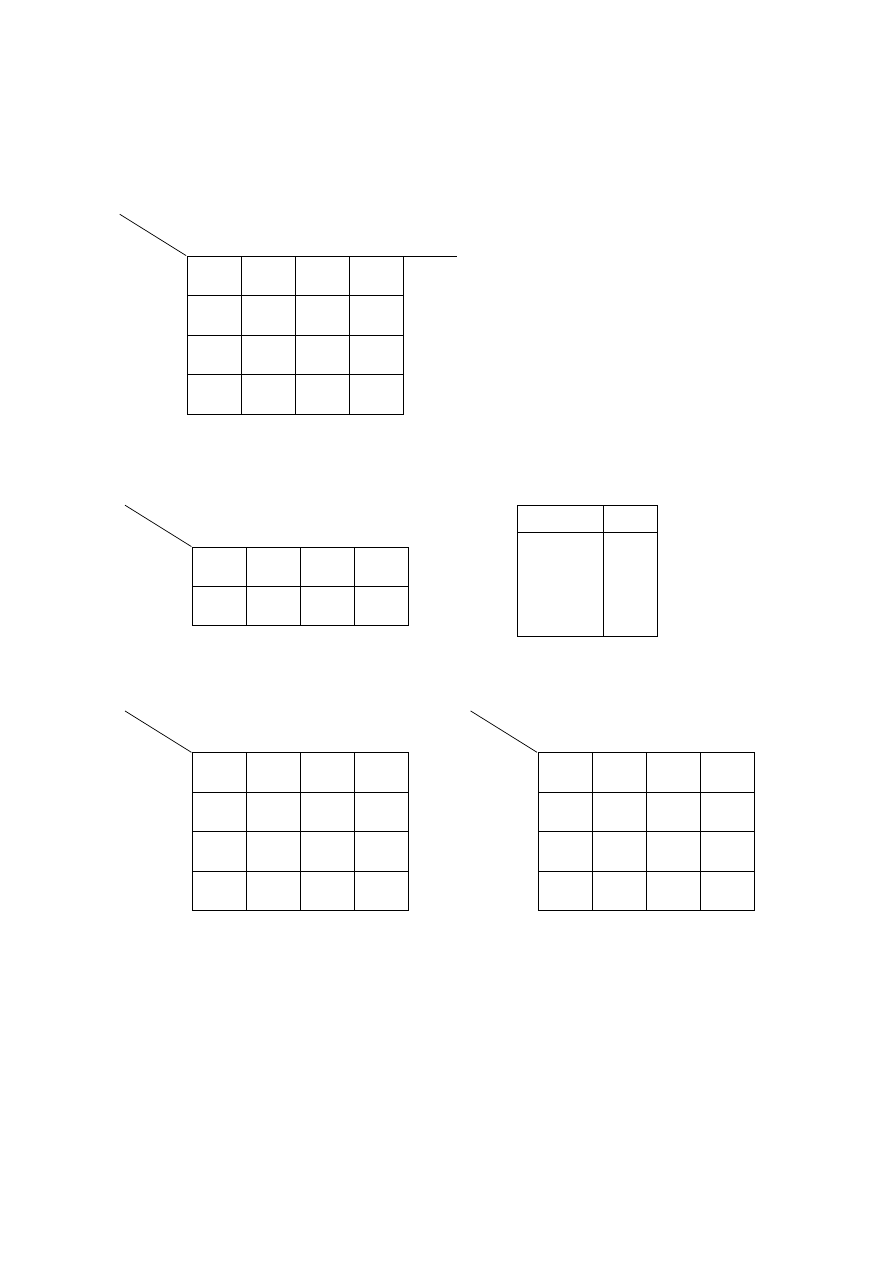
6

Projektowanie układu z wydzielonym blokiem przerzutników wz
(wariant z dodatkowym stanem wewnętrznym)

Tablica przejść i wyjść

x

1

x

2

Q

1

Q

2

00

01

11

10

y

00

01

11

10

,

1

1



t

Q

1

2



t

Q

Tablica przejść przerzutnika wz

Macierz przejść przerzutnika wz

wz

Q

t

00

01

11

10

0

0

0

-

1

1

1

0

-

1

Q

t+1

Q

t



Q

t+1

wz

0



0

0



1

1



1

1



0

0-

10

-0

01

Tablica wzbudzeń przerzutnika Q

1

Tablica wzbudzeń przerzutnika Q

2

x

1

x

2

Q

1

Q

2

00

01

11

10

00

01

11

10

w

1

z

1

x

1

x

2

Q

1

Q

2

00

01

11

10

00

01

11

10

w

2

z

2

Funkcje wzbudzeń:

w

1

=

w

2

=

z

1

=

z

2

=

Funkcja wyjść:

y =

7

Uniwersalna tablica przejść i wyjść

x

1

x

2

Q

1

Q

2

00

01

11

10

y





w

F1 (F1, F-)





z

F0 (F0, F-)

00

01

11

10

,

1

1



t

Q

1

2



t

Q

Schemat układu

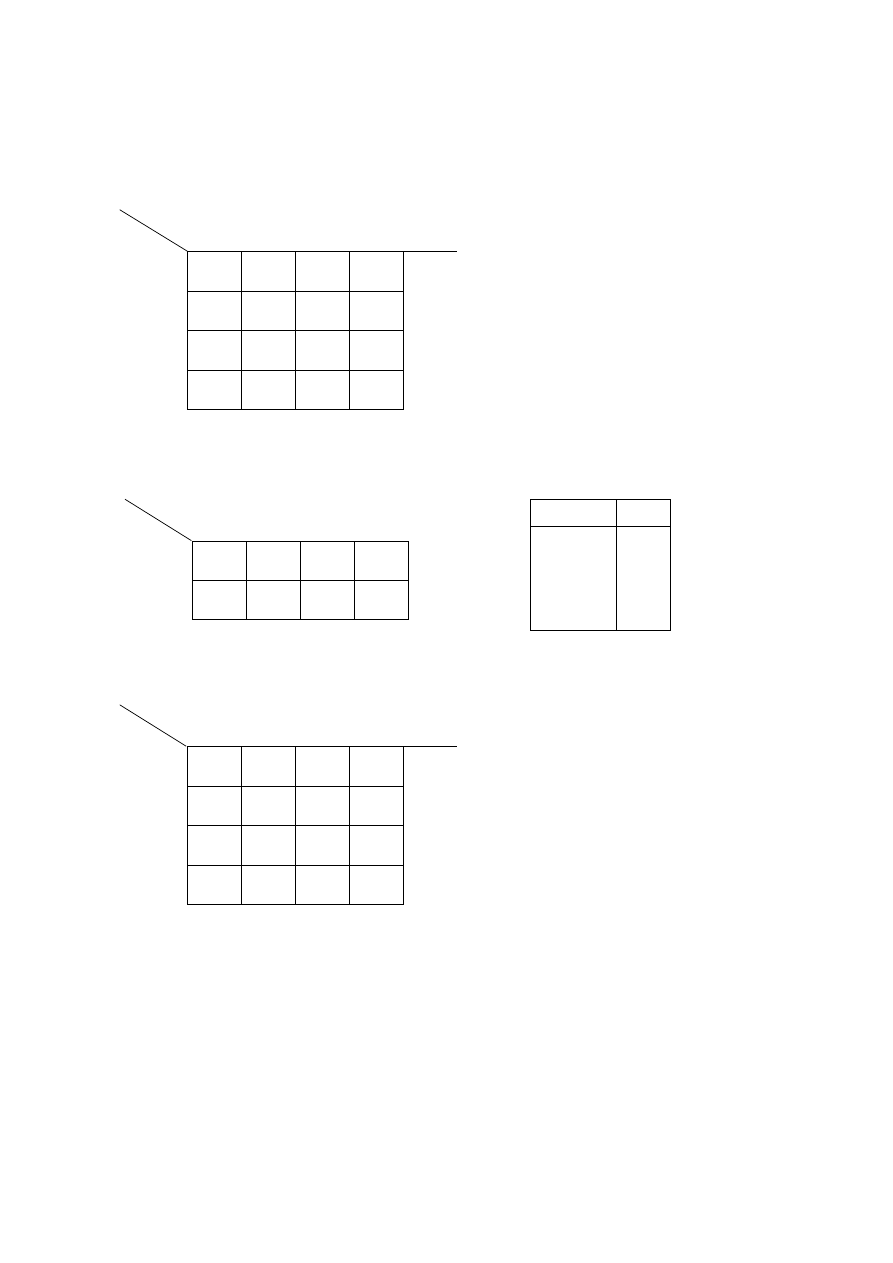
8

Układ synchroniczny z blokiem przerzutników JK
(oryginalna wersja układu)

x

1

x

2

Q

1

Q

2

00

01

11

10

y





J

F1 (F0, F1, F-)





K

F0 (F1, F0, F-)

00

01

11

10

,

1

Q



2

Q



Tablica przejść przerzutnika JK

Macierz przejść przerzutnika JK

JK

Q

t

00

01

11

10

0

0

0

1

1

1

1

0

0

1

Q

t+1

Q

t



Q

t+1

JK

0



0

0



1

1



1

1



0

0-

1-

-0

-1

Tablica wzbudzeń przerzutnika Q

1

x

1

x

2

Q

1

Q

2

00

01

11

10

y

00

01

11

10

J

1

K

1

Funkcje wzbudzeń:

J

1

=

J

2

=

K

1

=

K

2

=

Fukcja wyjść:

y =

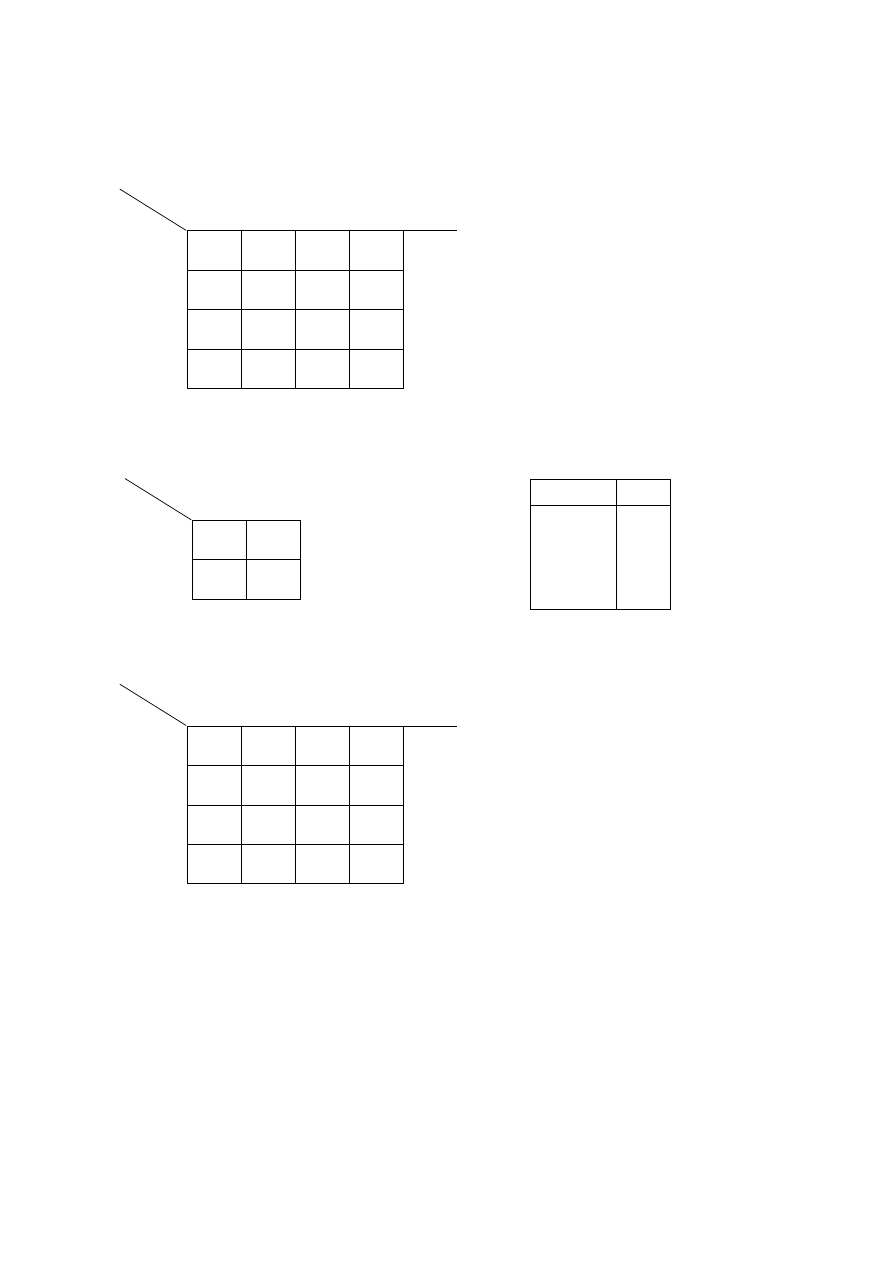
9

Układ synchroniczny z blokiem przerzutników D
(oryginalna wersja układu)

x

1

x

2

Q

1

Q

2

00

01

11

10

y

00

01

11

10

,

1

Q



2

Q



Tablica przejść przerzutnika D

Macierz przejść przerzutnika D

D

Q

t

0

1

0

0

1

1

0

1

Q

t+1

Q

t



Q

t+1

D

0



0

0



1

1



1

1



0

0

1

1

0

Tablica wzbudzeń przerzutnika Q

1

x

1

x

2

Q

1

Q

2

00

01

11

10

y

00

01

11

10

1

D

Funkcje wzbudzeń:

D

1

=

D

2

=

Funkcja wyjść:

y =

Układ Mealy’ego asynchroniczny

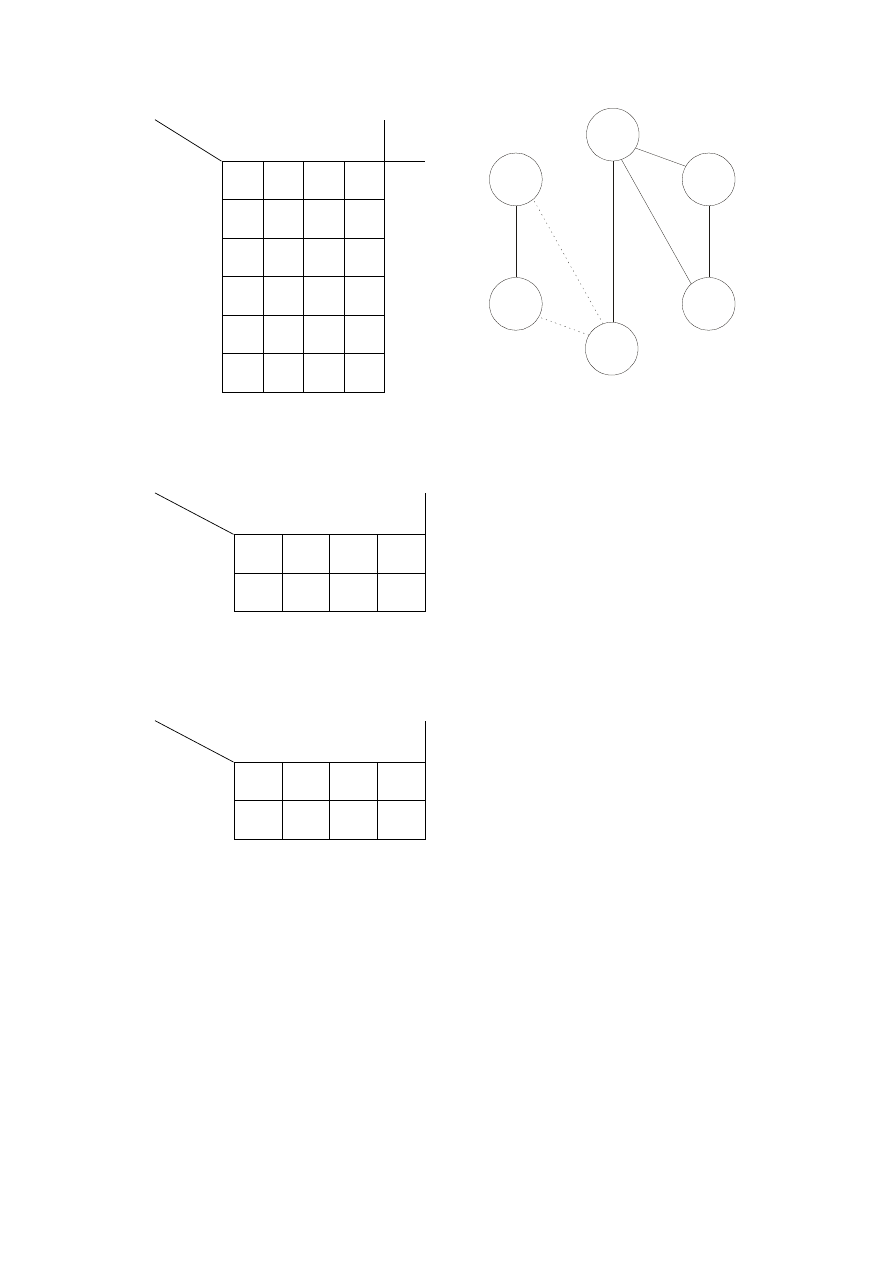
10

0

1

2

3

4

5

Q

t+1

Tablica przejść uproszczona (skrócona)










Tablica wyjść

x

1

x

2

Q

t

00

01

11

10

y

0

0

3

-

1

0

1

0

-

2

1

0

2

-

3

2

1

0

3

0

3

4

-

0

4

-

3

4

5

1

5

0

-

4

5

1

x

1

x

2

Q

t

00

01

11

10

0

1

Q’

x

1

x

2

Q

t

00

01

11

10

0

1

y

a)

b)