Czy neutrina

Czy neutrina

mogą nam coś powiedzieć

mogą nam coś powiedzieć

na temat asymetrii

na temat asymetrii

między materią i antymaterią

między materią i antymaterią

we Wszechświecie?

we Wszechświecie?

Czy neutrina

Czy neutrina

mogą nam coś powiedzieć

mogą nam coś powiedzieć

na temat asymetrii

na temat asymetrii

między materią i antymaterią

między materią i antymaterią

we Wszechświecie?

we Wszechświecie?

Seminarium IFJ PAN, Kraków, 05.12.2013

Tomasz Wąchała

Zakład Neutrin i Ciemnej Materii (NZ16)

2

Plan

Plan

Plan

Plan

●

Neutrina w Modelu Standardowym fizyki cząstek.

●

Oscylacje neutrin.

●

Ostatni kąt mieszania neutrin a symetria CP.

●

Eksperymenty T2K i Daya Bay.

●

Przyszłe pomiary dotyczące symetrii CP w oscylacjach
neutrin.

●

Asymetria między materią i antymaterią we

wszechświecie.

●

Bariogeneza, leptogeneza i symetria CP.

●

,,Ciężkie” neutrina.

3

Neutrina w Modelu Standardowym

Neutrina w Modelu Standardowym

fizyki cząstek

fizyki cząstek

Neutrina w Modelu Standardowym

Neutrina w Modelu Standardowym

fizyki cząstek

fizyki cząstek

●

Neutrino w Modelu Standardowym
jest cząstką elementarną o
następujących własnościach:

➔

Jest bezmasowe

➔

Występuje w trzech zapachach

(elektronowe: ν

e

, mionowe: ν

μ

,

taonowe: ν

τ

)

➔

Spin ½

➔

Jest obojętne elektrycznie (ładunek

zerowy)

➔

Oddziałuje wyłącznie słabo

➔

Obserwowane są tylko lewoskrętne

neutrina (skrętność = rzut spinu na

kierunek pędu)

➔

Może być cząstką Majorany (w teorii

Majorany cząstka = antycząstka)

4

Oscylacje neutrin

Oscylacje neutrin

Oscylacje neutrin

Oscylacje neutrin

●

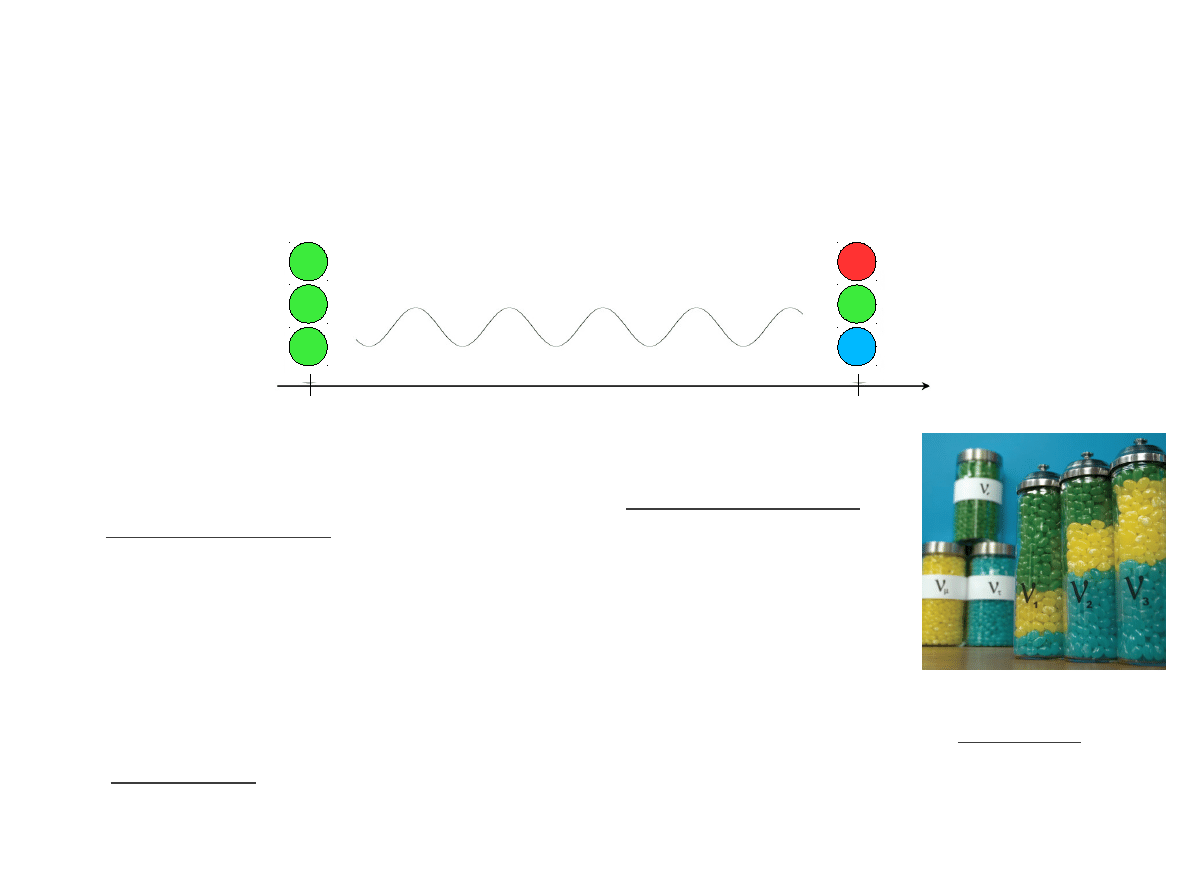
Neutrina oscylują, czyli zmieniają swój zapach.

●

Neutrina są produkowane i rejestrowane poprzez oddziaływania

słabe ale propagują się w przestrzeni jako kombinacje liniowe

stanów masowych (

stany masowe ≠ stany zapachowe

)

[

ν

e

ν

μ

ν

τ

]

=

U

PMNS

[

ν

1

ν

2

ν

3

]

Stany

zapachowe

Stany

masowe

●

Prawdopodobieństwo oscylacji P(ν

α

→ ν

β

) zależy od elementów macierzy

mieszania U

PMNS

oraz od sin

2

(Δm

ij

2

L/E), gdzie Δm

ij

2

= m

i

2

-m

j

2

Źródło neutrin

o energii E

(tylko neutrina

mionowe)

Detektor

(neutrina

trzech zapachów)

ν

μ

ν

μ

ν

μ

ν

e

ν

μ

ν

τ

L

Oscylacje

5

Oscylacje neutrin – stan wiedzy

Oscylacje neutrin – stan wiedzy

eksperymentalnej

eksperymentalnej

Oscylacje neutrin – stan wiedzy

Oscylacje neutrin – stan wiedzy

eksperymentalnej

eksperymentalnej

Neutrina mają masę
(małą < eV
ale niezerową!

Δ

m

ij

2

~10

-3

10

-5

eV

2

)

Neutrina
oscylują

U

PMNS

=

(

1
0
0

0

c

23

−

s

23

0

s

23

c

23

)

⋅

(

c

13

0

−

s

13

e

−

i δ

CP

0
1
0

s

13

e

−

i δ

CP

0

c

13

)

⋅

(

c

12

s

12

0

s

12

c

12

0

0
0
1

)

Parametryzacja

macierzy

mieszania

neutrin

c

ij

=

cosθ

ij

s

ij

=

sin θ

ij

●

Szereg eksperymentów w ciągu ostatnich 15 lat

potwierdziło istnienie zjawiska oscylacji neutrin

●

Wartości parametrów oscylacji neutrin takich jak

trzy kąty mieszania θ

ij

i dwie różnice kwadratów

mas neutrin Δm

2

ij

są różne od zera!

Zdaniem wielu
teoretyków fizyka
poza Modelem
Standardowym!

6

Czego jeszcze nie wiemy i co

Czego jeszcze nie wiemy i co

możemy zmierzyć?

możemy zmierzyć?

Czego jeszcze nie wiemy i co

Czego jeszcze nie wiemy i co

możemy zmierzyć?

możemy zmierzyć?

Faza Diraca δ

CP

= ?

→ Łamanie lub zachowanie

symetrii CP w oscylacjach neutrin

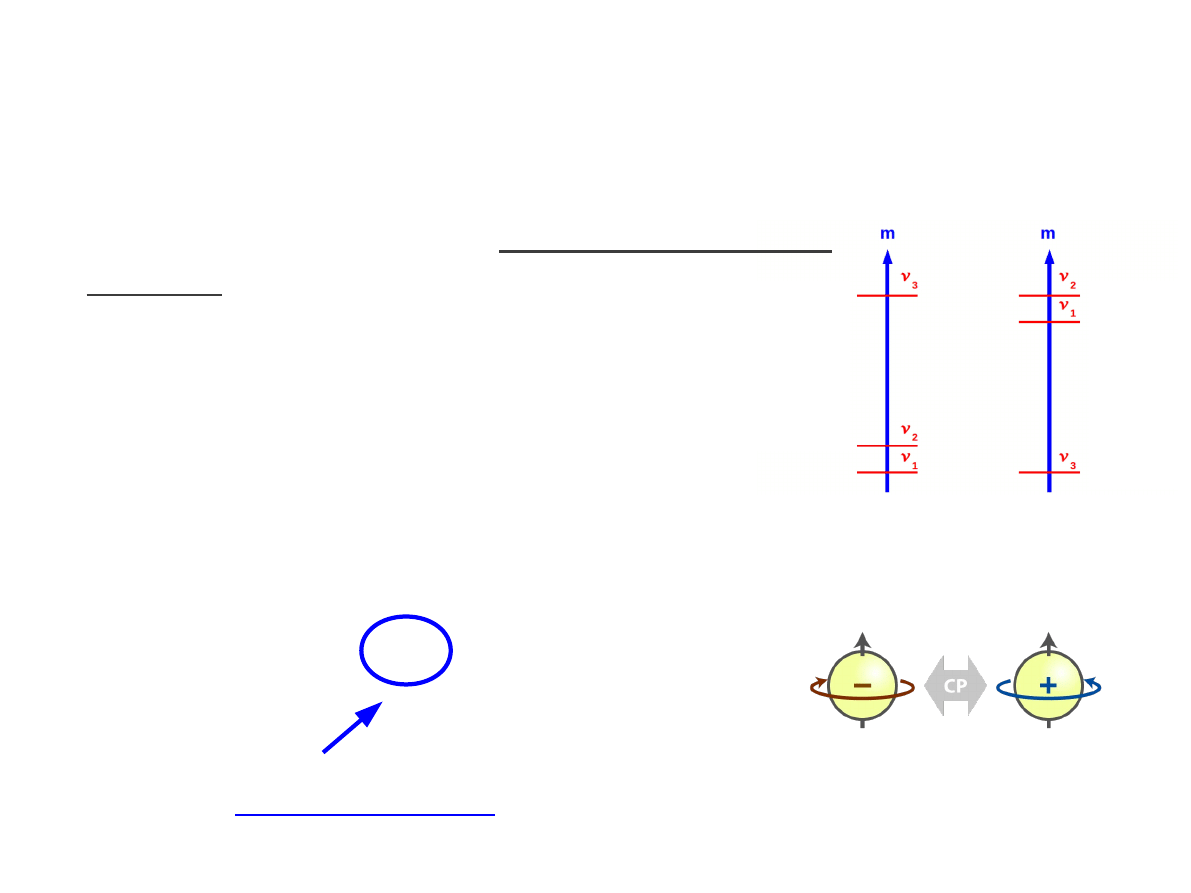
Hierarchia mas neutrin

Normalna? Odwrócona?

U

PMNS

=

(

1
0
0

0

c

23

−

s

23

0

s

23

c

23

)

⋅

(

c

13

0

−

s

13

e

−

i δ

CP

0
1
0

s

13

e

−

i δ

CP

0

c

13

)

⋅

(

c

12

s

12

0

s

12

c

12

0

0
0
1

)

●

Co możemy zmierzyć poprzez oscylacje
neutrin:

➔

Kąt mieszania θ

23

< 45̊ czy θ

23

> 45̊?

➔

Jaka hierarchia mas neutrin (znak

Δ

m

2

23

)

?

➔

Jaka wartość fazy δ

CP

?

elektron

pozyton

7

Kąt mieszania

Kąt mieszania

θ

θ

13

13

oraz

oraz

δ

δ

CP

CP

Kąt mieszania

Kąt mieszania

θ

θ

13

13

oraz

oraz

δ

δ

CP

CP

●

Można zmierzyć δ

CP

tylko jeśli kąt mieszania θ

13

jest

niezerowy. Najlepiej aby był duży!

●

Jak wyznaczyć kąt θ

13

?

➔

Pomiar ile neutrin elektronowych pojawiło się
w akceleratorowej wiązce neutrin

mionowych

➔

Pomiar ile neutrin elektronowych z reaktora zanikło

(,,przeoscylowało” w neutrina innego zapachu):

P(ν

μ

→ν

e

)≈

sin

2

2θ

13

sin

2

θ

23

sin

2

(

1.27 Δ m

23

2

L

E

)

P(ν

e

→ν

e

)≈

1−

sin

2

2θ

13

sin

2

(

1.27Δ m

31

2

L

E

)

+ człony zależne od δ

CP

+ człony mocno zależne
od hierarchii mas neutrin

+ człony słabo zależne
od hierarchii mas neutrin

ν

ν

e

e

ν

ν

μ

μ

ν

ν

τ

τ

ν

ν

e

e

ν

ν

μ

μ

ν

ν

τ

τ

8

Krótka historia kąta mieszania

Krótka historia kąta mieszania

θ

θ

13

13

Krótka historia kąta mieszania

Krótka historia kąta mieszania

θ

θ

13

13

➔

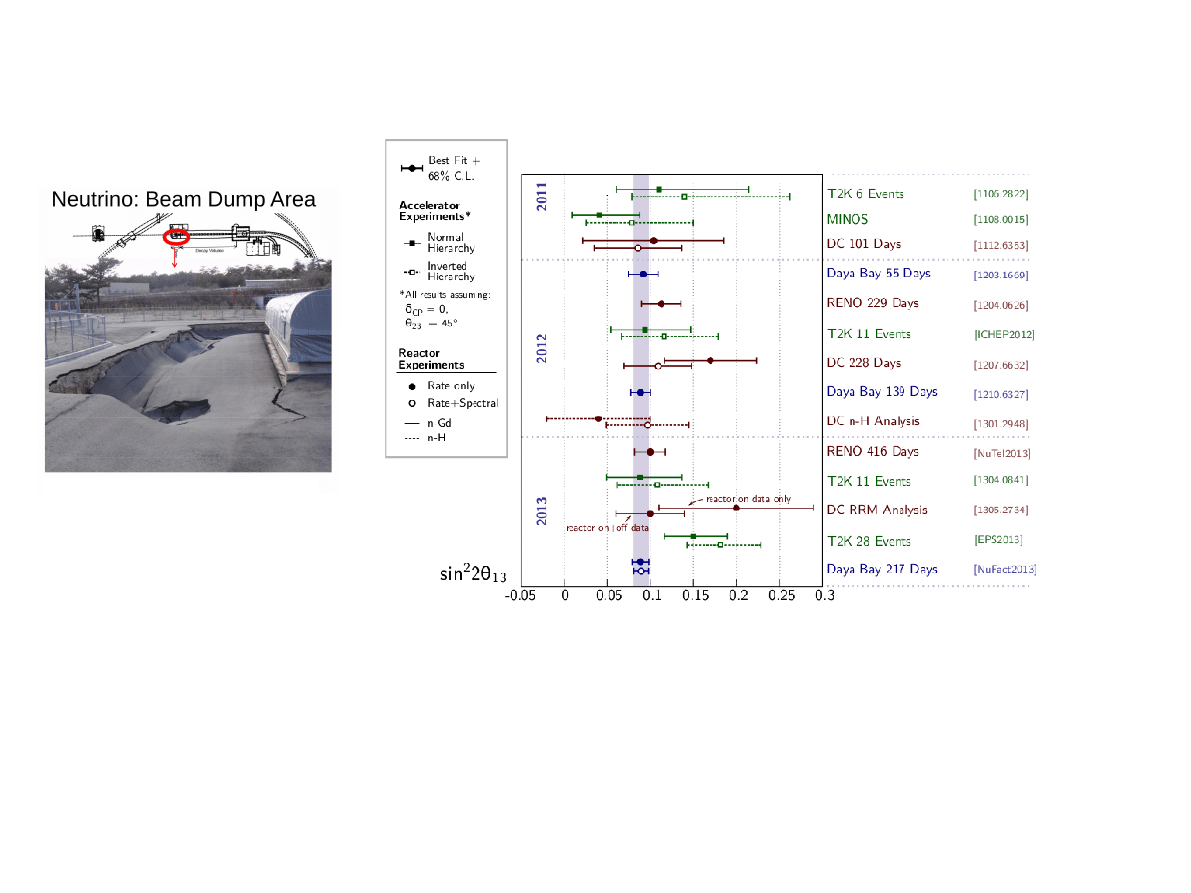
Czerwiec 2011: Pierwsze wyniki T2K (dane sprzed trzęsienia ziemi Tohoku). Kąt θ

13

rózny

od zera na poziomie 2.5 odchylenia standardowego (

Top Cite: 694 cytowań w Inspire

),

➔

Marzec 2012: Eksperyment Daya Bay: sin

2

2θ

13

= 0.0890.010(stat)0.005(syst.)

➔

Lipiec 2013: Ulepszona analiza w T2K (28 zarejestrowanych neutrin elektronowych). Kąt

θ

13

różny od zera na poziomie 7.3 odchyleń standardowych

➔

Sierpień 2013: Daya Bay i najdokładniejszy pomiar θ

13

: sin

2

2θ

13

= 0.0890.009

Marzec 2011
J-PARC zaraz po
trzęsieniu ziemi Tohoku

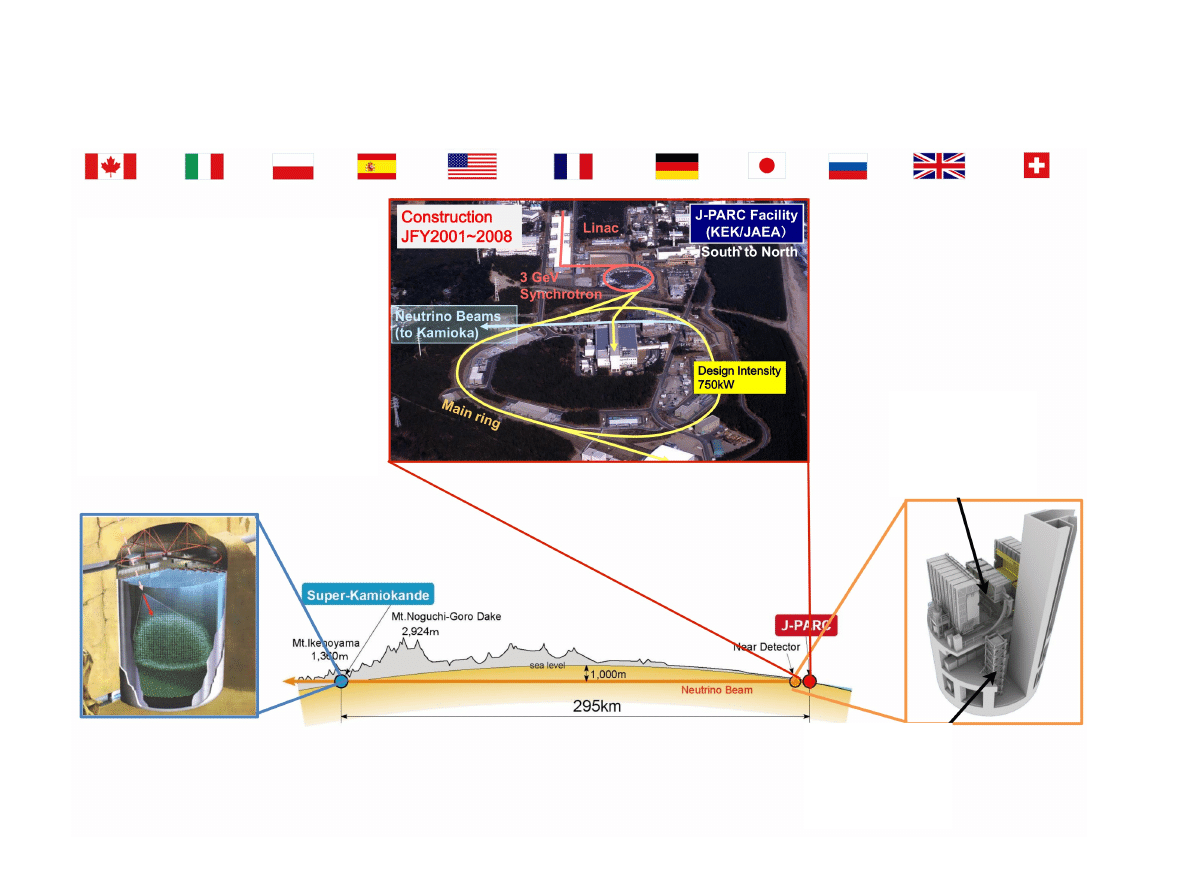
Eksperyment T2K

Eksperyment T2K

Eksperyment T2K

Eksperyment T2K

●

11 krajów,

●

59 instutucji (w
tym IFJ PAN)

●

~500 ludzi

Detektor daleki

(Super-Kamiokande)

→ Tutaj ,,wyłapuje” się neutrina,

które przeoscylowały.

Ośrodek akceleratorowy

J-PARC

→ Tutaj produkuje

się neutrina mionowe

Detektor bliski

→ Tutaj mierzy się

parametry neutrin

zanim zaszły

oscylacje.

10

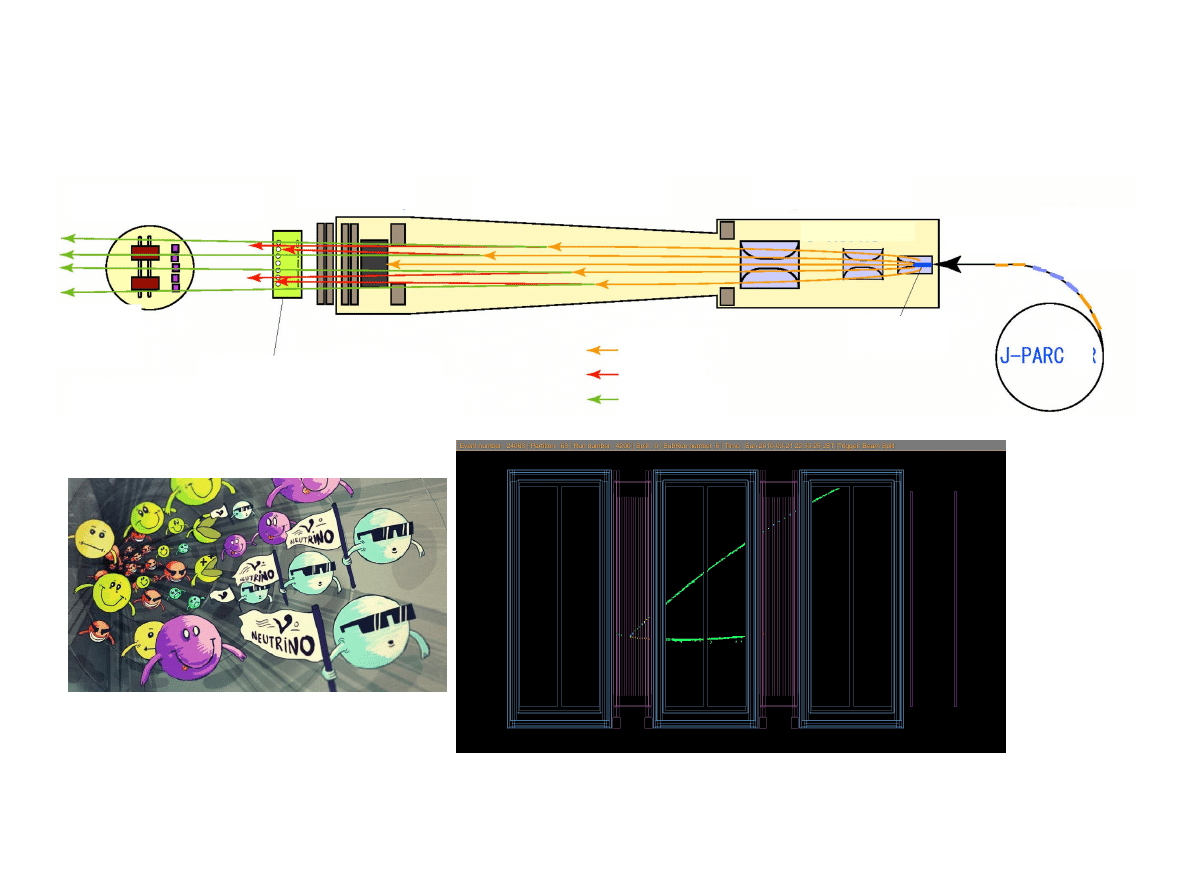
Wiązka neutrin z akceleratora

Wiązka neutrin z akceleratora

i detektor bliski

i detektor bliski

Wiązka neutrin z akceleratora

Wiązka neutrin z akceleratora

i detektor bliski

i detektor bliski

Detektor bliski

Detektor (monitor)

mionowy

Tunel rozpadu

Tarcza

Protony

piony
miony
neutrina

Do
detektora

dalekiego

(akcelerator)

Oddziaływanie neutrina w det. bliskim

Oddziaływanie neutrina w det. bliskim

●

Po co nam detektor bliski? Urządzenie do pomiaru parametrów wiązki neutrin

mionowych (widmo energetyczne) zanim zaszły oscylacje.

11

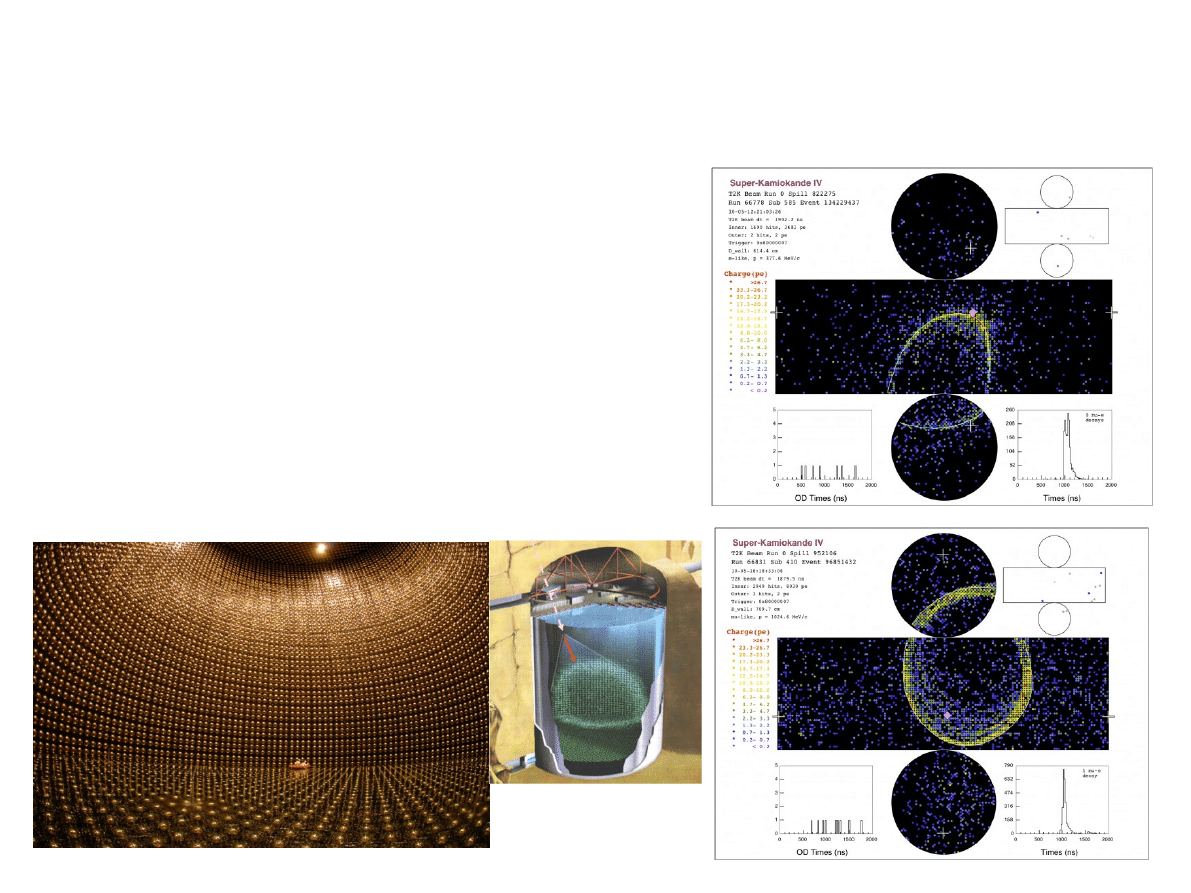
Największy garnek z wodą?

Największy garnek z wodą?

Największy garnek z wodą?

Największy garnek z wodą?

●

Detektor Super-Kamiokande, to obecnie największy

detektor neutrin na świecie:

➔

Zbiornik w kształcie walca o średnicy i

wysokości

40m,

➔

Umiejscowiony w kopalni Kamioka

1km pod

ziemią

(aby uwolnić się od tła od promieni

kosmicznych),

➔

Zawiera

50 tysięcy ton

bardzo czystej wody

●

11 tyś. fotopowielaczy

rejestruje promieniowanie

Czerenkowa wysyłane przez cząstki naładowane

powstające w oddziaływaniach neutrin.

Elektron

Elektron

(neutrino

(neutrino

elektronowe)

elektronowe)

Mion

Mion

(neutrino

(neutrino

mionowe)

mionowe)

Wewnątrz Super Kamiokande

Wewnątrz Super Kamiokande

12

Polacy w T2K

Polacy w T2K

Polacy w T2K

Polacy w T2K

●

Uniwersytet Warszawski, Narodowe Centrum Badań
Jądrowych, Politechnika Warszawska

●

Uniwersytet Wrocławski

●

Uniwersytet Śląski

●

Instytut Fizyki Jądrowej PAN:

➔

Projekt i budowa system montażu detektora mionowego.

Montaż detektora mionowego.

➔

Rozwój oprogramowania (przewodnictwo grupie rekonstrukcji

zdarzeń w detektorze bliskim).

➔

Analiza danych – pomiary przekrojów czynnych w detektorze

bliskim (3 różne analizy w naszym zakładzie)

Montaż elementów

Montaż elementów

detektora bliskiego

detektora bliskiego

13

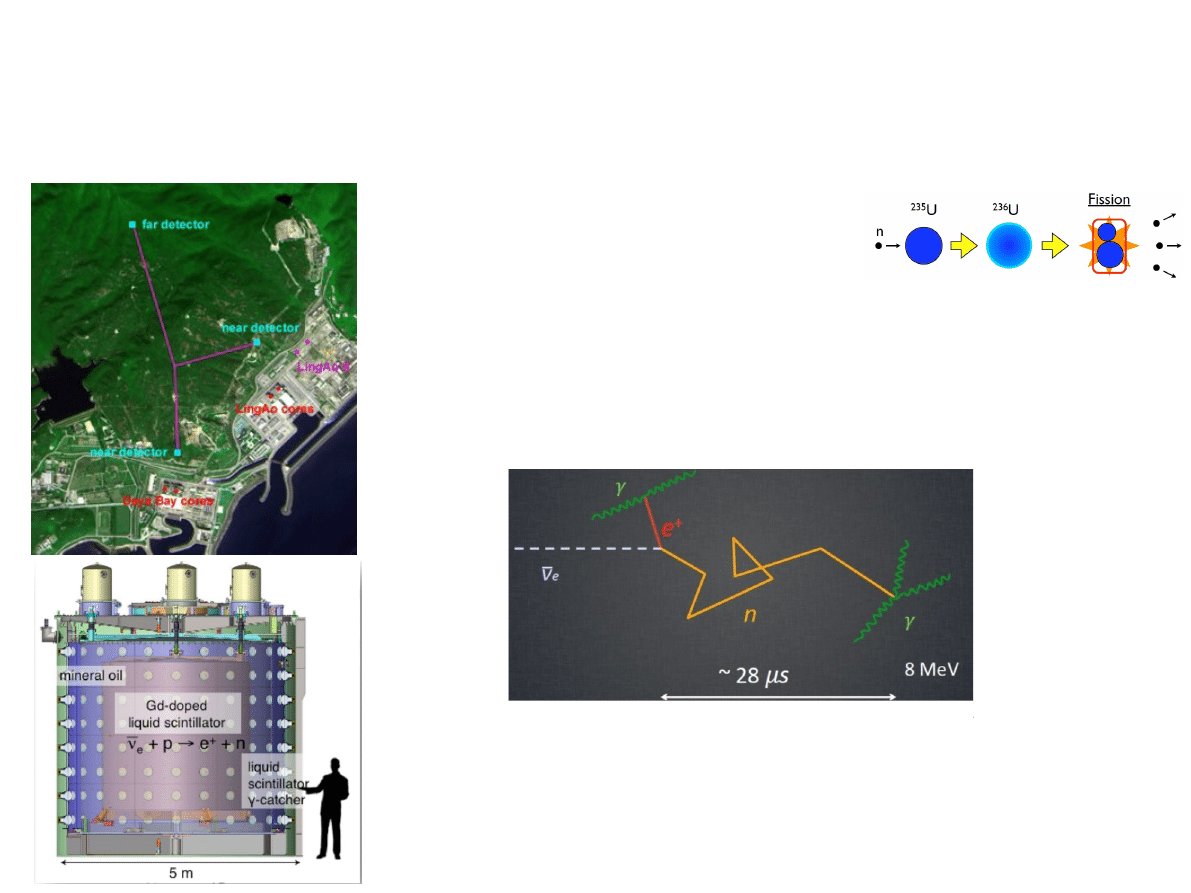
Neutrina z reaktorów -

Neutrina z reaktorów -

eksperyment Daya Bay

eksperyment Daya Bay

Neutrina z reaktorów -

Neutrina z reaktorów -

eksperyment Daya Bay

eksperyment Daya Bay

●

Neutrina produkowane są również

w reaktorach jądrowych w procesach

rozszczepienia (rozpady β neutronów)

●

W eksperymencie Daya Bay (Chiny) dwa detektory bliskie i

jeden daleki rejestrują neutrina z dwóch elektrowni: Daya

Bay i Ling Ao.

Chiny

Chiny

●

Wykorzystanie znanej od dawna techniki pomiaru opartej o tzw.
odwrotny rozpad β oraz wychwyt neutronu.

●

Detektory, to zbiorniki wypełnione ciekłym scyntylatorem
dopowanym Gadolinem z fotopowielaczami na ściankach,
które rejestrują fotony.

14

T2K dostarcza pierwszych

T2K dostarcza pierwszych

wskazówek na temat

wskazówek na temat

δ

δ

CP

CP

T2K dostarcza pierwszych

T2K dostarcza pierwszych

wskazówek na temat

wskazówek na temat

δ

δ

CP

CP

●

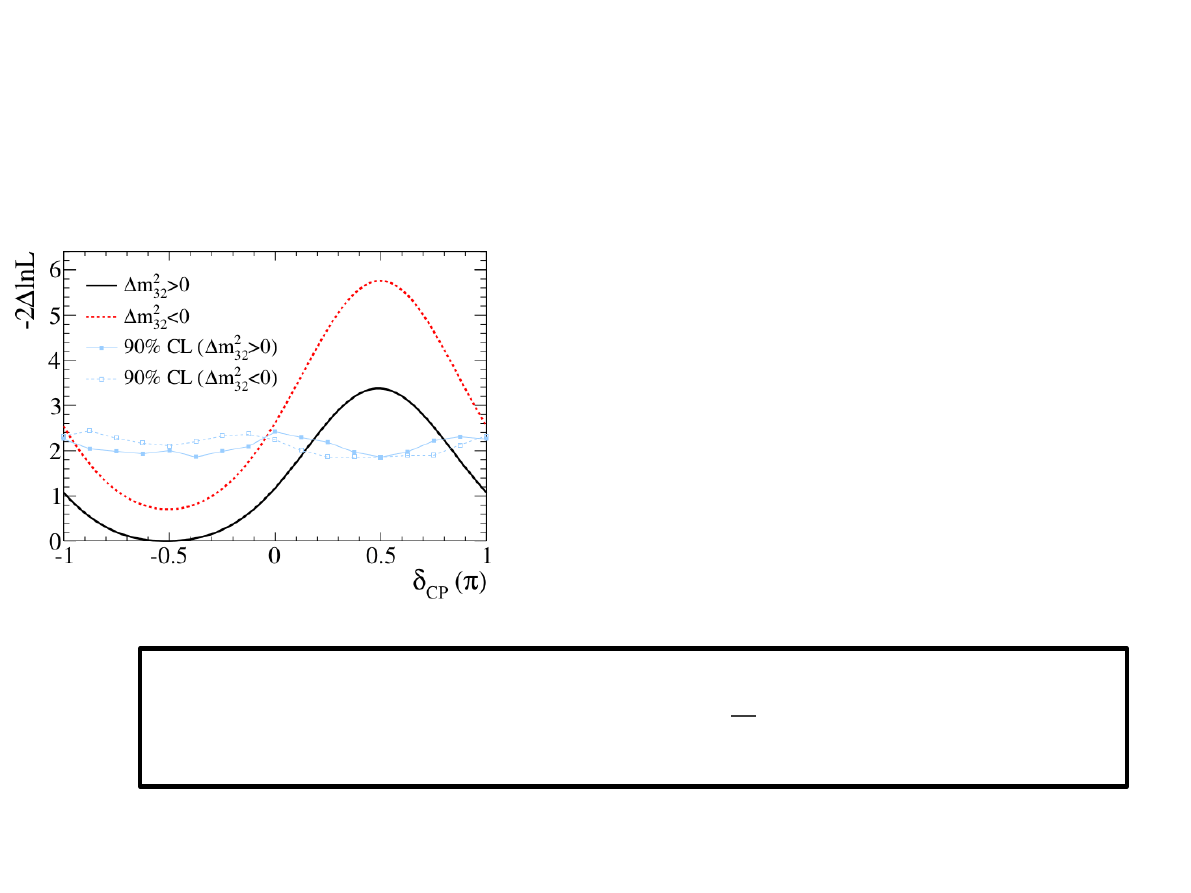
Wykorzystując ostatnie wyniki z eksperymentu T2K
(28 neutrin elektronowych w wiązce neutrin
mionowych) oraz wartość kąta θ

13

zmierzoną przez

eksperymenty reaktorowe.

●

T2K wyklucza na poziomie ufności 90% wartości δ

CP

:

●

Preferowana wartość δ

CP

to -π/2

P(ν

μ

→ν

e

)≈

sin

2

2θ

13

sin

2

θ

23

sin

2

(

1.27 Δ m

23

2

L

E

)

+ człony zależne od δ

CP

+ człony mocno zależne
od hierarchii mas neutrin

( 0.35 π ,0 .63 π )
(−π ,−0.97 π )∪(−0.04 π , π )

Hierarchia normalna

Hierarchia odwrócona

19 listopad 2013

15

Perspektywa najbliższych 10 lat w

Perspektywa najbliższych 10 lat w

pomiarach

pomiarach

δ

δ

CP

CP

Perspektywa najbliższych 10 lat w

Perspektywa najbliższych 10 lat w

pomiarach

pomiarach

δ

δ

CP

CP

●

T2K w ciągu najbliższych 10 lat powinno wykluczyć 50% wartości δ

CP

z

połowy przedziału wartości δ

CP

gdy hierarchia mas nie będzie znana.

●

Jeśli uda się wcześniej zmierzyć hierarchię mas neutrin będziemy w stanie
wykluczyć 50% wartości δ

CP

z całego jej przedziału wartości

●

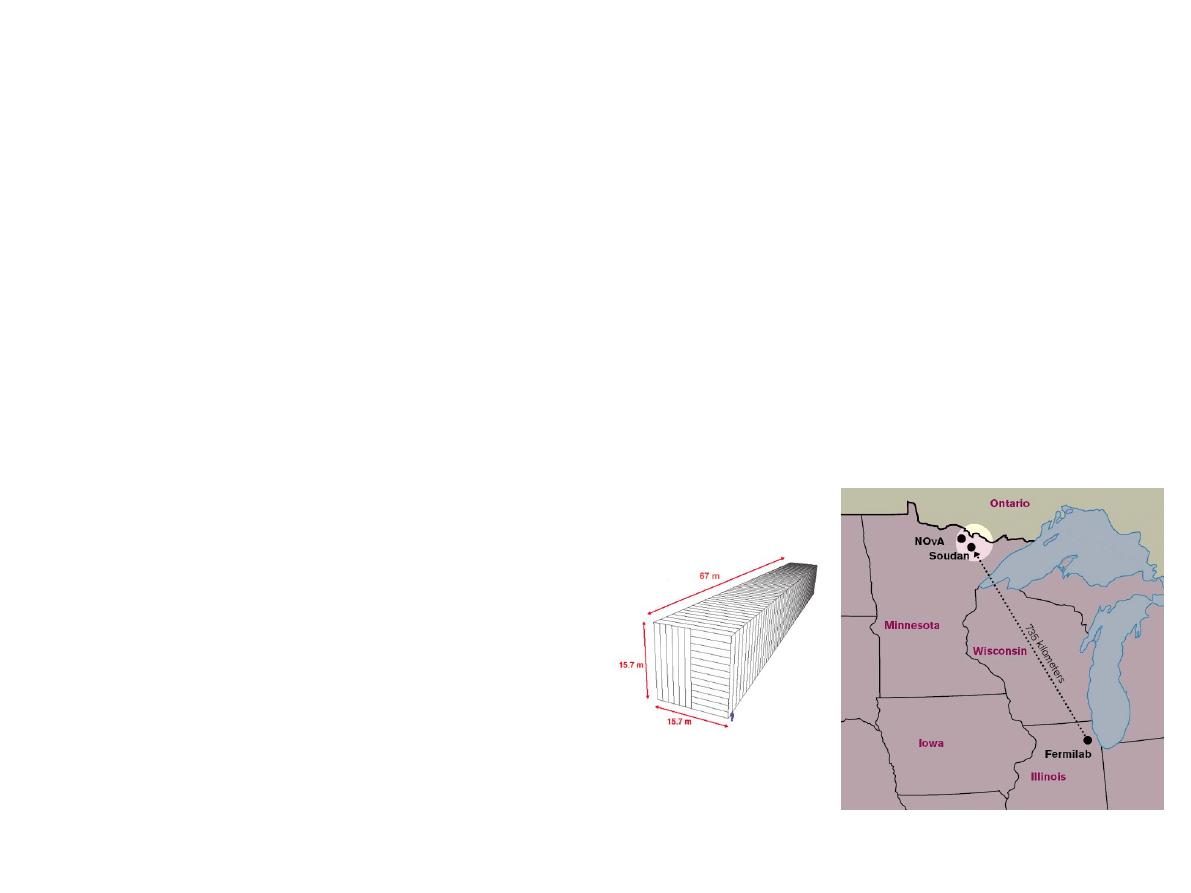
Eksperyment NOvA (USA):

➔

Wiązka neutrin mionowych z akceleratorowego ośrodka Fermilab

➔

Daleki detektor w odległości 735 km od
Fermilabu w kopalni Soudan

●

Połączenie wyników eksperymentów

T2K i NOvA powinno pozwolić na

wykluczenie 60% wartości δ

CP

z

pełnego jej przedziału wartości

.

Eksperyment NOvA

Eksperyment NOvA

16

Precyzyjne pomiary

Precyzyjne pomiary

δ

δ

CP

CP

- ,,super

- ,,super

wiązki” neutrin

wiązki” neutrin

Precyzyjne pomiary

Precyzyjne pomiary

δ

δ

CP

CP

- ,,super

- ,,super

wiązki” neutrin

wiązki” neutrin

●

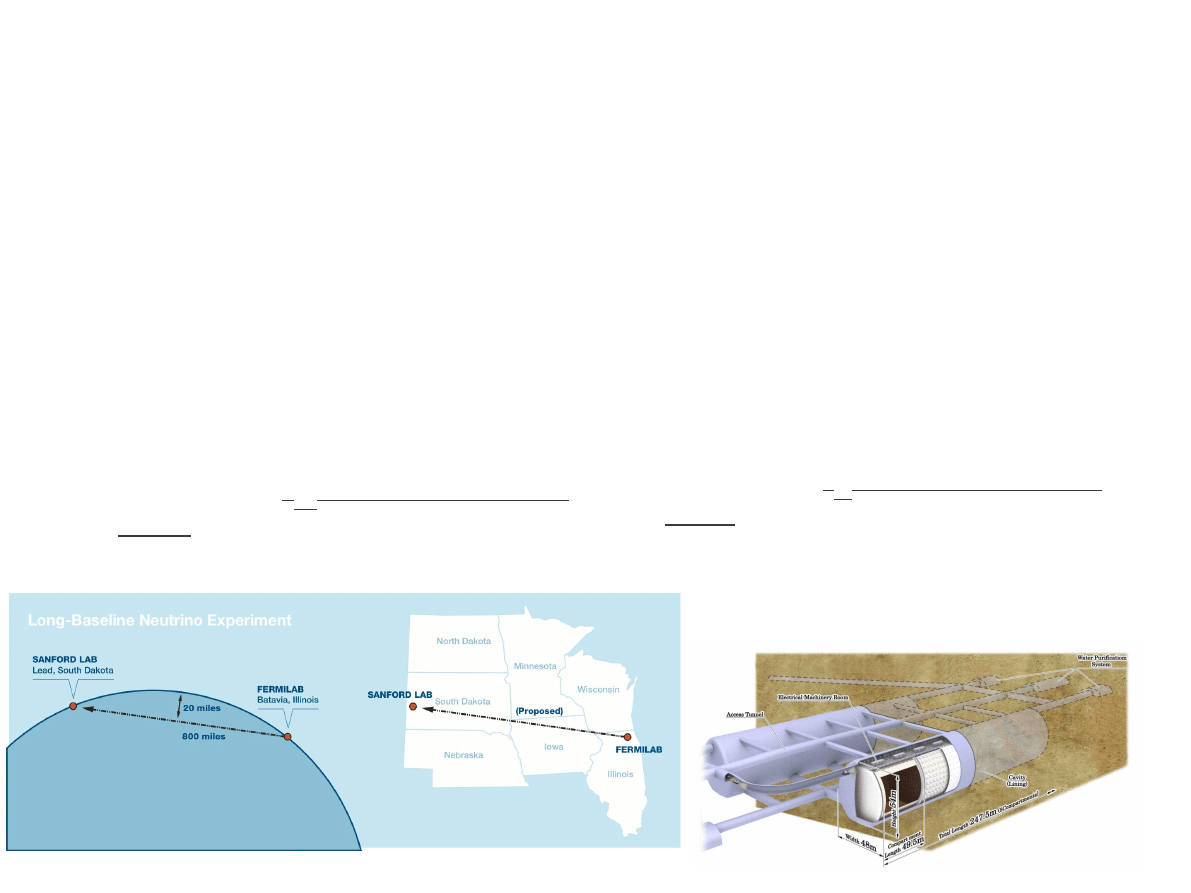
LBNE (USA)

➔

Flagowy projekt z fizyki cząstek w

Stanach Zjednoczonych.

➔

Wiązka neutrin z ośrodka Fermilab

(Chicago)

➔

Detektor z 10 tyś. ton ciekłego argonu

w stanie Południowa Dakota

oddalonego o 1300 km od Fermilabu.

➔

Wyznaczenie δ

CP

z dokładnością do 20

stopni (do 10 stopni po podniesieniu

mocy wiązki).

●

Hyper-Kamiokande (Japonia)

➔

Naturalne rozszerzenie eksperymentu

T2K

➔

Bardzo intensywną wiązką neutrin (1.7

MW) z ośrodka J-PARC

➔

Większym dalekim detektorem (wodny

detektor Czerenkowa o masie miliona

ton!) w odległości 300 km od J-PARC.

➔

Wyznaczenie δ

CP

z dokładnością do 18

stopni ale dokładność zależy od tego,

czy znamy hierarchię mas neutrin.

17

Asymetria między materią i

Asymetria między materią i

antymaterią we Wszechświecie

antymaterią we Wszechświecie

Asymetria między materią i

Asymetria między materią i

antymaterią we Wszechświecie

antymaterią we Wszechświecie

●

Wszechświat zbudowany w większości z cząstek materii (protony, neutrony etc.) a
nie antymaterii (anty-protony, anty-neutrony, etc.).

●

Opis asymetrii materia i antymateria poprzez stosunek liczby barionów do liczby
fotonów:

●

Dwa niezależne oszacowania parametru η:

➔

Zawartości lekkich pierwiastków
we wszechświecie:

η

= (5.1 – 6.5) x 10

-10

➔

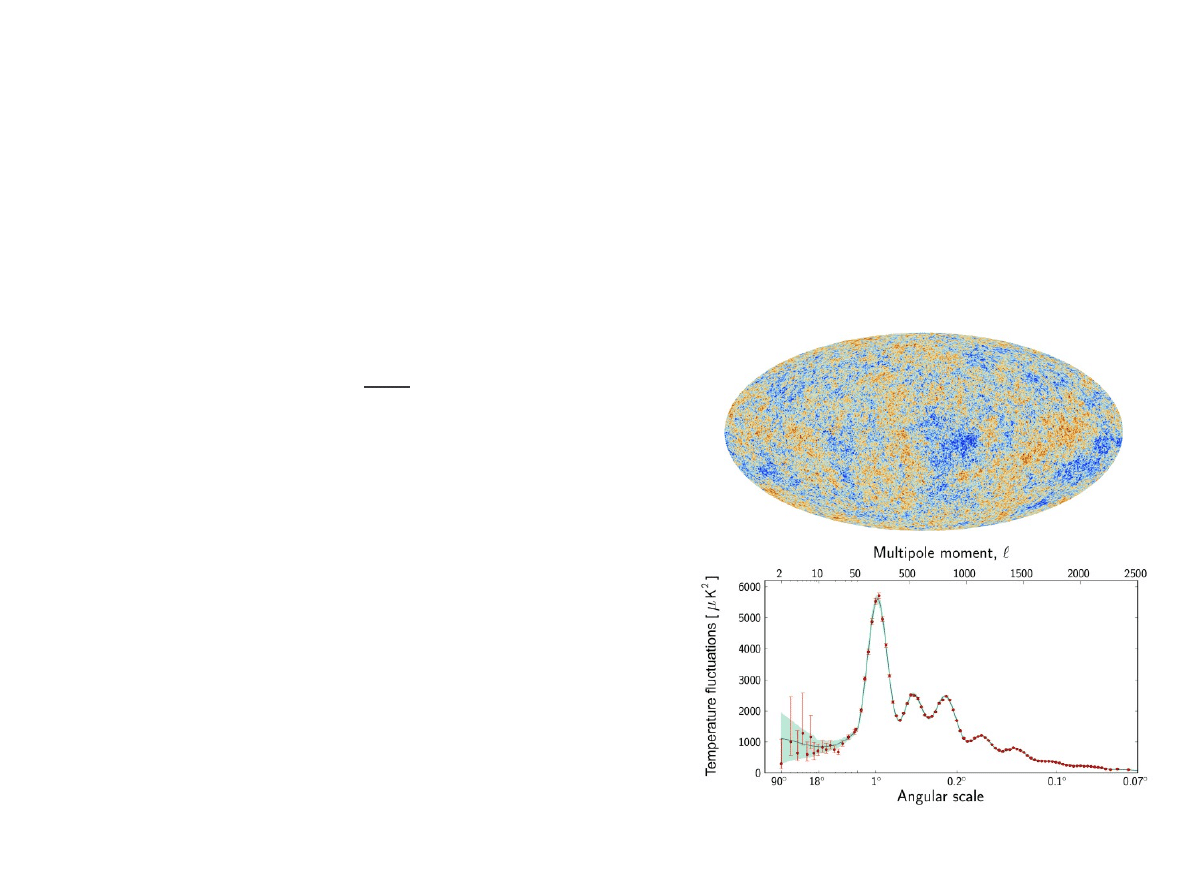
Anizotropie kosmicznego promieniowania tła:

η

= (6.04  0.08) x 10

-10

(Planck)

●

Wszechświat po Wielkim Wybuchu

składał się z równych ilości materii i antymaterii.

➔

W symetrycznym Wszechświecie:

η

= 5 x 10

-19

Mikrofalowe promieniowanie tła widziane przez

Mikrofalowe promieniowanie tła widziane przez

satelitę Planck

satelitę Planck

η=

n

B

n

γ

18

Bariogeneza i symetria CP

Bariogeneza i symetria CP

Bariogeneza i symetria CP

Bariogeneza i symetria CP

●

Jak w dynamiczny sposób z symetrycznego Wszechświata

rozwinęła się asymetria między liczbą barionów i anty-
barionów? →

model bariogenezy

●

Warunki niezbędne do zajścia
bariogenezy (1967r. Sacharow):

➔

Łamanie liczby barionowej (B)

➔

Łamanie symetrii ładunkowo-

przestrzennej (CP)

➔

Brak równowagi termodynamicznej

●

Co z łamaniem CP w rozpadach
mezonów K i B?

➔

Obliczenia pokazują, że jest ono o wiele

rzędów wielkości za małe zjawisko
(~10

-20

) aby wyjaśnić zmierzoną wartość

asymetrii.

M. C. Escher

M. C. Escher

19

Leptogeneza

Leptogeneza

Leptogeneza

Leptogeneza

●

Procesy mogące prowadzić do łamania symetrii CP a w

rezultacie także do łamania liczby barionowej to rozpady
ciężkich cząstek sprzęgających się do neutrin np.

●

Gdzie kwantowe poprawki wyższego rzędu sprawiają, że
częstości rozpadu na lepton i anty-lepton są różne:

●

Jest to tzw. model

leptogenezy,

który w rezultacie

prowadzi do bariogenezy i

może wyjaśniać asymetrię

między materią i antymaterią.

Γ (

N

i

→

LH )≠Γ( N

i

→ ̄

L H

*

)

N

i

→

L

α

H

N

i

→ ̄

L

α

H

*

20

,,Ciężkie neutrina”

,,Ciężkie neutrina”

,,Ciężkie neutrina”

,,Ciężkie neutrina”

●

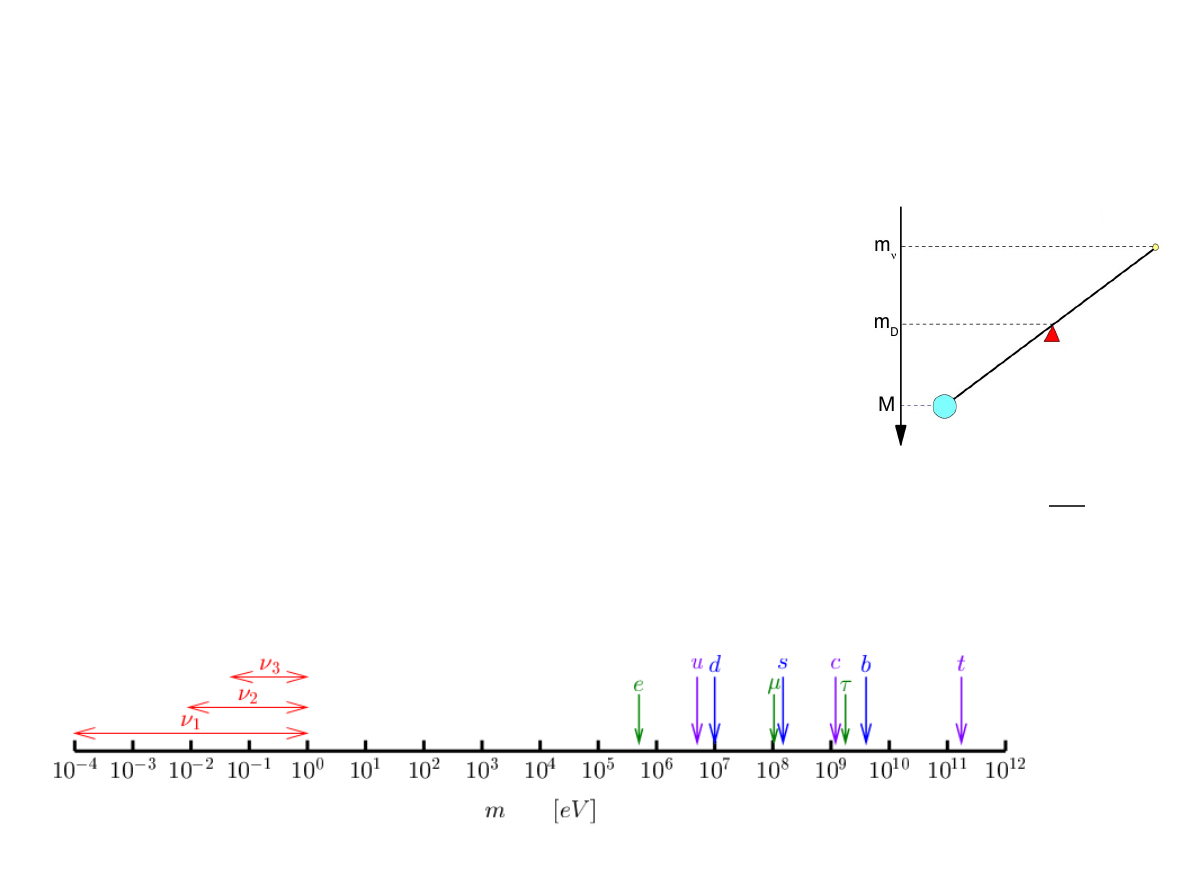
Mechanizm huśtawki

(Minkowski,

Gell-Mann,...) tłumaczy dlaczego
masy lekkich neutrin są takie małe
w porównaniu z kwarkami i innymi
leptonami.

➔

Wiąże on lekkie neutrina ze swoimi
ciężkimi odpowiednikami

(,,ciężkimi

neutrinami”).

m

ν

=−

m

D

1

M

m

D

T

M∼m

GUT

(∼10

14

GeV )

Ciężkie neutrino

Ciężkie neutrino

Lekkie neutrino

Lekkie neutrino

(które obserwujemy)

(które obserwujemy)

21

,,Ciężkie neutrina”

,,Ciężkie neutrina”

,,Ciężkie neutrina”

,,Ciężkie neutrina”

●

Model leptogenezy postuluje łamanie symetrii CP w rozpadach ciężkich
cząstek sprzęgających się do neutrin (,,lekkich” neutrin).

●

Mechanizm huśtawki

dostarcza nam tychże ciężkich cząstek – ciężkich

neutrin.

●

Odkrycie łamania symetrii CP w oscylacjach lekkich neutrin →

ważny

argument na korzyść modelu leptogenezy

z uwagi na ich związek poprzez

mechanizm huśtawki z ciężkimi neutrinami.

●

Ponadto istnienie ciężkich neutrin to:

➔

,,Proste” rozszerzenie Modelu Standardowego.

➔

Ciężkie neutrina – kandydaci na ciemną materię?

➔

Jeśli mechanizm huśtawki jest prawdziwy, to jesteśmy w stanie badać obiekty w

skali GUT poprzez badania lekkich neutrin o masach mniejszych niż elektronowolt!

Leptogeneza i bariogeneza

Łamanie symetrii CP
dla ,,lekkich” neutrin

Asymetria między
materią i antymaterią

22

Podsumowanie

Podsumowanie

Podsumowanie

Podsumowanie

●

Ostatnie lata, to bardzo ciekawy okres dla fizyki neutrin:

➔

Dzięki pomiarom w eksperymencie T2K oraz w eksperymentach reaktorowych

poznaliśmy wartość

ostatniego z kątów mieszania neutrin i wiemy, że jest on niezerowy.

➔

,,Otwarła się furtka” do pomiaru fazy odpowiedzialnej za łamanie lub zachowanie symetrii CP w
sektorze neutrin.

➔

W tym roku eksperyment T2K dostarczył

pierwszych wskazówek eksperymentalnych na temat

wartości δ

CP

.

●

Najbliższe lata w tej dziedzinie badań także zapowiadają się bardzo obiecująco:

➔

Eksperymenty T2K (IFJ PAN) oraz NOvA będą w stanie dostarczyć dalszych informacji na temat
symetrii CP w ciągu najbliższych 10 lat.

➔

W planach są eksperymenty, w których zasięgu jest wyznaczenie δ

CP

z dużą dokładnością i

ostateczne sprawdzenie czy symetria CP jest łamana w sektorze neutrin.

➔

Z pewnością neutrina będą mogły dostarczyć wskazówek na temat asymetrii między materią i
antymaterią we Wszechświecie.

●

Szereg innych bardzo ciekawych eksperymentów z fizyki neutrin:

✔

Poszukiwanie podwójnego bezneutrinowego rozpadu β → sprawdzenie, czy neutrina są cząstkami Majorany i
łamanie CP poprzez fazy Majorany,

✔

Sprawdzenie hierarchii mas neutrin,

✔

Pomiary ,,kosmologiczne”: suma mas neutrin, neutrina kosmiczne.