1. Równowaga względna.

Występuje, gdy siła bezwzględna jest równoważona przez siłę unoszenia. Zakładamy, że punkt znajduje się w

równowadze względem układu ruchomego, który porusza się względem innego układu mającego cechy układu
Galileusza.

Równanie ruchu punktu względem układu ruchomego

mp

W

= F - mp

U

- mp

C

w przypadku równowagi w=0 pw=0 pc=0 Równanie równowagi względnej

F - mp

U

= 0 F + F

U

= 0

2. Przyspieszenie Coriolisa.

P.C. jest to przyspieszenie wynikające z ruchu unoszenia

p

C

=2ω×w.

P.C. jest równe podwojonemu iloczynowi wektorowemu prędkości kątowej i prędkości względnej, jest

prostopadłe do wektorów ω i w

p

C

=2ωwsinϕ

gdzie ϕ kąt między wektorami w i ω. Zwrot tego przyspieszenia wynika z przyjętego przez nas zwrotu,

określonego przez prawoskrętny prostokątny układ współrzędnych.

P.C. jest równe 0 gdy:

(1) ruch unoszenia jest postępowy ω=0,
(2) w pewnej chwili prędkość względna punktu jest równa 0 w=0,
(3) prędkość względna punktu jest równoległa do osi obrotu układu ruchomego sinϕ=0 ωπ=0 (ruch śrubowy).

P.C. występuje gdy układ unoszenia dokonuje obrotu. Występuje, gdy punkt znajduje się w początku ruchomego

układu wsp. Np. ruch obrotowy ziemi powoduje powstawanie przyspieszenia coriolisa.

3. Przyspieszenie unoszenia

P.U. jest to przyspieszenie złożone z przyspieszenia punktu ruchomego oraz przyspieszenia stycznego i

normalnego

p

U

=p

A

+p

UT

+p

UN

p

A

=dV

A

/dt

p

UT

=ε×ρ

p

UN

=ω×(ω×ρ)

p

U

= p

A

+ε×ρ+ω×(ω×ρ)

4. Równanie dynamiki ruchu względnego (Człowiek w jadącym tramwaju, itp. )

Dynamiczne równania ruchu p.m. w ruchomym układzie odniesienia są takie, jak gdyby układ był inercjalny pod

warunkiem, że do siły

F

B

dodamy siłę unoszenia

F

U

= -mp

U

i Coriolisa

F

C

= -mp

C

.

F

W

=F+F

U

+F

C

F

U

= -mp

U

- siła bezwładności unoszenia

F

C

= -mp

C

- siła bezwładności Coriolisa

mp

w

= F -mp

U

-mp

C

równowaga względna układu: prędkość względna i przyspieszenie względne jest równe 0
w = 0 p

w

= 0

F – mp

u

= 0

5. Uderzenie punktu mat o przegrodę.

Punkt uderzenia o powierzchnię przegrody będącej w spoczynku z prędkością v1 której kierunek tworzy kąt α

(padania) z normalną powierzchni przegrody. Po uderzeniu punkt odbija się i porusza się z prędkością v2 tworząc kąt β
(odbicia) z normalną. W trakcie zderzenia wystąpi reakcja mająca charakter siły zderzeniowej

mV

2

cosβ + mV

1

cosα = J

RN

mV

2

sinβ – mV

1

sinα = 0 J

RT

=0

J – impuls reakcji normalnej.
J

RT

= hipoteza idealności więzów

Współczynnik restytucji – stosunek bezwzględnych wartości normalnych składowych prędkości po i przed

zderzeniem i jest niezależny od prędkości i wymiarów ciał zderzających się tylko od materiałów, z których są wykonane.

k = V

2n

/V

1n

k = v

2

cosβ/v

1

cosα

Przy uderzeniu idealnie sprężystym k = 1 przy plastycznym k = 0.

6. Współczynnik restytucji przy zderzeniu dwóch kul

W.R. jest to stosunek prędkości względnych obu kul po i przed zderzeniem. Prędkości względne mają różne

znaki gdyż kule przed zderzeniem się zbliża-ją a po zderzeniu oddalają się od siebie

k=

v

12

–v

22

/v

11

–v

21



7. Prawo zmienności pędu w postaci całkowej.

Przyrost pędu układu w przeciągu pewnego czasu = sumie impulsów wektora głównego sił zew i wektora

głównego reakcji w przeciągu tego czasu.

B-B

0

=∫(t-t

0

) Sdt + ∫(t-t

0

) Rdt

Prawo zmienności pędu pozwala na wyciagnięcie ogólnych wniosków dotyczących ruchu układu:
dB=0 B= const

B

X

=C

X

B

Y

=C

Y

B

Z

=C

Z

– rów skalarowe pędu

8*. Ruch ciała sztywnego pod działaniem sił zderzeniowych

Uderzenie jest to suma impulsów sił zderzeniowych J oraz reakcji zderz R jeżeli ciało nie jest swobodne.

Moment główny impulsów sił zderzeniowych-L, a moment reakcji – H Ruch ten bada się za pomocą prawa zmienności
pędu i krętu.

B

2

-B

1

=J+R,

K

2

-K

1

=L+H

2-po zderzeniu, 1-przed. Rzutując te równania na osie układu współrzędnych. Otrzymamy równania określające

przyrosty prędkości postępowej i kątowej ciała wywołanej impulsami sił zderzeniowych: m.(x’

2

-x’

1

)=J

x

+R

x

itd.

9. Środek uderzenia

Jest to punkt, w którym nie zaobserwuje się wstrząsu wywołanego uderzeniem ciała. Współrzędna tego punktu:

y

a

=k

x

2

/y

c

Uderzenie nie wywoła wstrząsu, jeżeli:
(1) kierunek jego jest prostopadły do płaszczyzny przechodzącej przez oś obrotu i środek masy,
(2) Oś obrotu jest osią główną punktu będącego rzutem punktu uderzenia na oś obrotu oraz
(3) punkt uderzenia leży w odległości danej od osi obrotu. Wykorzystuje się to przy projektowaniu narzędzi i

maszyn.

10. Rozpraszanie en. Kinetycznej przy zderzeniu.

Punkt uderza w przegrodę prostopadle do jej powierzchni α=β=0 k=v2/v1 v2=kv1. Różnica energii kinetycznej

po i przed zderzeniem wynosi

E2-E1= 0.5m(V

2

2

– V

1

2

) = 0.5 mV

1

2

cos

2

α (1+k)

Następuje więc ubytek energii kinetycznej tym większy im mniejszy jest współczynnik restytucji. W przypadku

zderzenia plastycznego cała energia kinetyczna zostaje stracona. W przypadku uderzenia idealnie sprężystego nie ma
straty energii. W przypadku częściowo sprężystego zderzenia część energii kinetycznej zostaje stracona, zamienia się w
ciepło.

11,12. Energia kinetyczna ciała sztywnego względem dowolnego punktu i środka masy. (tw. Koniga).

E=0.5 (mV

2

C

+ I

lc

ω

2

)

Energia kinetyczna jest równa sumie energii kinetycznej ruchu postępowego z prędkością środka masy i energii

ruchu obrotowego wokół osi przechodzącej przez środek masy. Energia kinetyczna ciała składa się więc z dwóch części.
Pierwsza to energia ruchu postępowego ciała z prędkością środka masy. Jeżeli prędkość środka masy = 0, to ruch bryły
jest chwilowym ruchem obrotowym wokół osi przechodzącej przez środek masy. Druga część wzoru przedstawia więc
energię kinetyczną w ruchu obrotowym.

13. Niewyrównoważenie statyczne i dynamiczne ciała sztywnego.

W maszynach zawierających elementy wirujące występuje okresowa zmiana siły działającej na łożyska, co

wywołuje drgania.

Dynamiczne – występują gdy środek masy ciała wirującego nie leży na osi obrotu oraz oś ta nie jest osią główną,

ponieważ przy wykonywaniu elementu nie zawsze da się to spełnić, więc każdy element jest poddawany sprawdzeniu.
Dodając lub odejmując masę można wpłynąć na położenie środka masy i rozkład momentów bezwładności –
wyrównoważenie.

14. Reakcje dynamiczne łożysk.

Jeżeli środek masy ciała leży na osi obrotu i jednocześnie oś ta jest osią główną ciała dla dowolnego jej punktu to

reakcje dynamiczne są równe 0. Reakcje dynamiczne występują, jeżeli środek masy ciała wirującego nie leży na osi
obrotu oraz jeżeli oś ta nie jest osią główną.

Do reakcji statycznych wynikających z obciążenia siłami dochodzą reakcje dynamiczne konieczne do utrzymania

ciała w określonym ruchu obrotowym. Reakcje te wynikają ze zmian pędu i krętu ciała. Gdy oś obrotu nie przechodzi
przez środek masy ciała występuje okresowa zmiana siły działającej na łożyska. Siła ta przenosząc się na elementy
fundamentu wywołuje drgania.

15. Zjawisko żyroskopowe.

Żyroskop jest to ciało mające kształt bryły obrotowej obracającej się szybko wokół swej osi symetrii. Oś obrotu

oprócz prędkości kątowej ω

1

ma jeszcze prędkość kątową ω

2

wokół osi Z przechodzącej przez środek masy O. Ciało

wykonuje ruch kulisty i ruch ten jest precesją regularną. Dla wywołania ruchu przykładamy moment sił zewnętrznych
M

o

. Zakładamy, że ω

2

obrotu osi wirującej jest dużo mniejsza od ω

1

obrotu własnego a więc kręt nie zależy od ω

2

tylko

od ω

1

i leży na osi obrotu własnego.

Moment żyroskopowy:

M

A

= I

X

ω

1

x ω

2

Żyroskop wykorzystywany jest jako wskaźnik położenia i zmian kierunku ruchu oraz do sterowania ruchem

obiektów ruchomych. W tym celu zostaje on zamocowany w przegubach umożliwiających swobodny ruch żyroskopu
względem obiektu ruchomego. Stosowany w samolotach (sztuczny horyzont) statki (stabilizacja)

16. Równanie ruchu punktu o zmiennej masie – równanie Mieszczerskiego.

v-prędkość punktu
u-prędkość dołączającej się cząstki

u – v = w

17. Równanie ruchu punktu materialnego o zmiennej masie w postaci II prawa Newtona

Gdy prędkość względna dołączającej się masy jest równa zero

w=0

Równanie ma formalnie postać identyczną z równaniem ruchu punktu o stałej masie, z tym że masa jest funkcją

czasu.

18. Kiedy równanie Mieszczerskiego ma postać II prawa Newtona

Gdy prędkość bezwzględna dołączającej się masy jest równa u=0. Otrzymujemy

d/dt(mv)=F.

19. Zdefiniować przyrost przygotowany, współrzędną uogólnioną i siłę uogólnioną.

Współrzędne uogólnione- niezależne wsp. których liczba jest najmniejszą potrzebną do określenia położenia

układu (3n-k) Mogą to być wsp kątowe bądź liniowe. Liczba wsp uogólnionych jest najmniejszą potrzebną do określenia
położenia i ruchu. Min liczbę wsp potrzebną do określenia położenia układu nazywamy liczba stopni swobody S=3n-k.

Siła uogólniona - wielkość, która pomnożona przez przyrost przygotowany wsp uogólnionej daje wartość pracy

wykonanej przez układ sił działających na dany układ materialny na przesunięciach przygotowanych wywołanych
przyrostem wsp uogólnionej

20. Zasda d’Lamberta, sformuowanie i zastosowanie.

Suma iloczynów skalarnych sum sił zewnętrznych i wewnętrznych działających na punkty układu oraz wektorów

(-mipi) i przesunięć przygotowanych punktów układu materialnego jest równa 0.

∑(F

i

+R

i

+W

i

-m

i

p

i

) ⋅ δr

i

=0.

Do badania ruchu układu swobodnego pod działaniem sił zewnętrznych może być zastosowana zasada:
Układ sił zewnętrznych działających na punkty układu materialnego swobodnego równoważy się w każdej chwili

z układem sił bezwładności S+SB=0 MO+MBO=0

Dla układu nieswobodnego: Układ wektorów złożony z sił bezwładności układu materialnego sił zewnętrznych

działających na ten układ oraz z sił reakcji ograniczających ruchy tego układu jest układem równoważnym 0. S+SB+R=0
MO+MBO+HO=0

21. Określenie przemieszczenia przygotowanego i pracy przygotowanej.

Przesunięciem przygotowanym nazywamy takie dowolnie pomyślane przez obserwatora przesunięcie będące

jednym z przesunięć możliwych niezwiązane ani z działającymi siłami ani z czasem. Jeżeli na punkt materialny działa
siła F

i

to po nadaniu punktom przesunięcia przygotowanego δr

i

zostanie wykonana praca elementarna

δL

i

=F

i

⋅δr

i

Pracę elementarną siły na przesunięciu przygotowanym nazywamy pracą przygotowaną. W położeniu równowagi

układu suma prac przygotowanych wszystkich sił zew i reakcji = 0. Zasada ta przedstawia warunek konieczny i
dostateczny równowagi układu mechanicznego. Zastosowanie – dla dowolnych układów materialnych

22. Zderzenia proste, centralne

Przy zderzeniu dwóch ciał powierzchnie tych ciał zetkną się w jednym punkcie. Punkt A 1 ciała zetknął się z

punktem D 2 ciała. Powierzchnie tych ciał w punkcie zetknięcia mają wspólną normalną (linia zderzenia). Prędkość
względna punktu A w stosunku do punktu D jest równa i przeciwna prędkości względnej punktu D w stosunku do punktu
A. Jeżeli te prędkości względne są położone na linii zderzenia to zderzenie nazywamy prostym w przeciwnym razie
ukośnym. Przy zderzeniu prostym siły chwilowe działają na linii zderzenia. Jeżeli linia zderzenia przechodzi przez
środek masy ciała to zderzenie nazywamy centralnym w odróżnieniu od zderzenia mimośrodowego w przypadku
przeciwnym.

23. Zderzenie dwóch kul

Zakładamy, że dwie kule o masach m

1

i m

2

poruszają się ruchem postępowym z prędkościami v

11

i v

12

przed

zderzeniem tak, że torem środka masy każdej z nich jest prosta, na której znajdują się ich środki O

1

i O

2

. Aby zderzenie

było możliwe v

11

-v

12

>0. Rzut wektora pędu na oś x wobec braku sił zewnętrznych jest stały. Po uderzeniu kule zaczną

poruszać się z prędkościami v

12

i v

22

skierowanymi także wzdłuż osi x.

Stałość pędu oznacza, że pęd układu po i przed zderzeniem jest taki sam

m

1

v

12

+m

2

v

22

= m

1

v

11

+m

2

v

21

Stosunek prędkości względnych obu kul po i przed zderzeniem jest równy współczynnikowi restytucji

k=

v

12

-

v

22

/

v

11

-

v

21



Przy zderzeniu plastycznym k=0 przy idealnie sprężystym k=1.

24. Co to jest ruch kulisty bryły. Precesja regularna.

Ruch kulisty ciała sztywnego występuje, gdy jeden z punktów układy związanego z ciałem jest nieruchomy.

Ruch ten jest ruchem o trzech stopniach swobody. K’=M. (można zrzutować na osie x,y,z w układzie nieruchomym). W
układzie ruchomym K’^+ωxK

0

=M

0

Precesja regularna jest to szczególny przypadek ruchu kulistego ciała, w którym prędkości kątowe obrotu

własnego i precesji są stałe ϕ’=ω

1

=const ψ’=ω

2

=const a prędkość kątowa nutacji jest równa 0, więc kąt nutacji jest stały

ϑ’=0 ϑ=ϑ0=const Ruch ten cechuje się tym, że ciało obraca się wokół osi własnej ζ z prędkością kątową ω

1

a oś ta

obraca się wokół osi stałej z z prędkością kątową ω2. Kąt między osiami jest stały. Stałe prędkości oznaczają, że kąty ψ i
ϕ zmieniają się w sposób jednostajny. Ruch opisany jest równaniami ruchu

ϕ=ω

1

t ψ=ω

2

t ϑ=ϑ0

przy założeniu, że w chwili początkowej t=0 kąty ϕ i ψ są równe 0 ω=ω

1

+ω

2

25. Równanie ruchu rakiety

Ruch rakiety w czasie działania silnika rakietowego jest ruchem ciała o zmiennej masie, podczas którego

następuje wypływ gazów spalinowych z dyszy silnika z prędkością względną uzyskiwaną w wyniku spalania paliwa.
Zakładamy, że prędkość względna gazów jest styczna do trajektorii oraz prędkość względna gazów jest stała w=u-v=-wτ

τ-wektor jednostkowy styczny do trajektorii.






26. Równania ruchu ciała sztywnego.

K

A

’+v

A

xmv

C

=M

A

mv

C

=B

B’=S

K

A

’+v

A

xB=M.

A

Występujące w powyższych wzorach pochodne są pochodnymi bezwzględnymi, odniesionymi do nieruchomego

układu odniesienia.

K

A

’+ωxK

A

+v

A

xB=M

A

R.r.c.s. otrzymamy jako szczególny przypadek równań ruchu układu materialnego. Możemy je otrzymać za pomocą
zasady pędu i krętu. Pochodna pędu względem czasu równa jest wektorowi głównemu sił zewnętrznych i reakcji a
pochodna krętu względem nieruchomego punktu momentowi głównemu sił zewnętrznych i reakcji. B’=S K’o=Mo
B’x=Sx ...K’x=Mx...

27. Równanie Lagrangea II rodzaju

Są to równania różniczkowe zwyczajne II rzędu. Rozwiązanie tych równań stanowi najkrótszy sposób badania

ruchu. Liczba równań różniczkowych jest przy tej metodzie najmniejsza i równa liczbie stopni swobody układu. W
równaniach tych występuje s niewiadomych przedstawiających s współrzędnych uogólnionych określających ruch
układu. Równania te nie zawierają reakcji toteż nie pozwalają one na wyznaczenie wartości tych reakcji

28.Równania Lagrange’a potencjalne

W przypadku gdy siły zewnętrzne działające na układ mają potencjał siłę uogólnioną można obliczyć jako

pochodną potencjału względem odpowiedniej współrzędnej

wtedy równania Lagrange’a

Potencjał kinetyczny L=E-V jest to różnica energii kinetycznej i potencjału sił. Ponieważ potencjał nie zależy od

prędkości uogólnionej d/dt(∂L/∂q’j)-∂L/∂qj=0 Potencjał kinetyczny przedstawia nadmiar energii kinetycznej nad
potencjalną.

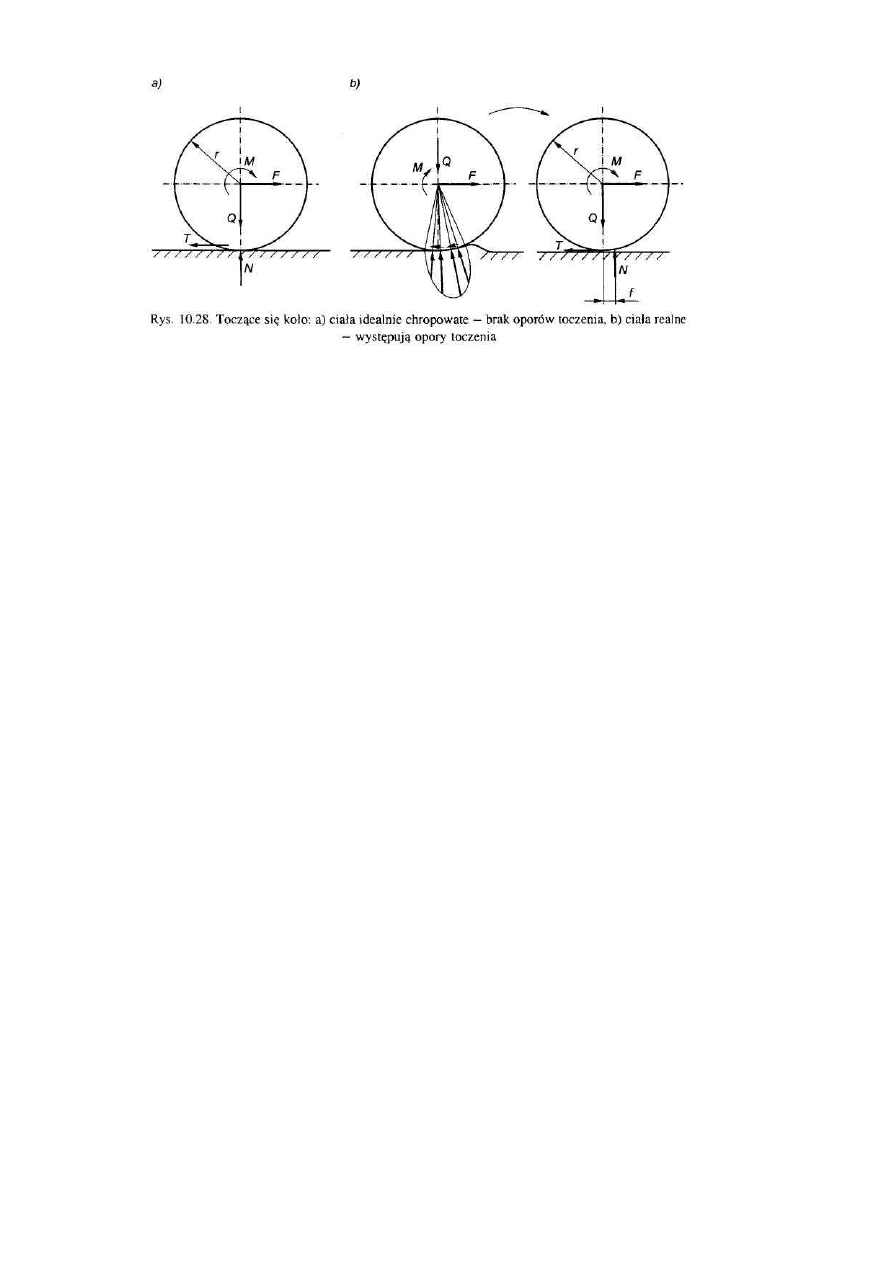
29. Dynamika toczącego się koła.

Ruch taki wykonują koła pojazdu, jeżeli pudło pojazdu wykonuje ruch postępowy po linii prostej. Przy takim

ruchu koło toczy się po jezdni obracając się jednocześnie. Koło obciążone jest siłami przekazanymi przez oś, na której
zostało osadzone oraz reakcjami prostej (jezdni) i własną siłą ciężkości. Przyjmujemy, że siły obciążające koło
przekazane przez oś z uwzględnieniem własnego ciężaru sprowadzają się do dwóch składowych pionowej P i poziomej F
oraz pary sił o momencie M. Siły te przyłożone są w punkcie C. Zakładamy, że punkt ten pokrywa się ze środkiem masy
koła. Ze strony toru (jezdni) działa na koło reakcja normalna N i siła tarcia T. Reakcja normalna ze względu na opór
toczny przesunięta jest o f w kierunku ruchu a siła tarcia skierowana w dodatnią stronę osi x gdyż przeciwstawia się
poślizgowi koła po szynie przy wskazanym kierunku działania momentu M.

Jeżeli koło toczy się bez poślizgu to między prędkością środka masy C a prędkością kątową istnieje związek

rω-vc=0 czyli ω=vc/r Równania ruchu są następujące

mv’c=F+T

0=N-P

Iω’=M-Nf-Tr

mV

C

’=F+T=F+(M.-Qfr-k

2

F)/r

2

+k

2

k-ramię bezwładności

30. Równania ruchu pojazdów.

Równanie ruchu środka masy (całego pojazdu)
∑F

X

=(GV

C

’-∑T

i

-W+F-Gsinα)g=0

Rów ruchu koła: -M.

Bi

-M.

Oi

+T

i

r

i

-N

i

f

i

=0 M

Bi

=J

i

ε=(Gk

2

V

C

’)/gr

i

z tych wzorów obliczamy

T

i

=(N

i

f

i

+M.

Oi

)/r

i

+(Q

i

V

i

’k

2

)/gr

i

podstawiając to równanie do pierwszego otrzymamy rów ruchu.

31. Dynamiczne równania Eulera dla bryły sztywnej.
Aω’

ξ

+(C-B)ω

η

ω

ψ

=Μ

ξ

Βω’

η

+(A-C)ω

ξ

ω

ψ

=Μ

η

Χω’

ψ

+(B-A)ω

ξ

ω

η

=M.

ψ

A,B,C- rzuty krętów na główne osie

bezwładności

32. Prawo zmienności energii u.p.m. w potencjalnym polu sił.

Przyrost energii kinetycznej układu = jest spadkowi potencjału. Suma energii kinetycznej i potencjalnej jest

równa energii całkowitej, czyli

E

p2

+E

v2

=E

p1

+E

v1

E

C2

=E

C1

Energia całkowita układu w polu potęcjalnym. Ma wartość stałą. Układy te nazywamy zachowawczymi.

33 inne jakieś pyatnie. Ogólne równanie mechaniki. Zasada d’Alamberta dla układu nieswobodnego
Suma iloczynów skalarnych sum sił zewnętrznych i wewnętrznych działających na punkty układu oraz wektorów (-mipi)
i przesunięć przygotowanych punktów układu materialnego jest równa 0. ∑(Fi+Wi-mipi)⋅δri=0. Do badania ruchu
układu swobodnego pod działaniem sił zewnętrznych może być zastosowana zasada: Układ sił zewnętrznych
działających na punkty układu materialnego swobodnego równo-waży się w każdej chwili z układem sił bezwładności
S+SB=0 MO+MBO=0 Dla układu nieswobodnego: Układ wektorów złożony z sił bezwładności układu materialnego sił
zewnętrznych działających na ten układ oraz z sił reakcji ograniczających ruchy tego układu jest układem równoważnym
0. S+SB+R=0 MO+MBO+HO=0

34*. Ruch obrotowy ciała sztywnego.

Ruch obrotowy ciała sztywnego dokoła osi stałej jest ruchem o jednym stopniu swobody. Ruch ciała określa się

jednym równaniem ruchu podającym zależność kąta obrotu od czasu. Najkorzystniej jest jako równanie to przyjąć jedno
z równań krętu

lub

Il⋅ε=Ml

Il-moment bezwładności względem osi obrotu Ml-moment sił zewnętrznych i reakcji względem osi obrotu

35 inne jakieś. Udowodnić że dla ciała idealnie sprężyst impuls jest dwukrotnie większy niż dla ciała idealnie plast.

J = mv

1

(k+1)cosα kspręż=1, kplast=0

36. Znane zasady mechaniki analitycznej.

Zasady różniczkowe i całkowe. Obszar tej mechaniki nie jest precyzyjnie określony. Oprócz omówienia zasad

mechaniki do mech analitycznej zalicza się równania ruchu zapisana za pomocą rów więzów, przesunięć i prac
przygotowanych. Należy więc zaliczyć do tej mechaniki równania Lagrangea i Hmiltona.

37. Równanie przyrostów prędkości postępowej

Impulsowi zderzenia odpowiadającemu niesk małemu przedziałowi czasu τ odpowiada skończony przyrost

prędkości p. m. Wynikający ze wzoru m.(v-v

0

)=J Stąd wartość prędkości po zderzeniu v=v

0

+J/m.

38. Pojęcie więzów układu mechanicznego, ich klasyfikacja.

Układ, którego punkty nie mogą zajmować dowolnych położeń i mieć dowolnych prędkości niezależnie od

działających sił nazywamy nieswobodnym.

Na położenie i prędkości wszystkich lub niektórych punktów układu nałożone są warunki ograniczające ich

swobodę zwane więzami.

Więzy określone równaniami nazywają się więzami dwustronnymi, nierównościami jedno-stronnymi. Jeżeli

równanie więzów zawiera tylko współrzędne punktów to nazywamy je więzami geometrycznymi.

Równania więzów mogą być także zależne od prędkości punktów (więzy kinematyczne). Oba rodzaje więzów

mogą być ponadto zależne od czasu (więzy niestacjonarne).

Więzy niezależne od czasu- więzy stacjonarne. Więzy całkowalne są to więzy kinematyczne, które można

przedstawić jako pochodną innej funkcji, która jest funkcją współrzędnych i czasu. Wtedy równaie więzów
kinematycznych może być zastąpione równoważnym równaniem więzów geometrycznych.

Wiezy idealne- są to więzy dwustronne, przy których suma prac przygotowanych i reakcji wywołanych tymi

więzami n1a dowolnym przesunięciu przygotowanym jest równa 0.

*--39. Zdefiniować i podać przykłady więzów niholonomicznych.
Są to więzy kinematyczne nie całkowalne.

40. Wyznaczenie siły uogólnionej odpowiadającej danej współrzędnej uogólnionej w równaniach Lagrnge’a,
przykład.

Siłę uogólnioną można obliczyć jako pochodną potencjału względem odpowiedniej współrzędnej w przypadku

gdy potencjał jest przedstawiony jako funkcja współrzędnych uogólnionych

Q

i

=-deltv/deltq

i

.

Niezależne współrzędne, których liczba jest najmniejszą potrzebną do określenia położenia układu nazywamy

współrzędnymi uogólnionymi. Mogą być dowolnymi współrzędnymi liniowymi lub kątowymi. Siłą uogólnioną
nazywamy taką wielkość, która pomnożona przez przyrost przygotowany δqj współrzędnej uogólnionej daje wartość
pracy wykonanej przez układ sił działających na dany układ materialny na przesunięciach przygotowanych wywołanych
przyrostem współrzędnej uogólnionej.

Qj=δLj/δqj.