Metody numeryczne w nauce i technice.

MATLAB

Laboratorium

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Plan zajęć:

Wprowadzenie – informacje wstępne:

1. Wstęp do programowania w środowisku Matlab.
2. Macierze, wektory, układy równań liniowych.
3. Interpolacja i aproksymacja.
4. Przybliżone rozwiązywanie równań nieliniowych.
5. Całkowanie i różniczkowanie numeryczne.
6. Rozwiązywanie równań różniczkowych zwyczajnych.
7. Kolokwium zaliczeniowe.

1.0 Wprowadzenie do metod numerycznych.

Metody numeryczne

są działem matematyki, zajmującej się opracowywaniem metod

przybliżonego rozwiązywania zagadnień matematycznych, których rozwiązanie sposobami
analitycznymi (ścisłymi) jest trudne, albo wręcz niemożliwe.

1.1 Oszacowanie dokładności obliczeń i analiza błędów.

Błędy opisu matematycznego analizowanego zjawiska

Błędy początkowe

(błędy danych wejściowych)

Błędy obcięcia

(skończona liczba działań)

Błędy zaokrągleń

(niedokładna reprezentacja liczb rzeczywistych)

Zadania źle uwarunkowane

– niewielka względna zmiana danych powoduje duże względne

zmiany jego rozwiązania.

Algorytm jest

numerycznie poprawny

, jeżeli dla dokładnych danych wejściowych daje

rozwiązania będące rozwiązaniami zadania dla niewiele zaburzonych tych danych.

(nie dotyczy deterministycznych układów chaotycznych☺)

1.2 Podstawowe komendy Matlaba

%

- komentarz, objaśnienia

clc

- czyści okno poleceń Command Window

clf

- czyści okno graficzne Figure

clear x

- usuwa zmienną x z pamięci

clear all

- usuwa wszystkie zmienne z pamięci

who,whos

- wyświetla zdefiniowane zmienne

lenght(x)

- zwraca długość wektora

size(M)

- zwraca rozmiar macierzy, ilość wierszy i kolumn

t=t1:Dt:t2

- definiuje wektor o poczatku t1, krok Dt, końcu t2.

M’

- transpozycja macierzy M

A*B

- iloczyn macierzy A i B

sum(x)

- suma elementów wektora x

prod(x)

- iloczyn elementów wektora x

det(A)

- wyznacznik macierzy kwadratowej A

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

2

Laboratorium z metod numerycznych – Informatyka Stosowana I .

lu

- rozkład macierzy na macierze trójkątne

[L,U]-lu(A)

- L*U=A

[L,U,P]=lu(A)

- L*U=PA

-

L

– macierz trójkątna dolna

-

U

– macierz trójkątna górna

-

P

– macierz permutacji

eye(n)

- macierz jednostkowa o wymiarze (n x n)

inv(A)

- macierz odwrotna

eig(A)

-

wektor

wartości własnych macierzy kwadratowej A

[V,D]=eig(A)

-

D

- diagonalna macierz wartości własnych A

-

V

– macierz, której kolumny odpowiadają wektorom własnym

spełniającym A*V=V*D

ones(m,n)

- macierz jedynek (m x n)

zeros(m,n)

- macierz zer (m x n)

2.0 Macierze, wektory, układy równań liniowych.

M-plik funkcyjny –

nazwa funkcji.m

Kod:

fun1.m

----------------------------

function y=fun1(x)

% opis fukcji

y=4*sin(3*x).*exp(-x/2);

============================

p2.m

----------------------------

clear all

t=1:0.2:10;
y=2*sin(2*t-1);

b=fun1(t);
plot(t,b,’xr’,t,y), grid on
pause(3)

grid off

Wynik przedstawia się następująco:

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

3

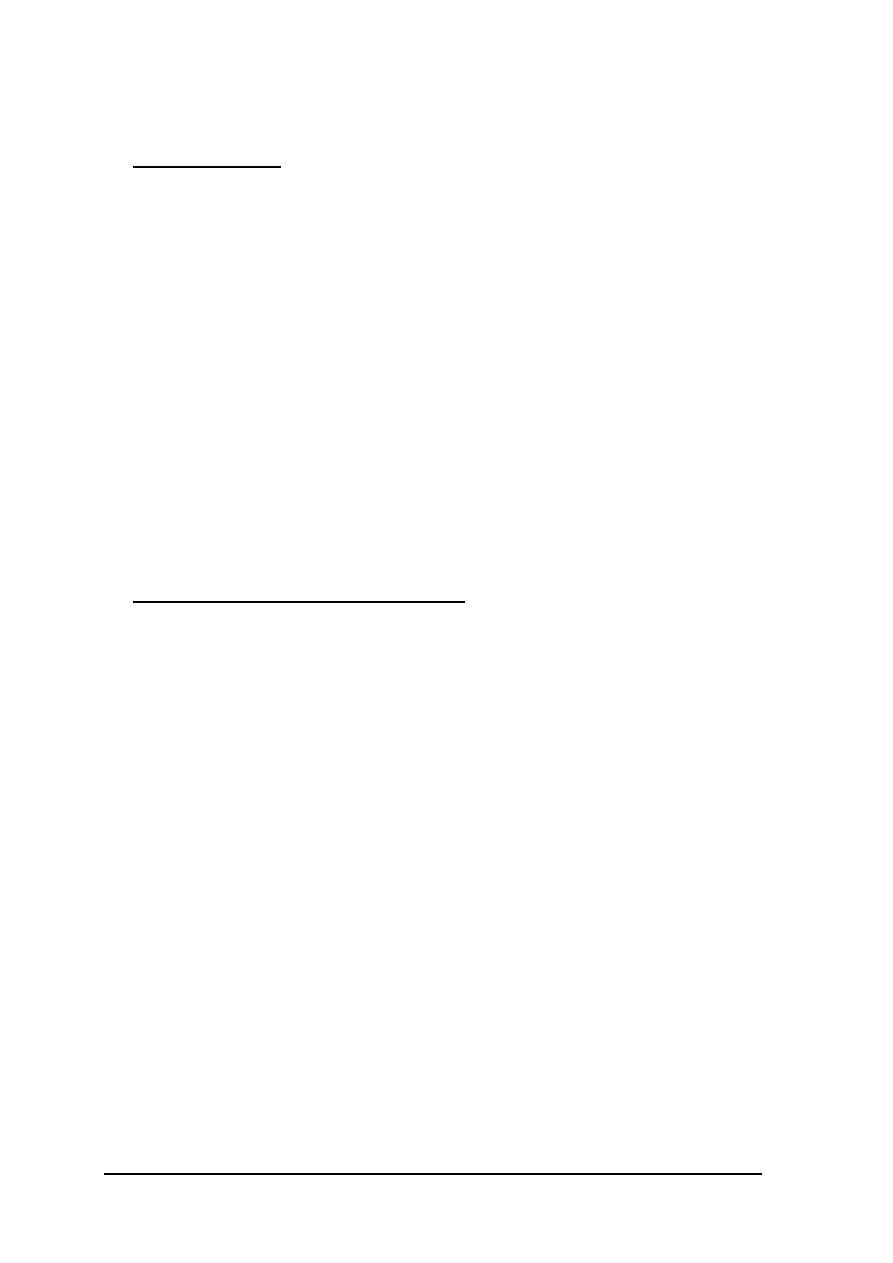
Laboratorium z metod numerycznych – Informatyka Stosowana I .

2.1 Macierze i wektory

M1=[1

2

3

W1=[1

2

3]

4 5 6]

M1=

W1=

1 2 3

1 2 3

4 5 6

W2=[1

2

3]’

M2=[1 2 3;4 5 6;7 8 9]

W2=

1

M2=

2

1 2 3

3

4 5 6

7 8 9

W3=1:2:8

W3=

1 3 5 7

2.2 Rozwiązywanie układów równań liniowych

Układ równań liczbowych

a

11

*x

1

+a

12

*x

2

+…+a

1k

*x

k

+…+a

1n

*x

n

=b

1

a

21

*x

1

+a

22

*x

2

+…+a

2k

*x

k

+…+a

2n

*x

n

=b

2

a

k1

*x

1

+a

k2

*x

2

+…+a

kk

*x

k

+…+a

kx

+x

n

=b

k

a

n1

*x

1

+a

n2

*x

2

+…+a

nk

*x

k

+…+a

xn

*x

n

=b

n

Przykład liczbowy

( )

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

=

≠

=

−

=

−

+

+

−

=

−

+

−

+

−

=

+

+

−

)

(

)

(

*

0

)

det(

*

15

4

2

4

11

4

2

9

7

2

21

2

6

6

7

3

3

2

1

1

3

x

2

x

1

x

x

x

x

z

y

x

x

B

A

x

B

x

A

A

x

z

y

x

x

z

y

x

y

x

z

y

x

Zapis w Matlabie

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

4

Laboratorium z metod numerycznych – Informatyka Stosowana I .

2.3

Rozkład LU

Kod:

% Równanie

A * x = B

(1)

% Rozkład LU

P * A = L * U

% Równanie (1) obustronnie mnożymy przez P

P * A *x = P * B

%

Stosujemy rozkład LU

L * U *x = P * B

% Wprowadzamy nową zmienną

U * x = y

% Otrzymujemy równanie o macierzy trójkątnej

L * y = P * B

Przykład m2.m

Kod:

A=[1 2 3;2 3 4;3 4 6];
B=[7;8;9];

[L,U,P]=lu(A);
n=length(B);

PB=P *B;

% dla macierzy L

y(1)=PB(1)/L(1,1);

for k=2:n
y(k)=(PB(k)-L(k,1:k-1)*y(1:k-1))’)/L(k,k);

end

% dla macierzy U

x(n)=y(n)/U(n,n);
for k=1:n-1

x(n-k)=(y(n-k)-U(n-k,n-k+1:n)*x(n-k+1:n))’)/U(n-k,n-k);
end
x’

2.4 Rozwiązania w Matlabie

Macierz kwadratowa → A * x = B

det(A) ≠ 0

Kod:

x=A

-1 *

B

x=inv(A) * B

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

5

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Inne przypadki: układy nadokreślone i niedookreślone

x=A\B

%Matrix left division \ of Galois arrays

x=pinv(A)B

%Moore-Penrose pseudoodwrotna macierz

Przykład 1

Rozwiąż równanie

Lx –B

T

=2* Ex

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

−

−

=

6

5

0

9

2

1

4

7

5

A

[

]

30

20

10

−

=

B

L – jest macierzą trójkątna dolna po permutacji macierzy A
E – jest macierzą jednostkową o wymiarach macierzy A

Kod:

A=[5 -7 4; =3 2 9; 0 5 6];

B=[-10 20 30];
[L,U,P]=lu(A);

E=eye(size(A));
X=(L-2*E)\B’

Otrzymujemy wynik:

x=

10.0000

-20.0000
-27.2000

2.5

Zadania

1.

4x+3y+6=14+3x-2y-8;
6y+15+3z=-4x+3;
2x-25+2y=3x+3y-3x;

Oblicz y oraz s = x

2

+y

2

+z

2

2.

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

6

Laboratorium z metod numerycznych – Informatyka Stosowana I .

7

⎤

⎢

⎢

⎢

⎣

⎡

−

−

=

9

2

3

4

7

5

A

⎥⎦

6

5

9

⎥

⎥

[

]

30

20

10

−

=

B

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

3

2

1

x

x

x

x

U – jest macierzą trójkątna górna macierzy A
E – jest macierzą jednostkową o wymiarach macierzy A
D – jest wyznacznikiem macierzy A

Rozwiąż równanie

Ux-5B

T

=d* Ex

Rozwiązania

1.

Kod:

A=[1 3 8;4 6 0;5 -1 -3];

B=[8;-15;25];
x=A\B;

y=x(2)
s=x’*x

Wynik:

y= -6.7000
s= 103.9400

2.

Kod:

A=[5 -7 4;-3 2 9;0 5 6];
B=[-10 20 30];
[L,U]=lu(A);

d=det(A);
E=eye(size(A));

x=(U-d*E)\(5*B’)

Wynik:

x=
-0.1397

0.2740

0.4109

2.6 Układ nadmiarowy – ilośc równań większa od ilości niewiadomych.

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Dla pomiarów [t

1

,y

1

]

t

1

0.1 0.3 0.5 0.9 1.2 1.6 2.2 2.8

y

1

2.5 2.3 2.7 2.9 2.5 2.0 1.4 1.2

Wyznaczyc współczynniki C

1

równania y=f(t)

2

-3t

3

-t

2

1

e

*

C

e

*

C

C

y(t)

+

+

=

Kod:

t=[0.1 0.3 0.5 0.9 1.2 1.6 2.2 2.8]’
y=[2.5 2.3 2.7 2.9 2.5 2.0 1.4 1.2]’
plot(t,y.’o’)

% y=C1+C2*exp(-t)+C3*exp(-3*t.^2)

A=[ones(size(t)) exp(-t) exp(-3*t.^2)]

C=A\y
pause

%dalej

–

“enter”

w oknie polecen matlaba

clf
tt=[0:0.01:3]’;

AA=[ones(size(tt)) exp(-tt) exp(-3*tt.^2)];
yy=AA*C;
plot(tt,yy,t,y,’o’),grid on, hold on

2.7 Układ niedookreślony – ilość równań mniejsza niż ilość niewiadomych

% R*x=B

m5.m

% R=[R1 R2],

R=[6

8

7

3

5

% x=[x1’ x2’]’

3 5 4 1 3

% R1*x1+R*x2=B

2 5 3 7 2]

% x1*x1=B-R2*x2

[n,m]=size(R)

R1=R(:,1:n)

R2=R(:,n+:m)

B=[2 1 4]’

x2=[1 1]’

x1=R1\)B-R2*x2)
x=[x1’

x2’]’

blad=B-R*x

3.0 Interpolacja i aproksymacja.

Interpolacja

Zadanie znalezienie funkcji F(x) przechodzącej przez zadane punkty (x,y) nazywamy

I N T E R P O L A C J Ą

(po łacinie inter – między, polus – węzeł)

Punkty (x,y) nazywamy węzłami interpolacji.

Istnieje funkcja:

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

8

Laboratorium z metod numerycznych – Informatyka Stosowana I .

]

[

),

(

0 n

x

x

x

x

f

y

∈

=

Należy wyznaczyć funkcję F(x), taką aby:

y

x

F

=

)

(

3.1 Metoda Funkcji bazowych

F(x) jest liniową kombinacją n=1 funkcji bazowych

∑

=

=

n

i

i

i

n

x

a

x

F

x

x

x

0

1

0

)

(

)

(

),

(

)

(

),

(

ϕ

ϕ

ϕ

ϕ

K

Wprowadzając macierz bazową

φ

[

]

)

(

)

(

)

(

)

(

1

0

x

x

x

x

n

ϕ

ϕ

ϕ

φ

K

=

i macierz współczynników A

[

]

T

n

a

a

a

A

K

1

0

=

A

x

x

F

∗

=

)

(

)

(

φ

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

=

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

∗

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

=

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

n

n

n

n

n

n

n

n

n

y

y

y

a

a

a

x

x

x

x

x

x

x

x

x

x

F

x

F

x

F

M

M

K

L

L

K

K

M

1

0

1

0

1

0

1

1

1

1

0

0

1

1

0

0

1

0

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

Y

x

x

F

Y

A

∗

∗

=

=

∗

−1

)

(

)

(

φ

φ

φ

Jeżeli funkcje bazowe są wielomianami to

interpolacja wielomianowa

np. interpolacja

wielomianami

Langrange`a

,

jednomianami

n

n

x

x

=

)

(

ϕ

3.2 Wielomiany

2

7

3

6

4

)

(

)

(

2

4

5

0

+

+

−

+

=

∈

=

∑

−

−

−

x

x

x

x

x

p

N

i

x

p

x

p

n

i

i

n

i

n

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

9

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Funkcje MATLABA

p= [4 6 0 -3 7 2]

% zapis wielomianu o współczynnikach p

y=polyval(p,x)

% oblicza wartość wielomianu dla x

p=polyfit(x,y,n)

% znajduje współczynniki wielomianu n-tego stopnia
aproksymującego dane (x

i

y

i

)

Kod:

xi=[ 2 4 6 8 9];

yi=[-5 0 2 -1 7];
plot(xi,yi,’o’),grid on,pause(2)

n=length(xi);
p=polyfit(xi,yi,n-1);
x=1:0.01:9.2;

y=polyval(p,x);
plot(xi,yi,’o’,x,y),grid on, pause(2)

pp=polyfit(xi,yi,8);
yy=polyval(pp,x);

plot(x1,yi,’o’,x,y,x,yy,’r’),grid on
axis([1 10 -10 12])

%dopasowanie osi wykresu

Interpolacyjne funkcje MATLABA

Matlab posiada rozbudowane funkcje interpolacyjne dedykowane do odpowiednich danych:

• Funkcje dla danych jednowymiarowych

interp1

• Funkcje dla danych dwuwymiarowych

inrerp2

• Funkcje dla danych wielowymiarowych

interp3, intern

Kod:

y=interp1(xi,yi,x,

’metoda’

)

%wykonuje interpolację w punktach określonych wektorami x dla zadanych węzłów (x

i

y

i

).

Elementy wektora

xi

muszą tworzyć ciąg rosnący.

metoda –

wybór metody interpolacji

linear

–

interpolacja funkcją łamaną

spline

–

interpolacja funkcjami sklejanymi

cubic

–

interpolacja wielomianami 3-go stopnia

nearest

– interpolacja wartościa najbliższych punktów

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

10

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Kod:

xi=[ 2 4 6 8 9];

yi=[-5 0 2 -1 6];
plot(xi,yi,’o’),grid on, pause(2)

x=1:0.01:9.1;
y1=interp1(xi,yi,x,’linear’);
plot(x,y1,xi,yi,’o’),grid on, pause(2)

y2=interp1(xi,yi,’o’,’spline’);
plot(x,y2,xi,yi,’o’),grid on, pause(2)

y3=interp1(xi,yi,x,’cubic’);
plot(x,y3,xi,yi,’o’),grid on, pause(2)

y4=interp1(xi,yi,x,’nearest’);
plot(x,y4,xi,yi,’o’),grid on, pause(2)
plot(x,y1,x,y2,x,y3,x,y4,xi,yi,’o’)

Wynik:

3.3

Aproksymacja

Aproksymacja

Zadaniem znalezienie funkcji F(x) z żądaniem, aby jak najbardziej zbliżała się do funkcji f(x) w
pewnym określonym przedziale (a,b) nazywamy

A P R O K S Y M A C J Ą.

Kryterium Aproksymacj metodą najmniejszych kwadratów jest minimalizacja całki:

∫

−

=

b

a

dx

x

F

x

f

Q

2

))

(

)

(

(

Dla przypadku funkcji dyskretnej, minimalizacja sumy:

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

11

Laboratorium z metod numerycznych – Informatyka Stosowana I .

[

]

∑

=

−

=

a

i

i

i

x

F

y

Q

1

2

)

(

Wyznaczanie współczynników prostej regresji

(

)

(

)

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

⎟

⎠

⎞

⎜

⎝

⎛ −

⎟

⎠

⎞

⎜

⎝

⎛ −

∗

⎟

⎠

⎞

⎜

⎝

⎛ −

=

∗

−

∗

−

∗

=

=

∗

−

∗

+

⎟

⎠

⎞

⎜

⎝

⎛

−

=

∗

−

∗

⎟⎟

⎟

⎠

⎞

⎜⎜

⎜

⎝

⎛

∗

−

+

∗

−

=

−

=

=

⎟

⎠

⎞

⎜

⎝

⎛

−

∗

+

=

−

+

∗

=

∂

∂

=

∗

−

+

∗

=

∂

∂

−

+

∗

=

−

=

∆

=

−

=

∆

+

∗

=

=

n

i

i

n

i

i

i

n

i

n

i

i

i

n

i

i

i

n

i

i

n

i

i

i

n

i

i

n

i

n

i

i

i

n

i

i

n

i

i

n

i

i

i

n

i

i

n

i

i

n

i

n

i

n

i

i

i

i

i

i

n

i

i

i

n

i

n

i

i

i

i

n

i

i

i

i

i

x

x

y

y

x

x

a

x

x

x

x

y

y

x

a

y

x

x

y

x

x

x

a

y

x

x

x

a

y

x

a

x

a

y

b

x

n

a

y

n

b

y

b

n

x

a

y

b

x

a

b

b

a

Q

x

y

b

x

a

a

b

a

Q

y

b

x

a

y

y

y

b

a

Q

y

y

y

b

x

a

y

n

i

y

x

1

2

__

1

__

__

1

1

__

2

1

__

1

1

1

__

1

1

__

2

1

1

1

__

__

2

__

__

1

1

1

1

1

1

1

2

2

1

2

0

0

1

1

0

2

2

)

,

(

0

2

)

,

(

)

(

)

(

)

,

(

..

1

)

(

∑

=1

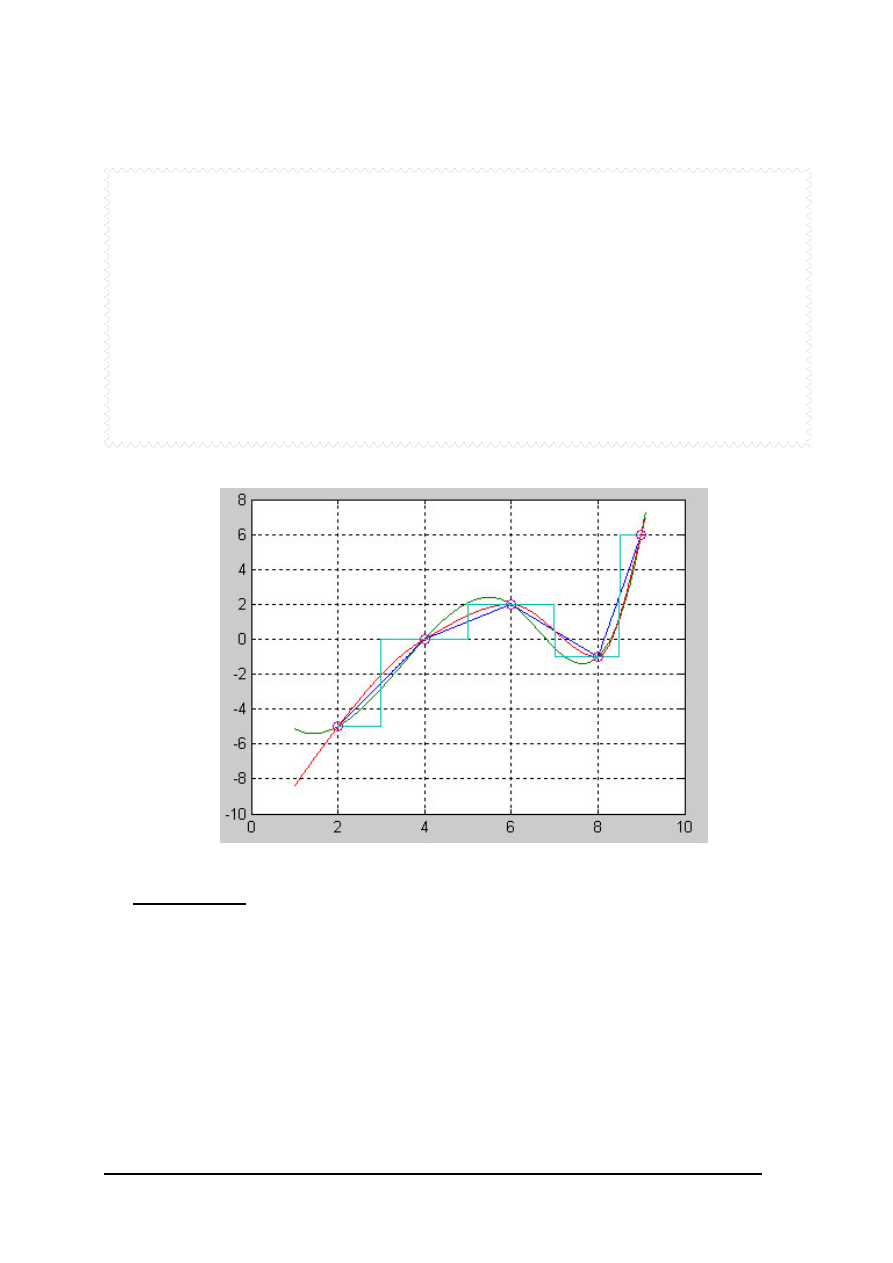
Kod:

xi=0:0.5:10;

n=length(xi);

y1=2*xi+3;
y2=3*(

rand

(1,n)-rand(1,n));

yi=y1+y2;
plot(xi,yi,’*’),pause(2)

xs=

sum

(xi)/n;

% wartość średnia x

ys=sum(yi)/n;

% wartość średnia y

a=(xi*yi’-n*xs*ys)/(xi*xi’-n*xs^2);
b=ys-a*xs;
x=0:0.01:10;

y=a*x+b;
plot(xi,yi,’*’,x,y),grid on

parametry_prostej=[a b]’

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

12

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Wynik:

parametry_prostej =

1.9143
3.9445

3.4 Zadania

Zadanie 1

Dokonano następujących pomiarów:

x

-5

-3

0 2 5 6 8

y 10 40 80 90 130 145 160

1. Wyznacz prostą regresji.
2. Oblicz y(1) i y(7).

Kod:

x=[ -5 -3 0 2 5 6 8];

y=[10 40 80 90 130 145 160];

c=polyfit(x,y,1)
y1_7=polyval(c,[1,7])

Wynik:

y= 11.2889x + 70.0444
y(1)= 81.3333

y(7)=149.0667

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

13

Laboratorium z metod numerycznych – Informatyka Stosowana I .

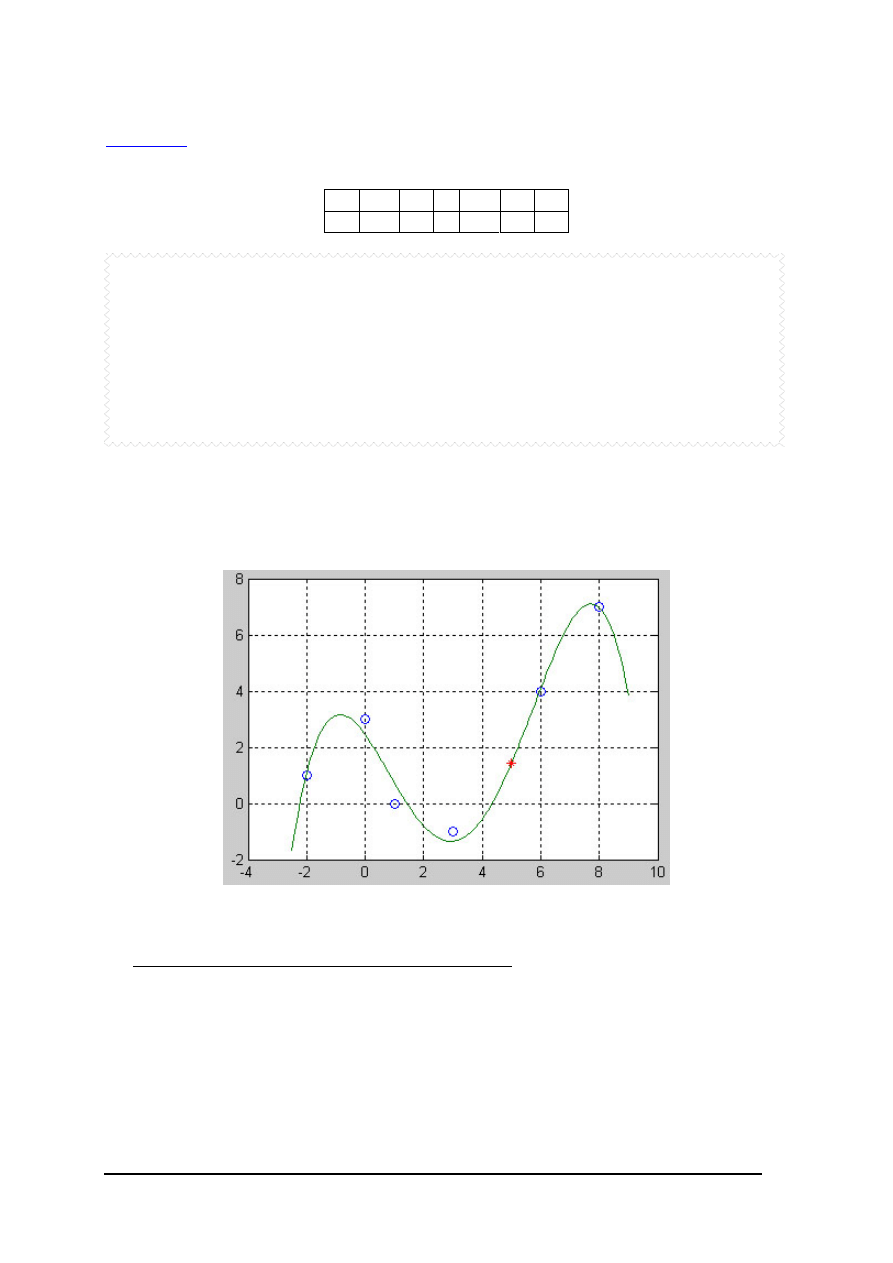
Zadanie 2.

Wyznacz współczynniki wielomianu 4 stopnia aporoksymującego punkty pomiarowe(x,y), a
następnie oblicz wartość y(5).

x -2 0 1

3 6 8

y 1 3 0

-1 4 7

Kod:

x=[-2 0 1 3 6 8];

y=[1 3 0 -1 4 7];

c=polyfit(x,y,4)

%wyznaczanie współczynników

y5=polyval(x,5)

%obliczanie y(5)

xx=-2.5:0.1:9;

yy=polyval(c,xx);
plot(x,y,’o’,xx,yy,5,y5,’*r’),grid on

Wynik:
c=

-0.0187 0.2.447 -0.5070 -1.4437 2.4623

y5= 1.4386

4.0 Przybliżone rozwiązywanie równań nieliniowych.

Twierdzenie Bolzano-Cauchy`ego

Jeżeli f(x) jest ciągła w przedziale [a,b] i f(a)•f(b)<0 to w przedziale (a,b) znajduje się co
najmniej jeden pierwiastek równania f(x)=0

Twierdzenie

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

14

Laboratorium z metod numerycznych – Informatyka Stosowana I .

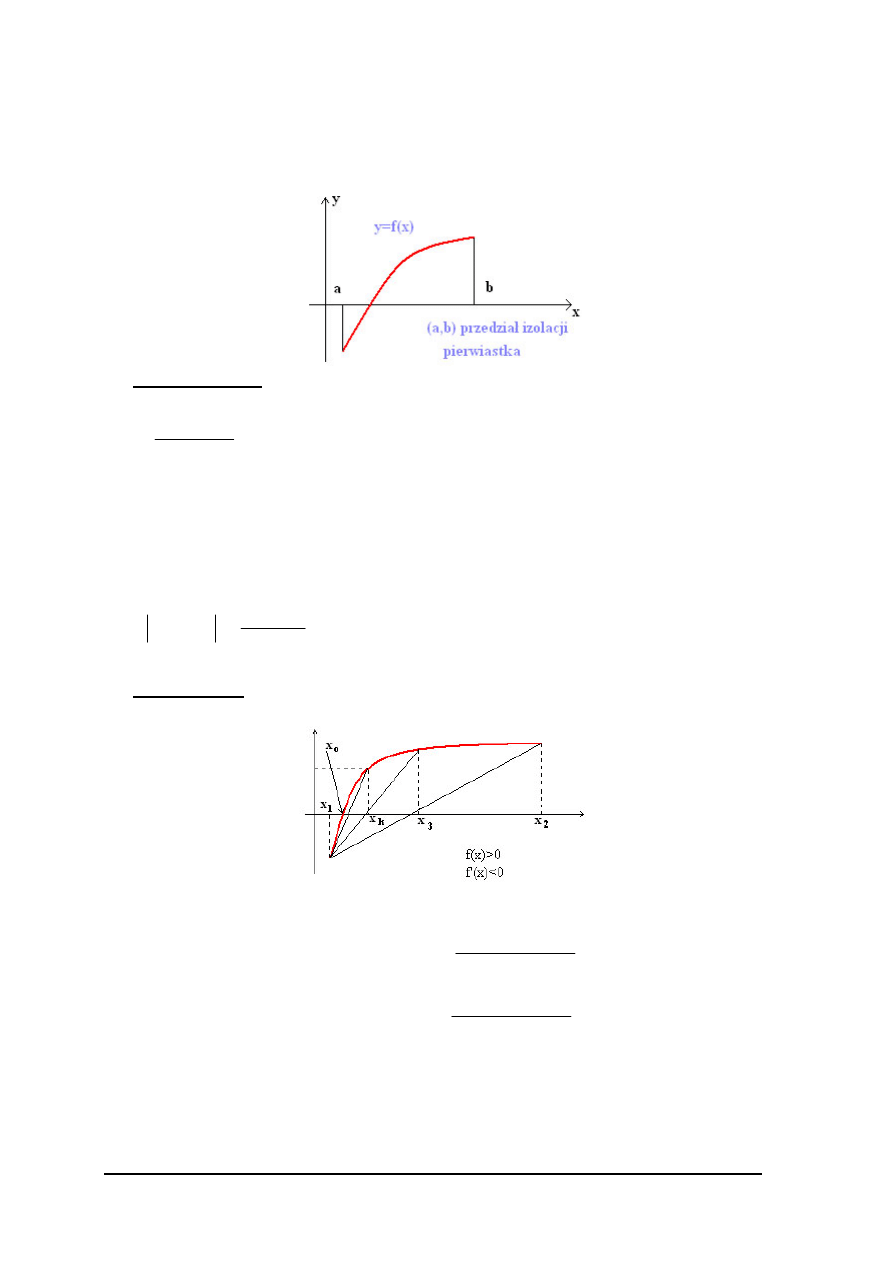
Jeżeli w przedziale [a,b] spełnione są założenia tw. Bolzano-Cauchy`ego i dodatkowo

sgn(f’(x))=const

dla

x

∈

[a,b],

to przedział ten jest przedziałem izolacji pierwiastka

równania

f(x)=0

4.1

Metoda bisekcji:

0

)

(

)

(

3

2

3

2

1

1

2

1

<

∗

>

−

=

∨

−

=

+

=

−

−

x

f

x

f

k

k

j

k

j

x

x

x

k

k

k

Błąd metody:

k

k

x

x

x

x

2

1

2

0

−

<

−

=

δ

4.2

Metoda cięciw

)

(

)

(

)

(

)

(

)

(

)

(

1

1

1

1

1

1

1

1

x

f

x

f

x

x

x

f

x

x

x

f

x

f

x

x

x

f

x

x

k

k

k

k

k

k

k

−

−

−

=

−

−

−

=

+

+

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

15

Laboratorium z metod numerycznych – Informatyka Stosowana I .

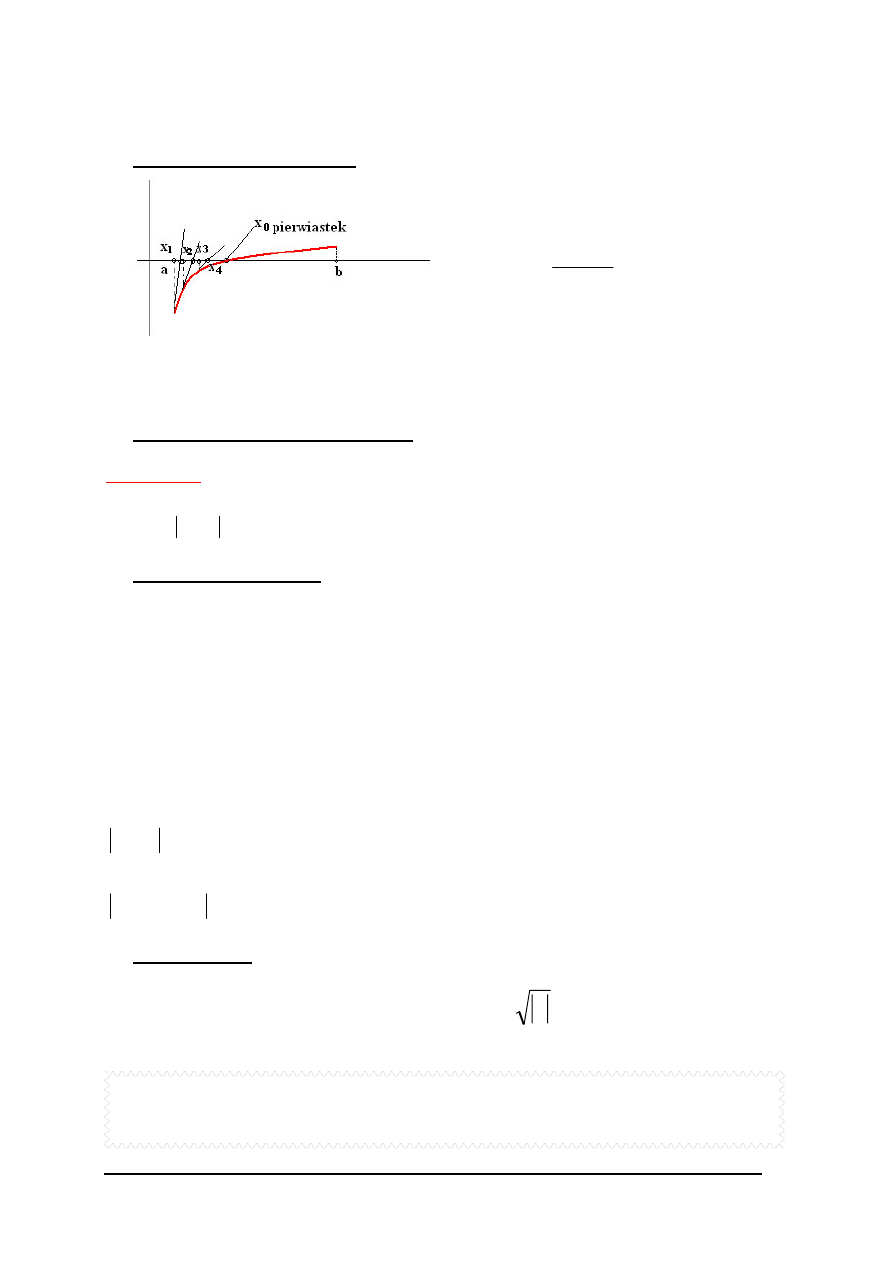
4.3

Metoda stycznych (Newtona)

b

x

x

f

x

f

a

x

x

f

x

f

k

k

k

k

=

→

<

∗

=

→

<

−

1

1

0

)

(

"

)

(

'

0

)

(

"

)

(

'

k

x

f

x

f

x

x

k

k

k

k

≥

−

=

+1

1

)

(

'

)

(

4.4

Metoda iteracji dla równania x=F(x)

Twierdzenie

Jeżeli w przedziale [a,b] izolacji pierwiastka równania x=F(x) pochodna funkcji F’(x) spelnia

warunek

1

)

(

'

<

≤ M

x

F

to proces iteracji jest zbieżny, przy czym x

0

∈

[a,b].

4.5 Wyprowadzanie metody

)

(

)

(

)

(

)

(

)

(

0

)

(

0

)

(

1

k

k

x

F

x

x

F

x

x

x

f

a

x

F

x

x

x

f

a

x

f

a

x

f

=

=

+

∗

=

=

+

∗

=

∗

=

+

Warunki zapewniające zbieżność

a

x

f

a

x

f

a

x

F

x

F

→

<

+

∗

+

∗

=

<

1

1

)

(

1

)

(

)

(

1

)

(

'

4.6 Metoda iteracji

x

x

x

y

−

+

+

−

=

3

4

2

Kod:
Plik funkcyjny f7.m: [f(x)]

function y=f7(x)

y=-x.^2+4*x+3-sqrt(abs(x));

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

16

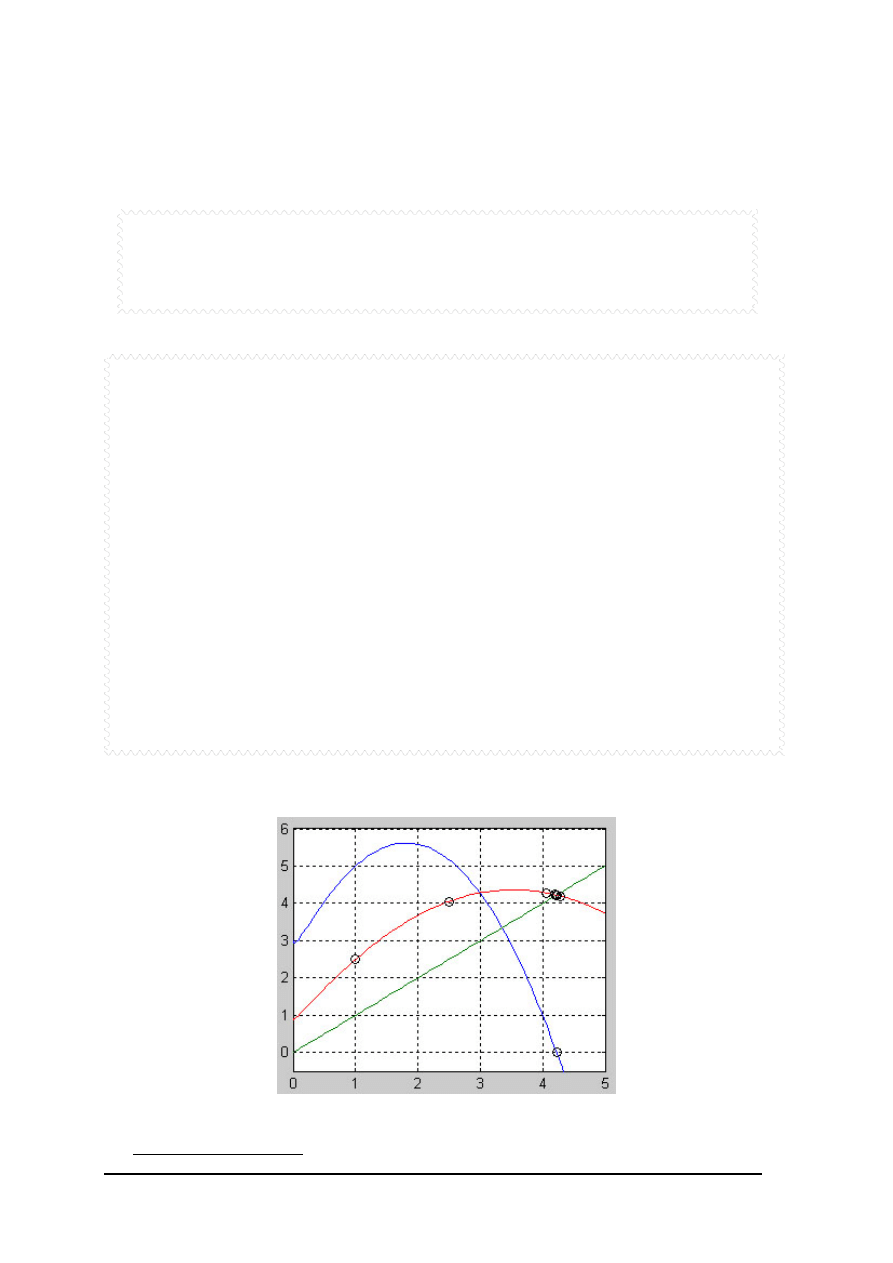
Laboratorium z metod numerycznych – Informatyka Stosowana I .

Plik fukncyjny f8.m: [F(x)]

function y=f8(x)

global a
Y=a*f7(x)+x;

Plik skryptowy:

clear all,clc,clf

global a
a=0.3;

fplot('[f7(x),x,f8(x)]',[0 5 -0.5 6])
grid on

hold on
x(1)=1;
b=1;

k=1;
while b>0.001

x(k+1)=f8(x(k));

b=abs(f7(x(k+1)));

k=k+1;

if k>10, break, end

end

n=length(x);
zo=x(n)

plot(zo,0,'ok',x,f8(x),'ok')

Wynik:

4.7

Polecenia MATLABA

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

17

Laboratorium z metod numerycznych – Informatyka Stosowana I .

xo = fzero(‘

plik_funkcyjny’

,

x

0

)

% oblicza miejsce zerowe funkcji podanej w m-

pliku_funkcjnym

%

x

0

punkt startowy

r=roots(p)

% oblicza pierwiastki wielomianu o współczynnikach zadanych wektorem p

fplot(‘

plik_funkcyjny’

,limits)

% wykreśla funkcję podana w m-

pliku_funkcyjnym

w przedziale określonym przez

limits

limits

jest wektorem określającym oś x

– [ x

min

x

max

],

lub osie x i y –

[x

min

x

max

y

min

y

max

].

4.8

Zadania

Zadanie 1

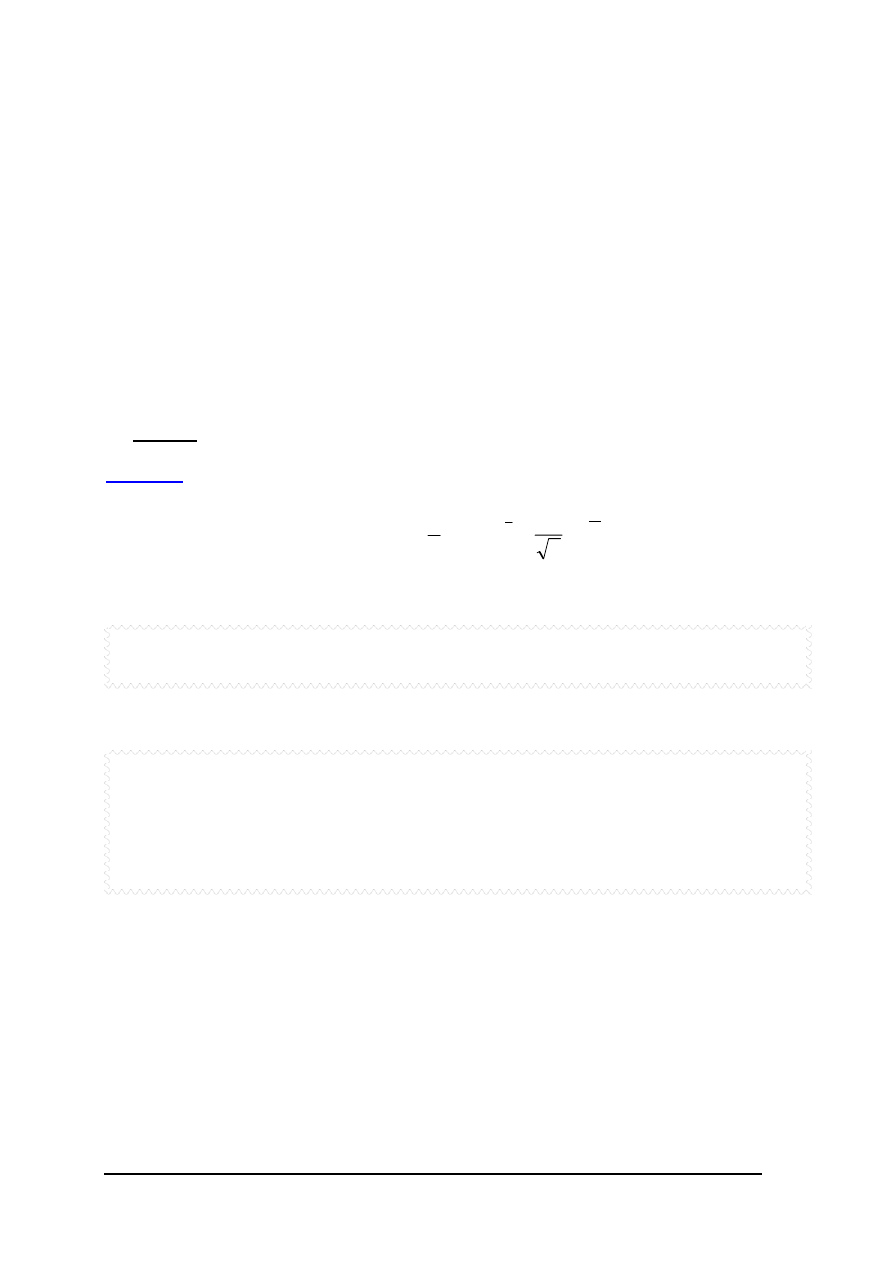
Wyznacz miejsca zerowe funkcji f(x)=0 w przedziale [0,9]

10

2

7

2

.

0

2

3

cos

2

)

(

x

x

e

e

x

x

f

∗

+

∗

⎟

⎠

⎞

⎜

⎝

⎛

−

∗

=

π

Kod:

Plik funkcyjny:

function t=fun2(x)

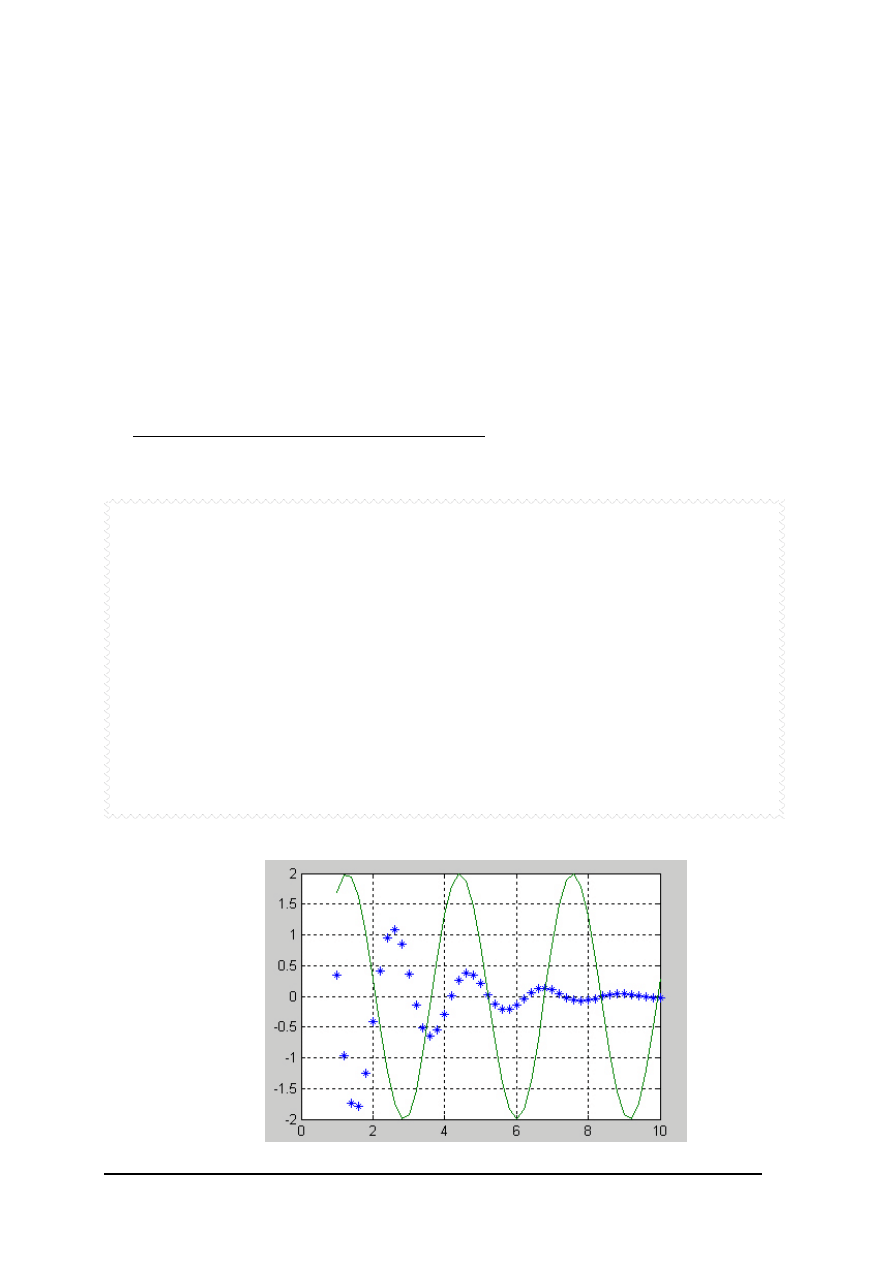
y=2*cos(pi*x/3-2).*exp(-x/2)-0.2/sqrt(7).*exp(-x/10);

Plik skryptowy:

fplot(‘fun2’,[-1 10 -2 2]), hold on

p1=fzero(‘fun2’,2);

p2=fzero(‘fun2’,6);
p3=fzero(‘fun2’,8);

p=[p1 p2 p3]’

plot(p,zeros(size(p)),’ok’), grid on

Wynik:

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

18

Laboratorium z metod numerycznych – Informatyka Stosowana I .

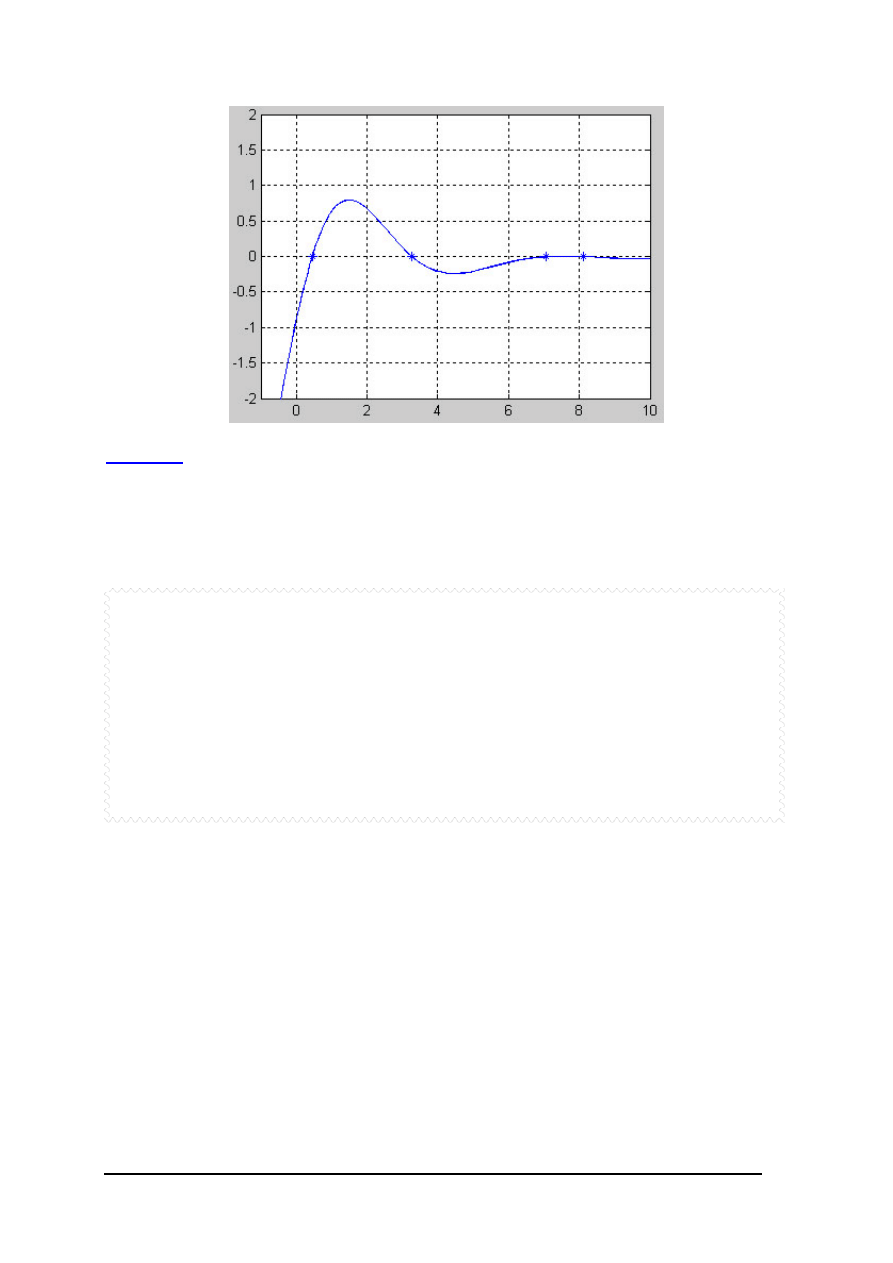
Zadanie 2

Znaleźć pierwiastki wielomianów:

a) p1(x)=2x

3

+6x

2

-20x-30

b) p2(x)=-1.5x

5

+2x

4

+20x

3

-100x

2

+80x+300

Kod:

p1=[2 6 -20 -30];

p2=[-1.5 2 20 -100 80 300];
r1=roots(p1)

r2=roots(p2)
x=-5:0.1:4;

y1=polyval(p1,x);
y2=polyval(p2,x);

subplot(2,1,1),plot(x,y1,r1,0,'o'), grid
subplot(2,1,2),plot(x,y2,r2,0,'o'), grid

Wynik:

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

19

Laboratorium z metod numerycznych – Informatyka Stosowana I .

5.0 Całkowanie i różniczkowanie numeryczne.


Dy=diff(y) %zwraca wektor różnic sąsiednich elementów wektora y

1

1

]

[

],

[

1

1

2

1

3

2

1

=

=

−

=

∆

∆

∆

∆

=

=

+

−

n

k

dla

y

y

y

y

y

y

Dy

y

y

y

y

y

k

k

k

n

n

K

K

K

Kod

x=0:0.1:7;
y=sin(x);
n=length(x)

yprim=diff(y)./fidd(x);

%pochodna

pot(x,y,x(1:n-1),yprim), grid

Kod f1.m

fumction y=f1(x)

y=2*x+5*cos(3*x).*exp(-x/2);

Kod

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

20

Laboratorium z metod numerycznych – Informatyka Stosowana I .

x=0:0.1:7;
y=f1(x);
n=length(x)

yprim=diff(y)./diff(x);

%pochodna

plot(x,y,x(1:n-1),yprim),grid

legend(‘funkcja’,’pochodna’);

5.1 Polecenia Matlaba

Dla wielomianów

P=[1 4 7 0 3 1 6]

P1=polyder(P)

Dla funkcji wymiernej

L=[-2 0 4 0 20 0]
M=[ 1 0 4 …]

[L1,M1]=polyder(L,M)

5.2 Przykłady

Wykreślić funkcję i jej pochodną dla x z przedziały -4 do 4

8

2

1

)

(

2

5

3

+

+

−

=

x

x

x

x

W

Rozwiązanie

h=0.05;
x=-4:h:4;

L=[1 0 -1];M=[1 0 2 0 8];
[L1,M1]=polder(L,M)

y=polyvel(L,x)./polyval(M,x);
yprim=polyval(L1,x)./polyval(M1,x);

plot(x,y,x,yprim,’-‘),grid
title(‘Funkcja wymierna i jej pochodna’)
legend(‘funkcja’,’pochodna’)

5.3

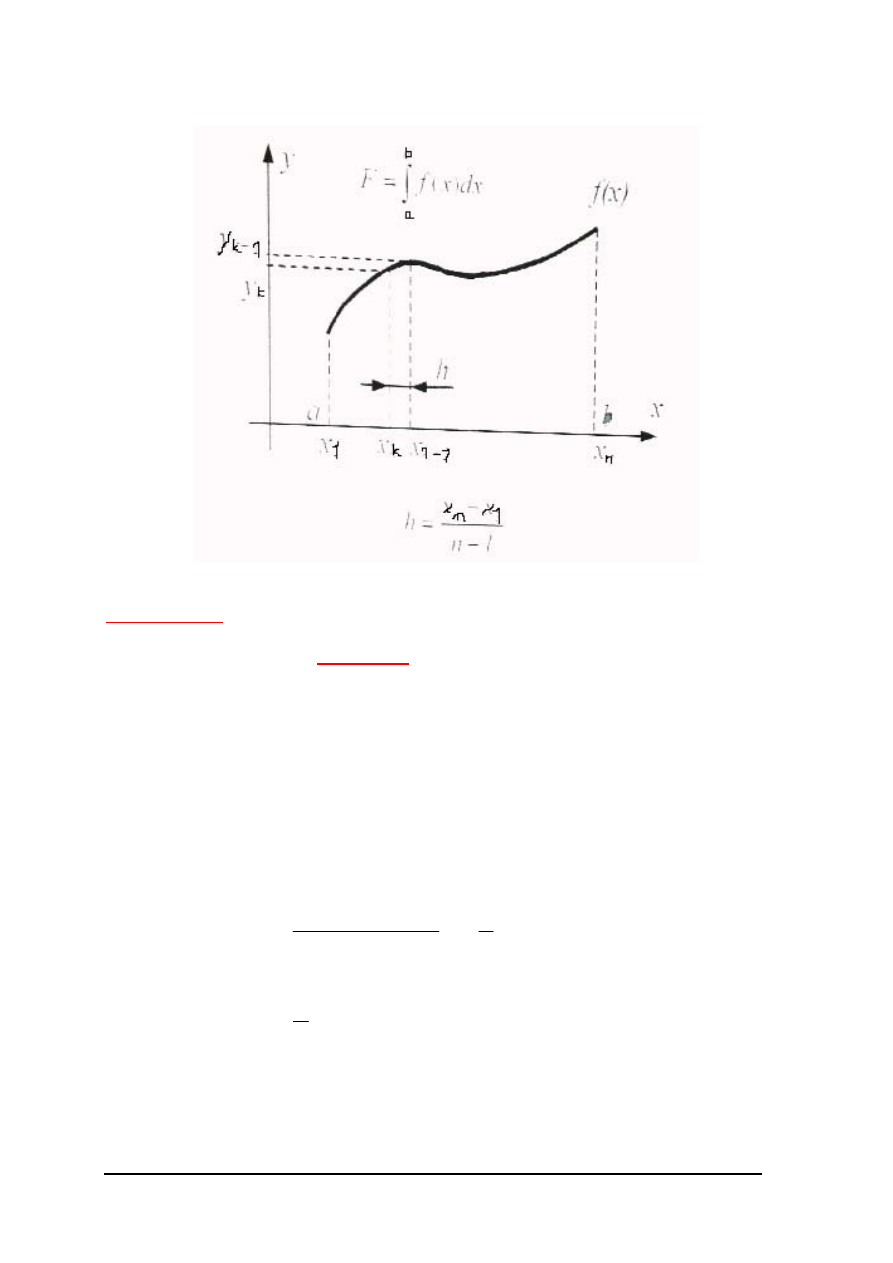
Całkowanie numeryczne

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

21

Laboratorium z metod numerycznych – Informatyka Stosowana I .

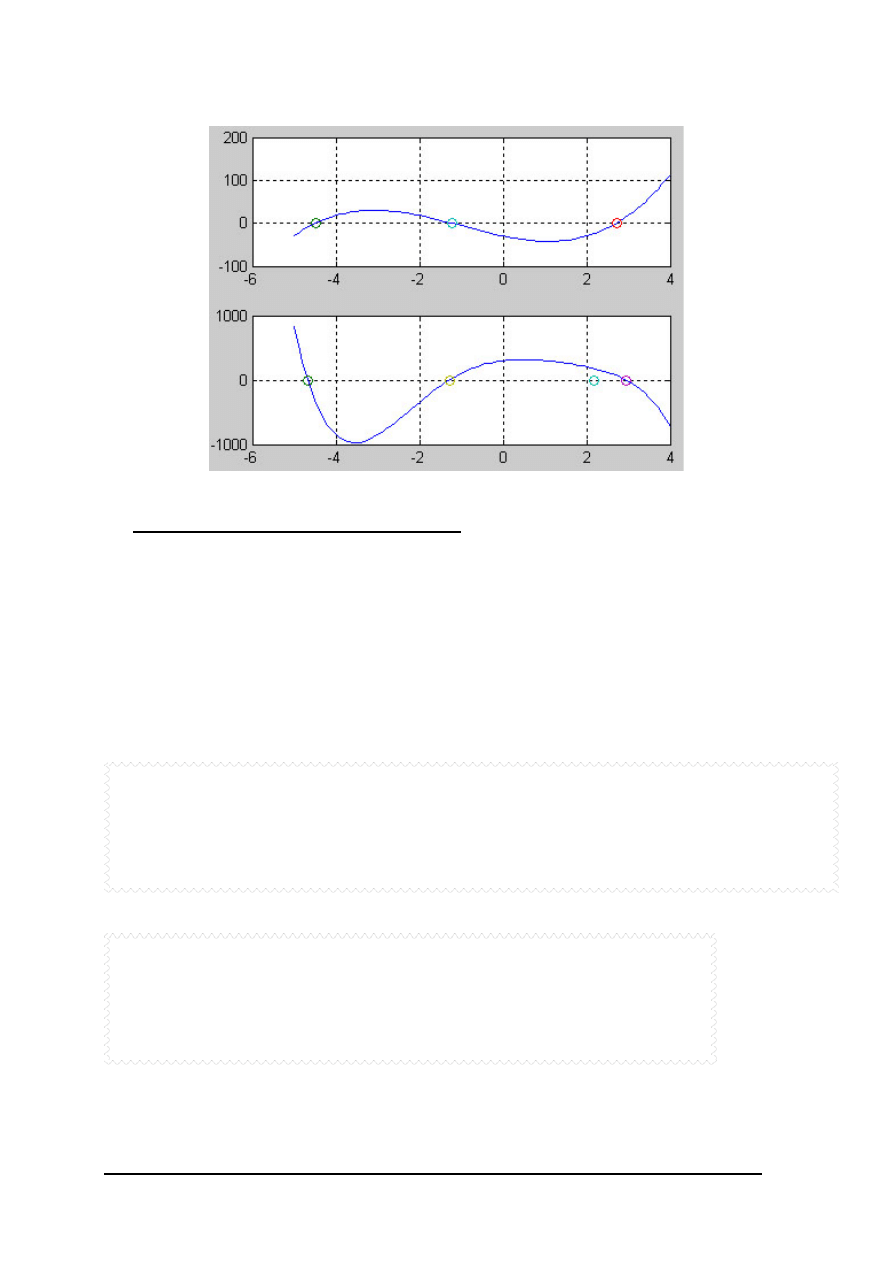
Wzory do numerycznego całkowania funkcji jednej zmiennej nazywane są

kwadraturami.

Funkcji wielu zmiennych –

kubaturami

Kwadratury interpolacyjne i aproksymacyjne:
Kwadratury Newtona-Cotesa
Kwadratury Gaussa
Kwadratury Lobatto

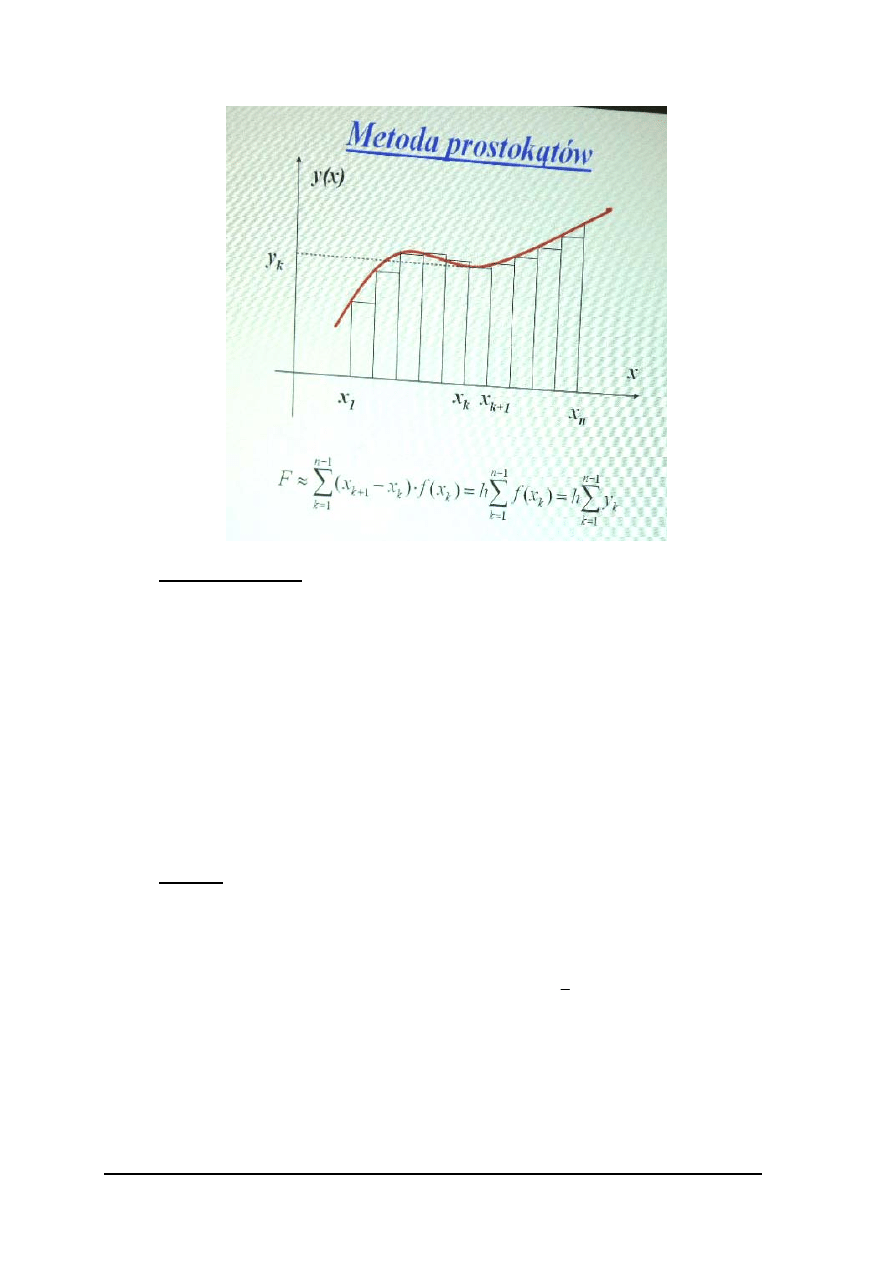
Metoda prostokątów

∑

∑

−

=

−

=

=

≈

1

1

1

1

)

(

n

k

n

k

k

k

y

h

x

f

h

F

Metoda trapezów

∑

∑

−

=

−

=

+

⎟

⎠

⎞

⎜

⎝

⎛

+

+

=

+

≈

1

1

1

2

1

1

2

2

2

)

(

)

(

n

k

n

k

n

k

k

k

y

y

y

h

h

x

f

x

f

F

Metoda parabol

)

)

(

)

(

4

)

(

(

3

2

/

1

1

2

2

1

2

∑

=

+

−

+

+

≈

n

k

k

k

k

x

f

x

f

x

f

h

F

Metoda Prostokątów

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

22

Laboratorium z metod numerycznych – Informatyka Stosowana I .

5.4

Polecenia Matlaba

∫

=

h

a

dx

x

f

F

)

(

F=quad(‘funk

% Simpson`s

cja’,a,b)

F=quad8(funkcja’a,b)

%Newton-Cotes(dawna)

felp quad

Quadv, quadl, dblquad, triplequad

5.5

Zadania

Oblicz całkę oznaczoną z funkcji f(x) w granicach a=1 b=10 metodą prostokątów,
trapezów I wbudowaną Matlaka

2

*

)

3

cos(

5

2

)

(

x

e

x

x

x

f

+

=

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

23

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Rozwiązanie

h=0.01;

x=1:h:10;
n=length(x)

fplot(‘f1’,[1 10]), grid
y=f1(x);
a=x(1);

b=x(n);
F(1)=h*sum(y(1:n-1));

%prostokątów

F(2)=h*(y(1)+2*sum(y(2:n-1))+y(n))/2;

%trapezów

F(3)=quad(‘f1’,a,b);

%Simpson`s

Wynik=F’

Oblicz całkę metodą prostokątów, trapezów i wbudowaną w Matlaba oraz wyznacz błąd
obliczeń numerycznych

∫

=

π

0

)

sin( dx

x

F

Rozwiązanie

h=0.1;
x=0:h:pi;

n=length(x)
fplot(‘sin’,[0 3*pi]), grid

y=sin(x);
a=x(1);

b=x(n);
format short
F1=h*sum(y:n-1));

%prostokątów

F2=h*(y(1)+2*sum(y(2:n-1))+y(n))/2;

%trapezów

F3=quad(‘sin’,a,b);

%Simpson`s

Wynik=[F1,F2,F3]’
Blad=2-Wynik

Wynik obliczeń

Wyniki=

∫

=

=

π

0

2

)

sin( dx

x

F

1,9954
1,9975
1,9991

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

24

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Błąd=
0,0046

metoda prostokątów

0,0025

metoda trapezów

0,0009

metoda Matlab

Oblicz pole figury leżącej w II-cwiartce układu współrzędnych ograniczonej wielomianem
W(x)=-x

4

+3x+4 oraz osiami OX i OY. Podaj pierwiastki wielomianu W(x), naszkicuj

wykres W(x) dla x z przedziału [-1.5 2]

Rozwiązanie

f2-inline(‘-x.^4+3*x+4’,’x’)

fplot(f2,[-1.5 2]), grid on
p2=[-1 0 0 3 4]

r2=roots(p2)
F2=quad(f2,r2(4),0)

z1=fzero(f2,-1);
z2=fzero(f2,2);
z=[z1;z2];

6.0 Równania różniczkowe zwyczajne (ordinary Differentia Equation ODE)

Równanie n-tego rzędu

(

)

)

1

(

)

2

(

)

1

(

)

(

,...

,

,

,

)

(

−

=

n

n

x

x

x

x

t

f

t

x

Równanie pierwszego rzędu

)

,

(

'

)

(

)

1

(

x

t

f

x

t

x

=

=

• Zagadnienia brzegowe (Boundary Valne Problem BVP)

• Równania różniczkowe cząstkowe (Partial Differentia Equation PDE)

6.1 Metody numeryczne

Numeryczne rozwiązywanie układów równań różniczkowych polega na poszukiwaniu
rozwiązania, startując z punktu, w którym jest ono znane (warunek początkowy). Jeśli znamy
rozwiązanie w punktach t

1

do t

k

to dla kolejnego t

k+1

wyznaczamy y(t

k+1

) stosując odpowiednią

aproksymację.

Prosta metoda Eulera

)

,

(

)

(

)

,

(

1

1

y

x

f

dx

x

dy

y

x

f

x

y

k

k

k

k

=

=

∆

∆

+

+

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

25

Laboratorium z metod numerycznych – Informatyka Stosowana I .

x

y

x

F

y

y

y

y

const

h

x

x

x

x

y

x

y

y

y

y

k

k

k

k

k

k

k

k

k

k

∆

+

=

=

=

=

∆

=

−

=

∆

=

−

=

∆

+

+

+

+

+

*

)

,

(

)

(

1

0

1

1

1

0

0

1

1

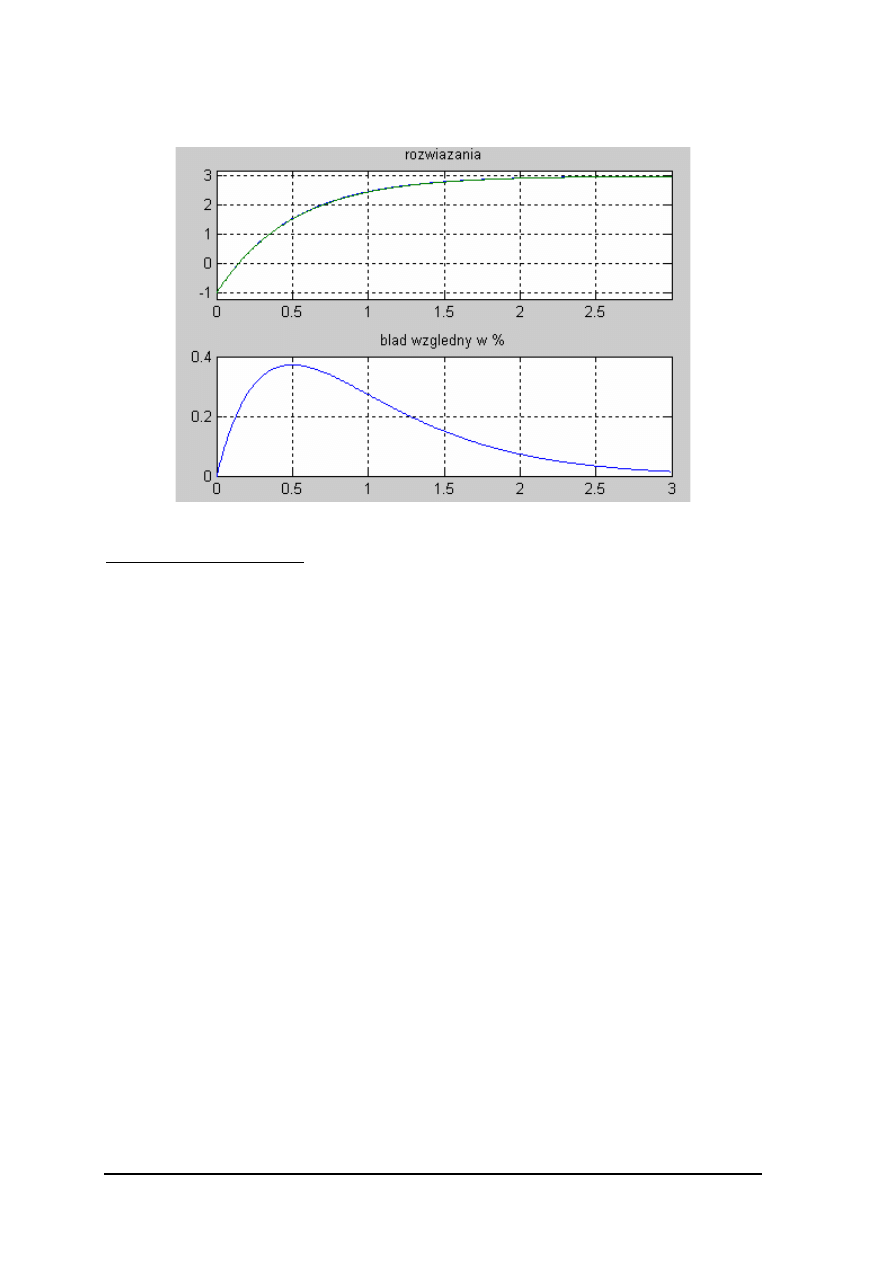
6.2 Rozwiązać numerycznie równanie w przedziale 0,3

b

y

a

dx

dy

+

−

=

*

Rozwiązanie analityczne

ax

e

a

b

y

a

b

x

y

−

−

+

=

*

)

(

)

(

0

Dane:

a=2, b=6, y(0)=y

0

=-1

Kod:

clear all, clf
f=inline(‘-2*y+6’,’x’,’y’);

x(1)=0;

% xo

y(1)=-1;

% yo

xk=3;
dx=0.01;

%krok

n=floor((xk-x(1))/dx);

%zaokraglenie

for k=1:n
y(k+1)=y(k)+f(x(k),y(k))*dx;

x(k+1)=x(k)+dx;
end

x1=min(x);x(2)=max(x);y1=min(y);y2=max(y);m=0.2;
yd=3+exp(-2*x)*(-3+y(1));

% rozw. dokładne

b=(y-yd)/(y2-y1)*100;

% blad w procentach

b1=min(b);b3=max(b);
subplot(2,1,1)

plot(x,y,x,yd),grid on, title(‘rozwiazania’)
axis([x1 x2 y1-m y2+m])

subplot(2,1,2)
plot(x,b),grid on,title(‘blad wzgledny w %’)

axis([x1 x2 b1-m b2+m])

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

26

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Wynik:

6.3

Funkcje ODE w Matlabie

[T,Y] = odexx(‘F’, przedzial, y0)

xx – liczba okreslajaca metode

powyższa instrukcja całkuje układ równań różniczkowych postacy y

n

=F(t,y)

w przedzale od

t_pocz

do

t-koniec

przedzial

= [

t_pocz t_koniec

]

z warunkami początkowymi podanymi w wektorze y0

‘F’ jest nazwą ODE pliku funkcyjnego.

Function

F(t,y) musi zawracać kolumnowy wektor.

[T Y] Każdy wiersz w macierzy rozwiązania Y odpowiada argumentowi t zwracanemu w
kolumnowym wektorze T.

Układy równań dobrze uwarunkowanych

ode45 - Runie-Kutta rzędu (4,5)

ode23 - Runie-Kutta rzędu (2,3)
ode113 – Adams-Bashforth-Moulton

Układy równań źle uwarunkowanych (sztywnych)

ode15s - Gear`s

ode23s - Rosenbrock
ode23t - trapez
ode23tb

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

27

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Przykład:
Rozwiązać numerycznie układ równań różniczkowych

0

)

0

(

5

.

0

1

)

0

(

2

2

2

1

1

1

2

=

−

−

=

=

=

y

y

y

dt

dy

y

y

dt

dy

w przedziale t [0,15], przy zadanych warunkach początkowych. Wykreślić przebiegi czasowe i
trajektorię. Podać wartość y

1

i y

2

dla t=1 i t=5

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

−

−

=

0

1

)

0

(

*

5

,

0

1

2

0

2

1

y

y

y

y

y

dt

dy

Pliki funkcyjny równanie różniczkowego row1.m

Kod:

function dy=row1(t,y)
dy=zeros(2,1);
dy(1)=2*y(2);

dy(2)=-y(1)-0.5*y(2);

Plik skryptowy rr1.m

Kod:

[t,y]=ode45(‘row1’,[0 14],[1;0]);
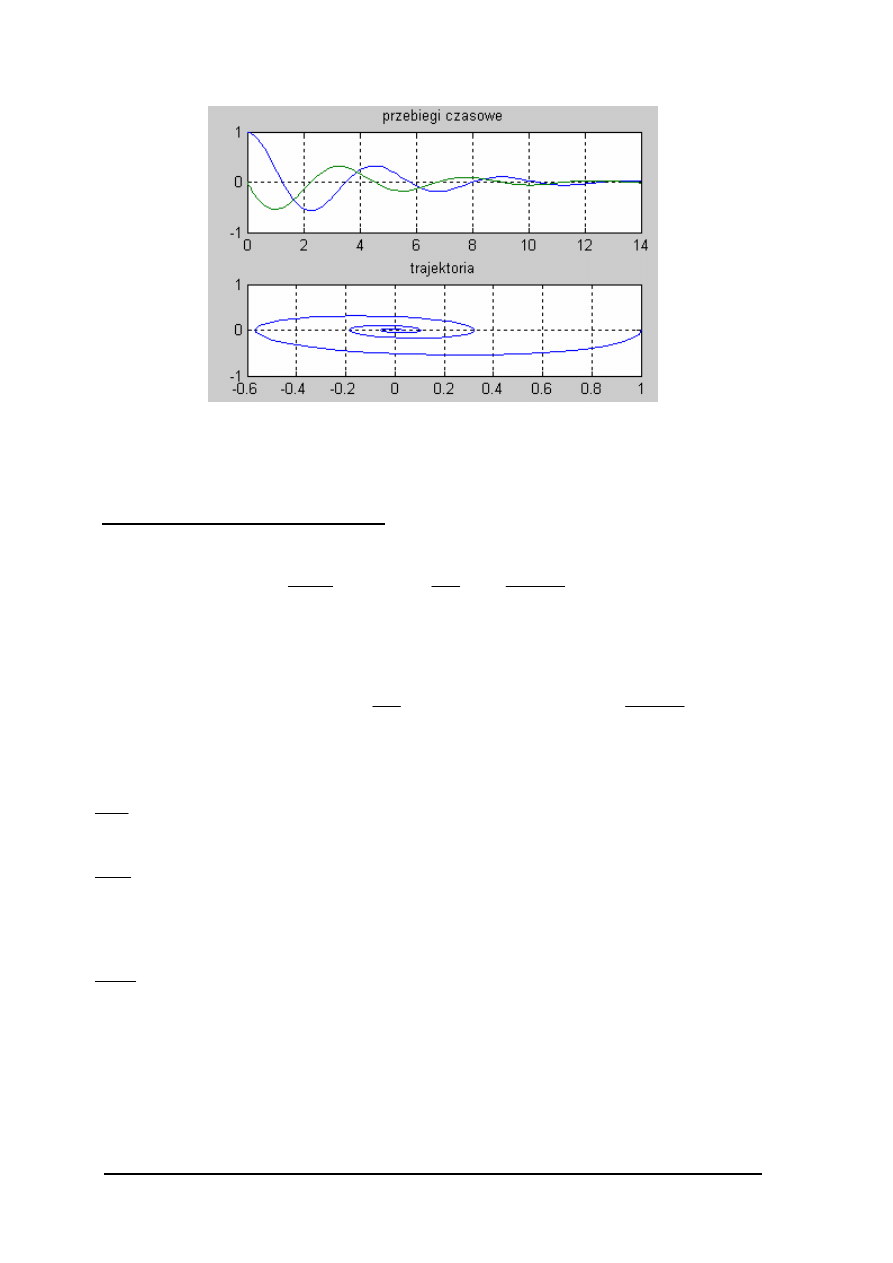
subplot(2,1,1)

plot(t,y(:,1),t,y(:,2)),grid on
title(‘przebiegi czasowe’)

subplot(2,1,2)
plot(y(:,1),y(:,2),grid on
title(‘trajektoria’)

y_p=interp1(t,y,[1,5],’linear’)

Wynik:

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

28

Laboratorium z metod numerycznych – Informatyka Stosowana I .

y_p =

0.2550 -0.1284

6.4 Równanie różniczkowe n-tego rzędu

0.2760 -0.5477

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

−

−

1

1

,

,

,

,

n

n

n

n

dt

y

d

dt

dy

y

t

f

dt

y

d

L

podstawiamy

1

1

2

1

−

−

=

=

=

n

n

n

dt

y

d

y

dt

dy

y

y

y

L

otrzymujemy uk

ład równań pierwszego rzędu

⎪

⎪

⎪

⎪

⎩

⎪⎪

⎪

⎪

⎨

⎧

=

2

1

y

dy

=

=

)

,

,

,

,

(

2

1

3

2

n

n

n

y

y

y

t

f

dt

y

d

y

dt

dy

dt

K

M

Przykład:

Rozwiąż równanie w przedziale 0 … 10

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

29

Laboratorium z metod numerycznych – Informatyka Stosowana I .

)

cos(

*

*

'

0

)

0

(

0

)

0

(

'

,

1

)

0

(

)

cos(

*

*

4

1

3

1

3

3

2

2

1

0

1

1

2

1

4

)

1

(

30

t

e

y

y

y

y

dt

d

y

y

dt

d

dt

y

y

y

y

y

y

y

y

y

t

e

y

y

n

n

+

+

−

=

=

=

=

=

=

=

−

=

=

−

−

−

6

y

y

+

y

y

d

=

.5

Równanie Van der Pola

al m

(1)^2)*y(2)];

0

'

*

)

1

(

2

=

+

−

+

y

y

y

y

n

µ

Kod:

function dy=row_vdp(t,y)

glob
dy=[y(2);-y(1)+m*(1-y

d:

r all

;

Ko

clea

global m
m=2;
[t,y]=ode45(‘row_vdp’,[0 20],[2:0]

plot(t,y(:,1)),grid on

e zadanie:

równanie różniczkowe

Kod:

function dx=de(t,x)

dx=[x(2);((2/t^2-1)*x(1))-x(2)/t];

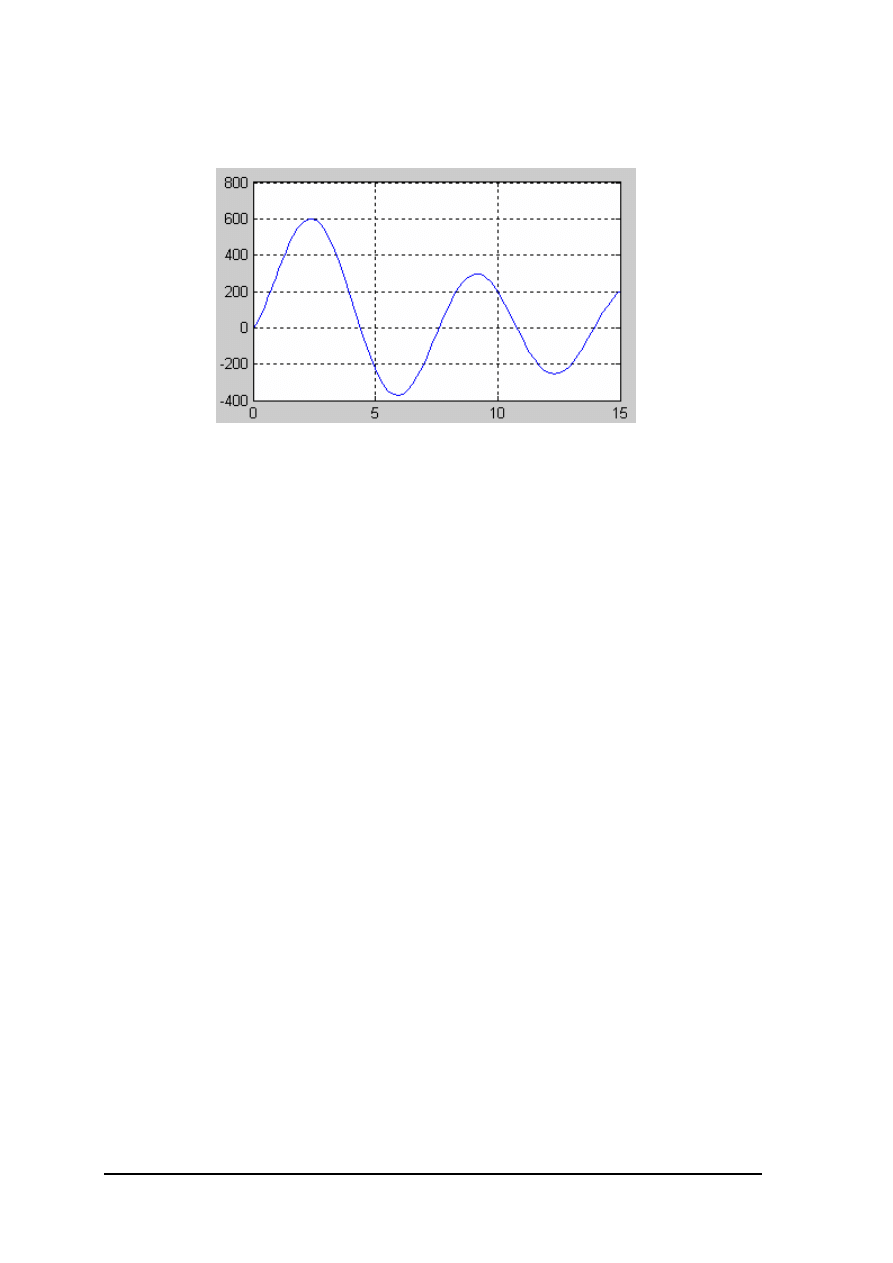
Przykładow
Rozwiąż

Kod:

[t,x]=ode45(‘de’,[0.01 15],[1 0]);
plot(t,x(:,1));grid on
x_5=interp1(t,x(:,1),5,’linear’)

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

Laboratorium z metod numerycznych – Informatyka Stosowana I .

Przepisał: Blick © Materiały dostarczył: qWest © Pomagał: L3Vy ©

PWSZ Tarnów 2007

31

Wynik: