Metoda Eulera rozwiązywania równań różniczkowych

1. Wykonanie

Przyjęte równanie różniczkowe z zadanym krokiem, warunkiem początkowym

oraz przedziałem różniczkowania:

+2

Krok różniczkowania; 0.1

Warunek początkowy: (0,1)

Przedział: (0,5)

2. M-plik metody Eulera:

x0=0;

y0=1;

h=0.1;

a=0;

b=5;

i=1;

m=1;

n=1;

t=1;

for x=[a:h:b];

y=y0+h*(x+1)

y0=y;

q=((3.*x.^2)/2+2*x+1);

e=abs(q-y);

y

m(i)=y

n(i)=q

t(i)=e

i=i+1;

end

subplot(2,1,1)

hold on

x=[a:h:b];

plot(x,m,'b')

title('Wykres rozwiazania dokladnego( obliczonego analitycznie ) i przyblizonego obliczonego z metody Eulera')

text(3,38,'Przyblizone rozwiazanie')

plot(x,n,'g')

text(4,9,'Analityczne rozwiazanie')

hold off

subplot(2,1,2)

x=[a:h:b];

plot(x,t,'r')

grid

title('Modul bledu metody')

3. Rozwiązanie analityczne

dla warunku początkowego: (0,1)

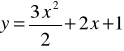
4. Dokładności metody Eulera

Uwzględniając wykres, zauważamy że błąd jest proporcjonalny co do wartości x. Wraz ze wzrostem wartości x, nasze rozwiązanie staje się bardziej niedokładne, a błąd rośnie liniowo. Aby uzyskać dokładniejszy wynik należy przyjąć mniejszą mniejszą wartość kroku.

5. Wnioski

Metoda Eulera nie daje zbyt dużej dokładności. Aby uzyskać wynik z większą dokładnością należy zmniejszyć wartość kroku. Innym rozwiązaniem polepszenia dokładności jest zastosowanie interpolacji Richardsona.

Łata Tomasz

Grupa 7

---