METODY NUMERYCZNE

Temat laboratorium: „Funkcje ODE23 i ODE45”

1. Cel ćwiczenia

Nauka rozwiązywania równań różniczkowych wyższych rzędów
w programie MATLAB 6.5.

2. Wykonanie:

Wybieramy równanie różniczkowe w następującej postaci:

3. Kod programu; (zapisujemy dwa m-pliki).

• Inplemetujący fukcje oscylatora:

function [dx]=f(t,x)

global M K B F w

dx=[x(2); -K/M*x(1)-(B/M)*x(2)+F*sin(w*t)/M];

• Inplemetujący funkcje ode23:

M=50; // masa

B=10; // współczynnik sprężystości

K=4; // współczynnik tłumienia

F=4; // siła

w=10; // prędkość kątowa

global M B K F w

t0=0;

tk=100;

x10=1;

x20=0;

WP=[x10,x20];

[T,x]=ode23('f',t0,tk,WP);

plot (T,x(:,1))

xlabel('Czas')

ylabel('Przemieszczenie')

4. Przykłady:

• Dla B > K:

• 
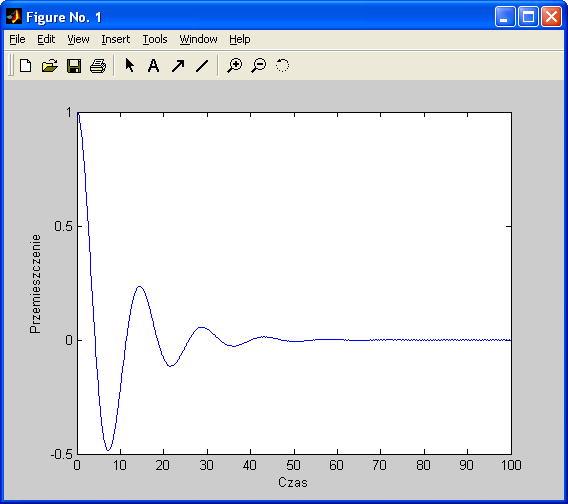
  Dla B = K

• Dla B < K

5. Wnioski

Funkcje ODE23 i ODE45 służą do numerycznego rozwiązywania zwyczajnych równań różniczkowych. Metoda rozwiązania Rungego-Kutty-Felberga, w której krok całkowania numerycznego jest zmieniany automatycznie ODE23 wykorzystuje zależności 2 i 3 (średnia dokładność), ODE45 wykorzystuje zależności 4 i 5 rzędu (duża dokładność).

Wynikiem funkcji jest zbiór wyników wyrażających zależność przemieszczenia od czasu w zakresie czasowym podanym w parametrach początkowych.

Jacek Łabusiewicz

Grupa 7

---