Przykładowe zadania z Metod numerycznych
Kolokwium 1
1. Dana jest 8. bitowa liczba stałoprzecinkowa (zapis binarny ze znakiem): 0.0111000
podać dokładność zapisu.
2. Jakie właściwości ma odwzorowanie
Ax
y
dla macierzy:
5
.
0
5
.
0
5
.
0
5
.
0
A
. Narysować obraz wektora
1
1
x
w tym
odwzorowaniu.
3. Narysować poziomice funkcji
2
2
2
1
2
)
2
(
4
x
x
y
. W punkcie (1,1) wyznaczyć równanie płaszczyzny stycznej do funkcji.
Narysować rzut płaszczyzny stycznej na płaszczyznę (
2
1
, x
x
). W punkcie (1,0) wyznaczyć równanie płaszczyzny stycznej do
funkcji.
Kolokwium 2
1. Dla równania:
0
16
4
x
zapisać algorytm iteracyjny Newtona-Raphsona oraz wyznaczyć przedział zbieżności algorytmu.
2. Dla równania iteracyjnego:
2
)
(
5
3
1
k
k
x
x
wyznaczyć przedział zbieżności i narysować kilka punktów początkowych
algorytmu.
3. Narysować przykłady algorytmu: monotonicznie zbieżnego, monotonicznie rozbieżnego, periodycznie zbieżnego,
periodycznie rozbieżnego, periodycznego.
Kolokwium 3
1. Metodą eliminacji Gaussa rozwiązać układ równań Ax=b dla
6
20
2
,
5
6
5
2
0
4
3
2
1
b
A
oraz wyznaczyć macierz odwrotną.
2. Wyznaczyć algorytm Newtona-Raphsona dla układu równań:
4
)
5
(
9
)
1
(
2
2
2
2
y
x
x
y
podać interpretację geometryczną rozwiązania.
Kolokwium 4
1. Wyznaczyć funkcję aproksymującą
)
(
)
(
)
(
2
2
1
1
x
f
a
x
f
a
x
f
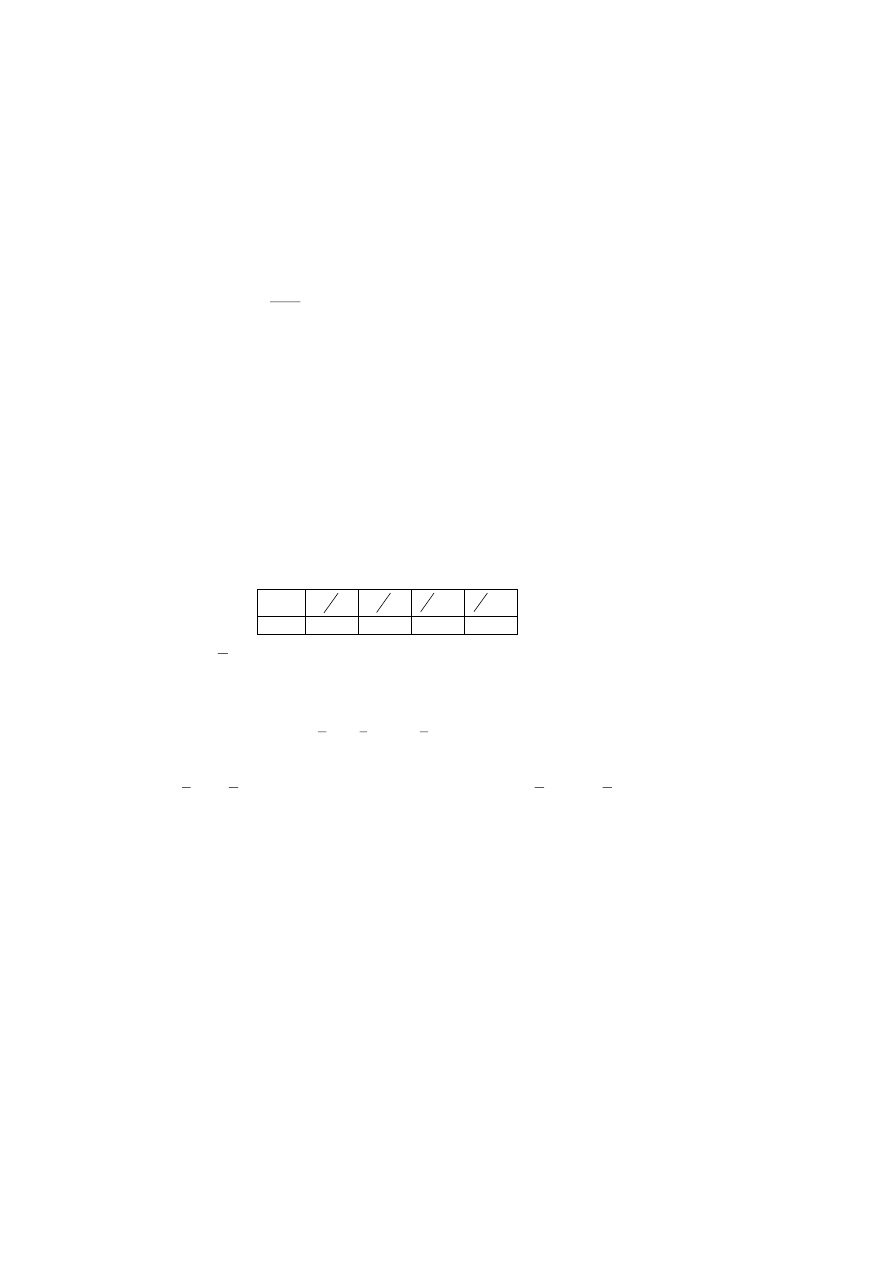
dla następujących punktów
X
2
3
3
2
Y
-3
-10
20
3
i funkcji bazowych
)
sin(
)
(
,
3
)
(
2
1
x
x
f
x
x
f
2. Dla funkcji aproksymującej
)
(x
f
i punktów (X,Y) wyznaczyć błąd średniokwadratowy.
Kolokwium 5
1. Omówić właściwości algorytmu:
1
n
1
n
n
1
n
y
3
2
h
y
3
1
y
3
4
y
2. Podać geometryczną interpretację rozwiązania równania różniczkowego w punkcie y(t
n+1
) stosując następującą metodę:
2
1
n
1
n
3
2
3
1
y
y
,
)
t
,
y
(
f
h
n
n
1
)
h
4
3
t
,
4
3
y
(
f
h
n
1
n
2
3. Wyznaczyć numeryczne kilka punktów rozwiązania (dowolną metodą) równania różniczkowego
2
t
y
. Dobrać prawidłowo krok całkowania h, aby metoda była stabilna.
Kolokwium 6
1. Omówić zasadę metody simpleks i podstawowe operacje na simpleksie:
* odbicie symetryczne
* wyznaczanie środka ciężkości
* ekspansję
* kontrakcję
* kurczenie simpleksu
2. Wyznaczyć zbiory kierunków dopuszczalnych w punkcie X
0
dla ograniczeń :
{ x
1
0 , x
2
0 , x
2
- (x
1
– 1)
3
} X
0
= [ 0 0 ]
T
X
0
= [ 0 1 ]
T
{ x
2
- (x
1
– 1)
3
+ , x
2
0 } X
0
= [ 0 1 ]
T
3. Wyznaczyć zbiory kierunków poprawy w punkcie X
0
dla następujących funkcji :
f(x) = (x
1
– 1)
2
+ 3x
2
2
- 6x
2
f(x) = x
1
- 2x
2
2
f(x) = x
1
2
- x
2
2
X
0
= [ 0 0 ]
T
X
0
= [ 0 1 ]
T
X
0
= [ 1 0 ]
T
X
0
= [ 1 1 ]
T