18.03.2013
SPRAWOZDANIE Z ĆWICZENIA NR 44
Olga Pawłowicz
TEMAT: Pomiar zależności oporu metali i półprzewodników od temperatury
CEL ĆWICZENIA: Pomiar oporu elektrycznego metalu i półprzewodnika w funkcji temperatury oraz wyznaczenie
temperaturowego współczynnika rezystancji (oporu) metalu i szerokości przerwy energetycznej w półprzewodniku.
1. Wstęp teoretyczny.
Budowa metali (przewodników).
Przewodniki, czyli substancje, w których istnieją mogące się swobodnie poruszać ładunki elektryczne to najczęściej
metale. Metal zbudowany jest z sieci krystalicznej jonów dodatnich oraz uwspólnionych ładunków elektrycznych (tu
elektronów). Zjawisko oporu elektrycznego polega na tym, że dodatnie jony metalu, stawiają opór poruszającym się
elektronom, które zderzając się z nimi tracą część swojej energii kinetycznej. Liczba zderzeń będzie tym większa, im
większe są wychylenia jonów z położenia równowagi, a te zwiększają się wraz ze wzrostem temperatury. Opór
przewodnika liniowo rośnie wraz ze wzrostem temperatury zgodnie ze wzorem:
R = R
0
+ αR
0
*t, gdzie:
R
0
to rezystancja w temperaturze odniesienia T
0
,
α to temperaturowy współczynnik rezystancji.
Model pasmowy półprzewodnika.
W półprzewodniku w temperaturze 0 K elektrony walencyjne zajmują wszystkie możliwe stany i nie mogą się poruszać
- zmieniać stanu. Pomiędzy pasmem walencyjnym a pasmem przewodnictwa istnieje przerwa energetyczna E
g
, czyli
wartość energi o jaką musi wzrosnąć energia elektronu, aby dostał się do pasma przewodnictwa. W paśmie
walencyjnym pojawiają się wtedy poziomy nieobsadzone (puste miejsca po elektronach, uzyskują miejscowy ładunek
dodatni, są miejscami, na które mogą przechodzić inne elektrony).
Za zwiększanie energi elektronów, odpowiedzialne są drgania międzyatomowe, które narastają ze wzrostem
temperatury.
Mówimy, że wraz ze wzrostem temperatury rośnie koncentracja nośników elektrycznych, czyli liczba elektronów w
paśmie przewodnictwa na jednostkę objętości.
2. Przyrządy pomiarowe.
grzałka z czujnikiem temperatury o dokładności C;
Miernik M-3850, którego dokładność pomiaru rezystancji wyrażamy wzorem: 0,5 % rdg + dgt.
3. Tabela Pomiarów
T[ C]
26
31,2
36
40,7
45,1
50,3
55,5
60,1
65
70,5
75,5
80
85,5
90,5
R3 [Ω]
33,4
27,1
22,6
18,9
16
13,6
11,3
9,9
8,3
7,1
6
5,3
4,8
4,4
R4 [Ω]
110,8
112,4
113,8
115,4
116,9
118,3
120
121,4
123,2
124,9
126,5
127,8
129,2
130,4
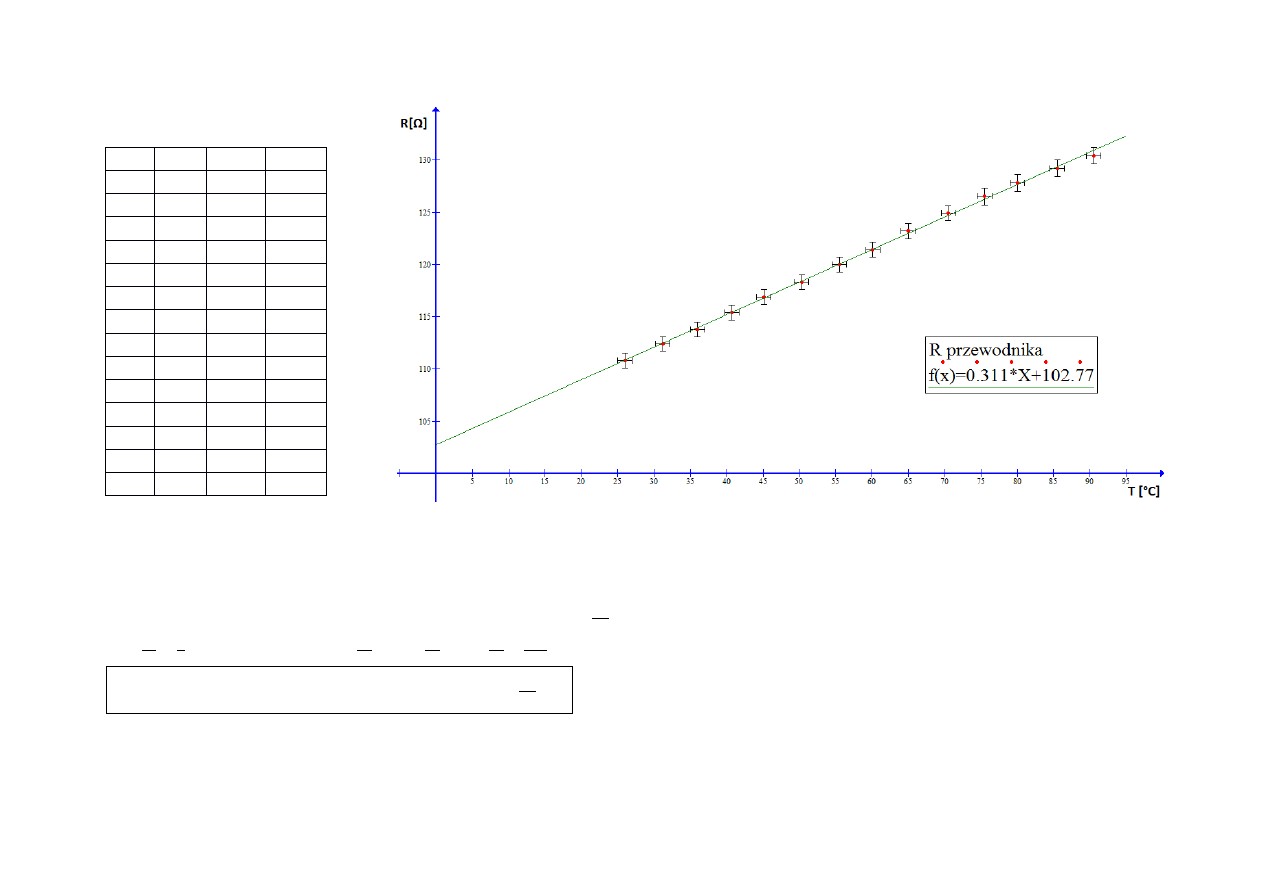
4. Analiza pomiarów dla przewodnika.
T [°C] R
4
[Ω] ΔT [°C] Δ R [Ω]
26
110,8
1
0,7
31,2 112,4
1
0,7
36
113,8
1
0,7
40,7 115,4
1
0,7
45,1 116,9
1
0,7
50,3 118,3
1
0,7
55,5
120
1
0,7
60,1 121,4
1
0,71
65
123,2
1
0,72
70,5 124,9
1
0,73
75,5 126,5
1
0,8
80
127,8
1
0,8
85,5 129,2
1
0,8
90,5 130,4
1
0,8
Wyniki pomiaru przedstawiono jako zależność R[T]. Jest to zależność liniowa y=ax + b; R = R
0
+ αR
0
*t gdzie R
0
= b, αR
0
= a
Współczynniki prostej a i b obliczono za pomocą regresji liniowej. Otrzymano wyniki: a = 0,3 0627 Δa = 0,002797 b= 02,77 6 Δb = 0, 7 549.
[
]
[ ]
, |
| |
|
[ ] [
]
5. Analiza pomiarów dla półprzewodnika.
T [°C] T [K] R
3
[Ω] ΔT [K] ΔR[Ω]
[
]
[
]
ln(R)[Ω] Δln(R)[Ω]
26,0
299 33,40
1
0,27
3,344
0,012
3,509
0,008
31,2 304,2 27,10
1
0,24
3,287
0,011
3,299
0,009
36,0
309 22,60
1
0,22
3,236
0,011
3,12
0,01
40,7 313,7 18,9
1
0,2
3,188
0,011
2,939
0,011
45,1 318,1 16,00
1
0,19
3,14
0,01
2,773
0,012
50,3 323,3 13,60
1
0,17
3,09
0,01
2,61
0,013
55,5 328,5 11,30
1
0,16
3,04
0,01
2,425
0,014
60,1 333,1 9,90
1
0,15
3,0021
0,0091
2,293
0,016
65,0
338
8,30
1
0,15
2,959
0,009
2,116
0,018
70,5 343,5 7,10
1
0,14
2,911
0,009
1,96
0,02
75,5 348,5 6,00
1
0,13
2,869
0,009
1,792
0,022
80,0
353
5,30
1
0,13
2,8329
0,0081
1,668
0,024
85,5 358,5 4,80
1
0,13
2,789
0,008
1,569
0,026
90,5 363,5 4,40
1
0,13
2,751
0,008
1,48
0,03
ΔR obliczono z wzoru na niepewność miernika: 0,5 % rdg + 1 dgt ( )
ΔT |
|
( )
ΔlnR ( ) |
|
( )
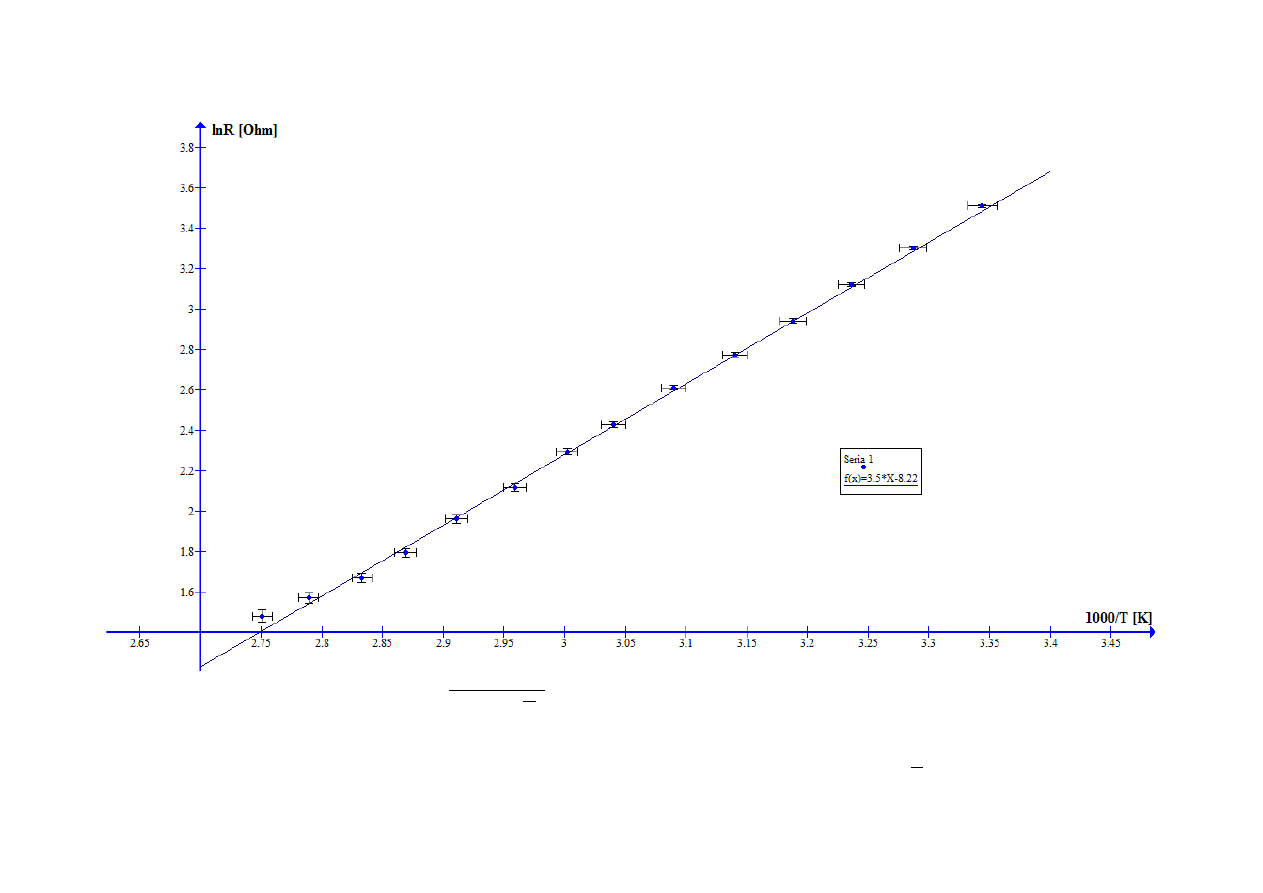
Wyniki pomiaru przedstawiono jako zależność ( ) (
). Otrzymano prostą o równaniu y=ax + b: ( (
))
(
)
, gdzie k = 1,3806 10-23 J/K - stała Boltzmanna. Wartość i niepewność współczynnika a odczytano z reglinp(): [
]
Wyliczamy
[
]
[
]
[
]
[ ]
Wnioski:
W pomiarze temperaturowego współczynnika rezystancji dla przewodnika uzyskano wynik [
]
Jest on porównywalny do współczynnika rezystancji takich metali jak: platyna, srebro, aluminium, jednakże nieco niższy. Najprawdopodobniej opornik został
wykonany z platyny, gdyż tego materiału używa się częściej. Różnica między tablicową wartością współczynnika (około 3,9 * 0
-3
K
-1
, podczas gdy w
pomiarach uzyskano wynik 3,03*10
-3
K
-1
) wynika najprawdopodobniej z błędu pomiaru, niedostatecznej ilości czasu potrzebnego na ustabilizowanie
temperatury, bądź niebezpośrednich pomiarach (nie było możliwości sprawdzenia np. gdzie grzałka mierzy temperaturę).
W przypadku wyznaczania przerwy energetycznej półprzewodnika uzyskano wynik:
[ ]
Zbliżoną wartość ma German. German jest ważnym półprzewodnikiem, wykorzystywanym do produkcji tranzystorów, diod i innych elementów
elektronicznych. Jego pasmo wzbronione ma szerokość 0,67 eV.
Na wykresie wyraźnie widać, że część punktów pomiarowych odbiega od prostej najlepszego dopasowania. Usunięcie pierwszych 4 powoduje wzrost
wartości E
g
do 0,615 eV.