`
1.Cel ćwiczenia.
Celem ćwiczenia jest :
a) pomiar rezystancji metalu i półprzewodnika w zakresie od temperatury pokojowej do około 450 K ,
b) wyznaczenie współczynnika temperaturowego rezystancji oraz szerokości pasma wzbronionego w półprzewodniku .
2 . WSTĘP TEORETYCZNY .
Przepływ prądu w metalu polega na uporządkowanym ruchu elektronów będących swobodnymi nośnikami ładunku . Zakłócenie przepływu strumienia elektronów powodujące spadek konduktywności metalu ( a tym samym wzrost rezystancji ) wywoływane jest przez dwie podstawowe przyczyny :
- w zakresie wysokich temperatur wzrasta amplituda drgan sieci krystalicznej , a tym samym przekrój czynny na rozpraszanie co powoduje osłabienie strumienia swobodnych nośników ładunku , czyli wzrost rezystancji . Dla czystych metali jednoskładnikowych zależność oporu elektrycznego od temperatury jest w przybliżeniu liniowa :
Rt=R0(1+0t)
Ro - rezystancja w temperaturze 0C ,
Rt - rezystancja w temperaturze t ,
o - temperaturowy współczynnik rezystancji w zakresie od 0 do t C :
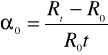
- rozpraszanie swobodnych nośników na wszelkich defektach sieciowych . W czystych jednoskładnikowych metalach ten typ rozpraszania jest dominujący w niskich temperaturach , natomiast w temperaturze pokojowej i wyższych nie ma większego znaczenia .
Dla półprzewodników prawdziwe są powyższe spostrzeżenia o rozpraszaniu swobodnych nośników w metalach , z tym że w niskich temperaturach głównymi defektami strukturalnymi są zjonizowane atomy domieszek . Dlatego w półprzewodnikach można zauważyć silną , wykładniczą zależność konduktancji od temperatury :
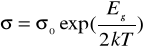
Eg - szerokość pasma wzbronionego ,
k= 1,38*10-23 JK - stała Boltzmanna ,
T - temperatura w kelvinach ,
o -stała niezależna od temperatury .
Z powyższego wzoru można bezpośrednio wyznaczyć zależność oporu od temperatury :
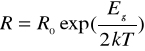
Ro - stała zależna od rodzaju i wymiarów geometrycznych półprzewodnika . Oznacza ona rezystancję jaką miałby w nieskończenie dużej temperaturze .
W celu wyliczenia szerokości pasma zabronionego Eg należy wyznaczyć wykres zależności lnR=f(1000/T) , odczytać z niego tg kąta nachylenia odcinka prostoliniowego charakterystyki i ostatnie równanie zlogarytmować stronami :
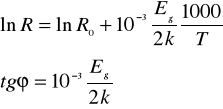
a następnie wyznaczyć Eg :
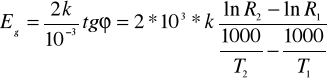
w powyższym wzorze (lnR1,1000/T1) i (lnR2,1000/T2) to współżędne punktów na początku i końcu prostoliniowego odcinka charakterystyki ln=f(1000/T) .
3 . PRZEBIEG POMIARÓW .
Układ pomiarowy składa się z komory pomiarowej K w której znajduje się walec miedziany (ze względu na dobrą przewodność cieplną) , we wnękach którego umieszczone są badane rezystory , termometr T i grzejnik G (zasilany z autotransformatora poprzez transformator ochronny , obniżający napięcie około dziesięciokrotnie) . Rezystancje mierzy się za pomocą multimetrów typu 1321 . Po odłączeniu napięcia zasilającego grzejnik temperatura walca obniża się , proces ten można przyspieszyć włączając wentylator (znajdujący się w dolnej części komory pomiarowej) i dodatkowo chłodzenie wodne dostępne za pośrednictwem zewnętrznej pompy.
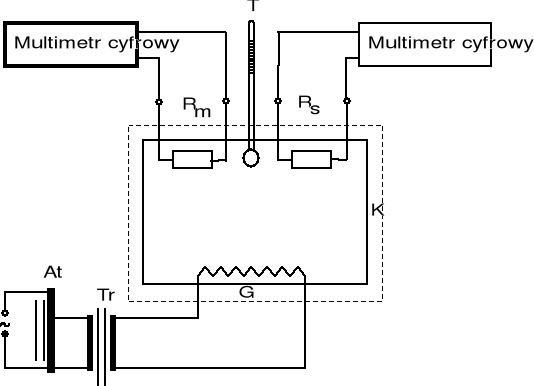
Pomiarów dokonywano podgrzewając rezystory od temperatury pokojowej(23C) do 83C odczytując co 5C wartości Rm i Rs . Następnie od 83C do 58C mierzono rezystancję przy spadku temperatury (przy wyłączonym grzejniku i działającym wentylatorze) . Wyniki odczytywane z multimetrów typu 1321 obarczone są błędem wynikającym z ich klasy dokładności :
![]()
W celu zamiany temperatury w C na temperature wyrażoną w K należy dokonać przekształcenia :
T=t+273,15
Następnie można przystąpić do sporządzenia wykresów :
Rm=f(t)
i
ln Rs=f(1000/T)
a później wyznaczyć szerokość pasma zabronionego w półprzewodniku :
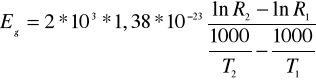
oraz temperaturowy współczynnik rezystancji metalu przyjmując jako rezystancję odniesienia rezystancję w temperaturze 23C :
Lp |
t |
T |
1000/T |
Rs |
ΔRs |
ln Rs |
Rm |
ΔRm |
|
[°C] |
[ K ] |
[ 1/K ] |
[ kΩ ] |
[ kΩ ] |
[ - ] |
[ Ω ] |
[ Ω ] |
1 |
23 |
296 |
3,378 |
11,01 |
0,04202 |
9,307 |
109,4 |
0,4188 |
2 |
28 |
301 |
3,322 |
8,56 |
0,03712 |
9,055 |
111,7 |
0,4234 |
3 |
33 |
306 |
3,268 |
6,96 |
0,03392 |
8,848 |
113,8 |
0,4276 |
4 |
38 |
311 |
3,215 |
5,63 |
0,03126 |
8,636 |
115,8 |
0,4316 |
5 |
43 |
316 |
3,165 |
4,59 |
0,02918 |
8,432 |
117,8 |
0,4356 |
6 |
48 |
321 |
3,115 |
3,75 |
0,0275 |
8,229 |
119,9 |
0,4398 |
7 |
53 |
326 |
3,067 |
3,04 |
0,02608 |
8,02 |
122,1 |
0,4442 |
8 |
58 |
331 |
3,021 |
2,51 |
0,02502 |
7,828 |
124,2 |
0,4484 |
9 |
63 |
336 |
2,976 |
2,03 |
0,02406 |
7,616 |
126,5 |
0,453 |
10 |
68 |
341 |
2,933 |
1,701 |
0,00540 |
7,439 |
128,6 |
0,4572 |
11 |
73 |
346 |
2,890 |
1,422 |
0,00484 |
7,26 |
130,6 |
0,4612 |
12 |
78 |
351 |
2,849 |
1,191 |
0,00438 |
7,082 |
132,7 |
0,4654 |
13 |
83 |
356 |
2,809 |
0,972 |
0,00394 |
6,879 |
135,2 |
0,4704 |
TABELA POMIARÓW I OBLICZEŃ PRZY WZROŚCIE TEMPERATURY
Lp |
t |
T |
1000/T |
Rs |
ΔRs |
ln Rs |
Rm |
ΔRm |
|
[°C] |
[ K ] |
[ 1/K ] |
[ kΩ ] |
[ kΩ ] |
[ - ] |
[ Ω ] |
[ Ω ] |
1 |
83 |
356 |
2,809 |
1,067 |
0,00413 |
6,973 |
133,9 |
0,4678 |
2 |
78 |
351 |
2,849 |
1,288 |
0,00458 |
7,161 |
131,6 |
0,4632 |
3 |
73 |
346 |
2,890 |
1,537 |
0,00507 |
7,338 |
129,5 |
0,459 |
4 |
68 |
341 |
2,933 |
1,830 |
0,00566 |
7,512 |
127,5 |
0,455 |
5 |
63 |
336 |
2,976 |
2,19 |
0,02438 |
7,692 |
125,4 |
0,4508 |
6 |
58 |
331 |
3,021 |
2,64 |
0,02528 |
7,878 |
123,4 |
0,4468 |
TABELA POMIARÓW I OBLICZEŃ PRZY SPADKU TEMPERATURY
WYKRES ZALEŻNOŚCI : LN Rt=f(1000/T)
WYKRES ZALEŻNOŚCI : Rm=f(t)
Wyznaczenie szerokości pasma zabronionego dla półprzewodnikowego rezystora Rt :
Wyznaczenie temperaturowego współczynnika rezystancji opornika Rm :
4. RACHUNEK BŁĘDÓW
Całkowity błąd wyznaczania współczynnika rezystancji wynika z błędu multimetru i błędu
odczytu z termometru. Otrzymamy go korzystając z metody różniczki zupełnej.
T2,T1 ,błędy odczytu temperatury (356 K ; 296 K) wynikające z błędu odczytu z termometru.:
T2, T1 =0,5 [K]
Rs i R23 - błędy bezwzględne pomiaru rezystancji w temperaturze 356K i 296K
R23=11,01kΩ
Rs=0,972 kΩ,
R23 =0,04202 kΩ,
Rs =0,00394 kΩ
Po wstawieniu wszystkich danych do wzoru na błąd bezwzględny uzyskujemy wynik:
![]()
= 0,000068 ![]()
0,0001
Ostatecznie =0.00390.0001
Błąd względny wyznaczenia współczynnika ![]()
wynosi:
Błąd wyznaczania wartości przerwy energetycznej półprzewodnika wyznaczamy również metodą różniczki zupełnej:
k=1,38∗10-23
T1=356K ΔT1 =0,5 K,
T2=296K ΔT2=0,5 K,
R1=0,972 kΩ ΔR1=0,00394 kΩ
R2=11,01 kΩ ΔR2= 0,04202 kΩ
Po podstawieniu tych wartości do powyższego wzoru otrzymujemy:
ΔEg![]()
0,0046[eV],
Ostatecznie Eg=0,7350,0046 [eV]
3 . DYSKUSJA BŁĘDÓW I WNIOSKI PŁYNĄCE Z ĆWICZENIA .
Błędy pomiarowe wynikają z wielu niedokładności i warunków:
-błąd paralaksy - niedokłady odczyt wartości temperatury z termometru labolatoryjnego,
-błędy wynikające z zakłóceń zewnętrznych (drgania, niestabilność zasilania multimetrów),
-błędy użytych mierników wynikające z dokładności i konstrukcji - miernik cyfrowy mierzy spadek
napięcia na rezystorze zasilanym z tzw. idealnego źródła prądowego; błędy pojawiają się przy
przekształcaniu napięcia na postać cyfrową metodą podwójnego całkowania i są spowodowane
niliniowością przetwarzania,
-błędy wynikające z warunków pomiaru (wyskalowanie mierników w innych warunkach ciśnienia,
temperatury i wilgotności),
-wpływ rezystancji przewodów i połączeń (długość przewodów),
- opóźnienie odczytu rezystancji względem odczytu temperatury (istotne znaczenie w przypadku wyznaczania szerokości pasma zabronionego przy ogrzewaniu i schładzaniu).
Różnice między ogrzewaniem i schładzaniem (dla metalu nieznaczne) wynikają z dużych i
szybkich zmian temperatury, w przypadku schładzania prędkość zmian temperatury ma istotne znaczenie dla dokładności wyników pomiarów ponieważ w doświadczeniu zakładaliśmy równowagę termodynamiczną dla badanych materiałów.
Zjawisko zmiany wartości rezystancji pod wpływem zmian temperatury znalazło szerokie zastosowanie w technice . Często stosowane są termometry oporowe platynowe pozwalające mierzyć temperatury w zakresie od -200 do +550C . Pomiar tą metodą może być bardzo dokładny po zastosowaniu odpowiednio wysokiej klasy miernika rezystancji wyskalowanego w jednostkach temperatury .
Termistor jest to element półprzewodnikowy , którego rezystancja silnie zależy od temperatury . W ćwiczeniu wykorzystany był element typu NTC-210 którego rezystancja rośnie wykładniczo wraz ze wzrostem temperatury . Istnieją także termistory typu PTC , których rezystancja maleje ze wzrostem temperatury , a również typu CTR o nagłym skokowym zmniejszeniu się rezystancji w wąskim przedziale temperatury . Typ NTC jest wytwarzany z tlenków manganu , tytanu , niklu , kobaltu , żelaza , glinu , miedzi i litu ; ich sproszkowane mieszaniny prasuje się a następnie spieka lub stapia w celu otrzymania elementów o wymaganych kształtach i rozmiarach . Termistory stosuje się przede wszystkim w termometrii jako wysokoczułe czujniki temperatury , a ponadto w układach kompensacji temperaturowej układów elektronicznych i do pomiaru mocy prądu wysokich częstotliwości .
Wyszukiwarka
Podobne podstrony:
Ćwiczenie nr 44 prawie dobre ale juz teraz lux, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA
Ćwiczenie nr 44, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
Ćwiczenie 44, Ćwiczenie 44 (2), Tomasz Pastor
Język polski 6 Ortografia Zasady i ćwiczenia fragment (strony 44 45)
ćwiczenie 44
cwiczenie 44 wyodrebianie chlorku potasu z sylwinitu, Technologia chemiczna, Technologia nieorganicz
Ćwiczenie nr 44, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare,
cwiczenie 44, Fizyka Sprawozdania, Ćw nr 44, Ćwiczenie 44
Cwiczenie 44 (1), 2.Elektryczność
Cwiczenie 44 (2), 2.Elektryczność
44, Cwiczenie 44 d, Politechnika Wroc˙awska
Mechanika - Dynamika, cwiczeniadynamika13, Przykład 47
Ćwiczenie 44, Ćwiczenie 44, Małgorzata
cwiczenie 44 (1), Politechnika Łódzka Biotechnologia, Chemia fizyczna LABORKI
więcej podobnych podstron