130410_0027 dr hab. Wojciech Bijak – matematyczne modele ryzyka i ich zastosowania - konspekt

1

Miary zgodności

Def.1. Dla zmiennych losowych

o łącznej dystrybuancie

funkcję

o

wartościach rzeczywistych nazywamy miarą zgodności gdy ma następujące własności:

P1

symetria,

P2

normalizacja,

P3

wiw gdy

są współmonotoniczne,

P4

wiw gdy

są przeciwmonotoniczne,

P5

Dla funkcji

ściśle monotonicznej

Def.2. Współmonotoniczność

Def.3. Przeciwmonotoniczność

Def.2. Zmienne łącznie wyłączające się

Miary zależności

W modelach kapitału obarczonego ryzykiem (RBC) uwzględnia się na ogół różne

rodzaje ryzyka, nośniki i czynniki ryzyka oraz jego źródła. Wchodzą one ze sobą w

interakcje, powodując, że występuje sieć skomplikowanych powiązań między nimi.

Atrakcyjne z punktu widzenia prostoty prowadzonych rozważań założenie o niezależności

wyróżnionych w modelu elementów nie znajduje więc uzasadnienia. Powstaje w związku z

tym istotna kwestia sposobu określania i mierzenia występujących w modelu zależności.

Wybór rozwiązania, podobnie jak w przypadku wyboru miary ryzyka, zależeć będzie od

przyjętej klasyfikacji i charakterystyki ryzyka (rodzajów, nośników i czynników oraz źródeł

ryzyka), ale również od założonego stopnia skomplikowania modelu i możliwości weryfikacji

przyjmowanych założeń. Szeroki przegląd zagadnień związanych z modelowaniem zależności

między zmiennymi losowymi znaleźć można m.in. w pracach: Nelsen 2006, Embrechts i in.

2001, Heilpern 2007.

130410_0027 dr hab. Wojciech Bijak – matematyczne modele ryzyka i ich zastosowania - konspekt

2

Do modelowania zależności między zmiennymi losowymi powszechnie wykorzystuje

się korelację liniową. Przyjmijmy, że rozpatrujemy wektor zmiennych losowych





T

Y

X

o

składowych reprezentujących np. różne rodzaje ryzyka i posiadających skończone wariancje.

Współczynnik korelacji liniowej określony jest jako:









 

 

Y

Var

X

Var

Y

X

Cov

Y

X

L

,

,





,

gdzie:





     

Y

E

X

E

XY

E

Y

X

Cov





,

oznacza kowariancję między zmiennymi X i Y, a

 

X

Var

,

 

Y

Var

wariancję odpowiednio zmiennej X i Y.

Współczynnik korelacji liniowej przyjmuje wartości z przedziału





1

,

1



. Wartości

skrajne 1 lub –1 przyjmowane są w przypadku liniowej zależności (dodatniej lub ujemnej)

między zmiennymi X i Y, natomiast wartość 0 w przypadku braku korelacji między tymi

zmiennymi (w szczególności niezależności stochastycznej zmiennych).

Korelacja liniowa jest przydatna ze względu na swoje własności i prostotę obliczeń.

Niech

1



n

X

oznacza n-elementowy wektor zmiennych losowych,

1



n

σ – wektor odchyleń

standardowych tych zmiennych,

 

n

n

diag



σ

– macierz diagonalną o elementach diagonalnych

równych składowym wektora

1



n

σ oraz

1



n

α – wektor liczb rzeczywistych. Wówczas:

 

 

 

α

σ

Ω

σ

α

X

α

diag

diag

Var

T

T



,

gdzie:

n

n



Ω

oznacza macierz korelacji między składowymi wektora

1



n

X

.

Wzór (3.14) pozwala uzależnić wariancję kombinacji liniowej zmiennych losowych

od wariancji poszczególnych składowych i korelacji między nimi.

Korelacja liniowa jest naturalną miarą zależności w szerokiej klasie rozkładów

eliptycznych (por. np. Landsman i Valdez 2003), do której należą m.in. wielowymiarowy

rozkład normalny, rozkład t Studenta, logistyczny, Laplace’a

1

. Pozwala ona na dekompozycję

ryzyka mierzonego za pomocą miary TVaR na poszczególne składowe (por. Panjer 2002,

Landsman i Valdez 2003).

Nieliniowe zależności mogą być mierzone za pomocą m.in. miary tau Kendala i rho

Spearmana (por. Nelsen 2006)).

1

Warto podkreślić, że do rodziny rozkładów eliptycznych należą rozkłady tzw. ciężkoogonowe, które

nie mają skończonej wariancji. Oznacza to, że nie można wykorzystywać współczynników korelacji liniowej

jako miary zależności między tymi rozkładami.

130410_0027 dr hab. Wojciech Bijak – matematyczne modele ryzyka i ich zastosowania - konspekt

3

Niech





T

1

1

Y

X

,





T

2

2

Y

X

będą niezależnymi wektorami zmiennych losowych o

identycznych rozkładach, określonych np. łączną dystrybuantą H. Współczynnik tau Kendala

określony jest jako:

























0

Pr

0

Pr

,

2

1

2

1

2

1

2

1

















Y

Y

X

X

Y

Y

X

X

Y

X



.

Oznacza to, że współczynnik tau Kendala jest równy różnicy prawdopodobieństw

uzyskiwania zgodnych i niezgodnych wartości poszczególnych zmiennych.

Niech





T

1

1

Y

X

,





T

3

2

Y

X

będą wektorami zmiennych losowych o identycznych

rozkładach brzegowych określonych dystrybuantami F i G, z których jeden wektor ma

rozkład określony łączną dystrybuantą H, natomiast składowe drugiego wektora są

stochastycznie niezależne. Współczynnik rho Spearmana określony jest jako:





























0

Pr

0

Pr

3

,

3

1

2

1

3

1

2

1

















Y

Y

X

X

Y

Y

X

X

Y

X

S



.

Współczynnik rho Spearmana jest proporcjonalny do różnicy prawdopodobieństw

uzyskiwania zgodnych i niezgodnych wartości poszczególnych zmiennych. Jeżeli

przyjmiemy, że wektor





T

1

1

Y

X

ma dystrybuantę o wartościach

 

y

x

H

,

, to drugi wektor





T

3

2

Y

X

ma łączną dystrybuantę o wartościach

   

y

G

x

F

.

Dla współczynników





Y

X ,



oraz





Y

X

S

,



mierzących zależność między ciągłymi

zmiennymi losowymi zachodzi związek (por. Nelsen 2006):









1

,

2

,

3

1









Y

X

Y

X

S





.

Przy określaniu ryzyka reprezentowanego przez zmienne losowe X i Y jesteśmy

czasami zainteresowani zależnościami, jakie zachodzą między nimi dla wartości skrajnych (w

ogonach rozkładów prawdopodobieństwa). Niech X, Y będą zmiennymi losowymi o

rozkładach ciągłych określonych przy pomocy dystrybuant F i G. Zależności wartości

skrajnych (w „górnym” lub „dolnym” ogonie rozkładu) definiuje się następująco:



Współczynnik zależności w „górnym” ogonie rozkładu

U



definiuje się jako granicę, o

ile ona istnieje, prawdopodobieństw warunkowych tego, że zmienna Y przekroczy wartość

kwantyla rzędu t, pod warunkiem, że ma to miejsce również dla zmiennej X:

 

 





.

|

Pr

lim

1

1

1

t

F

X

t

G

Y

t

U



















Współczynnik zależności w „dolnym” ogonie rozkładu

L



definiuje się jako granicę, o ile

ona istnieje, prawdopodobieństw warunkowych tego, że zmienna Y nie przekroczy

wartości kwantyla rzędu t, pod warunkiem, że ma to miejsce również dla zmiennej X:

130410_0027 dr hab. Wojciech Bijak – matematyczne modele ryzyka i ich zastosowania - konspekt

4

 

 





.

|

Pr

lim

1

1

0

t

F

X

t

G

Y

t

L

















W modelach kapitału obarczonego ryzykiem (RBC) konstruowanych na potrzeby

wewnętrzne zakładów ubezpieczeń coraz częściej uwzględnia się, wykorzystując kopule

2

,

złożone zależności między różnymi rodzajami ryzyka, nośnikami lub czynnikami ryzyka.

Takie podejście rekomendowane jest m.in. przez Międzynarodowe Stowarzyszenie

Aktuariuszy (IAA 2004).

Niech

1



n

X

będzie wektorem zmiennych losowych o dystrybuancie łącznego rozkładu

prawdopodobieństwa H i o dystrybuantach brzegowych rozkładów poszczególnych

składowych

n

i

F

i

,...,

1

,



. Wówczas istnieje taka funkcja C (kopula), że dla każdego

 

n

n

i

R

x







1

x

zachodzi:





   

 





n

n

n

x

F

x

F

x

F

C

x

x

x

H

,...,

,

,...,

,

2

2

1

1

2

1



.

Kopula C wprowadza strukturę zależności między poszczególnymi zmiennymi

losowymi tworzącymi wektor X . W przypadku zmiennych losowych o ciągłych rozkładach

prawdopodobieństwa funkcja C określona jest jednoznacznie (na mocy twierdzenia Sklara);

por. Nelsen 2006.

Kopulę C (

   

1

,

0

1

,

0

:



n

C

) można traktować jako dystrybuantę wielowymiarowego

rozkładu o jednostajnych rozkładach brzegowych:





 

 

 





n

n

n

u

F

u

F

u

F

H

u

u

u

C

1

2

1

2

1

1

1

2

1

,...,

,

,...,

,









.

Przykładowymi kopulami są: kopula normalna, kopula t Studenta, kopula Gumbela.

Kopula normalna (gaussowska) z macierzą korelacji

 

n

n

ij

r





R

ma postać:

 

 

 

 





n

n

G

u

u

u

C

1

2

1

1

1

,...,

,

















R

R

u

,

gdzie:

n
R



– dystrybuanta n-wymiarowego standardowego rozkładu normalnego z macierzą

korelacji

R ;

1





funkcja odwrotna do dystrybuanty standardowego jednowymiarowego

rozkładu normalnego. Kopula normalna nie nadaje się do modelowania zależności w ogonie

rozkładów prawdopodobieństwa, gdyż jeżeli

1



ij

r

, to

0





L

U





(por. Embrechts i in.,

2001).

2

W pracy: Heilpern 2007 zaproponowany został termin funkcje łączące.

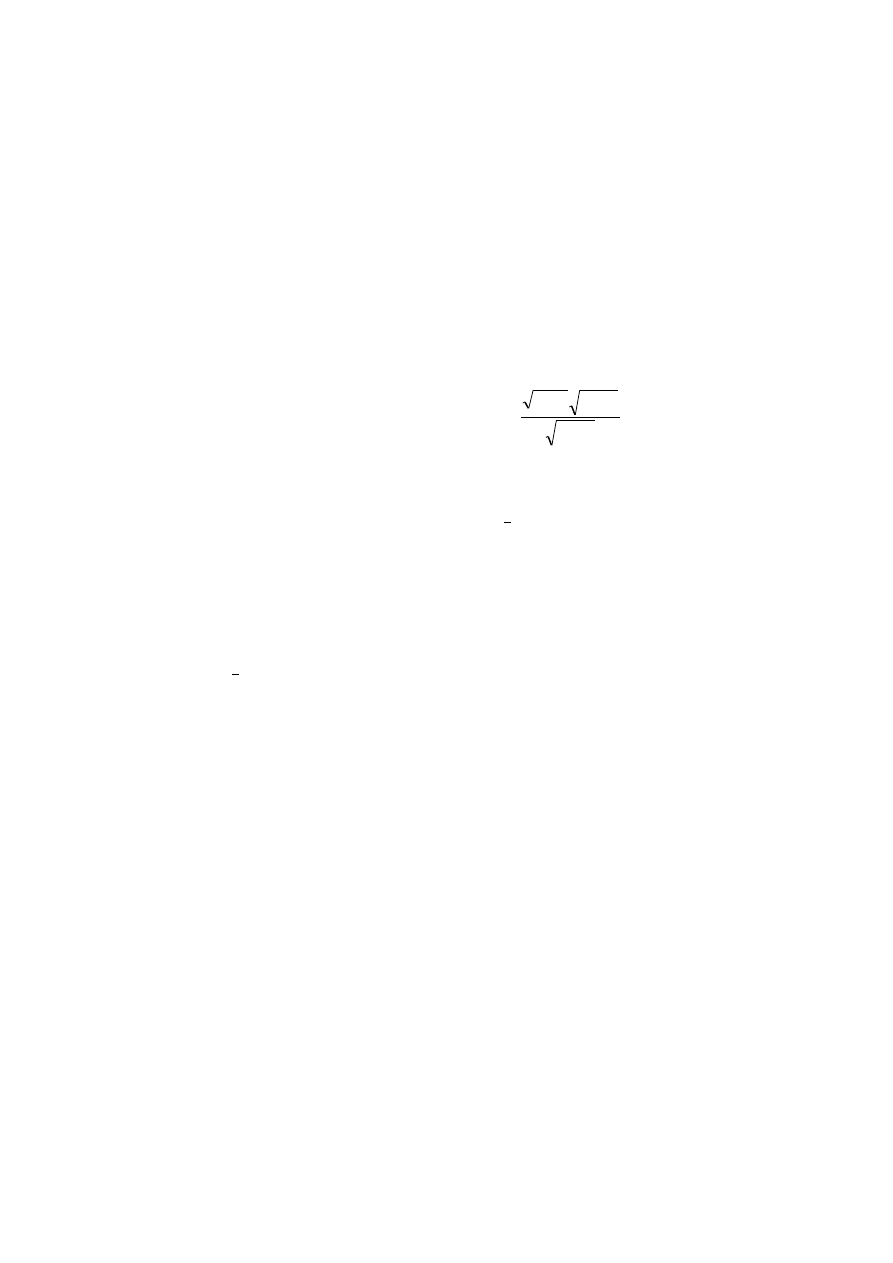
130410_0027 dr hab. Wojciech Bijak – matematyczne modele ryzyka i ich zastosowania - konspekt

5

Kopula t Studenta o



stopniach swobody i z macierzą korelacji

 

n

n

ij

r





R

ma

postać:

 

   

 





n

n

t

u

t

u

t

u

t

t

C

1

2

1

1

1

,

,

,...,

,



















R

R

u

,

gdzie:

n

t

R

,



– dystrybuanta n-wymiarowego rozkładu t Studenta o



stopniach swobody z

macierzą korelacji R ;

1





t

funkcja odwrotna do dystrybuanty jednowymiarowego rozkładu t

Studenta o



stopniach swobody. Kopula t Studenta określa jednakową zależność górną i

dolną w ogonie rozkładu prawdopodobieństwa równą:





































ij

ij

j

i

L

j

i

U

r

r

t

X

X

X

X

1

1

1

2

2

,

,

1









.

Kopulę Gumbela (por. np. Faivre 2005) można przedstawić w postaci:

 





1

,

ln

exp

1

1











































n

i

i

G

u

C

u

.

Może być ona wykorzystywana do modelowania niezależności lub zależności dodatniej.

Określa zależność dolną w ogonie rozkładu prawdopodobieństwa równą zero





0



L



i górną

równą





1

2

2





U

. Z tego względu może stanowić dobre narzędzie do modelowania sytuacji

stresowych na potrzeby określania zapotrzebowania na kapitał zabezpieczający wypłacalność.

Przy ustalaniu zależności między rozkładami prawdopodobieństwa można wyróżnić

trzy skrajne struktury (por. Nelsen 2006):

 





n

n

u

u

u

M

,...,

,

min

2

1



u

,

 









n

i

i

n

u

1

u

,

(3.25)

 























0

;

1

max

1

n

u

W

n

i

i

n

u

.

Funkcje

 

u

n

M

,

 

u

n

W

określają ograniczenia Frecheta–Hoeffdinga. Funkcja

 

u

n

M

oznacza skrajną dodatnią zależność, funkcja

 

u

n

W

skrajną ujemną zależność, natomiast

 

u

n



niezależność rozkładów. Funkcje

 

u

n

M

,

 

u

n



są kopulami dla każdego wymiaru n,

podczas gdy funkcja

 

u

n

W

jest kopulą jedynie wtedy, gdy

2



n

.

130410_0027 dr hab. Wojciech Bijak – matematyczne modele ryzyka i ich zastosowania - konspekt

6

Z punktu widzenia określania wymogów kapitałowych funkcja

 

u

n

M

opisuje

najgorszą sytuację – jednoczesnego zachodzenia niekorzystnych zdarzeń. W modelach

wykorzystujących wielowymiarowe rozkłady normalne odpowiada to przyjmowaniu

założenia, że współczynniki korelacji między zmiennymi są równe 1. W takim przypadku

miary VaR i TVaR stają się miarami addytywnymi.