Miary współzależności

Mogą być badane w populacjach co
najmniej dwucechowych gdzie cechy
oznaczamy odpowiednio X oraz Y.
Zmienne są powiązane w pary poprzez
przynależność każdej pary obserwacji
do tego samego elementu w próbie
N-elementowa próba losowa będzie
rerezentowana przez układ par (X

1

,Y

1

),

(X

2

,Y

2

),…, (X

n

,Y

n

),

Miary współzależności

Kowariancja S

xy

lub cov(X,Y)

pozwala uchwycić współzmienność
cech

Wady – zależy od przyjętych jednostek, w których
wyrażone są cechy
Z tej samej próby otrzymamy inną wartość
kowariancji, jeśli obserwacje będą wyrażone w
gramach i centymetrach, a inną wartość, jeśli będą
wyrażone w kilogramach i metrach

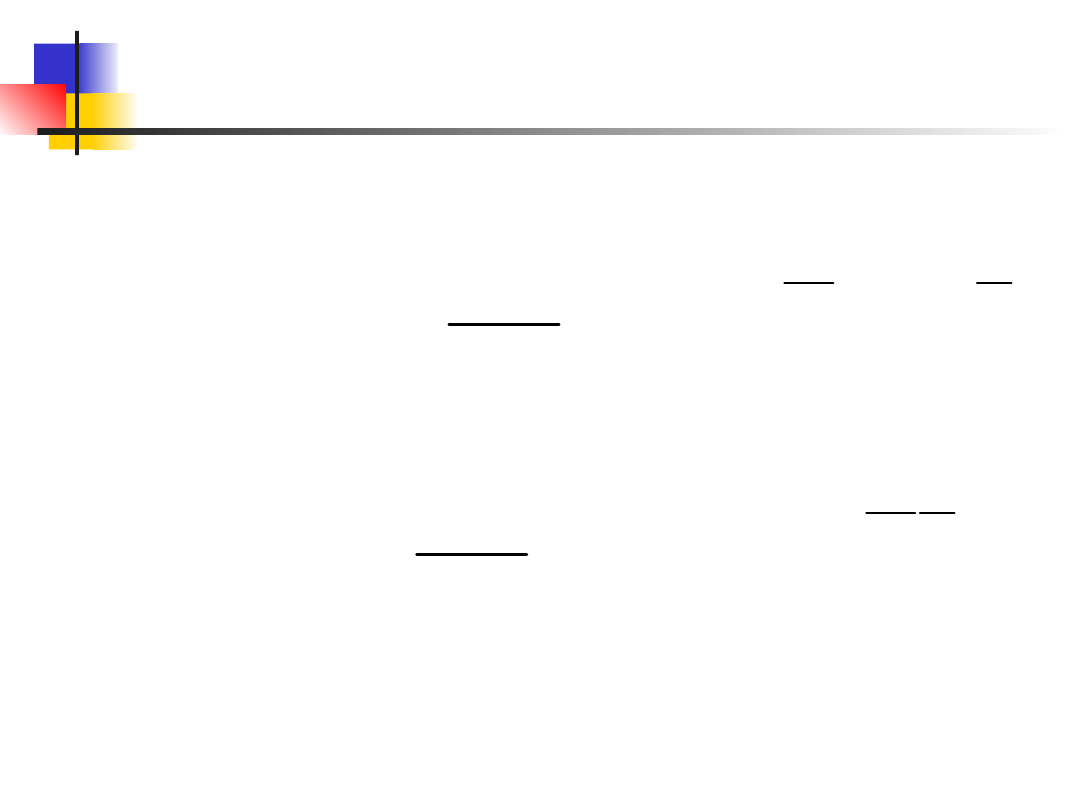
Miary współzależności

Kowariancja S

xy

lub cov(X,Y)

określona jest wzorem

lub wzorem równoważnym
(w inny sposób obliczamy sumę iloczynów odchyleń)

przy dużych liczebnościach próby, gdy n/(n-1) zmierza do 1, w obu

wzorach w miejsce wyrażenia (n-1) wstawia się tylko n











)

)(

(

1

1

Y

Y

X

X

n

S

i

i

xy

)

)

((

1

1









Y

X

n

Y

X

n

S

i

i

xy

Miary współzależności

Współczynnik korelacji liniowej

Pearsona r

xy

pozwala uchwycić współzmienność cech

I pozbawiony jest wady jaką ma kowariancja
Czyli nie zależy od przyjętych jednostek, w których

wyrażone są cechy
Z tej samej próby otrzymamy tą samą wartość współczynnika,

niezależnie od tego czy obserwacje będą wyrażone w

gramach i centymetrach, czy będą wyrażone w kilogramach i

metrach

Gdzie S

xy

jest kowariancją z próby,

s

x

oraz s

y

są odchyleniami standardowymi

odpowiednio dla zmiennej X oraz Y

Przy obliczaniu korelacji Excel korzysta
z wzorów na kowariancję i
odchylenia standardowe z wyrażeniem n/(n-1)

y

x

xy

xy

s

s

S

r 

Miary współzależności

Kowariancja jest nieskalowana
(zależy od jednostek przyjętych dla
badanych cech )

Współczynnik korelacji liniowej jest
skalowany (nie zależy od jednostek
przyjętych dla badanych cech)
przyjmuje wartości z zakresu -1 do 1

Wartość 0 oznacza brak korelacji
Im wartość współczynnika jest bliższa 1 lub -1 tym
zmienne są bardziej skorelowane

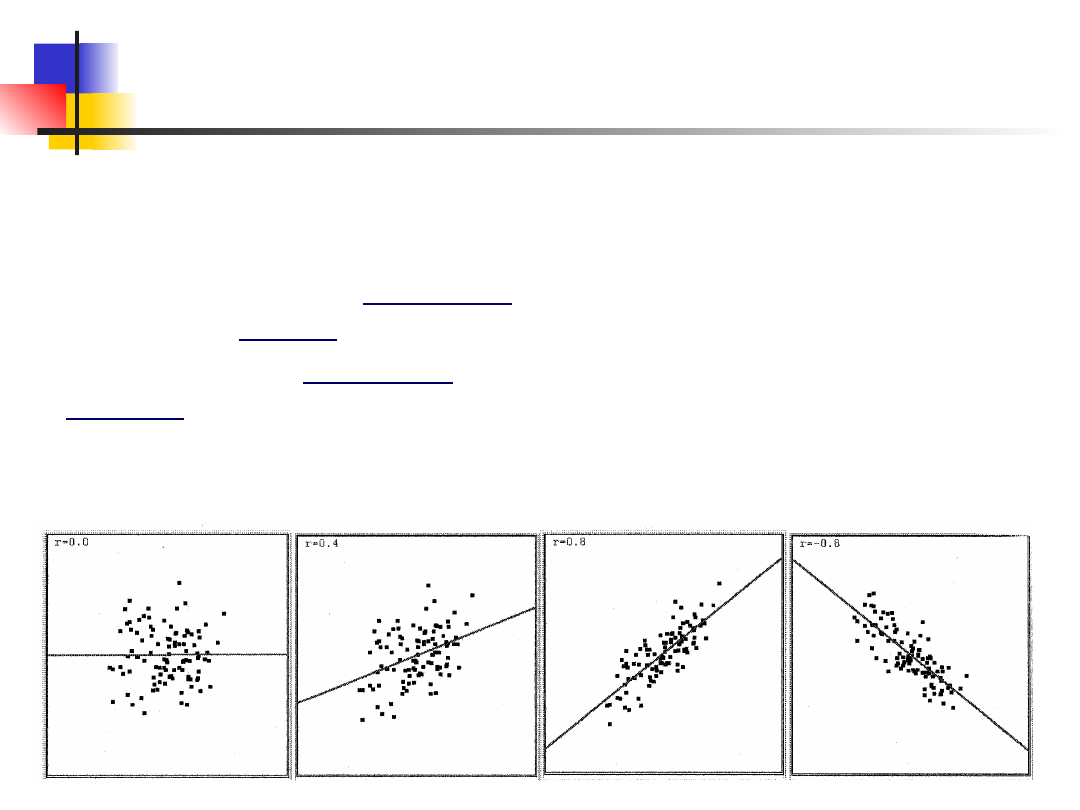
Korelacje

Bezwzględna wartość współczynnika informuje nas o sile
związku Znak współczynnika informuje nas o kierunku
korelacji,
+ K. DODATNIA - wzrostowi wartości jednej cechy
odpowiada wzrost wartości drugiej cechy
- K. UJEMNA – wzrostowi wartości jednej cechy odpowiada
spadek wartości drugiej cechy
0 – brak korelacji – zmienne są niezależne
Założeniem stosowalności tego współczynnika jest liniowość
związku
r=0,0

r=0,4

r=0,8

r=-0,8

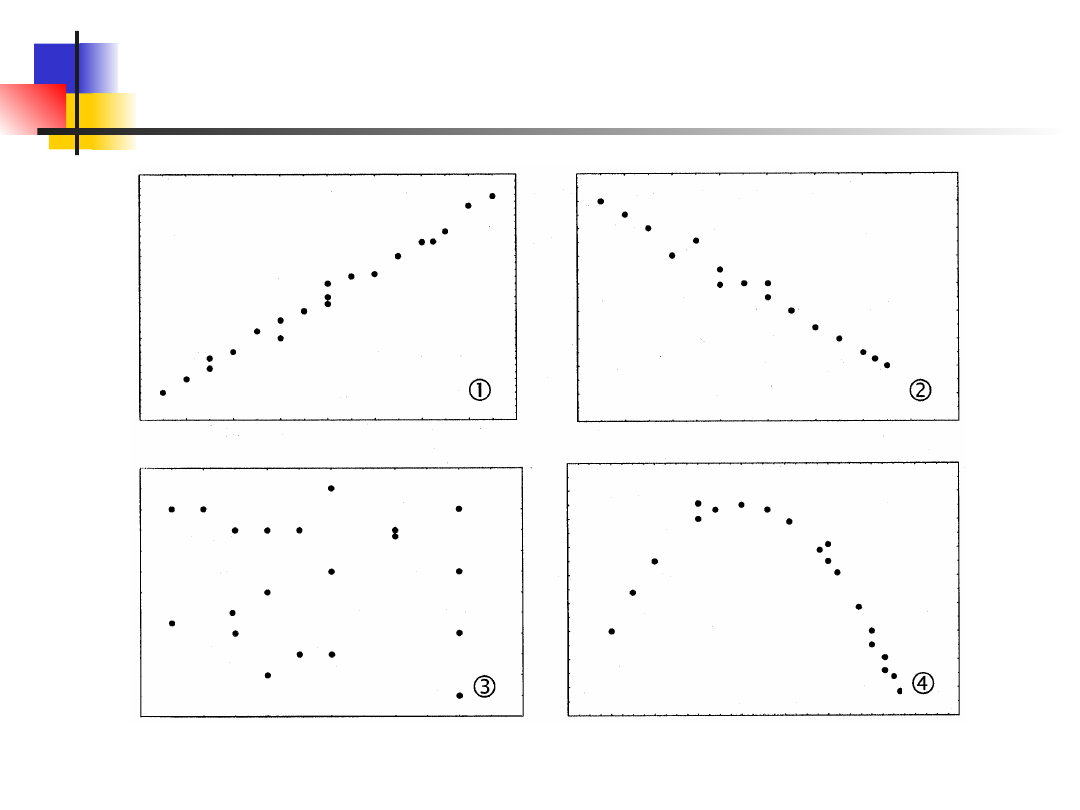
Korelacyjne wykresy rozrzutu

1. Korelacja liniowa dodatnia

2.Korelacja liniowa ujemna

3. Brak korelacji

4. Korelacja krzywoliniowa

Korelacje

Przy interpretacji wartości współczynnika korelacji

liniowej Pearsona należy pamiętać że:



Wielkość współczynnika podlega wpływom wartości

skrajnych i odstających



Najważniejsza jest istotność korelacji. Niepotrzebna

nam korelacja nawet bardzo wysoka, jeżeli nie jest

istotna



Wartość współczynnika bliska 0 nie zawsze oznacza brak

zależności, a jedynie brak zależności prostoliniowej

Przybliżone określenie stopnia zależności cech
r

xy=

= 0

brak korelacji

0 ≤ r

xy

< 0,1 korelacja nikła

0,1 ≤ r

xy

< 0,3 korelacja słaba

0,3 ≤ r

xy

< 0,5 korelacja przeciętna

0,5 ≤ r

xy

< 0,7 korelacja wysoka

0,7 ≤ r

xy

< 0,9 korelacja bardzo wysoka

0,9 ≤ r

xy

< 1 korelacja prawie pełna

Metody badania istotności
korelacji

Przy interpretacji współzależności
występujących pomiędzy badanymi
zmiennymi ważna jest nie tylko siła
tego związku ale również jego
statystyczna istotność.

Najważniejsza jest istotność
korelacji.

Niepotrzebna nam korelacja nawet
bardzo wysoka, jeżeli nie jest istotna

Metody badania istotności
korelacji

W celu określenia statystycznej istotności
korelacji obliczamy F

czyli

wartość stosunku

wariancji wyjaśnionej do niewyjaśnionej

gdzie r – współczynnik korelacji
N – liczba par pomiarów

2

2

1

)

2

(

r

N

r

F







Metody badania istotności
korelacji

Po obliczeniu wartości stosunku F sprawdzamy jaka
jest krytyczna wartość F dla poziomu istotności
0,05. Przy korzystaniu z tablic zakładamy, iż liczba
stopni swobody dla wariancji większej wynosi df=1
a liczba stopni swobody dla wariancji mniejszej
wynosi df= N-2.

Jeżeli wartość F odczytana z tablic wartości
krytycznych rozkładu F jest mniejsza od obliczonej
to korelacja jest istotna statystycznie

Jeżeli wartość F odczytana z tablic wartości
krytycznych rozkładu F jest większa od obliczonej to
korelacja jest nieistotna statystycznie

Metody badania istotności
korelacji

Istotność korelacji można również sprawdzić
wykorzystując narzędzia Excela W tym celu
wybieramy:
Narzędzia /Analiza danych/Regresja
Po zaznaczeniu zakresu danych osobno dla y i x,
narzędzie oblicza wartość F oraz podaje wartość
istotności F.
Jeżeli wartość istotności F jest mniejsza od
przyjętego przez nas poziomu istotności np. 0,05 to
korelacja jest istotna statystycznie

Jeżeli wartość istotności F jest większa od
przyjętego przez nas poziomu istotności np. 0,05 to
korelacja jest nieistotna statystycznie