ANALIZA 

WSPÓŁZALEŻNOŚCI 

ZMIENNYCH

Badanie zależności pomiędzy 
wyodrębnionymi cechami musi być 
poprzedzone analizą merytoryczną 
badanego związku. Jej celem  jest 
stwierdzenie, czy pomiędzy badanymi 
cechami występuje związek przyczynowo-
skutkowy. Pozytywna odpowiedź daje 
podstawę do badania zależności. 
Pominięcie tej analizy może skutkować 
badaniem zależności pozornej.

ZALEŻNOŚĆ FUNKCYJNA A 

STATYSTYCZNA

Można wyróżnić dwa rodzaje zależności pomiędzy cechami:

•  funkcyjna

•  statystyczna.
Zależność funkcyjna oznacza występowanie jednoznacznego 

przyporządkowania 

wartościom cechy niezależnej odpowiednich wartości cechy zależnej (każdej 
Wartości zmiennej niezależnej odpowiada tylko jedna wartość zmiennej zależnej). 
Ten typ zależności nie odnosi się w zasadzie do relacji zachodzących w przypadku
 zjawisk społeczno-gospodarczych. Wynika to między innymi z następujących 
przyczyn:

• zjawiska tego typu podlegają zwykle oddziaływaniu bardzo wielu czynników, 

• w większości przypadków trudno jednoznacznie zidentyfikować wszystkie 

czynniki, 

• nie wszystkie z ustalonych czynników mają charakter mierzalny by można je 

było uwzględnić w analizie współzależności, 

• wpływ wielu czynników, nawet tych mierzalnych, trudno jednoznacznie 

określić liczbowo z uwagi na często występujące złożone powiązania z innymi 

czynnikami,

• uwzględnienie w badaniach zbyt dużej liczby czynników znacznie komplikuje 

procedury obliczeniowe, a niekiedy wręcz je uniemożliwia.

W związku z powyższym w przypadku zjawisk społeczno-gospodarczych można 

mówić jedynie o występowaniu zależności typu statystycznego. Jest to 
zależność niejednoznaczna, tzn. każdej wartości zmiennej niezależnej może 
być przyporządkowanych kilka wartości zmiennej zależnej .

Metody badania 

współzależności

W literaturze wyodrębnia się różne 

podejścia do badania współzależności 

o zróżnicowanym stopniu precyzji 

wyników jej badania. Należą do nich:

a) metoda graficzna,
b) metoda tabelaryczna,
c) metody formalne oparte na 

wykorzystaniu parametrycznych i 

nieparametrycznych miar zależności.

Metoda graficzna 

Punktem wyjścia dla metody graficznej są 

szeregi szczegółowe zawierające dane o 

wartościach dwóch wybranych cech Y i X 

opisujących badaną zbiorowość. Sporządzony 

na ich podstawie diagram korelacyjny stanowi 

wykres punktowy umieszczony w układzie 

współrzędnych prostokątnych, na którym 

zaznacza się punkty o współrzędnych 

(współrzędne te należy traktować jako 

wartości cech X i Y zaobserwowane w i-tej 

jednostce). Na podstawie uzyskanego układu 

punktów dokonuje się oceny zależności 

między badanymi cechami.

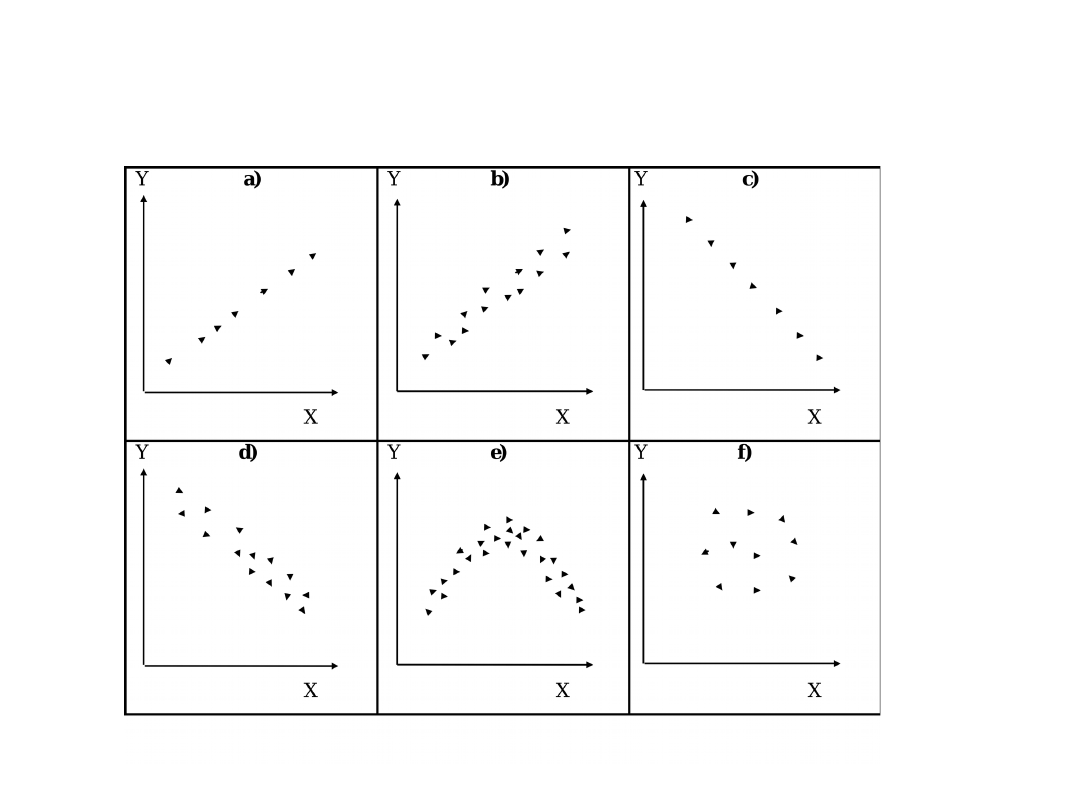
Kształty diagramów 

korelacyjnych

Kształty diagramów korelacyjnych - 

interpretacja

a) występuje zależność funkcyjna, dodatnia (ma miejsce jednoznaczne porządkowanie 
wzajemne wartości cech X i Y; każdej wartości cechy X odpowiada tylko jedna wartość cechy Y
 przy czym rosnącym wartościom cechy X odpowiadają rosnące wartości cechy Y lub
 malejącym wartościom cechy X odpowiadają malejące wartości cechy Y,
b) zależność prostoliniową o kierunku dodatnim; w tym przypadku poszczególnym 
wartościom cechy X może odpowiadać dowolna liczba wartości  cechy Y; dodatkowo  - wraz ze
 wzrostem wartości cechy X wzrastają (średnio) wartości cechy Y (lub odwrotnie),
c) ten kształt diagramu ilustruje zależność funkcyjną o kierunku ujemnym; w  tym przypadku 
również występuje jednoznaczne, wzajemne przyporządkowanie wartości  cech X i Y, przy
 czym rosnącym wartościom cechy X odpowiadają malejące wartości cechy Y lub malejącym 
wartościom cechy X odpowiadają rosnące wartości cechy Y,
d) ten przypadek ilustruje zależność prostoliniową o kierunku ujemnym; poszczególnym 
wartościom cechy X może odpowiadać dowolna liczba wartości cechy Y, przy czym rosnącym 
wartościom cechy X odpowiadają malejące (średnio)  wartości cechy Y (lub odwrotnie),
e) ilustruje jeden z przypadków związku krzywoliniowego; w tym przypadku występuje 
niejednoznaczne przyporządkowanie wartości obu cech, a dodatkowo nie ma miejsca jednolita 
tendencja zmian wartości tych cech, 
f) ten przypadek jest ilustracją brak zależności między cechami.
Na podstawie powyższego można stwierdzić, że metoda graficzna oprócz informacji o 
charakterze związku (liniowy lub krzywoliniowy) i kierunku związku  (dodatni lub ujemny) 
dostarcza również wskazówek umożliwiających wstępną ocenę siły związku miedzy cechami.
 Może ona stanowić punkt wyjścia dla  stosowania formalnych metod opisu współzależności.

Metoda tabelaryczna

• Metoda tabelaryczna badania współzależności – 

wykorzystująca dane ujęte zarówno w szeregach 

jak i tablicach statystycznych - pozwala na 

uzyskanie wyników badania o stopniu precyzji 

zbliżonym do metody graficznej. Diagram 

korelacyjny to przecież nic innego, jak 

zaprezentowany w postaci graficznej materiał 

statystyczny ujęty w szeregach bądź tablicy 

statystycznej. W przypadku danych w szeregach 

statystycznych ocena charakteru związku jak i 

natężenia oraz kierunku zależności odbywa się na 

podstawie określenia charakteru wzajemnych 

powiązań wartości dwóch badanych cech. 

Metoda tabelaryczna

Dla licznych zbiorowości (przyjmuje się 

zwykle, że ich liczebność przekracza 30) 

materiał statystyczny opisujący je ujmuje 

się w formie tablicy statystycznej zwanej w 

tym przypadku tablicą korelacyjną.  

Tablica taka prezentuje jednoczesny 

rozkład badanej zbiorowości ze względu na 

dwie cechy, stąd też spotykane w 

literaturze określenie, iż przedstawia ona 

dwuwymiarowy rozkład zbiorowości. 

W tablicy takiej dla cech typu liczbowego 

ich wartości ujmowane są najczęściej w 

postaci przedziałów klasowych, zaś dla 

cech typu opisowego przyjmuje się 

występujące w zbiorowości ich warianty. 

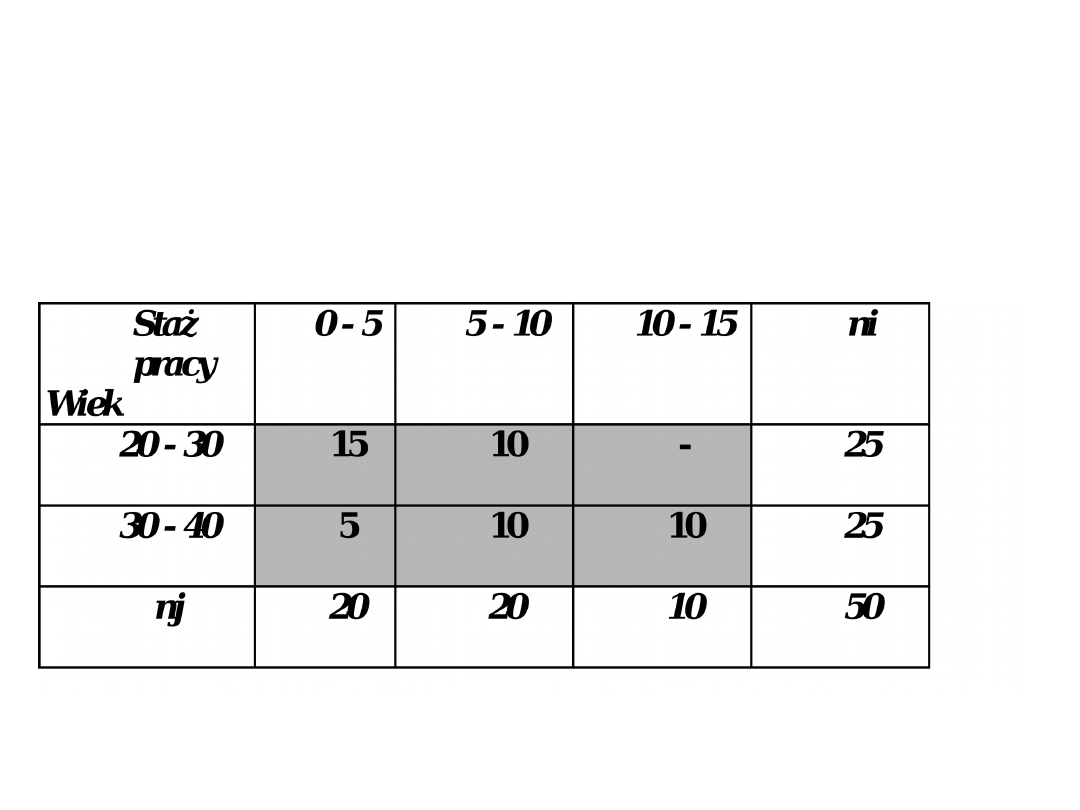
Przykład tablicy korelacyjnej

Pracownicy firmy „M” ze względu 

na wiek i staż pracy

Metoda tabelaryczna

• Typy rozkładów występujących w 

tablicy korelacyjnej:

• rozkład łączny
• rozkład brzegowy 
• rozkład warunkowy

Metoda tabelaryczna

Ocena zależności na podstawie materiału statystycznego ujętego 

w tablicy korelacyjnej opierać się może na ocenie rozkładu 

liczebności (częstości) w tablicy jak również na ocenie 

podobieństwa rozkładów warunkowych.

Koncentracja liczebności (częstości) wzdłuż przekątnych tablicy 

korelacyjnej wskazuje na występowanie znacznego natężenia 

zależności; jeśli jest to przekątna biegnąca z lewego górnego 

narożnika tablicy do prawego dolnego – to sytuacja taka 

oznacza występowanie zależności o kierunku dodatnim; w 

przeciwnym przypadku będzie to zależność o kierunku 

ujemnym. 

Dokonując oceny zależności na podstawie rozkładów warunkowych 

należy kierować się zasadą: im wyższy stopień podobieństwa 

rozkładów warunkowych określonej cechy (przy zmieniających 

się warunkach nałożonych na cechę przeciwną) tym mniejsze 

jest natężenie zależności. Jeśli są one identyczne, zależność nie 

występuje. Dodać należy, iż na badaniu podobieństwa 

rozkładów warunkowych opierają się niektóre z miar zależności.

Metody formalne badania zależności

• Omówione wyżej sposoby badania zależności pozwalają 

jedynie na wstępną jej ocenę. Precyzyjniejszych wyników 

badania dostarczają metody formalne wykorzystujące 

miary zależności cech. 

• Metody formalne można ująć w dwie grupy tj. metody 

nieparametryczne (stochastyczne) i metody  

parametryczne (korelacyjne) badania 

współzależności. 

• Pierwsza grupa opiera się na badaniu podobieństwa 

rozkładów warunkowych (analiza dotyczy jedynie 

rozkładów cech a nie ich wartości) cechy zależnej. 

Natężenie zależności w tym przypadku określamy na 

podstawie stopnia podobieństwa warunkowych rozkładów 

tej cechy. 

• W drugim przypadku przedmiotem analizy jest badanie 

podobieństwa parametrów warunkowych ( średnich 

warunkowych) cechy zależnej. Wyższe podobieństwo 

średnich warunkowych cechy zależnej oznaczać będzie 

mniejsze natężenie zależności. 

Własności idealnej miary zależności

a) winna być niemianowana, gdyż umożliwia to prowadzenie analizy 

porównawczej zależności różnych cech,

b) winna być unormowana, tzn. winna przyjmować wartości ze skończonego 

przedziału liczbowego; umożliwia to ocenę natężenia zależności pomiędzy 

badanymi cechami. Miary spełniające ten postulat przyjmują najczęściej 

wartości z przedziału liczbowego <0 ; 1> Dla oceny natężenia zależności 

można przyjąć następujące kryteria:
0 - niezależność (brak zależności)
( 0 – 0,33>zależność słaba,
( 0,33 – 0,66>zależność wyraźna
( 0,66 – 1,00)zależność silna
1,00 -zależność funkcyjna

c) oprócz natężenia winna wskazywać również kierunek zależności; jej wartość 

winna informować, czy w określonym przypadku mamy do czynienia z 

zależnością o kierunku dodatnim bądź ujemnym. Miary wskazujące kierunek 

zależności przyjmują wartości zarówno dodatnie jak i ujemne; w przypadku 

miar unormowanych przyjmują one wartości z przedziału liczbowego <-1; 

1>. Badanie kierunku zależności odnosi się do relacji zachodzących między 

cechami, których wartości są wyrażone przynajmniej na skali porządkowej,

d) winna być symetryczna;  wówczas wartość miary jest identyczna bez 

względu na „kierunek” badania zależności, co oznacza, iż wartość miary 

zależności Y od X jest identyczna jak miara zależności X od Y. Własność ta 

jest spełniona w przypadku związków prostoliniowych lub w przypadku 

badaniach związków zachodzących między cechami opisowymi,

Własności idealnej miary zależności – 

c.d.

e) istnieje możliwość jej stosowania do badania zależności w związkach prosto- 

i krzywoliniowych. Spełnienie tej własności wyklucza konieczność badania 

"charakteru" związku przed zastosowaniem określonej miary do badania 

zależności. W przypadku miar, które mogą być stosowane do badania 

zależności w związkach prostoliniowych, właściwe badanie zależności musi 

być poprzedzone badaniem potwierdzającym występowanie związku 

prostoliniowego między badanymi cechami. Negatywny wynik takiego 

badania zmusza nas do wyboru innej miary zależności. Brak możliwości 

zbadania charakteru związku (np. gdy dane zawarte są w tablicy 

korelacyjnej) wymaga przynamniej przyjęcia założenia o występowaniu 

związku prostoliniowego.  Należy dodać, iż problem badania "charakteru" 

związku nie odnosi się do zależności występujących między cechami 

opisowymi,

f) istnieje możliwość jej stosowania do badania zależności w dowolnym 

układzie rodzajowym cech; badanie zależności może dotyczyć trzech 

następujących sytuacji: badamy zależność między dwiema cechami 

liczbowymi, np. między stażem pracy i zarobkami pracowników; badanie 

zależności między dwiema cechami opisowymi, np. między poziomem 

wykształcenia pracowników a miejscem zajmowanym w strukturze 

organizacyjnej firmy; wreszcie zależności między cechą liczbową a opisową, 

np. między poziomem wykształcenia pracowników a ich zarobkami. Idealną 

miarą zależności byłaby taka, którą można zastosować w każdej z 

wymienionych sytuacji,

g) winna spełniać własność jednolitej preferencji wartości, co oznacza, iż 

wzrostowi wartości miary towarzyszy wzrost natężenia zależności między 

cechami,

h) winna być prosta rachunkowo.

Nieparametryczne miary zależności

Nieparametryczne badanie zależności polega na badaniu prawidłowości
 występujących w zakresie współwystępowania wariantów cechy 
zależnej przyporządkowanych poszczególnym wariantom cechy 
niezależnej i stwierdzeniu, na ile rozkład wariantów cechy zależnej jest
 zdeterminowany zmieniającymi się odmianami cechy niezależnej. 
Praktycznie oznacza to badanie podobieństwa rozkładów warunkowych 
częstości cechy zależnej. Identyczność tych rozkładów oznacza 
występowanie niezależności w sensie nieparametrycznym. Formalnie 

warunek 

niezależności można ująć w sposób następujący:
jeśli dla wszystkich kombinacji wariantów cech zależnej i niezależnej 
(czyli wszystkich pól rozkładu łącznego w tablicy korelacyjnej) zachodzi 
relacja:

wówczas występuje niezależność badanych cech. 

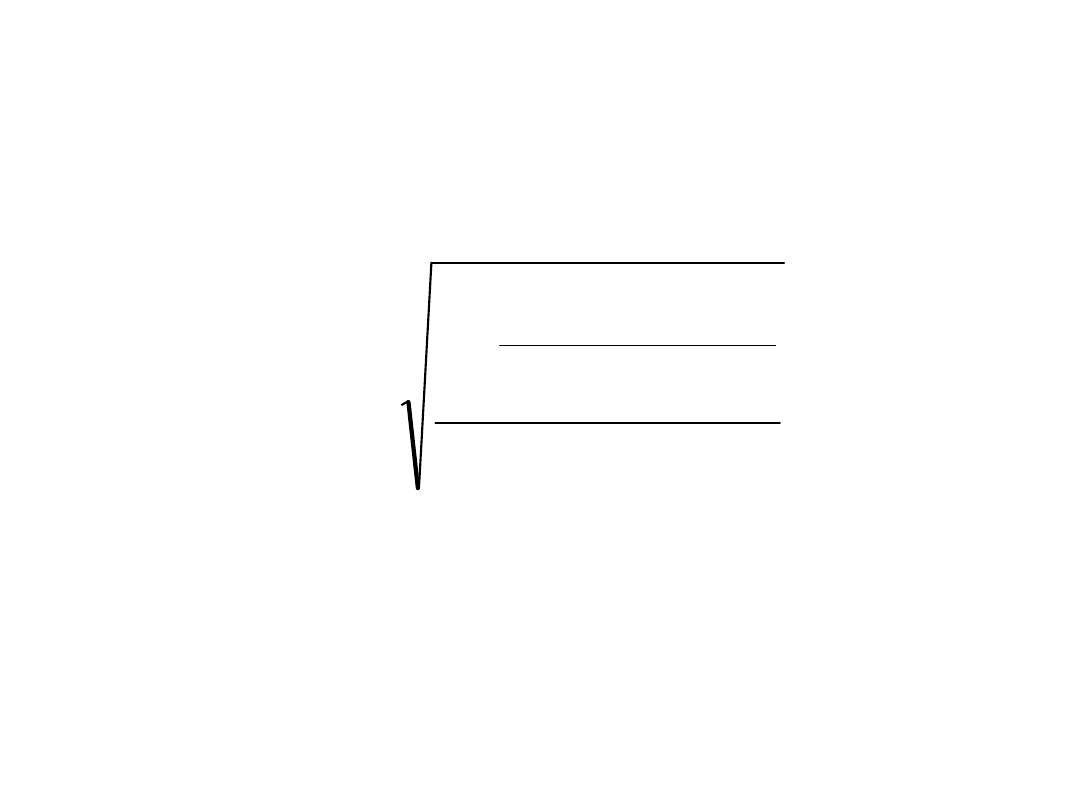
Współczynnik zbieżności Czuprowa





 

1

,

min

*

*

,

2









s

r

f

f

f

f

f

d

j

i

j

i

j

i

ij

c

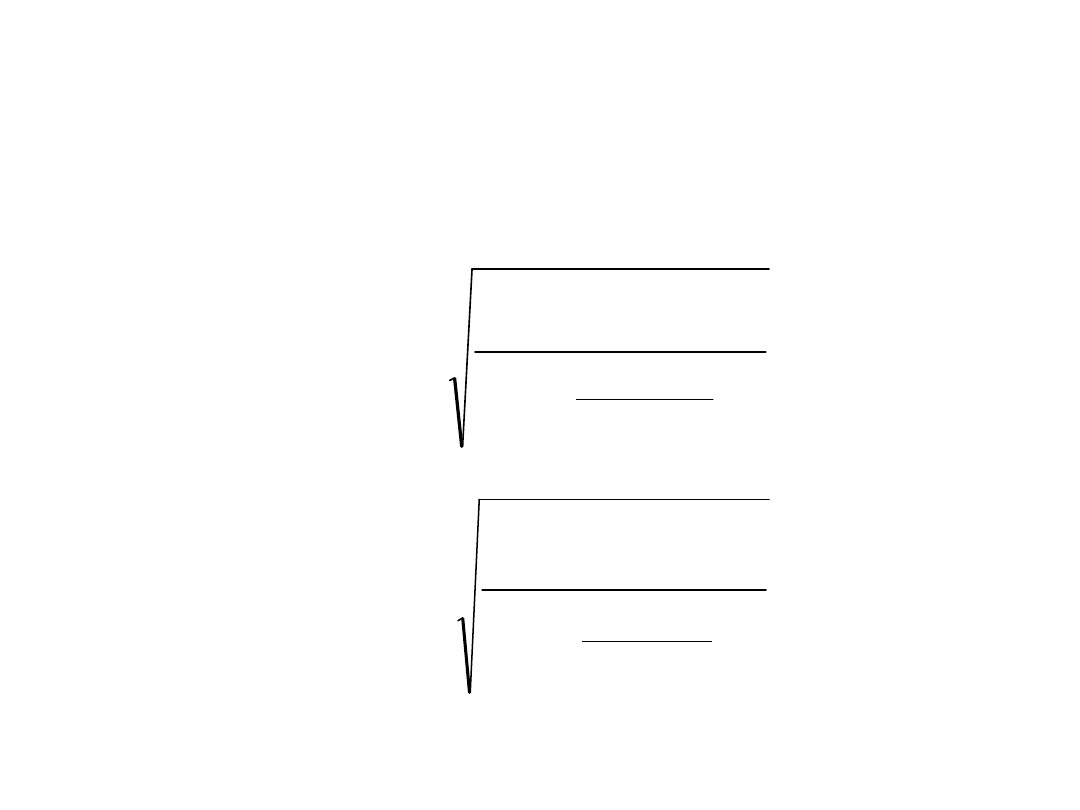
Współczynnik zależności 

Hellwiga

Dwie wersje współczynnika: 

- dla podzbioru G

- dla podzbioru M

 

s

r

f

f

f

d

G

j

i

G

j

i

j

i

ij

H

G

,

min

1

1

*

,

,















 

s

r

f

f

f

d

M

j

i

M

j

i

ij

j

i

H

M

,

min

1

1

*

,

,















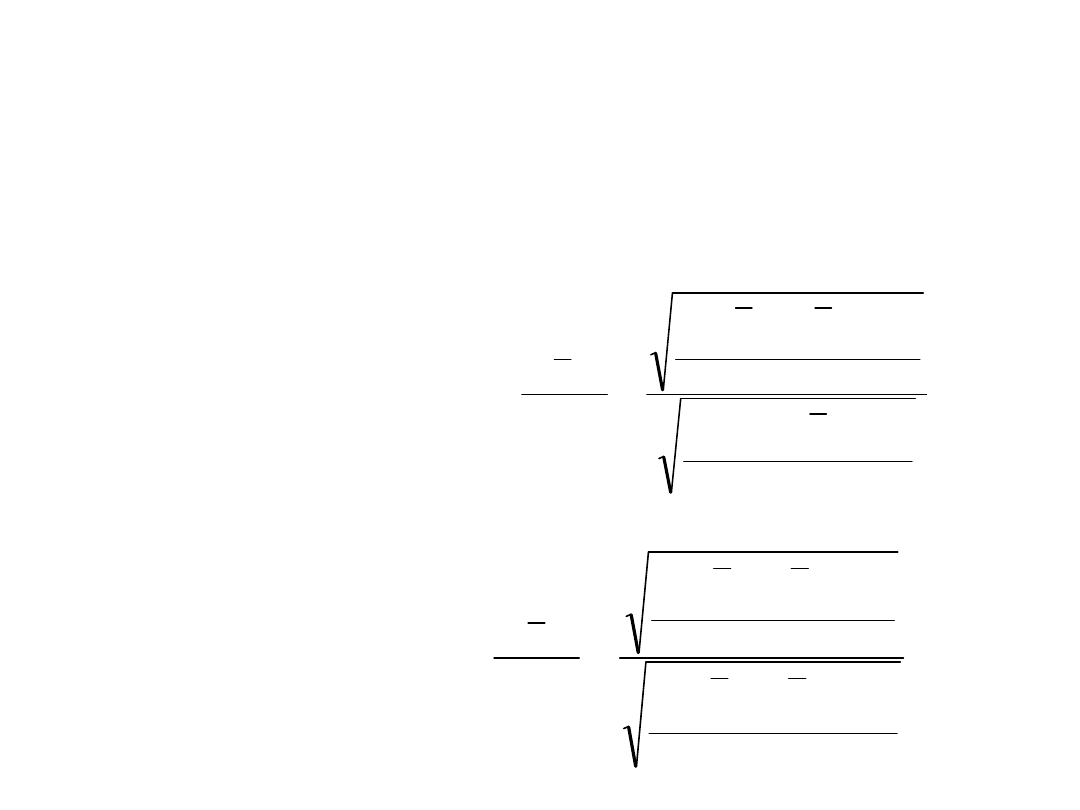
Stosunek korelacyjny

Dwie wersje miary dla układu tablicy korelacyjnej, w 

której:

- warianty cechy Y występują w wierszach

- warianty cechy Y występują w kolumnach

 

 









N

n

y

y

N

n

y

y

y

s

y

s

r

i

i

i

j

j

x

x

k

j

j













*

*

2

2

 

 









N

n

y

y

N

n

y

y

y

s

y

s

r

j

j

x

i

i

x

x

k

i

i

i













*

*

2

2

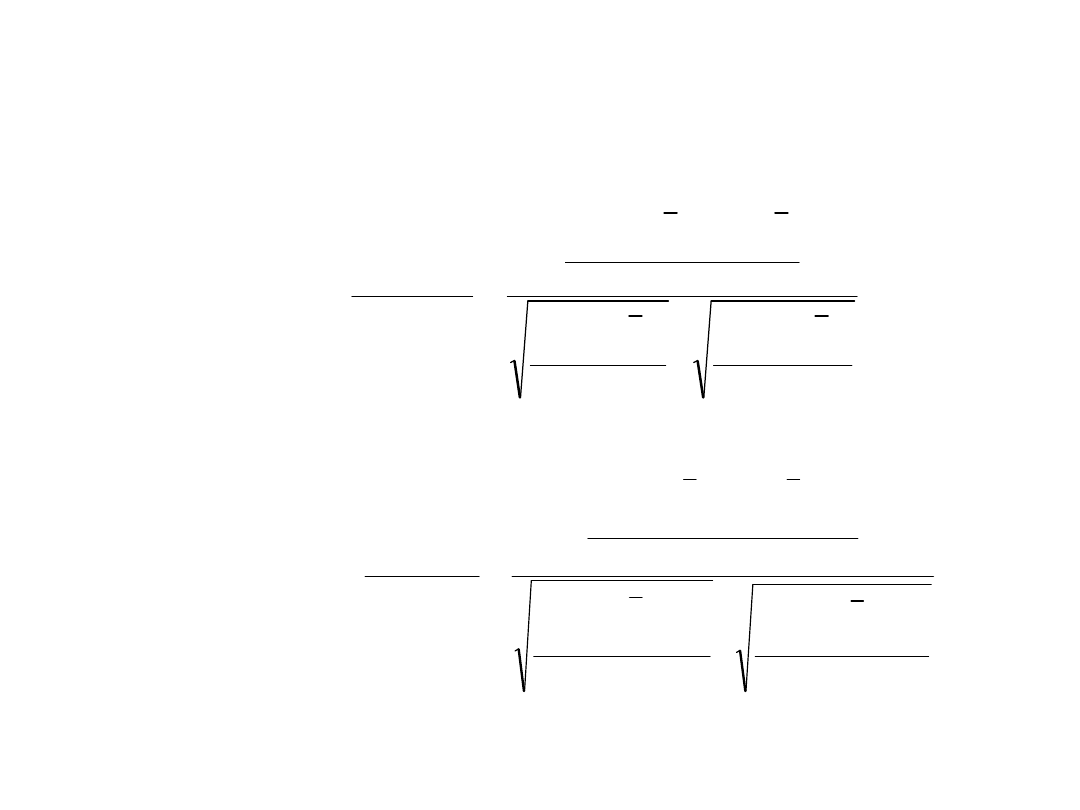
Współczynnik korelacji liniowej 

Pearsona

- dla szeregów szczegółowych

- dla tablicy korelacyjnej

 

   



 











N

y

y

N

x

x

N

y

y

x

x

y

s

x

s

y

x

c

r

i

i

i

i

i

i

i

P



















2

2

*

*

*

,

 

   

















N

n

y

y

N

n

x

x

N

n

y

y

x

x

y

s

x

s

y

x

c

r

i

i

i

j

j

j

j

i

ij

i

j

P



















*

*

*

*

*

*

,

2

2

,

Współczynnik korelacji rang 

Spearmana

 





N

N

d

d

r

i

y

x

Sp

i

i











3

2

6

1

Analiza regresji

Celem analizy regresji jest skonstruowanie
funkcji regresji charakteryzujących związek
 cech X oraz Y: 
• regresja Y względem X:
określa, jakie zmiany Y powoduje wzrost X o 
jednostkę,
• regresja X względem Y:
określa, jakie zmiany X powoduje wzrost Y o
 jednostkę.

b

x

a

y

y



 *

ˆ

b

y

a

x

x



 *

ˆ

Szacowanie parametrów funkcji 

regresji

• Równanie regresji : 

• Parametr      :

• Parametr b:

b

x

a

y

y



 *

ˆ

y

a

 

 



 







N

x

x

N

y

y

x

x

x

s

y

x

C

a

i

i

i

i

i

y















2

2

*

,

x

a

y

b

y

*





Współczynnik dopasowania      (fi 

kwadrat)

 

• określa, jaka część zmiennej zależnej 

(objaśnianej) nie jest wynikiem oddziaływania 
zmiennej niezależnej (objaśniającej).



















i

i

i

i

i

y

y

y

y

y

2

2

2

ˆ



2



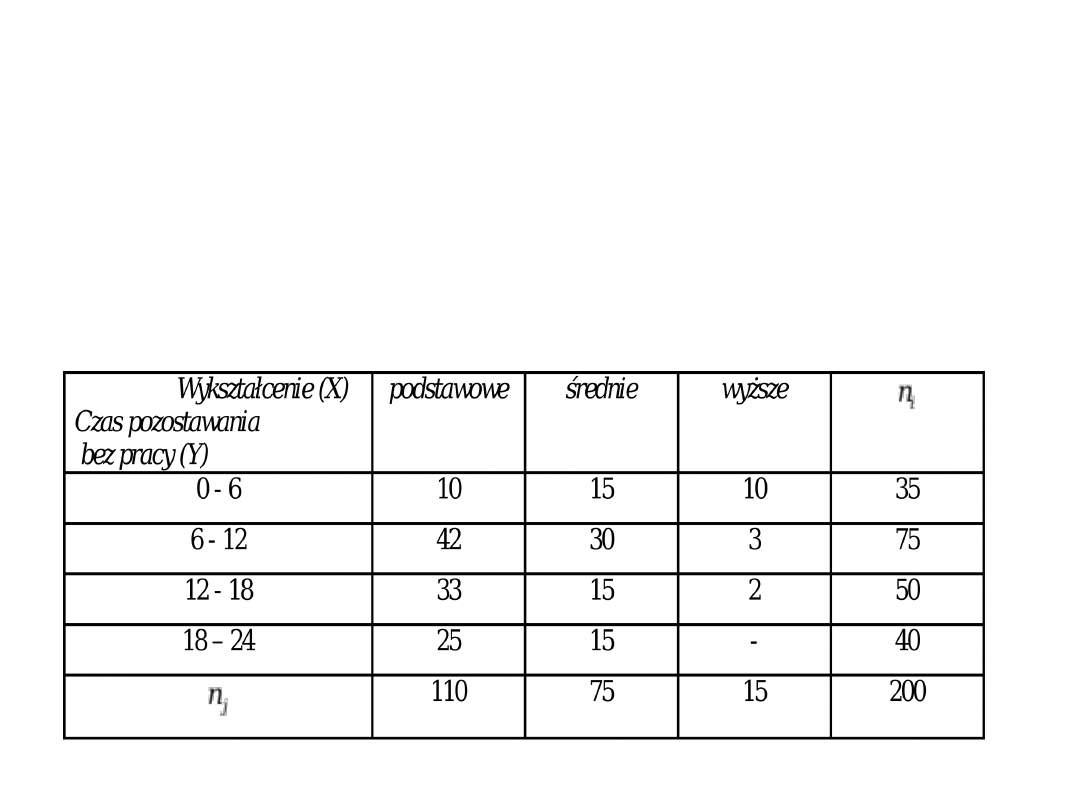
Przykład 1. Zebrano dane dotyczące czasu pozostawania 

bez pracy oraz poziomu wykształcenia badanej grupy 

bezrobotnych i ujęto je w poniższej tablicy korelacyjnej. 

Przy pomocy nieparametrycznej miary zależności 

zbadać, czy występuje zależność czasu pozostawania 

bez pracy od poziomu wykształcenia badanej grupy 

bezrobotnych

Tablica 1. Bezrobotni miasta „K” według czasu pozostawania bez 

pracy (Y – w miesiącach) oraz poziomu wykształcenia (X) – stan na 

30.06.2009 r.

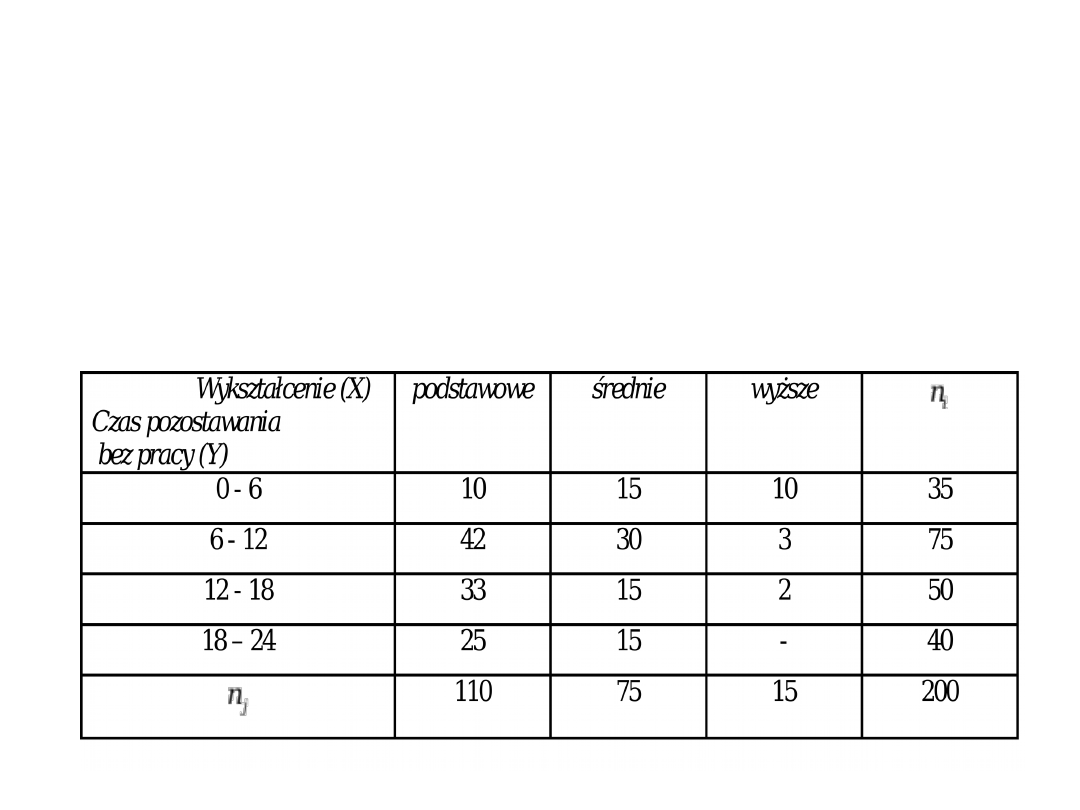
Przykład 2.  Zebrano dane dotyczące czasu 

pozostawania bez pracy oraz poziomu wykształcenia 

badanej grupy bezrobotnych i ujęto je w poniższej 

tablicy korelacyjnej. Przy pomocy parametrycznej miary 

zależności zbadać, czy występuje zależność czasu 

pozostawania bez pracy od poziomu wykształcenia 

badanej grupy bezrobotnych

Tablica 2. Bezrobotni miasta „K” według czasu pozostawania bez 

pracy (Y – w miesiącach) oraz poziomu wykształcenia (X) – stan na 

30.06.2009 r.

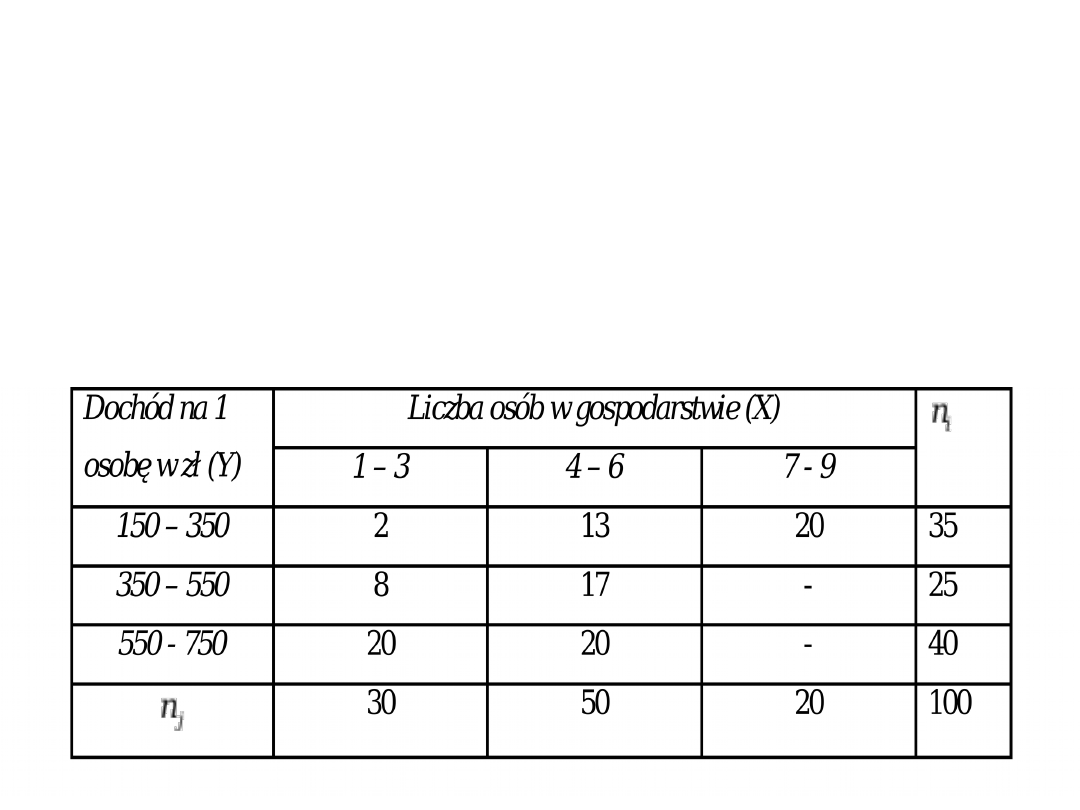
Przykład 3. W poniższej tablicy zawarto wyniki badania 

warunków materialnych losowej grupy gospodarstw domowych 

miasta „L” uwzględniające wysokość dochodów na 1 członka 

gospodarstwa domowego (Y) oraz liczbę osób w gospodarstwie 

(X). Przy pomocy parametrycznej miary zależności zbadać 

natężenie i kierunek zależności wielkości dochodów na 1 osobę 

od liczby osób w badanej grupie gospodarstw domowych

Tabela 3. Gospodarstwa domowe miasta „L” według dochodów 

na 1 osobę w zł oraz liczbę osób w gospodarstwie

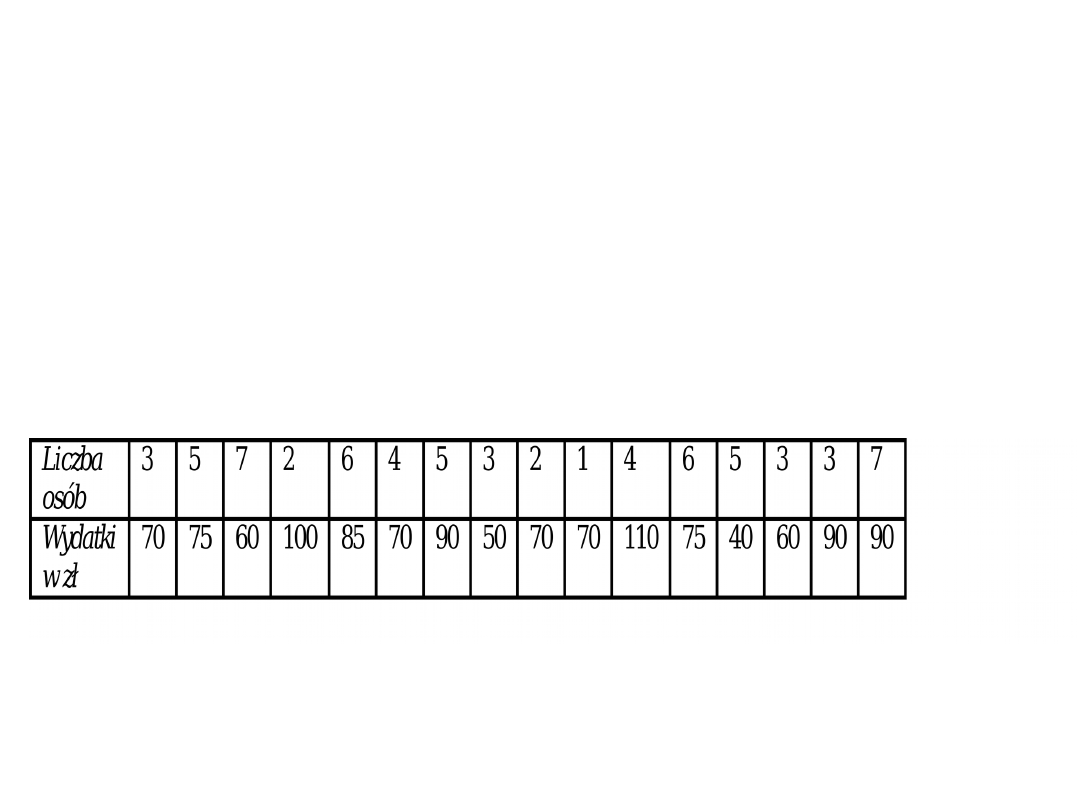
Przykład 4. Dla zbadania zależności między wielkością 

miesięcznych wydatków na cele kulturalne (Y) a liczbą 

osób w gospodarstwie domowym (X) zebrano informacje 

dla 16 wylosowanych gospodarstw gminy „Z” i  ujęto je 

w poniższej tablicy. Przy pomocy współczynnika korelacji 

liniowej Persona zbadać, czy występuje zależność 

wysokości wydatków od liczby osób w gospodarstwie 

domowym?

 

Tablica 4. Gospodarstwa domowe gminy „Z” według liczby osób oraz 

wysokości miesięcznych wydatków na cele kulturalne