WSPÓŁZALEŻNOŚĆ

WSPÓŁZALEŻNOŚĆ

ZMIENNYCH

ZMIENNYCH

MIERZALNYCH

MIERZALNYCH

WSPÓŁZALEŻNOŚĆ

WSPÓŁZALEŻNOŚĆ

ZMIENNYCH

ZMIENNYCH

MIERZALNYCH

MIERZALNYCH

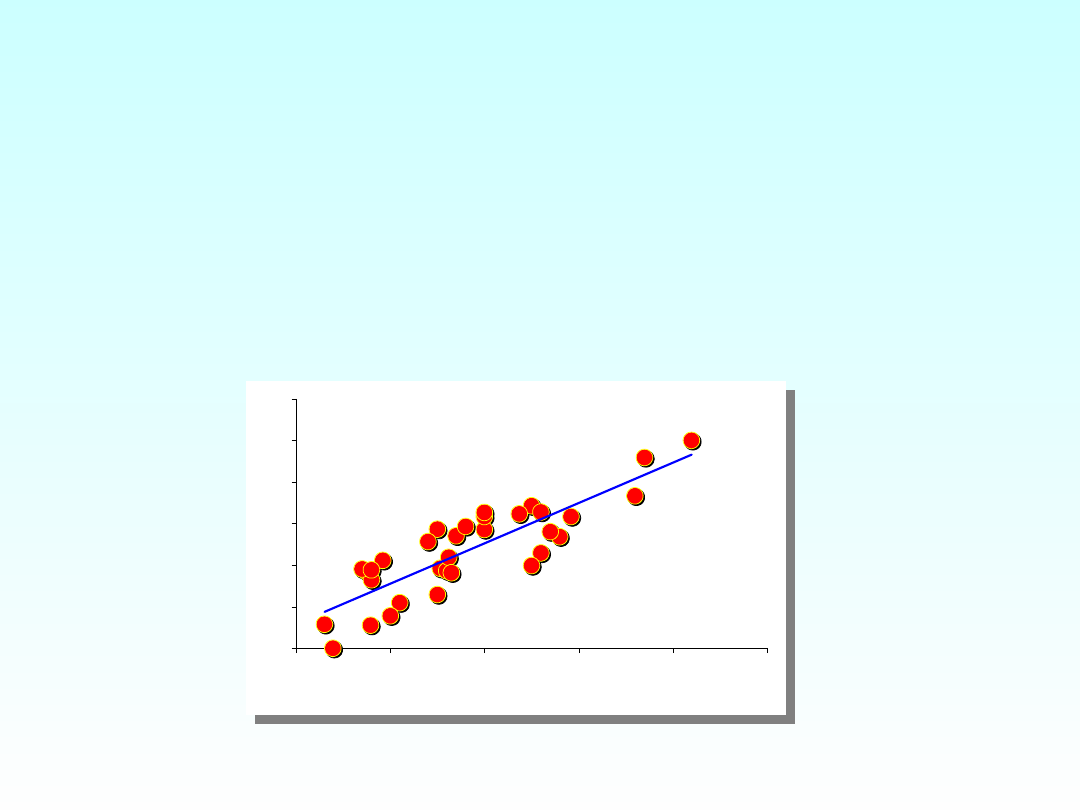
y = 0,0194x - 1,0467

R

2

= 0,729

0,0

0,2

0,4

0,6

0,8

1,0

1,2

60

70

80

90

100

110

x

y

y = 0,0194x - 1,0467

R

2

= 0,729

0,0

0,2

0,4

0,6

0,8

1,0

1,2

60

70

80

90

100

110

x

y

ZWIĄZKI MIĘDZY DWIEMA

ZWIĄZKI MIĘDZY DWIEMA

ZMIENNYMI MIERZALNYMI

ZMIENNYMI MIERZALNYMI

• Związek przyczynowy - istnieje zależność jednej

ze zmiennych od tej drugiej (masa ciała i
podnoszony ciężar maksymalny).

• Współzależność - bezpośrednia, przyczynowa

zależność obu rozpatrywanych zmiennych nie
zachodzi - obie warunkowane są przez inną
(inne) zmienne (odległość skoku w dal i czas w
biegu na 60 m).

• Źródło współzależności może być oczywiste lub

może pozostać niewyjaśnione.

PRZYKŁADY ZALEŻNOŚCI

PRZYKŁADY ZALEŻNOŚCI

• wysokość ciała 



masa ciała ,

• masa ciała





siła mięśni,

• długość podudzia





długość ramienia,

• wysokość wyskoku 



czas biegu na 60

m,

• maks. stężenie LA 



(

(





)

)

czas biegu na

400 m.

KORELACJA POZORNA

KORELACJA POZORNA

Straty wywołane
pożarem korelują z
liczbą strażaków
biorących udział w
akcji gaśniczej.

KORELACJA POZORNA

KORELACJA POZORNA

Pewnego razu w
Szwecji
stwierdzono, że
liczba urodzonych
w danej gminie
dzieci koreluje z
liczbą bocianów
zamieszkujących
gminę

WSPÓŁCZYNNIK KORELACJI

WSPÓŁCZYNNIK KORELACJI

- ILOŚCIOWA MIARA

- ILOŚCIOWA MIARA

ZALEŻNOŚCI

ZALEŻNOŚCI

• Współczynnik korelacji Pearsona:

• r

2

- współczynnik determinacji - określa,

jaka część zmienności jednej cechy jest
wyjaśniana przez drugą zmienną.

n

y

x

r

n

i

i

i







1

*

*

ZAŁOŻENIA DOTYCZĄCE

ZAŁOŻENIA DOTYCZĄCE

ZMIENNYCH

ZMIENNYCH

• Obie zmienne są ilościowe, mierzalne

(wyrażone na skali interwałowej).

• Obie zmienne mają rozkłady normalne

(w szczególności nie są to rozkłady
skośne).

• W przypadku niespełnienia założeń

stosuje się inne miary korelacji (np.
współczynnik korelacji Spearmana)

WŁASNOŚCI

WŁASNOŚCI

WSPÓŁCZYNNIKA

WSPÓŁCZYNNIKA

KORELACJI

KORELACJI

• r  <-1,1>,

• wartość bezwzględna r świadczy o sile

związku,

• ujemne wartości r oznaczają zależność

malejącą - „im więcej tym mniej”,

• dodatnie wartości r oznaczają zależność

rosnącą - „im więcej tym więcej”,

• liniowe przekształcenie zmiennych nie

zmienia korelacji między nimi.

• Współczynnik korelacji jest przemienny:

r(x,y)=r(y,x)

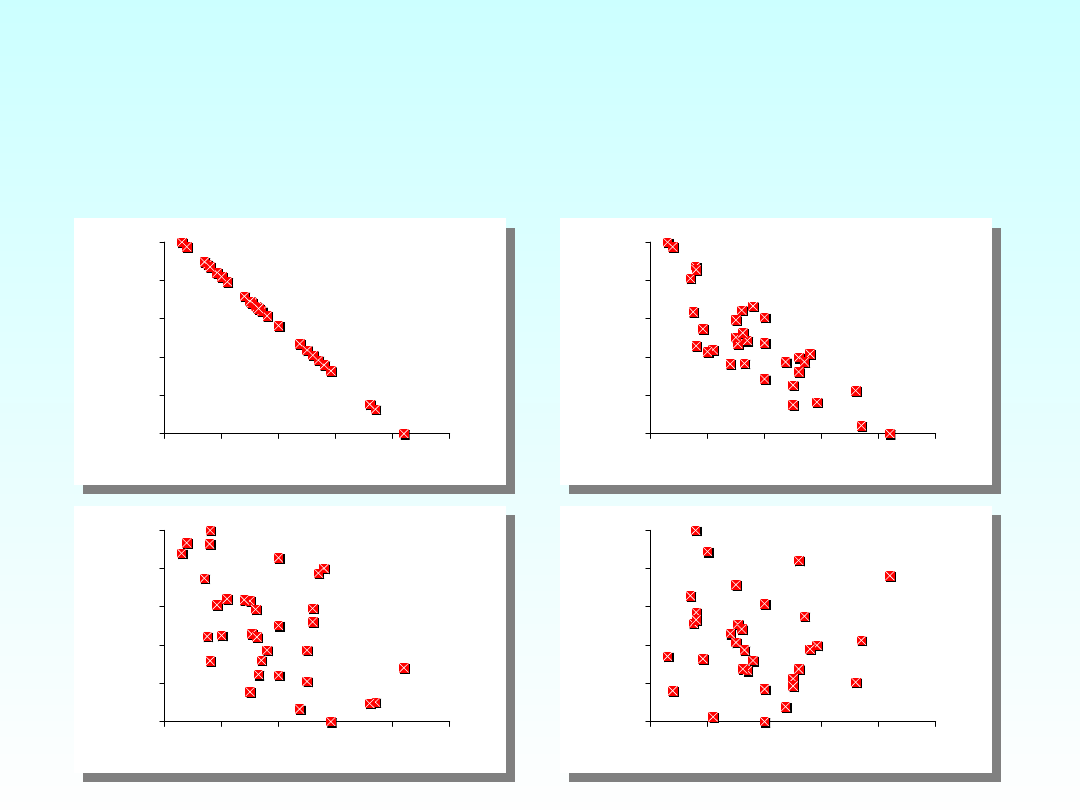
RÓŻNE ZALEŻNOŚCI

RÓŻNE ZALEŻNOŚCI

KORELACYJNE (r<=0)

KORELACYJNE (r<=0)

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = -1

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = -1

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = -0,8

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = -0,8

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = -0,5

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = -0,5

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 0

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 0

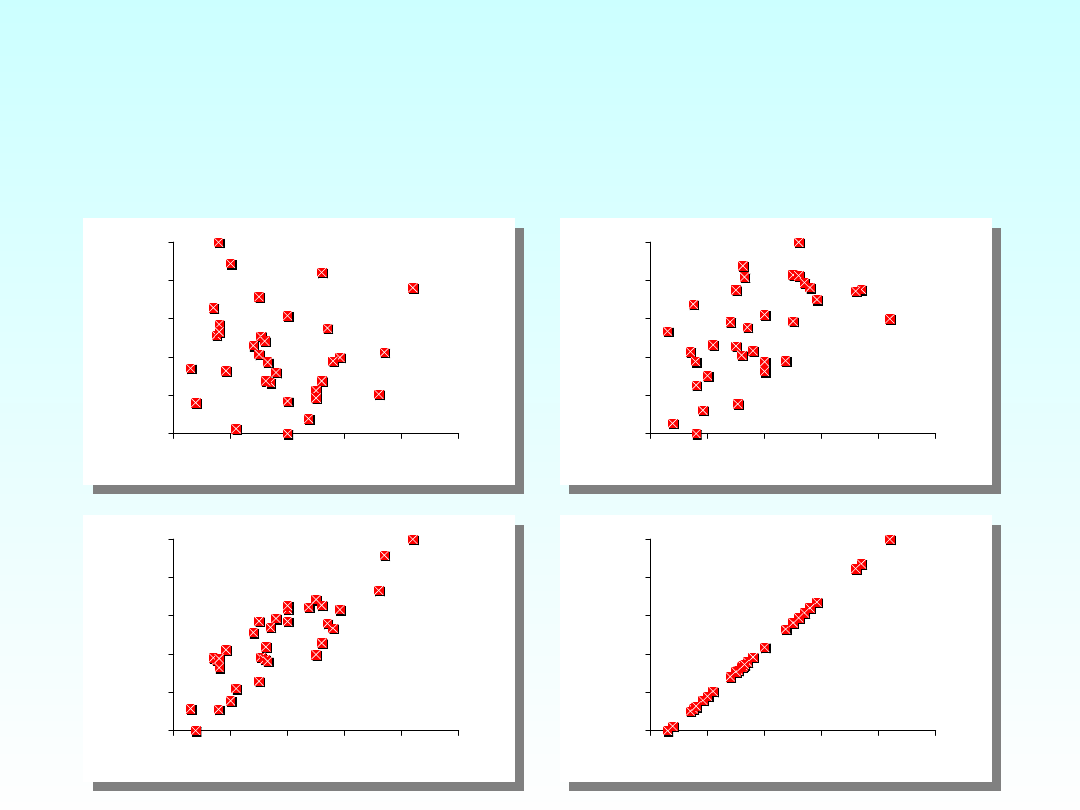
RÓŻNE ZALEŻNOŚCI

RÓŻNE ZALEŻNOŚCI

KORELACYJNE (r>=0)

KORELACYJNE (r>=0)

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 0

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 0

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 0,5

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 0,5

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 0,8

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 0,8

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 1

0,0

0,2

0,4

0,6

0,8

1,0

60

70

80

90

100

110

x

y

r = 1

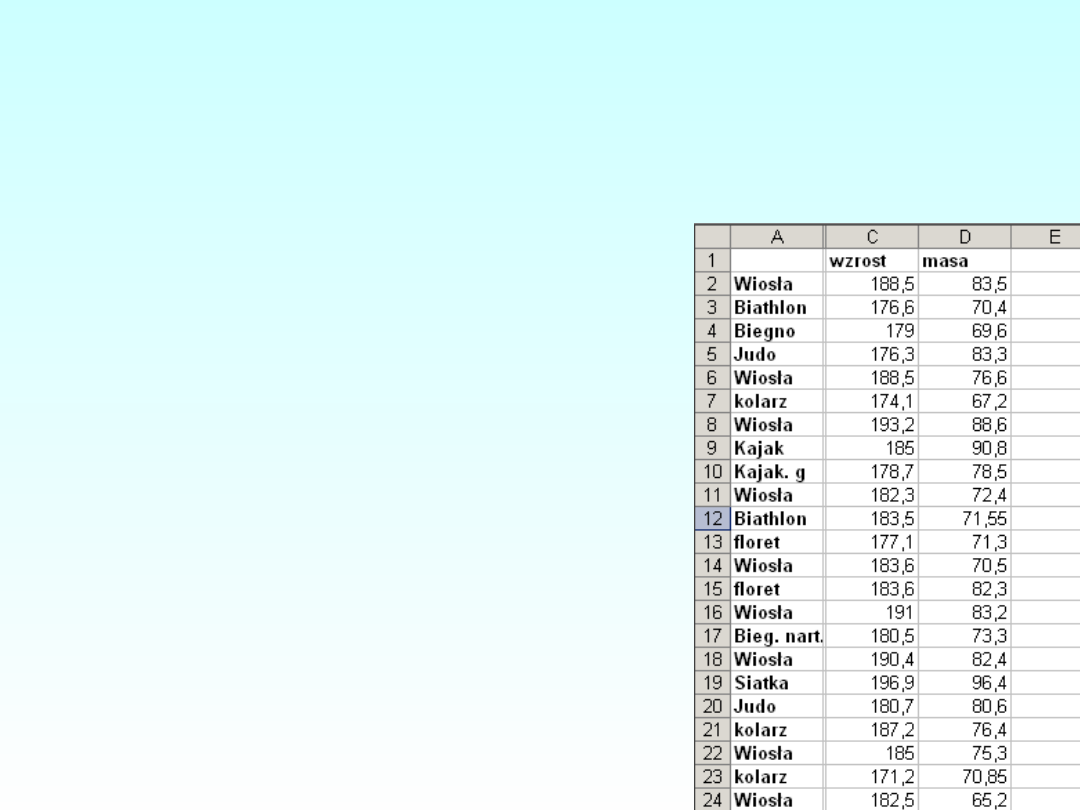
OBLICZANIE

OBLICZANIE

WSPÓŁCZYNNIKA

WSPÓŁCZYNNIKA

KORELACJI W EXCELU

KORELACJI W EXCELU

=wsp.korelacji(

C2:C24

;

D2:D24

)
Oba obszary muszą mieć ten sam

rozmiar!

Z uwagi na przemienność tę samą

zależność można uzyskać

zamieniając obszary:

=wsp.korelacji(

D2:D24

;

C2:C24

)

TESTOWANIE ISTOTNOŚCI

TESTOWANIE ISTOTNOŚCI

WSPÓŁCZYNNIKA

WSPÓŁCZYNNIKA

KORELACJI

KORELACJI

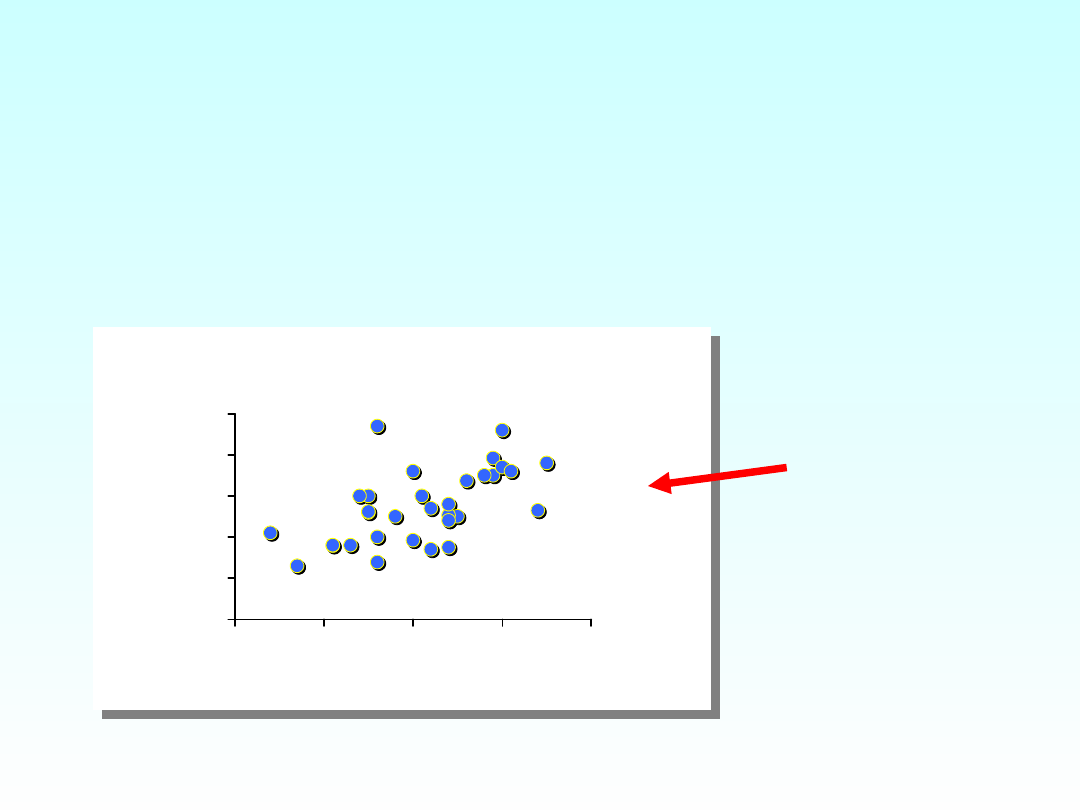
• W przypadku danych uzyskanych z

próbki szczególnie ważne jest
stwierdzenie, czy obserwowane
ułożenie punktów jest wyrazem
rzeczywistej tendencji właściwej
populacji, czy powstało w wyniku
przypadkowego charakteru próby.

H

H

0

0

: związek między dwiema

: związek między dwiema

zmiennymi mierzalnymi nie

zmiennymi mierzalnymi nie

zachodzi - rzeczywista

zachodzi - rzeczywista

wartość współczynnika

wartość współczynnika

korelacji dla populacji

korelacji dla populacji

wynosi r = 0.

wynosi r = 0.

Związek masy ciała z wysokością

50

60

70

80

90

100

160

170

180

190

200

Wysokość [cm]

M

a

sa

[

k

g

]

Związek masy ciała z wysokością

50

60

70

80

90

100

160

170

180

190

200

Wysokość [cm]

M

a

sa

[

k

g

]

Czy to może

Czy to może

być

być

przypadkow

przypadkow

e ułożenie?

e ułożenie?

• Formułujemy H

o

, dobieramy 



,

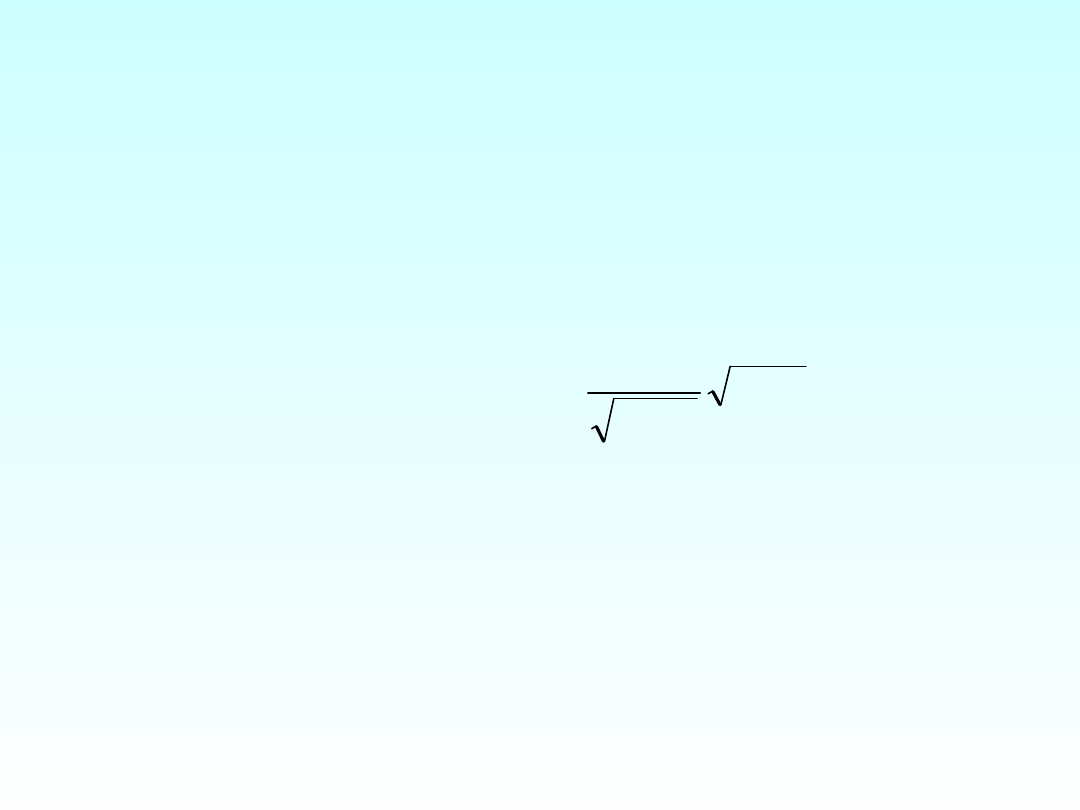
• obliczamy t - Studenta:

n - liczebność, r - wsp. korelacji;

• odnajdujemy krytyczną wartość t

k

dla f = n-2 i 



,

• jeżeli |t |>t

k

to p<



i odrzucamy H

0

,

w przeciwnym przypadku p>=



i nie odrzucamy H

0

.

TESTOWANIE ISTOTNOŚCI

TESTOWANIE ISTOTNOŚCI

WSPÓŁCZYNNIKA

WSPÓŁCZYNNIKA

KORELACJI - kolejność

KORELACJI - kolejność

czynności

czynności

2

1

2







n

r

r

t

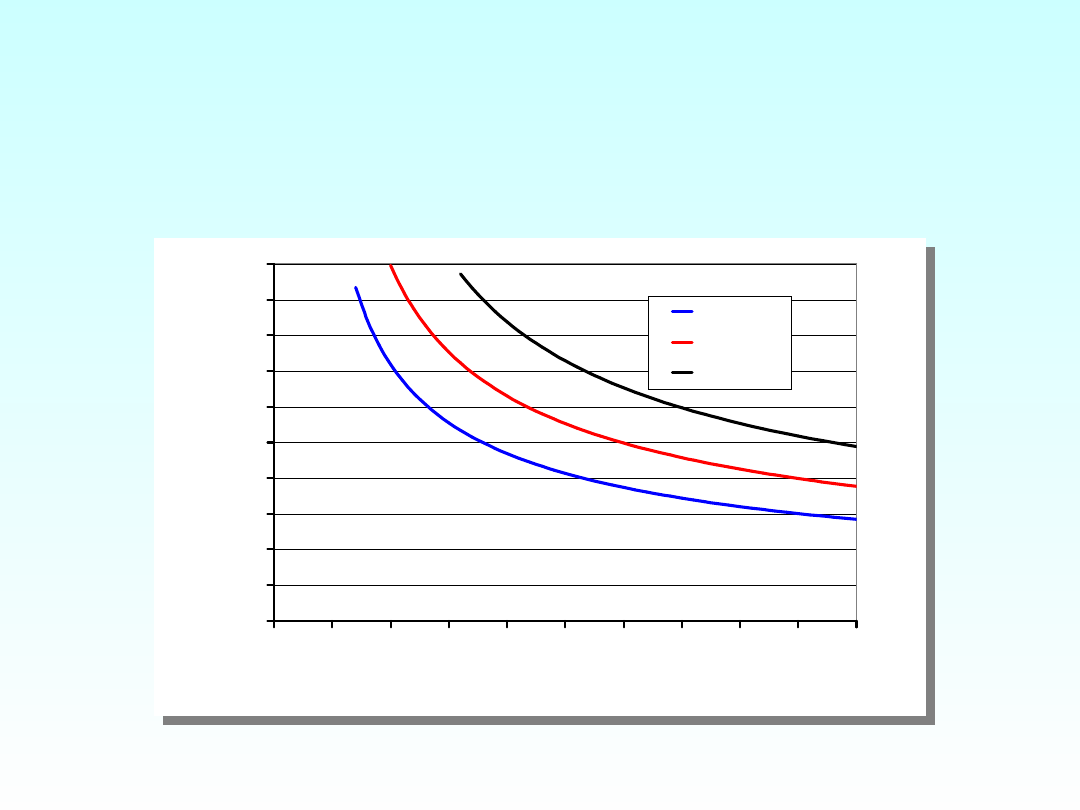
ISTOTNOŚĆ WSP.

ISTOTNOŚĆ WSP.

KORELACJI

KORELACJI

A LICZEBNOŚĆ PRÓBY

A LICZEBNOŚĆ PRÓBY

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0

5

10

15

20

25

30

35

40

45

50

liczebność [-]

w

sp

ó

łc

zy

n

n

ik

k

o

re

la

c

ji

[

-]

p<0,05
p<0,01
p<0,001

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0

5

10

15

20

25

30

35

40

45

50

liczebność [-]

w

sp

ó

łc

zy

n

n

ik

k

o

re

la

c

ji

[

-]

p<0,05
p<0,01
p<0,001

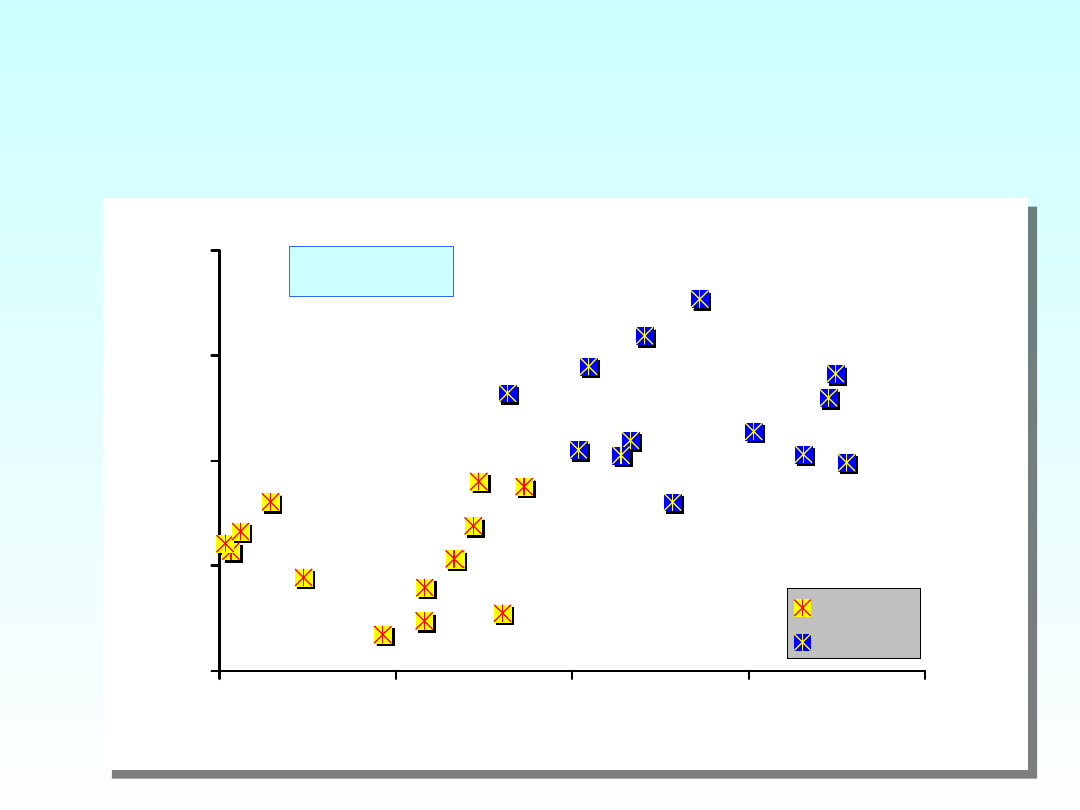
NIEJEDNORODNOŚĆ

NIEJEDNORODNOŚĆ

GRUPY A WSP.

GRUPY A WSP.

KORELACJI

KORELACJI

0,0

0,5

1,0

1,5

2,0

0

0,5

1

1,5

2

Cecha X

C

ec

ha

Y

Grupa A
Grupa B

r

1

= 0,033

r

2

= 0,082

r

1+2

= 0,652

0,0

0,5

1,0

1,5

2,0

0

0,5

1

1,5

2

Cecha X

C

ec

ha

Y

Grupa A
Grupa B

r

1

= 0,033

r

2

= 0,082

r

1+2

= 0,652

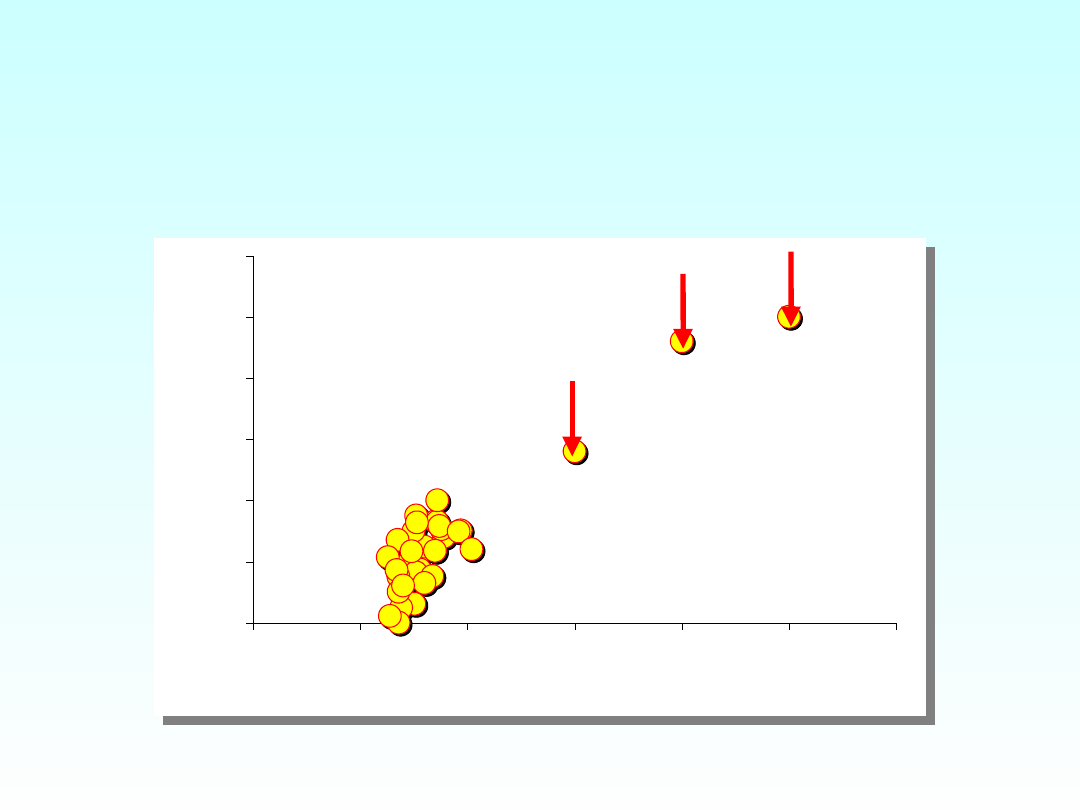
SKOŚNOŚĆ ROZKŁADU

SKOŚNOŚĆ ROZKŁADU

A WSP. KORELACJI

A WSP. KORELACJI

0

0,5

1

1,5

2

2,5

3

0

50

100

150

200

250

300

x

y

r = 0,57

r = 0,92

bez odstających punktów

z odstającymi punktami

0

0,5

1

1,5

2

2,5

3

0

50

100

150

200

250

300

x

y

r = 0,57

r = 0,92

bez odstających punktów

z odstającymi punktami

WSPÓŁCZYNNIK KORELACJI

WSPÓŁCZYNNIK KORELACJI

SPEARMANA

SPEARMANA

)

1

(

)]

(

)

(

[

6

1

2

1

2















n

n

y

d

x

d

r

n

i

i

i

s

Gdzie:
n - liczebność próbki,

d(x

i

), d(y

i

) – rangi wartości x

i

i y

i

OBLICZANIE KORELACJI

OBLICZANIE KORELACJI

SPEARMANA W EXCELU

SPEARMANA W EXCELU

60

65

70

75

80

85

90

95

100

165

170

175

180

185

190

195

200

Wzrost [cm]

M

as

a

[k

g]

60

65

70

75

80

85

90

95

100

165

170

175

180

185

190

195

200

Wzrost [cm]

M

as

a

[k

g]

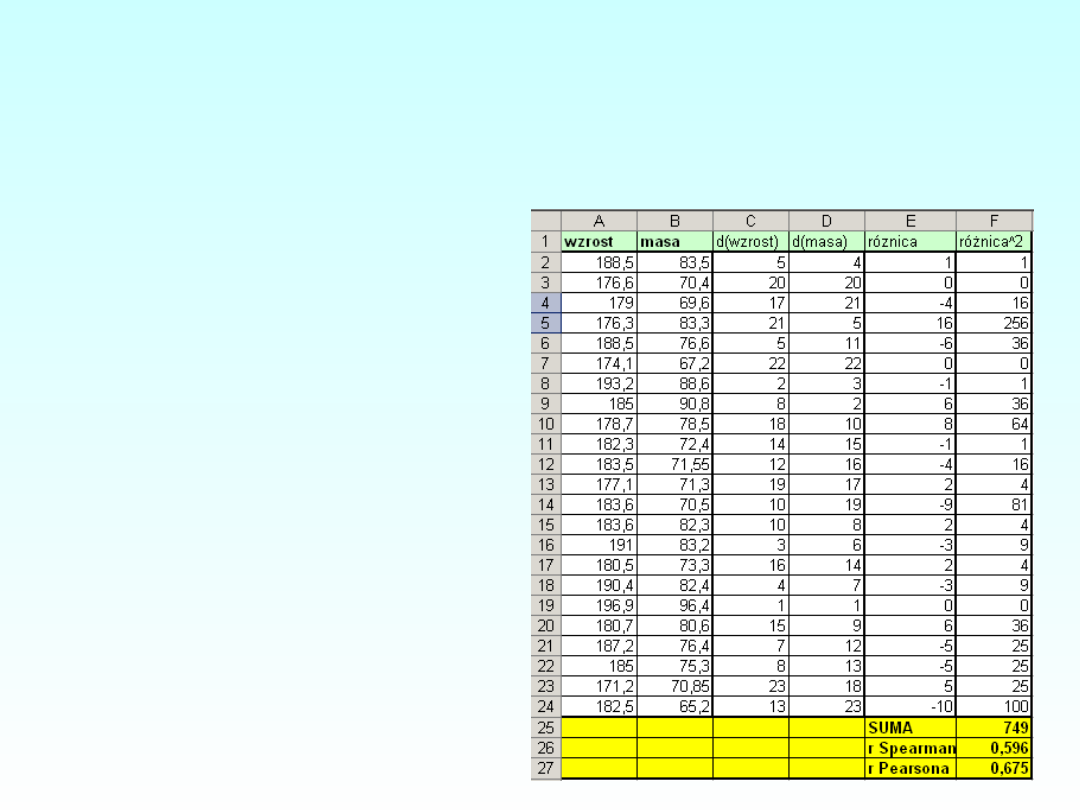
OBLICZANIE RANG W

OBLICZANIE RANG W

EXCELU

EXCELU

=pozycja(

A2

;

A2:A24

;0)

Szukamy rangi

A2

w

zbiorze liczb

A2:A24

.

0 oznacza, że
kolejność rangowania
będzie malejąca (im
większa wartość, tym
większa ranga)