Równowaga chemiczna

1. Reakcje w układach jednofazowych
2. Obliczanie liczby moli i stężeń reagentow z uwzględnieniem przebiegu reakcji chemicznej
3. Reakcje w układach heterofazowych – przykłady obliczeń.

Reakcje chemiczne mogą biec aż do całkowitego zużycia substratow, lub też osiagać stan, w 

którym substraty współistnieją z produktami. Przykładami reakcji, w których zużycie substratów jest 
całkowite   są   eksplozje   materiałow   wybuchowych   lub   reakcje   denaturacji   białek   -   zachodzą   one 
nieodwracalnie   i   nie   ma   możliwości   ponownego   odzyskania   substratow.   Jeżeli   jednak   istnieje 
możliwość   przemiany   substratów   w   produkty   i   odwrotnie   -   produktow   w   substraty,   to   nawet   po 
dłuższym czasie prowadzenia reakcji układ może zawierać znaczne ilości substratow. Takie zachowanie 
układu wynika z ustalenia się stanu rownowagi, w którym stopień przereagowania substratow nie jest 
całkowity, ale zatrzymuje się na pewnej wartości, w miejscu określonym przez tzw. stałą rownowagi.  
Przykładem  reakcji  równowagowych   mogą  być   reakcje  estryfikacji,  w   których  z   alkoholu  i  kwasu 
otrzymujemy ester i wodę. Reakcją odwrotną w tym przypadku jest hydroliza estru z powrotem do 
kwasu i alkoholu.

1.

Reakcje w układach jednofazowych (reakcje homogeniczne)

1.1. Wszystkie substancje (substraty i produkty) znajdują się w jednej fazie, np. wszystkie są gazami lub 
wszystkie tworzą jednorodną fazę ciekłą. W stanie równowagi stężenia substancji nie zmieniają się w 
czasie ponieważ szybkość powstawania produktów jest równa szybkości ich zużywania w procesie 
odwrotnym . Osiągnięcie stanu równowagi nie oznacza więc, że ustały wszelkie reakcje chemiczne, 
oznacza jednak że szybkości obu reakcji (powstawania produktów i ich przekształcania w substraty) są 
sobie równe.
 Przykład: reakcja otrzymywania octanu etylu z alkoholu etylowego i kwasu octowego (r.estryfikacji).

C

2

H

5

OH + CH

3

COOH 

→ CH

3

COOC

2

H

5

 

+ H

2

O

Załóżmy, że początkowo zmieszano ze sobą tylko kwas octowy i etanol. Na podstawie ogólnej teorii 
kinetyki chemicznej możemy założyć, że szybkość powstawania octanu etylu i wody (szybkość 
estryfikacji - v

e

) będzie proporcjonalna do iloczynu stężeń molowych substratow – alkoholu i kwasu:

v

e 

= k

e

[C

2

H

5

OH][CH

3

COOH]

Wspołczynnik k

e 

nazywany jest stałą szybkości reakcji. 

Z kolei szybkość reakcji odwrotnej – reakcji hydrolizy estru (szybkość hydrolizy – v

h 

) będzie 

zależna od stężeń octanu etylu i wody:

v

h 

= k

h

[CH

3

COOC

2

H

5

][H

2

O]

Na początku szybkość reakcji estryfikacji, v

e,  

ma dużą wartość, bo stężenia substratow są duże, zaś 

szybkość reakcji hydrolizy, v

h, 

 jest mała, gdyż ww wczesnych etapach reakcji stężenia produktow są 

bliskie zeru. Z upływem czasu osiągany jest stan, w którym w jednostce czasu powstaje dokładnie tyle
samo moli estru, ile rozkłada się do alkoholu i kwasu. Wowczas stężenia składników mieszaniny 
reakcyjnej nie zmieniają się już w czasie. Mówimy wówczas, że osiągnięty został stan równowagi 
dynamicznej. 

Z warunku na jednakową szybkość reakcji w obie strony (v

e 

= v

h

) otrzymujemy:

k

e

[C

2

H

5

OH][CH

3

COOH] = k

h

[CH

3

COOC

2

H

5

][H

2

O]

czyli:

K

c

=

k

e

k

h

=

[

CH

3

COOC

2

H

5

]∗[

H

2

O]

[

CH

3

COOH ]∗[C

2

H

5

OH ]

Iloraz stałych szybkości k

e

/k

h 

oznaczony K

c

  nazywamy stężeniową stałą rownowagi.

Wartość stałej równowagi dla danej reakcji obliczonej z powyższego równania jest zależna jedynie od 
temperatury (dla gazow rownież od ciśnienia i objętości). Zależność stałej równowagi od temperatury 
wynika z wpływu temperatury na stałe szybkości reakcji k

e 

i k

h 

(jakościowo wpływ temperatury na 

szybkość reakcji chemicznych opisuje reguła van't Hoffa, a ilościowo równanie Arrheniusa).

 Uogólnieniem podanej wyżej zależności jest jest prawo działania mas, sformułowane przez 

Guldberga i Waagego:

W danej temperaturze w stanie równowagi iloczyn ułamków molowych produktów reakcji

podniesionych do odpowiednich potęg podzielony przez iloczyn ułamków molowych substratów
podniesionych do odpowiednich potęg ma wartość stałą.

Wykładnikami potęgowymi w prawie działania mas są wspołczynniki występujące w 

zbilansowanym rownaniu reakcji chemicznej.
 Zatem dla reakcji danej równaniem: aA + bB 

↔ cC + dD

wyrażenie na stałą rownowagi K

X  

będzie miało postać:

K

x

=

x

C

c

∗

x

D

d

x

A

a

∗

x

B

b

Tak zdefiniowana stała rownowagi zdefiniowana dobrze opisuje układy znajdujące się w stałej 
temperaturze oraz przy stałym całkowitym ciśnieniu gazow (jeśli faza gazowa nie jest obecna, to 
ciśnienie nie ma dużego wpływu na wartość stałej). Przyjmując, że dla niezbyt stężonych roztworów  
ułamek molowy jest proporcjonalny do stężenia molowego możemy w wyrażeniu na stałą K

x

 zastąpić 

ułamki molowe równowagowymi stężeniami molowymi reagentów. Otrzymujemy wówczas wyrażenie 
na stężeniową stałą równowagi K

c

 (nawiasy kwadratowe oznaczają stężenie molowe reagenta):

K

c

=

[

C ]

c

∗[

D]

d

[

A]

a

∗[

B]

b

Stała   stężeniowa   obowiązuje   wyłącznie   dla   układow   spełniających   warunek   stałości   temperatury, 
ciśnienia   i   objętości   układu.   Jest   ona   najczęściej   stosowana   do   opisu   równowag   zachodzących   w 
rozcieńczonych roztworach wodnych, co przy nieznacznej zmianie gęstości, a tym samym i objętości 
mieszaniny   reakcyjnej   powoduje,   że   stężenia   molowe   dla   takiej   mieszany   są   dość   dobrym 
przybliżeniem ułamkow molowych, a tak otrzymana stała stężeniowa K

c 

jest w przybliżeniu 

równa K

x

.

Przez podstawienie ciśnień cząstkowych p

x 

w miejsce stężeń, uzyskujemy ciśnieniową stałą 

rownowagi K

p

, ktora zależy tylko od temperatury i rodzaju układu:

K

p

=

p

C

c

∗

p

D

d

p

A

a

∗

p

B

b

Reakcje   przebiegające   w   fazie   gazowej   można   opisywać   stałymi   ciśnieniowymi   lub 

stężeniowymi, ktorych wartości zazwyczaj się różnią. W razie potrzeby stałe te można między soba 
wzajemnie   przeliczać   w   oparciu   o   stechiometrię   zbilansowanej   reakcji   chemicznej   oraz   równanie 
Clapeyrona. Ze stechiometrii reakcji wyznacza się różnicę liczby moli produktów i substratów reakcji 
Δn. Przykładowo dla reakcji:

aA +bB → cC + dD 
Δn = (c + d) – (a + b)

Następnie, po podstawieniu  p

i 

= n

i

RT/V = (n

i

/V)RT = c

i

RT w wyrażeniu na ciśnieniową stałą 

równowagi K

p

 otrzymujemy:

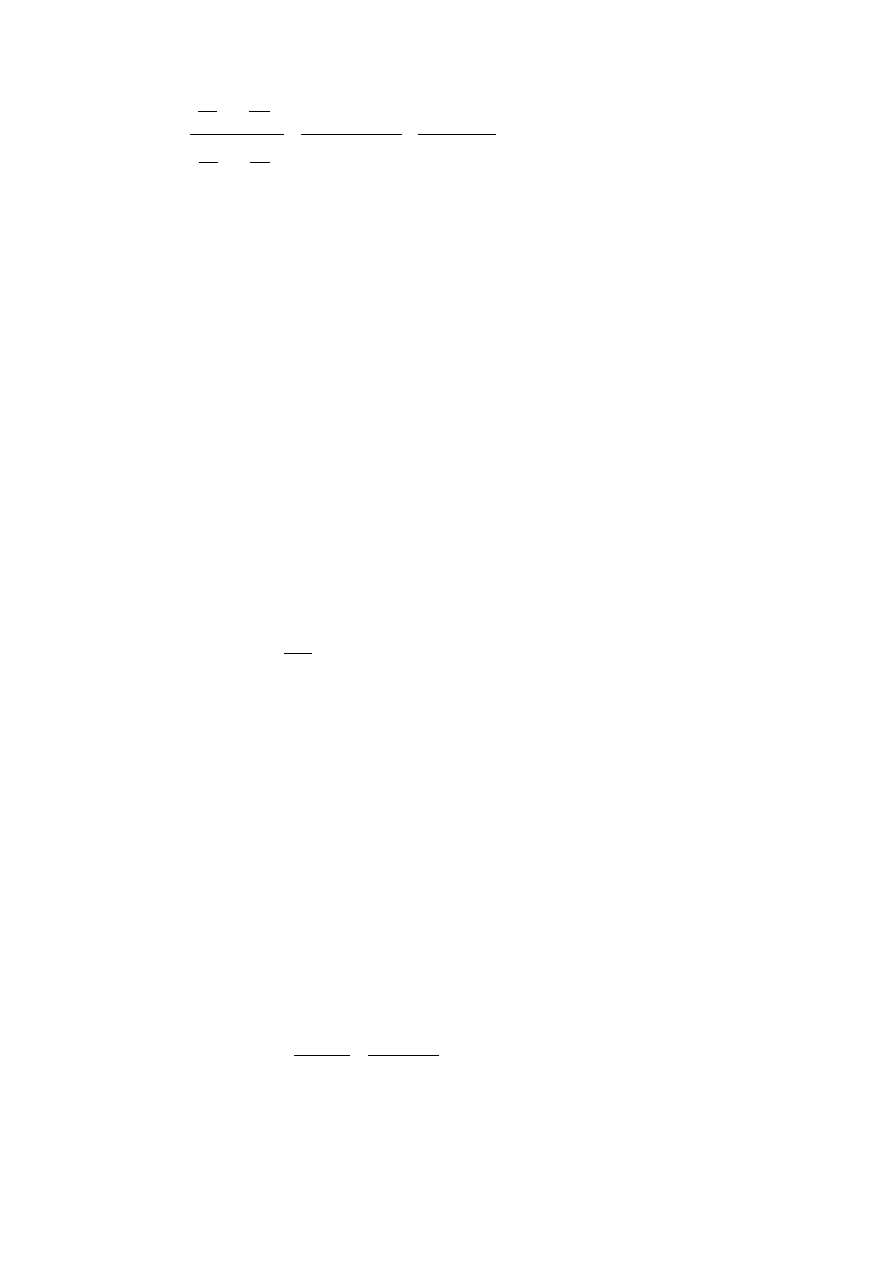
K

p

=

(

n

C

V

)

c

∗(

n

D

V

)

d

(

n

A

V

)

a

∗(

n

B

V

)

b

−

(

RT )

c

∗(

RT )

d

(

RT )

a

∗(

RT )

b

=

[

C ]

c

∗[

D]

d

[

A]

a

∗[

B]

b

−(

RT )

Δ

n

=

K

c

∗(

RT )

Δ

n

Otrzymuje się w ten sposób wyrażenie pozwalające na wzajemne przeliczanie stałych
stężeniowych: 

K

p

=

K

c

∗(

RT )

Δ

n

Dla reakcji, w których sumy moli reagentów są stałe (liczby moli substratów są równe liczbie 

moli produktów)   

Δn  = 0, przy założeniu że pomijamy aktywności bądź lotności reagentów, można 

przyjąć, że odpowiednie stałe równowagi są sobie równe, czyli: K

x

 = K

c

 = K

p

. 

Ponadto   w   tych   przypadkach   do   obliczenia   stałej  równowagi   zamiast   ułamków  molowych,  ciśnień 
cząstkowych lub stężeń, można użyć liczby moli reagentow w stanie rownowagi.

W razie potrzeby jakościowego określenia kierunku przebiegu reakcji chemicznej przy znanych 

początkowych   „ilościach”   wszystkich   reagentow   (wyrażonych   w   molach,   jednostkach   stężenia 
molowego, ułamkach molowych) lub po zaburzeniu stanu równowagi w układzie przez dodanie (lub  
usunięcie)   jednego   lub   więcej   reagentow   wykorzystuje   się   zwykle   tzw.   ilorazu   reakcyjnego   Q, 
analogicznego   do   wyrażenia   na   stałą   rownowagi,   z   tym,   że   ilości   reagentów   dotyczą   określonego 
momentu reakcji i porównuje się wartość Q z wartością odpowiedniej stałej równowagi.
 

Zatem jeśli Q > K to mamy nadmiar produktow reakcji, czyli reakcja będzie przebiegała w lewo, 

natomiast jeśli Q < K to mamy nadmiar substratow, czyli reakcja będzie przebiegała w prawo. 
Ten  sam efekt  uzyskamy  obliczając   tzw.  postęp   reakcji  chemicznej  x,  kierunek przebiegu  reakcji 
wynika wówczas ze znaku postępu reakcji.

Postęp reakcji chemicznej x jest równy stosunkowi zmiany (przyrostu lub ubytku) liczby moli 

danego reagenta n

i  

do jego współczynnika stechiometrycznego  v

i 

w zbilansowanym równaniu reakcji 

przedstawionej zapisem standardowym.

x=

Δ

n

i

v

i

  Jednostką   postępu   reakcji   jest   mol.   W   procesie,   w   którym   przybywa   substratów,   a   maleje   ilość 
produktów, postęp reakcji ma znak ujemny. 

Liczba   moli  

n

i

 

dowolnego   reagenta,  po   zajściu   reakcji   chemicznej   w   stopniu   określonym 

postępem x jest określona zależnością:

n

i

=

n

i

o

+

x v

i

2. Przykłady obliczeń w reakcjach homogenicznych:

Przykład 1. 
W naczyniu o pojemności 2 dm

3

 

umieszczono po 0,02 mola N

2

O

4 

i NO

2

. Czy należy oczekiwać 

dysocjacji N

2

O

4 

czy asocjacji NO

2

, jeżeli stała K

c 

dla reakcji 

N

2

O

4

(g)  

↔ 2NO

2

(g)

wynosi dla tych warunkow 4,6?

Rozwiązanie.  Obliczamy iloraz reakcyjny Q i porównujemy go z podaną stałą K

c

.

Wyrażenie na stałą równowagi dla podanej reakcji jest następujące: 

K

c

=

[

NO

2

]

2

[

N

2

O

4

]

=

(

n

NO

2

/

V )

2

n

N

2

O

4

/

V

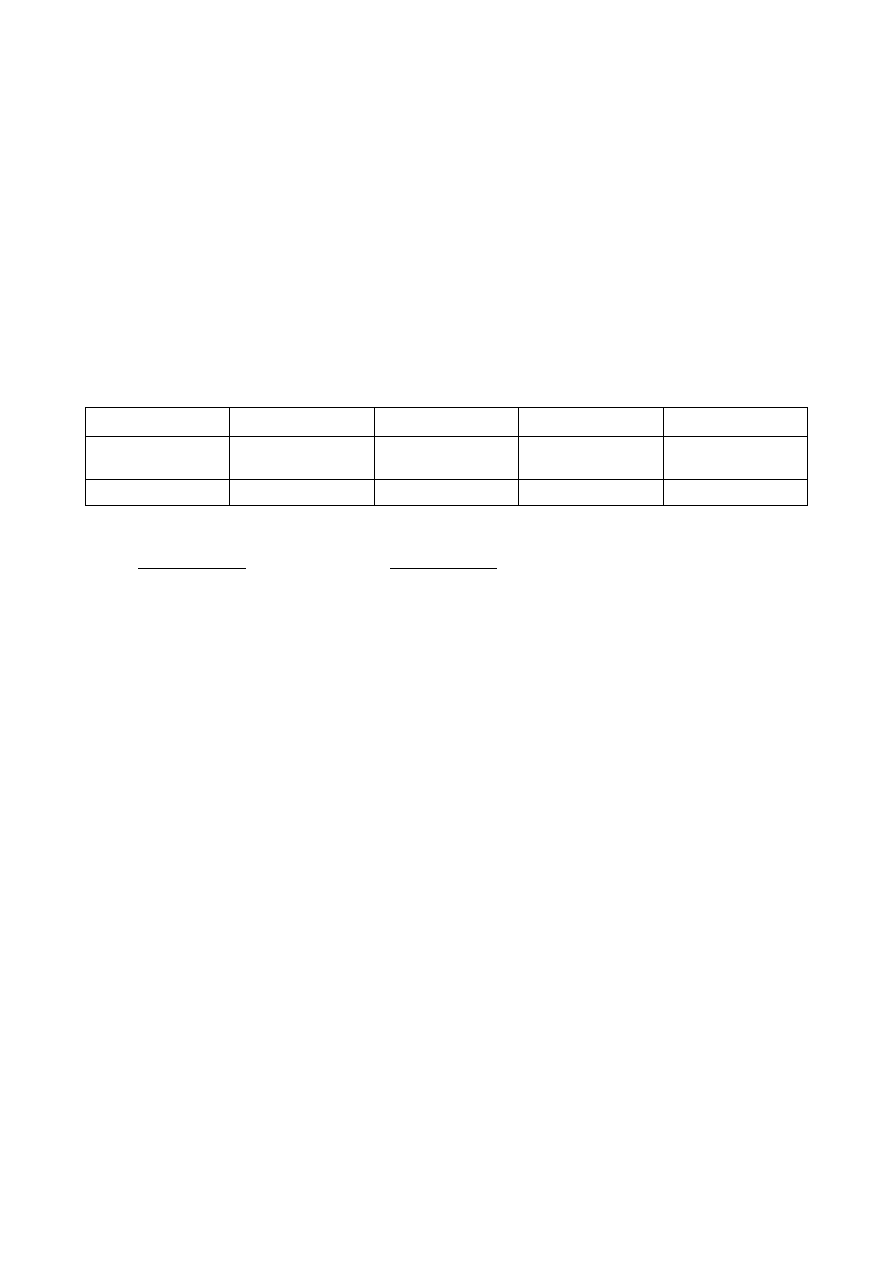
Wykorzystując dane z zadania i stechiometrię reakcji obliczamy stężenia reagentów  i iloraz reakcyjny:

[N

2

O

4

] = [NO

2

] = 0,02 mol / 2dm

3

 

= 0,01 mol/dm

3

Q = (0,01)

2

/(0,01) = 0,01 

Z   uwagi  na  to,  że   Q  <  K,  to  dla   osiągnięcia  równowagi  należy zwiększyć   stężenie  NO

2

  (licznik) 

wówczas zmniejszy się stężenie N

2

O

4 

(mianownik). Reakcja będzie biec w prawo w i powstanie więcej 

produktu czyli

, 

czyli nastąpi dysocjacja części N

2

O

4

 do NO

2

.

Przykład 2.

Zmieszano   5,0   moli   etanolu   z   8,0   mola   kwasu   octowego.   Jakie   będą   liczby   moli   poszczególnych 
reagentow w stanie rownowagi jeżeli stała stężeniowa reakcji estryfikacji K

C

=4,0?

Rozwiązanie:
CH

3

COOH(c) + C

2

H

5

OH(c) = CH

3

COOC

2

H

5

(c) + H

2

O(c)

Bilans moli – zakładamy, że powstanie x moli produktu:

Równanie reakcji

CH

3

COOH

 C

2

H

5

OH

CH

3

COOC

2

H

5

H

2

O

Początkowa liczba 
moli

8

5

0

0

Liczba moli po reakcji

8-x

5-x

x

x

Korzystając z wyrażenia na stałą równowagi reakcji estryfikacji mamy:

 

K

c

=

x

2

(

8−x )∗(5−x )

, czyli

4=

x

2

(

8− x)∗(5− x)

rozwiązujemy równanie kwadratowei obliczamy wartość x = 4. 
W stanie równowagi będzie więc po 4 mole octanu etylu i wody. Ilości kwasu octowego i etanolu
obliczamy z bilansu:

(8-x) = 4,0 mole CH

3

COOH i (5-x) = 1 mol etanolu.

Przykład 3.

Określ postęp reakcji estryfikacji kwasu mrówkowego metanolem, jeśli: a) w reakcji powstało 0,1 mola  
mrówczanu metylu; b) w reakcji ubyło 0,2 mola mrówczanu metylu.

Rozwiązanie. Zapis reakcji estryfikacji:

HCOOH + CH

3

OH 

↔ HCOOCH

3 

+ H

2

O

a) Jeżeli w reakcji kwasu mrówkowego z metanolem powstało 0,1 mola estru i współczynnik 
stechiometryczny przy mrowczanie metylu jest 1 (ubyło jednocześnie po tyle samo moli kwasu i
metanolu) to postęp reakcji wynosi:

 

x

i

 

= 

n

i

 /v 

= 0,1/1 = 0,1 mola

b) Jeżeli w reakcji kwasu HCOOH z metanolem ubyło 0,2 mola estru (przybyło jednocześnie po tyle 
samo moli kwasu i metanolu) to postęp reakcji wynosi:

 

x

i

 

= 

n

i

 /v 

= -0,2/1 = -0,2 mola 

Odpowiedź. Postęp reakcji estryfikacji wynosi: a) 0,1 mola; b) –0,2 mola

Przykład 4.
Oblicz postęp reakcji oraz liczbę moli wszystkich reagentow na podstawie reakcji syntezy amoniaku 

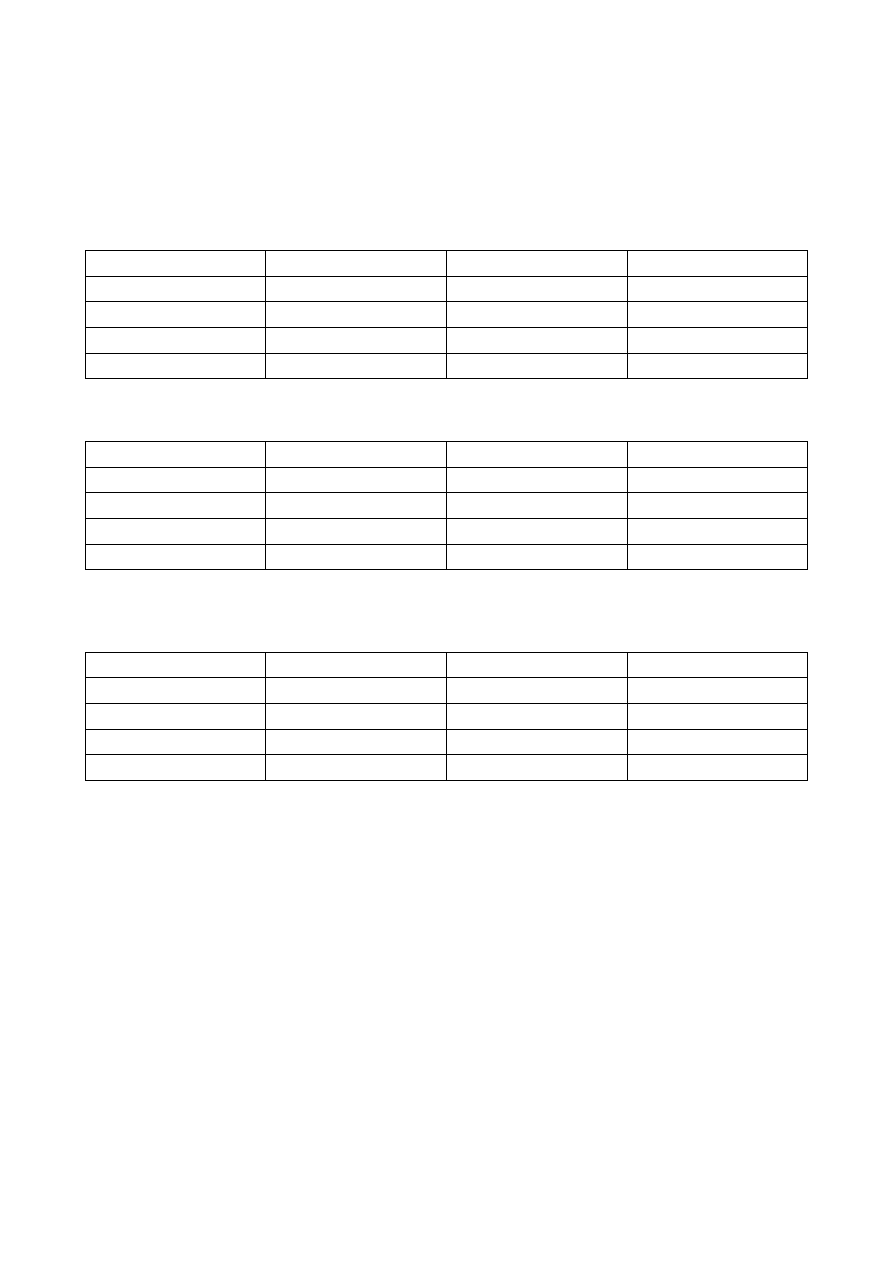
opisanej równaniem: 3H

2

 +

 N

2

 

= 2NH

3

 

oraz zawartość wszystkich reagentów w mieszaninie 

poreakcyjnej, jeżeli dla trzech oddzielnych eksperymentow w mieszaninie po reakcji stwierdzono 
obecność: a) 1,5 mola NH

3

; b) 0,7 mola NH

3

  

oraz c) 2 moli H

2

, a mieszanina początkowa zawierała po 

1,00 molu wszystkich gazow: H

2

, N

2

 

oraz NH

3

.

Rozwiązanie:

a) 

z bilansu amoniaku NH

3 

mamy: 1,50 = 1,0 + x・2 czyli 

 

x = 0,250

Równanie reakcji

3 H

2

+ N

2

2NH

3

Stan początkowy 

1 mol

1mol

1 mol

zmiana

-3x

-x

+2x

równowaga

1-3x

1-x

1+2x

Po reakcji

0,25

0,75

1,50

b) z bilansu amoniaku 

0,700 = 1 + x・2 czyli:

 

x = –0,150

Równanie reakcji

3 H

2

+ N

2

2NH

3

Stan początkowy

1 mol

1mol

1 mol

zmiana

-3x

-x

+2x

równowaga

1-3x

1-x

1+2x

Po reakcji

1,45

1,15

0,70

c) z bilansu wodoru H

2 

mamy: 2,00 = 1,00 – x・3 czyli:

 

x = –0,333

Równanie reakcji

3 H

2

+ N

2

2NH

3

Stan początkowy

1 mol

1mol

1 mol

zmiana

-3x

-x

+2x

równowaga

1-3x

1-x

1+2x

Po reakcji

2

1,333

0,334

Odpowiedź. Postępy reakcji i liczby moli reagentów wynoszą odpowiednio:
a) x = 0,250, n(H

2

) = 0,250 mola, n(N

2

) = 0,750 mola;

b) x = –0,150, n(H

2

) = 1,45 mola, n(N

2

) = 1,15 mola;

c) x = –0,333, n(N

2

)= 1,333 mola, n(NH

3

) = 0,333 mola.

Przykład 5.

Mieszanina zawierająca 4 mole octanu etylu, 1 mol wody, 1 mol etanolu i 1 mol kwasu octowego 
znajduje   się   w   stanie   rownowagi.   Do   układu   dodano   36   gramow   wody,   wymieszano   całość   i 
pozostawiono   do  przereagowania   aż   do  ustalenia   się   nowego   stanu   równowagi.   Oblicz   ilości   moli 
poszczególnych substancji w nowym stanie rownowagi.

C

2

H

5

OH + CH

3

COOH ↔CH

3

COOC

2

H

5 

+ H

2

O

Z warunków początkowych obliczamy stałą równowagi: Kc = 4
Konstruujemy tabelę, wstawiając sumaryczną liczbę moli wody w układzie (1 mol + 36g wody czyli 
dodatkowe 2 mole, M(H

2

O)=18 g/mol):

Równanie reakcji

CH

3

COOH

 C

2

H

5

OH

CH

3

COOC

2

H

5

H

2

O

Początkowa liczba 
moli

1

1

4

(1+2)=3

Liczba moli po reakcji

1-x

1-x

4+x

3+x

 Po podstawieniu wartości z tabeli do wyrażenia na stałą równowagi obliczamy wartość x:

K

c

=

4=

(

4+ x)∗(3+ x)

(

1−x )

2

 otrzymujemy rownanie kwadratowe, 3x

2 

-15x -8 = 0, z którego wyliczamy wartość postępu reakcji x. Z 

dwóch  pierwiastkow  rownania,  x

1

=  5,486 i  x

2

= -0,486,  wybieramy x

2

,  ponieważ    x

1    

prowadzi  do 

ujemnych stężeń etanolu i kwasu. Postęp reakcji jest ujemny, co oznacza że po dodaniu wody reakcja 
pobiegnie w kierunku odtworzenia substratów. 
Liczby moli w nowym stanie równowagi oliczamy korzystając z  x= -0,486.
n(C

2

H

5

OH) = 1,0–x = 1,0–(–0,4861) = 1,486

n(CH

3

COOH) = 1,0–x = 1,486

n(CH

3

COOC

2

H

5

) = 4,0+x = 4,0+(–0,4861) = 3,514

n(H

2

O) = 3,0+x = 2,514

Odpowiedź: W nowym stanie równowagi mamy po 1,486 mola etanolu i kwasu octowego, 3,514 mola 
octanu etylu i 2,514 mola wody.

3. Reakcje zachodzące w układach heterofazowych

Dla układow, w których w równowadze wspołistnieje kilka faz, reakcje chemiczne zachodzą tak 

długo aż wyrównają się potencjały chemiczne.   Z warunku na równość potencjału chemicznego faz  
wynika, że do wyrażenia na stałą równowagi nalezy wstawić ułamki molowe (ciśnienia cząstkowe, 
stężenia) substancji w obrębie fazy, w której ona występuje. Przykładowo w przypadku reakcji między  
fazą   stałą   i   roztworami   wyrażenie   na   stałą   równowagi   zawiera   jedynie   stężenia   (ułamki   molowe) 
substancji obecnych w  fazie  ciekłej (roztworze),  a pomijamy  ciała stałe ponieważ ułamek molowy 
substancji w ciele stałym nie ulega zmianie i wynosi 1. Do opisu tej równowagi wystarczy podanie 
stężenia substancji w roztworze nasyconym (co oczywiście zależy od temperatury). 

Podobnie, w reakcji wspołistnienia ze sobą gazów i ciał stałych w wyrażeniu na stałą rownowagi 

pomija się człony dotyczące fazy stałej. Tak więc niektóre reakcje równowagi rozkładu ciał stałych daje 
się opisać za pomocą stałych ciśnieniowych z pominięciem substancji stałych, podając równowagową 
prężność gazów powstających w danej reakcji w określonej temperaturze. W taki sposób opisuje się 
często np. reakcje rozkładu węglanow metali do tlenku metalu i dwutlenku węgla:
CaCO

3

(s)  

↔  CaO(s) + CO

2

(g) lub reakcje odwodnienia hydratów: CaSO

4

・

2H

2

O(s)  

↔  CaSO

4

・

0,5H

2

O(s)   +   1,5H

2

O(g).   W   takich   przypadkach   podaje   się   równowagową   prężność   CO

2  

w   danej 

temperaturze   w   przypadku   rozkładu   węglanu   lub   prężność   pary   wodnej   w   danej   temperaturze   dla  
reakcji   odwodnienia   hydratu.   Niezwykle   ważne   jest   podawanie   stanu   skupienia   dla   wszystkich 
reagentow.

Przykład 6
Podaj wyrażenia na stałe równowagi reakcji syntezy siarkowodoru z pierwiastków w temperaturze a) 
1000°C, b) 200°C, c) -100°C.

Rozwiązanie:
a)W temperaturze 1000°C wszystkie reagenty są gazowe, siarka w tej temperaturze występuje głównie 
jako cząsteczka dwuatomowa, a więc tę reakcję można przedstawić rownaniem:

2H

2

(g) + S

2

(g) 

↔ 2H

2

S(g)

K

p

=

p

H

2

S

2

p

H

2

2

∗

p

S

2

b) 

W temperaturze 200°C równanie syntezy siarkowodoru będzie miało postać:

8H

2

(g) + S

8

(c) 

↔ 8H

2

S(g)

 

  K

p

=

p

H

2

S

8

p

H

2

8

c) 

W temperaturze –100°C tylko wodor będzie gazem, a pozostałe reagenty ciałami stałymi.

Wowczas reakcję można zapisać następująco:

8H

2

(g) + S

8

(s) 

↔ 8H

2

S(s)

K

p

=

1

p

H

2

8

Wynika stąd, ze niezwykle istotne jest podanie stechiometrii i stanu skupienia reagentów ponieważ 
wartości stałych znacznie różnia się od siebie.

Przykład 7.
Podaj rownanie na stałą równowagi dla następujących reakcji chemicznych w układow dwu- lub 
wielofazowych:
1) MgCO

3 

(s) 

↔ MgO (s) + CO

2

(g)

2 ) 2NaHCO

3 

(s) 

↔ Na

2

CO

3

(s) + H

2

O(g) + CO

2

(g)

3) 2CaSO

4

・

2H

2

O(s) 

↔ 2CaSO

4

・

H

2

O(s) + 2H

2

O(g)

4) C(grafit) + O

2

(g) 

↔ CO

2

(g)

5) PbI

2

(s) 

↔ Pb

2+

(aq) + 2 I

–

(aq)

6) 2NaHCO

3

(aq) 

↔ Na

2

CO

3

(aq) + CO

2

(g) + H

2

O(c)

Rozwiązanie:

1) K

p 

= p(CO

2

)

2) K

p 

= p(H

2

O) p(CO

2

)

3) K

p

= p(H

2

O)

4 ) K

p 

= p(CO

2

)/p(O

2

)

5) K

c 

= [Pb

2+

(aq)

][I

–

(aq)

]

2

6) 

K

p

= p(CO

2

)

Równowagi w roztworach elektrolitów. 

[zagadnienia do samodzielnego przygotowania: elektrolity mocne i słabe, teorie kwasów i zasad, 
dysocjacja elektrolityczna, prawo działania mas]

 

W roztworze doskonałym wszystkie jego właściwości fizyczne zależą  liniowo od składu i 

właściwości   fizycznych   składników   tego   roztworu.   Prawa   równowag   chemicznych   są   ściśle 
spełniane tylko przez roztwory doskonałe. Z dobrym przybliżeniem możemy je również stosować 
do roztworów bardzo rozcieńczonych. 

W przypadku roztworów rzeczywistych, w prawie działania mas zamiast stężeń używa się 

aktywności reagentów (czyli efektywnych stężeń). Równowagę w takim układzie można zapisać 
następująco:

 mA + nB 

↔ pC + qD

a ilościową zależność między aktywnościami a

i

 reagentów takiej reakcji równowagowej 

przedstawić jako: 

K =

a

C

p

∗

a

D

q

a

A

m

∗

a

B

n

gdzie K jest termodynamiczną stałą równowagi w danej temperaturze i przy danym ciśnieniu (czyli 
stałą równowagi dla roztworu doskonałego), a współczynniki stechiometryczne reakcji we wzorach 
na stałą równowagi są potęgami aktywności reagentów (w liczniku wyrażenia występują produkty 
reakcji, a w mianowniku – substraty). 
Aktywności poszczególnych składników wiąże ze stężeniami następująca zależność: 

a

i

=

f

i

∗

c

i

gdzie  fi  oznacza współczynnik aktywności a  ci  – oczekiwane lub teoretyczne równowagowe 
stężenie   danego   reagenta.   Aktywność  posiada   jednostkę  taką  samą  jak   stężenie   molowe   a 
współczynnik aktywności jest bezwymiarowy. Do zapisu stężeń reagentów w stanie równowagi 
używa się nawiasów kwadratowych, zatem wyrażenie na termodynamiczną stałą równowagi można 
zapisać w postaci:  

K =

f

C

p

∗

f

D

q

f

A

m

∗

f

B

n

∗

[

C ]

p

∗[

D]

q

[

A]

m

∗[

B]

n

Przenosząc współczynniki aktywności na stronę stałej termodynamicznej otrzymamy: 

K '= K

f

A

m

∗

f

B

n

f

C

p

∗

f

D

q

=

[

C ]

p

∗[

D]

q

[

A]

m

∗[

B]

n

gdzie K' jest warunkową stałą równowagi wyrażoną w stężeniach równowagowych dla danej siły 
jonowej  I  roztworu w danej temperaturze. Siła jonowa jest miarą oddziaływań międzyjonowych 
wystepujacych w roztworze i definiujemy ją (wg. Lewisa i Randalla, 1921) jako: 

I =

1
2

Σ

z

i

2

∗

c

i

gdzie  zi  oznacza   liczbę   ładunków   elementarnych   i-tego   jonu   o   stężeniu   molowm  ci 

znajdującego się w roztworze.

 

Jednostką siły jonowej jest mol/dm

3

.

Jeśli w roztworze istnieją  również  elektrolity słabe, wstępne wartości siły jonowej oblicza się 

tylko dla elektrolitów mocnych uwzględniając stechiometrię   reakcji. W przypadku konieczności 
bardzo   dokładnych   obliczeń,   siłę  jonową  z   uwzględnieniem   elektrolitów   słabych   koryguje   się 
później metodami iteracyjnymi. 

Współczynniki   aktywności   można   wyznaczać  dla   związków   chemicznych   z   właściwości 

koligatywnych   roztworów   (ciśnienie   osmotyczne,   obniżenie   temperatury   krzepnięcia   lub 
podwyższenie temperatury wrzenia roztworu, obniżenie prężności pary nasyconej rozpuszczalnika 
nad   roztworem),   albo   poprzez   pomiary  sił  elektromotorycznych   odpowiednio   skonstruowanych 
ogniw. Są to wówczas tak zwane średnie współczynniki aktywności będące średnią geometryczną 
współczynników   aktywności   wszystkich   jonów   danego   związku.   Takie   uśrednienie 
współczynników aktywności powoduje, że za odstępstwa od idealnego roztworu w równym stopniu 
odpowiadają wszystkie rodzaje jonów tego zwiazku. Niestety jest to tylko grube przybliżenie w 
miarę  dobrze spełniane dla bardzo rozcieńczonych roztworów elektrolitów złożonych z jonów o 
takiej samej liczbie ładunków. 

Alternatywną  metodą  jest obliczanie współczynników aktywności indywidualnych jonów na 

podstawie odpowiednich zależności, do których potrzebna jest znajomość siły jonowej roztworu. 

Poprawne obliczenia dla stężonych roztworów elektrolitów mocnych wymagają znajomości 

współczynników aktywności, które wyznacza się zwykle z granicznego prawa Debye'a-Hückla 

−

logf

i

=

Az

i

2

∗

√

I

1+

√

I

 

gdzie z

i

 jest ładunkiem jonu i, A - stała,  której wartość zależy od temperatury i właściwości 

rozpuszczalnika, dla roztworu wodnego w temperaturze 25°C wynosi ona około 0,5. 
Graniczne prawo  Debye'a-Hückla jest adekwatne w przypadku jonów jednowartościowych gdy siła 
jonowa I ≤ 0,05; dla jonów dwuwartościowych gdy I ≤ 0,014  i trójwartościowych gdy I ≤ 0,005.
Dla roztworów bardziej rozcieńczonych, gdy I ≤ 0,01 można obliczać współczynniki aktywności 
jonów z uproszczonej zależności:  −logf

i

=

Az

i

2

∗

√

I

Wartości współczynników aktywności w roztworach stężonych wyznacza się korzystając z 
zależności logarytmu f  od siły jonowej (Z.Galus, Ćwiczenia z Chemii analitycznej,  str. 338).

Przykłady obliczeń:

Przykład  1
Obliczyć siłę jonową wodnego roztworu Na

2

SO

4

 o stężeniu 0,2 mol/dm

3

. 

Rozwiązanie:
W oparciu o reakcję dysocjacji soli: 

Na

2

SO

4 

→ 2 Na

+

 + SO

4

2-

 

obliczamy stężenia molowe poszczególnych jonów. 

Stężenie jonów sodowych wynosi 0.4 mol/dm

3

, a jonów siarczanowych 0.2 mol/dm

3

. Podstawiając 

te wartości do wzoru na siłę jonowa uzyskujemy wartość:

I =

1
2

∗(

0.4

mol
dm

3

∗

1+0.2

mol
dm

3

∗

4)=0.6

mol
dm

3

Przykład 2

Jakie jest stężenie jonów chlorkowych w roztworze CaCl

2

 o sile jonowej 0,21 mol/dm

3

? 

Rozwiązanie: Stężenie CaCl

2

 oznaczamy jako C. W wyniku dysocjacji soli 

CaCl

2

 → Ca

2+

 + 2Cl‾ 

stężenie jonów wapniowych w roztworze wynosi C, a jonów chlorkowych 2C Siła jonowa I = 0.21 
mol/dm

3

 = 1/2(4C + 2C) Stąd C = 0,07 mol/dm

3 

(stężenie jonów wapniowych). Stężenie jonów 

chlorkowych wynosi 0,14 mol/dm

3

.

Iloczyn jonowy wody i pH

[przypomnieć: iloczyn jonowy wody, definicję pH]

Zadania:

1.

Do   naczynia   wprowadzono   gazowy   azot   i   wodór   w   proporcji   stechiometrycznej   (1:3).   Układ 
wygrzewano   w   temperaturze   900K   pod   stałym   ciśnieniem,   wynoszącym   30398hPa.   Analiza 
wykazała,   że   azot   N2  wywiera   w   stanie   rownowagi   ciśnienie   cząstkowe   4053   hPa.   Oblicz 
ciśnieniową stałą równowagi K

P

. [Odp: 0.0276]

2.

W zbiorniku o objętości 1 dm3 i w temperaturze 740K badano równowagę reakcji:

2 NOCl(g) 2NO(g) + Cl2(g)

Wprowadzono 2 mole NOCl do pustego zbiornika i po osiągnięciu stanu równowagi stwierdzono, że 
stopień dysocjacji tego związku wynosi 33%. Oblicz stałą równowagi reakcji. [odp: 0,080]

3.

 Zmieszano 1,0 mola kwasu octowego ze 100 gramami wodnego roztworu alkoholu
etylowego o zawartości 30% wagowych etanolu. Oblicz, ile moli octanu etylu powstanie w stanie 
rownowagi, jeśli stała równowagi reakcji estryfikacji K

c

 wynosi 4,0. [odp: 0,269 mola (uwzględnić 

obecność wody w roztworze etanolu!]

4.

W naczyniu o pojemności 2,0 dm

3

  umieszczono 4,0 mola SO

2

  i 3,0 mola NO

2

. Ile gramów SO

3 

powstanie w stanie równowagi, jeśli stała stężeniowa dla tej temperatury wynosi 1,0. Równanie 
reakcji: SO

2

(g) + NO

2

(g) = SO

3

(g) + NO(g). [odp: 137g SO

3

]

5.

Reakcja   metalicznego   żelaza   z   wodą   zachodzi   wg   równania   3Fe(s)   +   4H2O(g)  

=  Fe3O4(s) + 

4H2(g). Jakie będzie stężenie pary wodnej w stanie równowagi w temperaturze 850°C, jeżeli reakcja 
została zapoczątkowana w naczyniu o pojemności 16,0 dm

3

 napełnionym 10,0 g H2 i odpowiednim 

nadmiarem Fe3O4, a stężeniowa stała równowagi Kc wynosi 4,60? [odp: 0,127M]

6.

W temperaturze 125

o

C dla następującej reakcji 2NaHCO3(s) 

↔Na2CO3(s) + CO2(g) + H2O(g) stała 

równowagi Kp wynosi 0,25. Do opróżnionego naczynia o pojemności 1,00 dm

3

 wprowadzono 11,9 g 

NaHCO3 i naczynie ogrzewano w tej temperaturze do ustalenia się stanu równowagi. Obliczyć: a) 
ciśnienia cząstkowe CO2 i H2O w stanie równowagi; b) masy NaHCO3 i Na2CO3 znajdujące się w  
naczyniu   po   ustaleniu   się   stanu   równowagi;   c)   minimalną   objętość   naczynia,   przy   ktorej   cały 
NaHCO3   ulegnie   rozkładowi.   [odp:   a)   pCO2=pH2O=50kPa,   b)   mNaHCO3=9,3627g; 
mNa2CO3=1,601g, c) V=4,689 dm

3

]

7.

Zmieszano   150ml   0.01M   roztworu   HCl   i   150ml   0.007M   roztworu   HNO

3

.   Jaka   jest   aktywność 

poszczególnych jonów w roztworze? [odp: a

Cl-

=0.0043, a

NO3

- 

=0.00315, a

H+

=0.00764]

8.

Jaka jest aktywność jonów potasowych w 1 litrze roztworu zawierajacym 0,101 g saletry potasowej 
oraz 0,085g saletry sodowej? [odp: 0.00095]

9.

Ile g NaOH musi zawierać 1 dm

3

 roztworu aby jego pH wynosiło 12?

10.

  Jaką objętość wodnego roztworu zasady sodowej o pH=10 należy użyć do zobojętnienia 25 cm

3 

kwasu siarkowego(VI) o stężeniu 0.075M?

11.

Oblicz pH roztworu kwasu solnego o stężeniu 10

-8

mol/dm

3

.

12.

  2g   metalicznego   wapnia   dodano   do   200ml   kwasu   solnego   o   pH=0,22.   Obliczyć   pH   i   pCl 
otrzymanego roztworu. [pH=1, pCl=0,22]

13.

Wykładnik stężenia jonów wodorowych w 0,15M roztworze kwasu octowego wynosi 2,79. Obliczyć 
wartość stałej dysocjacji kwasu octowego.

14.

Stężenia   molowe   jonów   wodorotlenkowych   w   dwóch   roztworach   są   następujące:
a)[OH

-

]=10

-4

, b)[OH

-

]=10

-6

. W którym  roztworze  jest  większe  stężenie  jonów H

+

,  a  w którym 

wyższe pH roztworu?