KONSPEKT LEKCJI MATEMATYKI

Autor:

Klasa: II liceum (matematyczna)

Dział tematyczny: Funkcje trygonometryczne

Temat: Równania trygonometryczne.

Program: Matematyka z plusem

Baza:
- Uczeń zna pojęcie sinusa, cosinusa, tangensa i cotangensa;
- Uczeń zna pojęcie funkcji trygonometrycznych dowolnego kąta;
- Uczen potrafi narysować wykresy funkcji trygonometrycznych;
- Uczeń zna wzory redukcyjne;
- Uczeń zna własności funkcji trygonometrycznych (dziedzina, parzystość, zbiór wartości,
okresowość);
- Uczeń potrafi rozwiązywać proste równania trygonometryczne;
- Uczeń potrafi rozwiązywać równania z wartością bezwzględną.

Cele:
Poznanie przez uczniów sposobów rozwiązywania różnych typów równań trygonometrycznych,
przećwiczenie tych sposobów oraz utrwalenie wiadomości związanych z równaniami try-
gonometrycznymi.

Metody:
- Podająca (wytłumaczenie metod rozwiązywania nowego typu równań trygonometrycznych;
pomoc w rozwiązaniu problemów o podwyższonym stopniu truności);
- Poszukująca (pytania pojawiające się w czasie rozwiązywania zadań);
- Praktyczna (liczenie zadań).

Zasady:
- Trwałości wiedzy (zadanie pracy domowej; sprawdzenie zadania domowego i rozwiązanie
ewentualnych problemów z nim związanych na początku lekcji);
- Świadomego i aktywnego udziału ucznia w procesie nauczania i uczenia się (samodzielne
rozwiązywanie zadań, próby rozwiązania pojawiających się problemów);
- Przystępności (dobór zadań według możliwości uczniów; stopniowanie trudności zadań);
- Systematyczności (wykorzystanie znajomości wykresów funkcji trygonometrycznych oraz
wzorów redukcyjnych do przedstawienia sposobów rozwiązań równań);
- Poglądowości (pomoc w postaci rysowania wykresów w początkowych przykładach).

1

Szczegółowy przebieg lekcji:

Czynności wstępne:

Witam się z uczniami i sprawdzam obecność.
Podaję uczniom temat lekcji: Równania trygonometryczne – ciąg dalszy.
Pytam uczniów, czy były problemy z zadaniem domowym. Jeśli uczniowie zgłoszą prob-
lemy, spróbujemy rozwiązać je wspólnie na tablicy. W przypadku, gdy będzie zbyt dużo
nierozwiązanych zadań postaram ograniczyć się do jednego przykładu z każdego typu. Tę
część lekcji traktuję jako przypomnienie.

Część wprowadzająca:

Następnie proszę uczniów o otwarcie zbiorów zadań na stronie 142.
Zapisuję na tablicy pierwszy przykład i rozwiązuję go samodzielnie, tłumacząc:

Zadanie 8.88
a) sin(2x +

π

4

) = −

√

2

2

Pytam uczniów, czego szukamy najpierw.

Odpowiedź: Tych argumentów t, dla których wartości funkcji y = sin t są równe −

√

2

2

,

zatem nasze równanie można zapisać w postaci: sin t = −

√

2

2

.

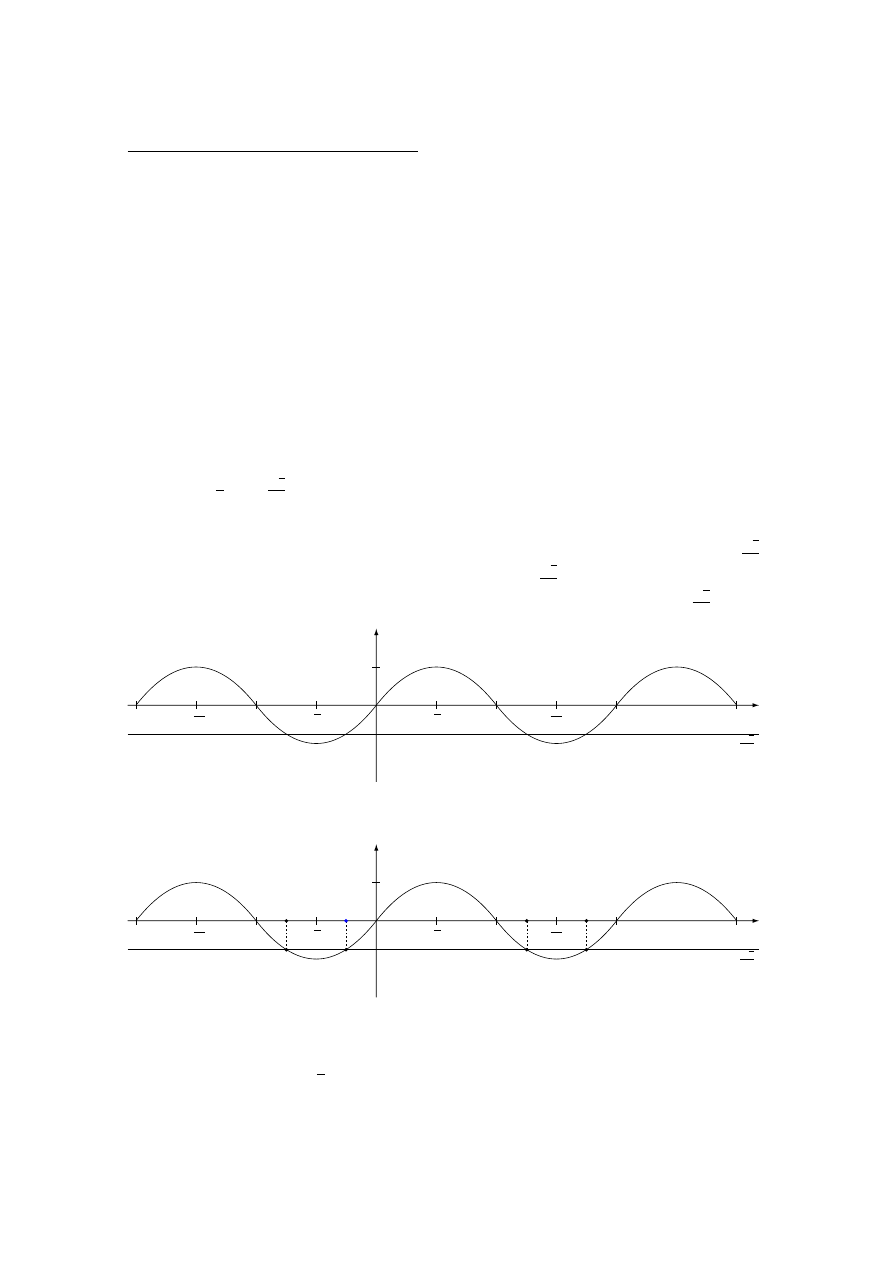
Rysuję pomocniczo wykres funkcji sinus i zaznaczam na wykresie prostą y = −

√

2

2

:

X

Y

O

1

π

2

π

3π

2

2π

3π

-

π

2

-π

-

3π

2

-2π

y = −

√

2

2

Mówię uczniom, że rozwiązaniem są te argumenty, dla których wykres funkcji sinus przecina
się z narysowaną prostą. Zaznaczam punkty przecięcia i argumenty im odpowiadające:

X

Y

O

1

π

2

π

3π

2

2π

3π

-

π

2

-π

-

3π

2

-2π

y = −

√

2

2

Pytam uczniów o współrzędną punktu zaznaczonego kolorem niebieskim.
Prawidłowa odpowiedź: −

π

4

.

2

Jeśli uczniowie będą mieli problem z podaniem prawidłowej odpowiedzi
przypominam, że funkcja sinus jest nieparzysta – zachodzi więc zależność:
sin(α) = − sin(−α)

Pytam wtedy dla jakiego kąta ostrego sin(α) =

√

2

2

.

Prawidłowa odpowiedź:

π

4

.

Piszę:

sin(

π

4

) =

√

2

2

⇔

sin(−

π

4

) = −

√

2

2

Zwracam uwagę, że co drugie „kropka” różni się od zaznaczonej o wielokrotności 2π. Zaz-
naczam wszystkie takie rozwiązania niebieskim kolorem i piszę na tablicy prosząc uczniów,
żeby dyktowali:

Pierwsze rozwiązania:
t = −

π

4

+ 2kπ, k ∈ C

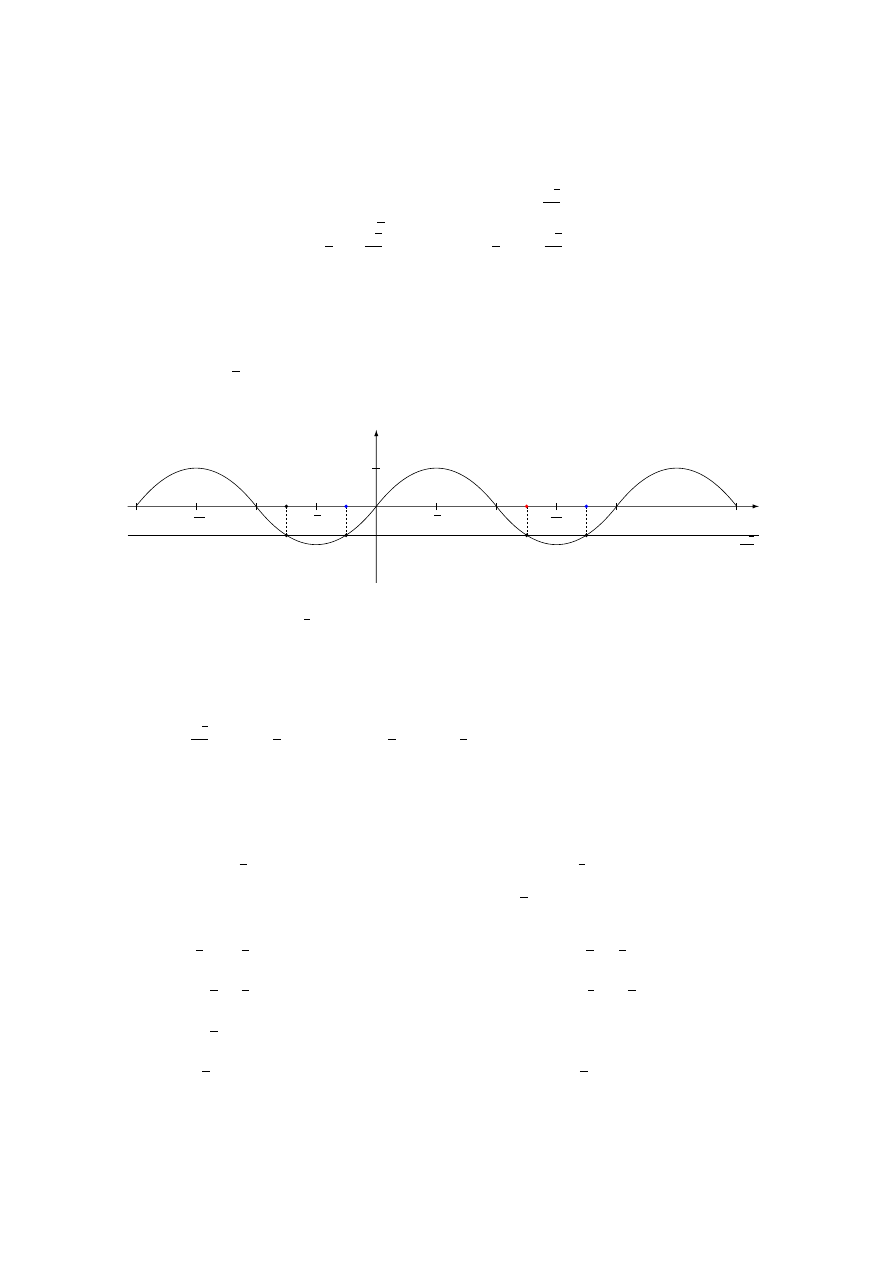
Zaznaczam czerwonym kolorem inne rozwiązanie:

X

Y

O

1

π

2

π

3π

2

2π

3π

-

π

2

-π

-

3π

2

-2π

y = −

√

2

2

Pytam uczniów o współrzędną tego punktu.
Prawidłowa odpowiedź:

5
4

π.

Jeśli uczniowie mają problem z podaniem prawidłowej odpowiedzi przypominam
wzór redukcyjny:
sin(π − α) = sin(α)
I liczę:

−

√

2

2

= sin(−

π

4

) = sin(π − (−

π

4

)) = sin(

5
4

π)

Tak jak w poprzednim przypadku zwracam uwagę, że co druga „kropka” różni się od wyz-
naczonej o wielokrotności liczby 2π. Zaznaczam wszystkie takie rozwiązania kolorem czer-
wonym. Zapisujemy na tablicy, obok poprzedniego rozwiązania:

Pierwsze rozwiązania:

Drugie rozwiązania:

t = −

π

4

+ 2kπ, k ∈ C

lub

t =

5
4

π + 2kπ, k ∈ C

Wracam do początku przykładu i mówię, że t = 2x +

π

4

Przypominam, że naszym celem

jest znalezienie x. Zapisuję rozwiązania:

2x +

π

4

= −

π

4

+ 2kπ, k ∈ C

lub

2x +

π

4

=

5
4

π + 2kπ, k ∈ C

2x = −

π

4

−

π

4

+ 2kπ, k ∈ C

lub

2x =

5
4

π −

π

4

+ 2kπ, k ∈ C

2x = −

π

2

+ 2kπ, k ∈ C

lub

2x = π + 2kπ, k ∈ C

x = −

π

4

+ kπ, k ∈ C

lub

x =

π

2

+ kπ, k ∈ C

3

Następnie proszę ucznia do tablicy, aby rozwiązał kolejny przykład:

b) cos(

1
2

x −

π

6

) =

1
2

Rozwiązanie:

cos t =

1
2

:

X

Y

O

1

π

4

π

2

π

3π

2

2π

5π

2

-

π

4

-

π

2

-π

-

3π

2

-2π

-

5π

2

y =

1
2

t =

π

3

+ 2kπ, k ∈ C

lub

t = −

π

3

+ 2kπ, k ∈ C

1
2

x −

π

6

=

π

3

+ 2kπ, k ∈ C

lub

1
2

x −

π

6

= −

π

3

+ 2kπ, k ∈ C

1
2

x =

π

3

+

π

6

+ 2kπ, k ∈ C

lub

1
2

x = −

π

3

+

π

6

+ 2kπ, k ∈ C

1
2

x =

π

2

+ 2kπ, k ∈ C

lub

1
2

x = −

π

6

+ 2kπ, k ∈ C

x = π + 4kπ, k ∈ C

lub

x = −

π

3

+ 4kπ, k ∈ C

Jeśli uczeń ma problem z podaniem drugiego rozwiązania,
przypominam o parzystości funkcji cosinus:
cos(α) = cos(−α).

Proszę kolejnego ucznia do tablicy:

c) tg(2x −

π

8

) = 1

W tym miejscu proszę ucznia, żeby spróbował rozwiązać przykład bez podstawiania zmi-
ennej t.

4

X

Y

O

π

4

π

2

π

-

π

2

-π

3π

2

-

3π

2

-

π

4

y = 1

W tym przykładzie zwracam uwagę, że należy najpierw wyznaczyć dziedzinę równania:

2x −

π

8

6=

π

2

+ kπ, k ∈ C

2x 6=

π

2

+

π

8

+ kπ, k ∈ C

2x 6=

5
8

π + kπ, k ∈ C

x 6=

5

16

π +

1
2

kπ, k ∈ C

Mówię, że tu mamy, w odróżnieniu od poprzednich przykładów, jedną grupę rozwiązań
postaci:

2x −

π

8

=

π

4

+ kπ, k ∈ C

2x =

π

4

+

π

8

+ kπ, k ∈ C

2x =

3
8

π + kπ, k ∈ C

x =

3

16

π +

1
2

kπ, k ∈ C

Proszę kolejnego ucznia do tablicy:

d) ctg(

1
3

x +

π

3

) =

√

3

5

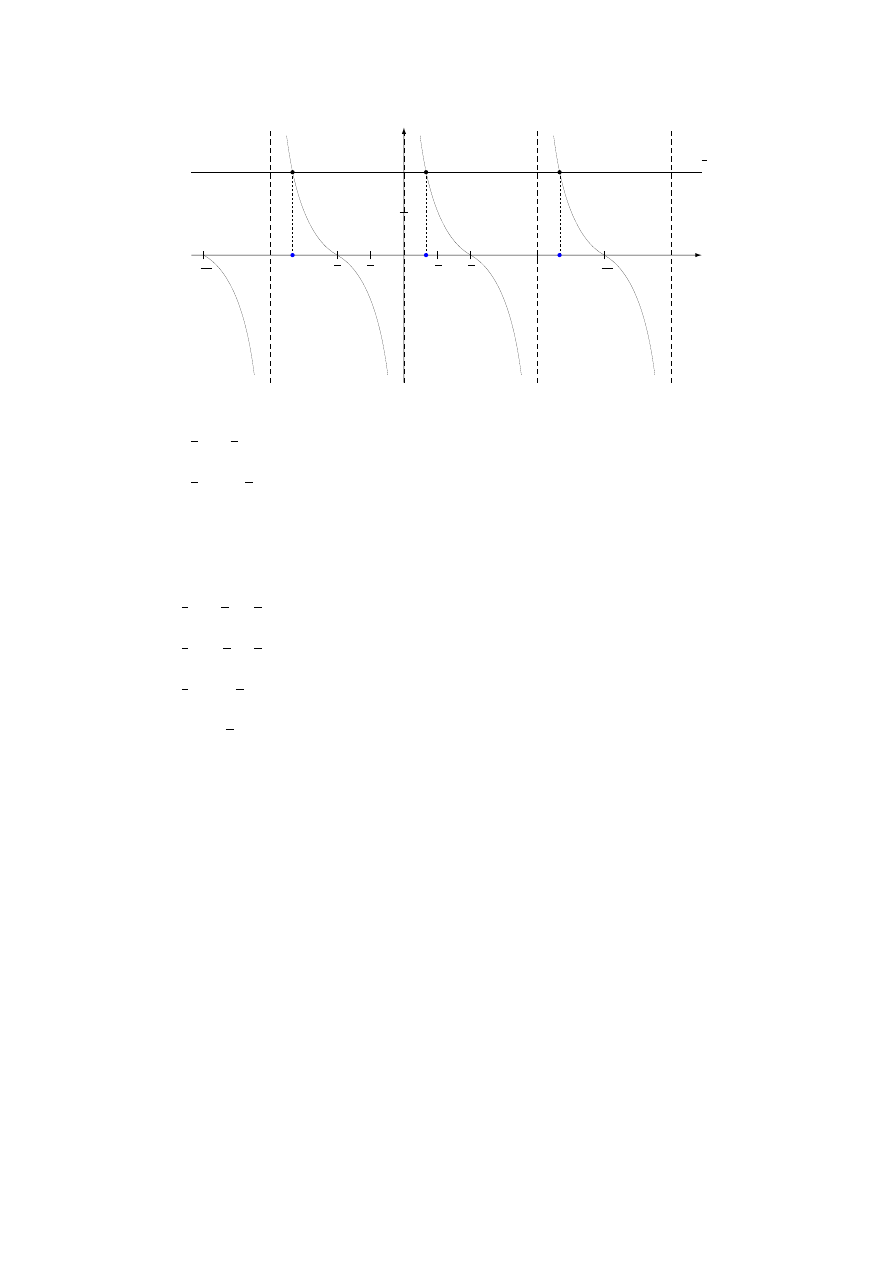
X

Y

O

1

π

4

π

2

π

2π

-

π

2

-π

3π

2

-

3π

2

-

π

4

y =

√

3

Dziedzina:

1
3

x +

π

3

6= kπ, k ∈ C

1
3

x 6= −

π

3

+ kπ, k ∈ C

x 6= −π + 3kπ, k ∈ C

Rozwiązanie:

1
3

x +

π

3

=

π

6

+ kπ, k ∈ C

1
3

x =

π

6

−

π

3

+ kπ, k ∈ C

1
3

x = −

π

6

+ kπ, k ∈ C

x = −

π

2

+ 3kπ, k ∈ C

Następnie przechodzę do kolejnego zadania. Proszę uczniów do tablicy.

Zadanie 8.89
a) 3 + 4 cos(0, 5x) = −1

Proszę ucznia, aby najpierw przekształcił równanie do postaci znanej nam z poprzedniego
zadania.

3 + 4 cos(0, 5x) = −1

4 cos(0, 5x) = −4

cos(0, 5x) = −1

6

X

Y

O

1

π

4

π

2

π

3π

2

2π

5π

2

-

π

4

-

π

2

-π

-

3π

2

-2π

-

5π

2

y = −1

Zwracam uwagę, że mamy tu tylko jedną grupę rozwiązań.

0, 5x = π + 2kπ, k ∈ C

x = 2π + 4kπ, k ∈ C

c) 3ctg(2x + π) = −

√

3

Rozpoczynamy od wyznaczenia dziedziny.

2x + π 6= kπ, k ∈ C

2x 6= −πkπ, k ∈ C

2x 6= (k − 1)π, k ∈ C

2x 6= kπ, k ∈ C

x 6=

1
2

kπ, k ∈ C

Przejście z (k − 1) do k w powyższym zapisie tłumaczę tym, że skoro k we wszystkich
naszych rozważaniach jest liczbą całkowitą, to również liczba mniejsza o 1 od k jest nadal
dowolną liczbą całkowitą.

Zwracam uwagę, że cotangens jest funkcją π-okresową, więc zamiast ctg(2x + π) możemy
zapisać ctg(2x).
Mamy zatem równanie: 3ctg(2x) = −

√

3

Przekształcamy równanie:

3ctg(2x) = −

√

3

ctg(2x) = −

√

3

3

7

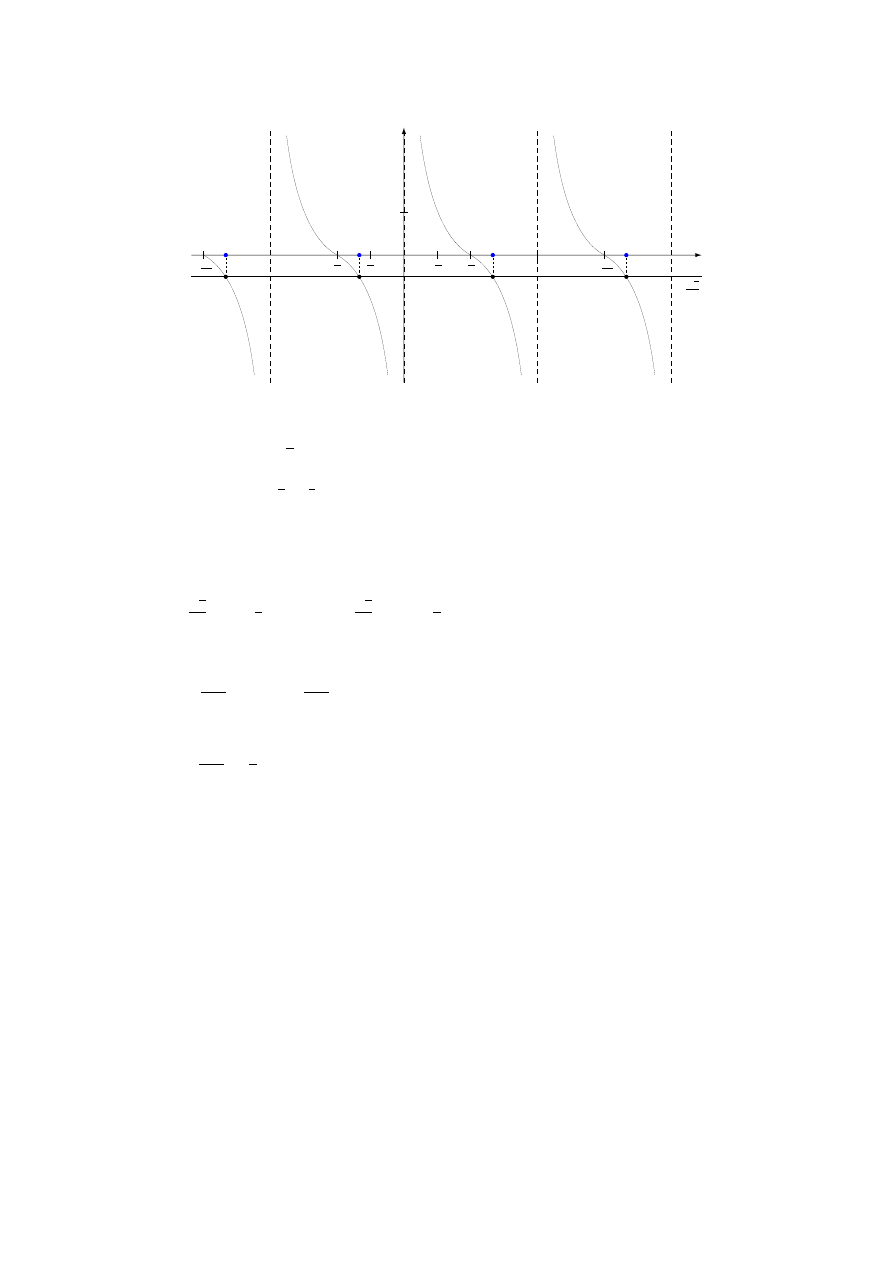
X

Y

O

1

π

4

π

2

π

2π

-

π

2

-π

3π

2

-

3π

2

-

π

4

y = −

√

3

3

Rozwiązanie:

2x = −

π

3

+ kπ, k ∈ C

x = −

π

6

+

1
2

kπ, k ∈ C

Jeśli uczniowie będą mieli problem ze znalezieniem podstawowego argumentu,
przypomnę o nieparzystości funkcji cotangens:
ctg(α) = −ctg(−α)

√

3

3

=ctg(

π

3

)

⇒

−

√

3

3

=ctg(−

π

3

)

d) 1+tg

2

(

π−x

2

) = [1+tg(

π−x

2

)]

2

Rozpoczynamy od wyznaczenia dziedziny:

π−x

2

6=

π

2

+ kπ, k ∈ C

π − x 6= π + 2kπ, k ∈ C

−x 6= π − π + 2kπ, k ∈ C

−x 6= 2kπ, k ∈ C

x 6= −2kπ, k ∈ C

Pytam uczniów jaka jest różnica między plusem a minusem przez wyrażeniem 2kπ.

Jeśli nie wiedzą podpowiadam, żeby wypisali wartości jakie może przyjmować k, sama
zapisuję na tablicy:

k ∈ {..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ...}

Następnie w podobny sposób zapisujemy 2kπ i −2kπ:

8

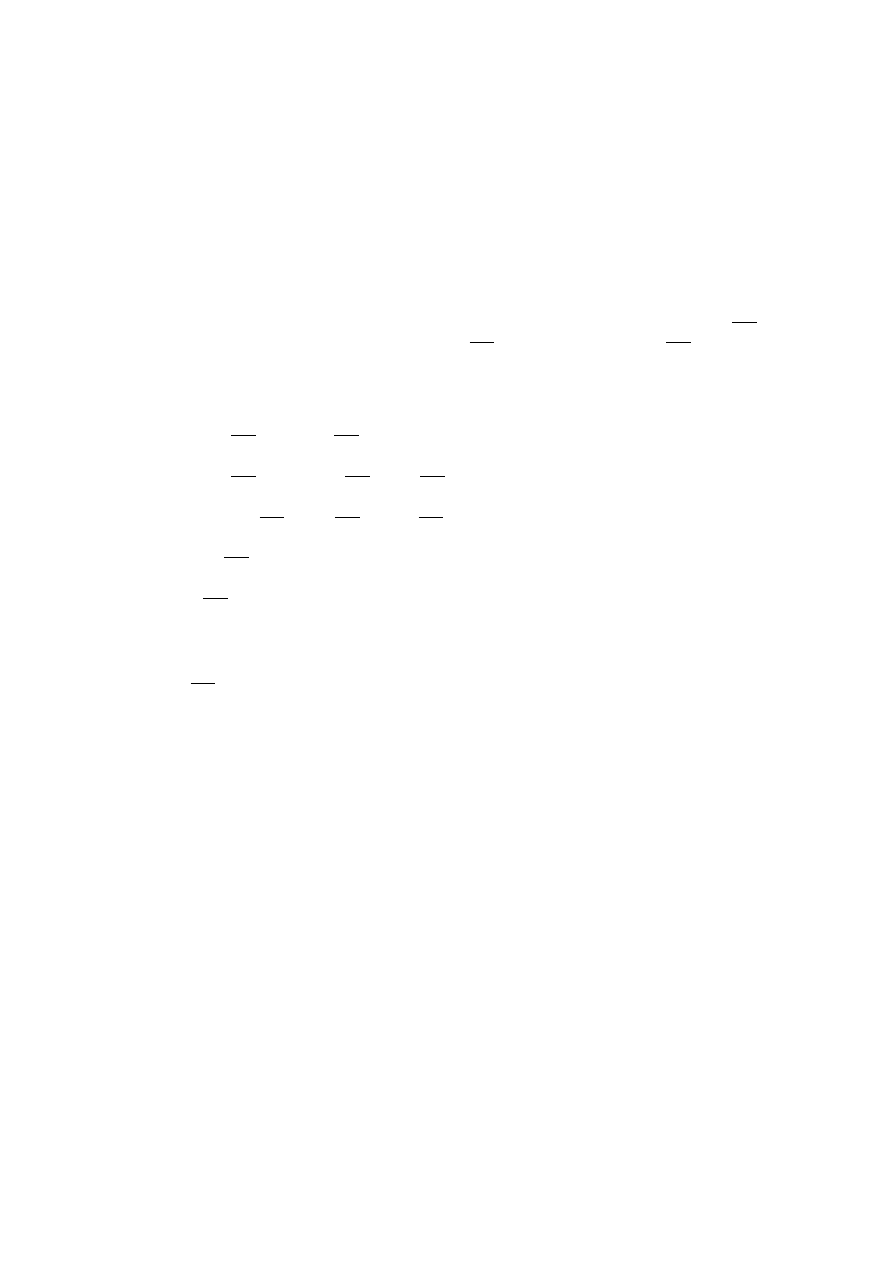
2kπ ∈ {..., −8π, −6π, −4π, −2π, 0, 2π, 4π, 6π, 8π, ...}

−2kπ ∈ {..., 8π, 6π, 4π, 2π, 0, −2π, −4π, −6π, −8π, ...}

Zauważamy, że są to te same zbiory. Nie ma zatem znaczenia jaki znak tam stoi.

Mówię uczniom, że zapisanie dziedziny może wyglądać również następująco:

x 6= 2kπ, k ∈ C

Następnie pytam uczniów, czy w wyznaczaniu dziedziny należy uwzględnić osobno tg

2

(

π−x

2

).

Dochodzimy do wniosku, że nie. Dziedzina tg

2

(

π−x

2

) jest taka sama jak tg(

π−x

2

), bo pod-

niesienie do kwadratu nie spowoduje przesunięcia asymptot.

Przekształcenia proponuję rozpocząć od zastosowania wzoru skróconego mnożenia:

1+tg

2

(

π−x

2

) = [1+tg(

π−x

2

)]

2

1+tg

2

(

π−x

2

) = 1 + 2tg(

π−x

2

)+tg

2

(

π−x

2

)

1 − 1+tg

2

(

π−x

2

)−tg

2

(

π−x

2

) − 2tg(

π−x

2

) = 0

−2tg(

π−x

2

) = 0

tg(

π−x

2

) = 0

Rozwiązanie:

π−x

2

= kπ, k ∈ C

π − x = 2kπ, k ∈ C

−x = −π + 2kπ, k ∈ C

x = π − 2kπ, k ∈ C

Pytam uczniów, czy możemy zapisać +2kπ zamiast −2kπ
w tym przypadku. Jeśli uczniowie zrozumieli
powyższe rozumowanie odpowiadają, że tak.

x = π + 2kπ, k ∈ C

Następnie przechodzimy do kolejnego zadania.
Pierwszy przykład rozwiązuję samodzielnie, tłumacząc.

9

Zadanie 8.91
a) |2 sin x −

√

3| =

√

3

Przypominam, że rozwiązując równania z wartością bezwględną dostajemy dwa przypadki:

2 sin x −

√

3 =

√

3

lub

2 sin x −

√

3 = −

√

3

2 sin x =

√

3 +

√

3

lub

2 sin x = −

√

3 +

√

3

2 sin x = 2

√

3

lub

2 sin x = 0

sin x =

√

3

lub

sin x = 0

Zwracam uwagę, że pierwsze rozwiązanie jest sprzeczne, ponieważ zawsze
sin x 6 1, a

√

3 > 1.

Rozwiązanie drugiego przypadku:

x = kπ, k ∈ C

Zatem rozwiązanie całego przykładu wygląda następująco:

x = kπ, k ∈ C

Do następnych przykładów proszę uczniów.

b) |

√

3tg(

x
3

)| = 1

Rozpoczynamy od wyznaczenia dziedziny:

x

3

6=

π

2

+ kπ, k ∈ C

x 6=

3
2

π + 3kπ, k ∈ C

Rozwiązanie:

10

√

3tg(

x

3

) = 1

lub

√

3tg(

x

3

) = −1

tg(

x
3

) =

1

√

3

·

√

3

√

3

=

√

3

3

lub

tg(

x
3

) = −

√

3

3

x
3

=

π

6

+ kπ, k ∈ C

lub

x
3

= −

π

6

+ kπ, k ∈ C

x =

π

2

+ 3kπ, k ∈ C

lub

x = −

π

2

+ 3kπ, k ∈ C

Pytam uczniów, czy rozwiązanie należy do dziedziny. Prowadzimy mała dyskusję na ten
temat. Jeśli uczniowie nie potrafią odpowiedzieć mi na to pytanie, wypisujemy zbiory ele-
mentów, które nie należą do dziedziny i elementów, które są rozwiązaniami i sprawdzamy,
czy zbiory te mają punkty wspólne. Ostatecznie dochodzimy do wniosku:

Rozwiązanie przykładu:

x =

π

2

+ 3kπ, k ∈ C

lub

x = −

π

2

+ 3kπ, k ∈ C

c) ctg(|2x|) = 1

Rozpoczynamy od wyznaczenia dziedziny:

|2x| 6= kπ

2x 6= kπ, k ∈ C

i

2x 6= −kπ, k ∈ C

x 6=

k
2

π, k ∈ C

i

x 6= −

k
2

π, k ∈ C

Zwracam uwagę, że obydwa te przypadki pokrywają się.

Pytam uczniów, czy widzą

dlaczego. Jeśli nie, to mówię, że skoro k ∈ C, to również −k ∈ C. Jeśli uczniowie nadal nie
rozumieją, tłumaczymy to podobnie jak prędzej – zapisując zbiory złożone z liczb postaci
k i −k, a następnie dochodzimy do wniosku, że są to te same zbiory. Zapisujemy dziedzinę:

x 6=

k
2

π, k ∈ C

Wracamy do liczenia przykładu:
Zwracam uwagę, że aby przejść do rozważania przypadków należy najpierw „wyjść” spod
cotangensa:

ctg(|2x|) = 1

|2x| =

π

4

+ kπ

Pytam uczniów, czy możemy zapisać tak jak zawsze k ∈ C.
Dochodzimy do wniosku, że nie można wstawiać tu liczb ujemnych w miejsce k, ponieważ
otrzymamy wtedy liczby ujemne, a wartość bezwzględna osiąga tylko wartości nieujemne.

Dopisuję:

11

|2x| =

π

4

+ kπ, k ∈ N

Rozwiązanie:

2x =

π

4

+ kπ

lub

2x = −

π

4

− kπ

x =

π

8

+

1
2

kπ, k ∈ N

lub

x = −

π

8

−

1
2

kπ, k ∈ N

Pytam uczniów, czy rozwiązanie należy do dziedziny. Prowadzimy dyskusję podobną do
tej z poprzedniego przykładu. Dochodzimy do wniosku, że całe rozwiązanie należy do
dziedziny.

d) 2 cos(|

x

3

|) = −1

Przekształcamy:

2 cos(|

x

3

|) = −1

cos(|

x
3

|) = −

1
2

Rozwiązujemy:

|

x
3

| =

2
3

π + 2kπ, k ∈ N

lub

|

x
3

| = −

2
3

π + 2kπ, k ∈ N

+

x
3

=

2
3

π + 2kπ

lub

x

3

= −

2
3

π − 2kπ

lub

x
3

= −

2
3

π + 2kπ

lub

x
3

=

2
3

π − 2kπ

k ∈ N

k ∈ N

k ∈ N

+

k ∈ N

+

x = 2π + 6kπ

lub

x = −2π − 6kπ

lub

x = −2π + 6kπ

lub

x = 2π − 6kπ

k ∈ N

k ∈ N

k ∈ N

+

k ∈ N

+

Proszę uczniów, aby zastanowili się, czy nie można tego rozwiązania zapisać krócej. Pod-
powiadam, że może niektóre przypadki się dopełniają. Jeśli uczniowie nie rozwiążą tego
problemu samodzielnie, mówię, że rozwiązania postaci x = 2π + 6kπ, k ∈ N oraz x =
2π − 6kπ, k ∈ N razem dają się zapisać w postaci: x = 2π + 6kπ, k ∈ C. Jeśli uczniowie
nie rozumieją, tłumaczę, że skoro k ∈ N , to wówczas −k reprezentuje wszystkie liczby
ujemne. Razem daje nam to zbiór liczb całkowitych.
To samo dotyczy rozwiązań x = −2π − 6kπ, k ∈ N oraz x = −2π + 6kπ, k ∈ N . Razem
możemy je zapisać w postaci: x = −2π + 6kπ, k ∈ C.
Zapisujemy zatem rozwiązanie całego przykładu:

x = −2π − 6kπ, k ∈ C

lub

x = −2π + 6kπ, k ∈ C

Przechodzimy do kolejnego zadania.
Do tablicy proszę ucznia.

Zadanie 8.92
a) tg

2

x − 3 = 0

Na początku wyznaczamy dziedzinę:

12

x 6=

π

2

+ kπ, k ∈ C

Jeśli uczeń nie wie, jak policzyć ten przykład, podpowiadam skorzystanie ze wzoru skró-
conego mnożenia w następujący sposób:

(tgx −

√

3)(tgx +

√

3) = 0

Rozwiązujemy dalej:

tgx =

√

3

lub

tgx = −

√

3

x =

π

3

+ kπ, k ∈ C

lub

x = −

π

3

+ kπ, k ∈ C

Pytam uczniów, czy rozwiązanie należy do dziedziny. Prowadzimy krótką dyskusję na ten
temat. Dochodzimy do wniosku, że całe rozwiązanie należy do dziedziny.

b) cos

2

3x −

1
2

cos 3x = 0

Podpowiadam, że można wyłączyć wspólny czynnik przed nawias, jeśli uczeń nie wie co
robić.

cos 3x(cos 3x −

1
2

) = 0

Rozwiązujemy dalej:

cos 3x = 0

lub

cos 3x =

1
2

3x =

π

2

+ kπ, k ∈ C

lub

3x =

π

3

+ 2kπ, k ∈ C

lub

3x = −

π

3

+ 2kπ, k ∈ C

x =

π

6

+

1
3

kπ, k ∈ C

lub

x =

π

9

+

2
3

kπ, k ∈ C

lub

3x = −

π

9

+

2
3

kπ, k ∈ C

c) sin

2

(

1
2

x) + 1 = 2 sin(

1
2

x)

Podpowiadam, że można przenieść wszystko na jedną stronę i zauważyć wówczas wzór
skróconego mnożenia:

sin

2

(

1
2

x) + 1 = 2 sin(

1
2

x)

sin

2

(

1
2

x) − 2 sin(

1
2

x) + 1 = 0

[sin(

1
2

x) − 1]

2

= 0

sin(

1
2

x) − 1 = 0

sin(

1
2

x) = 1

13

Rozwiązanie:

1
2

x =

π

2

+ 2kπ

x = π + 4kπ, k ∈ C

d) ctg

3

x = 3ctgx

Rozpoczynamy od wyznaczenia dziedziny:

x 6= kπ, k ∈ C

Proponuję przeniesienie wszystkiego na jedną stronę i wyłączenie wspólnego czynnika przed
nawias.

ctg

3

x = 3ctgx

ctg

3

x − 3ctgx=0

ctgx(ctg

2

x − 3) = 0

ctgx(ctgx −

√

3)(ctgx +

√

3) = 0

Rozwiązanie:

ctgx = 0

lub

ctgx =

√

3

lub

ctgx = −

√

3

x =

π

2

+ kπ, k ∈ C

lub

x =

π

6

+ kπ, k ∈ C

lub

ctgx =

5
6

π + kπ, k ∈ C

Pytam uczniów, czy rozwiązanie należy do dziedziny. Prowadzimy krótką dyskusję i do-
chodzimy do wniosku, że całe rozwiązanie należy do dziedziny.

Później przechodzę do następnego zadania.
Proszę uczniów do tablicy.

Zadanie 8.93
a)

sin x

4x

= 0

Zaczynamy od wyznaczenia dziedziny równania:

4x 6= 0

x 6= 0

Przechodzimy do rozwiązania:

14

sin x

4x

= 0

x 6= 0

sin x = 0

x 6= 0

x = kπ, k ∈ C

x 6= 0

Zwracam uwagę, że jeśli w otrzymanym rozwiązaniu wstawimy k = 0 dostaniemy x = 0,
ale to nie należy do dziedziny równania.
Ostateczne rozwiązanie wygląda więc następująco:

x = kπ, k ∈ C\{0}

c)

cos

2

x−1

sin x

+ sin

3

x = 0

Na początku wyznaczamy dziedzinę:

sin x 6= 0

x 6= kπ, k ∈ C

Proponuję przekształcenie:

cos

2

x−1

sin x

+ sin

3

x = 0

cos

2

x−cos

2

x−sin

2

x

sin x

+ sin

3

x = 0

− sin

2

x

sin x

+ sin

3

x = 0

− sin x + sin

3

x = 0

sin x(sin

2

x − 1) = 0

sin x = 0

lub

sin

2

x − 1 = 0

x = kπ, k ∈ C

lub

(sin x − 1)(sin x + 1) = 0

nie należy do

sin x = 1

lub

sin x = −1

dziedziny

x =

π

2

+ 2kπ, k ∈ C

lub

x = −

π

2

+ 2kπ, k ∈ C

Zwracam uwagę, że otrzymane przez nas rozwiązania można zapisać razem jako:

x =

π

2

+ kπ, k ∈ C

Jeśli uczniowie nie rozumieją dlaczego, tłumaczę im to rysując obydwa rozwiązania na osi
liczbowej.

15

d) tg

2

x cos x + 4 cos

3

x =ctgx sin x +

1

cos x

Na początku wyznaczamy dziedzinę:

cos x 6= 0

tgx

ctgx

x 6=

π

2

+ kπ, k ∈ C

i

x 6=

π

2

+ kπ, k ∈ C

i

x 6= kπ, k ∈ C

Mówię, że razem dziedzinę możemy zapisać następująco:

x 6=

1
2

kπ, k ∈ C

Jeśli uczniowie tego nie rozumieją tłumaczę również na osi liczbowej.

Proponuję przekształcenie:

tg

2

x cos x + 4 cos

3

x =ctgx sin x +

1

cos x

sin

2

x

cos

2

x

cos x + 4 cos

3

x =

cos x

sin x

sin x +

1

cos x

sin

2

x

cos x

+ 4 cos

3

x = cos x +

1

cos x

sin

2

x + 4 cos

4

x = cos

2

x + 1

sin

2

x + 4 cos

4

x − cos

2

x − 1 = 0

sin

2

x + 4 cos

4

x − cos

2

x − sin

2

x − cos

2

x = 0

4 cos

4

x − 2 cos

2

x = 0

2 cos

4

x − cos

2

x = 0

cos

2

x(2 cos

2

x − 1) = 0

cos

2

x = 0

cos x = 0

x =

π

2

+ kπ, k ∈ C

lub

cos

2

x =

1
2

cos x =

√

2

2

lub

cos x = −

√

2

2

x =

π

4

+ 2kπ, k ∈ C lub x = −

π

4

+ 2kπ, k ∈ C

lub

x =

3
4

π + 2kπ, k ∈ C lub x = −

3
4

π + 2kπ, k ∈ C

Proponuję uczniom, żeby zapisali rozwiązanie w jednym wyrażeniu,tak jak robiliśmy to
wcześniej.
Prawidłowe rozwiązanie:

16

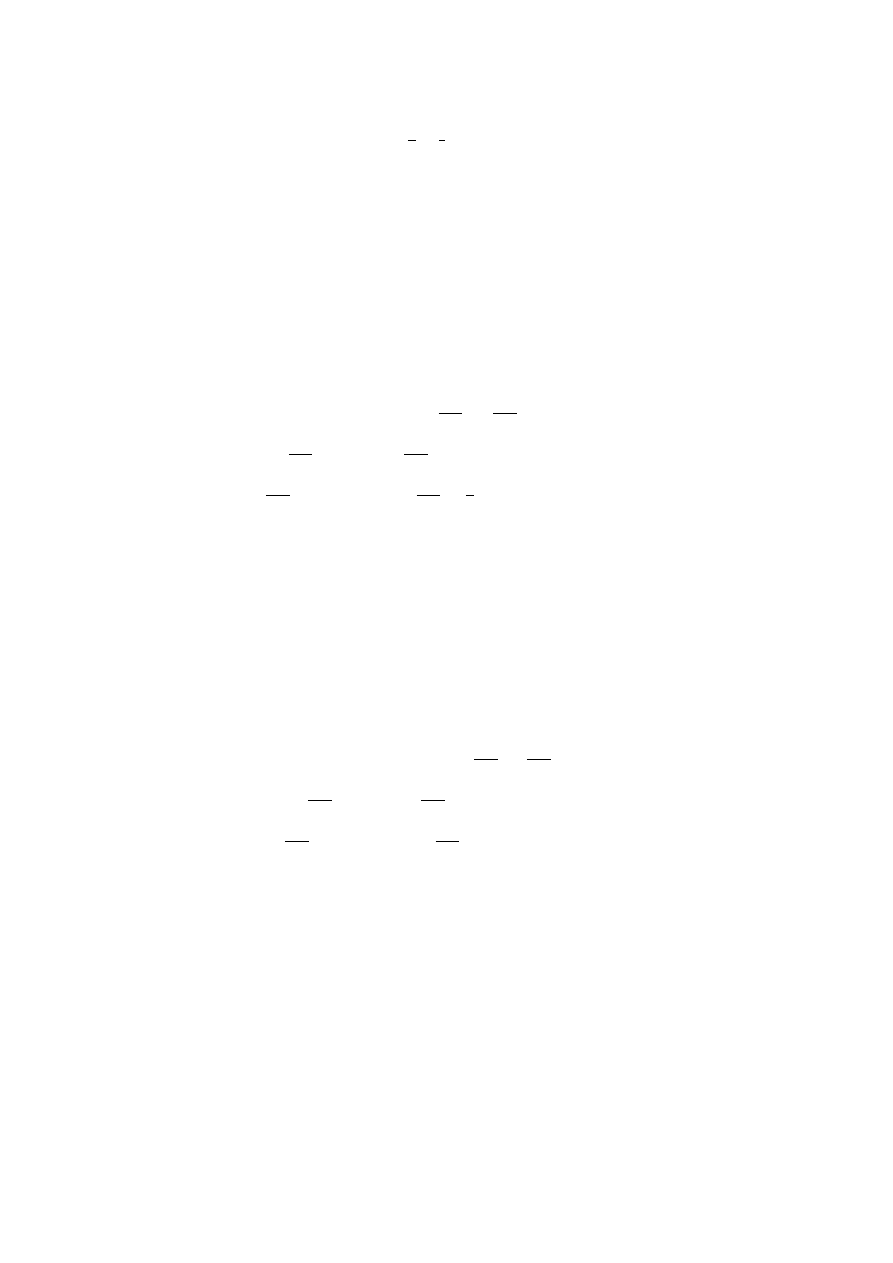
x =

π

4

+

1
2

kπ, k ∈ C

Następnie przechodzimy do kolejnego zadania.
Wprowadzam wzory, które będą przydatne w rozwiązaniach.

sin x = sin y

Aby rozwiązać takie równanie wygodnie jest użyć wzoru na różnicę sinusa:

sin x − sin y = 0 ⇔ 2 sin

x−y

2

cos

x+y

2

= 0 ⇔

sin

x−y

2

= 0 lub cos

x+y

2

= 0 ⇔

x−y

2

= kπ, k ∈ C lub

x+y

2

=

π

2

+ kπ, k ∈ C ⇔

x − y = 2kπ, k ∈ C lub x + y = 2π + 2kπ, k ∈ C ⇔

x = y + 2kπ, k ∈ C lub x = −y + 2kπ, k ∈ C

cos x = cos y

Aby rozwiązać takie równanie wygodnie jest użyć wzoru na różnicę cosinusa:

cos x − cos y = 0 ⇔ −2 sin

x+y

2

sin

x−y

2

= 0 ⇔

sin

x+y

2

= 0 lub sin

x−y

2

= 0 ⇔

x+y

2

= kπ, k ∈ C lub

x−y

2

= kπ, k ∈ C ⇔

x + y = 2kπ, k ∈ C lub x − y = 2kπ, k ∈ C ⇔

x = −y + 2kπ, k ∈ C lub x = y + 2kπ, k ∈ C

tgx =tgy

Aby rozwiązać takie równanie wygodnie jest użyć wzoru na różnicę tangensa:

17

Tutaj musimy ustalić dziedzinę:
x 6=

π

2

+ kπ, k ∈ C i y 6=

π

2

+ kπ, k ∈ C

tg x−tg y = 0 ⇔

sin(x−y)

cos x·cos y

= 0 ⇔

sin(x − y) = 0 ⇔

x − y = kπ, k ∈ C ⇔

x = y + kπ, k ∈ C

ctgx =ctgy

Aby rozwiązać takie równanie wygodnie jest użyć wzoru na różnicę cotangensa:

Tutaj musimy ustalić dziedzinę:
x 6= kπ, k ∈ C i y 6= kπ, k ∈ C

ctg x−ctg y = 0 ⇔ −

sin(x−y)

sin x·sin y

= 0 ⇔

sin(x − y) = 0 ⇔

x − y = kπ, k ∈ C ⇔

x = y + kπ, k ∈ C

Proszę ucznia do tablicy.

Zadanie 8.90
a) tg2x =tgx

Na początku wyznaczamy dziedzinę:

2x 6=

π

2

+ kπ, k ∈ C

i

x 6=

π

2

+ kπ, k ∈ C

x 6=

π

4

+

1
2

kπ, k ∈ C

Pytam uczniów, czy nie można zapisać dziedziny krócej. Razem dochodzimy do wniosku,
że tak – w postaci:

x 6=

k
4

π, k ∈ C

Następnie przechodzimy do liczenia wykorzystując odpowiedni wzór z tych, które wcześniej
wyprowadziłam.

18

tg2x =tgx

2x = x + kπ, k ∈ C

x = kπ, k ∈ C

Pytam uczniów, czy rozwiązanie należy do dziedziny. Wspólnie dochodzimy do wniosku,
że tak.

b) cos(2x −

π

6

) − cos(x +

π

6

) = 0

Podpowiadam, że najlepiej jest przekształcić to równanie do postaci z poprzedniego
przykładu:

cos(2x −

π

6

) = cos(x +

π

6

)

Rozwiązanie:

2x −

π

6

= x +

π

6

+ 2kπ, k ∈ C

lub

2x −

π

6

= −x −

π

6

+ 2kπ, k ∈ C

2x − x =

π

6

+

π

6

+ 2kπ, k ∈ C

2x + x = −

π

6

+

π

6

+ 2kπ, k ∈ C

lub

3x = 2kπ, k ∈ C

x =

π

3

+ 2kπ, k ∈ C

lub

x =

2
3

kπ, k ∈ C

d) sin 3x = sin(x +

π

4

)

Rozwiązanie:

3x = x +

π

4

+ 2kπ, k ∈ C

lub

3x = π − (x +

1
4

π) + 2kπ, k ∈ C

3x = x +

π

4

+ 2kπ, k ∈ C

lub

3x =

3
4

π − x + 2kπ, k ∈ C

3x − x =

π

4

+ 2kπ, k ∈ C

lub

3x + x =

3
4

π + 2kπ, k ∈ C

2x =

π

4

+ 2kπ, k ∈ C

lub

4x =

3
4

π + 2kπ, k ∈ C

x =

π

8

+ kπ, k ∈ C

lub

x =

3

16

π +

1
2

kπ, k ∈ C

Zadanie domowe:

Jako zadanie domowe proponuję uczniom, żeby dokończyli zadanie, w którym ewentualnie
znajdziemy się na końcu lekcji oraz zastanowili się nad wszystkimi przykładami do zadania
8.93, których nie zdążymy zrobić.

19

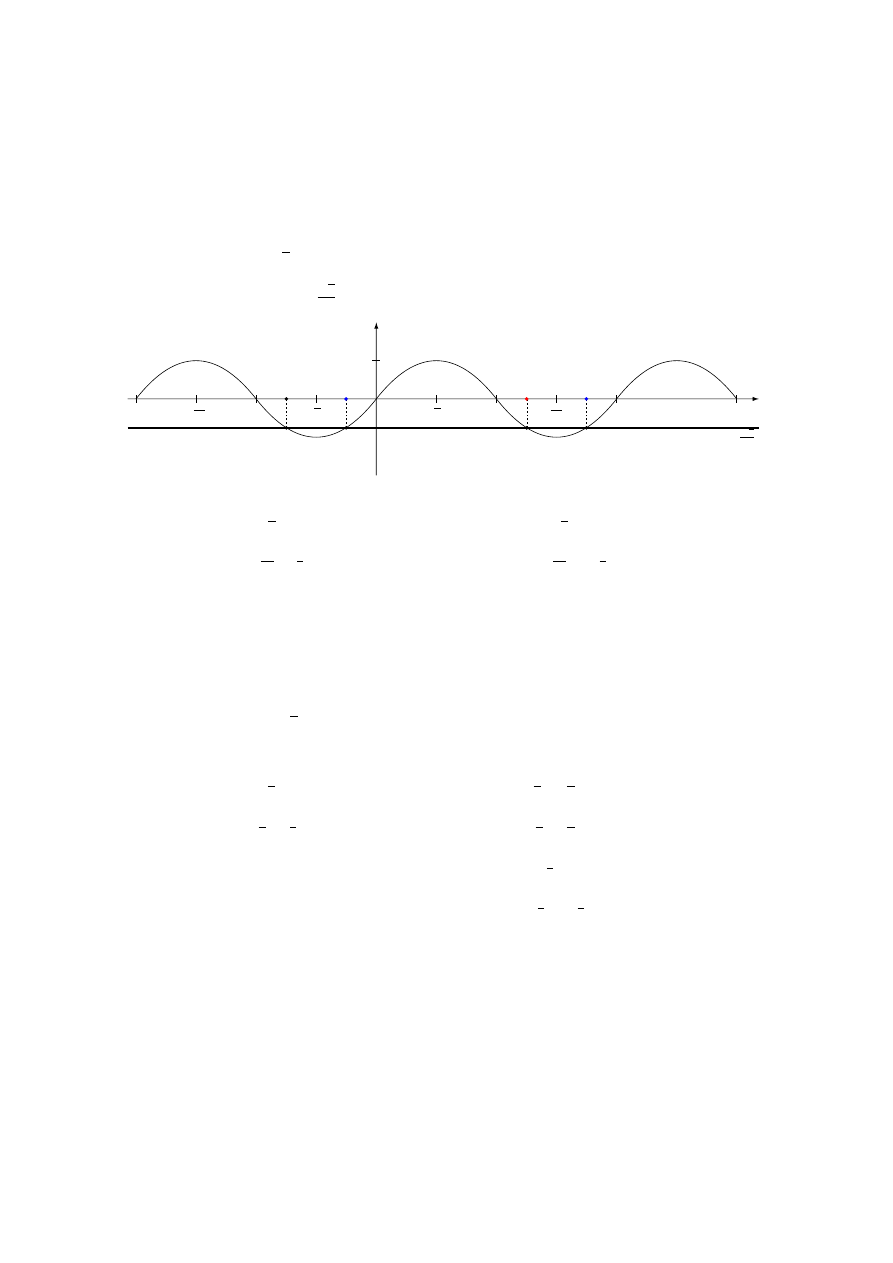
Ponadto zadaję:
Zadanie 8.89 b)
Zadanie 8.90 c)
Zadanie 8.93 b)

Rozwiązania:
8.89 b) 2 sin 3x = −

√

2

sin 3x = −

√

2

2

X

Y

O

1

π

2

π

3π

2

2π

3π

-

π

2

-π

-

3π

2

-2π

y = −

√

2

2

3x = −

π

4

+ 2kπ, k ∈ C

lub

3x =

5
4

π + 2kπ, k ∈ C

x = −

π

12

+

2
3

kπ, k ∈ C

lub

x =

5

12

π +

2
3

kπ, k ∈ C

8.90 c) tg2x =tg(3x −

π

6

)

Dziedzina:

2x 6=

π

2

+ kπ, k ∈ C

i

3x −

π

6

6=

π

2

+ kπ, k ∈ C

x 6=

π

4

+

1
2

kπ, k ∈ C

i

3x 6=

π

2

+

π

6

+ kπ, k ∈ C

3x 6=

2
3

π + kπ, k ∈ C

x 6=

2
9

π +

1
3

kπ, k ∈ C

Rozwiązanie:

20

2x = 3x −

π

6

+ kπ, k ∈ C

2x − 3x = −

π

6

+ kπ, k ∈ C

−x = −

π

6

+ kπ, k ∈ C

x =

π

6

− kπ, k ∈ C

x =

π

6

+ kπ, k ∈ C

Rozwiązanie należy do dziedziny.

8.93 b) sin x cos x − sin

2

x − cos x + sin x = 0

sin x cos x − sin

2

x − cos x + sin x = 0

cos x(sin x − 1) − sin x(sin x − 1) = 0

(sin x − 1)(cos x − sin x) = 0

sin x = 1

lub

cos x = sin x

Wykorzystujemy wzór redukcyjny, aby pozbyć się sinusa lub cosinusa, np. sin(

π

2

− α) =

cos(α).

sin x = 1

lub

sin(

π

2

− x) = sin x

x =

π

2

+ 2kπ, k ∈ C

lub

π

2

− x = x + 2kπ, k ∈ C

lub

π

2

− x = π − x + 2kπ, k ∈ C

−x − x = −

π

2

+ 2kπ, k ∈ C

lub

−x + x = π −

π

2

+ 2kπ, k ∈ C

−2x = −

π

2

+ 2kπ, k ∈ C

lub

0 =

π

2

+ 2kπ, k ∈ C

x =

π

4

+ kπ, k ∈ C

lub

r-nie sprzeczne

Odpowiedź:

x =

π

2

+ 2kπ, k ∈ C

lub

x =

π

4

+ kπ, k ∈ C

21