Część 2
7. METODA MIESZANA
1
7.
7. METODA MIESZANA
Metoda mieszana polega na jednoczesnym wykorzystaniu metody sił i metody przemieszczeń przy
rozwiązywaniu układów statycznie niewyznaczalnych. Nawiązuje ona do twierdzenia o wzajemności reakcji i
przemieszczeń. Jej celem jest ograniczenie liczby niewiadomych. Układ dzieli się na część, którą korzystniej
jest rozwiązać metodą sił i część, którą łatwiej rozwiązać metodą przemieszczeń.
W celu zobrazowania zastosowania metody mieszanej rozwiążmy następujące zadania:
Zadanie 1
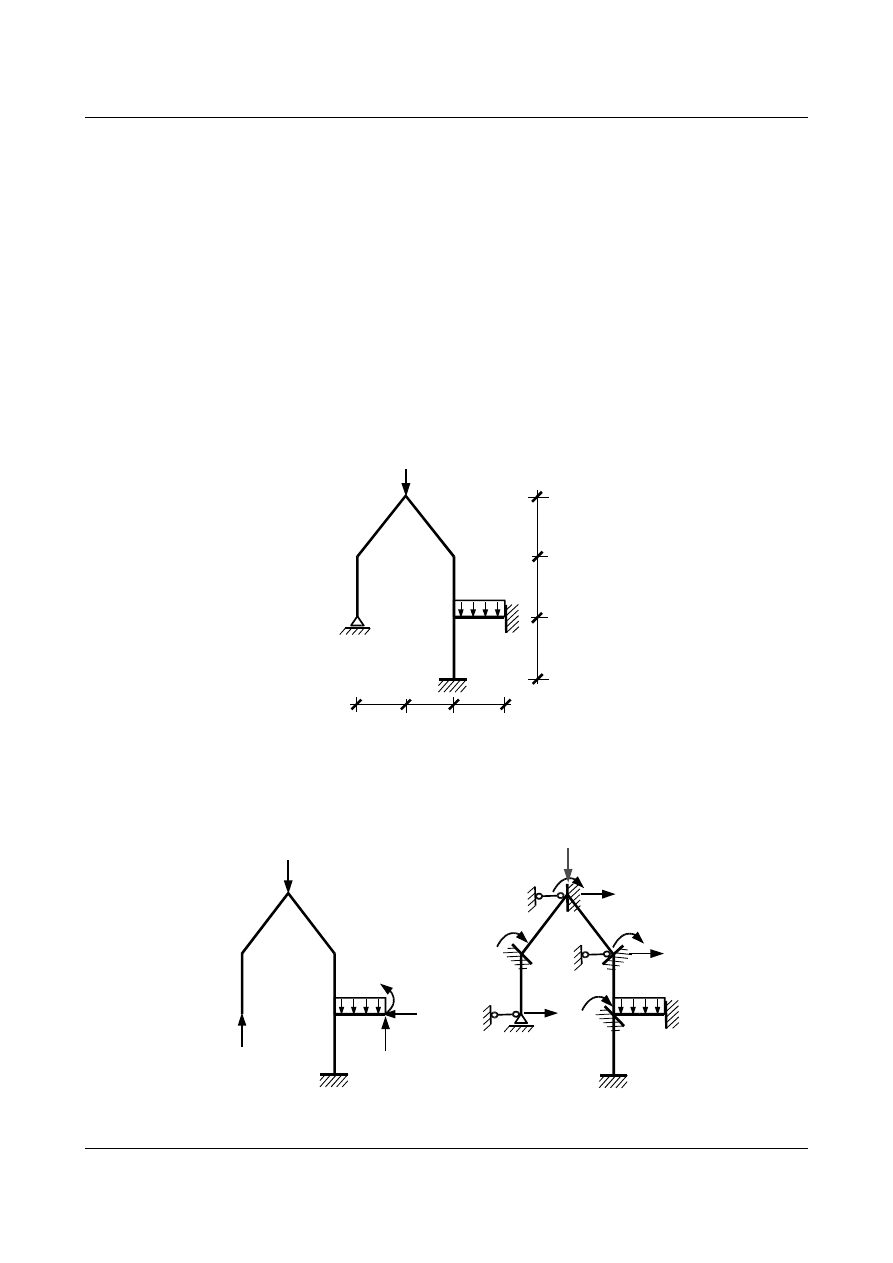
Znajdź siły wewnętrzne w prętach ramy statycznie niewyznaczalnej:
P
a
q
a
a
b
b
b
Rys. 7.1. Rama statycznie niewyznaczalna
Zauważmy, że rozwiązując powyższą ramę klasycznie metodą sił liczba nadliczbowych niewiadomych
wynosiłaby 4, natomiast analizując dany przykład w metodzie przemieszczeń liczba niewiadomych wzrosłaby
do 7 (rys. 7.2).
P
q
a)
X
1
X
2
X
3
X
4
φ
1
φ
2
φ
3
φ
4
u
5
u
7
u
6
P
q
b)
Rys. 7.2. Liczba niewiadomych dla a) metody sił b) dla metody przemieszczeń
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
2
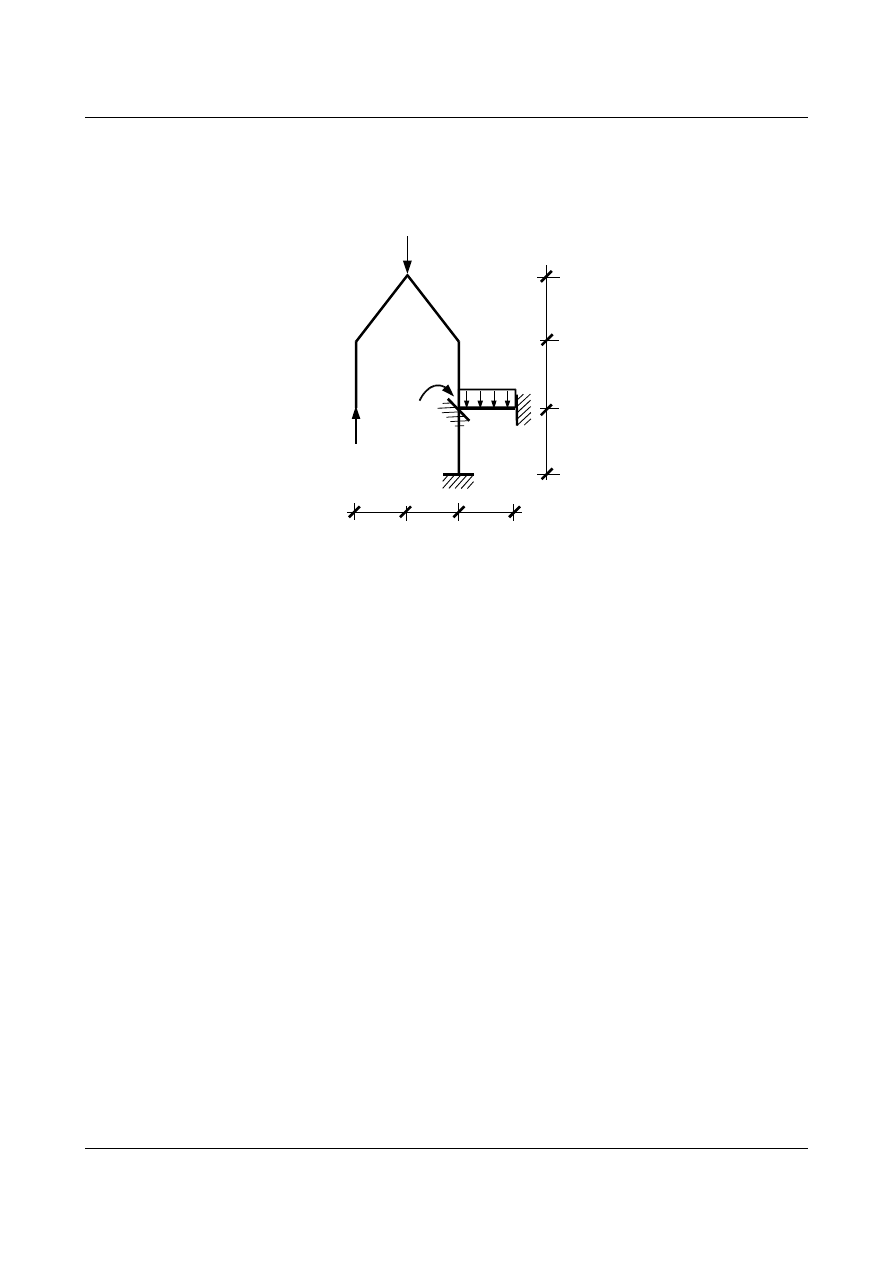
Rozwiązanie powyższego układu znacznie uprości odpowiednie połączenie metody przemieszczeń z metodą
sił. W metodzie mieszanej najkorzystniejszy będzie następujący układ podstawowy:
P
q
X
1
φ
2
A
B
b
b
b
a
a
a
Rys. 7.3. Układ podstawowy w metodzie mieszanej
W tak przyjętym schemacie statyczna zgodność z układem rzeczywistym zachowana została przez
wprowadzenie siły
X
1
, ale zakłócona przez wprowadzenie wewnętrznego utwierdzeniem. Kinematyczna
zgodność została zakłócona odrzuceniem podpory w punkcie
A.
Układy podstawowy i rzeczywisty będą identyczne jeśli spełnimy następujące warunki:
A
=0
M
B
=0
Po ich rozpisaniu uzyskujemy układ równań kanonicznych
{
11
X
1
12
2
1 P
=0
r
21
X
1
r
22
2
R
2 P
=0
W metodzie mieszanej ważna jest interpretacja niektórych współczynników:
-
12
jest przemieszczeniem pionowym punktu
A wywołanym jednostkowym obrotem podpory B (o kąt
φ
2
=
1),
- r
21
jest reakcją (momentem) w punkcie
B wywołaną jednostkową siłą przyłożoną w punkcie A (X
1
=
1).
Kolejnym etapem jest wykonanie wykresów momentów w poszczególnych stanach.
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
3
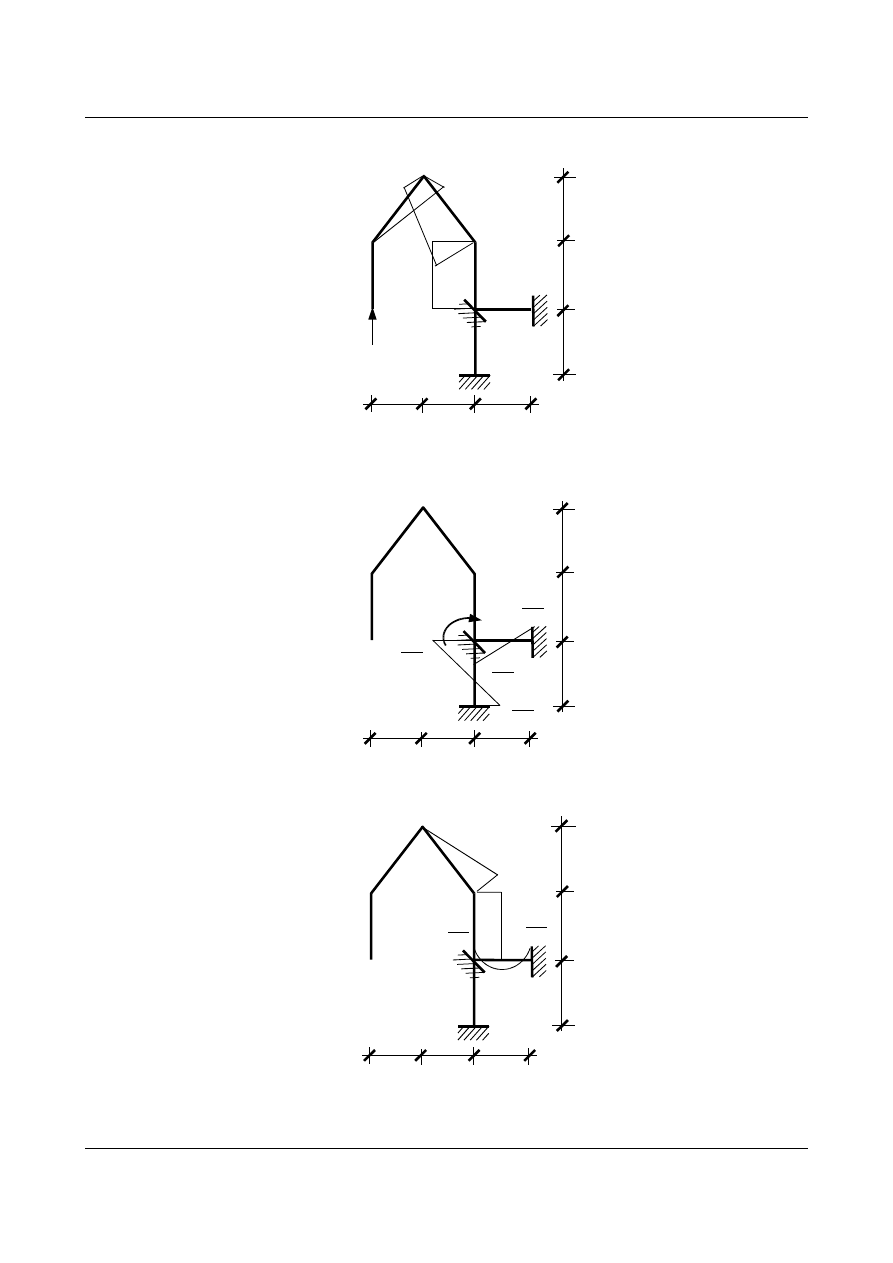
Stan dla pierwszej niewiadomej, czyli
X
1
=
1
X
1
A
B
b
b
b
a
a
a
0
0
0
a
a
2a
2a
M
1
[m]
Rys. 7.4. Wykres momentów dla stanu X
1
= 1
Stan dla drugiej zmiennej, czyli
φ
2
=
1
b
b
b
a
a
a
φ
2
=1
M
2
[m]
4EJ
b
4EJ
a
2EJ
b
2EJ
a
0
0
0
0
Rys. 7.5. Wykres momentów dla stanu φ
2
= 1
Stan
P
b
b
b
a
a
a
0
0
M
P
[kNm]
qa
2
12
qa
2
12
Pa
Pa
0
Rys. 7.6. Wykres momentów dla stanu P
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
4
Obliczmy współczynniki układu równań kanonicznych. W celu obliczenia współczynnika
δ
11
korzystamy z
równania pracy wirtualnej (jak w klasycznej metodzie sił):
11
=
∫
s
M
1
2
EJ
ds
(7.1)
11
=
1
EJ
⋅
[
1
2
⋅
a
2
b
2
⋅a⋅
2
3
⋅a
1
2
⋅
a
2
b
2
⋅2 a
2
3
⋅2 a
1
3
⋅a
1
2
⋅
a
2
b
2
⋅a
2
3
⋅a
1
3
⋅2 a
b⋅2 a⋅2 a
]
=
=
1
EJ
⋅
a
2
3
⋅
a
2
b
2
5 a
2
3
⋅
a
2
b
2
2 a
2
3
⋅
a
2
b
2
4 a
2
b
=
1
EJ
⋅
8
3
a
2
l
4 a
2
b
gdzie l=
a
2
b
2
Do wyznaczenia współczynnika
r
21
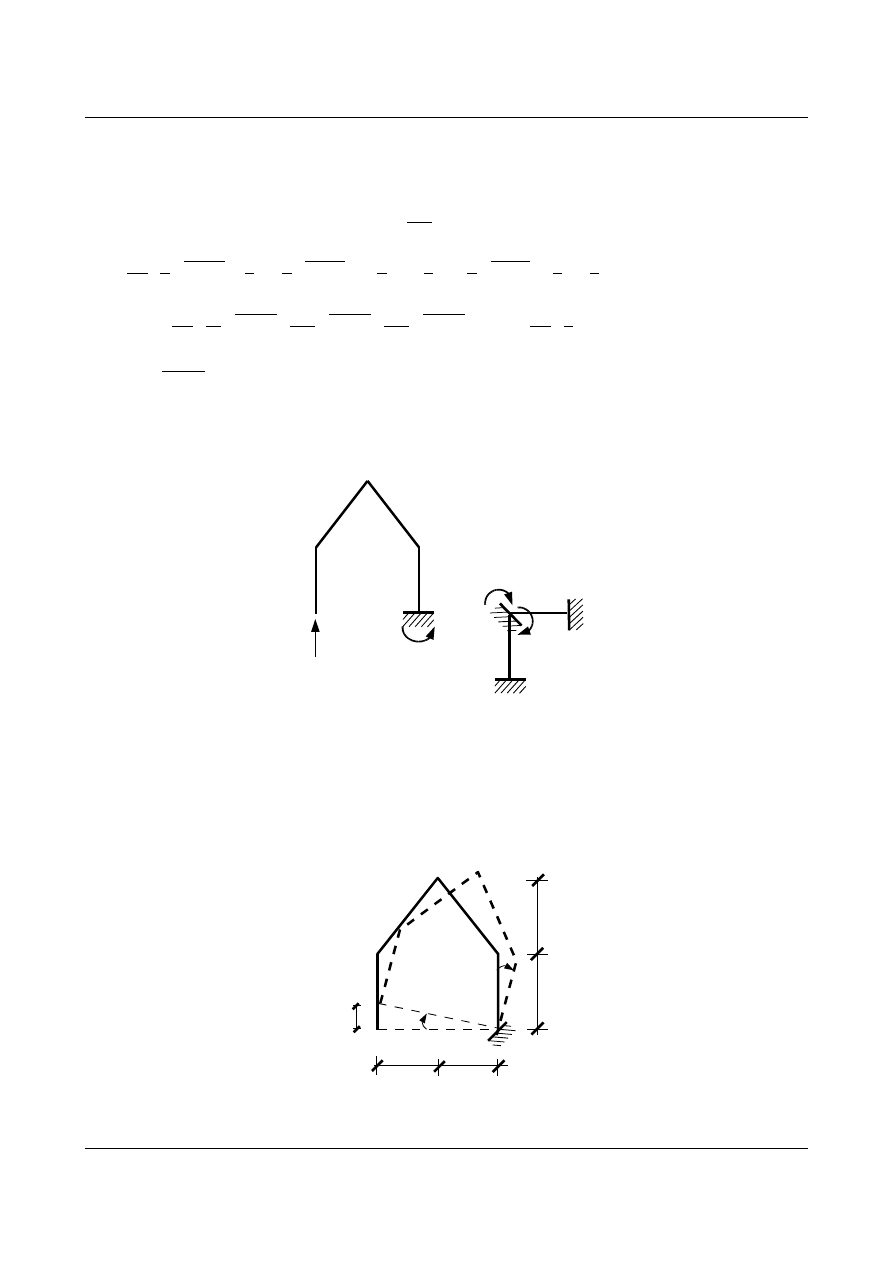
potrzebna jest głębsza analiza. Moment zginający w podporze
B wywołany
działaniem siły
X
1
= 1 wyznaczamy zapisując równanie równowagi dla węzła B.
r
21
2a
2a
X
1
= 1
Rys. 7.7. Moment w podporze B wywołany jednostkową siłą
r
21
=−2 a
(7.2)
Podobnie współczynnik
δ
12
trzeba wyznaczyć inaczej niż w klasycznej metodzie sił (jest to przemieszczenie
wywołane przemieszczeniem). Przemieszczenie po kierunku niewiadomej
X
1
, wywołane obrotem węzła
B o kąt
φ
2
=
1.
a
a
b
b
φ
2
=1
δ
12
φ
2
=1
Przyjmując, że
tg φ
2
≈ φ
2
=
1 otrzymujemy:
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
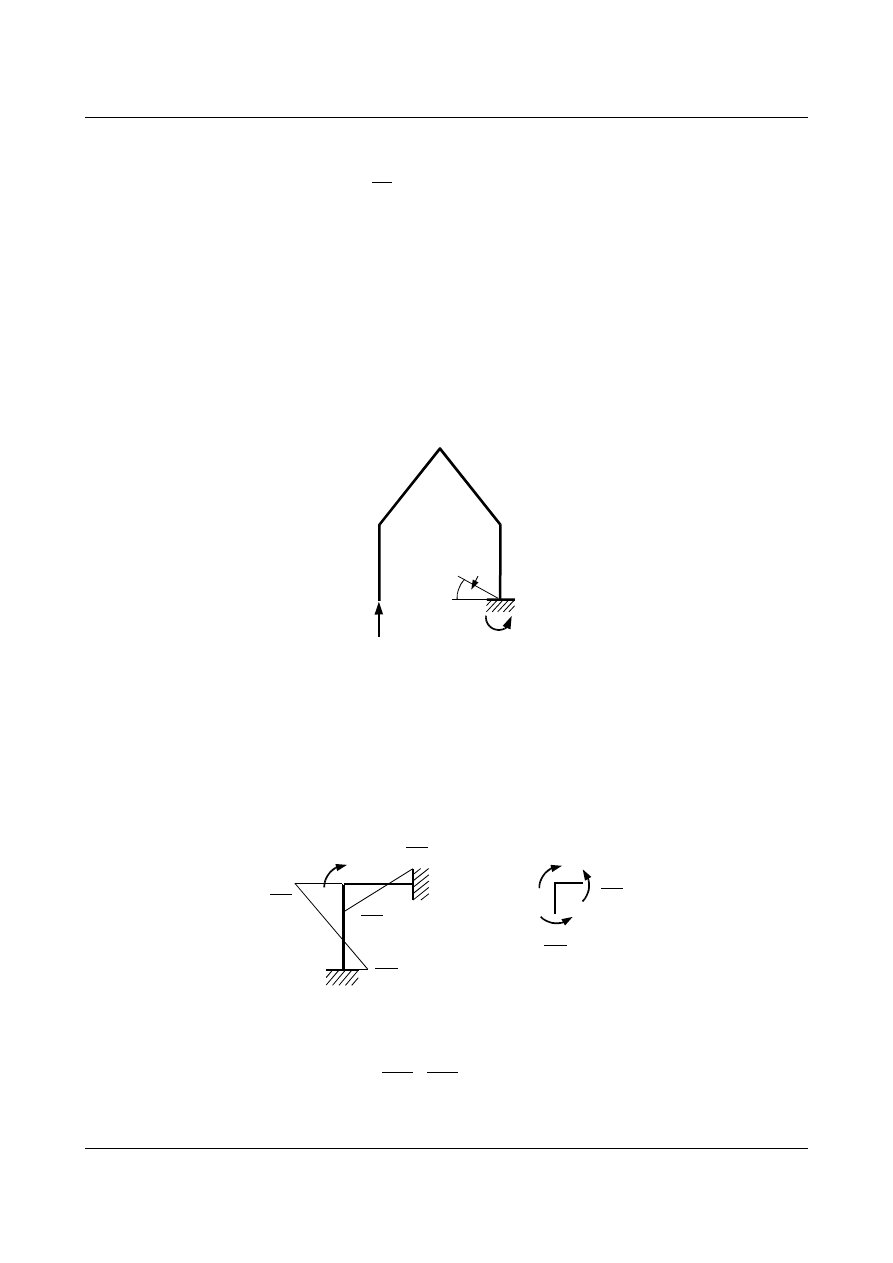
Część 2
7. METODA MIESZANA
5
12
2 a
=tg
2
12
=2 a
(7.3)
W bardziej skomplikowanych przypadkach wykorzystujemy równanie pracy wirtualnej stosowane do
obliczania przemieszczeń w układach statycznie wyznaczalnych.
1⋅
i
=−
∑
R
i
⋅
i
W naszym przypadku
12
=−
∑
R
1
⋅
2
(7.3)
2a
X
1
= 1
φ
2
= 1
12
=−−2 a⋅1=2 a
(7.3)
Warto zauważyć, że zgodnie z twierdzeniem o wzajemności przemieszczeń i reakcji
r
21
= -
δ
12
.
Reakcję uogólnioną po kierunku niewiadomej
2 spowodowaną obrotem kąta φ
2
wyznaczymy z równania
równowagi węzła
B zgodnie z klasyczną metodą przemieszczeń (stan φ
2
=
1).
r
22
4EJ
b
4EJ
a
2EJ
b
2EJ
a
4EJ
b
4EJ
a
r
22
stąd:
r
22
=
4 EJ
a
4 EJ
b
(7.4)
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
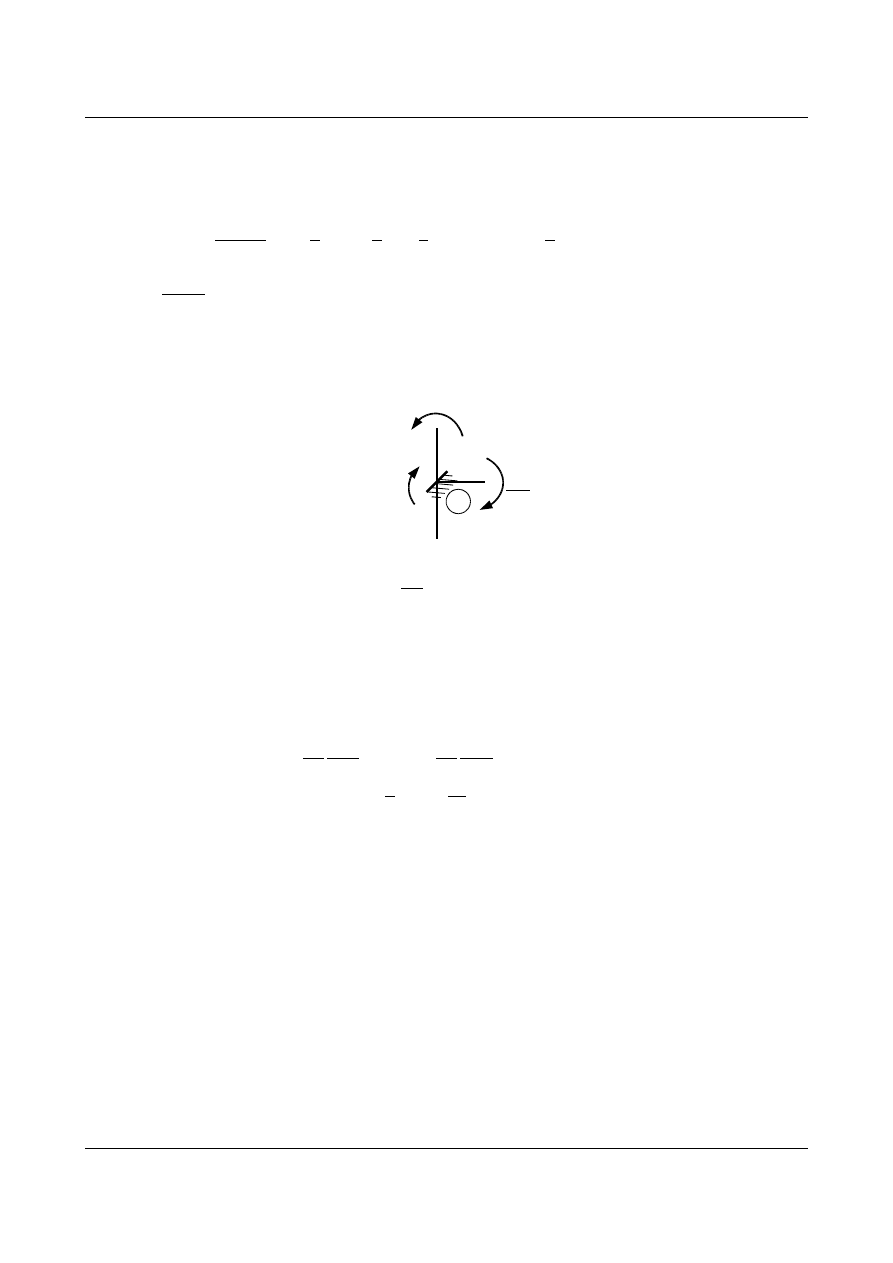
Część 2
7. METODA MIESZANA
6
Przemieszczenie po kierunku niewiadomej
1 spowodowane obciążeniem zewnętrznym wyznaczymy stosując
równanie pracy wirtualnej, mnożąc wykres z rys. 7.4 przez wykres z rys. 7.6:
1 P
=
∫
s
M
1
⋅M
P
o
EJ
⋅ds=−
1
2
⋅P⋅a⋅l⋅
2
3
⋅2 a
1
3
⋅a
−P⋅a⋅b⋅2 a=−
5
6
Pa
2
l
−2 Pa
2
b
(7.5)
gdzie l=
a
2
b
2
Reakcję po kierunku niewiadomej
2 spowodowaną działaniem obciążenia zewnętrznego obliczymy z równania
równowagi zapisanego dla węzła
B w stanie P:
R
2P
Pa
qa
2
12
0
B
R
2 P
=−
qa
2
12
Pa
(7.6)
Dalsze obliczenia przeprowadzono przyjmując następujące wielkości liczbowe:
a = 4m, b = 3m, l = 5m,
q = 8 kN/m, P = 10 kN, EJ [kNm
2
].
Po ich podstawieniu otrzymano następujący układ równań kanonicznych metody przemieszczeń:
{
1
EJ
1216
3
⋅X
1
8
2
−
1
EJ
4480
3
=0
−8 X
1
7
3
EJ
2
88
3
=0
Rozwiązanie tego układu prowadzi do wartości nadliczbowej reakcji
X
1
i nieznanego przemieszczenia w węźle
B:
•
X
1
= 3,991197183 [kN]
•
EJφ
2
= 1,112676056
Ostateczne wykresy sił wewnętrznych uzyskamy obciążając układ obliczonymi zmiennymi lub z zasady
superpozycji przez zsumowanie wykresów jednostkowych przemnożonych przez wartości zmiennych
X
1
i
φ
2
.
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
7
4
4
4
3
3
3
M
[kNm]
0
15,965
8,070
11,223
9,554
1,484
0,742
[m]
Rys. 7.9. Wykres momentów w układzie niewyznaczalnym
T [kN]
0
3,193
16,417
15,583
0,742
0,742
3,193
-
4,807
4,807
+
0
-
+
-
[m]
3
3
3
4
4
4
Rys. 7.10. Wykres sił tnących
-
-
-
[m]
3
3
3
4
4
4
N [kN]
0,742
9,574
3,991
3,605
6,009
+
-
-
2,394
Rys. 7.11. Wykres sił normalnych
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
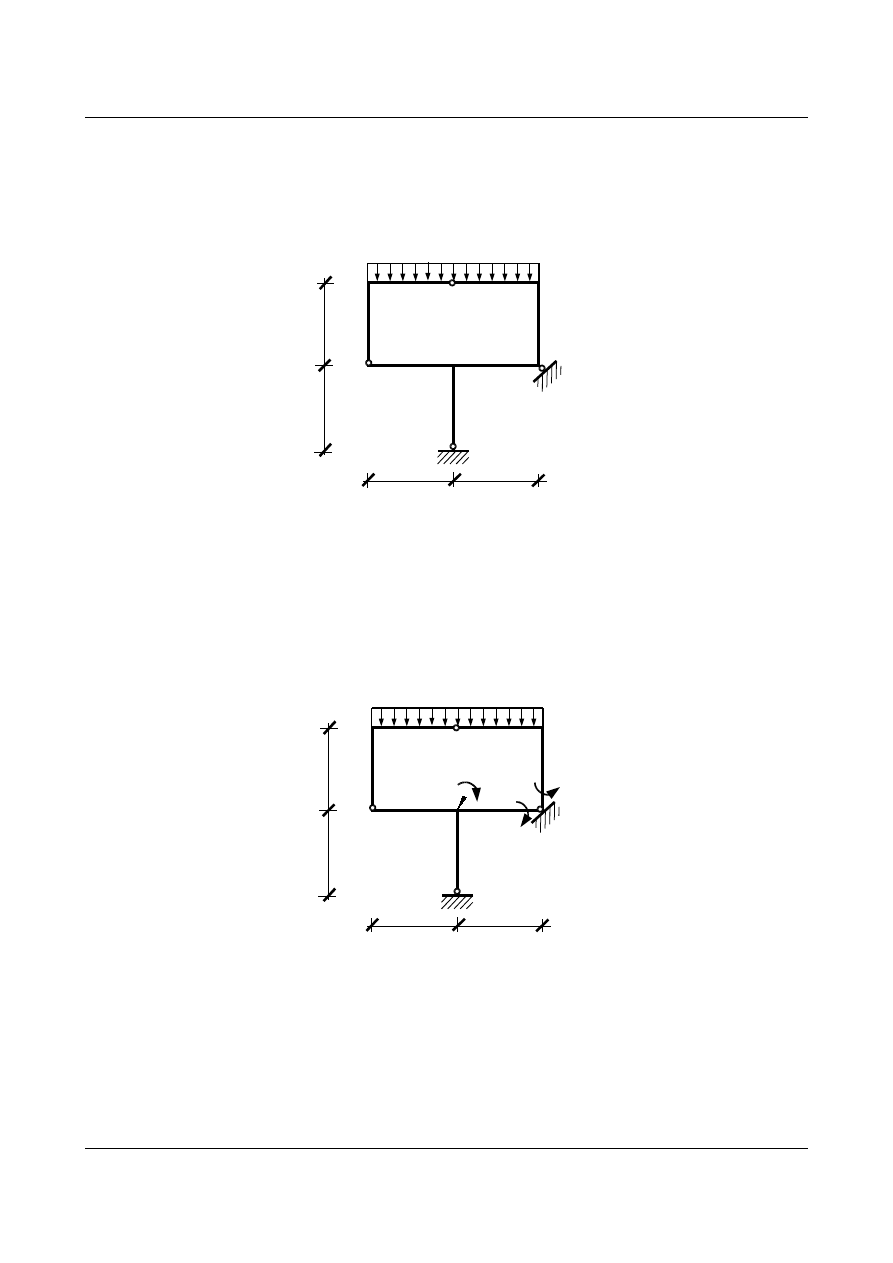
Część 2
7. METODA MIESZANA
8
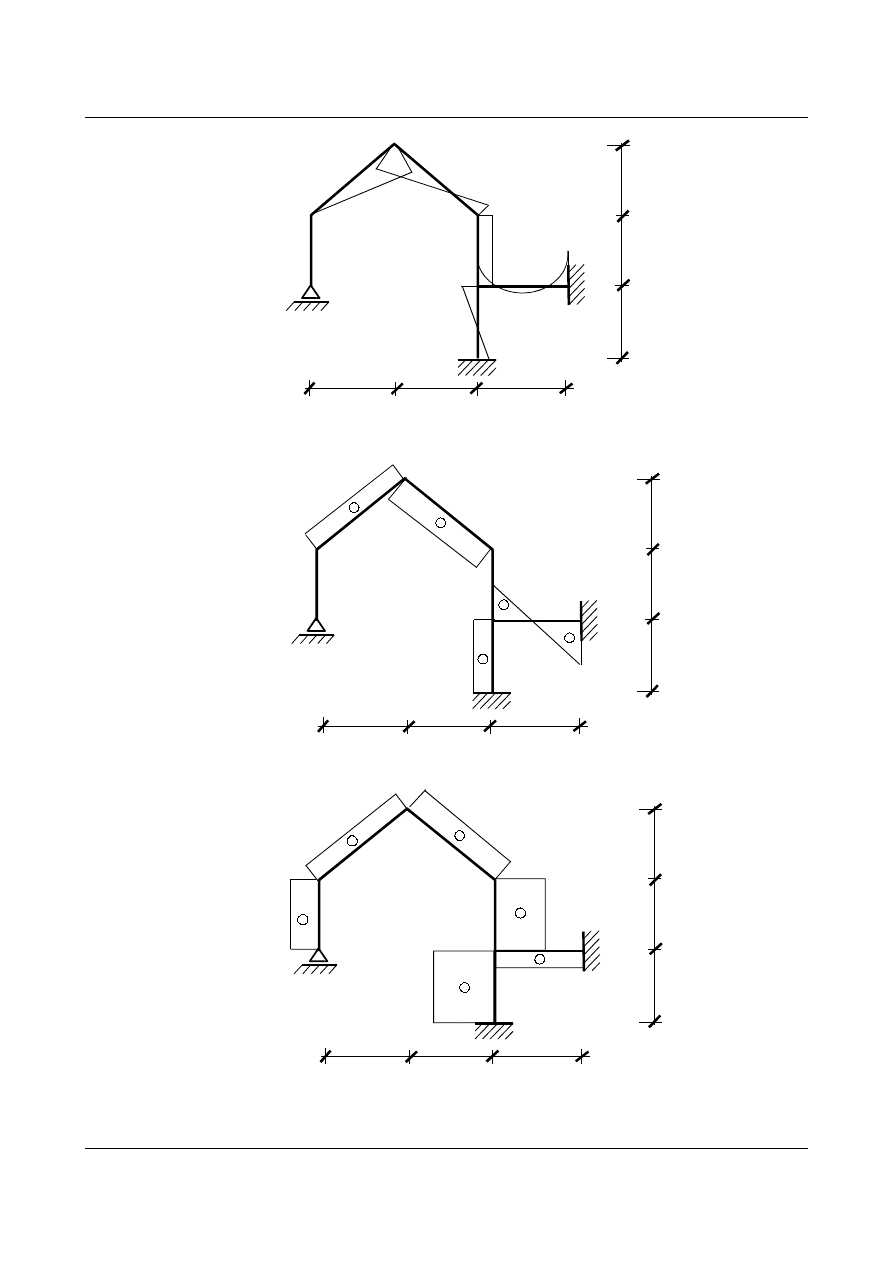
Zadanie 2
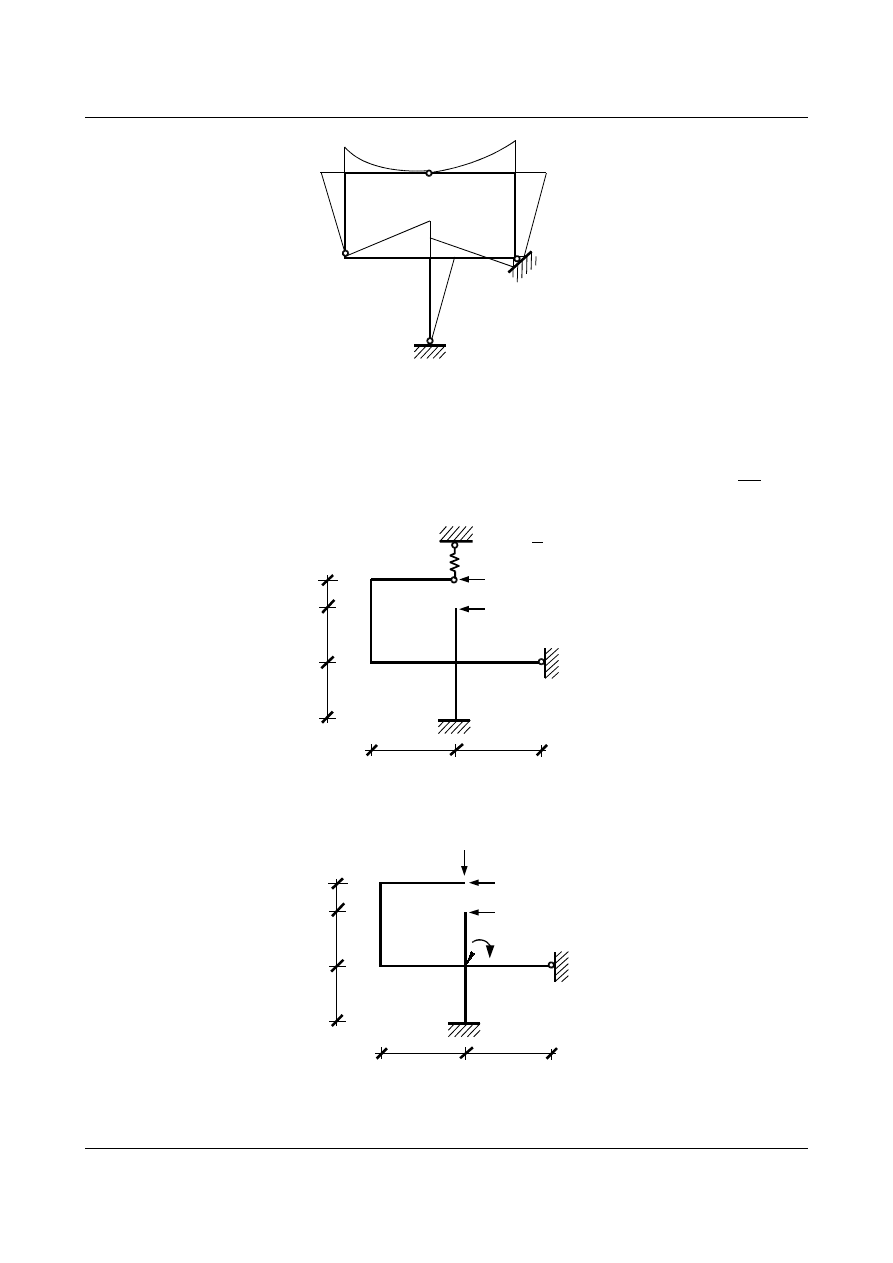
Wyznaczyć wykres momentów rzeczywistych dla ramy o następującym schemacie, (
EJ = const.):
3
3
3
3kN/m
EJ = const
3
B
A
C
[m]
Rys. 7.12. Schemat ramy
Żeby rozwiązanie tego układu było jak najprostsze, górną część ramy wraz z dolnym lewym ryglem należy
rozwiązać metodą sił, natomiast prawy rygiel i słup dolny rozwiązać metodą przemieszczeń. W tym celu
górną część zamieniamy na układ trójprzegubowy przez wprowadzenie przegubu w sztywne naroże ramy przy
podporze
C. Pociąga to za sobą konieczność wprowadzenia niewiadomej w postaci momentu X
1
. Natomiast w
miejscu zbiegania się trzech prętów wprowadzamy utwierdzenie blokujące obrót co wiąże się z potrzebą
uwzględnienia niewiadomej
φ
2
. (Rys. 7.13).
3
3
3
φ
2
3kN/m
3
[m]
X
1
X
1
Rys. 7.13. Układ podstawowy
Otrzymaliśmy zatem układ dwukrotnie niewyznaczalny z tym, że jedną niewiadomą jest siła, a drugą
przemieszczenie. Napiszmy zatem układ równań kanonicznych:
{
11
X
1
12
2
1 P
=0
r
21
X
1
r
22
2
R
2 P
=0
(7.7)
Aby otrzymać odpowiednie przemieszczenia i reakcje narysujmy wykresy momentów w stanach
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
9
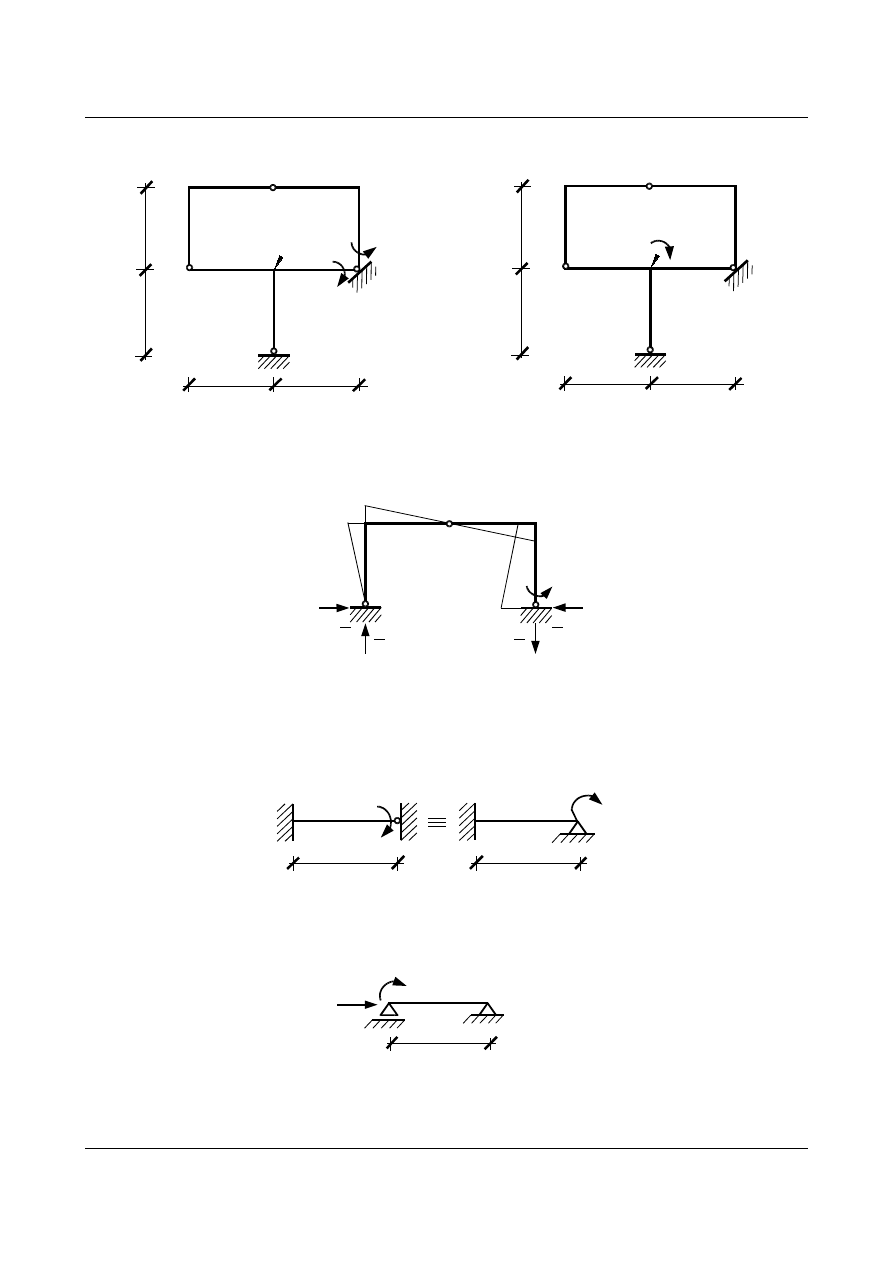
jednostkowych poszczególnych niewiadomych.
3
3
3
3
[m]
X
1
X
1
B
A
C
Rys. 7.14. Stan X
1
= 1
3
3
3
3
[m]
B
A
C
φ
2
=1
Rys. 7.15. Stan φ
2
=1
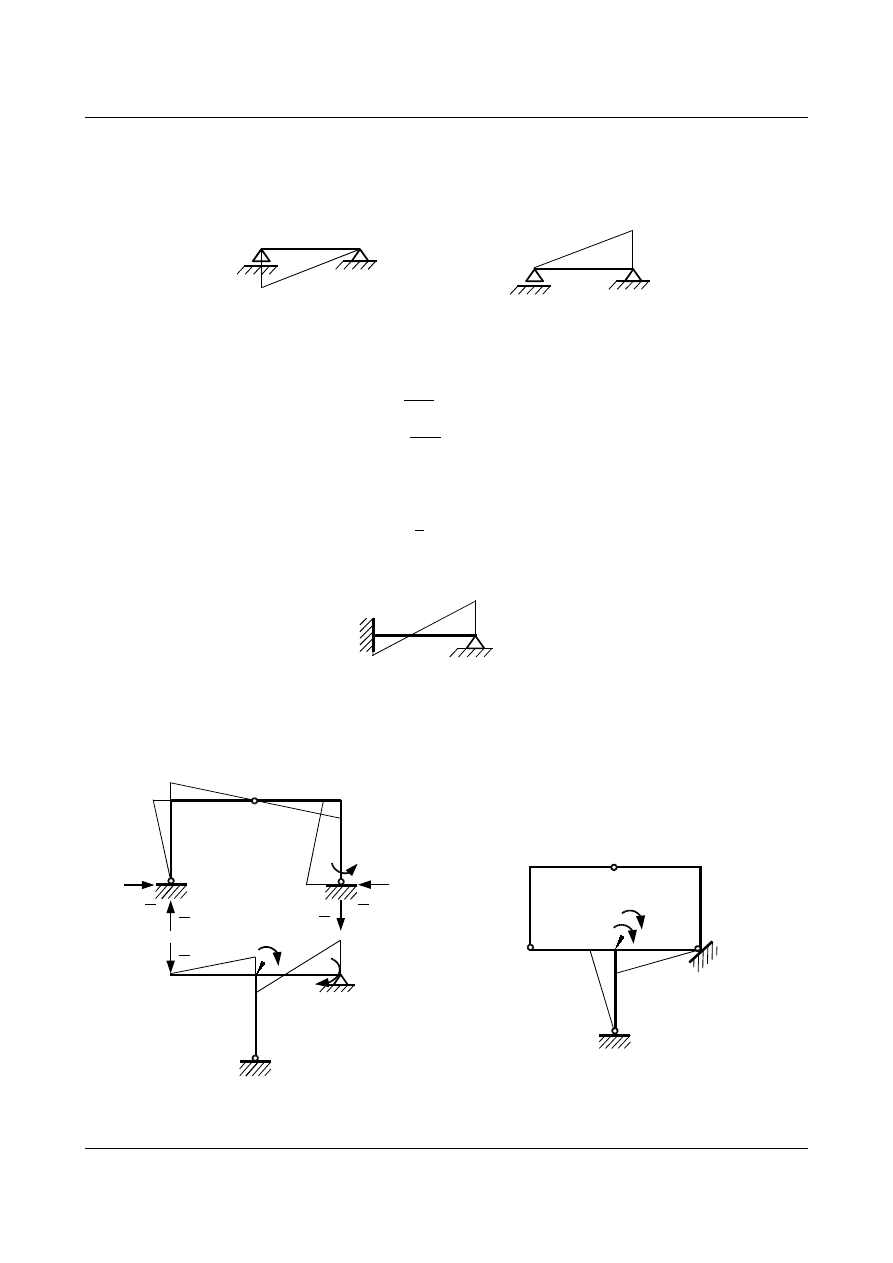
Aby otrzymać wykres od
X
1
=
1 rozwiążmy najpierw układ trójprzegubowy obciążony momentem
jednostkowym działającym powyżej przegubu
C.
1
1
6
1
6
1
6
1
6
0,5
1,0
0,5
Rys. 7.16. Wykres momentów w statycznie wyznaczalnej części układu podstawowego (układ trójprzegubowy)
Analizując działanie momentu jednostkowego z drugiej strony przegubu
C okazuje się, że obciąża on część
ramy statycznie niewyznaczalną. Aby wyznaczyć wykres momentów od tego obciążenia rozwiążemy belkę jak
na poniższym schemacie.
1
l
l
1
Rys. 7.17. Belka utwierdzona z jednej strony i podparta przegubowo z drugiej
Rozwiążemy kolejne, nowe zadanie metodą sił dlatego dla odróżnienia symboli będziemy używać oznaczeń z
(*).
X
1
*
l
X
2
*
Rys. 7.18. Układ podstawowy
Siła
X
2
* nie wywołuje momentów zginających, co w konsekwencji ogranicza układ dwóch równań
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
10
kanonicznych do jednej równości:
11
*
X
1
*
1 P
*
=0
(7.8)
1
M
1
*
1
M
P
*
Rys. 7.19. Wykresy momentów dla belki od X
1
* = 1 i od obciążenia zewnętrznego
Po wyznaczeniu współczynników
11
*
=
l
3 EJ
1 P
*
=−
l
6 EJ
Wyliczamy wartość nadliczbowej
X
1
*
=
l
2
(7.9)
i tworzymy wykres momentów w belce niewyznaczalnej z rys. 7.17.
1
0,5
M
(n)
Rys. 7.20. Wykresy momentów rzeczywistych dla belki
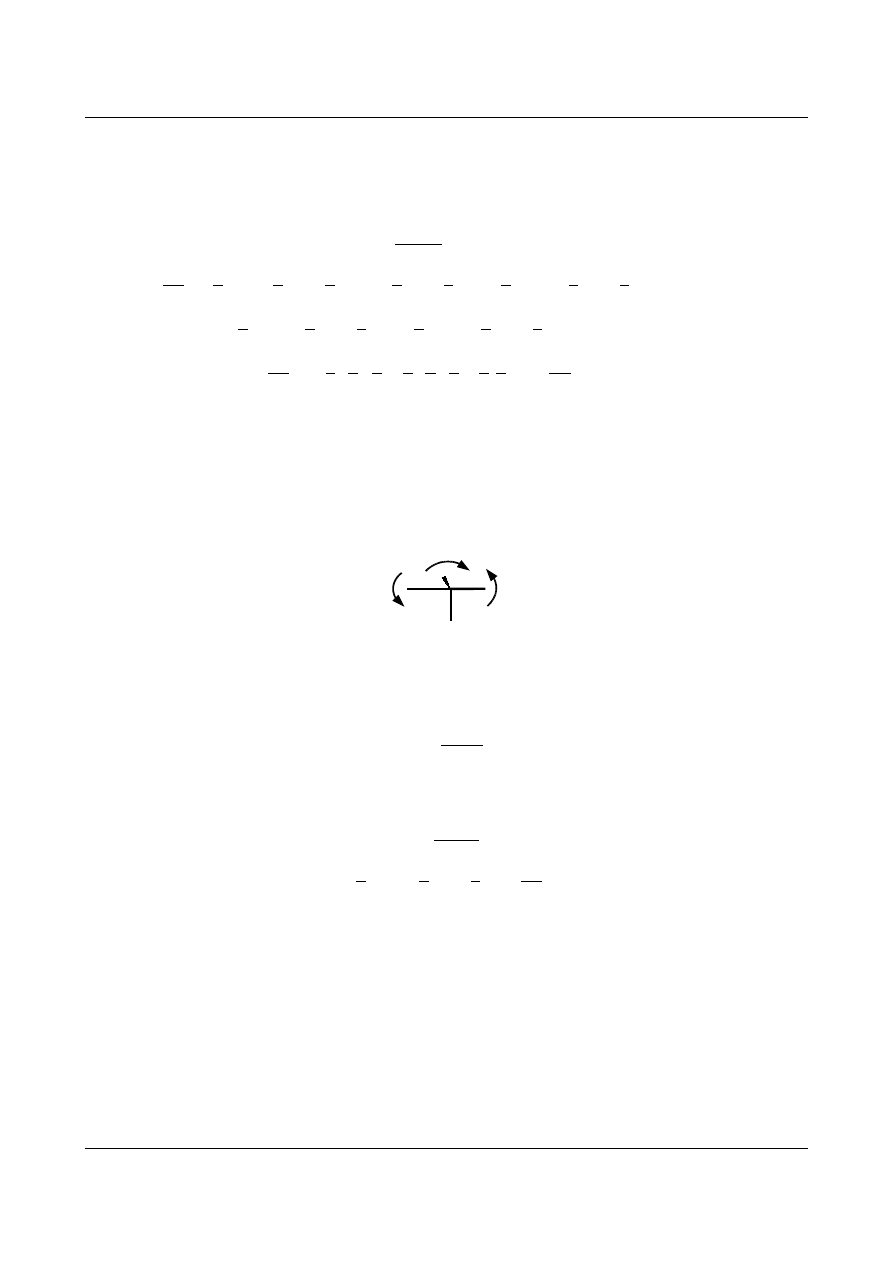
Na podstawie rys. 7.16 i 7.20 oraz wzorów transformacyjnych (patrz wykład 1) otrzymaliśmy wykresy
od poszczególnych stanów jednostkowych.
X
1
= 1
1
6
1
6
1
6
1
6
0,5
1,0
0,5
1
6
1,0
0,5
0,5
M
1
r
21
X
1
= 1
Rys. 7.21. Wykres momentów w stanie X
1
= 1
EJ
M
2
EJ
φ
2
=1
r
22
Rys. 7.22. Wykres momentów w stanie φ
2
= 1
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
11
Teraz możemy wyznaczyć współczynniki równania kanonicznego metody mieszanej:
•
według zasad metody sił:
11
=
∫
M
1
M
1
EJ
ds
11
=
1
EJ
⋅
[
4
⋅
1
2
⋅0,5 ⋅3 ⋅
2
3
⋅0,5
1
2
⋅1,0 ⋅3 ⋅
2
3
⋅1,0
1
3
⋅0,5
1
2
⋅0,5 ⋅3 ⋅
1
3
⋅1,0
2
3
⋅0,5
1
2
⋅1,0 ⋅3 ⋅
2
3
⋅1,0 −
1
3
⋅0,5
1
2
⋅0,5 ⋅3 ⋅
2
3
⋅0,5 −
1
3
⋅1,0
]
11
=
1
EJ
⋅
[
1
3
2
⋅
2
3
1
6
3
4
⋅
2
6
1
3
3
2
⋅
1
2
0
]
=
3,5
EJ
•
według zasad metody przemieszczeń
r
22
=EJ EJ =2 EJ
•
reakcję w węźle
B w stanie X
1
= 1 (z równowagi węzła):
r
21
0,5
0,5
r
21
=1,0
•
przemieszczenie (wzajemny obrót) po kierunku
1 w stanie φ
2
=
1 (z równania pracy wirtualnej):
1⋅
i
=−
∑
R
i
⋅
i
∫
s
M M
EJ
ds
zapisujemy:
12
=−
∑
R
2
⋅
1
∫
s
M
1
M
2
EJ
ds
12
=−r
21
⋅
1
2
⋅EJ⋅3 ⋅
2
3
⋅0,5 −
1
3
⋅1,0
⋅
1
EJ
12
=−1 ⋅1 =−1,0
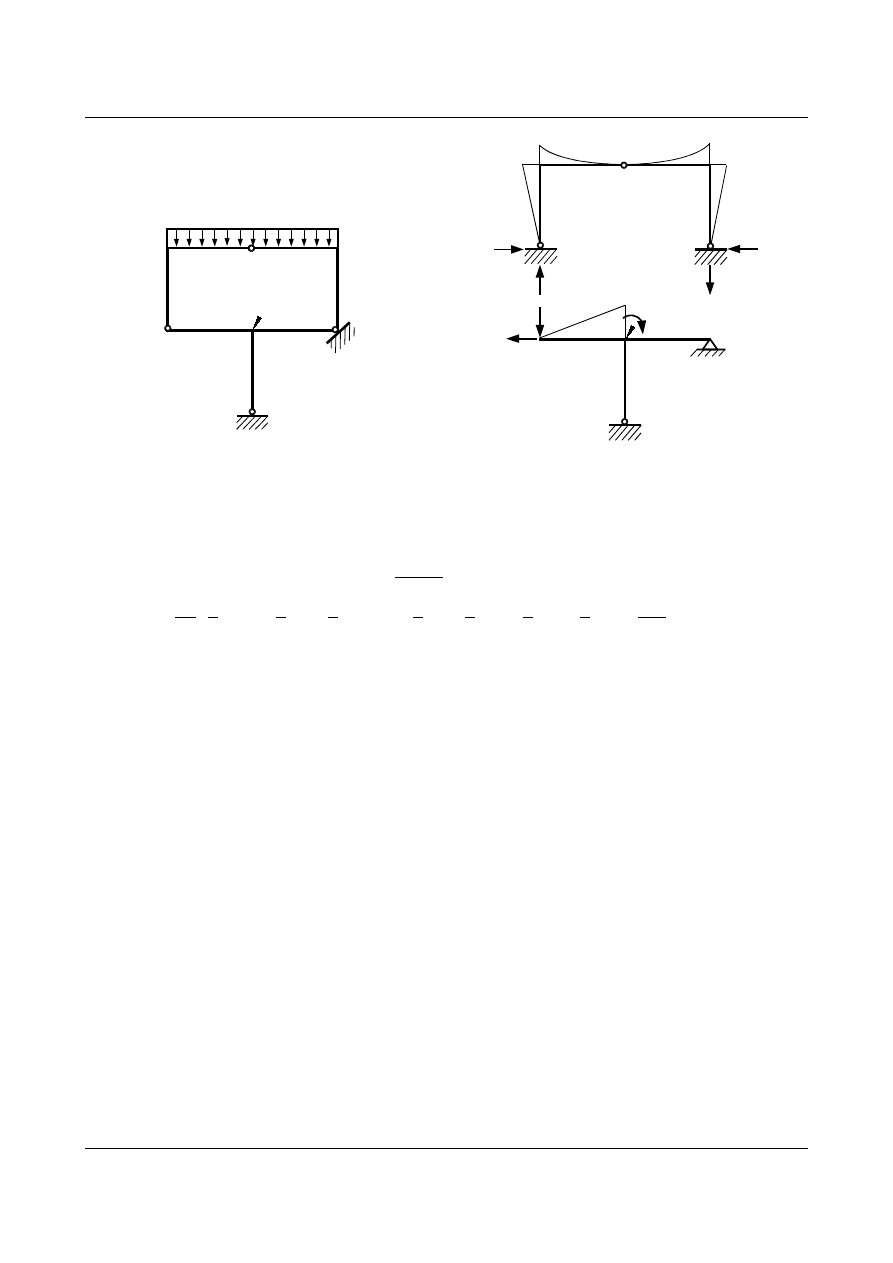
Żeby rozwiązać zadanie potrzebujemy jeszcze wykres od obciążenia zewnętrznego w układzie podstawowym.
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
12
B
A
C
3kN/m
Rys. 7.23. Stan P
4,5
0,5
1,0
13,5
27,0
4,5
9,0
9,0
9,0
4,5
13,5
M
P
(o)
r
2p
Rys. 7.24. Wykres momentów M
P
(o)
Na podstawie rys. 7.21 i rys. 7.24 wyznaczamy współczynniki
δ
1P
oraz r
2P
. Przemieszczenie po kierunku 1,
czyli wzajemny obrót przekrojów przy przegubie
C od obciążenia zewnętrznego wynosi:
1 P
=
∫
M
1
M
P
EJ
ds
1 P
=
1
EJ
⋅
[
1
2
⋅13,5 ⋅3 ⋅
2
3
⋅0,5
1
2
⋅13,5 ⋅3 ⋅
−
2
3
⋅0,5 −
1
3
⋅1,0
1
2
⋅27 ⋅3 ⋅
2
3
⋅0,5
]
=
6,75
EJ
Reakcję po kierunku
2 obliczamy z równowagi węzła B:
r
2 P
=27 [kNm]
Równania kanoniczne będą miały postać:
{
3,5
⋅X
1
−1,0 ⋅
2
⋅EJ =−6,75
1,0
⋅X
1
2,0 ⋅
2
⋅EJ =−27
(7.10)
Z nich wyznaczamy niewiadome
X
1
=−5,0625 [kNm]
EJ
2
=−10,96875
Korzystając z zasady superpozycji wyznaczamy wykres momentów rzeczywistych (rys. 7.25).
M
n
=M
P
o
M
1
⋅X
1
M
2
⋅
2
(7.11)
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
13
10,96875
10,96875
24,46875
16,03125
5,0625
13,5
M
(n)
[kNm]
Rys. 7.25. Wykres momentów rzeczywistych
Zadanie 3
Wyznaczyć wykres momentów rzeczywistych dla ramy o następującym schemacie (
EJ = const, k
=
EJ
9
).
3
3
2
6 kN
2
6 kN
1
[m]
EJ = const
k=
A
B
EJ
1
9
Rys. 7.26. Schemat ramy niewyznaczalnej
Na początek przyjmujemy układ podstawowy metody mieszanej.
3
3
2
X
1
6 kN
2
6 kN
1
φ
2
[m]
Rys. 7.27. Układ podstawowy metody mieszanej
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
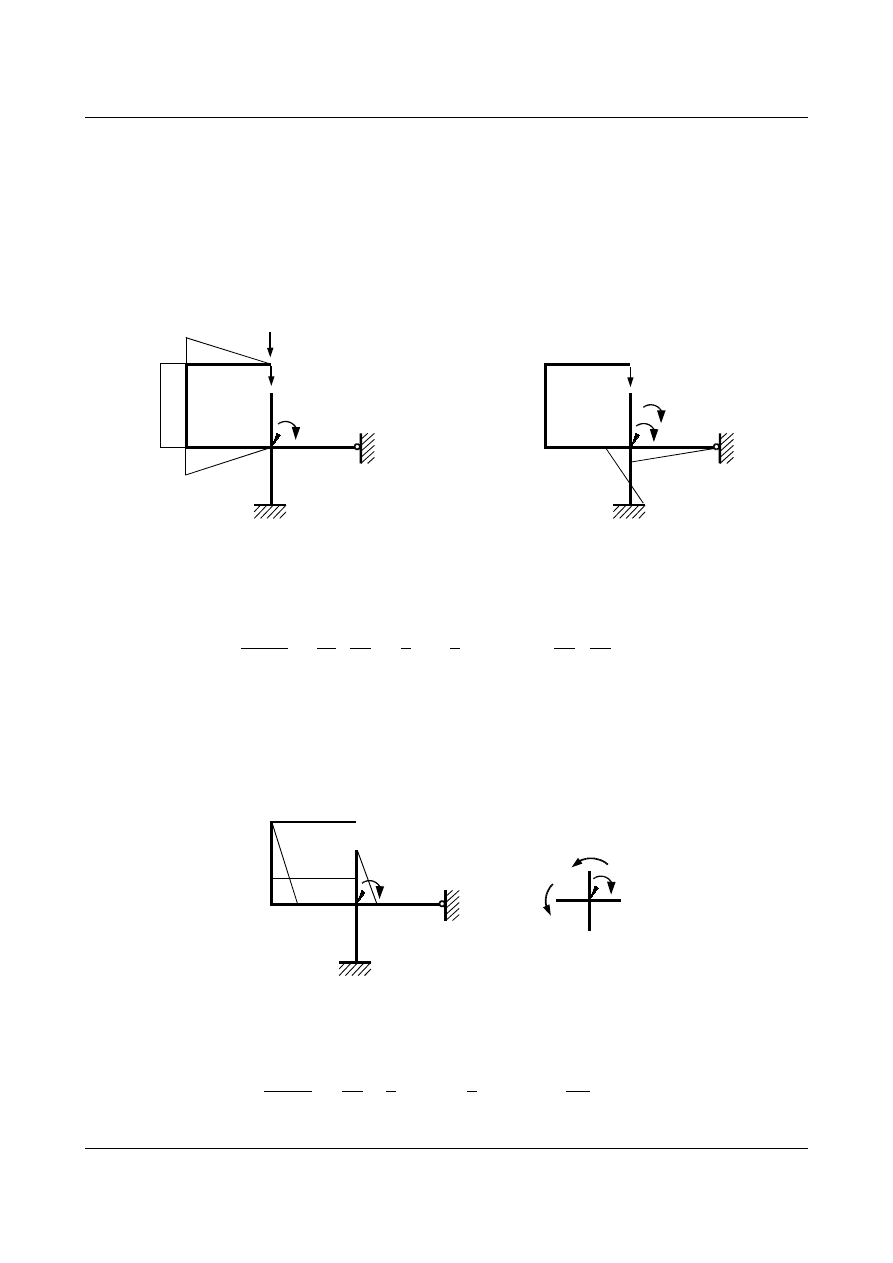
Część 2
7. METODA MIESZANA
14
Przemieszczenie po kierunku odrzuconej podpory
A oraz reakcja w punkcie B od wszystkich wpływów muszą
być równe zeru:
{
1
=
11
X
1
12
2
1 P
=0
r
2
=r
21
X
1
r
22
2
R
2 P
=0
(7.12)
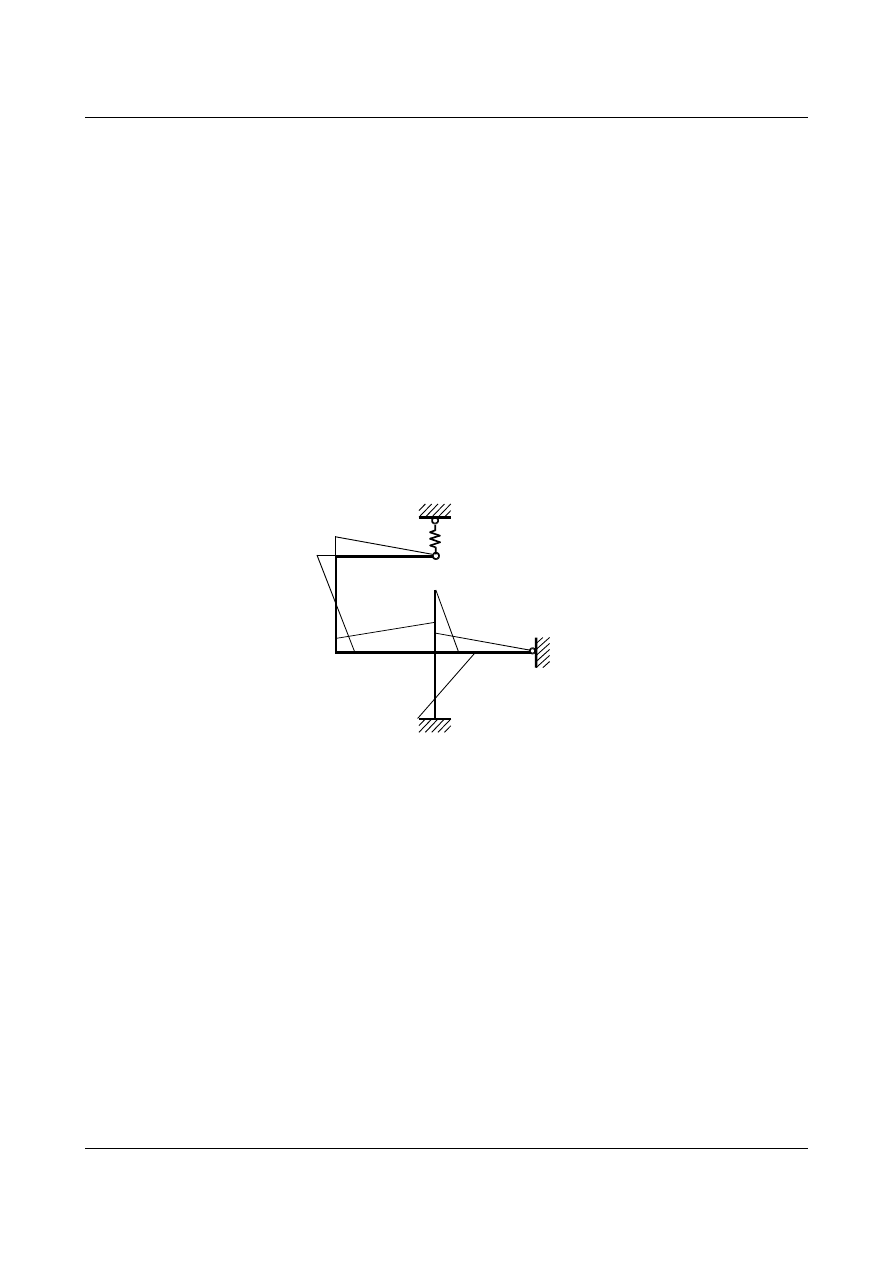
Narysujmy wykresy od siły jednostkowej i od przemieszczenia jednostkowego w układzie podstawowym:
X
1
=1
3
3
M
1
r
21
δ
22
Rys. 7.28. Stan X
1
= 1
φ
2
=1
EJ
EJ
2EJ
M
2
δ
12
r
22
Rys. 7.29. Stan φ
2
= 1
Na podstawie powyższych wykresów (rys. 7.28 i rys. 7.29) obliczamy odpowiednie przemieszczenia i reakcje:
11
=
∫
M
1
M
1
EJ
ds
R
1
2
k
=
1
EJ
⋅
2
⋅
1
2
⋅3 ⋅3 ⋅
2
3
⋅3 3 ⋅3 ⋅3
9
EJ
=
54
EJ
r
22
=2 EJ EJ =3 EJ
r
21
=
12
=0
Następnie rysujemy wykres momentów od stanu
P:
18
12
M
P
(o)
r
2P
r
2P
12
18
Rys. 7.30. Stan P
i obliczamy wyrazy wolne:
1 P
=
∫
s
M
1
M
P
o
EJ
ds
=
1
EJ
⋅
−
1
2
⋅18 ⋅3 ⋅3 −
1
2
⋅3 ⋅3 ⋅18
=−
162
EJ
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
7. METODA MIESZANA
15
r
2 P
=1218 =30 [kNm]
Jeśli przemnożymy pierwsze równanie przez
EJ, to układ uzyska postać:
{
54
⋅X
1
=162
3
⋅
2
⋅EJ =−30
A zatem niewiadome wynoszą:
X
1
=3 [kN ]
EJ
2
=−10
Na postawie tych wyników, zgodnie z zasadą superpozycji możemy wyznaczyć momenty rzeczywiste w
ramie.
M
n
=M
P
o
M
1
⋅X
1
M
2
⋅
2
18
12 20
10
9
9
10
M
(n)
[kNm]
Rys. 7.31. Wykres momentów rzeczywistych
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater