9

CAŁKI NIEWŁAŚCIWE.

Def.

Niech funkcja f(x) będzie całkowalna (w sensie Riemanna) na przedziale [ a, T]

dla każdego T > a, wówczas

)

(

lim

dx

T

a

x

f

T

nazywać będziemy całką

niewłaściwą funkcji f(x) na przedziale [a, ) i oznaczać

dx

T

a

f(x)

T

lim

df

dx

a

f(x)

,

przy czym jeżeli granica powyższa jest skończona , to całkę nazywamy zbieżną,
jeżeli zaś nieskończona lub nie istnieje, to całkę nazywamy rozbieżną.

Analogicznie określamy całkę niewłaściwą funkcji f(x) na przedziale

]

,

(

b

dx

b

T

)

x

(

f

T

lim

df

=

dx

b

)

x

(

f

.

Natomiast , jeżeli f(x) jest całkowalna na każdym przedziale domkniętym na OX,
to

dx

T

c

)

x

(

f

T

lim

+

dx

c

T

)

x

(

f

T

lim

df

=

dx

)

x

(

f

,

(&)

gdzie c jest dowolnym punktem osi OX, z zachowaniem reguł zbieżności j. w.
Całkę

dx

T

T

)

x

(

f

T

lim

df

=

dx

)

x

(

f

określamy jako wartość główną całki na przedziale

)

,

(

w sensie Cauchy'ego,

której istnienie nie jest równoważne definicji (&).
Całki niewłaściwe na przedziałach nieskończonych
nazywamy całkami niewłaściwymi pierwszego rodzaju.

Określmy teraz całki niewłaściwe drugiego rodzaju.
Niech funkcja f(x) będzie nieograniczona w lewostronnym sąsiedztwie punktu b
i całkowalna na każdym przedziale domkniętym [a , b- ]
dla każdego

(0 , b - a ), to jej całkę niewłaściwą na przedziale [a , b ]

określamy następująco

.

dx

b

a

)

x

(

f

b

a

0

lim

df

=

dx

)

x

(

f

Analogicznie określamy całkę niewłaściwą na przedziale [a , b] funkcji f(x)
nieograniczonej na prawostronnym sąsiedztwie punktu a

.

dx

b

a

f(x)

b

a

0

lim

df

=

f(x)dx

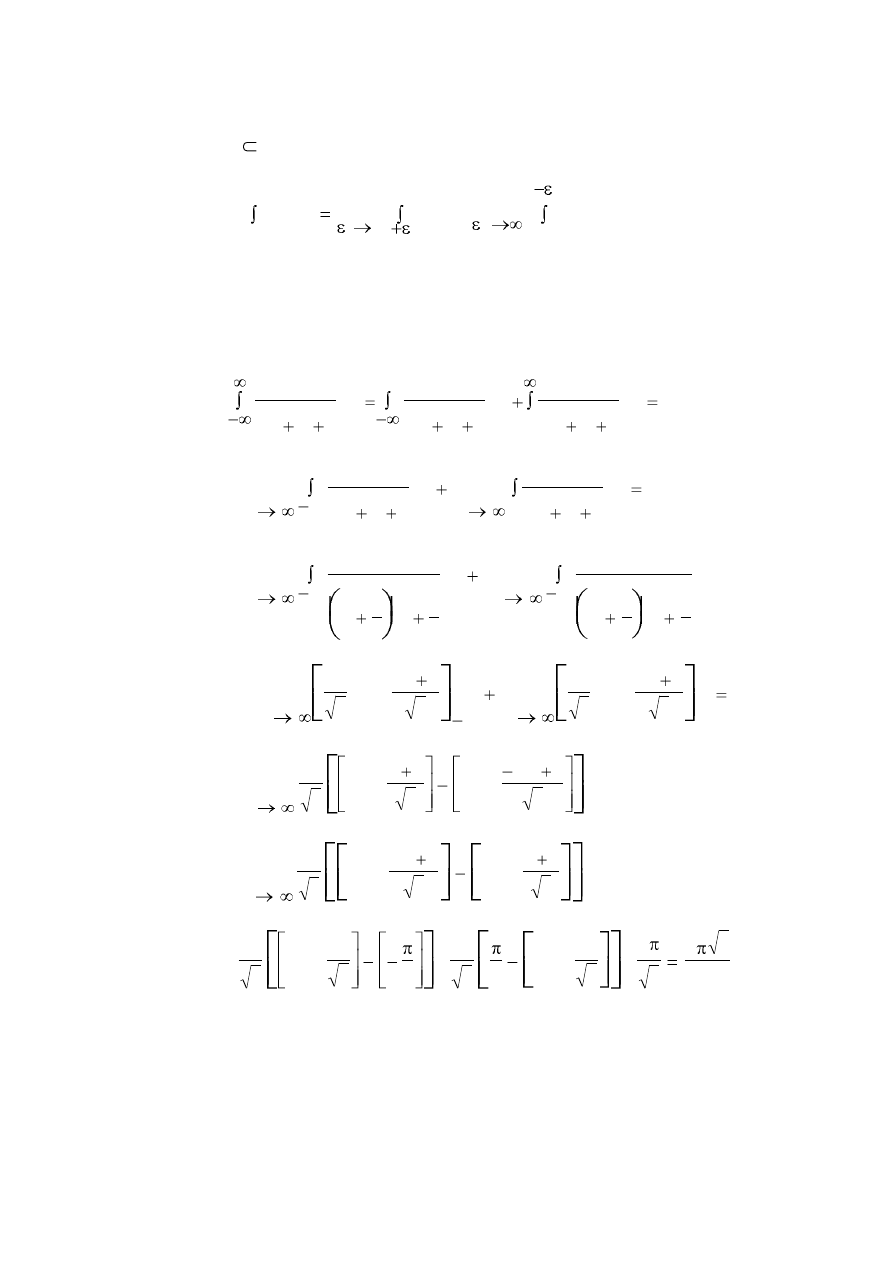
10

Natomiast , jeżeli f(x) jest całkowalna na każdym przedziale domkniętym
[c , d ]

(a , b ), przy czym a oraz b są punktami nieograniczoności funkcji f,

to

+

df

dx

2

b

e

)

x

(

f

2

lim

dx

e

1

a

)

x

(

f

0

1

lim

dx

b

a

)

x

(

f

,

gdzie e jest dowolnym punktem przedziału (c , d ), z zachowaniem reguł
zbieżności j. w.

Przykład.

dx

x

x

dx

dx

x

x

dx

dx

x

x

dx

2

1

2

1

0

2

1

0

=

lim

lim

A

dx

x

x

dx

A

B

dx

x

x

dx

B

2

1

0

2

1

0

=

lim

A

dx

x

dx

A

1

2

2

3

4

0

lim

A

dx

x

dx

A

1

2

2

3

4

0

=

=

lim

lim

A

arctg

x

A

B

arctg

x

B

2

3

2

1

3

0

2

3

2

1

3

0

=

lim

A

arctg

arctg

A

2

3

0

1

3

2

1

3

+

+

lim

B

arctg

B

arctg

2

3

2

1

3

0

1

3

=

=

2

3

1

3

2

arctg

+

2

3

2

1

3

arctg

=

2

3

2

3

3

.

Całka jest zbieżna.

11

Przykład

Oblicz:

1

2

0

1

x

x

dx

e

ln

1

0

1

2

x

x

dx

e

ln

lim

ln

A

x

x

dx

A

e

0

1

1

2

=

ln

ln

ln

x t

x

dx dt

dla x A

t

A

dla x

e

t

e

1

1

1

1

=

lim

ln

A

t

dt

A

0

1
2

1

lim

ln

A

t

A

0

1

1

lim

ln

A

A

0

1

1

1

=

lim

ln

A

A

0

1

1

0 + 1 = 1

Całka jest zbieżna.

Przykład.

Oblicz:

1

2

1

1

x

x

dx

e

ln

1

2

1

1

x

x

dx

e

ln

=

lim

ln

B

x

x

dx

e

B

1

1

1

2

==

ln

ln

x t

x

dx dt

dla x B

t

B

dla x

e

t

1

1

1

=

lim

ln

B

t

B

1

1

1

lim

ln

B

B

1

1

1

1

=

1

B

ln

1

1

1

B

lim

Całka jest rozbieżna.

Przykład.

Oblicz:

1

0

1

x

dx dla

1
2

3

0 1

1

1

o

o

o

,

,

1

o

1

0

1

x

dx = lim

0

1

1

1

1

x

=

lim

0

1

1

1

1

1

1

1

Całka zbieżna.

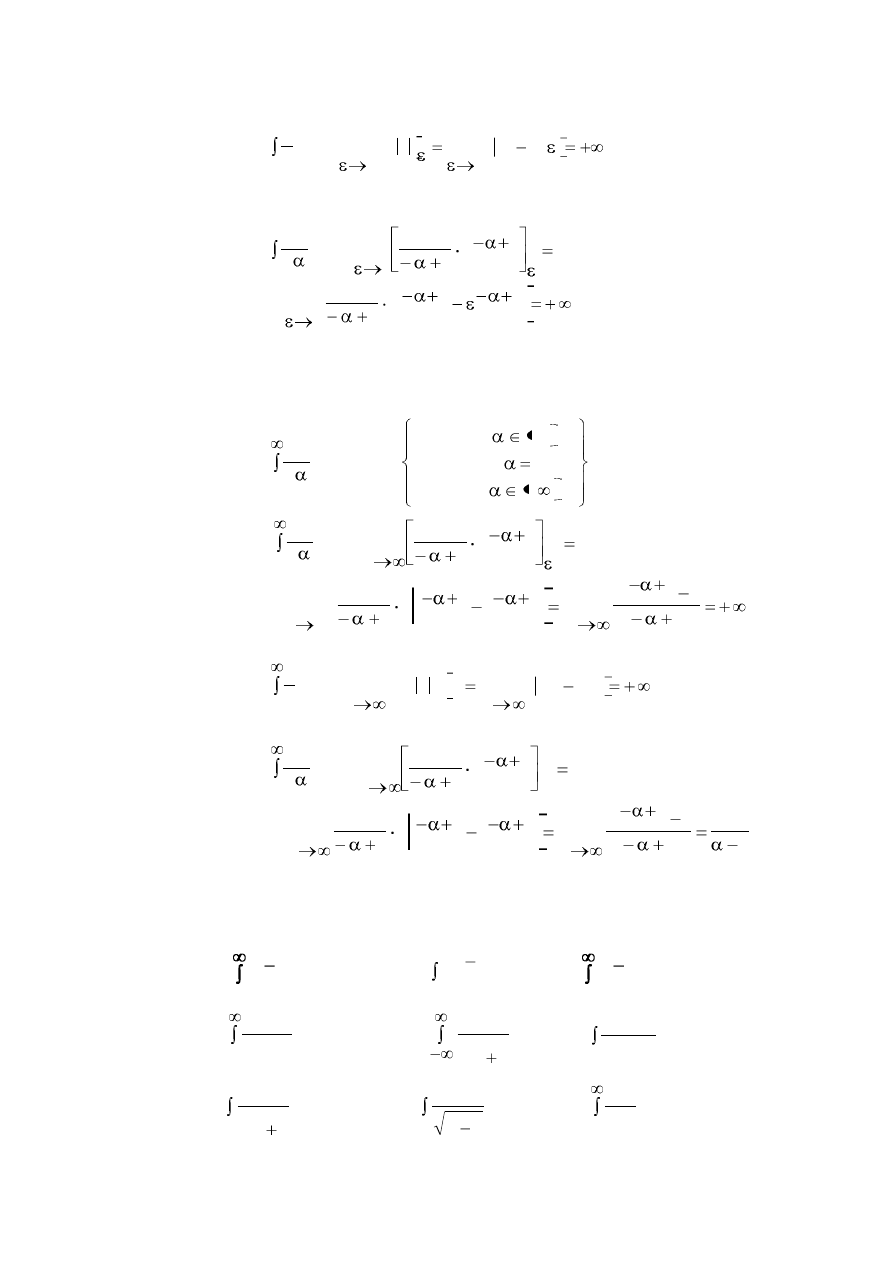
12

2

o

1

0

1

x

dx =

lim ln

lim ln

ln

0

1

0

1

x

Całka rozbieżna.

3

o

1

0

1

x

dx = lim

0

1

1

1

1

x

=

lim

0

1

1

1

1

1

Całka rozbieżna.

Przykład.

Oblicz:

1

1 x

dx dla

1
2
3

0 1

1

1

o

o

o

,

,

1

o

1

1 x

dx = lim

A

x

A

1

1

1

=

lim

lim

A

A

A

A

0

1

1

1 1

1

1 1

1

Całka rozbieżna.

2

o

1

1 x

dx =

lim

ln

lim ln

ln

B

x

B

B

B

1

1

Całka rozbieżna.

3

o

1

1 x

dx = lim

C

x

C

1

1

1

1

=

lim

lim

C

C

C

C

1

1

1 1

1

1 1

1

1

1

Całka zbieżna.

Ćwiczenia.

Oblicz:

1.

0

dx

2

x

e

x

,

2. x e

x

dx

2

0

1

,

3.

1

dx

2

x

e

x

,

4.

1

1 x

x

dx

ln

,

5.

x

x

dx

4

1

,

6.

1

0

1

x

x

dx

ln

,

7.

x

x

dx

4

1

1

0

,

8.

dx

x

1

3

0

2

,

9.

1

3

0 x

dx .