1
Równania Maxwella
i fale elektromagnetyczne
Strumie
ń
pola magnetycznego
B
przez powierzchni
ę
S
(analogicznie jak strumie
ń
pola elektrycznego
E
)
∫
=
S
B
S
B d
φ
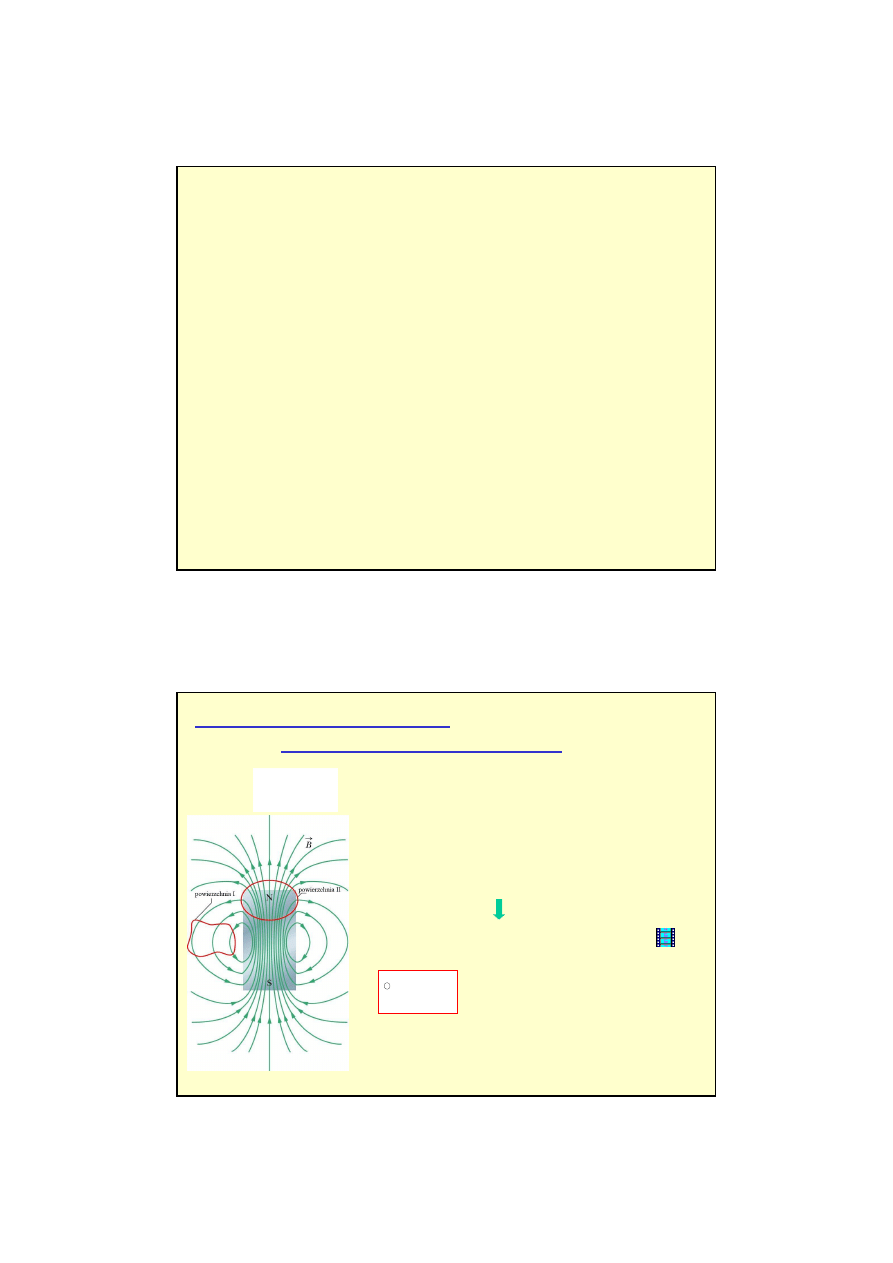
Poniewa
ż
linie pola
B
s
ą
krzywymi zamkni
ę
tymi, wi
ę
c
dowolna powierzchnia zamkni
ę
ta otaczaj
ą
ca
ź
ródło pola
magnetycznego jest przecinana przez tyle samo linii
wychodz
ą
cych ze
ź
ródła co wchodz
ą
cych do niego.
strumie
ń
pola magnetycznego przez
zamkni
ę
t
ą
powierzchni
ę
jest równy zeru
0
d
=
∫
S
S
B
prawo Gaussa dla pola magnetycznego
Nie udało si
ę
zaobserwowa
ć
w przyrodzie
pojedynczych biegunów magnetycznych
analogicznych do ładunków elektrycznych.
Prawo Gaussa dla pola magnetycznego
RÓWNANIA MAXWELLA
2
Je
ż
eli w zmiennym polu magnetycznym umie
ś
cimy przewodz
ą
c
ą
kołow
ą
p
ę
tl
ę
(obwód) to
w tym obwodzie popłynie pr
ą
d (prawo Faradaya).
Oznacza to,
ż
e w miejscu gdzie znajduje si
ę
przewodnik istnieje pole elektryczne
E
, które
działa na ładunki elektryczne w przewodniku wywołuj
ą
c ich ruch.
To pole elektryczne E zostało wytworzone (wyindukowane)
przez zmieniaj
ą
ce si
ę
pole magnetyczne
B
.
Obecno
ść
p
ę
tli (obwodu) nie jest konieczna.
Je
ż
eli go nie b
ę
dzie, to nie b
ę
dziemy obserwowa
ć
przepływu pr
ą
du jednak indukowane pole elektryczne
E
b
ę
dzie nadal istnie
ć
.
Indukowane pola elektryczne nie s
ą
zwi
ą
zane z ładunkiem,
ale ze zmian
ą
strumienia magnetycznego.
Zmianom pola magnetycznego towarzyszy zawsze powstanie pola elektrycznego.
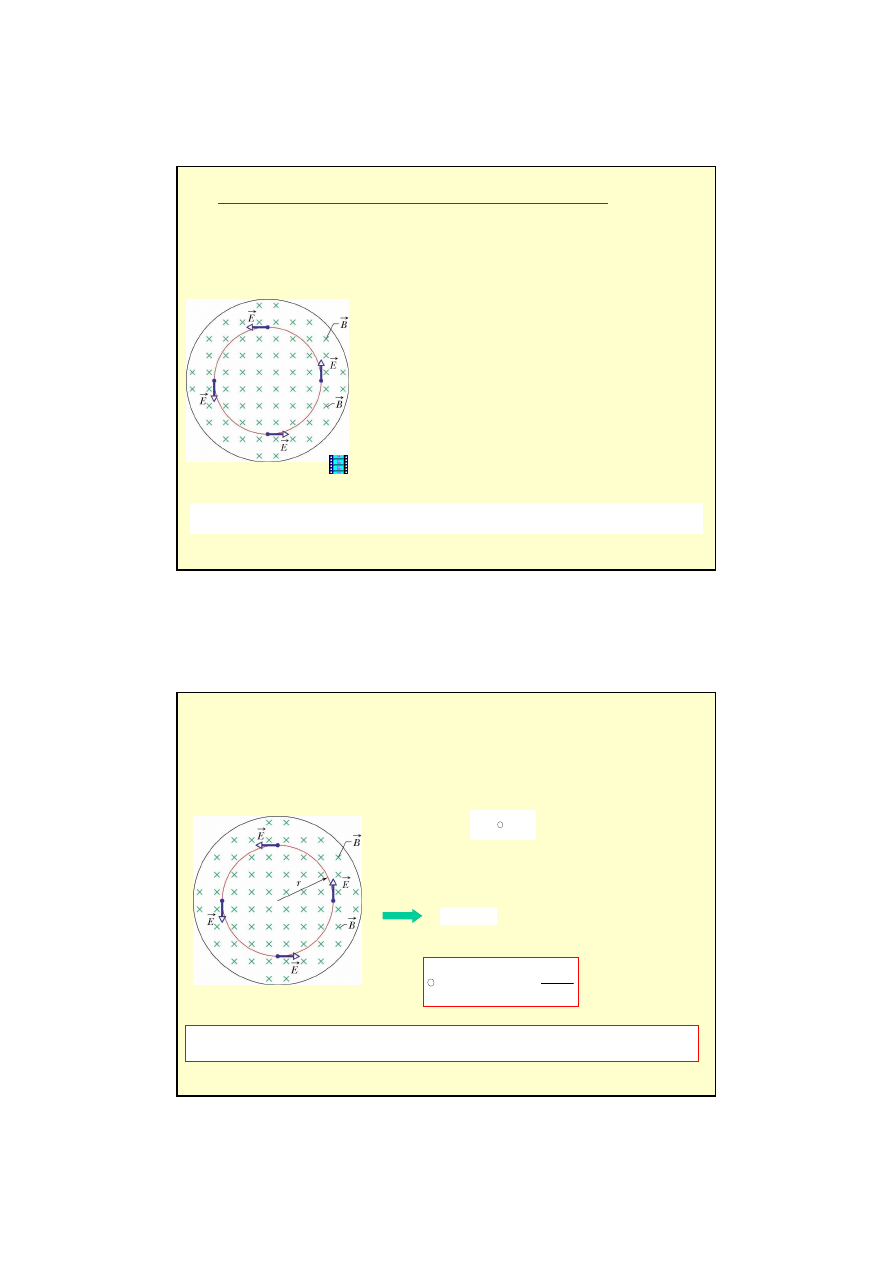
Indukowane wirowe pole elektryczne (prawo Faradaya)
Indukowane pole elektryczne nazywamy (ze wzgl
ę
du na kształt linii)
wirowym polem elektrycznym
Nat
ęż
enia kołowego pola elektrycznego jest zwi
ą
zane z indukowan
ą
sił
ą
elektromotoryczn
ą
∫
=
l
E d
ε
całkowanie odbywa si
ę
po drodze, na której
działa siła tj. wzdłu
ż
linii pola elektrycznego
r
E
π
ε
2
=
∫
−
=
=
t
B
d
d
)
(
d
φ
ε
l
E
Cyrkulacja wektora nat
ęż
enia pola
E
po dowolnym zamkni
ę
tym konturze jest równa szybko
ś
ci
zmiany strumienia magnetycznego przechodz
ą
cego przez ten kontur.
3
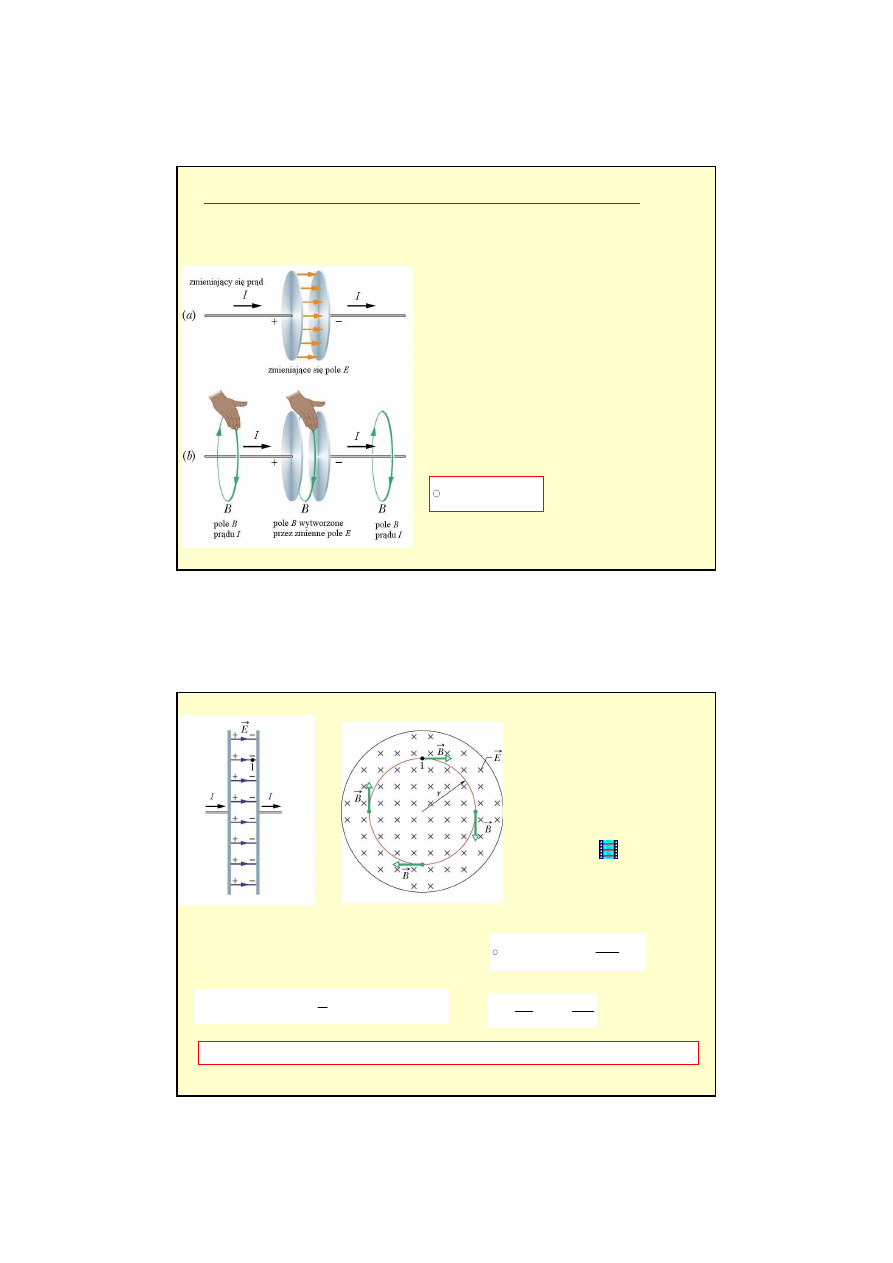
Indukowane pole magnetyczne (uogólnione prawo Ampère'a)
Gdy ładujemy lub rozładowujemy kondensator to do okładek dopływa (lub z nich ubywa)
ładunek i w konsekwencji zmienia si
ę
pole elektryczne
E
w kondensatorze.
Zmieniaj
ą
cy si
ę
w obwodzie pr
ą
d I jest
"uzupełniony„ polem
E
zmieniaj
ą
cym si
ę
mi
ę
dzy
okładkami w kondensatorze.
Do
ś
wiadczenie pokazuje,
ż
e pomi
ę
dzy
okładkami kondensatora powstaje pole
magnetyczne wytworzone przez zmieniaj
ą
ce si
ę
pole elektryczne.
∫
=
I
r
0
d
µ
µ
l
B
pole
B
pr
ą
du I
pole
B
równie
ż
w kondensatorze
Linie pola, maj
ą
kształt
okr
ę
gów tak jak linie pola
wokół przewodnika z pr
ą
dem.
E
r
r
r
E
S
E
d
d
S
E
Cd
CU
Q
φ
ε
ε
ε
ε
ε
ε
0
0
0
=
=
=
=
=
t
t
Q
I
E
r
p
d
d
d
d
0
φ
ε
ε
=
=
pr
ą
d przesuni
ę
cia
∫
+
=
I
t
E
r
r
d
d
d
0
0
φ
ε
ε
µ
µ
l
B
Pole magnetyczne mo
ż
e by
ć
wytwarzane zarówno przez przepływ pr
ą
du (prawo Ampère'a) jak
i przez zmienne pole elektryczne.
Maxwell uogólnił prawo Ampère'a do postaci
Zmianom pola elektrycznego towarzyszy zawsze powstanie pola magnetycznego.
4
Równania Maxwella (dla pró
ż
ni)
uogólnione prawo Ampère'a
4
uogólnione prawo Faradaya
3
prawo Gaussa dla magnetyzmu
2
prawo Gaussa dla elektryczno
ś
ci
1
Równanie
Prawo
∫
=
0
d
ε
ε
r
Q
S
E
∫
=
0
d S
B
∫
−
=
t
B
d
d
d
φ
l
E
I
t
r
E
r
r
0
0
0
d
d
d
µ
µ
φ
ε
ε
µ
µ
+
=
∫
l
B
Wszystkie powy
ż
sze prawa s
ą
słuszne zarówno w przypadku statycznym
(pola niezale
ż
ne od czasu) jak i w przypadku pól zale
ż
nych od czasu.
Równania Maxwella
∫
−
=
=
t
B
d
d
)
(
d
φ
ε
l
E
I
t
E
0
0
0
µ
φ
ε
µ
+
=
∫
d
d
d l
B
Ka
ż
da zmiana w czasie pola elektrycznego wywołuje
powstanie zmiennego pola magnetycznego, które z kolei
indukuje wirowe pole elektryczne itd.
Taki ci
ą
g sprz
ęż
onych pól elektrycznych i magnetycznych
tworzy fal
ę
elektromagnetyczn
ą
.
Przyspieszony ładunek elektryczny wypromieniowuje pole elektryczne i magnetyczne
w postaci fali elektromagnetycznej.
s
m
.
8
0
0
10
9979
2
1
⋅
=
=
ε
µ
c
0
0
B
E
c
=
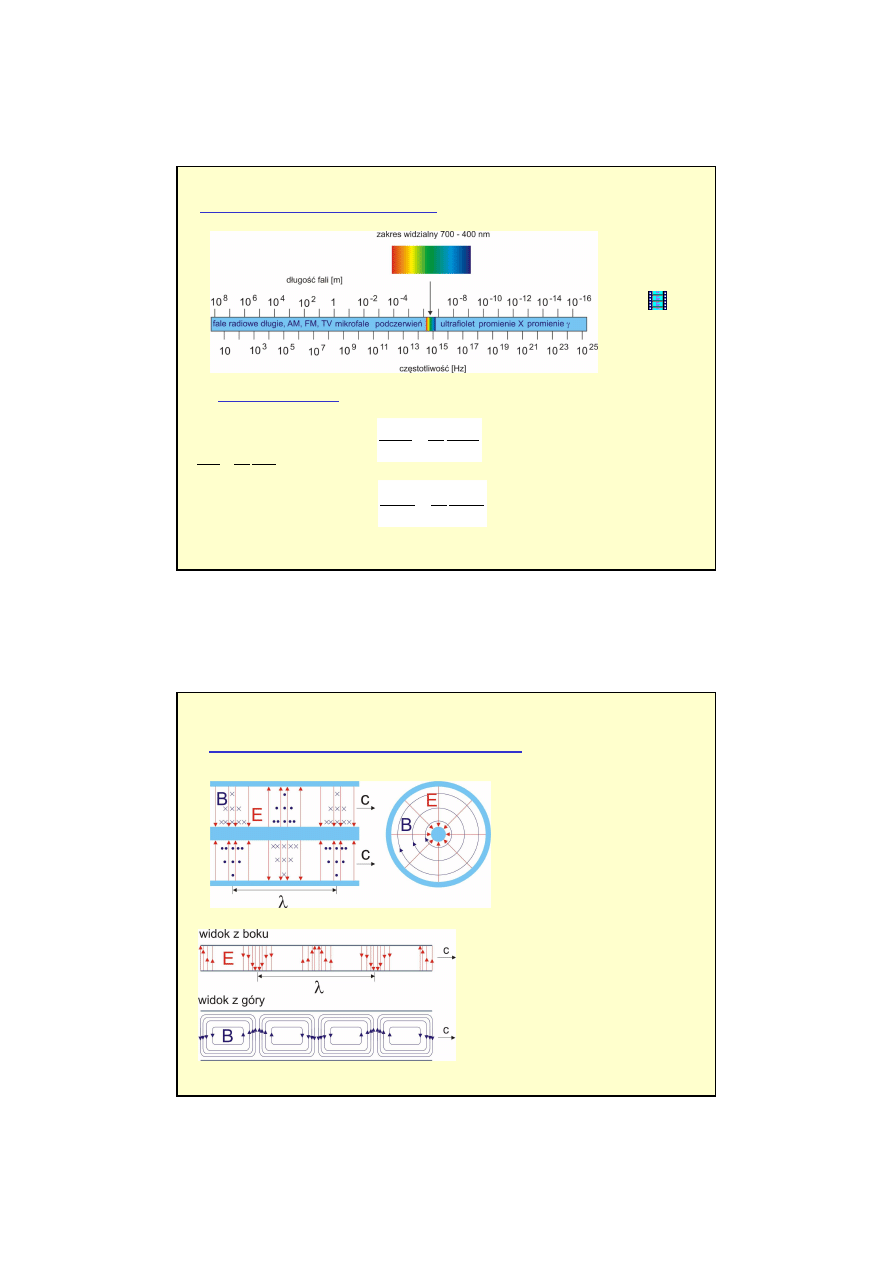
Fala poprzeczna
FALE ELEKTROMAGNETYCZNE
w pró
ż
ni:
5
Widmo fal elektromagnetycznych
2
2
2
2
2
1
t
y
x
y
∂
∂
∂
∂
v
=
równanie struny
2
2
2
2
2
1
t
B
c
x
B
z
z
∂
∂
∂
∂
=
2
2
2
2
2
1
t
E
c
x
E
y
y
∂
∂
∂
∂
=
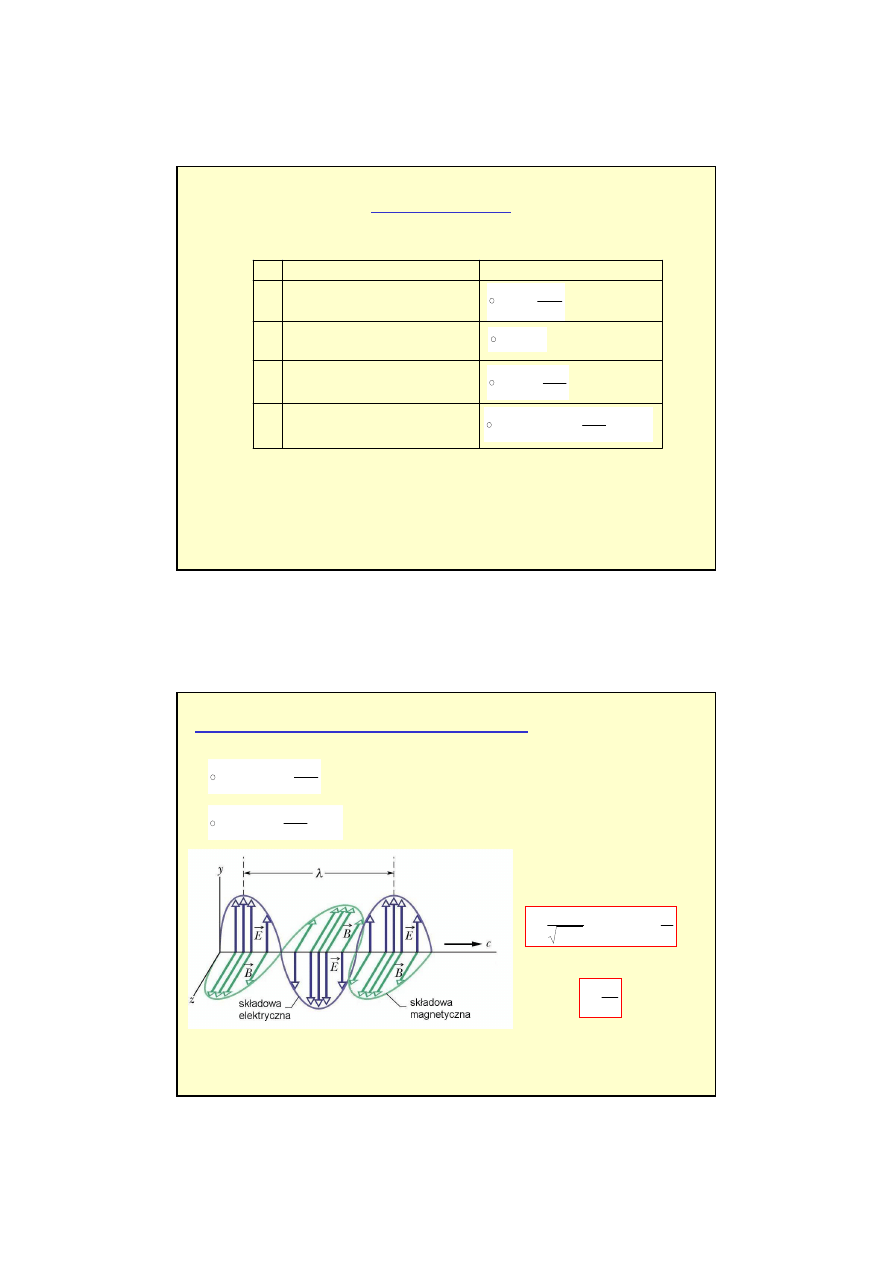
Pola E i B s
ą
do siebie
prostopadłe i prostopadłe
do kierunku rozchodzenia
si
ę
fali.
Równanie falowe
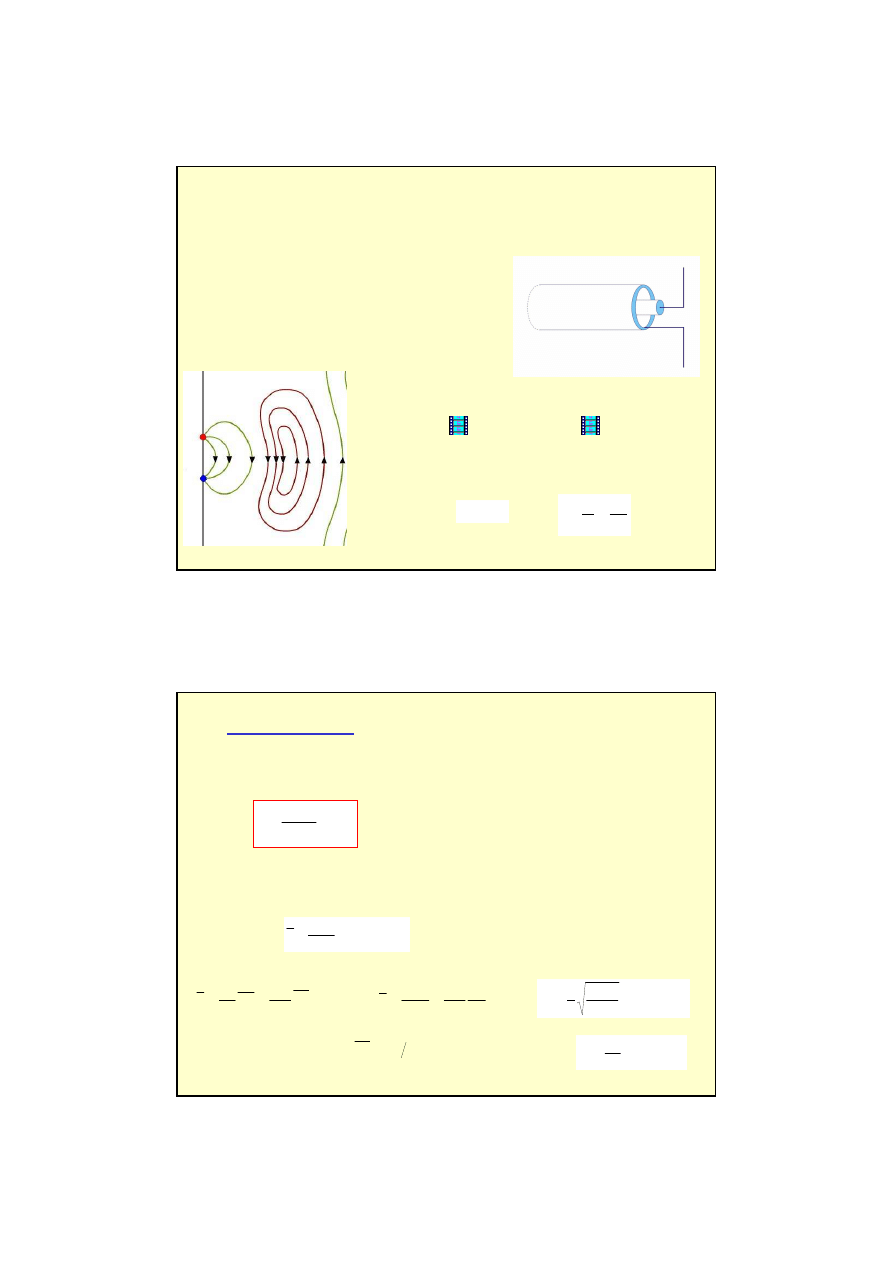
Rozkład pola elektrycznego
i magnetycznego w kablu
koncentrycznym w danej
chwili t.
Pola te poruszaj
ą
si
ę
wzdłu
ż
kabla z pr
ę
dko
ś
ci
ą
c.
Przykładowy rozkład pól
E, B
dla
prostok
ą
tnego falowodu.
Rozkład pól nie musi by
ć
sinusoidalnie zmienny.
Rozchodzenie si
ę
fal elektromagnetycznych
6
Elektromagnetyczna linia transmisyjna mo
ż
e by
ć
zako
ń
czona w sposób umo
ż
liwiaj
ą
cy
wypromieniowanie energii elektromagnetycznej do otaczaj
ą
cej przestrzeni.
antena dipolowa
Je
ż
eli ró
ż
nica potencjałów pomi
ę
dzy mi
ę
dzy drutami
zmienia si
ę
sinusoidalnie to taka antena zachowuje si
ę
jak dipol elektryczny, którego moment dipolowy zmienia
si
ę
co do wielko
ś
ci jak i kierunku.
Energia jest wypromieniowywana przez anten
ę
w postaci fali elektromagnetycznej.
Fala elektromagnetyczna emitowana
przez drgaj
ą
cy dipol elektryczny
Fale elektromagnetyczne mog
ą
rozchodzi
ć
si
ę
w pró
ż
ni
v
c
λ
=
0
0
B
E
k
c
=
=
ω
Szybko
ść
przepływu energii przez jednostkow
ą
powierzchni
ę
płaskiej fali
elektromagnetycznej opisujemy wektorem
S
zwanym wektorem Poyntinga
B
E
S
×
=
0
1
µ
µ
r
Kierunek wektora
S
pokazuje kierunek przenoszenia
energii. Wektory
E
i
B
s
ą
chwilowymi warto
ś
ciami pola
elektromagnetycznego w rozpatrywanym punkcie.
Przykład : Radiostacja o mocy P
0
= 30 kW wysyła fale EM izotropowo. Obliczamy nat
ęż
enie
sygnału (moc na jednostk
ę
powierzchni) w odległo
ś
ci r = 10 km od nadajnika.
ś
rednia warto
ść
wektora Poyntinga w
odległo
ś
ci r od
ź
ródła
2
2
0
m
/
µ
W
24
4
=
=
r
P
S
π
2
0
0
1
1
E
c
EB
S
µ
µ
=
=
2
1
4
2
0
0
2
0
E
c
r
P
S
µ
π
=
=
m
/
V
13
.
0
2
1
0
0
0
=
=
π
µ
cP
r
E
cB
E
=
2
2
0
2
E
E
=
fala sinusoidalna
T
10
4
10
0
0
−
⋅
=
=
c
E
B
Wektor Poyntinga
Wyszukiwarka
Podobne podstrony:
5IMIR fale EM prawa Maxwella id Nieznany
14 prawa Maxwella
14 przejscia fazoweid 15265 Nieznany (2)
piel 38 1 14 79 id 356923 Nieznany
14 Zmaganie sie z choroba1id 1 Nieznany (2)
Pojecie zrodel prawa id 370403 Nieznany
14 Prowadzenie roznych kierunko Nieznany (4)
14 Poslugiwanie sie dokumentacj Nieznany
PROGRAM AKT PRAWA MIEJSCOW PWS Nieznany
2009 05 30 14;58;17id 26810 Nieznany (2)
2009 05 30 14;58;14id 26809 Nieznany
14 spiaczki cukrzycoweid 15553 Nieznany (2)
14 rozdzial 13 w2pa42u4da5r3dcm Nieznany (2)
10 Zasady prawa cywilnegoid 11 Nieznany (2)
AAS piatek 14 30 id 50013 Nieznany
14 elementy i uklady elektronic Nieznany
2009 05 30 14;57;36id 26802 Nieznany
Encyklopedia prawa wyklady id 1 Nieznany
14 Stosowanie technik laczenia Nieznany (2)
więcej podobnych podstron