1

Równania Maxwella

i fale elektromagnetyczne

Strumie

ń

pola magnetycznego

B

przez powierzchni

ę

S

(analogicznie jak strumie

ń

pola elektrycznego

E

)

∫

=

S

B

S

B d

φ

Poniewa

ż

linie pola

B

s

ą

krzywymi zamkni

ę

tymi, wi

ę

c

dowolna powierzchnia zamkni

ę

ta otaczaj

ą

ca

ź

ródło pola

magnetycznego jest przecinana przez tyle samo linii
wychodz

ą

cych ze

ź

ródła co wchodz

ą

cych do niego.

strumie

ń

pola magnetycznego przez

zamkni

ę

t

ą

powierzchni

ę

jest równy zeru

0

d

=

∫

S

S

B

prawo Gaussa dla pola magnetycznego

Nie udało si

ę

zaobserwowa

ć

w przyrodzie

pojedynczych biegunów magnetycznych
analogicznych do ładunków elektrycznych.

Prawo Gaussa dla pola magnetycznego

RÓWNANIA MAXWELLA

2

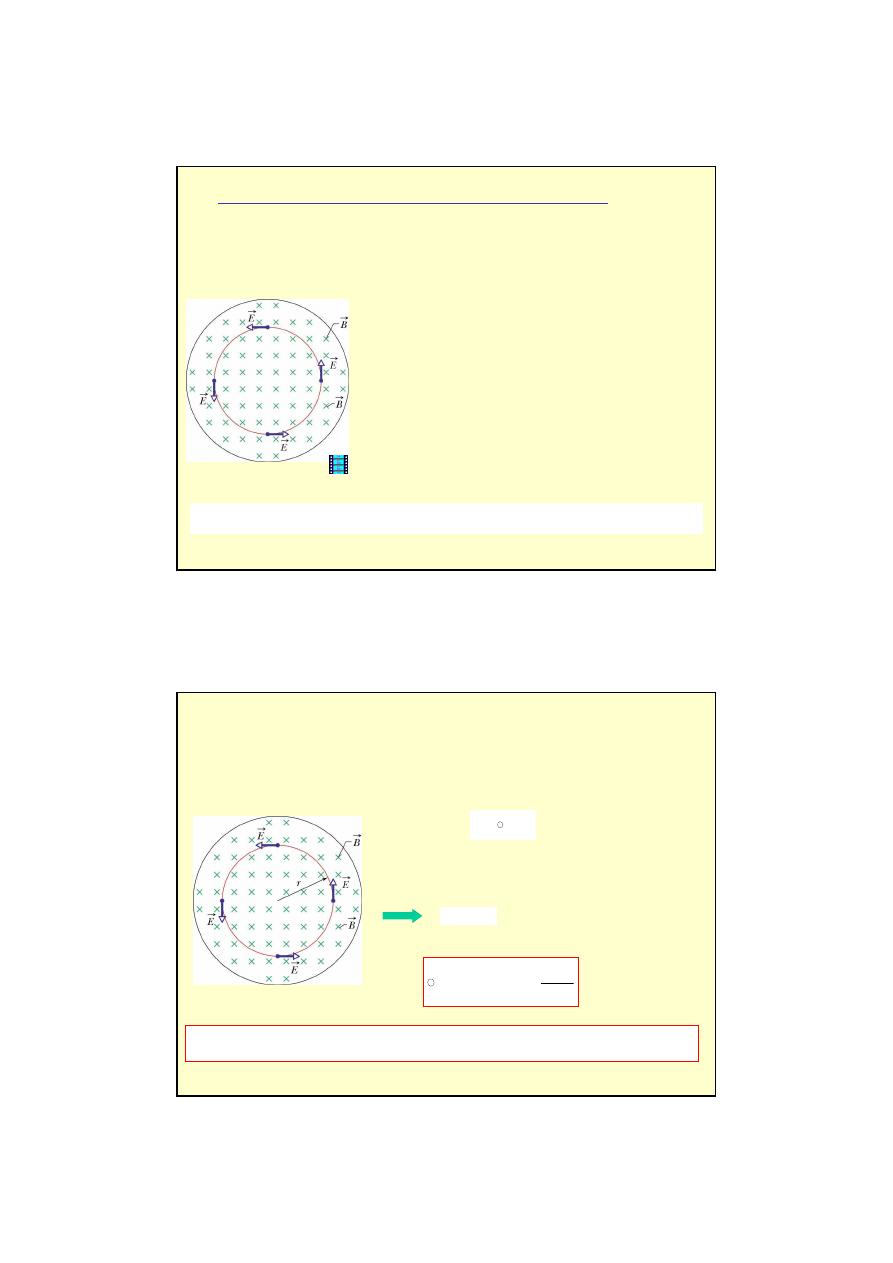
Je

ż

eli w zmiennym polu magnetycznym umie

ś

cimy przewodz

ą

c

ą

kołow

ą

p

ę

tl

ę

(obwód) to

w tym obwodzie popłynie pr

ą

d (prawo Faradaya).

Oznacza to,

ż

e w miejscu gdzie znajduje si

ę

przewodnik istnieje pole elektryczne

E

, które

działa na ładunki elektryczne w przewodniku wywołuj

ą

c ich ruch.

To pole elektryczne E zostało wytworzone (wyindukowane)
przez zmieniaj

ą

ce si

ę

pole magnetyczne

B

.

Obecno

ść

p

ę

tli (obwodu) nie jest konieczna.

Je

ż

eli go nie b

ę

dzie, to nie b

ę

dziemy obserwowa

ć

przepływu pr

ą

du jednak indukowane pole elektryczne

E

b

ę

dzie nadal istnie

ć

.

Indukowane pola elektryczne nie s

ą

zwi

ą

zane z ładunkiem,

ale ze zmian

ą

strumienia magnetycznego.

Zmianom pola magnetycznego towarzyszy zawsze powstanie pola elektrycznego.

Indukowane wirowe pole elektryczne (prawo Faradaya)

Indukowane pole elektryczne nazywamy (ze wzgl

ę

du na kształt linii)

wirowym polem elektrycznym

Nat

ęż

enia kołowego pola elektrycznego jest zwi

ą

zane z indukowan

ą

sił

ą

elektromotoryczn

ą

∫

=

l

E d

ε

całkowanie odbywa si

ę

po drodze, na której

działa siła tj. wzdłu

ż

linii pola elektrycznego

r

E

π

ε

2

=

∫

−

=

=

t

B

d

d

)

(

d

φ

ε

l

E

Cyrkulacja wektora nat

ęż

enia pola

E

po dowolnym zamkni

ę

tym konturze jest równa szybko

ś

ci

zmiany strumienia magnetycznego przechodz

ą

cego przez ten kontur.

3

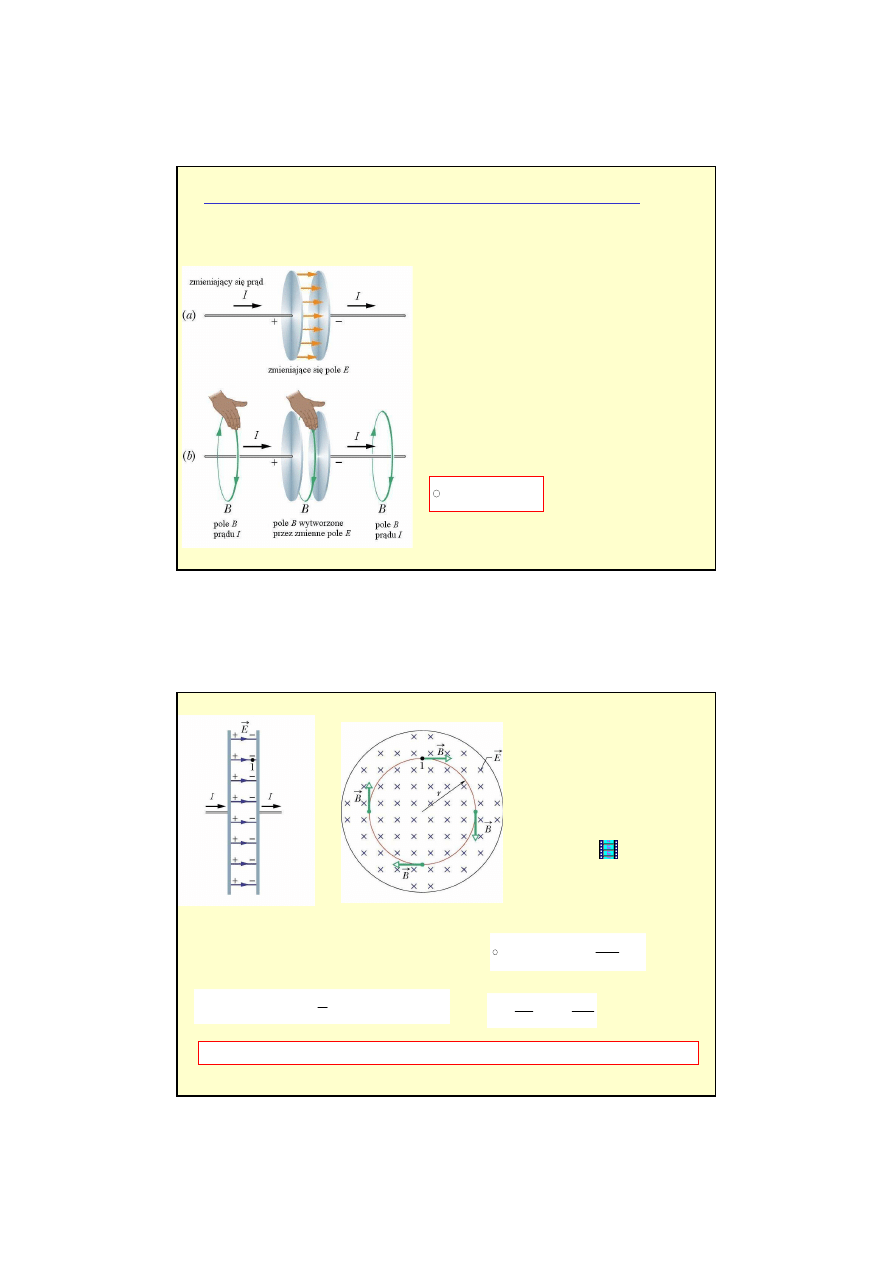
Indukowane pole magnetyczne (uogólnione prawo Ampère'a)

Gdy ładujemy lub rozładowujemy kondensator to do okładek dopływa (lub z nich ubywa)
ładunek i w konsekwencji zmienia si

ę

pole elektryczne

E

w kondensatorze.

Zmieniaj

ą

cy si

ę

w obwodzie pr

ą

d I jest

"uzupełniony„ polem

E

zmieniaj

ą

cym si

ę

mi

ę

dzy

okładkami w kondensatorze.

Do

ś

wiadczenie pokazuje,

ż

e pomi

ę

dzy

okładkami kondensatora powstaje pole
magnetyczne wytworzone przez zmieniaj

ą

ce si

ę

pole elektryczne.

∫

=

I

r

0

d

µ

µ

l

B

pole

B

pr

ą

du I

pole

B

równie

ż

w kondensatorze

Linie pola, maj

ą

kształt

okr

ę

gów tak jak linie pola

wokół przewodnika z pr

ą

dem.

E

r

r

r

E

S

E

d

d

S

E

Cd

CU

Q

φ

ε

ε

ε

ε

ε

ε

0

0

0

=

=

=

=

=

t

t

Q

I

E

r

p

d

d

d

d

0

φ

ε

ε

=

=

pr

ą

d przesuni

ę

cia

∫













+

=

I

t

E

r

r

d

d

d

0

0

φ

ε

ε

µ

µ

l

B

Pole magnetyczne mo

ż

e by

ć

wytwarzane zarówno przez przepływ pr

ą

du (prawo Ampère'a) jak

i przez zmienne pole elektryczne.

Maxwell uogólnił prawo Ampère'a do postaci

Zmianom pola elektrycznego towarzyszy zawsze powstanie pola magnetycznego.

4

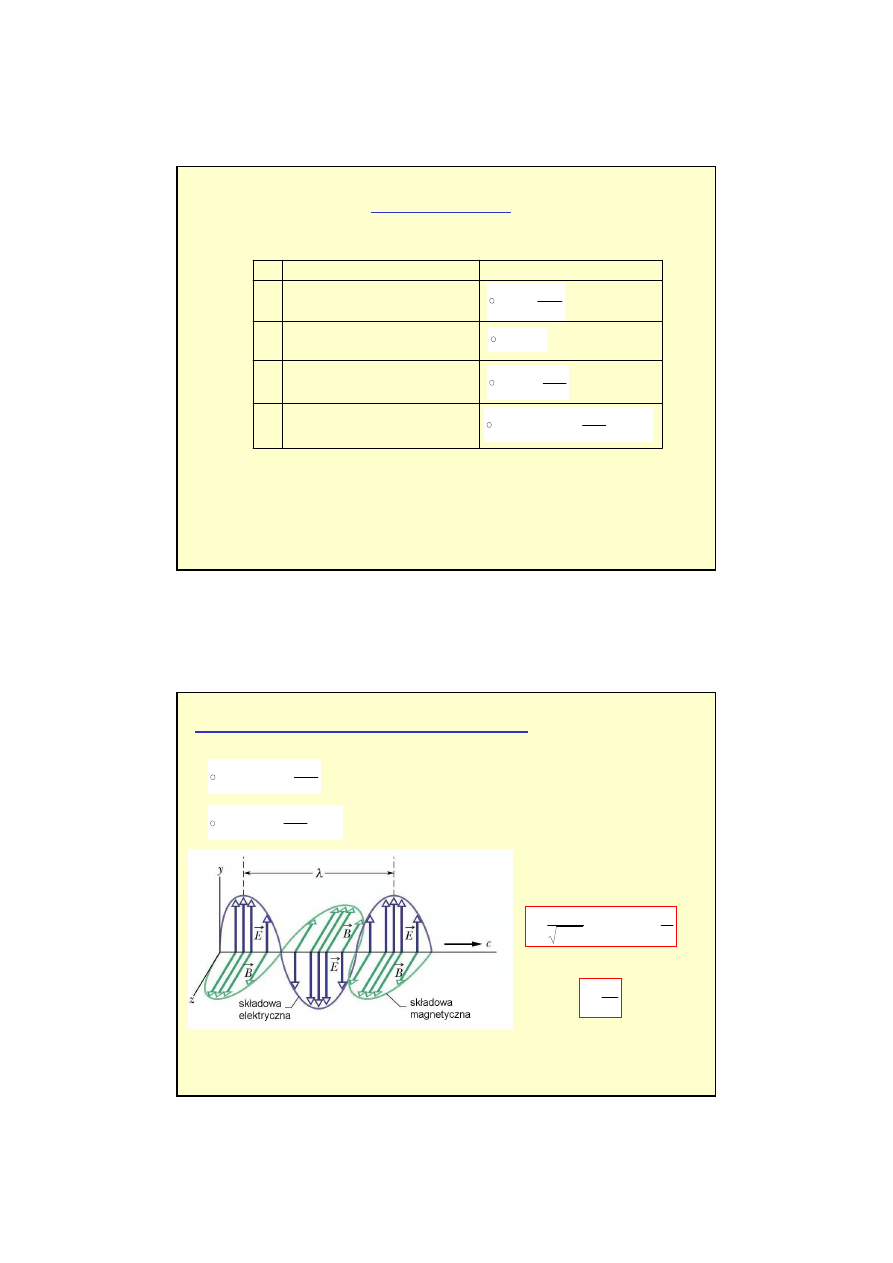
Równania Maxwella (dla pró

ż

ni)

uogólnione prawo Ampère'a

4

uogólnione prawo Faradaya

3

prawo Gaussa dla magnetyzmu

2

prawo Gaussa dla elektryczno

ś

ci

1

Równanie

Prawo

∫

=

0

d

ε

ε

r

Q

S

E

∫

=

0

d S

B

∫

−

=

t

B

d

d

d

φ

l

E

I

t

r

E

r

r

0

0

0

d

d

d

µ

µ

φ

ε

ε

µ

µ

+

=

∫

l

B

Wszystkie powy

ż

sze prawa s

ą

słuszne zarówno w przypadku statycznym

(pola niezale

ż

ne od czasu) jak i w przypadku pól zale

ż

nych od czasu.

Równania Maxwella

∫

−

=

=

t

B

d

d

)

(

d

φ

ε

l

E

I

t

E

0

0

0

µ

φ

ε

µ

+

=

∫

d

d

d l

B

Ka

ż

da zmiana w czasie pola elektrycznego wywołuje

powstanie zmiennego pola magnetycznego, które z kolei
indukuje wirowe pole elektryczne itd.
Taki ci

ą

g sprz

ęż

onych pól elektrycznych i magnetycznych

tworzy fal

ę

elektromagnetyczn

ą

.

Przyspieszony ładunek elektryczny wypromieniowuje pole elektryczne i magnetyczne
w postaci fali elektromagnetycznej.

s

m

.

8

0

0

10

9979

2

1

⋅

=

=

ε

µ

c

0

0

B

E

c

=

Fala poprzeczna

FALE ELEKTROMAGNETYCZNE

w pró

ż

ni:

5

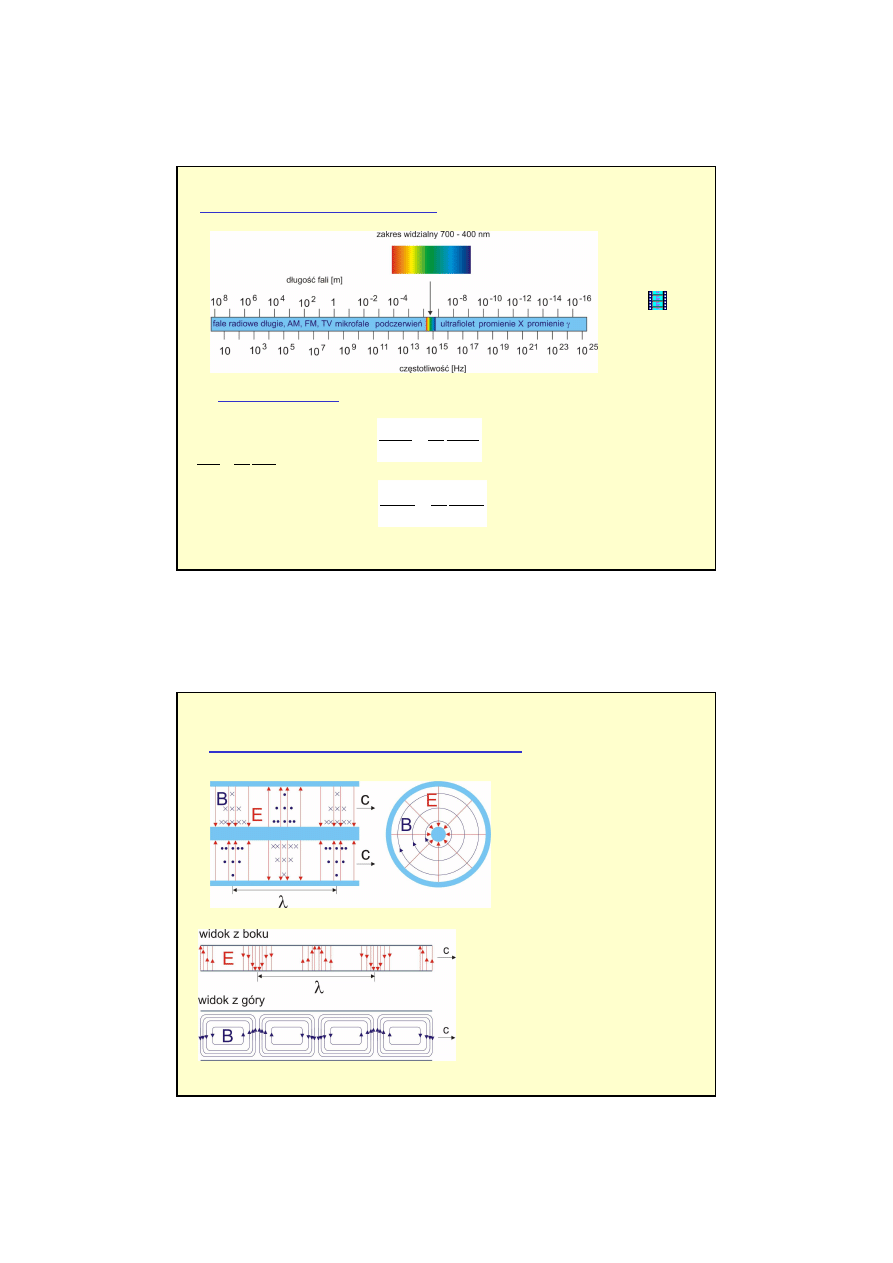
Widmo fal elektromagnetycznych

2

2

2

2

2

1

t

y

x

y

∂

∂

∂

∂

v

=

równanie struny

2

2

2

2

2

1

t

B

c

x

B

z

z

∂

∂

∂

∂

=

2

2

2

2

2

1

t

E

c

x

E

y

y

∂

∂

∂

∂

=

Pola E i B s

ą

do siebie

prostopadłe i prostopadłe
do kierunku rozchodzenia
si

ę

fali.

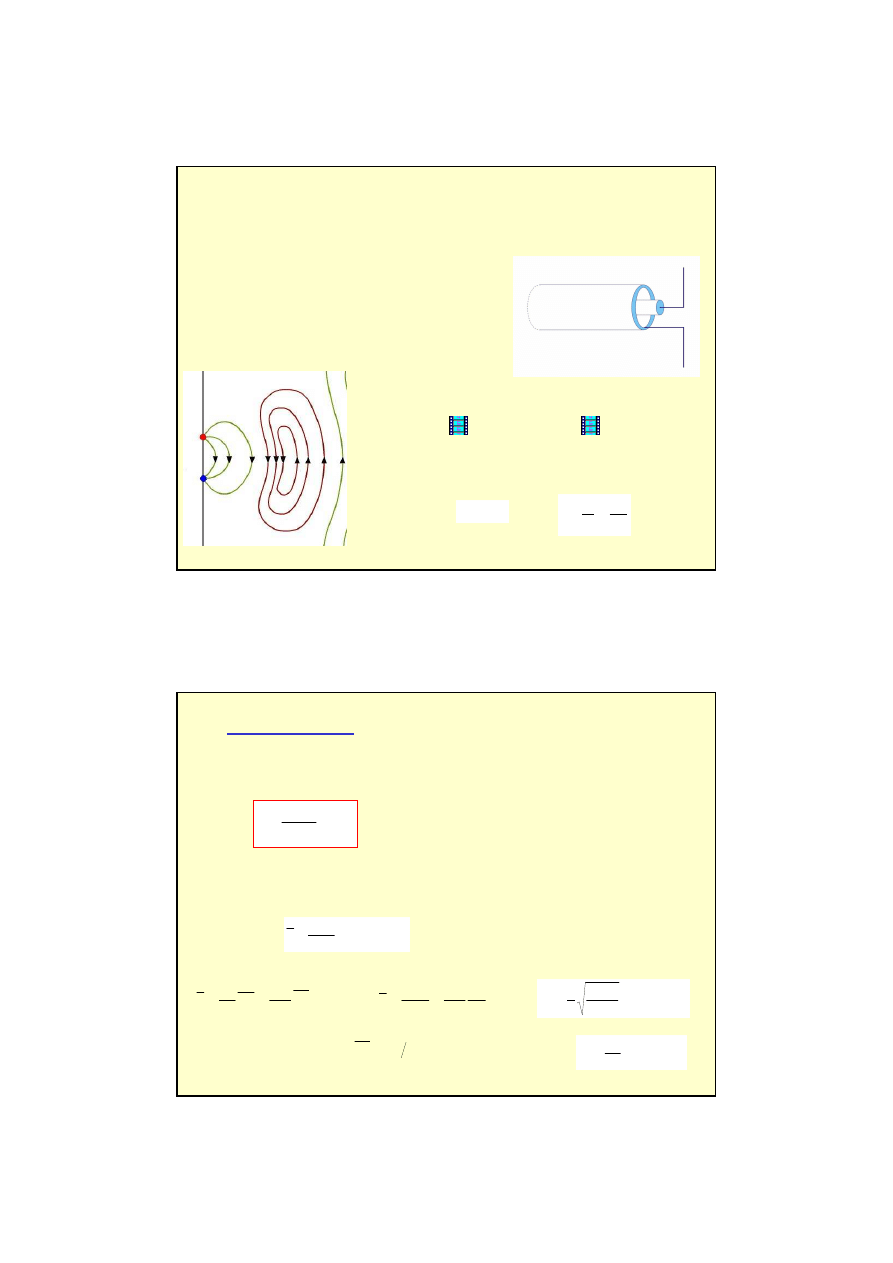
Równanie falowe

Rozkład pola elektrycznego
i magnetycznego w kablu
koncentrycznym w danej
chwili t.

Pola te poruszaj

ą

si

ę

wzdłu

ż

kabla z pr

ę

dko

ś

ci

ą

c.

Przykładowy rozkład pól

E, B

dla

prostok

ą

tnego falowodu.

Rozkład pól nie musi by

ć

sinusoidalnie zmienny.

Rozchodzenie si

ę

fal elektromagnetycznych

6

Elektromagnetyczna linia transmisyjna mo

ż

e by

ć

zako

ń

czona w sposób umo

ż

liwiaj

ą

cy

wypromieniowanie energii elektromagnetycznej do otaczaj

ą

cej przestrzeni.

antena dipolowa

Je

ż

eli ró

ż

nica potencjałów pomi

ę

dzy mi

ę

dzy drutami

zmienia si

ę

sinusoidalnie to taka antena zachowuje si

ę

jak dipol elektryczny, którego moment dipolowy zmienia
si

ę

co do wielko

ś

ci jak i kierunku.

Energia jest wypromieniowywana przez anten

ę

w postaci fali elektromagnetycznej.

Fala elektromagnetyczna emitowana

przez drgaj

ą

cy dipol elektryczny

Fale elektromagnetyczne mog

ą

rozchodzi

ć

si

ę

w pró

ż

ni

v

c

λ

=

0

0

B

E

k

c

=

=

ω

Szybko

ść

przepływu energii przez jednostkow

ą

powierzchni

ę

płaskiej fali

elektromagnetycznej opisujemy wektorem

S

zwanym wektorem Poyntinga

B

E

S

×

=

0

1

µ

µ

r

Kierunek wektora

S

pokazuje kierunek przenoszenia

energii. Wektory

E

i

B

s

ą

chwilowymi warto

ś

ciami pola

elektromagnetycznego w rozpatrywanym punkcie.

Przykład : Radiostacja o mocy P

0

= 30 kW wysyła fale EM izotropowo. Obliczamy nat

ęż

enie

sygnału (moc na jednostk

ę

powierzchni) w odległo

ś

ci r = 10 km od nadajnika.

ś

rednia warto

ść

wektora Poyntinga w

odległo

ś

ci r od

ź

ródła

2

2

0

m

/

µ

W

24

4

=

=

r

P

S

π

2

0

0

1

1

E

c

EB

S

µ

µ

=

=

2

1

4

2

0

0

2

0

E

c

r

P

S

µ

π

=

=

m

/

V

13

.

0

2

1

0

0

0

=

=

π

µ

cP

r

E

cB

E

=

2

2

0

2

E

E

=

fala sinusoidalna

T

10

4

10

0

0

−

⋅

=

=

c

E

B

Wektor Poyntinga