Obwody trójfazowe ... /11

2008 K.M.Gawrylczyk

1

O

BWODY TRÓJFAZOWE

Znikanie sumy napięć ïród»owych i sumy prądów

w wielofazowym układzie symetrycznym

n – liczba faz układu,

α = 2π / n - kąt pomiędzy kolejnymi napięciami fazowymi,

e

j

nα

= 1, e

-j

nα

= 1

Napięcie k-tej fazy:

e

k

= |E

m

| sin[ωt − (k − 1)α]

Przy n - fazach:

[

]

(

)

(

)

(

)

1

j t

j( t- )

j[ -( -1) ]

- j t

- j( t- )

- j[ -( -1) ]

j t

- j

- j( -1)

- j t

j

( -1)

- j

j

- j

=

sin + sin(

) +... + sin[

( 1) ]

1

e +e

+...+e

e

e

... e

2j

1

e 1+e +...+e

e

1+e +...+e

2j

1

1 e

e

2j

1 e

n

k

m

k=

t n

t n

m

n

n

m

n

t

m

e

E

t

t

t

n

E

E

E

ω

ω α

ω

α

ω

ω α

ω

α

ω

α

α

ω

α

α

α

ω

α

ω

ω

α

ω

α

−

−

−

=

=

−

−

− −

=





=

−

=





−

=

−

−

∑

j

- j

j

1 e

e

= 0.

1 e

n

t

α

ω

α





−





−





Użyty został wzór na sumę ciągu geometrycznego:

1

j

1

1

,

e

1

n

n

k

k

a

a

a

a

α

−

±

=

−

=

=

−

∑

.

Analogicznie dla funkcji typu cosinus:

=1

cos[

( 1) ] = 0.

ω

α

−

−

∑

n

k

t

n

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

2

Wyrównanie układu symetrycznego o liczbie faz n $ 3

Moc chwilowa wytwarzana w k-tej fazie źródła:

p

k

= e

k

·i

k

= |E

m

|·|I

m

|·sin[ωt − (k − 1)·α]·sin[ωt − (k − 1)·α − n] =

= |E|·|I|·{cos n − cos[2ωt − 2(k − 1)·α − n]}

Przy n $ 3 zachodzi :

n

=

= | || | cos

k=1

k

p

p n E I

φ

⋅

⋅ ⋅

∑

Dla n = 2 α = 2π/n = π , wi“c:

2(k−1)·α = 0 przy k = 1,

2(k−1)·α = 2π przy k = 2,

stąd moc chwilowa pobierana w dwóch fazach :

p = p

1

+ p

2

= |E|·|I|·2 [cosn − cos(2ωt − n)]

i wyrównanie nie występuje (moc jest funkcją czasu).

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

3

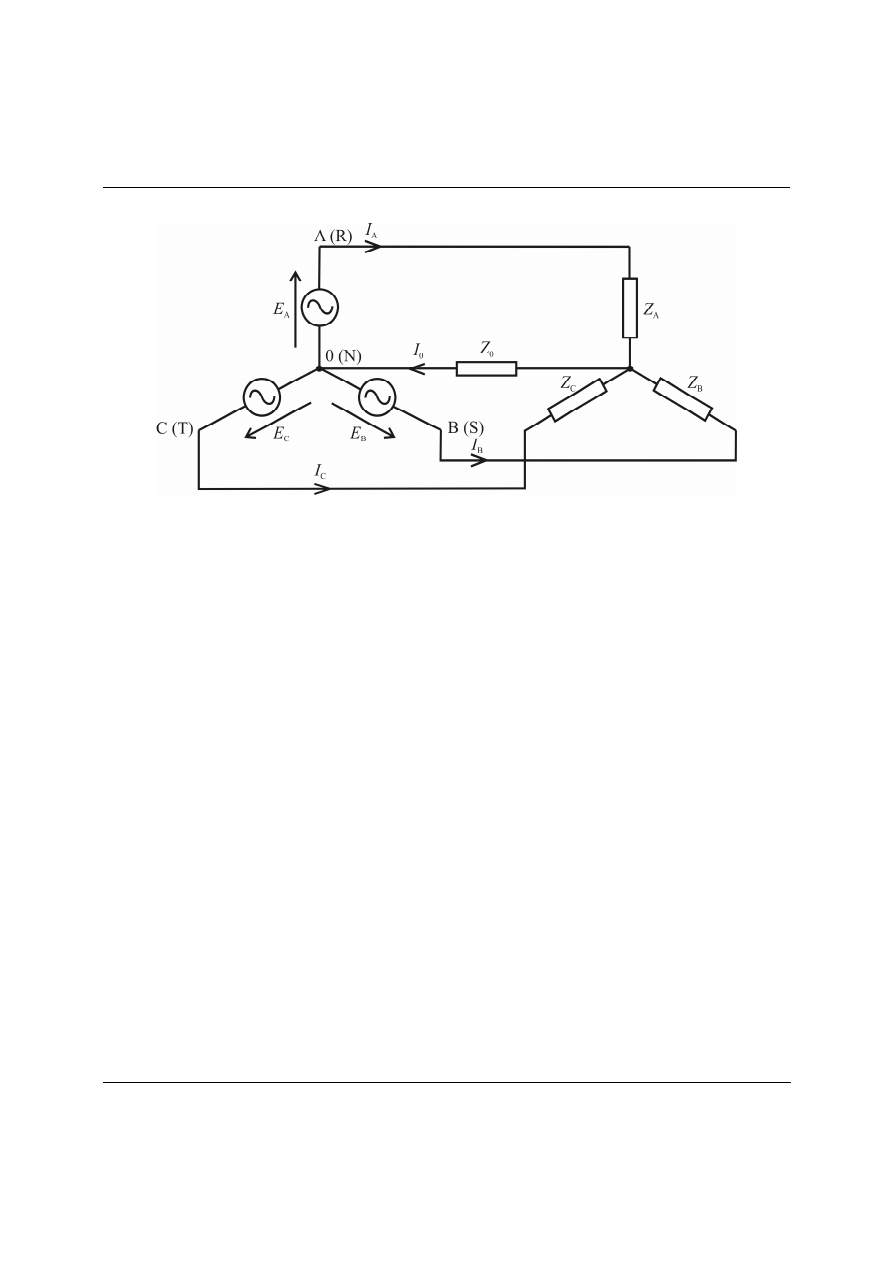
Układ trójfazowy skojarzony w gwiazdę

Rys. 1. Generator i odbiornik skojarzone w gwiazdę.

Suma prądów w węźle środkowym odbiornika:

I

A

+ I

B

+ I

C

=I

0

,

i

A

+ i

B

+ i

C

=i

0

.

Przy symetrycznym generatorze:

e

A

= |E

m

| sin ωt

e

B

= |E

m

| sin (ωt−120°)

e

C

= |E

m

| sin (ωt−240°) = |E

m

| sin (ωt+120°)

i symetrycznym odbiorniku prądy w gałęziach odbiornika wynoszą:

i

A

= |I

m

| sin (ωt − φ)

i

B

= |I

m

| sin (ωt − 120°− φ)

i

C

= |I

m

| sin (ωt − 240°− φ)

i tworzą układ trójfazowy symetryczny (trójkąt zamknięty), a ich suma,

prąd i

0

= 0. Układ jest wyrównany, a jego moc czynna wynosi

P = 3·|E|·|I|·cosφ.

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

4

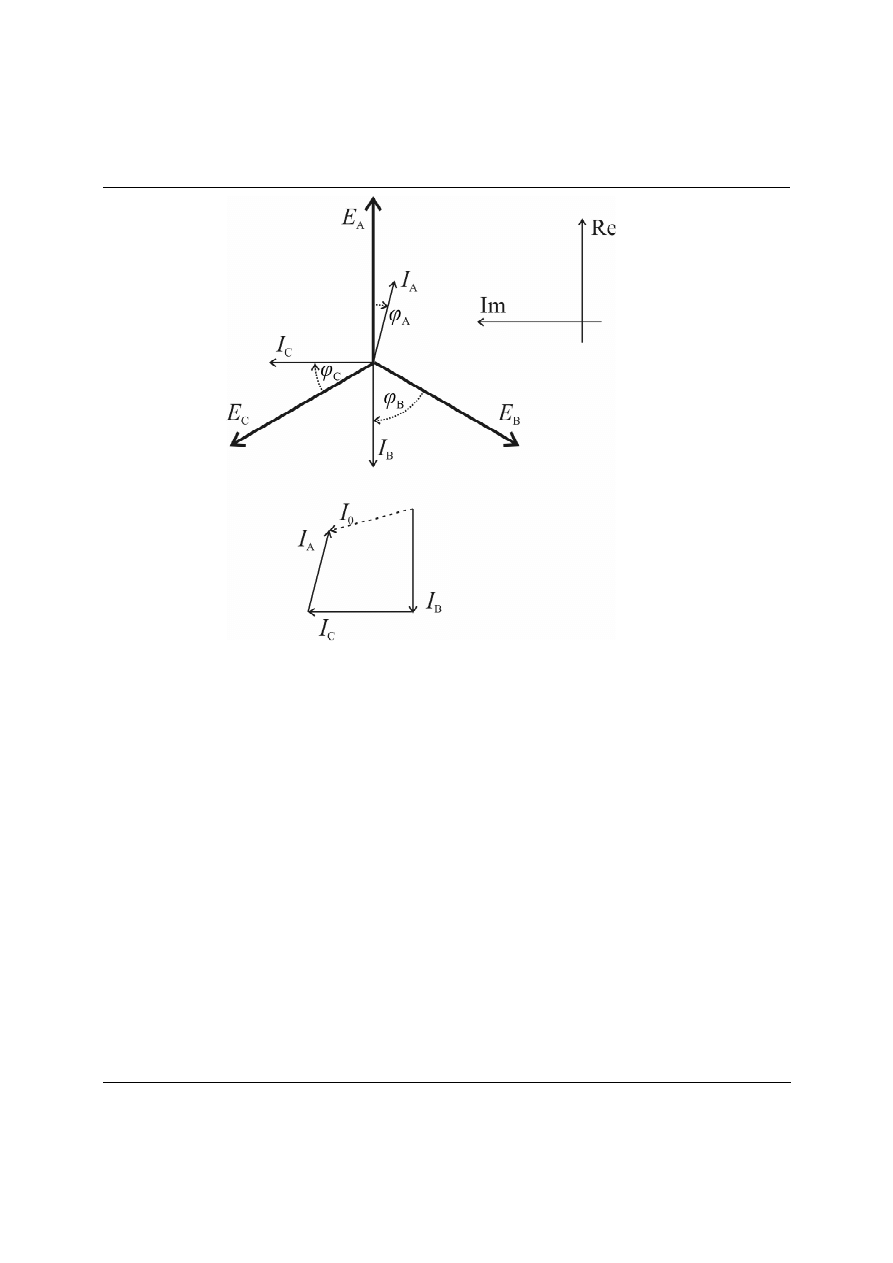
Rys. 2. Wykres wskazowy dla generatora symetrycznego, lecz odbiornika niesymetrycznego.

Jeżeli odbiornik nie jest symetryczny, płynie prąd I

0

w przewodzie

zerowym. Moc czynna odbiornika, wraz z mocą traconą w impedancji Z

0

wynosi wtedy:

P = |E

A

|·|I

A

|·cosφ

A

+|E

B

|·|I

B

|·cosφ

B

+|E

C

|·|I

C

|·cosφ

C

lub:

P = Re(E

A

·I

A

*

+E

B

·I

B

*

+E

C

·I

C

*

)

Moc czynna samego odbiornika wynosi:

P' = |I

A

|

2

·Re(Z

A

) + |I

B

|

2

·Re(Z

B

) + |I

C

|

2

·Re(Z

C

).

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

5

A

NALIZA ODBIORNIKA NIESYMETRYCZNEGO

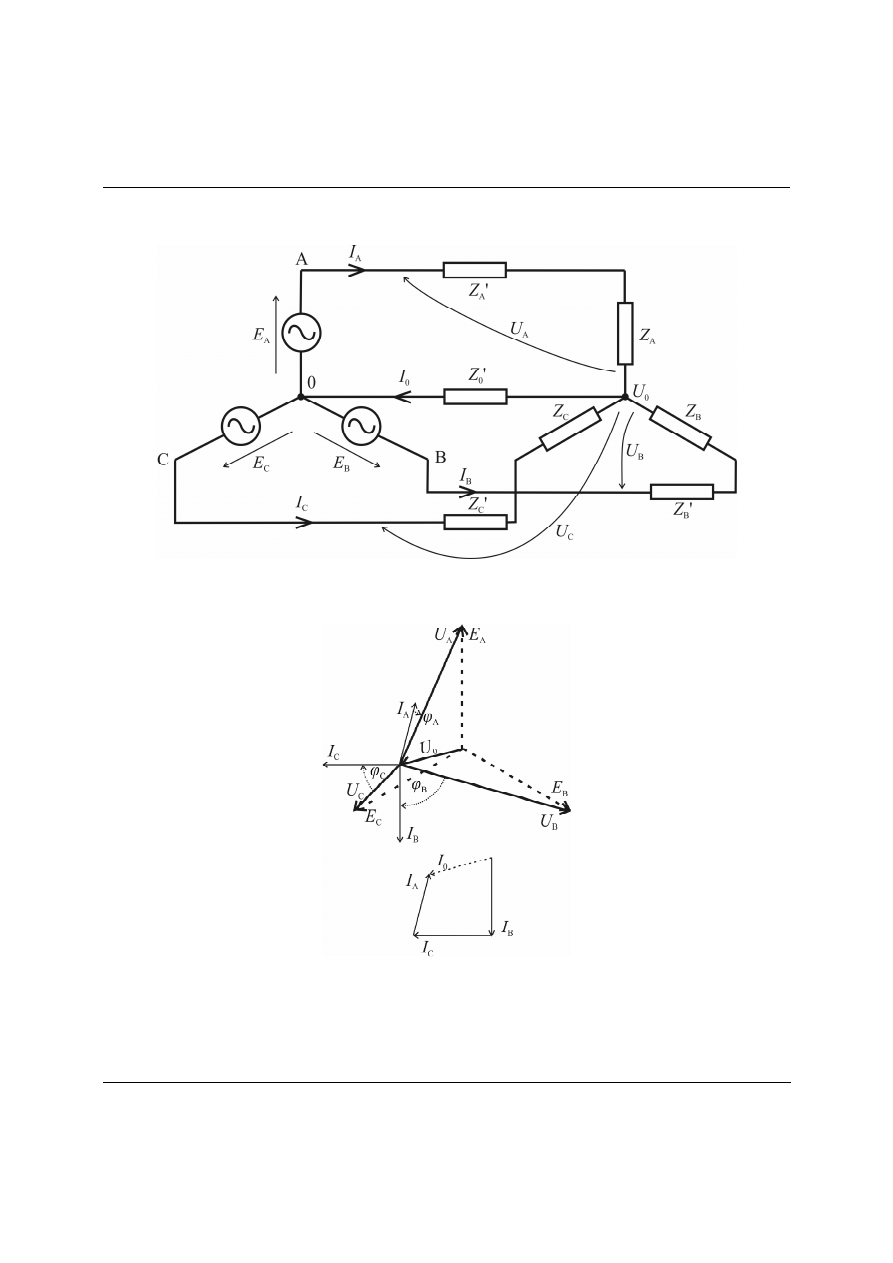
Rys. 3. Odbiornik gwiaździsty niesymetryczny z impedancjami przewodów.

Rys. 4. Wykres wskazowy dla odbiornika niesymetrycznego.

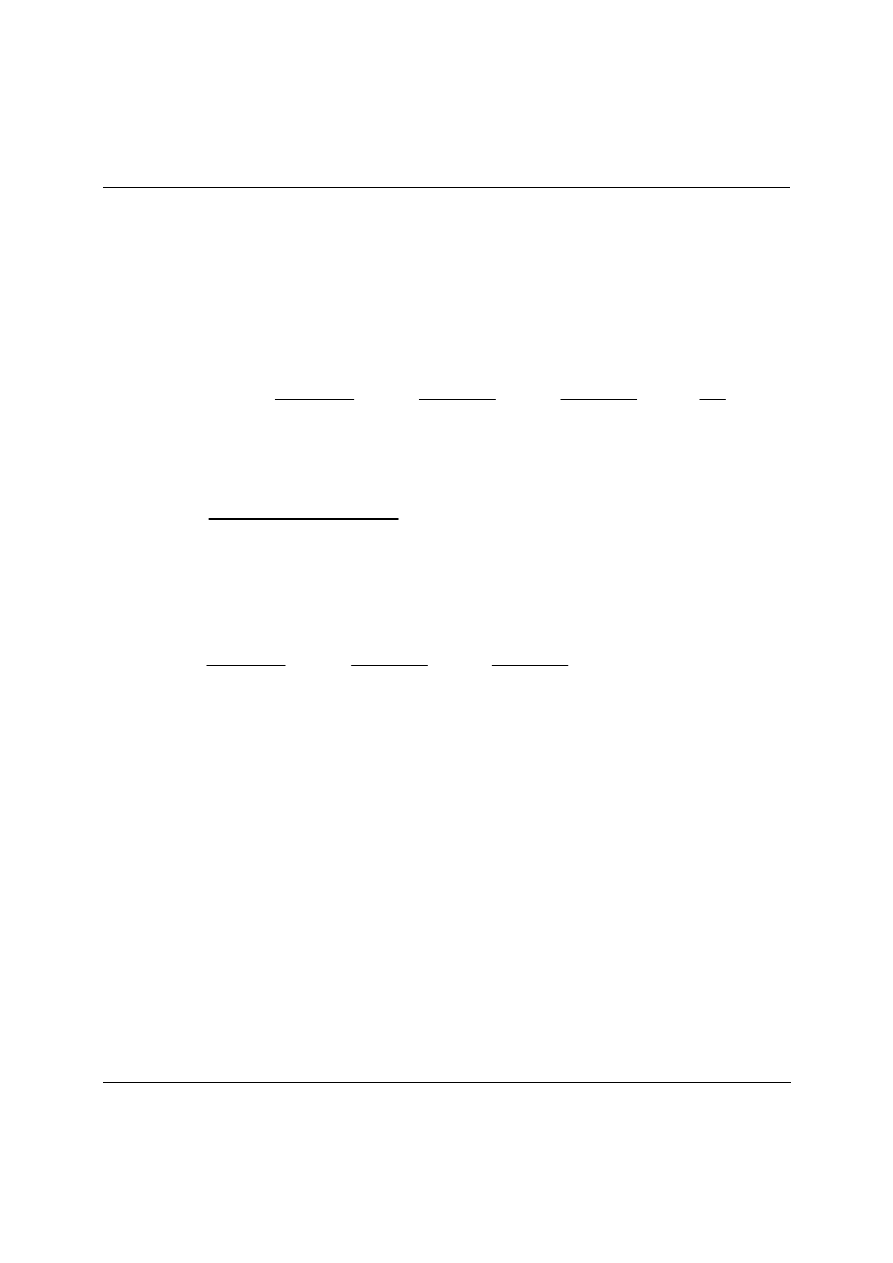
Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

6

W celu wyznaczenie prądów faz odbiornika trzeba najpierw

wyznaczyć potencjał punktu zerowego odbiornika U

0

, odniesiony do

punktu zerowego generatora. W tym celu użyjemy metody węzłowej:

(

)

0

A

B

C

0

A A

B B

C C

A

B

C

0

A

A

B

B

C

C

0

'

'

'

'

,

1

1

1

1

gdzie:

,

,

,

.

U Y

Y

Y

Y

E Y

E Y

E Y

Y

Y

Y

Y

Z

Z

Z

Z

Z

Z

Z

+ + +

=

+

+

=

=

=

=

+

+

+

czyli:

A A

B B

C C

0

A

B

C

0

E Y

E Y

E Y

U

Y

Y

Y

Y

+

+

=

+ + +

.

Prądy poszczególnych faz odbiornika wynoszą:

A

0

B

0

C

0

A

A

C

A

A

B

B

C

C

'

'

'

,

,

E

U

E

U

E

U

I

I

I

Z

Z

Z

Z

Z

Z

−

−

−

=

=

=

+

+

+

.

Np. przy symetrycznym generatorze (230V):

E

A

= |E

m

| = 230[V]

E

B

= |E

m

| e

-j120°

= −115−j200[V]

E

C

= |E

m

| e

-j240°

= |E

m

| e

j120°

=−

115+j200[V]

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

7

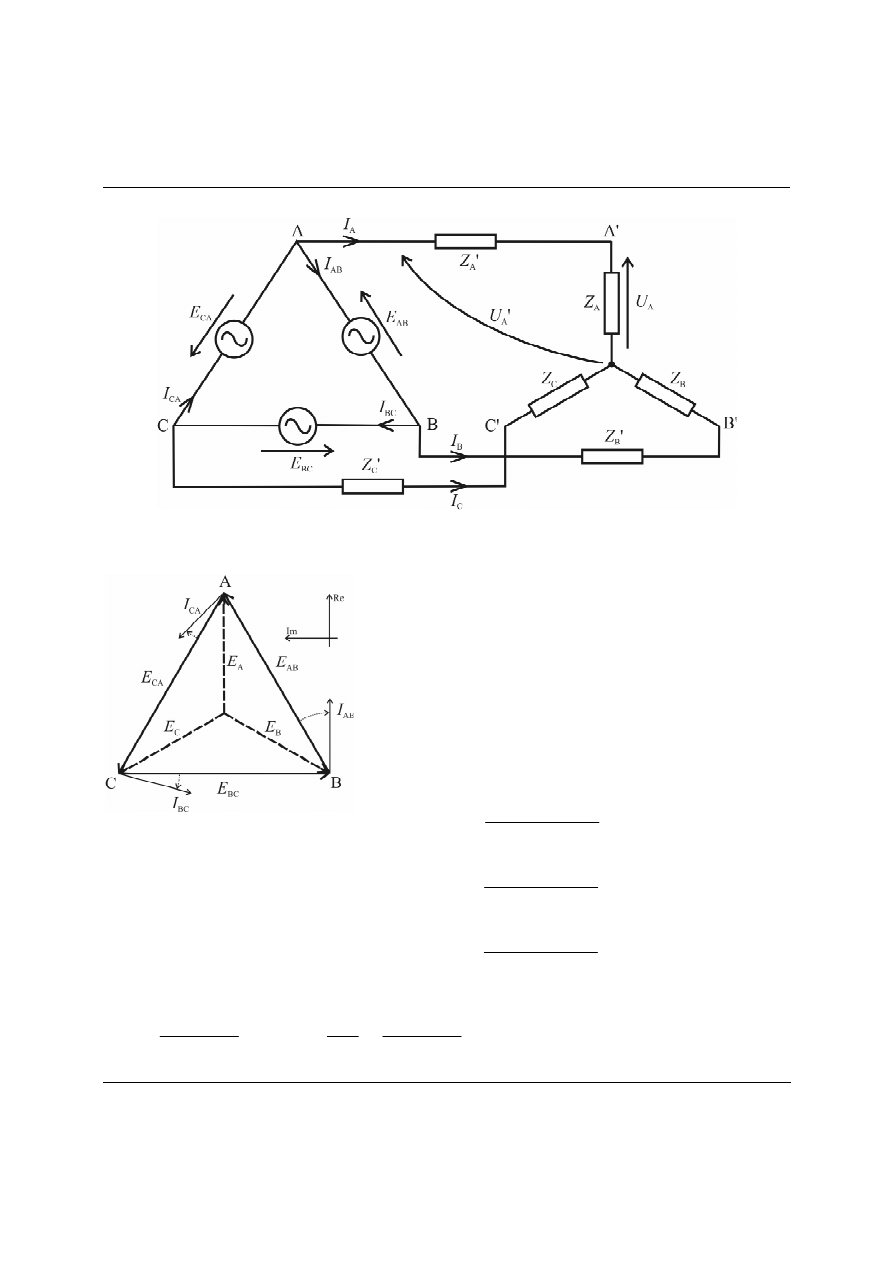
U

KŁAD TRÓJKĄT

-

GWIAZDA

Rys. 5. Odbiornik gwiaździsty połączony z generatorem w układzie trójkąta.

|E

fm

| = 400[V]

E

AB

= E

A

−

E

B

= |E

fm

| e

j30°

= 345 + j200,

E

BC

= E

B

−

E

C

= |E

fm

| e

-j90°

= −j400

E

CA

= E

C

−

E

A

= |E

fm

| e

j150°

= −345 + j200

stąd:

Z dzielnika napięć:

A

A

A

A

A

A

A

A

A

A

A

'

'

'

'

,

Z

U

U

U

U I

Z

Z

Z

Z

Z

=

=

=

+

+

, itd. kolejno dla pozostałych faz.

A

A

B B

C C

A

B

AB

A

C

CA

'

'

'

'

'

'

'

0

Y U

Y U

Y U

U

U

E

U

U

E

+

+

=

−

=

−

+ =

(

)

(

)

(

)

A

B AB

C CA

A

B

C

B

C BC

A AB

A

B

C

C

A CA

B BC

A

B

C

'

'

'

1

1

1

U

Y E

Y E

Y

Y

Y

U

Y E

Y E

Y

Y

Y

U

Y E

Y E

Y

Y

Y

=

−

+ +

=

−

+ +

=

−

+ +

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

8

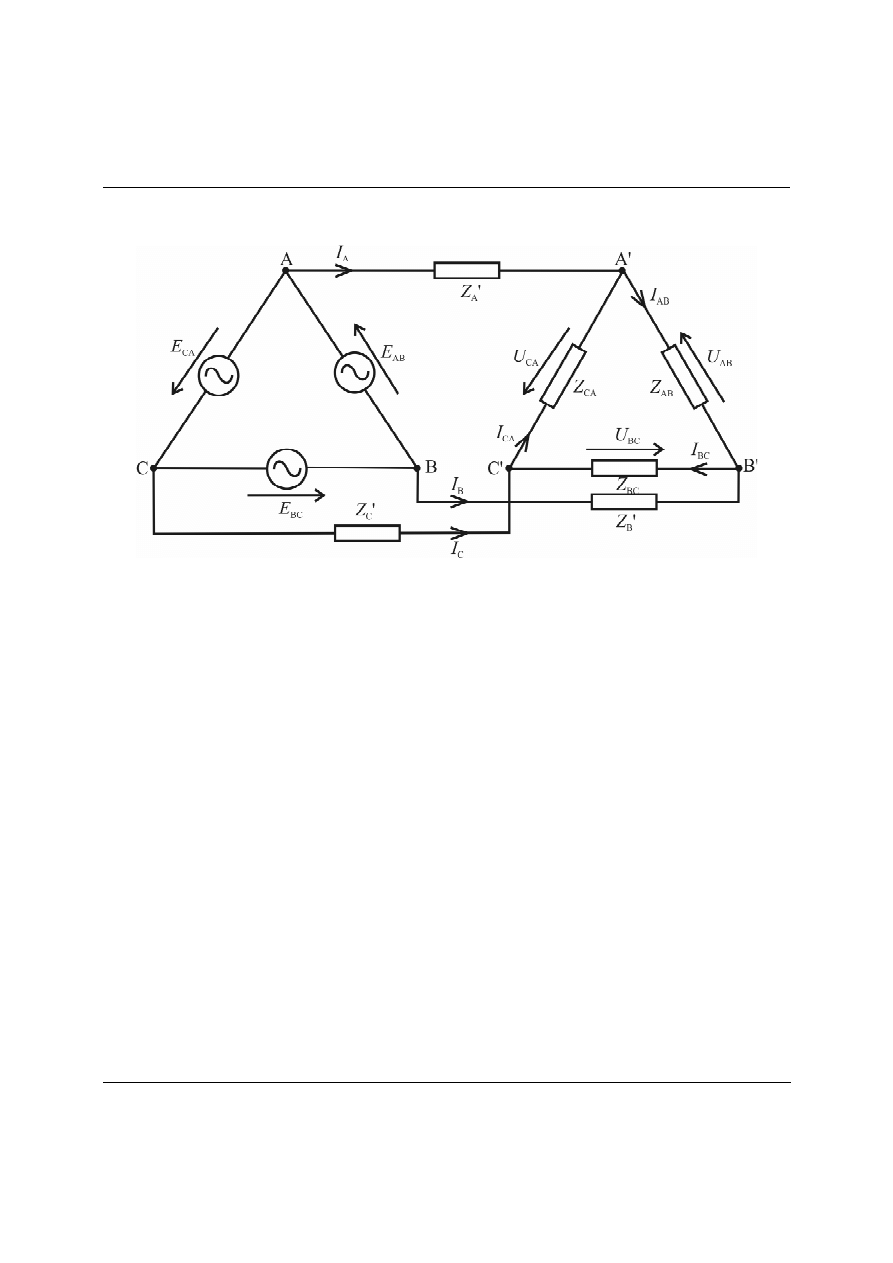
U

KŁAD TRÓJKĄT

-

TRÓJKĄT

Rys. 6. Odbiornik trójkątowy połączony z generatorem w układzie trójkąta.

Bilans napięć w oczku:

A A

AB AB

B B

AB

'

'

Z I

Z I

Z I

E

+

−

=

Prądy liniowe w funkcji prądów fazowych:

A

AB

CA

B

BC

AB

,

I

I

I

I

I

I

=

−

=

−

Stąd otrzymujemy pierwsze równanie, kolejne przez przestawienie

wskaźników:

(

)

(

)

(

)

A

AB

B

AB

B BC

A CA

AB

B AB

B

BC

C

BC

C CA

BC

A AB

C BC

C

CA

A

CA

CA

'

'

'

'

'

'

'

'

'

'

'

'

Z

Z

Z I

Z I

Z I

E

Z I

Z

Z

Z I

Z I

E

Z I

Z I

Z

Z

Z I

E

+

+

−

−

=

−

+

+

+

−

=

−

−

+

+

+

=

Z tego układu równań można wyznaczyć prądy fazowe odbiornika:

I

AB

, I

BC

, I

CA

.

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

9

P

OMIAR MOCY W UKŁADACH TRÓJFAZOWYCH

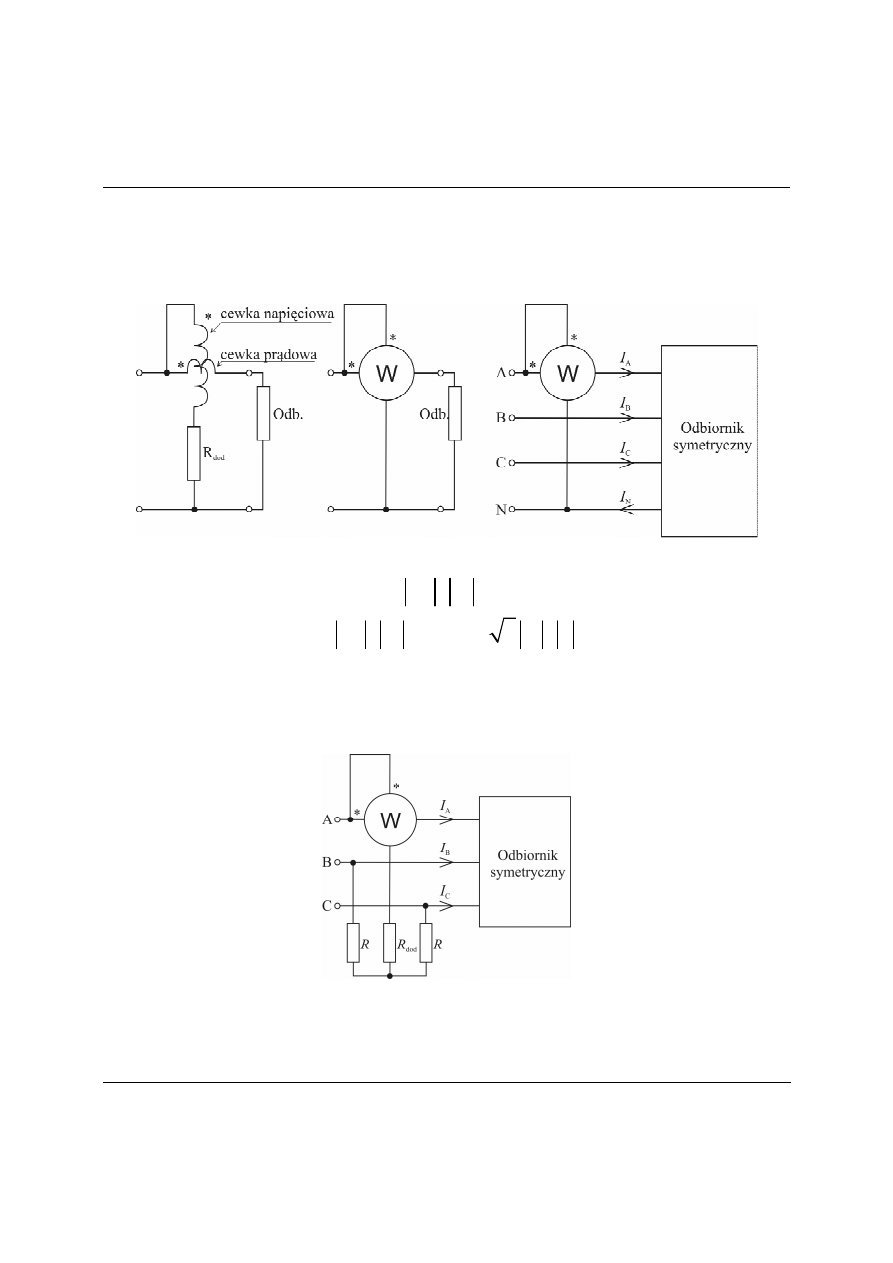
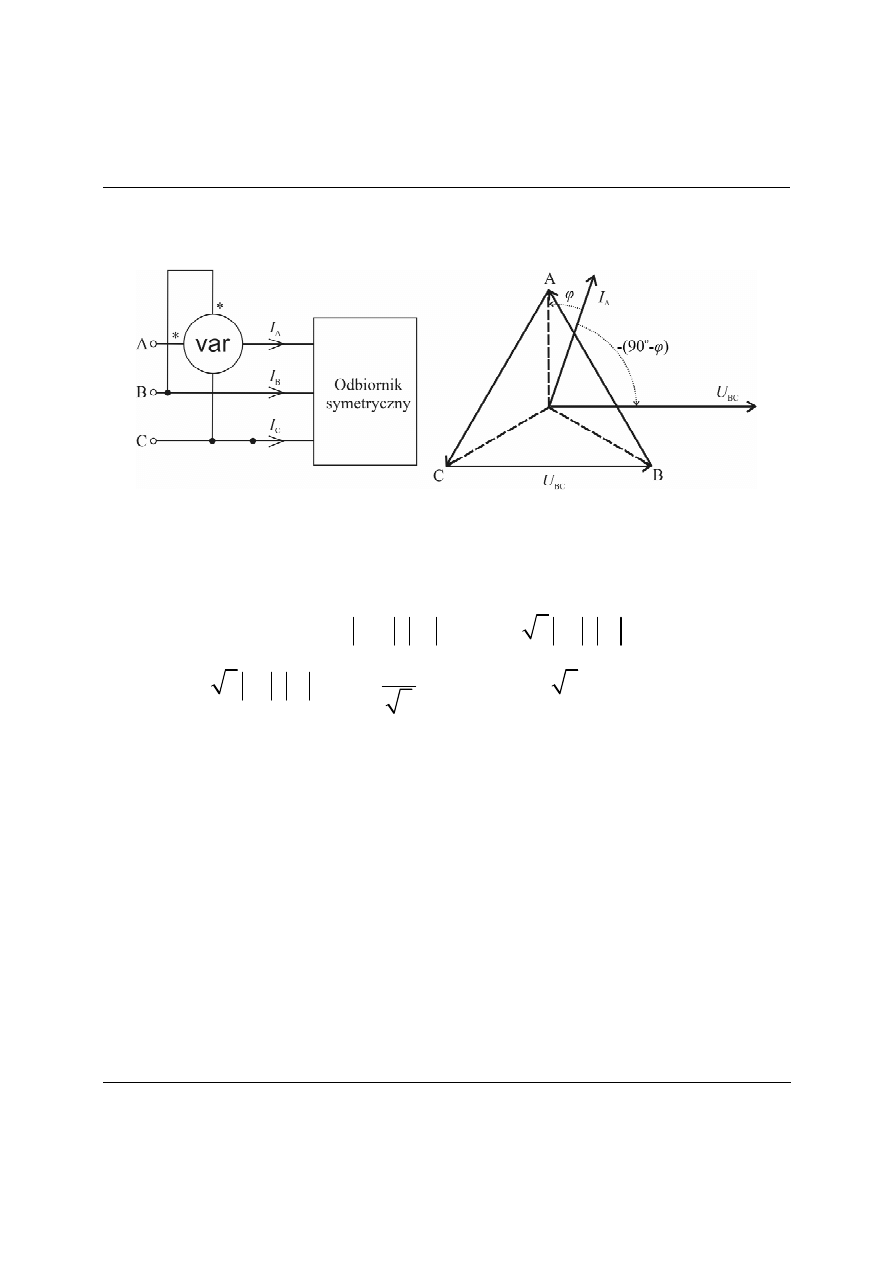
Pomiar mocy w układzie symetrycznym

Rys. 7. Użycie watomierza do pomiaru mocy w układzie trójfazowym symetrycznym.

W

V

I

f

f

W

f

f

cos

cos ,

3

3

cos

3

cos ,

P

U

I

U

I

P

P

U

I

U I

ϕ

ϕ

ϕ

ϕ

=

⋅ ⋅

=

⋅

⋅

=

= ⋅

⋅

⋅

=

⋅ ⋅

gdzie:

U

f

, I

f

– napięcie i prąd fazowy,

U, I – napięcie i prąd liniowy.

Rys. 8. Pomiar mocy czynnej w układzie symetrycznym ze sztucznym zerem,

R

V

+

R

dod

=

R

.

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

10

Pomiar mocy biernej w układzie symetrycznym

Rys. 9. Układ do pomiaru mocy biernej w układzie symetrycznym.

Wskazanie waromierza wynosi P

W

:

(

)

o

W

V

I

BC

A

f

f

3f

f

f

3f

W

cos

cos

3

cos 90

3

sin

, czyli:

3 .

3

P U I

U

I

U I

Q

U I

Q

P

ϕ

ϕ

ϕ

ϕ

=

⋅ ⋅

=

⋅

⋅

=

⋅

−

=

=

⋅

=

=

Obwody trójfazowe ...

/11

2008

K.M.Gawrylczyk

11

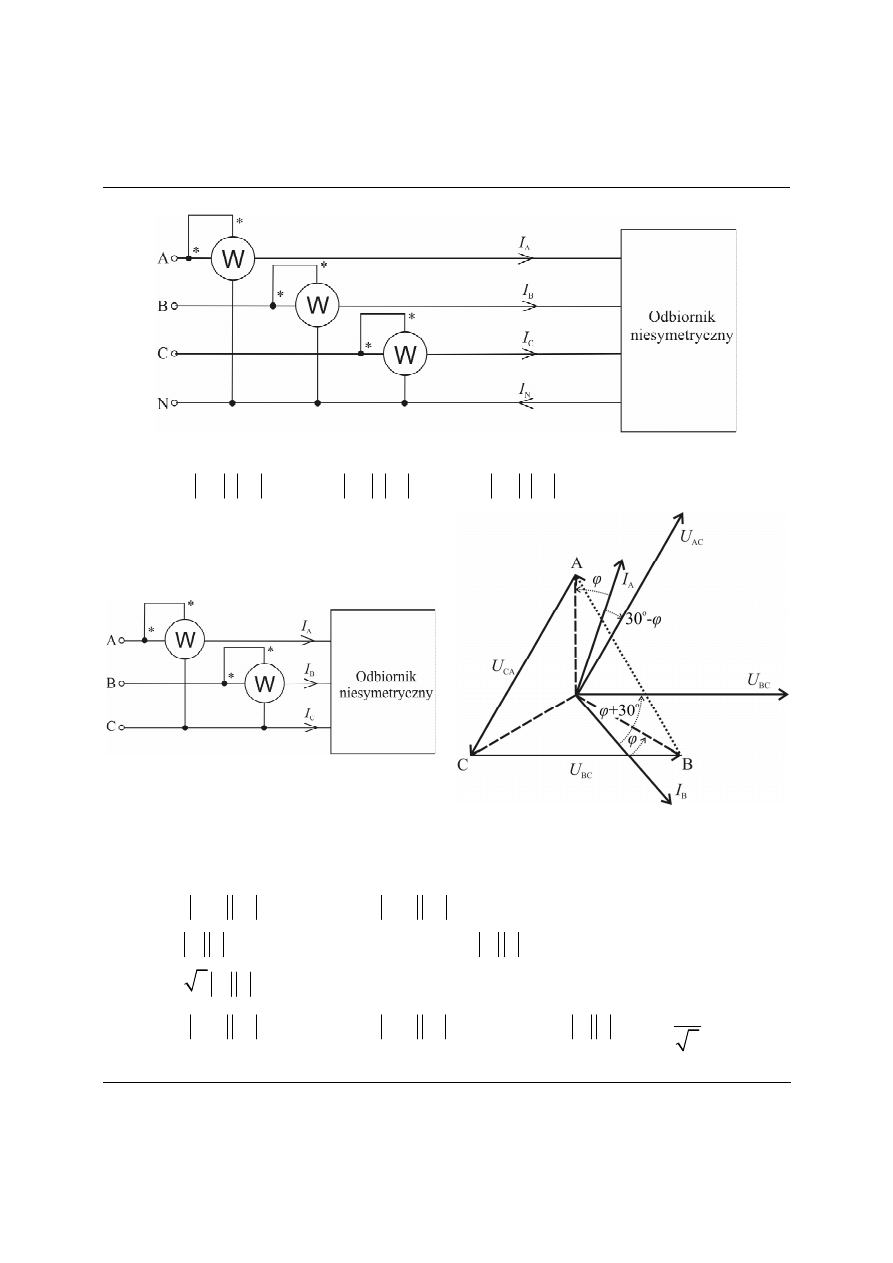
Pomiar mocy w układzie niesymetrycznym

Rys. 10. Pomiar mocy czynnej układu niesymetrycznego trzema watomierzami.

A

A

A

B

B

B

C

C

C

cos

cos

cos

P

U

I

U

I

U

I

ϕ

ϕ

ϕ

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

Rys.11. Pomiar mocy w układzie Arona.

Na przykładzie odbiornika symetrycznego:

(

)

(

)

o

o

1

2

AC

A

BC

B

o

o

o

o

odb

o

o

1

2

AC

A

BC

B

odb

cos(30

)

cos(

30 )

cos cos30 sin sin30

cos cos30 sin sin30

3

cos

,

1

cos(30

)

cos(

30 )

sin

.

3

W W U

I

U I

U I

U I

U I

P

W W U

I

U I

U I

Q

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

+

=

− +

+

=

=

+

+

−

=

=

=

−

=

− −

+

=

=