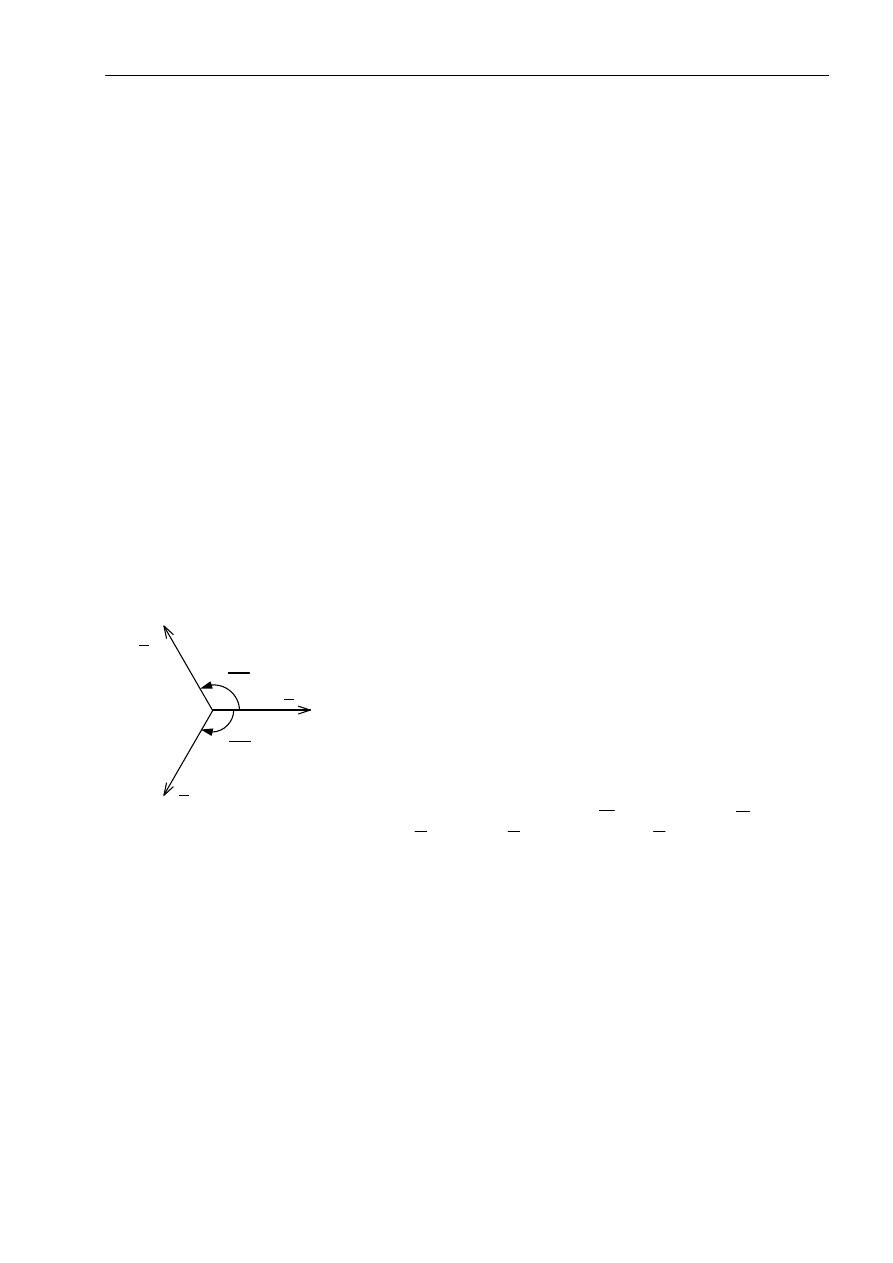
7. Rozwiązywanie obwodów prądu sinusoidalnego

143

Wykład XVII. PODSTAWOWE STRUKTURY OBWODÓW TRÓJFAZOWYCH

Układ wielofazowy i układ trójfazowy

Terminem układ wielofazowy określa się zbiór – w liczbie dwa lub większej – takich, związanych
ze sobą strukturalnie obwodów elektrycznych, że w każdym z nich działa jedno źródło napięcia
sinusoidalnego o częstotliwości takiej samej jak w obwodach pozostałych, oraz początkowym kącie
fazowym różnym niż w obwodach pozostałych.
Obwody tworzące układ wielofazowy noszą nazwę faz tego układu. Jak wiadomo, termin „faza”
oznacza też bieżącą wartość argumentu przebiegu sinusoidalnego, tj.

ω

t

+

ψ

, dlatego aby nie po-

wodować nieporozumień, zaznacza się zwykle, czy chodzi o fazę układu, czy o fazę przebiegu
(unika się też używania skróconej nazwy początkowego kąta fazowego: „faza początkowa”).
Uporządkowanie początkowych kątów fazowych

ψ

u

napięć źródłowych w fazach układu – wg ma-

lejących wartości – wyznacza kolejność faz układu. Jeśli punkty o tych wartościach dzielą prze-
dział o długości równej 2

π

=

360

°

(okres funkcji sinus) na równe odcinki, a przy tym wartości sku-

teczne napięć w fazach są jednakowe, to taki układ wielofazowy nazywa się symetrycznym.
Fazy układu oznacza się kolejnymi literami alfabetu (oznaczeniem pierwszej fazy może, ale nie
musi być litera A) lub cyframi (w takim wypadku oznaczeniem pierwszej fazy jest zawsze cyfra 1).
Warto zaznaczyć, że kolejność faz nie jest równoznaczna z ich numeracją (oznaczeniem faz). Za
pierwszą fazę można obrać dowolną fazę układu. Używa się też pojęć: zgodna i przeciwna kolej-
ność faz, np. w związku ze sposobem przyłączenia zacisków odbiornika do zacisków źródła.

Układ trójfazowy to układ o trzech fazach (obwodach fazowych). Fazy układu trójfazowego ozna-
cza się literami, np. A, B, C, albo cyframi 1, 2, 3. Fazom układu oznaczonym cyframi 1, 2, 3 odpo-
wiadają kolejności faz zgodne: 1, 2, 3; 2, 3, 1 i 3, 1, 2, oraz przeciwne: 1, 3, 2; 2, 1, 3 i 3, 2, 1.

Różnice faz początkowych napięć źródłowych symetrycznego
układu trójfazowego są równe

±

120

°

, jak na rys. obok, gdzie dla

wskazu w fazie A przyjęto początkowy kąt fazowy równy 0.
Funkcje czasu wyrażające te napięcia są następujących postaci:

t

E

t

e

m

A

ω

sin

)

(

⋅

=

, (7.19a)

)

120

sin(

)

(

o

−

⋅

=

t

E

t

e

m

B

ω

, (7.19b)

)

120

sin(

)

(

o

+

⋅

=

t

E

t

e

m

C

ω

, (7.19c)

a wartości symboliczne -

E

E

A

=

,

3

2

π

⋅

−

⋅

=

j

B

e

E

E

,

3

2

π

⋅

⋅

=

j

C

e

E

E

. (7.20)

Gdy obwody fazowe nie są połączone ze sobą galwanicznie, to układ wielofazowy (trójfazowy)
określa się jako nieskojarzony, gdy natomiast występuje tego rodzaju połączenie – jako skojarzony.
Ź

ródłowe napięcia fazowe są zwykle „pobierane” z trójfazowego uzwojenia generatora lub trans-

formatora, toteż w praktyce spotyka się wyłącznie układy trójfazowe skojarzone o zasilaniu syme-
trycznym. Takie właśnie obwody są dalej omawiane.

Źródło, odbiornik i linia skojarzonego układu trójfazowego

W układach trójfazowych występują źródła trójfazowe, odbiorniki trójfazowe oraz – pomijane czę-
sto w obliczeniach – linie trójfazowe (między źródłami i odbiornikami). W układach trójfazowych
skojarzonych, elementy fazowe źródła oraz odbiornika trójfazowego mogą być łączone w gwiazdę
lub w trójkąt.
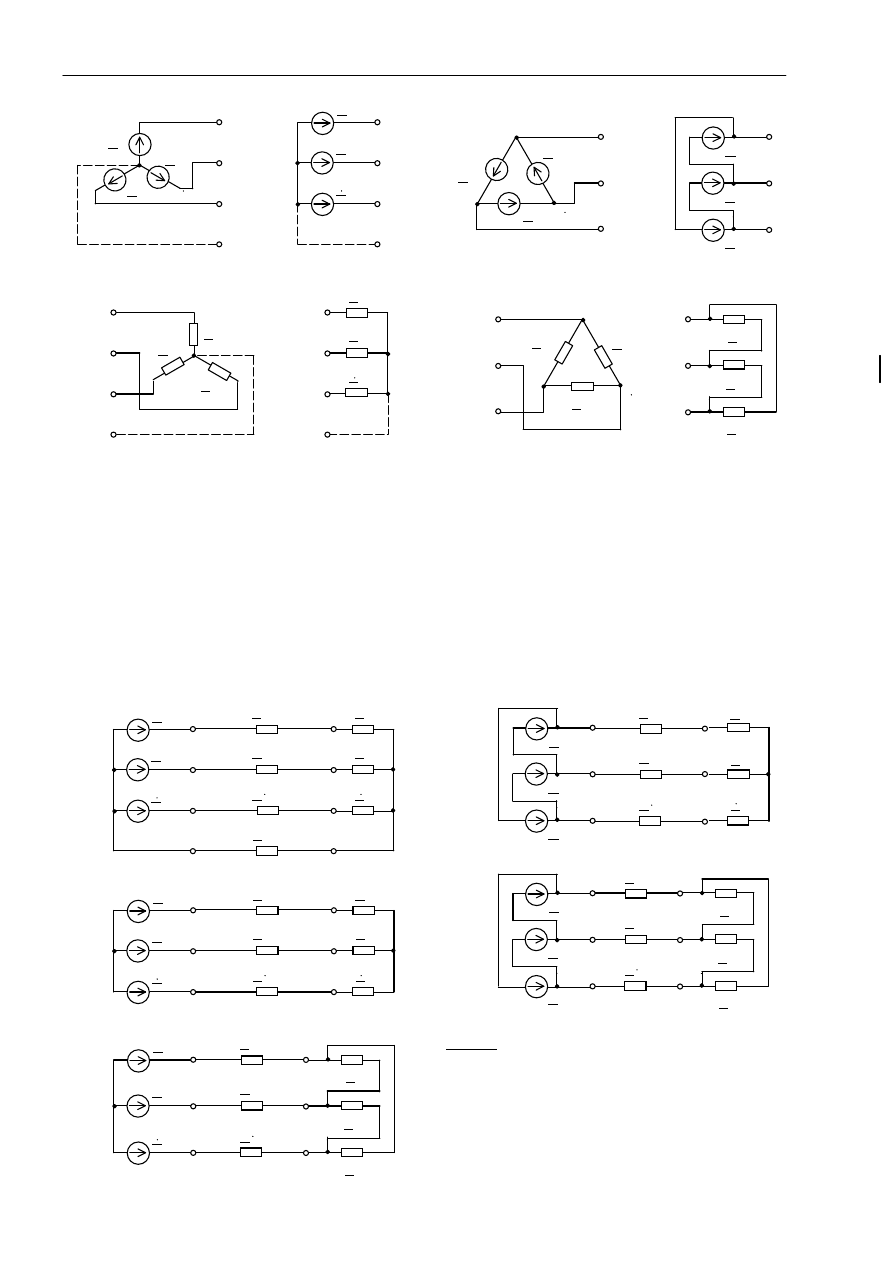
Układy „gwiazdowe” i „trójkątowe” można rysować sytuując elementy fazowe: 1) pod kątami od-
powiadającymi mniej więcej symetrycznemu przesunięciu wskazów, 2) równolegle do siebie.
Na poniższym rysunku pokazano obie wersje graficzne: a) źródła „gwiazdowego”, b) źródła „trój-
kątowego” (dla uproszczenia przyjęto źródła idealne), c) odbiornika „gwiazdowego”, d) odbiorni-
ka „trójkątowego”.

E

A

E

C

E

B

2

π

3

–

2

π

3

Wykład XVII

144

W układach gwiazdowych źródła i odbiornika występują punkty wspólne, nazywane neutralnymi
(oznaczenie: N, jak na rys.) lub zerowymi (oznaczenie: 0). Zależnie od tego, czy punkty te są połą-
czone z resztą układu, czy też nie (linia przerywana), źródła oraz odbiorniki są czterozaciskowe lub
trójzaciskowe. Oczywiście, źródła i odbiorniki „trójkątowe” są zawsze trójzaciskowe.

W linii trójfazowej występują 3 przewody, nazywane fazowymi, i ewentualnie – przewód czwarty,
nazywany neutralnym lub zerowym, który łączy punkty neutralne (zerowe) układów gwiazdowych
ź

ródła i odbiornika. Zależnie od tego, czy w linii jest przewód neutralny (zerowy), czy też nie, na-

zywa się ją czteroprzewodową lub trójprzewodową. Na poniższym rysunku pokazano: a’) układ z
linią czteroprzewodową – w jedynej możliwej konfiguracji ze źródłem i odbiornikiem (gwiazda-
gwiazda); a’’, a’’’, b’, b’’) układy z linią trójprzewodową – we wszystkich konfiguracjach ze źró-
dłem i odbiornikiem (gwiazda-gwiazda, gwiazda-trójkąt, trójkąt-gwiazda, trójkąt-trójkąt).

Uwaga. Terminy „neutralny” i „zerowy”
(punkt, przewód) są używane zamiennie, ale
preferuje się nazwę pierwszą. Pojęcie punktu
lub przewodu zerowego bywa bowiem zawę-
ż

ane do takiego, który jest uziemiony (połą-

czony galwanicznie z ziemią, dokładniej – z
jej wierzchnią warstwą przewodzącą).

c) d)

≡

A

B

C

Z

AB

Z

CA

Z

BC

A

B

C

Z

AB

Z

CA

Z

BC

≡

A

B

C

N

Z

A

Z

C

Z

B

A

B

C

N

Z

A

Z

C

Z

B

a) b)

≡

A

B

C

E

AB

E

CA

E

BC

A

B

C

E

AB

E

CA

E

BC

A

B

C

N

E

A

E

C

E

B

≡

A

B

C

N

E

A

E

C

E

B

a’)

a’’)

a’’’)

A’

B’

C’

N’

Z

A

Z

C

Z

B

A

B

C

N

E

A

E

C

E

B

Z

AA’

Z

CC’

Z

BB’

Z

N’N

A’

B’

C’

Z

A

Z

C

Z

B

A

B

C

E

A

E

C

E

B

Z

AA’

Z

CC’

Z

BB’

A

B

C

E

A

E

C

E

B

Z

AA’

Z

CC’

Z

BB’

A’

B’

C’

Z

AB

Z

CA

Z

BC

Z

AA’

Z

CC’

Z

BB’

A’

B’

C’

Z

AB

Z

CA

Z

BC

A

B

C

E

AB

E

CA

E

BC

b’)

b’’)

Z

AA’

Z

CC’

Z

BB’

A’

B’

C’

Z

A

Z

C

Z

B

A

B

C

E

AB

E

CA

E

BC

7. Rozwiązywanie obwodów prądu sinusoidalnego

145

Obwód trójfazowy. Prąd trójfazowy i napięcie trójfazowe

Ź

ródłowe napięcia występujące w układach trójfazowych tworzą trójfazowe układy napięć źródło-

wych; podobnie można mówić o trójfazowych układach napięć: w linii zasilającej i w odbiorniku,
oraz o trójfazowych układach prądów: w źródle, linii i odbiorniku. Aby uniknąć niejednoznaczności
terminu „układ”, określającego: 1) zbiór elementów tworzących pewną strukturę (powiązane ze
sobą obwody fazowe), 2) zbiór wielkości tego samego rodzaju, występujących w jakimś obiekcie
(powiązane ze sobą napięcia albo prądy), używa się, odpowiednio, terminów: 1) obwód trójfazowy,
2) napięcie trójfazowe i prąd trójfazowy.

Uwaga. Termin „obwód trójfazowy” jest powszechnie stosowany w elektroenergetyce, gdzie wy-
stępują układy trójfazowe o rozbudowanej strukturze. Przyjęło się tu mówić o obwodach jedno- i
trójfazowych jako układach „widzianych” przez grupę odbiorów. Obwody takie to podsystemy
rozdzielczo-odbiorcze, związane z odbiornikami zasilanymi z jednej linii układu elektroenergetycz-
nego. Część układu nazywana obwodem trójfazowym jest więc tu układem złożonym z zastępczego
ź

ródła trójfazowego, linii trójfazowej i przyłączonych do niej odbiorników. Pełna analiza funkcjo-

nowania systemu elektroenergetycznego prowadzona jest na różnych poziomach, odpowiadających
hierarchii podsystemów.

Napięcia, prądy i moce w obwodach trójfazowych

W obwodach trójfazowych można wyróżnić następujące napięcia oraz prądy:

a) napięcia fazowe źródła oraz odbiornika, tj. napięcia na ich elementach fazowych,

b) napięcia fazowe układu i linii zasilającej, tj. napięcia między przewodami fazowymi i przewo-

dem neutralnym, a w układzie z uziemionym punktem neutralnym źródła, bez przewodu neu-
tralnego (zerowego) – napięcia między przewodami fazowymi a wnętrzem ziemi (tzw. ziemią
odległą),

c) napięcia międzyfazowe źródła oraz odbiornika, tj. napięcia między punktami (zaciskami) źró-

dła oraz odbiornika, przyłączonymi do przewodów fazowych,

d) napięcie międzyfazowe, inaczej: międzyprzewodowe lub liniowe, układu i linii zasilającej, tj.

napięcia między przewodami fazowymi,

e) prądy fazowe źródła oraz odbiornika, tj. prądy w ich elementach fazowych,

f)

prądy liniowe, inaczej: przewodowe, oraz prąd powrotny (neutralny, zerowy) układu i linii za-
silającej, tj. prądy w przewodach fazowych oraz prąd w przewodzie neutralnym, a w układzie z
uziemionym punktem neutralnym źródła – w ziemi.

Symbole napięć i prądów fazowych (źródła, linii, odbiornika) opatruje się czasami indeksem „f”.
Wartości skuteczne fazowego i międzyfazowego (międzyprzewodowego) symetrycznego napięcia
trójfazowego linii zapisuje się w związku z tym jako: U

f

i U, a np. fazowe napięcia źródłowe ukła-

du „trójkątowego”, które są jednocześnie w tym wypadku napięciami międzyfazowymi źródła oraz
linii (E

AB

, E

BC

,

E

CA

), mogą być zapisane jako E

fA

, E

fB

, E

fC

.

Moce: czynna P, bierna Q oraz zespolona S, wydawane przez źródło trójfazowe lub pobierane przez
odbiornik trójfazowy, są równe odpowiednio:

fC

fB

fA

P

P

P

P

+

+

=

,

fC

fB

fA

Q

Q

Q

Q

+

+

=

,

fC

fB

fA

S

S

S

S

+

+

=

. (7.21a, b, c)

Omawiane będą obwody trójfazowe z idealnym (zwykle też symetrycznym) źródłem i bezimpedan-
cyjną linią zasilającą odbiornik.

Jeśli w tzw. gałęzi powrotnej układu gwiazda-gwiazda (między punktami neutralnymi źródła i od-
biornika) występuje impedancja Z

N’N

, to będzie ona traktowana jako element odbiornika Z

N

. W

takim wypadku, całkowite moce pobierane w odbiorniku są obliczane z zależności:

N

fC

fB

fA

P

P

P

P

P

+

+

+

=

,

N

fC

fB

fA

Q

Q

Q

Q

Q

+

+

+

=

,

N

fC

fB

fA

S

S

S

S

S

+

+

+

=

. (7.22a, b, c)

gdzie: P

N

, Q

N

, S

N

– moce tracone w gałęzi powrotnej, w impedancji Z

N

=

Z

N’N

odbiornika.

Wykład XVII

146

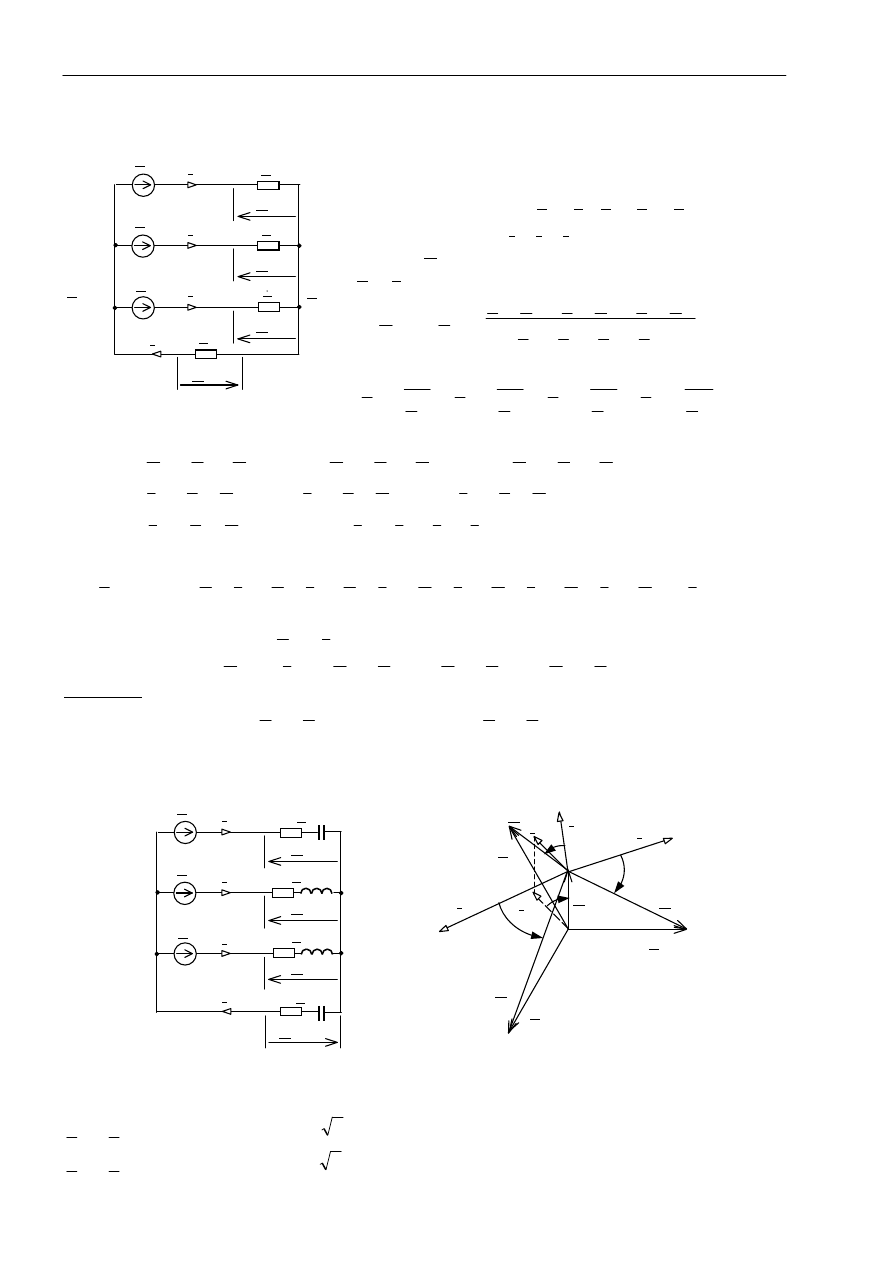
Odbiornik zasilany czteroprzewodowo

Na rys. obok pokazano obwód trójfazowy z odbiornikiem
o układzie gwiazdowym, zasilanym czteroprzewodowo.

W ogólnym przypadku: Z

N

≠

0 , Z

A

≠

Z

B

≠

Z

C

.

Aby obliczyć prądy: I

A

, I

B

, I

C

, trzeba najpierw wyznaczyć

napięcie U

N’N

. Stosując metodę węzłową, przy założeniu

V

N

=

0

, otrzymuje się:

N

C

B

A

C

C

B

B

A

A

N

N

N

Y

Y

Y

Y

E

Y

E

Y

E

Y

V

U

+

+

+

⋅

+

⋅

+

⋅

=

=

'

'

, (7.23a)

gdzie:

A

A

Z

Y

1

=

,

B

B

Z

Y

1

=

,

C

C

Z

Y

1

=

,

N

N

Z

Y

1

=

. (7.23b)

Następnie korzysta się z zależności:

N

N

A

A

U

E

U

'

−

=

,

N

N

B

B

U

E

U

'

−

=

,

N

N

C

C

U

E

U

'

−

=

, (7.23c)

A

A

A

U

Y

I

⋅

=

,

B

B

B

U

Y

I

⋅

=

,

C

C

C

U

Y

I

⋅

=

, (7.23d)

N

N

N

N

U

Y

I

'

⋅

=

albo

C

B

A

N

I

I

I

I

+

+

=

. (7.23e)

Moc wydawana przez źródło idealne, a pobierana przez odbiornik wraz z gałęzią powrotną, wynosi:

*

'

*

*

*

*

*

*

N

N

N

C

C

B

B

A

A

C

C

B

B

A

A

I

U

I

U

I

U

I

U

I

E

I

E

I

E

jQ

P

S

⋅

+

⋅

+

⋅

+

⋅

=

⋅

+

⋅

+

⋅

=

+

=

. (7.24)

Szczególnym przypadkiem jest czteroprzewodowy układ gwiazda-gwiazda z bezimpedancyjnym
przewodem neutralnym, tzn.

0

=

N

Z

, wobec czego:

0

'

=

N

N

U

,

A

A

E

U

=

,

B

B

E

U

=

,

C

C

E

U

=

.

Przykład 1. Odbiornik gwiazdowy o impedancjach faz i gałęzi powrotnej (przyłączonej do punktu
neutralnego odbiornika):

)

100

100

(

j

Z

Z

N

A

−

=

=

Ω

,

)

100

100

(

j

Z

Z

C

B

+

=

=

Ω

, jest zasilany

czteroprzewodowo napięciem symetrycznym 3

×

230/400 V. Należy obliczyć wartości napięć i prą-

dów występujących w obwodzie, przedstawić wykres wskazowy odpowiadający tym wartościom
oraz sporządzić bilans mocy obwodu.

Schemat obwodu z zaznaczeniem charakteru gałęzi – rys. a.

Wartości admitancji fazowych i admitancji gałęzi powrotnej, obliczone wg wzorów (7.23b):

o

45

2

2

10

2

5

,

0

10

)

5

,

0

5

,

0

(

j

N

A

e

j

Y

Y

⋅

⋅

=

⋅

+

=

=

−

−

S,

o

45

2

2

10

2

5

,

0

10

)

5

,

0

5

,

0

(

j

C

B

e

j

Y

Y

−

−

−

⋅

⋅

=

⋅

−

=

=

S.

N’

Z

A

Z

B

Z

C

I

A

I

B

I

C

E

A

E

C

E

B

Z

N

N

I

N

U

A

U

B

U

C

U

N’N

V

N

=

0

V

N’

U

A

U

B

U

C

N’

Z

A

Z

B

Z

C

I

A

I

B

I

C

E

A

E

C

E

B

Z

N

N

I

N

U

N’N

a) b)

E

A

E

C

E

B

U

A

U

C

U

B

I

N

I

C

I

A

I

B

ϕ

A

ϕ

B

ϕ

C

U

N‘N

ϕ

N

I

N

7. Rozwiązywanie obwodów prądu sinusoidalnego

147

Napięcie zasilające 3

×

230/400 V, określające znamionowe napięcia: fazowe U

f

=

230 V i między-

fazowego U

=

400 V, odpowiada w przybliżeniu warunkowi U

=

3 U

f

. Bliższe spełnienia tego

związku są np. wartości: U

f

=

231 V i U

=

400 V (230

3

≅

398,37 ; 231

3

≅

400,10). Dla ogra-

niczenia niepotrzebnych błędów – w tym i następnych przykładach – używać się będzie w oblicze-
niach tych drugich wartości.

Przyjęte wartości początkowych kątów fazowych napięć źródła:

o

0

.

=

A

e

ψ

,

o

120

.

−

=

B

e

ψ

,

o

120

.

=

C

e

ψ

.

Wartości symboliczne napięć źródła:

231

231

0

=

⋅

=

o

j

A

e

E

V,

)

200

5

,

115

(

231

120

j

e

E

j

B

−

−

=

⋅

=

−

o

V,

)

200

5

,

115

(

231

120

j

e

E

j

C

+

−

=

⋅

=

o

V.

Wartość symboliczna napięcia na impedancji w gałęzi powrotnej, obliczona wg wzoru (7.23a):

o

90

'

'

5

,

115

5

,

115

j

N

C

B

A

C

C

B

B

A

A

N

N

N

e

j

Y

Y

Y

Y

E

Y

E

Y

E

Y

V

U

⋅

=

=

+

+

+

⋅

+

⋅

+

⋅

=

=

V.

Wartości symboliczne napięć fazowych odbiornika, obliczone wg wzorów (7.23c):

o

6

,

26

'

3

,

258

5

,

115

231

j

N

N

A

A

e

j

U

E

U

−

⋅

≅

−

=

−

=

V,

o

1

,

110

'

0

,

336

5

,

315

5

,

115

j

N

N

B

B

e

j

U

E

U

−

⋅

≅

−

−

=

−

=

V,

o

8

,

143

'

1

,

143

5

,

84

5

,

115

j

N

N

C

C

e

j

U

E

U

⋅

≅

+

−

=

−

=

V.

Wartości symboliczne prądów, obliczone wg wzorów (7.23d, e):

o

4

,

18

826

,

1

j

A

A

A

e

U

Y

I

⋅

≅

⋅

=

A,

o

1

,

155

376

,

2

j

B

B

B

e

U

Y

I

−

⋅

≅

⋅

=

A,

o

8

,

98

012

,

1

j

C

C

C

e

U

Y

I

⋅

≅

⋅

=

A,

o

135

'

817

,

0

j

N

N

N

N

e

U

Y

I

⋅

≅

⋅

=

A.

Wykres wskazowy odpowiadający wartościom napięć i prądów – rys. b (obok schematu obwodu).

Bilans mocy:

- moc zespolona obwodu, wydawana przez źródło i pobierana przez odbiornik, wg wzoru (7.24)

(VA),

267

1067

012

,

1

231

376

,

2

231

826

,

1

231

2

,

21

1

,

35

4

,

18

*

*

*

j

e

e

e

I

E

I

E

I

E

S

j

j

j

C

C

B

B

A

A

gen

+

≅

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

+

⋅

+

⋅

=

−

o

o

o

(VA),

267

1067

817

,

0

5

,

115

012

,

1

1

,

143

376

,

2

0

,

336

826

,

1

3

,

258

45

45

45

45

'

*

'

*

*

*

j

e

e

e

e

e

I

U

e

I

U

e

I

U

e

I

U

I

U

I

U

I

U

I

U

S

j

j

j

j

j

N

N

N

j

C

C

j

B

B

j

A

A

N

N

N

C

C

B

B

A

A

odb

N

C

B

A

+

≅

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

+

⋅

+

⋅

+

⋅

=

−

−

o

o

o

o

ϕ

ϕ

ϕ

ϕ

- moc elementów rezystancyjnych

1067

817

,

0

100

012

,

1

100

376

,

2

100

826

,

1

100

2

2

2

2

2

≅

⋅

+

⋅

+

⋅

+

⋅

=

⋅

=

∑

k

k

k

I

R

P

W,

- moc elementów reaktancyjnych

267

817

,

0

100

012

,

1

100

376

,

2

100

826

,

1

100

2

2

2

2

2

≅

⋅

−

⋅

+

⋅

+

⋅

−

=

⋅

=

∑

k

k

k

I

X

Q

var.

Równanie

Q

j

P

S

S

odb

gen

+

=

=

jest spełnione, tzn. moce się bilansują.

Wykład XVII

148

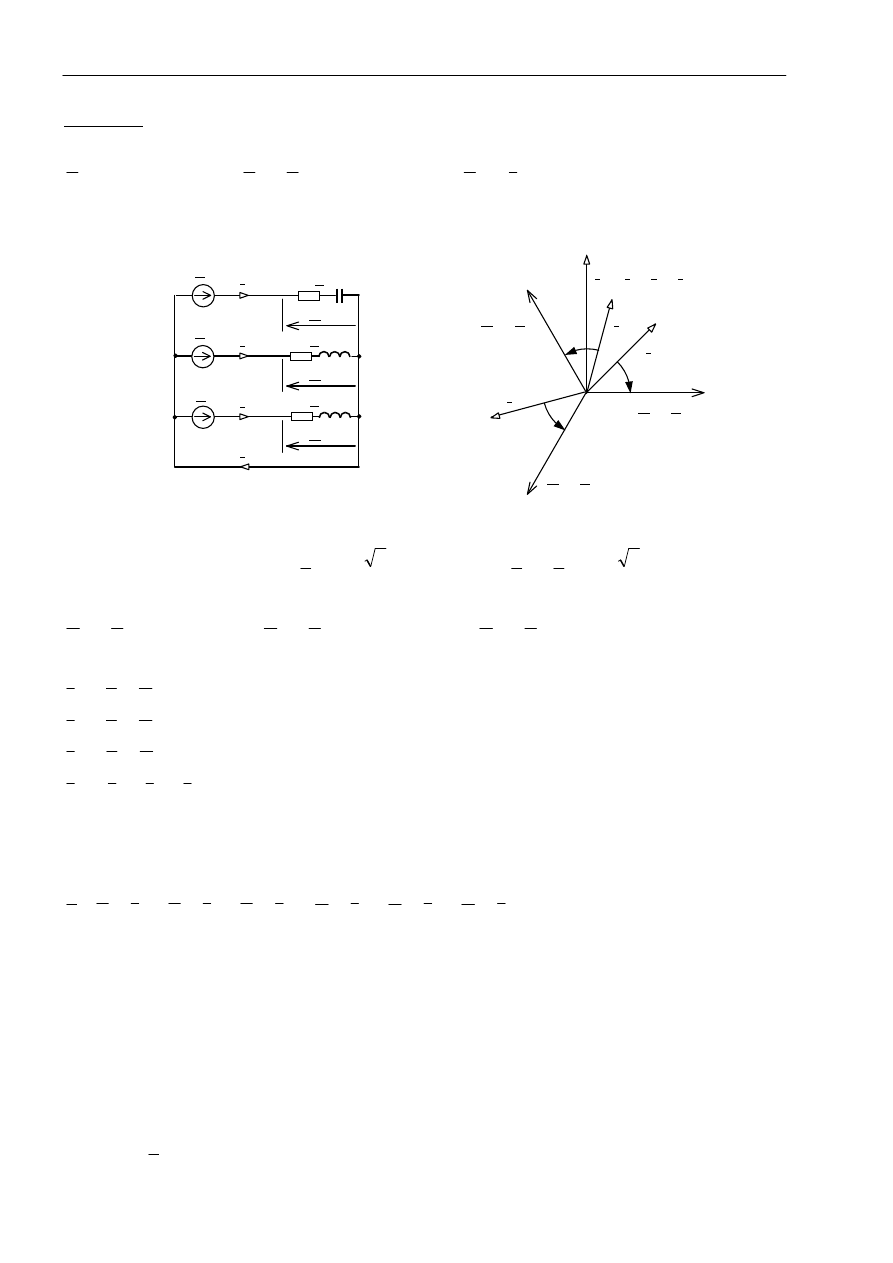
Przykład 2. Odbiornik gwiazdowy o wartościach impedancji faz – jak poprzednio, i bezimpedan-
cyjnej gałęzi powrotnej (bezpośrednio połączone punkty neutralne źródła i odbiornika):

)

100

100

(

j

Z

A

−

=

Ω

,

)

100

100

(

j

Z

Z

C

B

+

=

=

Ω

,

)

0

0

(

0

j

Z

N

+

=

=

Ω

, jest zasilany cztero-

przewodowo napięciem symetrycznym 3

×

230/400 V. Należy obliczyć wartości napięć i prądów

występujących w obwodzie, przedstawić wykres wskazowy odpowiadający tym wartościom oraz
sporządzić bilans mocy obwodu.

Schemat obwodu z zaznaczeniem charakteru gałęzi – rys. a.

Wartości admitancji fazowych:

o

45

2

10

2

5

,

0

j

A

e

Y

⋅

⋅

=

−

S,

o

45

2

10

2

5

,

0

j

C

B

e

Y

Y

−

−

⋅

⋅

=

=

S.

Napięcia fazowe – w zadanych warunkach i przy założonych jak poprzednio napięciach źródła:

o

0

231

j

A

A

e

E

U

⋅

=

=

V,

o

120

231

j

B

B

e

E

U

−

⋅

=

=

V,

o

120

231

j

C

C

e

E

U

⋅

=

=

V.

Wartości symboliczne prądów, obliczone wg wzorów (7.23d, e):

o

45

633

,

1

j

A

A

A

e

U

Y

I

⋅

≅

⋅

=

A,

o

165

633

,

1

j

B

B

B

e

U

Y

I

−

⋅

≅

⋅

=

A,

o

75

633

,

1

j

C

C

C

e

U

Y

I

⋅

≅

⋅

=

A,

o

90

309

,

2

j

C

B

A

N

e

I

I

I

I

⋅

≅

+

+

=

A.

Wykres wskazowy odpowiadający wartościom napięć i prądów – rys. b (obok schematu obwodu).

Bilans mocy:

- moc zespolona obwodu, wydawana przez źródło i pobierana przez odbiornik, wg wzoru (7.24)

(VA),

267

800

633

,

1

231

633

,

1

231

633

,

1

231

45

45

45

*

*

*

*

*

*

j

e

e

e

e

I

U

e

I

U

e

I

U

I

U

I

U

I

U

I

E

I

E

I

E

S

j

j

j

j

C

C

j

B

B

j

A

A

C

C

B

B

A

A

C

C

B

B

A

A

C

B

A

+

≅

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

+

⋅

+

⋅

=

⋅

+

⋅

+

⋅

=

−

o

o

o

ϕ

ϕ

ϕ

- moc elementów rezystancyjnych

800

633

,

1

100

633

,

1

100

633

,

1

100

2

2

2

2

≅

⋅

+

⋅

+

⋅

=

⋅

=

∑

k

k

k

I

R

P

W,

- moc elementów reaktancyjnych

267

633

,

1

100

633

,

1

100

633

,

1

100

2

2

2

2

≅

⋅

+

⋅

+

⋅

−

=

⋅

=

∑

k

k

k

I

X

Q

var.

Równanie

Q

j

P

S

+

=

jest spełnione, tzn. moce się bilansują.

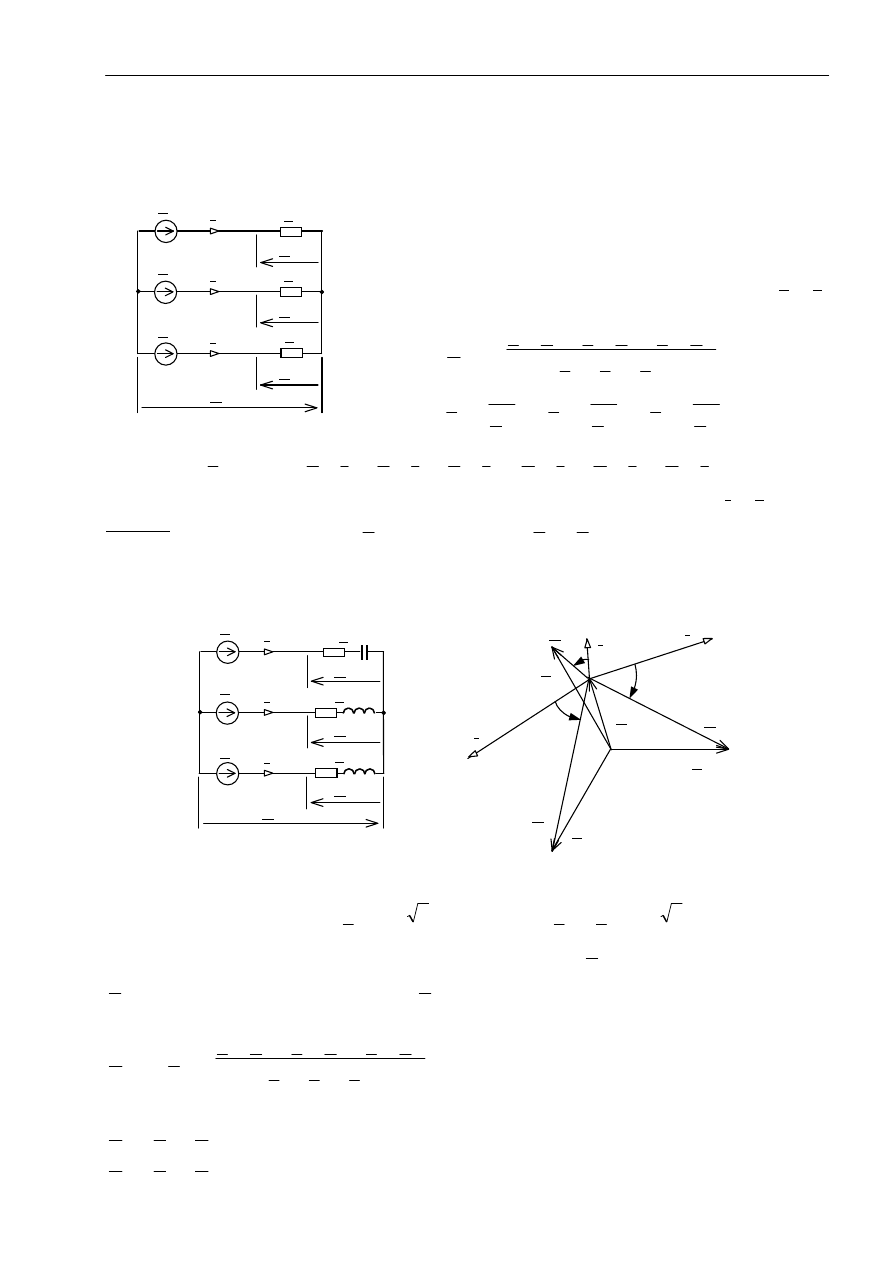
U

A

U

B

U

C

N’

Z

A

Z

B

Z

C

I

A

I

B

I

C

E

A

E

C

E

B

N

I

N

a) b)

U

A

=

E

A

I

N

=

I

A

+

I

B

+

I

C

I

C

I

A

I

B

ϕ

A

ϕ

B

ϕ

C

U

B

=

E

B

U

C

=

E

C

7. Rozwiązywanie obwodów prądu sinusoidalnego

149

Odbiornik o układzie gwiazdowym zasilany trójprzewodowo

Na rysunku pokazano obwód trójfazowy z odbiornikiem źródła o układzie gwiazdowym, zasilanym
trójprzewodowo ze źródła o układzie gwiazdowym.

Z punktu widzenia pracy odbiornika, sposób połączenia ele-
mentów źródła nie ma znaczenia. Gwiazdowy układ źródła,
istniejący rzeczywiście lub zastępczy, pozwala traktować za-
silanie trójprzewodowe jako przypadek zasilania czteroprze-
wodowego z gałęzią powrotną o zerowej admitancji Y

N

=

0

.

Wtedy to wzory (7.23a), (7.23b) i (7.24) przyjmują formy:

C

B

A

C

C

B

B

A

A

N

N

Y

Y

Y

E

Y

E

Y

E

Y

U

+

+

⋅

+

⋅

+

⋅

=

'

, (7.25a)

A

A

Z

Y

1

=

,

B

B

Z

Y

1

=

,

C

C

Z

Y

1

=

, (7.25b)

*

*

*

*

*

*

C

C

B

B

A

A

C

C

B

B

A

A

I

U

I

U

I

U

I

E

I

E

I

E

jQ

P

S

⋅

+

⋅

+

⋅

=

⋅

+

⋅

+

⋅

=

+

=

. (7.26)

Zależności (7.23c, d) stosuje się w niezmienionej postaci, a miejsce (7.23e) zajmuje: I

N

=

0

.

Przykład. Odbiornik gwiazdowy:

)

100

100

(

j

Z

A

−

=

Ω

,

)

100

100

(

j

Z

Z

C

B

+

=

=

Ω

, jest zasilany

trójprzewodowo napięciem symetrycznym 3

×

400 V. Należy obliczyć wartości napięć i prądów

występujących w obwodzie, przedstawić wykres wskazowy odpowiadający tym wartościom oraz
sporządzić bilans mocy obwodu.

Schemat obwodu z zaznaczeniem charakteru gałęzi – rys. a.

Wartości admitancji fazowych:

o

45

2

10

2

5

,

0

j

A

e

Y

⋅

⋅

=

−

S,

o

45

2

10

2

5

,

0

j

C

B

e

Y

Y

−

−

⋅

⋅

=

=

S.

Wartości symboliczne napięć źródła (umownie – gwiazdowego):

231

231

0

=

⋅

=

o

j

A

e

E

V,

)

200

5

,

115

(

231

120

j

e

E

j

B

−

−

=

⋅

=

−

o

V,

)

200

5

,

115

(

231

120

j

e

E

j

C

+

−

=

⋅

=

o

V.

Wartość symboliczna napięcia między punktami N’ i N, obliczona wg wzoru (7.25a):

o

4

,

108

'

'

1

,

146

6

,

138

2

,

46

j

C

B

A

C

C

B

B

A

A

N

N

N

e

j

Y

Y

Y

E

Y

E

Y

E

Y

V

U

⋅

=

+

−

=

+

+

⋅

+

⋅

+

⋅

=

=

V.

Wartości symboliczne napięć fazowych odbiornika, obliczone wg wzorów (7.23c):

o

6

,

26

'

9

,

309

6

,

138

2

,

277

j

N

N

A

A

e

j

U

E

U

−

⋅

≅

−

=

−

=

V,

o

6

,

101

'

6

,

345

6

,

338

3

,

69

j

N

N

B

B

e

j

U

E

U

−

⋅

≅

−

−

=

−

=

V,

Z

C

U

A

U

B

U

C

N’

Z

A

Z

B

I

A

I

B

I

C

E

A

E

C

E

B

N

U

N

’N

U

A

U

B

U

C

N’

Z

A

Z

B

Z

C

I

A

I

B

I

C

E

A

E

C

E

B

N

U

N

’N

a) b)

E

A

E

C

E

B

U

A

U

C

U

B

I

C

I

A

I

B

ϕ

A

ϕ

B

ϕ

C

U

N

‘N

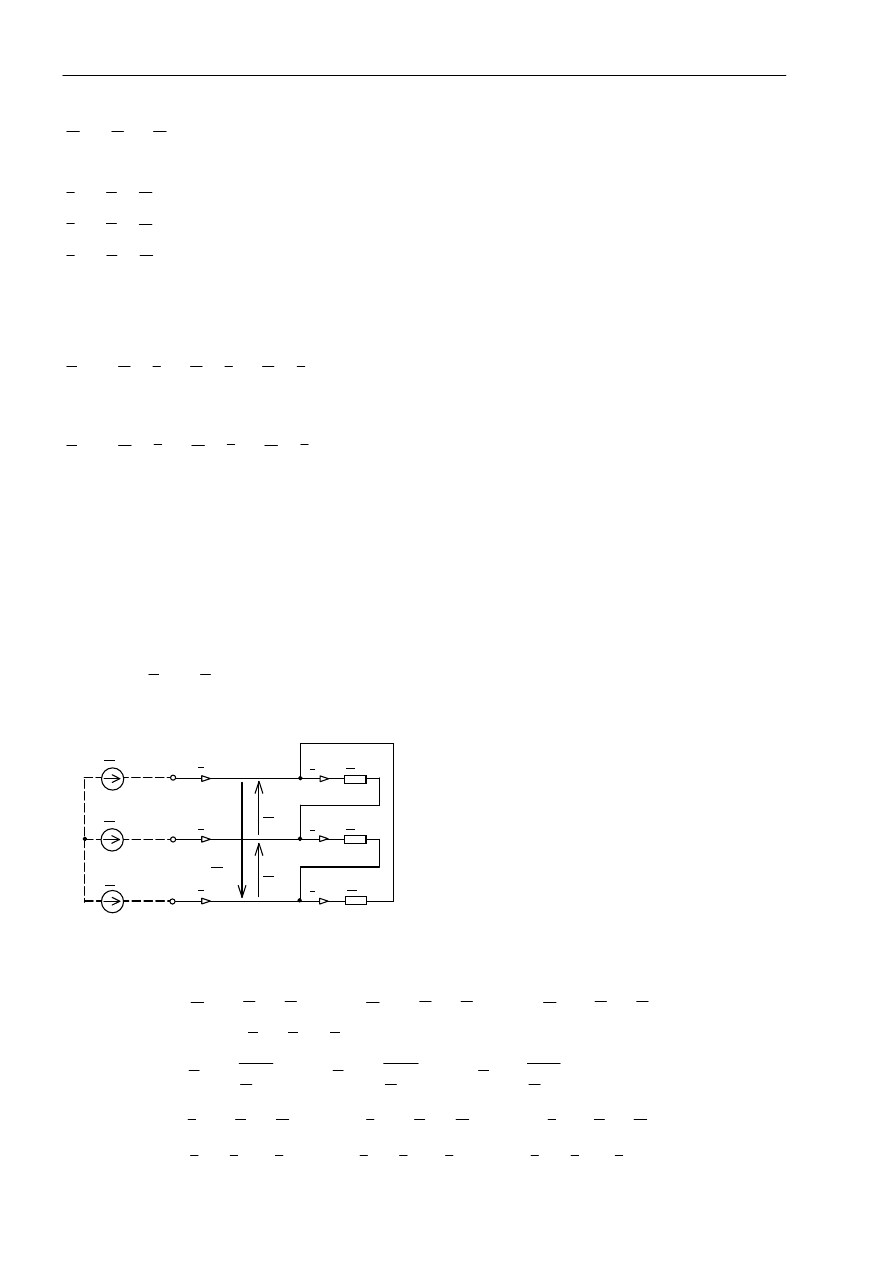
Wykład XVII

150

o

5

,

138

'

6

,

92

1,4

6

3

,

69

j

N

N

C

C

e

j

U

E

U

⋅

≅

+

−

=

−

=

V.

Wartości symboliczne prądów, obliczone wg wzorów (7.23d):

o

4

,

18

191

,

2

j

A

A

A

e

U

Y

I

⋅

≅

⋅

=

A,

o

6

,

146

444

,

2

j

B

B

B

e

U

Y

I

−

⋅

≅

⋅

=

A,

o

5

,

93

655

,

0

j

C

C

C

e

U

Y

I

⋅

≅

⋅

=

A.

Wykres wskazowy odpowiadający wartościom napięć i prądów – rys. b (obok schematu obwodu).

Bilans mocy:

- moc zespolona obwodu, wydawana przez źródło i pobierana przez odbiornik, wg wzoru (7.26)

(VA),

60

1

1120

655

,

0

231

444

,

2

231

191

,

2

231

5

,

26

6

,

26

4

,

18

*

*

*

j

e

e

e

I

E

I

E

I

E

S

j

j

j

C

C

B

B

A

A

gen

+

≅

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

+

⋅

+

⋅

=

−

o

o

o

(VA),

60

1

1120

655

,

0

6

,

92

444

,

2

6

,

345

191

,

2

9

,

309

45

45

45

*

*

*

j

e

e

e

e

I

U

e

I

U

e

I

U

I

U

I

U

I

U

S

j

j

j

j

C

C

j

B

B

j

A

A

C

C

B

B

A

A

odb

C

B

A

+

≅

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

⋅

+

⋅

+

⋅

=

−

o

o

o

ϕ

ϕ

ϕ

- moc elementów rezystancyjnych

1120

655

,

0

100

444

,

2

100

191

,

2

100

2

2

2

2

≅

⋅

+

⋅

+

⋅

=

⋅

=

∑

k

k

k

I

R

P

W,

- moc elementów reaktancyjnych

160

655

,

0

100

444

,

2

100

191

,

2

100

2

2

2

2

≅

⋅

+

⋅

+

⋅

−

=

⋅

=

∑

k

k

k

I

X

Q

var.

Równanie

Q

j

P

S

S

odb

gen

+

=

=

jest spełnione, tzn. moce się bilansują.

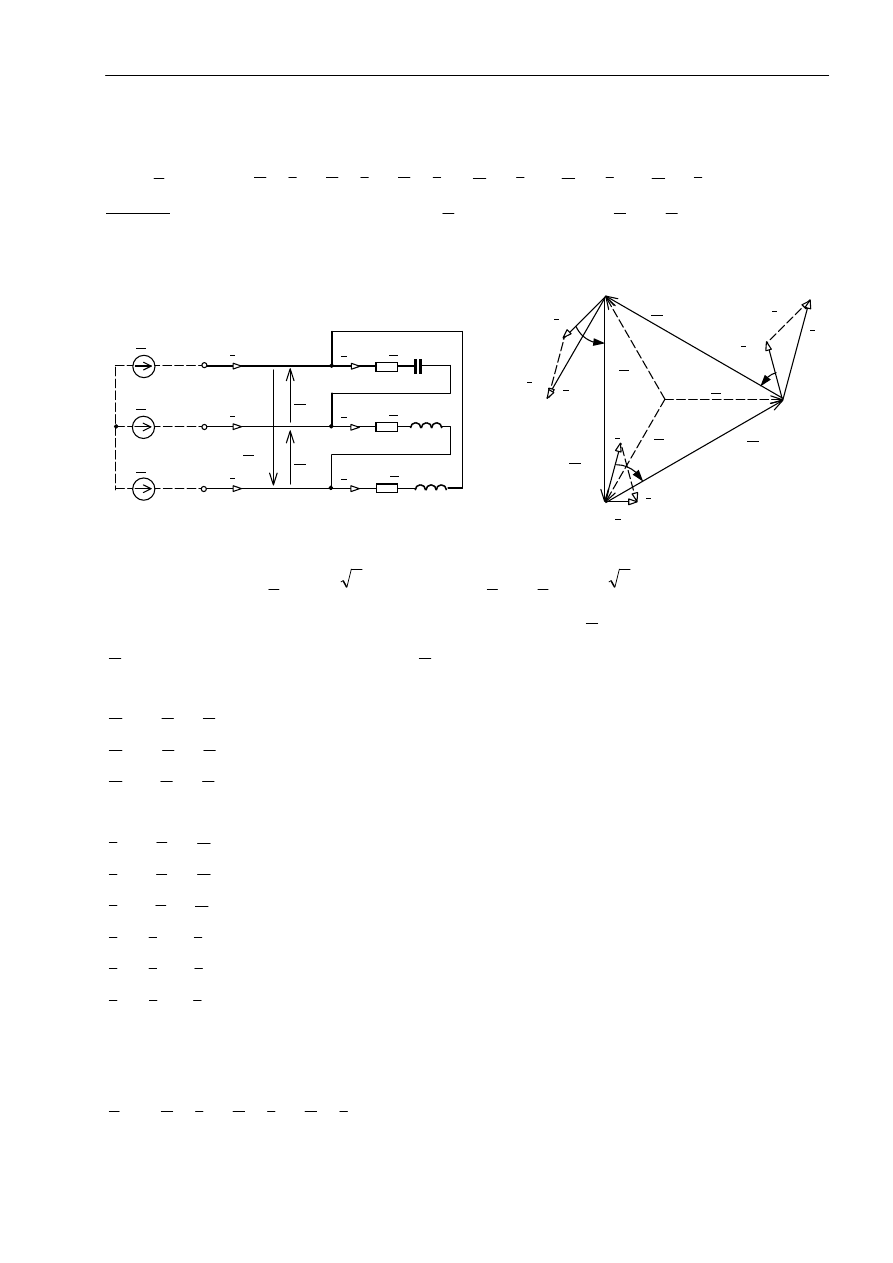
Odbiornik o układzie trójkątowym

Na rys. obok pokazano obwód trójfazowy z
odbiornikiem o układzie trójkątowym, zasila-
nym trójprzewodowo ze źródła o układzie
gwiazdowym.
Z punktu widzenia pracy odbiornika, sposób
połączenia elementów źródła nie ma znacze-
nia, dlatego zaznaczono je liniami przerywa-
nymi. Fazy linii zasilającej opatrzono symbo-
lami L1, L2, L3 – alternatywnymi do A, B, C.

Napięcia fazowe odbiornika są jednocześnie jego napięciami międzyfazowymi. Między nimi a fa-
zowymi napięciami źródła o układzie gwiazdowym zachodzą następujące związki:

B

A

AB

E

E

U

−

=

,

C

B

BC

E

E

U

−

=

,

A

C

CA

E

E

U

−

=

. (7.27)

W ogólnym przypadku (

Z

AB

≠

Z

BC

≠

Z

CA

) korzysta się z zależności:

AB

AB

Z

Y

1

=

,

BC

BC

Z

Y

1

=

,

CA

CA

Z

Y

1

=

, (7.28a)

AB

AB

AB

U

Y

I

⋅

=

,

BC

BC

BC

U

Y

I

⋅

=

,

CA

CA

CA

U

Y

I

⋅

=

, (7.28b)

CA

AB

A

I

I

I

−

=

,

AB

BC

B

I

I

I

−

=

,

BC

CA

C

I

I

I

−

=

. (7.28c)

Z

CA

I

AB

I

BC

I

CA

Z

AB

Z

BC

I

A

I

B

I

C

E

A

E

C

E

B

A (L1)


B (L2)


C (L3)

U

CA

U

AB

U

BC

7. Rozwiązywanie obwodów prądu sinusoidalnego

151

Moc wydawana przez źródło idealne o układzie gwiazdowym, a pobierana przez odbiornik o ukła-
dzie trójkątowym, wynosi:

*

*

*

*

*

*

CA

CA

BC

BC

AB

AB

C

C

B

B

A

A

I

U

I

U

I

U

I

E

I

E

I

E

jQ

P

S

⋅

+

⋅

+

⋅

=

⋅

+

⋅

+

⋅

=

+

=

. (7.29)

Przykład. Odbiornik o układzie trójkątowym:

)

100

100

(

j

Z

AB

−

=

Ω

,

)

100

100

(

j

Z

Z

CA

BC

+

=

=

Ω

,

jest zasilany napięciem symetrycznym 3

×

400 V. Należy obliczyć wartości napięć i prądów wystę-

pujących w obwodzie, przedstawić wykres wskazowy odpowiadający tym wartościom oraz sporzą-
dzić bilans mocy obwodu.

Schemat obwodu z zaznaczeniem charakteru gałęzi – rys. a.

Wartości admitancji:

o

45

2

10

2

5

,

0

j

AB

e

Y

⋅

⋅

=

−

S,

o

45

2

10

2

5

,

0

j

CA

BC

e

Y

Y

−

−

⋅

⋅

=

=

S.

Wartości symboliczne napięć źródła (umownie – gwiazdowego):

231

231

0

=

⋅

=

o

j

A

e

E

V,

)

200

5

,

115

(

231

120

j

e

E

j

B

−

−

=

⋅

=

−

o

V,

)

200

5

,

115

(

231

120

j

e

E

j

C

+

−

=

⋅

=

o

V.

Wartości symboliczne napięć fazowych (międzyfazowych) odbiornika, wg wzorów (7.27):

o

30

400

00

2

5

,

346

j

B

A

AB

e

j

E

E

U

⋅

≅

+

=

−

=

V,

o

90

400

00

4

j

C

B

BC

e

j

E

E

U

−

⋅

≅

−

=

−

=

V,

o

150

400

00

2

5

,

346

j

A

C

CA

e

j

E

E

U

⋅

≅

+

−

=

−

=

V.

Wartości symboliczne prądów, obliczone wg wzorów (7.28b, c):

≅

⋅

≅

⋅

=

o

75

828

,

2

j

AB

AB

AB

e

U

Y

I

(0,732

+

j

2,732) A,

≅

⋅

≅

⋅

=

−

o

135

828

,

2

j

BC

BC

BC

e

U

Y

I

(

–

2

–

j

2) A,

≅

⋅

≅

⋅

=

o

105

828

,

2

j

CA

CA

CA

e

U

Y

I

(

–

0,732

+

j

2,732) A.

o

0

464

,

1

0

464

,

1

j

CA

AB

A

e

j

I

I

I

⋅

≅

+

=

−

=

A,

o

120

464

,

5

732

,

4

732

,

2

j

AB

BC

B

e

j

I

I

I

−

⋅

≅

−

−

=

−

=

A,

o

75

899

,

4

732

,

4

268

,

1

j

BC

CA

C

e

j

I

I

I

⋅

≅

+

=

−

=

A.

Wykres wskazowy odpowiadający wartościom napięć i prądów – rys. b (obok schematu obwodu).

Bilans mocy:

- moc zespolona obwodu, wydawana przez źródło i pobierana przez odbiornik, wg wzoru (7.29)

(VA),

800

2400

899

,

4

231

464

,

5

231

464

,

1

231

45

0

0

*

*

*

j

e

e

e

I

E

I

E

I

E

S

j

j

j

C

C

B

B

A

A

gen

+

≅

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

+

⋅

+

⋅

=

−

o

o

o

I

AB

I

BC

I

CA

Z

AB

Z

BC

Z

CA

I

A

I

B

I

C

E

A

E

C

E

B

A (L1)


B (L2)


C (L3)

U

CA

U

AB

U

BC

a) b)

-I

CA

I

A

I

C

I

B

ϕ

AB

ϕ

BC

E

B

U

AB

U

BC

U

CA

E

A

E

C

I

AB

-I

AB

I

BC

-I

BC

I

CA

ϕ

CA

Wykład XVII

152

(VA),

00

8

2400

828

,

2

400

828

,

2

400

828

,

2

400

45

45

45

*

*

*

j

e

e

e

e

I

U

e

I

U

e

I

U

I

U

I

U

I

U

S

j

j

j

j

CA

CA

j

BC

BC

j

AB

AB

CA

CA

BC

BC

AB

AB

odb

CA

BC

AB

+

≅

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

=

⋅

+

⋅

+

⋅

=

−

o

o

o

ϕ

ϕ

ϕ

- moc elementów rezystancyjnych

2400

828

,

2

100

828

,

2

100

828

,

2

100

2

2

2

2

≅

⋅

+

⋅

+

⋅

=

⋅

=

∑

k

k

k

I

R

P

W,

- moc elementów reaktancyjnych

800

828

,

2

100

828

,

2

100

828

,

2

100

2

2

2

2

≅

⋅

+

⋅

+

⋅

−

=

⋅

=

∑

k

k

k

I

X

Q

var.

Równanie

Q

j

P

S

S

odb

gen

+

=

=

jest spełnione, tzn. moce się bilansują.

Uwaga. Zadanie powyższe można rozwiązać z powodzeniem na podstawie starannie narysowane-
go wykresu wskazowego. Procedura postępowania jest następująca:

1. Oblicza się wartości kątów fazowych impedancji gałęzi, wartości impedancji gałęzi i wartości

skuteczne prądów w gałęziach:

o

45

−

=

AB

ϕ

,

o

45

=

=

CA

BC

ϕ

ϕ

;

4

,

141

2

100

≅

=

=

=

=

CA

BC

AB

Z

Z

Z

Z

Ω

,

828

,

2

2

2

2

100

400

≅

=

=

=

=

=

Z

U

I

I

I

CA

BC

AB

A .

2. Przyjmuje się skale napięcia i prądu.

3. Rysuje się trójkąt napięć: U

AB

, U

BC

, U

CA

.

4. Przy właściwych napięciach i pod odpowiednimi kątami nanosi się wskazy prądów: I

AB

o 45

°

przed U

AB

, I

BC

o 45

°

za U

BC

, I

CA

o 45

°

za U

CA

. Następnie dodaje się graficznie wskazy: -I

CA

do

I

AB

, -I

AB

do I

BC

, -I

BC

do I

CA

, otrzymując prądy w linii (przewodach zasilających): I

A

, I

B

, I

C

.

5. Z zależności geometrycznych na wykresie wskazowym, określa się początkowe kąty fazowe i

wartości skuteczne prądów (wartościom skutecznym odpowiadają długości wskazów). Można

tak wyznaczyć np. :

o

o

o

120

15

135

.

−

=

+

−

=

B

i

ψ

,

46

,

5

15

cos

2

828

,

2

≅

⋅

⋅

=

o

B

I

A.

6. Moce wydawane lub pobierane w poszczególnych fazach oblicza się jako iloczyny długości

wskazów napięcia i prądu oraz cosinusa (dla mocy czynnej) lub sinusa (dla mocy biernej) kąta
między tymi wskazami. Trzeba przy tym określić znak tego kąta (jest on dodatni, gdy prąd
„opóźnia się” względem napięcia).

Wniosek. Szkic wykresu wskazowego jest zawsze potrzebny do kontroli wyników obliczeń. Jeśli
związki geometryczne między wskazami są w miarę proste, to można uzyskać rozwiązanie obwodu
bez stosowania rachunku symbolicznego. Widać to dobrze np. dla innego obwodu (rys. poniżej), w

którym szuka się wartości I

2

i I

3

, przy danych: wartości I

1

=

3 A i związku liczbowym

3

R

X

C

=

.

Oblicza się (z danych):

o

60

31

23

−

=

=

ϕ

ϕ

;

R

Z

Z

2

31

23

=

=

,

stąd

12

31

23

5

,

0

I

I

I

⋅

=

=

.

Wyznacza się (z wykresu):

2

12

=

I

A,

1

31

=

I

A,

73

,

1

3

2

≅

=

I

A,

73

,

1

3

3

≅

=

I

A.

I

1

-I

23

U

12

ϕ

U

23

U

31

I

31

-I

31

I

12

ϕ

-I

12

ϕ

I

23

ϕ

I

2

I

3

I

12

R
R
I

23

C
R
C I

31

I

1

I

2

I

3

U

31

U

12

U

23

L1



L2




L3