
POLITECHNIKA GDA ´
NSKA
WYDZIAÃL FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ
S.B. Leble
D.W. Rohraff
ELEKTRODYNAMIKA
22 maja 2005
Gda´nsk 2005


Spis tre´sci
1 UkÃlady inercjalne
5
1.1 UkÃlady inercjalne . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
1.2 Referencje do rozdziaÃlu: 1.UkÃlady inercjalne . . . . . . . . . . . . . .
7
2 Podstawowe poje
ι
cia elektrodynamiki
9
2.1 Elektrodynamika w pr´o˙zni . . . . . . . . . . . . . . . . . . . . . . . .
9
2.2 PotencjaÃly wektorowe i skalarne . . . . . . . . . . . . . . . . . . . . .
15
2.3 Zasady zachowania. Twierdzenie Poyntinga. . . . . . . . . . . . . . .
18
2.4 Fale elektromagnetyczne. Fala pÃlaska . . . . . . . . . . . . . . . . . .
20
2.5 Niejednorodne r´ownanie falowe. Generacja fal E-M. . . . . . . . . . .
25
2.6 Promieniowanie fal elektromagnetycznych. Przybli˙zenie dipolowe. . .
27
3


RozdziaÃl 1
UkÃlady inercjalne
1.1
UkÃlady inercjalne
Fizyka opiera sie
ι
na pewnych zaÃlo˙zeniach, kt´orych cecha
ι
jest to, ˙ze sa
ι
zdefiniowane
bezwzgle
ι
dnie. Oznacza to, ˙ze podstawa
ι
ich wprowadzenia jest nie do´swiadczenie,
lecz zaÃlo˙zenie (umowa). PrzykÃladem mo˙ze by´c jednostka dÃlugo´sci - 1 metr [m]. In-
nymi jednostkami podstawowymi sa
ι
: kilogram [kg] - okre´slenie masy, sekunda [s] -
czasu, amper [A] - nate
ι
˙zenia pra
ι
du elektrycznego, Kelvin [K] - jednostka temperatury,
mol [mol] - okre´slenie ilo´sci materii. ´SwiatÃlo´s´c ´zr´odÃla emituja
ι
cego promieniowanie
okre´slamy w kandelach [cd].
Nie mo˙zemy m´owi´c o bezwzgle
ι
dnym ruchu lub te˙z bezwzgle
ι
dnym spoczynku. Ruch
ciaÃl opisujemy wzgle
ι
dem jakiego´s ukladu, czyli ruch ten jest wzgle
ι
dny. ZaÃlo˙zenie to
jest opisywane przez zasade
ι
wzgle
ι
dno´sci Galileusza.
Poje
ι
cie ukÃladu inercjalnego jest r´ownie˙z poje
ι
ciem bezwzgle
ι
dnym.
Co to jest ukÃlad inercjalny? Zgodnie z defincja
ι
: jest to taki ukÃlad odniesienia, w
kt´
orym ciaÃlo punktowe, w przypadku braku siÃl zewne
ι
trznych lub gdy siÃly
dziaÃlaja
ι
ce na to ciaÃlo sie
ι
r´
ownowa˙za
ι
, to porusza sie
ι
ono ze staÃla
ι
pre
ι
dko´scia
ι
.
Wektor pre
ι
dko´sci ~v tego ciaÃla jest w takim przypadku staÃly.
~v(t) =
d~v
dt
= const
(1.1.1)
Obecno´s´c powy˙zszych ukÃlad´ow opisuje I zasada dynamiki Newtona, kt´ora wprowadza
poje
ι
cie bezwÃladno´sci. M´owia
ι
, ˙ze ruch ciaÃla jest bezwÃladny, gdy nie dziaÃla na niego
˙zadna siÃla zewne
ι
trzna lub gdy siÃly dziaÃlaja
ι
ce sie
ι
r´ownowa˙za
ι
.
Pierwsza zasada dynamiki zostaÃla sprawdzona do´swiadczalnie, potwierdzaja
ι
c teo-
retyczne zaÃlo˙zenia. Okazuje sie
ι
, zgodnie z okre´sleniem, ˙ze Ziemia nie jest ukÃladem
inercjalnym. Empirycznie mo˙zna to wykaza´c analizuja
ι
c ruch wahadÃla Foucault.
Skoro najbli˙zsza nam planeta nie speÃlnia powy˙zszych zaÃlo˙ze´n, powstaje pytanie: gdzie
mo˙zna spotka´c ukÃlady inercjalne? By je znale˙z´c musimy nasze poszukiwania posze-
rzy´c o Wszech´swiat. UkÃlady takie (z do´s´c dobrym przybli˙zeniem) tworza
ι
gwiazdy, z
5

6
RozdziaÃl 1. UkÃlady inercjalne
kt´orymi zwia
ι
zany jest np. heliocentryczny ukÃlad odniesienia - to jest taki, w kt´orym
masywna gwiazda znajduje sie
ι
w ´srodku ukÃladu pokrywaja
ι
cego sie
ι
ze ´srodkiem masy.
Przeprowadzaja
ι
c eksperymenty, dosy´c cze
ι
sto mo˙zemy uwa˙za´c Ziemie
ι
jako inerc-
jalny ukÃlad odniesienia (zaniedbuja
ι
c przy tym ,,siÃle
ι
Coriolisa”). Czasami ruch Ziemi
nie ma znacza
ι
cego wpÃlywu na zjawiska znane z ˙zycia codziennego jak praca wykony-
wana z udziaÃlem maszyn, przemiany energii dokonywane w domu i w laboratorium,
procesy zwia
ι
zane z przesyÃlaniem faÃl elektromagnetycznych (m.in. wsp´oÃlczesna ko-
munikacja). Poprawiaja
ι
c nasze zaÃlo˙zenia w celu idealizacji zmierzaja
ι
cej do idealnego
ukÃladu inercjalnego, jest ukÃlad zwia
ι
zany ze ´srodkiem Ziemi. Taki ukÃlad nazywamy
ukÃladem geocentrycznym. Kolejnym przybli˙zeniem mo˙ze by´c ukÃlad heliocentryczny,
gdzie w centrum ukÃladu znajduje sie
ι
SÃlo´nce. (Nale˙zy pamie
ι
ta´c, ˙ze Ziemia porusza sie
ι
dookoÃla SÃlo´nca ruchem przyspieszonym). Nasza
ι
idealizacje
ι
mo˙zemy stosowa´c dalej,
w zale˙zno´sci od dokÃladno´sci, kt´ora
ι
chcemy uzyska´c.
Eksperyment, tak bardzo przydatny w wielu dziedzinach fizyki, w przypadku
bada´n nad ukÃladami inercjalnymi zawodzi, gdy˙z nie jest w stanie wyr´o˙zni´c ukÃladu
,,czysto” inercjalnego - tego szczeg´olnego przypadku, kt´ory posÃlu˙zyÃlby za wz´or -
etalon.
UkÃlady inercjalne sa
ι
do siebie r´
ownowa˙zne
Zasada wzgle
ι
dno´sci we wsp´oÃlczesnym sformuÃlowaniu rozszerza poje
ι
cie ukÃladu in-
ercjalnego:
W ka˙zdym ukÃladzie inercjalnym wszystkie zjawiska fizyczne przebiegaja
ι
tak samo
Podsumowuja
ι
c:
- w ka˙zdym ukÃladzie inercjalnym obowia
ι
zuja
ι
te same prawa przyrody.
- zachowanie formy r´owna´n fizyki (matematycznej) podczas transformacji z ukÃladu
S
1
do S
2
, mianowicie, r´ownania fizyki matematycznej powinny by´c r´ownaniami ten-
sorowymi wzgle
ι
dem pewnej grupy transformacji (tj. forma ka˙zdego r´ownania po-
zostaje taka sama - patrz [Ref 2]).
- istnienie jednego ukÃladu inercjalnego S, stwarza mo˙zliwo´s´c wyznaczenia kolejnych
ukÃlad´ow inercjalnych, gdy˙z ka˙zdy ukÃlad poruszaja
ι
cy sie
ι
ruchem jednostajnym ze staÃla
pre
ι
dko´scia
ι
wzgle
ι
dem ukÃladu S, te˙z jest ukÃladem inercjalnym.

1.2. Referencje do rozdziaÃlu: 1.UkÃlady inercjalne
7
1.2
Referencje do rozdziaÃlu: 1.UkÃlady inercjalne
[Ref 1] J.D. Jackson, Elektrodynamika klasyczna, wyd 2, PWN, Warszawa 1987.
[Ref 2] V.A. Fok, Teori prostranstva, vremeni i t gomeri , Moskva 1955.
[Ref 3] L.B. Okun, Fundamental units: physics and metrology, (2003), arXiv, physics
0310069.
[Ref 4] A. Einstein, The meaning of relativity, 4th edn, Princeton 1953.
[Ref 5] D.J. Griffiths, Podstawy elektrodynamiki, PWN, Warszawa 2001.
[Ref 6] D. Stauffer, H. Eugene Stanley, Od Newtona do Mandelbrota. Wste
ι
p do fizyki
teoretycznej, WNT, Warszawa 1996.
[Ref 7] A. Puankare, O nauke, Izdatel~stvo «Nauka» 1983. X


RozdziaÃl 2
Podstawowe poje
ι
cia
elektrodynamiki
2.1
Elektrodynamika w pr´
o˙zni
Fundamentem elektrodynamiki jest obecno´s´c p´ol: elektrycznego i magnetycznego,
wytworzonych przez poruszaja
ι
ce sie
ι
Ãladunki elektryczne. Pola te wyste
ι
puja
ι
ze soba
ι
w ´scisÃlym zwia
ι
zku, dlatego te˙z okre´slamy je wsp´olnym mianem pola elektromagnety-
cznego (E-M). Zasada interakcji pomie
ι
dzy Ãladunkami a polem E-M dziaÃla r´ownie˙z na
odwr´ot: pole elektromagnetyczne wpÃlywa na ruch Ãladunk´ow elektrycznych. Po´sre-
dniczy ono w oddziaÃlywaniu pomie
ι
dzy nimi, co przejawia sie
ι
tym, i˙z cza
ι
stka pr´obna
zachowa sie
ι
identycznie w dw´och r´o˙znych ukÃladach odniesienia, je´sli podziaÃlaja
ι
na
nia
ι
takie same E i B.
Analize
ι
pola elektromagnetycznego rozpocznijmy od okre´slenia nate
ι
˙zenia pola
elektrycznego w danym punkcie:
~
E =
~
F
q
(2.1.1)
co oznacza, i˙z badaja
ι
c nate
ι
˙zenie pola E mierzymy siÃle
ι
wywierana
ι
na Ãladunek pun-
ktowy. ÃLadunek pr´obny powinien by´c maÃly, aby jego obecno´s´c nie zaburzaÃla istnieja
ι
-
cego pola elektrycznego (przez wpÃlyw na Ãladunki tworza
ι
ce to pole).
Aby dokona´c peÃlnego opisu pola elektromagnetycznego, opr´ocz zdefiniowania pola
elektryczego, nale˙zy poda´c r´ownie˙z okre´slenie pola magnetycznego. W tym celu
przeprowad´zmy naste
ι
puja
ι
ce rozwa˙zania. Wybierzmy dowolna
ι
poruszaja
ι
ca
ι
sie
ι
cza
ι
stke
ι
punktowa
ι
i umie´s´cmy ja
ι
w polu B. Na te
ι
cza
ι
stke
ι
dziaÃla´c be
ι
dzie siÃla magnetyczna F
B
,
kt´ora zale˙zy od kierunku ~v, przez co jej warto´s´c mo˙ze zmienia´c sie
ι
od 0 do pewnej
warto´sci granicznej F
max
. Podczas obserwacji zauwa˙zymy, ˙ze wektor siÃly magnety-
cznej jest zawsze prostopadÃly do wektora pre
ι
dko´sci cza
ι
stki: ~
F
B
⊥~v. Oznacza to, ˙ze
siÃla magnetyczna nie wpÃlywa na warto´s´c ruchu cza
ι
stki (czyli brak przyspieszenia lub
op´o´znienia co jest zwia
ι
zane ze zmiana
ι
energii kinetycznej cza
ι
stki) a jedynie mo˙ze
zmienia´c tor ruchu, a to oznacza ˙ze praca wykonana przez F
B
jest zawsze r´owna 0
9
10
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
(zero). Zatem siÃle
ι
magnetyczna
ι
zdefiniujemy jako:
~
F
B
= q
·
~v × ~
B
¸
= qvBsin(~v ~
B)
(2.1.2)
Przyjmujemy, i˙z kierunek wektora indukcji magnetycznej B, jest zgodny z kierunkiem
pre
ι
dko´sci w przypadku gdy F
B
= 0.
Kontynuuja
ι
c, zawsze mo˙zemy tak dostroi´c ukÃlad pomiarowy przez odpowiednie
ustawienie zwrotu B, aby cza
ι
stka poruszaÃla sie
ι
pod ka
ι
tem prostym do B, a to oz-
nacza, ˙ze siÃla dziaÃlaja
ι
ca na nia
ι
be
ι
dzie maksymalna, gdy˙z sin(~v ~
B) = sin(90
◦
) = 1.
Otrzymamy zatem r´ownanie:
F
B
= qvB
(2.1.3)
kt´ore posÃlu˙zy nam do okre´slenia pola B:
B =
F
B
qv
(2.1.4)
WÃlasno´sci pola magnetycznego sa
ι
wykorzystywane bardzo cze
ι
sto w fizyce i tech-
nice. Dzie
ι
ki wiedzy o tym, jak zachowa sie
ι
naÃladowana cza
ι
stka elektryczna w B,
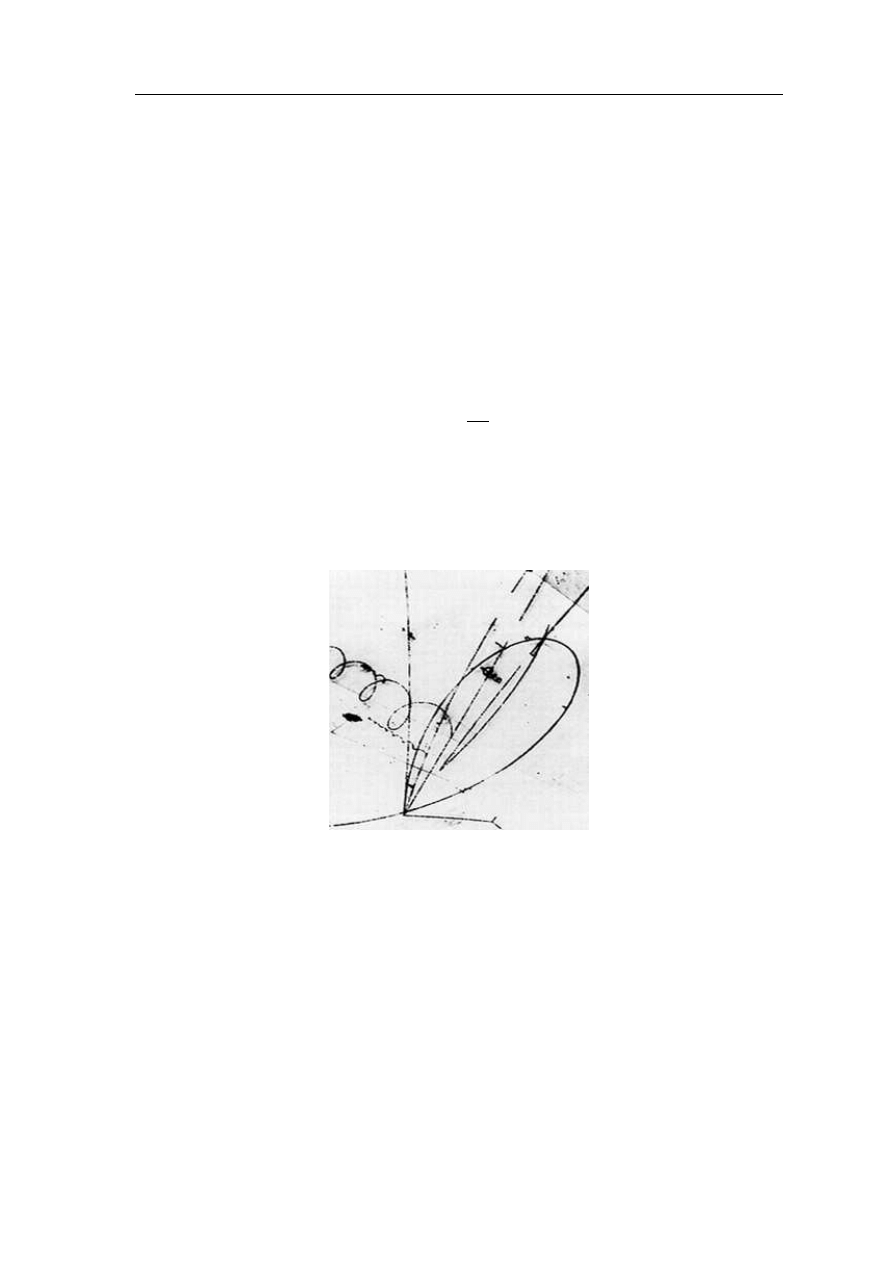
mo˙zliwe byÃlo zbudowanie takich urza
ι
dze´n jak cyklotron (1932) lub komora Wilsona
(1912). Cyklotrony stosowane sa
ι
do przyspieszania cza
ι
stek, natomiast komora Wilsona
sÃlu˙zy do detekcji cza
ι
stek lub promieniowania [Ref 5].
Rys 2.1. ´
Slady po przej´sciach naÃladowanych cza
ι
stek w komorze Wilsona. Widoczne sa
ι
zakrzywienia
tor´ow cza
ι
stek pod wpÃlywem pola magnetycznego. Ilustracja pochodzi ze zbior´ow Brookhaven Na-
tional Laboratory http://www.bnl.gov/bnlweb/history/charmed.asp
PeÃlny opis oddziaÃlywania pola EM z naÃladowana
ι
cza
ι
stka
ι
mo˙zna zatem przedstawi´c
naste
ι
puja
ι
co:
~
F
L
= q
µ
~
E + ~v × ~
B
¶
(2.1.5)
2.1. Elektrodynamika w pr´
o˙zni
11
SiÃle
ι
~
F
L
nazywamy siÃla
ι
Lorentza. R´ownanie (2.1.3) zostaÃlo wprowadzone w opar-
ciu o eksperyment (np. przez analize
ι
zachowania sie
ι
dw´och przewodnik´ow podczas
przepÃlywu przez nie pra
ι
d´ow elektrycznych).
Po wprowadzeniu okre´slenia pola elektromagnetycznego, mo˙zemy przej´s´c do r´owna´n
dla tego pola. Do opisu pola E-M u˙zywamy r´owna´n Maxwella [Ref 1, Ref 2], kt´ore
wyra˙zaja
ι
cztery podstawowe prawa elektryczno´sci i magnetyzmu:
- prawo Coulomba (1785 r.)
- brak Ãladunk´ow magnetycznych!
- prawo Faradaya (1831 r.)
- r´ownanie Amp`ere’a-Maxwella (1864 r.)
Dokonajmy opisu wy˙zej wymienionych praw:
1. Prawo Coulomba.
Rozwa˙zmy oddziaÃlywania o charakterze centralnym (pochodza
ι
ce od Ãladunk´ow
punktowych). SiÃly pochodza
ι
ce od takich Ãladunk´ow podlegaja
ι
zasadzie liniowej su-
perpozycji:
~
E
1
+ ~
E
2
+ ~
E
3
+ ... =
n
X
i=1
~
E
i
= ~
E
kt´ora mo˙ze by´c zapisana w spos´ob cia
ι
gÃly zamieniwszy sume
ι
na caÃlke
ι
, oraz zasadzie i˙z
siÃla oddziaÃlywania pomie
ι
dzy Ãladunkami jest odwrotnie proporcjonalna do kwadratu
ich odlegÃlo´sci.
Aby wyprowadzi´c prawo Coulomba posÃlu˙zymy sie
ι
prawem Gaussa, kt´ore zasto-
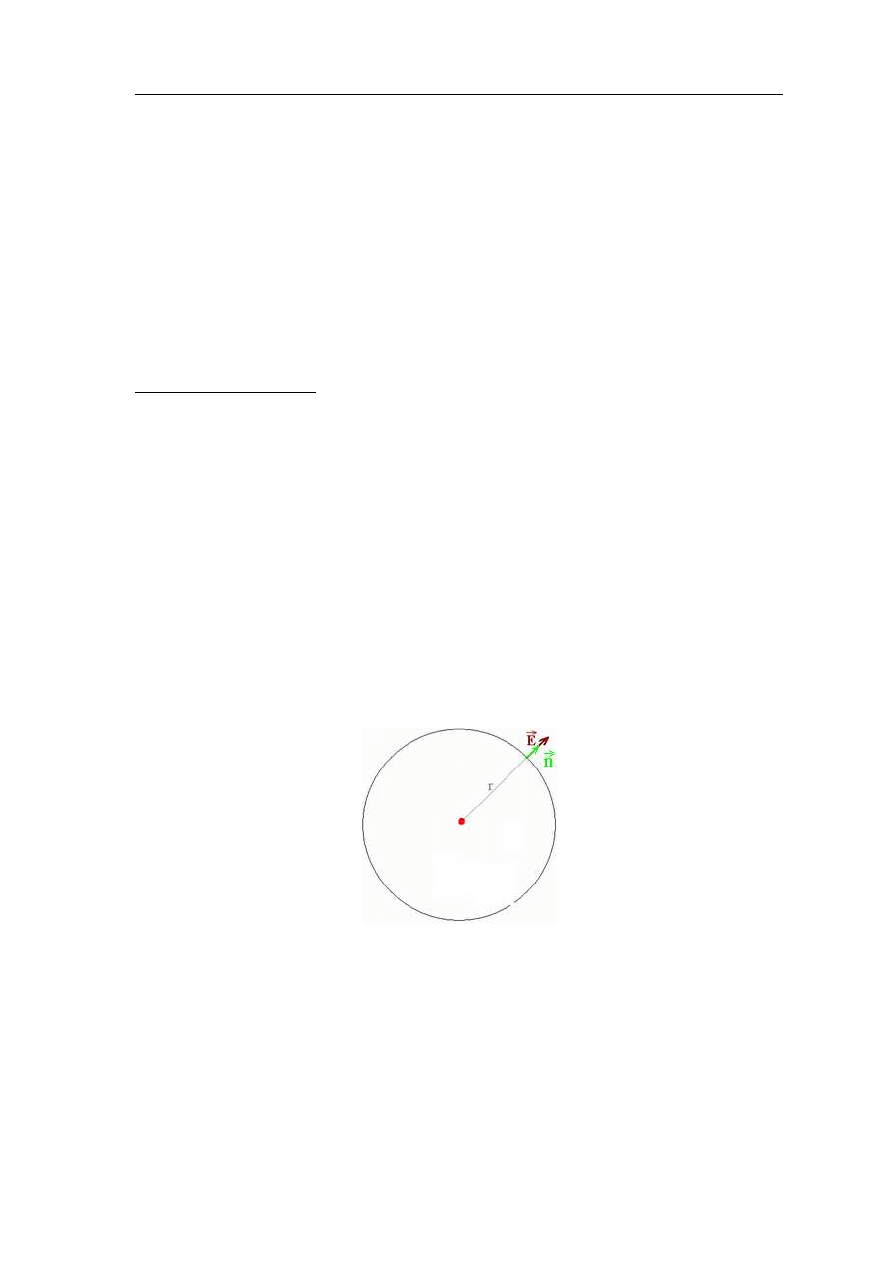
sujemy do opisu pojedynczego Ãladunku q. Prawo to mo˙zna zastosowa´c do dowolnej
sfery, jednak my, dla uÃlatwienia wykorzystamy powierzchnie
ι
kulista
ι
o promieniu r,
ze wzgle
ι
du na symetrie
ι
, gdy˙z wtedy pole E jest takie same na caÃlej jej powierzchni.
W ´srodku sfery znajduje sie
ι
Ãladunek punktowy q.
Rys 2.2. Hipotetyczna sfera dla naszych rozwa˙za´
n, gdzie: r - to jej promie´
n, ~n - jednostkowy wektor
skierowany na zewnatrz da (infinitezymalnej cze
ι
´sci powierzchni sfery)

12
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
Policzmy teraz strumie´n przechodza
ι
cy przez wybrana
ι
sfere
ι
:
Φ =
I
S
~
E · d~
S
(2.1.6)
Ka
ι
t pomie
ι
dzy wektorem pola elektrycznego a wektorem stycznym do powierzchni
wynosi zero. Wiemy r´ownie˙z z rozwa˙za´n nad symetria
ι
, i˙z pole E jest w ka˙zdym
punkcie takie same, czyli:
I
S
~
E · d~
S = E
I
S
dS = 4πr
2
E
(2.1.7)
gdzie 4πr
2
jest powierzchnia
ι
sfery. Strumie´n dla pojedynczego Ãladunku mo˙zemy
r´ownie˙z zapisa´c jako:
Φ =
q
ε
(2.1.8)
co pozwala, po przyr´ownaniu (2.1.7) i (2.1.8) wyznaczy´c nate
ι
˙zenie pola E pochodza
ι
ce
od Ãladunku q.
E =
q
4πε
0
r
2
(2.1.9)
Gdy w pobli˙zu Ãladunku q pojawi sie
ι
drugi Ãladunek Q, to wielko´s´c siÃly dziaÃlaja
ι
cej na
ten Ãladunek wynosi F = Eq
0
, a uwzgle
ι
dniaja
ι
c wcze´sniej otrzymany wynik, dostajemy:
F =
1
4πε
0
r
2
(2.1.10)
czyli r´ownanie Coulomba. Prawo Gaussa mo˙zemy stosowa´c do dowolnej powierzchni,
przez co jest ono wygodne przy znajdowaniu zale˙zno´sci pomie
ι
dzy strumieniem pola
elektrycznego Φ przechodza
ι
cym przez dana
ι
powierzchnie
ι
a Ãladunkiem, kt´ory jest
przez nia
ι
otoczony. Je˙zeli rozkÃlad Ãladunk´ow jest cia
ι
gÃly, to pewnym uÃlatwieniem
mo˙ze by´c wprowadzenie ge
ι
sto´sci Ãladunku elektrycznego ρ. Pozwoli to zapisa´c prawo
Coulomba w formie caÃlkowej:
I
S
~
E · d~
S = 4πρ
(2.1.11)
Gdy skorzystamy z twierdzenia Gaussa-Ostrogradskiego:
I
S
~
K · d~
S =
Z
V
div ~
KdV
be
ι
dziemy mogli przedstawi´c prawo Gaussa w postaci r´o˙zniczkowej:
div ~
E = 4πρ
(2.1.12)
2. Brak Ãladunk´
ow magnetycznych.

2.1. Elektrodynamika w pr´
o˙zni
13
Prawo to mo˙zna wykaza´c naste
ι
puja
ι
co: wybieraja
ι
c jaka
ι
´s powierzchnie
ι
zamknie
ι
ta
ι
,
a naste
ι
pnie policzy´c (na podstawie pomiar´ow) caÃlke
ι
wedÃlug okre´slenia Riemanna:
I
S
~
B · d~
S
kt´ora, jak mo˙zna stwierdzi´c (empirycznie!), wynosi 0.
Oznacza to, ˙ze jedynym
´zr´odÃlem pola magnetycznego sa
ι
pra
ι
dy elektryczne.
Gdyby istniaÃl Ãladunek magnetyczny, wytwarzaÃlby pole magnetyczne skierowane ra-
dialnie od obiektu. Pole to (analogicznie do pola elektrycznego) malaÃloby jak
1
r
2
. Ist-
nienie Ãladunku magnetycznego - pojedynczego bieguna magnetycznego (o poszukiwa-
niach monopolu magnetycznego [Ref 3]), spowodowaÃloby, ˙ze z obszaru, w kt´orym zna-
jdowaÃlby sie
ι
, wypÃlywaÃlby strumie´n indukcji B. IstniaÃlaby r´ownie˙z symetria pomie
ι
dzy
r´ownaniami opisuja
ι
cymi Ãladunki elektryczne (prawo Coulomba) i Ãladunki magne-
tyczne. Jednak zastosowanie twierdzenia Ostrogradskiego-Gaussa (podobnie jak to
zrobili´smy dla E), daje wÃla´snie r´ownanie rotB = 0 zgodne z wynikami pomiar´ow.
3. Prawo Faradaya.
Rozwa˙zmy przewodnik umieszczony w polu magnetycznym B. Gdy wycia
ι
gniemy
go z tego pola, okazuje sie
ι
, ˙ze przewodniku popÃlyna
ι
Ãl pra
ι
d elektryczny. M´owimy,
˙ze zaindukowaÃla sie
ι
siÃla elektromotoryczna SEM. Gdy wprowadzimy przewodnik
ponownie do B, powstanie znowu siÃla elektromotoryczna tylko, ˙ze o przeciwnym
znaku. Oznacza to, i˙z na umieszczony w zmiennym polu magnetycznym przewod-
nik dziaÃla SEM. Pod jej wpÃlywem, w przewodniku powstaje pra
ι
d indukcyjny. SiÃla
elektromotoryczna jest proporcjonalna (ze znakiem minus) do szybko´sci zmian stru-
mienia magnetycznego przenikaja
ι
cego przez powierzchnie
ι
, czego skutkiem jest reguÃla
Lenza: zmiana strumienia magnetycznego przechodza
ι
cego przez powierzchnie
ι
nad ob-
wodem powoduje powstanie pra
ι
du indukcyjnego, kt´orego w Ãlasne pole magnetyczne
przeciwdziaÃla zmianom strumienia magnetycznego, kt´ore wywoÃluje pra
ι
d indukcyjny.
4. R´
ownanie Amp`
ere’a-Maxwella.
R´ownanie to okre´sla zale˙zno´s´c pomie
ι
dzy polem magnetycznym a predko´scia
ι
zmian
pola elektrycznego oraz pre
ι
dko´scia
ι
ruchu Ãladunk´ow elektrycznych. CzÃlon
1
c
∂ ~
E
∂t
w tym
r´ownaniu, wprowadzony przez Maxwella, uwzgle
ι
dniÃl symetrie
ι
r´owna´n, zawieraja
ι
cych
rotacje
ι
, czym potwierdziÃl do´swiadczalna
ι
zasade
ι
zachowania Ãladunku elektrycznego.
Podsumowywuja
ι
c, r´ownania Maxwella (w pr´o˙zni) przyjmuja
ι
posta´c:
r´ownianie Coulomba:
div ~
E = 4πρ
(2.1.13)
brak Ãladunk´ow magnetycznych:
div ~
B = 0
(2.1.14)

14
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
prawo Faraday’a:
rot ~
E = −
1
c
∂ ~
B
∂t
(2.1.15)
r´ownanie Amp`ere’a-Maxwella:
rot ~
B =
1
c
∂ ~
E
∂t
+
4π
c
~j
(2.1.16)
gdzie: ρ(~r, t) - ge
ι
sto´s´c Ãladunku elektrycznego, ~j(~r, t) - ge
ι
sto´s´c pra
ι
du elektrycznego.
Korzystaja
ι
c z wÃlasno´sci r´ownania (2.1.7), mo˙zemy wyprowadzi´c zasade
ι
zachowania
Ãladunku elektrycznego. Policzmy zatem dywergencje
ι
r´ownania (2.1.9):
div(rot ~
B) =
1
c
∂(div ~
E)
∂t
+
4π
c
div~j
(2.1.17)
pamie
ι
taja
ι
c jednak, ˙ze:
¡
∇, [∇ × B]
¢
=
¡
∇, [B × ∇]
¢
=
¡
B, [∇ × ∇]
¢
= 0
(2.1.18)
Otrzymujemy:
0 =
1
c
∂(4πρ)
∂t
+
4π
c
div~j
(2.1.19)
Porza
ι
dkuja
ι
c r´ownanie (2.1.12) oraz dziela
ι
c przez czynnik
4π
c
, dostajemy:
∂ρ
∂t
+ div~j = 0
(2.1.20)
R´ownanie (2.1.13) przedstawia prawo zachowania Ãladunku elektrycznego (= r´ownanie
cia
ι
gÃlo´sci). Prawo to nie jest zaÃlo˙zeniem a priori, lecz bezpo´srednio wynika z r´owna´n
Maxwella, co zreszta
ι
udowodnili´smy. Jest ono speÃlnione dla cia
ι
gÃlego rozkÃladu Ãladunk´ow.
Wprowadzenie p´ol: elektrycznego i magnetycznego pozwala na niezale˙zne rozpa-
trzenie ´zr´odeÃl i Ãladunk´ow podlegaja
ι
cych dziaÃlaniu siÃl elektromagnetycznych. Dla
ka˙zdego (wybranego) Ãladunku obecno´s´c innych Ãladunk´ow wpÃlywa na jego ruch z
przyspieszeniem, co z kolei opisujemy r´ownaniem ruchu. Aby zamkna
ι
´c ukÃlad r´owna´n
Maxwella (tj. dokona´c peÃlnego opisu) konieczne jest dopisanie r´owna´n ruchu. Kiedy
jednak istnieje mo˙zliwo´s´c zaniedbania przyspieszenia, korzystamy z r´owna´n Maxwella,
rozpatruja
ι
c opis Ãladunk´ow tylko na podstawie ge
ι
sto´sci Ãladunku i ge
ι
sto´sci pra
ι
du.
Je˙zeli na Ãladunki pr´obne be
ι
da
ι
dziaÃla´c jednakowe siÃly, to rozkÃlad p´ol E i B jest
jednakowy w okre´slonym punkcie przestrzeni. Bardzo wa˙zne jest stwierdzenie, i˙z pola
elektromagnetyczne moga
ι
istnie´c w obszarach, w kt´orych brak jest ´zr´odeÃl. Istotnym
faktem jest r´ownie˙z to, E i B ˙ze moga
ι
by´c one no´snikami energii, pe
ι
du, momentu
pe
ι
du.
Podsumowywuja
ι
c, sformuÃlujmy matematyczna
ι
podstawe
ι
opisu E i B. Og´olna
liczna r´owna´n Maxwella wynosi osiem. Dwa z nich sa
ι
r´ownaniami, w kt´orych nie

2.2. PotencjaÃly wektorowe i skalarne
15
ma pochodnych po czasie, co oznacza, ˙ze mo˙zemy w dowolnej chwili wyznaczy´c jedna
ι
ze skÃladowych obu p´ol E i B a naste
ι
pnie podstawi´c do pozostalych (dynamicznych,
tj. zawieraja
ι
cych pochodne po czasie) r´owna´n.
SformuÃlowanie zagadnienia pocza
ι
tkowego (tj. zagadnienia Cauchy’ego) dla ukÃladu
r´owna´n Maxwella zawiera sze´s´c warunk´ow pocza
ι
tkowych, po jednym dla ka˙zdej zmi-
ennej. R´ownania (2.1.1) i (2.1.4) [?] wprowadzaja
ι
pewne wie
ι
zy dla podstawowych
zmiennych (tj. E i B), wa˙znych w dowolnym czasie, a wie
ι
c i w chwili pocza
ι
tkowej.
To oznacza, ze tylko cztery ze skÃladowych p´ol sa
ι
dynamicznie niezale˙zne, czyli mo˙zna
zostawi´c cztery r´ownania przy uzyskaniu zale˙zno´sci od czasu.
2.2
PotencjaÃly wektorowe i skalarne
Rozwa˙zmy r´ownania (2.1.7) i (2.1.9). Wynika z nich i˙z rotacja B w (2.1.9)
w og´olnym przypadku nie musi by´c r´owna zero. Skutkiem tego, pole B (w przeci-
wie´nstwie do pola E) nie mo˙ze by´c ju˙z przedstawione za pomoca
ι
gradientu. Jednak
uwzgle
ι
dniaja
ι
c i˙z divB = 0, pole B mo˙zna wyrazi´c za pomoca
ι
innego pola wek-
torowego. Wprowad´zmy zatem potencjaÃl wektorowy A, kt´ory zdefiniujemy naste
ι
pu-
ja
ι
co:
~
B = rot ~
A
(2.2.1)
co automatycznie daje div(rot ~
B) = 0. Podstawmy potencjaÃl wektorowy A do r´ow-
nania Faradaya (2.1.8):
rot ~
E = −
1
c
∂
∂t
rot ~
A
=⇒
rot
µ
~
E +
1
c
∂ ~
A
∂t
¶
= 0
(2.2.2)
W elektrostatyce potencjaÃl definiowali´smy jako:
~
E = −∇φ = −gradϕ
(2.2.3)
Na podstawie (2.2.2) i (2.2.3) wprowad´zmy nowa
ι
definicje
ι
potencjaÃlu:
~
E +
1
c
∂ ~
A
∂t
= −gradϕ
(2.2.4)
kt´ory mo˙zemy zapisa´c naste
ι
puja
ι
co:
~
E = −gradϕ −
1
c
∂ ~
A
∂t
(2.2.5)
Stosuja
ι
c okre´slenie potencjaÃlu (2.2.3) do r´ownania Coulomba (2.1.6) stwierdzamy, ˙ze
zasada zachowania Ãladunku elektrycznego jest speÃlniona.
div ~
E = −4ϕ −
1
c
∂
¡
div ~
A
¢
∂t
= 4πρ
(2.2.6)
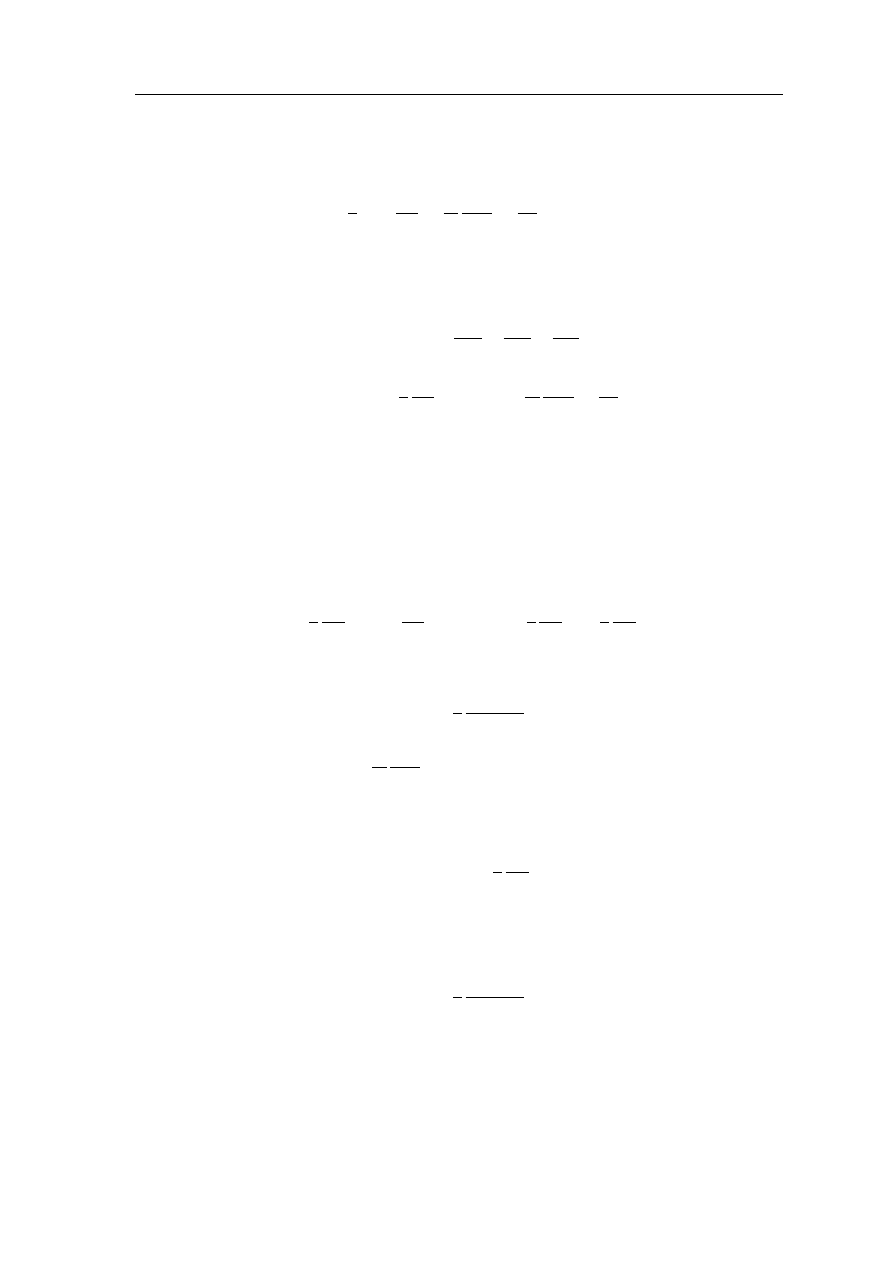
16
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
Podobnie mo˙zemy posta
ι
pi´c z pozostaÃlymi r´ownaniami Maxwella (2.1.7) i (2.1.9):
div ~
B = div
¡
rot ~
A
¢
= 0
(2.2.7)
rot ~
B = rot
¡
rot ~
A
¢
= −
1
c
grad
∂ϕ
∂t
−
1
c
2
∂
2
A
∂t
2
+
4π
c
~j = ∇
¡
div ~
A
¢
− ∇
2
~
A
(2.2.8)
W r´ownaniu (2.2.8) wykorzystali´smy zale˙zno´s´c:
rot
¡
rot ~
A
¢
=
£
∇ × [∇ × ~
A]
¤
= ∇
¡
∇, ~
A
¢
− ∇
2
~
A
gdzie:
¡
∇, ~
A
¢
= div ~
A =
∂A
x
∂x
+
∂A
y
∂y
+
∂A
z
∂z
oraz
grad
µ
div ~
A +
1
c
∂ϕ
∂t
¶
= 4 ~
A −
1
c
2
∂
2
~
A
∂t
2
+
4π
c
~j
(2.2.9)
Z powy˙zszych wzor´ow wynika naste
ι
puja
ι
ca transformacja:
~
A → ~
A
0
+ ∇Λ(t, ~r)
(2.2.10)
z kt´orej wynika, i˙z pole wektorowe ~
A jest okre´slone do pewnej staÃlej, kt´ora znika przy
r´o˙zniczkowaniu, wie
ι
c og´olna posta´c r´ownania nie ulegnie zmianie. Nasza
ι
staÃla
ι
jest
gradient pola skalarnego ∇Λ(t, ~r).
Gdy podstawimy (2.2.10) do r´ownania (2.2.4):
~
E = ∇ϕ −
1
c
∂ ~
A
∂t
− 1c∇
∂Λ
∂t
= −∇
µ
ϕ +
1
c
∂Λ
∂t
¶
−
1
c
∂ ~
A
∂t
(2.2.11)
otrzymamy zale˙zno´s´c okre´slaja
ι
ca
ι
potencjaÃl ϕ:
ϕ → ϕ
0
= −
1
c
∂Λ(t, ~r)
∂t
+ ϕ
(2.2.12)
−
1
c
2
∂
2
Λ
∂t
2
+ div(gradΛ) = 0
(2.2.13)
Mo˙zemy opisa´c skÃladowe E pola elektromagnetycznego przy pomocy wprowadzonych
przez nas potencjaÃl´ow Ai ϕ:
~
E = −∇ϕ
0
−
1
c
∂ ~
A
∂t
(2.2.14)
Uzyskana
ι
transformacje
ι
tj. (2.2.10) i (2.2.12) nazywamy transformacja
ι
cechowania:
~
A → ~
A
0
+ ∇Λ(t, ~r)
ϕ → ϕ
0
= −
1
c
∂Λ(t, ~r)
∂t
+ ϕ

2.2. PotencjaÃly wektorowe i skalarne
17
Powy˙zsze zwia
ι
zki (transformacje) pozwalaja
ι
nam zachowa´c pewna
ι
dowolno´s´c przy
wyborze potencjaÃlu wektorowego. Funkcja Λ jest dowolna, a to oznacza, ˙ze mo˙zemy
wybra´c funkcje
ι
ϕ i A takie, aby m´oc upro´sci´c r´ownanie (2.2.9), jednak pod warunk-
iem, ˙ze:
1
c
∂ϕ
∂t
+ div ~
A = 0
(2.2.15)
R´ownanie (2.2.15) jest okre´sleniem warunku cechowania Lorentza.
W przypadku, gdy
div ~
A = 0
(2.2.16)
mamy do czynienia z warunkiem cechowania Coulomba.
Z przedstawienia E i B za pomoca
ι
potencjaÃl´ow: wektorowego i skalarnego, korzys-
tamy maja
ι
c na celu uproszczenie oblicze´n. Startuja
ι
c z r´owna´n Maxwella dysponujemy
sze´scioma zmiennymi (E
x
,E
y
,E
z
,B
x
,B
y
,B
z
), podczas gdy wprowadzaja
ι
c potencjaÃly :
wektorowy i skalarny, pozostana
ι
ju˙z tylko cztery zmienne (A
x
,A
y
,A
z
,ϕ). Z wÃlasno´sci
potencjaÃlu wektorowego A korzystamy w obliczeniach dla p´ol magnetycznych, nato-
miast potencjaÃl skalarny ϕ stosujemy rozpatruja
ι
c pola elektryczne.
Jakie mo˙zliwo´sci daje nam cechowanie? - rozwa˙zania teoretyczne
Warunek na cechowanie Lorentza jest bardzo cze
ι
sto wykorzystywany ze wzgle
ι
du na
dwie, bardzo wa˙zne wÃlasno´sci. Przede wszystkim mo˙zna uzyska´c niezale˙zne r´ownania
falowe speÃlniane przez A i ϕ:
−
1
c
∂
2
~
A
∂t
2
+ 4 ~
A = −
4π
c
~j
(2.2.17)
oraz
¤ϕ = −4πρ
(2.2.18)
gdzie: ¤ = −
1
c
∂
2
∂t
2
+ 4
oraz zawsze mo˙zemy tak dobra´c A i ϕ aby uzyska´c to cechowanie.
Natomiast z warunk´ow cechowania Coulomba korzystamy kiedy wygodnie jest
zastosowa´c r´ownanie Poissona dla potencjaÃlu ϕ. PotencjaÃl skalarny w tym przypadku,
to po prostu dobrze znany potencjaÃl kulombowski.
1
c
∇ϕ = −
1
c
∂
2
~
A
∂t
2
+ 4 ~
A +
4π
c
~j
(2.2.19)
gdzie: 4 = ∇
2
oraz
4ϕ = −4πρ
(2.2.20)
Po rozwia
ι
zaniu powy˙zszych r´owna´n, mo˙zemy obliczy´c pole A.

18
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
2.3
Zasady zachowania. Twierdzenie Poyntinga.
Zasady zachowania tworza
ι
fundamenty fizyki. Na nich opieraja
ι
sie
ι
wszelkie prawa
oraz zjawiska zachodza
ι
ce w przyrodzie. GÃl´owna
ι
cecha
ι
zasad zachowania jest ich
niepodwa˙zalno´s´c! Do tych podstawowych praw, zaliczamy m.in. zachowanie Ãladunku
elektrycznego, zasady zachowania energii, pe
ι
du, momentu pe
ι
du [Ref 3, Ref 4]. Z
punktu widzenia elektrodynamiki, najbardziej interesuja
ι
nas zasady zachowania ener-
gii oraz pe
ι
du, kt´ore dotycza
ι
podstawowych wÃlasno´sci pola elektromagnetycznego oraz
poruszaja
ι
cych sie
ι
Ãladunk´ow.
Jako pierwsza
ι
rozpatrzmy zasade
ι
zachowania energii, nazywana
ι
r´ownie˙z twierdze-
niem Poyntinga. W tym celu skorzystamy z r´owna´n Maxwella:
rot ~
E = −
1
c
∂ ~
B
∂t
rot ~
B =
1
c
∂ ~
E
∂t
+
4π
c
~j
Korzystaja
ι
c z powy˙zszych wzor´ow mo˙zemy obliczy´c naste
ι
puja
ι
ce iloczyny skalarne:
( ~
B, rot ~
E) = −
1
c
µ
~
B,
∂ ~
B
∂t
¶
= −
1
2c
∂ ~
B
2
∂t
(2.3.1)
( ~
E, rot ~
B) =
1
2c
∂ ~
E
2
∂t
+
4π
c
( ~
E,~j)
(2.3.2)
Gdy odejmiemy stronami (2.3.1) od (2.3.2), otrzymamy:
1
2c
∂ ~
E
2
∂t
+
4π
c
¡
~
E,~j
¢
+
1
2c
∂ ~
B
2
∂t
=
1
2c
∂
¡
~
E
2
+ ~
B
2
¢
∂t
+
4π
c
¡
~
E,~j
¢
+
¡
~
B, rot ~
E
¢
−
¡
~
E, rot ~
B
¢
= 0
(2.3.3)
Korzystaja
ι
c z zale˙zno´sci wektorowej:
div
£
~
E × ~
B
¤
=
¡
~
B, rot ~
E
¢
−
¡
~
E, rot ~
B
¢
ostatecznie mo˙zemy zapisa´c prawo zachowania energii w postaci:
1
8π
∂
∂t
µ
~
E
2
+ ~
B
2
¶
= −
c
4π
div
£
~
E × ~
B
¤
−
¡
~
E,~j
¢
(2.3.4)
Powy˙zsze r´ownanie (2.3.4) skÃlada sie
ι
z dw´och czÃlon´ow: div
¡
c
4π
£
~
E × ~
B
¤¢
oraz z ( ~
E,~j).
W pierwszym z nich, wyra˙zenie
¡
c
4π
£
~
E × ~
B
¤¢
nazywamy wektorem Poyntinga i oz-
naczamy jako:
~
S =
c
4π
£
~
E × ~
B
¤
(2.3.5)
Wektor ten reprezentuje ge
ι
sto´s´c strumienia energii, tj. energie
ι
przenoszona
ι
przez pola
w jednosce czasu na jednostke
ι
powierzchni. Zdolno´s´c p´ol do przenoszenia i maga-
zynowania energii, jest jedna
ι
z wa˙zniejszych wÃlasno´sci fal elektromagnetycznych.
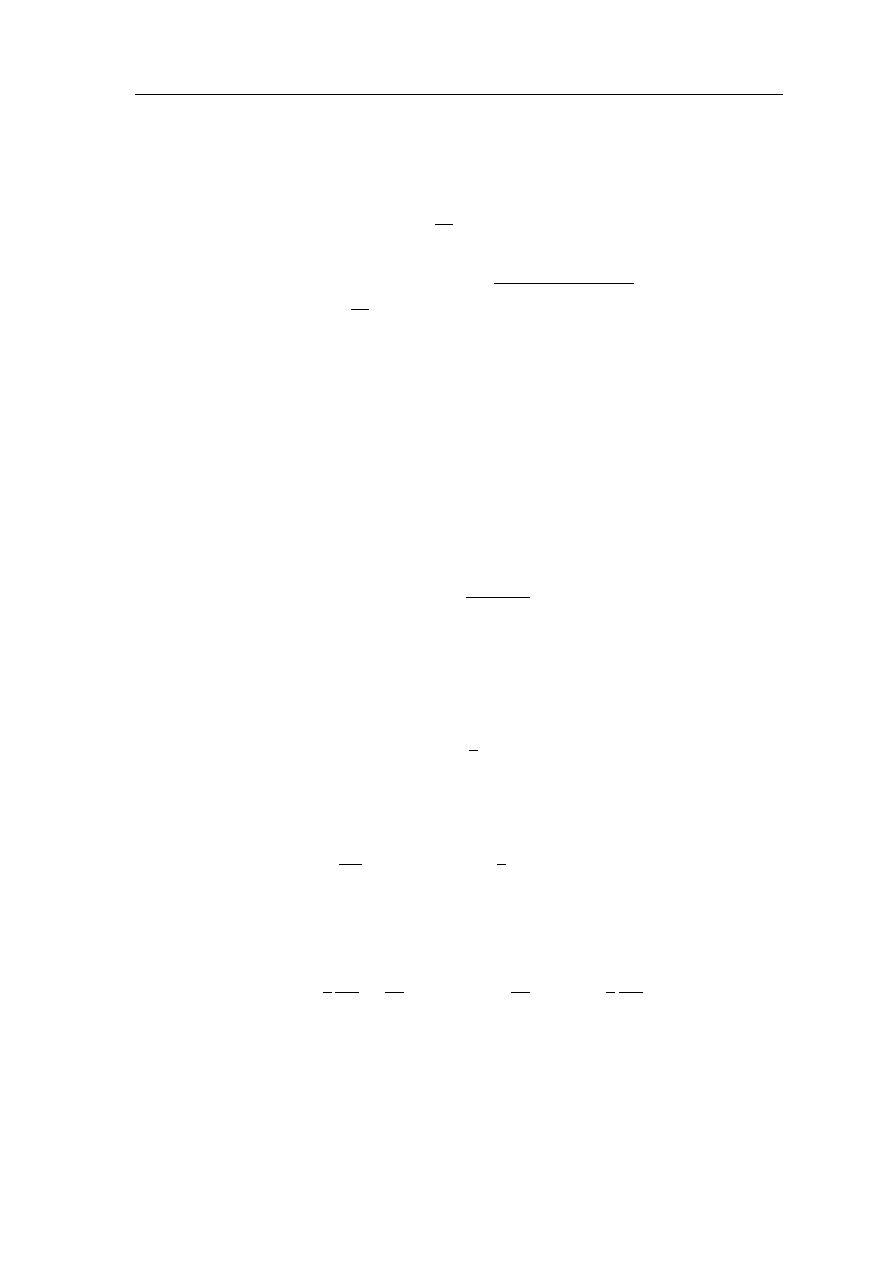
2.3. Zasady zachowania. Twierdzenie Poyntinga.
19
Korzystaja
ι
c z wÃlasno´sci wektora Poyntinga mo˙zemy opisa´c pre
ι
dko´s´c przepÃlywu
energii przez jednostkowa
ι
powierzchnie
ι
dla pÃlaskiej fali elektromagnetycznej. Wektor
ten, korzystaja
ι
c ze zwia
ι
zk´ow pomie
ι
dzy c i µ
0
, mo˙zna zapisa´c tak˙ze w r´ownowa˙zny
spos´ob:
~
S =
1
µ
0
£
~
E × ~
B
¤
(2.3.6)
gdzie: µ
0
to przenikalno´s´c magnetyczna pr´o˙zni.
Wymiar wektora Poyntinga okre´slamy jako
[energia]
[pole powierzchni]·[czas]
, co w ukÃladzie jed-
nostek SI przyjmuje posta´c
W
m
2
.
W r´ownaniu opisuja
ι
cym prawo zachowania energii, liczymy div ~
S. Oznacza to, i˙z
wektor Poyntinga jest okre´slony z dokÃladno´scia
ι
do pewnej staÃlej, w naszym przy-
padku jest to dowolne pole wektorowe (analogicznie jak w przypadku potencjaÃlu
wektorowego i skalarnego). Natomiast drugi z czÃlon´ow, okre´slaja
ι
cy iloczyn skalarny
¡
~
E,~j
¢
okre´sla ge
ι
sto´s´c mocy (prace
ι
wykonana
ι
w jednostce czasu w jednostkowej
obje
ι
to´sci).
Zatem zasada zachowania energii to suma zmian energii elektromagnetycznej na
jednostke
ι
czasu w pewnej obje
ι
to´sci oraz energii elektromagnetycznej wypÃlywaja
ι
cej w
jednostce czasu przez powierzchnie
ι
ograniczaja
ι
ca
ι
te
ι
obje
ι
to´s´c, przy czym jest r´owna
(−) pracy wykonanej w jednostce czasu przez pola nad ´zr´odÃlami w tej obje
ι
to´sci.
Ge
ι
sto´s´c energii definiujemy jako:
w
energii
=
~
E
2
+ ~
B
2
8π
(2.3.7)
Druga
ι
z rozpatrywanych przez nas zasad jest zasada zachowania pe
ι
du.
Wybie˙zmy zatem dowolny Ãladunek punktowy, kt´ory porusza sie
ι
w polu E ruchem
jednostajnym z pre
ι
dko´scia
ι
v. Na Ãladunek ten, dziaÃla´c be
ι
dzie siÃla Lorentza F
L
, kt´ora
ι
wcze´sniej zdefiniowali´smy naste
ι
puja
ι
co:
~
F
L
= q
µ
~
E +
1
c
£
~v × ~
B
¤
¶
PosÃluguja
ι
c sie
ι
druga
ι
zasada
ι
dynamiki Newtona, oznaczmy sume
ι
pe
ι
d´ow wszystkich
cza
ι
stek w pewnej obje
ι
to´sci V przez P. Otrzymamy:
dP
dt
=
Z
V
d
3
x
µ
ρ ~
E +
1
c
£
~j × ~
B
¤
¶
(2.3.8)
Aby m´oc wyeliminowa´c ze wzoru (2.3.8) ge
ι
sto´s´c Ãladunku elektrycznego ρ(t, ~r) oraz
ge
ι
sto´s´c pra
ι
du elektrycznego ~j(t, ~r) posÃlu˙zymy sie
ι
r´ownaniami Maxwella (2.1.6) i
(2.1.9):
rot ~
B =
1
c
∂ ~
E
∂t
+
4π
c
~j
⇒
~j =
c
4π
µ
rot ~
B −
1
c
∂ ~
E
∂t
¶
(2.3.9)
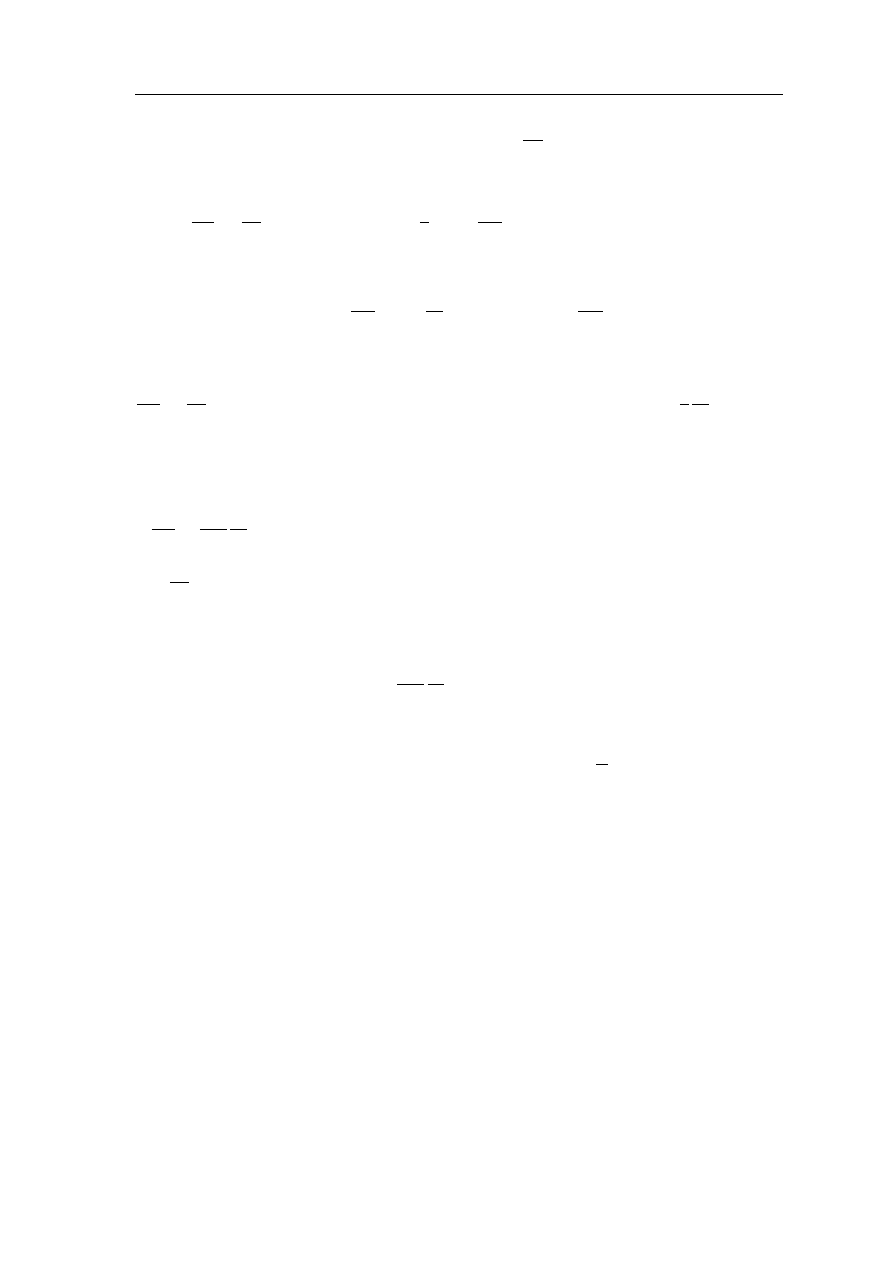
20
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
div ~
E = 4πρ
⇒
ρ =
1
4π
div ~
E
(2.3.10)
Gdy podstawimy (2.3.9) i (2.3.10) do (2.3.8) otrzymamy naste
ι
puja
ι
ce wyra˙zenie:
dP
dt
=
1
4π
Z
V
d
3
x
µ
~
E
¡
∇, ~
E
¢
+
1
c
·
~
B ×
∂ ~
E
∂t
¸
−
·
~
B ×
£
∇ × ~
B
¤
¸¶
(2.3.11)
W powy˙zszym r´ownaniu skorzystamy z wÃlasno´sci iloczynu wektorowego:
·
~
B ×
∂ ~
E
∂t
¸
= −
∂
∂t
£
~
E × ~
B
¤
+
·
~
E ×
∂ ~
B
∂t
¸
a naste
ι
pnie gdy dodamy B(∇, B) = 0, dostaniemy:
dP
dt
=
1
4π
Z
V
d
3
x
Ã
~
E(∇, ~
E)+ ~
B(∇, ~
B)−
·
~
E×
£
∇× ~
E
¤
¸
−
·
~
B×
£
∇× ~
B
¤
¸
−
1
c
∂
∂t
£
~
E× ~
B
¤
!
(2.3.12)
Wz´or (2.3.8), przedstawiaja
ι
cy pre
ι
dko´s´c zmiany pe
ι
du, w postaci (2.3.12) mo˙zna za-
pisa´c naste
ι
puja
ι
co:
dP
dt
+
1
4πc
∂
∂t
Z
V
d
3
x
£
~
E × ~
B
¤
=
=
1
4π
Z
V
d
3
x
Ã
~
E(∇, ~
E) + ~
B(∇, ~
B) −
·
~
E ×
£
∇ × ~
E
¤
¸
−
·
~
B ×
£
∇ × ~
B
¤
¸!
(2.3.13)
gdzie caÃlka po lewej stronie r´ownania (2.3.13) opisuje caÃlkowity pe
ι
d pola elektromag-
netycznego P
p
.
~
P
p
=
1
4πc
∂
∂t
Z
V
d
3
x
£
~
E × ~
B
¤
(2.3.14)
Funkcje
ι
podcaÃlkowa
ι
[E × B] mo˙zna zinterpretowa´c jako ge
ι
sto´s´c pe
ι
du pola elektro-
magnetycznego. Jest ona proporcjonalna do wektora Poyntinga (ge
ι
sto´sci strumienia
energii), przy czym wsp´oÃlczynnik proporcjonalno´sci wynosi
1
c
2
.
Zgodnie z zasada
ι
zachowania pe
ι
du, poruszaja
ι
ce sie
ι
cza
ι
stki oraz pola E i B posiadaja
ι
pe
ι
d. Oznacza to, i˙z aby zasada ta byÃla speÃlniona, pe
ι
d tracony przez cza
ι
stki, jest
przekazywany polom.
2.4
Fale elektromagnetyczne. Fala pÃlaska
Przedstawmy r´ownania Maxwella za pomoca
ι
potencjaÃl´ow: wektorowego i skalarnego,
podobnie jak to uczynili´smy w podrozdziale (2.2). Wprowad´zmy jednak pewne ogra-
niczenie dotycza
ι
ce Ãladunk´ow elektrycznych, a mianowicie ich brak. Oznacza to, ˙ze

2.4. Fale elektromagnetyczne. Fala pÃlaska
21
czÃlony zawieraja
ι
ce ge
ι
sto´s´c Ãladunku ρ oraz ge
ι
sto´s´c pra
ι
du elektrycznego ~j znikna
ι
. Poz-
woli nam to uzyska´c warunek na ¤ ~
E :
1
c
2
∂
2
~
E
∂t
2
=
1
c
∂
∂t
µ
1
c
∂ ~
E
∂t
¶
=
1
c
∂
∂t
µ
rot ~
B
¶
=
1
c
rot
∂ ~
B
∂t
=
=
1
c
rot
¡
− crot ~
B
¢
= −rot(rot ~
B) =
= −grad(div ~
E) + ∇
2
~
E = ∇
2
~
E (2.4.1)
W r´ownaniu (2.4.1) div ~
E = 0, poniewa˙z nasze zaÃlo˙zenia dotycza
ι
pr´o˙zni. Tak wie
ι
c:
¤ ~
E = 0
(2.4.2)
gdzie ¤ jest operatorem d’Alemberta. Powy˙zsze r´ownanie (2.4.2) tworzy ukÃlad r´owna´n
dla skÃladowych (t, x, y, z) :
1
c
2
∂
2
~
E
∂t
2
=
∂
2
~
E
∂x
2
+
∂
2
~
E
∂y
2
+
∂
2
~
E
∂z
2
(2.4.3)
kt´ory rozwia
ι
˙zemy metoda
ι
Fouriera. Metoda ta polega na rozdzieleniu zmiennych
funkcji:
E
i
(t, x, y, z) = T (t)X(x)Y (y)Z(z)
(2.4.4)
a naste
ι
pnie scaÃlkowaniu po parametrze zewne
ι
trznym k
i
. Rozwia
ι
zanie szczeg´olnego
r´ownania falowego przyjmie posta´c:
E
i
= E
i0
e
i(~k~r−ωt)
+ c.c.
(2.4.5)
przy czym wprowadzili´smy oznaczenie ~k~r = k
x
x + k
y
y + k
z
z, w kt´orym k
x
, k
y
,
k
z
stanowia
ι
parametry separacji zmiennych. Sa
ι
to wspomniane wy˙zej parametry
zewne
ι
trzne, niezale˙zne od siebie.
Podobny algorytm poste
ι
powania, przeprowad´zmy dla pola B. Ostatecznie otrzy-
mamy wzory dla p´ol E i B stowarzyszonych z fala
ι
pÃlaska
ι
:
E = E
0
e
i(~k~r−ωt)
+ c.c.
(2.4.6a)
B = B
0
e
i(~k~r−ωt)
+ c.c
(2.4.6b)
W r´ownaniach (2.4.6), E
0
oraz B
0
stanowia
ι
amplitudy fal.
Naszym kolejnym etapem be
ι
dzie policzenie rotacji pola elektrycznego wyste
ι
puja
ι
cego
w (2.4.6). Skorzystamy przy tym z r´ownania Faradaya (2.1.15):
∇ × ~
E = −
1
c
∂ ~
B
∂t
= −
1
c
¡
~
B
0
e
iϕ
(−iω)
¢
= i
ω
c
~
B
0
e
iϕ
(2.4.7a)
∇ × ~
E =
£
∇ × ~
E
0
e
iϕ
¤
= e
iϕ
£
∇ϕ × ~
E
0
¤
= ie
iϕ
£
~k × ~E
0
¤
(2.4.7b)
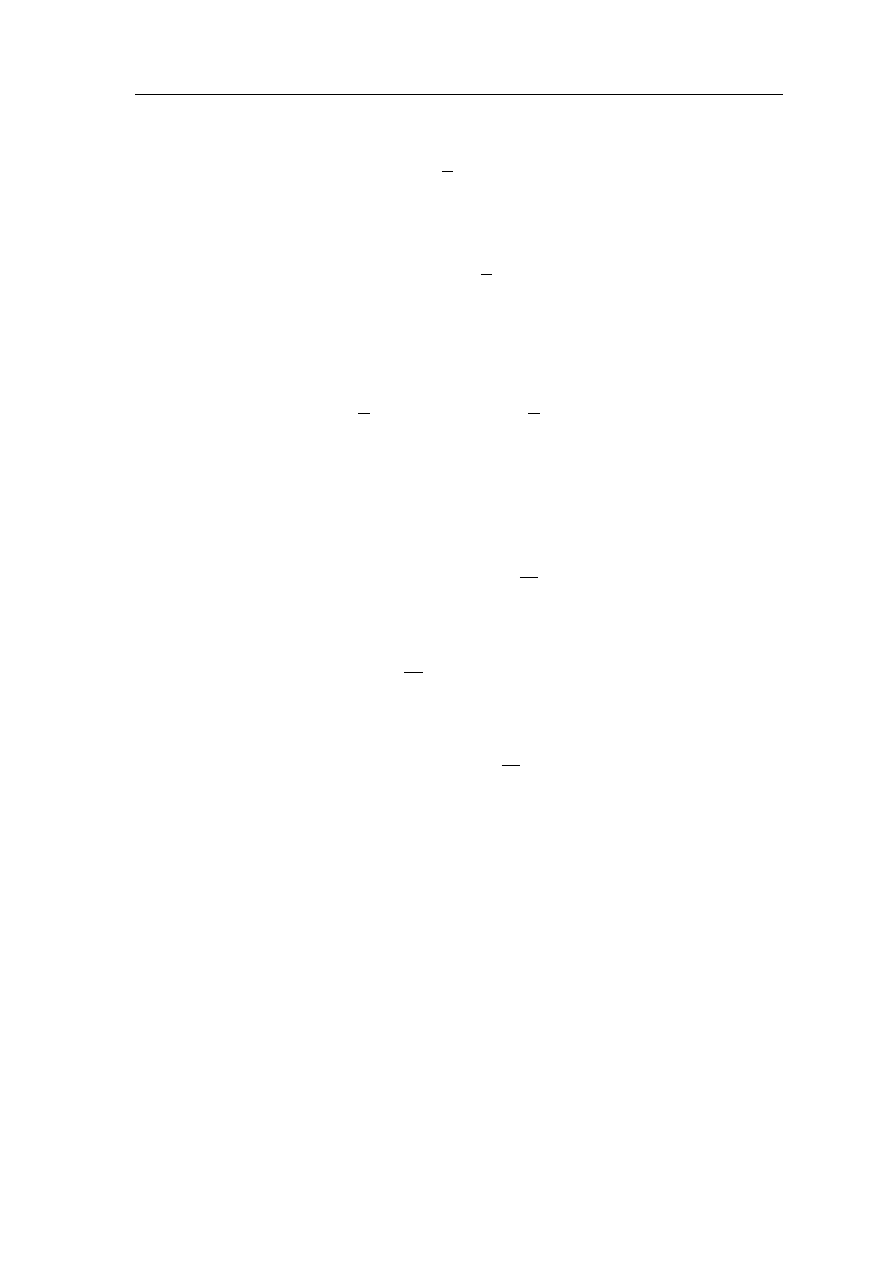
22
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
Przyr´ownujemy stronami powy˙zsze wyra˙zenia, aby wyznaczy´c B:
~
B
0
=
c
ω
£
~k × ~E
0
¤
(2.4.8)
Podobny algorytm poste
ι
powania zastosujemy obliczaja
ι
c rotacje
ι
pola magnetycznego.
Wykorzystamy r´ownania (2.4.6) oraz Amp´ere’a-Maxwella.
∇ × ~
B = −i
ω
c
~
E
0
e
iϕ
(2.4.9a)
∇ × ~
B = ie
iϕ
£
~k × ~B
0
¤
(2.4.9b)
Ponownie musimy przyr´owna´c stronami wyra˙zenia r´owno´sci(2.4.9), jednak tym razem
wykorzystamy warto´s´c B otrzymana
ι
w (2.4.8).
c
ω
·
~k ×
£
~k × ~E
0
¤
¸
= −
ω
c
~
E
0
(2.4.10)
Wyra˙zenie po lewej stronie r´ownania (2.4.10) upro´scimy, gdy skorzystamy z zale˙zno´sci
”bac-cab”:
£
a × [b × c]
¤
= b(a, c) − c(a, b)
czyli w naszym przypadku:
~k
¡
~k, ~E
0
¢
− ~
E
0
~k
2
= −
ω
2
c
2
~
E
0
(2.4.11)
Poniewa˙z wektory k i E sa
ι
ortogonalne, wie
ι
c wyra˙zenie (2.4.11) zredukuje sie
ι
do
postaci
µ
ω
2
c
2
− ~k
2
¶
~
E
0
= 0
(2.4.12)
Rozwia
ι
zanie r´ownania (2.4.12) be
ι
dzie jedno, gdy zaÃlo˙zymy, ˙ze jest ono nietrywialne,
tzn. E
0
6= 0.
gdy :
~
E
0
6= 0
⇒
ω
2
c
2
− ~k
2
= 0
ω
2
= c
2
~k
2
(2.4.13)
R´ownanie postaci (2.4.13) jest warunkiem dyspersyjnym dla fali pÃlaskiej, kt´ory wraz z
powy˙zszym rozumowaniem, stanowi potwierdzenie poprawno´sci otrzymanych wzor´ow
(2.4.6). Gdy rozwa˙zamy ruch falowy jako og´oÃl zjawisk, to oka˙ze sie
ι
, ˙ze zachowanie
fal mo˙ze by´c dwojakie: moga
ι
ulega´c dyspersji lub te˙z nie. Zale˙zy to od pewnych
czynnik´ow tj. rodzaju fali oraz wÃlasno´sci fizycznych o´srodka propagacji.
Rozwia
ι
zanie szczeg´olne r´ownania falowego (2.4.6) m´owi nam, ˙ze czoÃlo fali pÃlaskiej
jest fala
ι
harmoniczna
ι
. O fali m´owimy, ˙ze jest harmoniczna
ι
, je˙zeli w chwili pocza
ι
tkowej
t
0
jej ksztaÃlt przyjmuje posta´c funkcji sinus lub cosinus. Oznacza to, ˙ze funkcje te
tworza
ι
baze
ι
, za pomoca
ι
kt´orej mo˙zemy przedstawi´c fale
ι
.

2.4. Fale elektromagnetyczne. Fala pÃlaska
23
Z propagacja
ι
fal nieodzownie zwia
ι
zane jest poje
ι
cie paczki falowej. Paczka falowa
jest skutkiem pracy (rzeczywistego) generatora. Generator wytwarza impuls, kt´ory
tworzy fale. Czas trwania tego impulsu jest ograniczony, wie
ι
c w miare
ι
oddalania sie
ι
fal od generatora utworza
ι
one paczke
ι
falowa
ι
. Z kolei paczka falowa stanowi pewna
ι
reprezenstacje
ι
caÃlki Fouriera, kt´ora
ι
liczymy w granicach od k do k + dk.
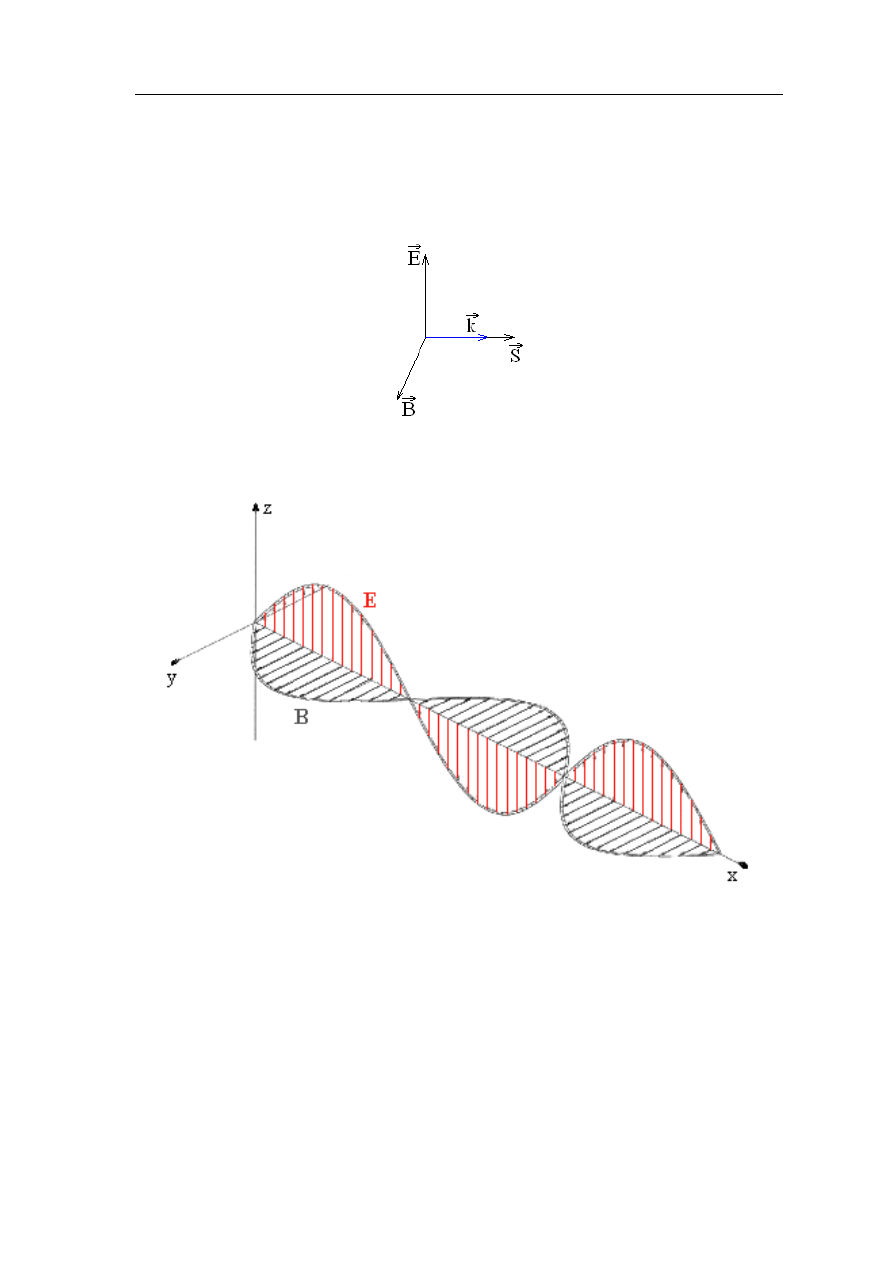
Rys 2.4.1 Model dwuwymiarowej paczki falowej.
Kontynuuja
ι
c rozwa˙zania dotycza
ι
ce fali pÃlaskiej w pro˙zni, posÃlu˙zymy sie
ι
superpozycja
ι
fourierowska
ι
paczek falowych. Z jej pomoca
ι
mo˙zemy r´ownie˙z skonstruowa´c r´ownanie
falowe. Pomijaja
ι
c warunki brzegowe, otrzymamy caÃlke
ι
Fouriera:
E
x
=
Z
dk
x
dk
y
dk
z
E
x
(k
x
, k
y
, k
z
)
(2.4.14)
oraz posta´c transformacji Fouriera w przestrzeni tr´ojwymiarowej:
E
x
(0, ~r) =
Z
d~kE
0x
(~k)e
i~k~r
(2.4.15)
E
0x
(~k) =
1
2π
Z
d~rE
x
(0, ~r)e
−i~k~r
(2.4.16)
kt´ora przy policzeniu dla ka˙zdej skÃladowej (x, y, z):
E
x
= E
0x
e
i(~k~r−ωt)
+ c.c.
(2.4.17a)
E
y
= E
0y
e
i(~k~r−ωt)
+ c.c.
(2.4.17b)
E
z
= E
0z
e
i(~k~r−ωt)
+ c.c.
(2.4.17c)
da warunek
k
x
E
0x
+ k
y
E
0y
+ k
z
E
0z
= 0
(2.4.18)
(~k, ~
E
0
) = 0
(2.4.19)
24
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
R´ownanie (2.4.19) oznacza, i˙z amplituda pola ~
E
0
(a przez to i ~
B
0
), jest prostopadÃla do
wektora falowego ~k. Wektor ~k okre´sla kierunek propagacji fali. Oznacza to, ˙ze w fali
pÃlaskiej skÃladowe pola elektromagnetycznego sa
ι
prostopadÃle do kierunku propagacji,
kt´ory z kolei jest zgodny z kierunkiem wektora Poyntinga ~
S. Wektor ten informuje o
´srednim kierunku strumienia energii (2.3.5).
Interesuja
ι
cy nas przypadek stanowi propaguja
ι
ca fala pÃlaska stowarzyszona z polem
elektromagnetycznym. Jej posta´c mo˙zna przedstawi´c naste
ι
puja
ι
co:
Rys 2.4.2. PÃlaskiej fali E-M towarzysza
ι
pola elektryczne E oraz magnetyczne B, kt´ore sa
ι
do siebie
prostopadÃle.
Poruszaja
ι
ca sie
ι
fala mo˙ze by´c no´snikiem informacji. Fala nie poddana modyfikacji
mo˙ze nas poinformowa´c tylko, czy dotarÃla do okre´slonego punktu (np. antena,

2.5. Niejednorodne r´
ownanie falowe. Generacja fal E-M.
25
odbiornik) czy te˙z nie. Wykorzystujemy przy tym dwie wÃlasno´sci fali, kt´ore mo˙zemy
modelowa´c. Sa
ι
to mianowicie amplituda oraz cze
ι
stotliwo´s´c. Taki mechanizm jest
wykorzystywany m.in. przy przesyÃlaniu fal radiowych. Stosujemy dwie techniki:
modulujemy amplitude
ι
(fale tzw. ,,AM”-Amplitude Modulation), wtedy w r´ownaniach
(2.4.6) zmieniaja
ι
sie
ι
w czasie E
0
i B
0
- amplitudy. Mo˙zna r´ownie˙z zmienia´c cze
ι
stotliwo´s´c
(fale tzw. ,,FM” - Frequency Modulation). Wtedy zmianom w r´ownaniach falowych
podlega ω. W uje
ι
ciu fizycznym, metoda wytwarzania fali zawarta jest w warunkach
brzegowych, kt´ore ograniczaja
ι
liczbe
ι
rozwia
ι
za´n do konkretnego modelu.
2.5
Niejednorodne r´
ownanie falowe. Generacja fal E-M.
W poprzednich rozdziaÃlach rozwa˙zali´smy liniowe r´ownanie falowe. W tym rozdziale
zajmiemy sie
ι
niejednorodnym (nieliniowym) r´ownaniem falowym, tj. w og´olnym przy-
padku gdy f 6= 0:
¤u(t, r) = f (t, r)
Rozwa˙zmy r´ownanie Poissona:
4u(t, r) = f (t, r)
(2.5.1)
w kt´orym r = (x, y, z) ∈ R
3
. W elektrostatyce f przyjmuje posta´c: f = 4πρ, gdy˙z:
divE = div(gradϕ) = 4πρ, przy czym ρ = ρ(t, ~r) jest ge
ι
sto´scia
ι
Ãladunku. ZakÃladamy
jednak, ˙ze Ãladunki sa
ι
staÃle w czasie, czyli: f (t, r) = f (r). Naste
ι
pnie chcemy wykaza´c,
i˙z rozwia
ι
zanie r´ownania falowego mo˙zna wyrazi´c za pomoca
ι
funkcji Greena G. Dla
fal poruszaja
ι
cych sie
ι
w trzech wymiarach, przy uwzgle
ι
dnieniu warunk´ow brzegowych
oraz funkcji u = u(~r) be
ι
da
ι
cej potencjaÃlem pochodza
ι
cym od Ãladunku, opisywanego
przez funkcje
ι
f , mamy:
u(~r) =
Z
V
G(~r, ~r
0
)f (~r
0
)d~r
0
gdzie d~r
0
= dx
0
dy
0
dz
0
. Funkcje
ι
Greena (w trzech wymiarach) definiujemy analogicznie:
¤G(~r − ~r
0
) = δ(~r − ~r
0
)δ(t − t
0
)
(2.5.2)
co inaczej mo˙zemy zapisa´c jako:
∂
2
G
∂x
2
+
∂
2
G
∂y
2
+
∂
2
G
∂z
2
−
1
c
2
∂
2
G
∂t
2
= δ(x − x
0
)δ(y − y
0
)δ(z − z
0
)δ(t − t
0
)
Wprowad´zmy oznaczenie dla |~r − ~r
0
| = R.
Funkcje
ι
G rozpatrzmy we wsp´oÃlrze
ι
dnych sferycznych. Operator 4 be
ι
dzie skÃladaÃl sie
ι

26
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
z naste
ι
puja
ι
cych czÃlon´ow:
4
R
=
1
R
2
∂
∂R
µ
R
2
∂
∂R
¶
(2.5.3a)
4
ϕ
=
1
R
2
1
sinϕ
∂
∂ϕ
µ
sinϕ
∂
∂ϕ
¶
(2.5.3b)
4
ϑ
=
1
R
2
1
sin
2
ϑ
∂
2
∂ϑ
2
(2.5.3c)
Stosuja
ι
c powy˙zszy zapis otrzymujemy:
4
R
G(R) = δ(R)
(2.5.4)
ZwÃlasno´sci funkcji Greena oraz z wÃlasno´sci funkcji δ-Diraca wiadomo, ˙ze
R
drδ(~r − ~r
0
) =
R
dRδ(R) = 1, caÃlkuja
ι
c to po powierzchni kuli o promieniu R, otrzymujemy:
Z
R
0
µ Z
π
0
µ Z
2π
0
4
R
G(R)R
2
cosϑdϑ
¶
dϕ
¶
dR = 1
(2.5.5)
Przy czym mo˙zemy zapisa´c:
R
2
4
R
G =
∂
∂R
R
2
∂G
∂R
co upro´sci caÃlke
ι
(2.5.4) do postaci:
4π
Z
R
0
dR
¡
R
2
4
r
G
¢
= 4πR
2
∂G
∂R
= 1
Po trywialnych przeksztaÃlceniach, otrzymujemy r´ownanie r´o˙zniczkowe:
dG
dR
=
1
4πR
2
kt´orego rozwia
ι
zanie przyjmuje posta´c:
G = −
1
4πR
(2.5.6)
Maja
ι
c posta´c funkcji Greena G, mo˙zemy ja
ι
naste
ι
pnie zastosowa´c do (2.5.3), pamie
ι
taja
ι
c
i˙z R = |~r − ~r
0
|
4
1
4πR
= δ(~r − ~r
0
)
(2.5.7)
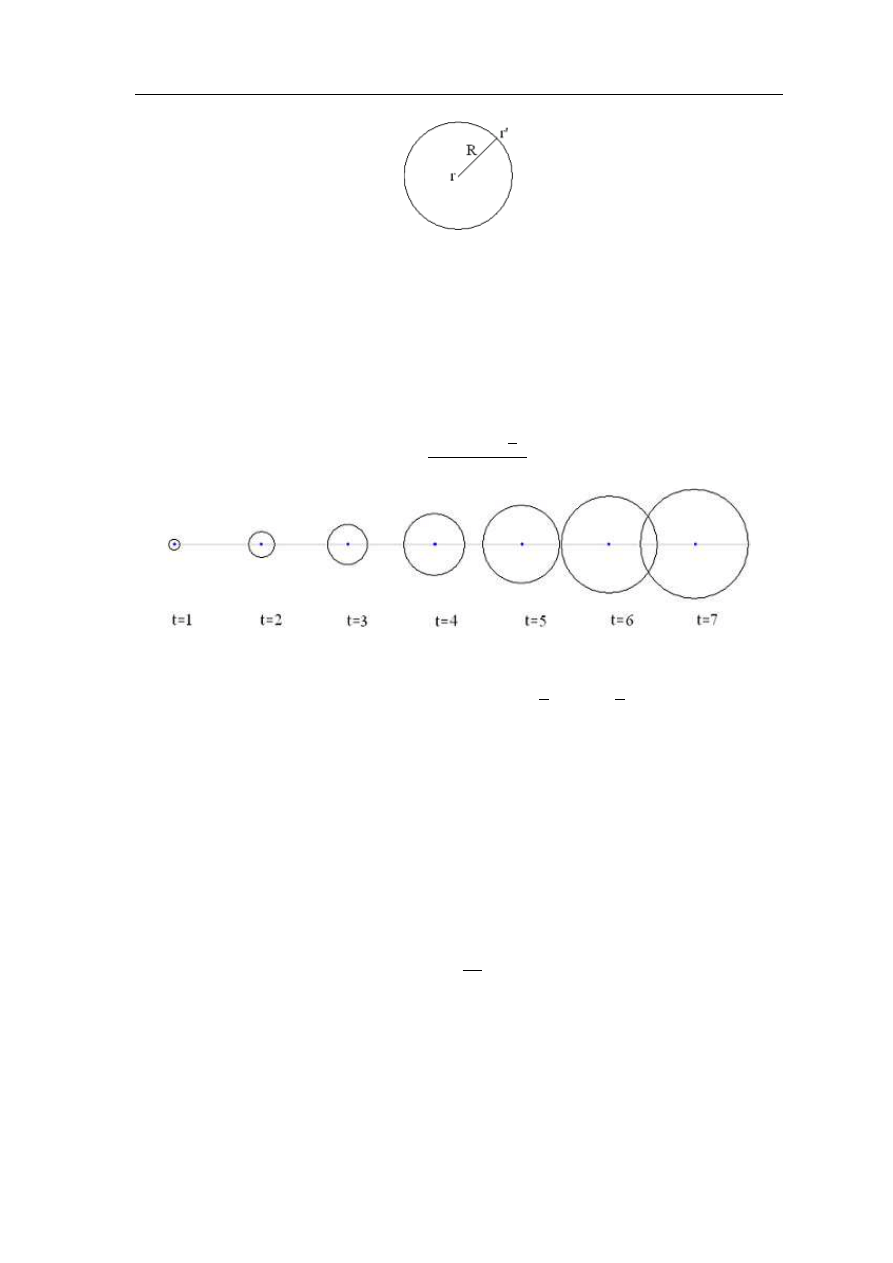
Omawiana przez nas fala eletromagnetyczna jest emitowana z punktu pocza
ι
tkowego
r. Rozchodzi sie
ι
ona w caÃlej przestrzeni z jednokowa
ι
pre
ι
dko´scia
ι
v tworza
ι
c kule
ι
o
promieniu R = |~r − ~r
0
|.
Gdy fala rozchodzi sie
ι
w pr´o˙zni, promie´n R mo˙zemy opisa´c r´ownie˙z zale˙zno´scia
ι
R = c
¡
t
0
− t
¢
, gdzie
¡
t
0
− t
¢
to czas, w kt´orym fala pokonuje dystans R =
¡
r
0
− r
¢
.
Schematycznie mo˙zna to przedstawi´c:
2.6. Promieniowanie fal elektromagnetycznych. Przybli˙zenie dipolowe.
27
Rozpatrywany przez nas przypadek, mo˙zna rozsze˙zy´c na peÃlne r´ownanie falowe (ana-
logicznie jak wy˙zej):
Z
δ
¡
~r
0
− ~r
¢
d~r
0
= 1
(2.5.8)
4u =
Z
¡
4G
¢
f dr = f
4G = δ
¡
~r − ~r
0
¢
¤G = δ
¡
~r − ~r
0
¢
δ
¡
t − t
0
¢
(2.5.9)
G =
δ
¡
t − t
0
−
R
c
¢
4πR
(2.5.10)
Powy˙zszy schemat przedstawia rozwia
ι
zanie funkcji Greena dla fali kulistej (prze-
dziaÃly czasowe t
i
sa
ι
r´owne). Cecha
ι
tej fali, wyra˙zonej (2.5.9) jest to, i˙z pokonuje ona
odlegÃlo´s´c |r − r
0
| w ´sci´sle okre´slonym czasie t
0
= t +
R
c
. CzÃlon
R
c
odpowiedzialny jest
r´ownie˙z za wzrost op´o´znienia propagacji fali kulistej. [ Fale
ι
kulista
ι
mo˙zemy zaob-
serwowa´c, detonuja
ι
c na pewnej wysoko´sci Ãladunek wybuchowy a naste
ι
pnie mierza
ι
c
rozchodzenie sie
ι
fali uderzeniowej ]
2.6
Promieniowanie fal elektromagnetycznych. Przybli˙zenie
dipolowe.
Nie ka˙zdy Ãladunek promieniuje.
¤ ~
A = −
4π
c
~j
(2.6.1a)
¤ϕ = −4πρ
(2.6.1b)
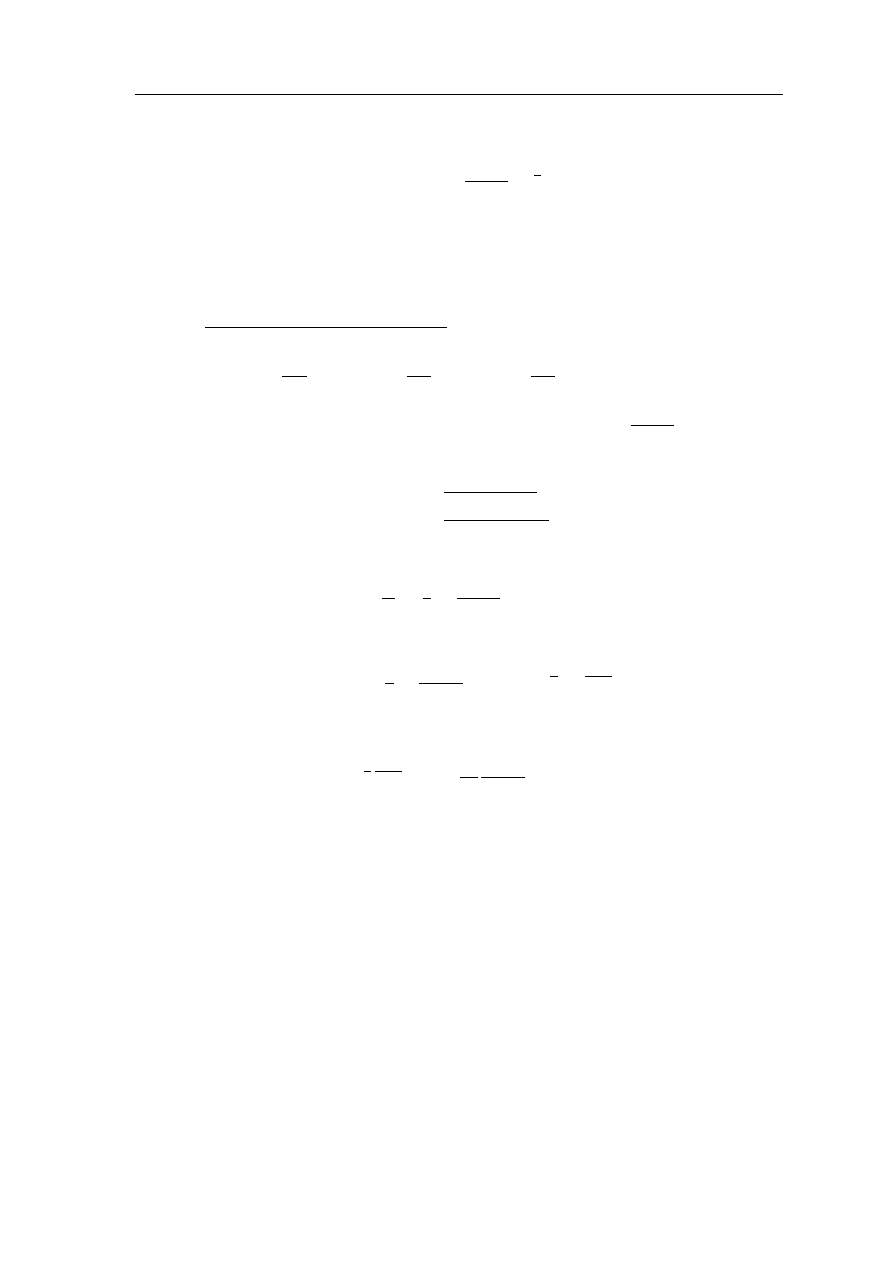
28
RozdziaÃl 2. Podstawowe poje
ι
cia elektrodynamiki
˙Zeby nie caÃlkowa´c wielokrotnie, stosujemy funkcje
ι
Greena:
ϕ(t, ~r) = e
iωt
Z
ρ
0
(~r
0
)
R
e
−i
ω
c
R
d~r
0
(2.6.2)
przy czym punkt R jest punktem obserwacji danym naste
ι
puja
ι
co:
R = |~r − ~r
0
| ¿ R
0
(2.6.3)
Rozwi´nmy R w szereg Taylorowski:
R =
p
(x − x
0
)
2
+ (y − y
0
)
2
+ (z − z
0
)
2
=
= r +
∂R
∂x
0
|
r
0
=0
(−x
0
) +
∂R
∂y
0
|
r
0
=0
(−y
0
) +
∂R
∂z
0
|
r
0
=0
(−z
0
) + . . . =
= r −
(~r, ~r
0
)
r
+ . . . (2.6.4)
gdzie:
r =
p
x
2
+ y
2
+ z
2
(2.6.5a)
r
0
=
p
x
0
2
+ y
0
2
+ z
0
2
(2.6.5b)
oraz odwrotno´s´c R:
1
R
=
1
r
+
(~r, ~r
0
)
r
3
+ ...
(2.6.6)
Uzyskane rozwinie
ι
cia stosuje
ι
do (2.6.2).
ϕ(t, ~r) = e
iωt
Z ·
1
r
+
(~r, ~r
0
)
r
3
+ ...
¸
ρ
0
e
−i
ω
c
£
r−
(~
r,~
r
0
)
r
+...
¤
d~r
0
(2.6.7)
W powy˙zszym r´ownaniu skorzystajmy z rozwinie
ι
cia funkcji e
x
w szereg:
e
i
ω
c
(~
r,~
r0)
r
≈ 1 +
iω
c
(~r, ~r
0
)
r
+ . . .
(2.6.8)
Wyszukiwarka
Podobne podstrony:
9) Powinowactwo elektronowe id Nieznany (2)
Indukcja elektromagnetyczna id Nieznany
Opracowanie egamin elektro id 3 Nieznany
Dysocjacja elektrolityczna id 1 Nieznany
GOSPODARKA ELEKTRONICZNA(1) id Nieznany
Oscyloskop elektroniczny 3 id 3 Nieznany
9) Powinowactwo elektronowe id Nieznany (2)
Echo elektroniczne id 149974 Nieznany
Fizyka Prad elektryczny test id Nieznany
33 Schemat elektryczny FM445 id Nieznany (2)
Mikroskopia elektronowa id 3018 Nieznany
elektro 3 id 157863 Nieznany
elektra 4 id 157704 Nieznany
5 Pole elektrostatyczne id 397 Nieznany
ELEKTRON przykladowe pytania id Nieznany
elektrae1 id 157847 Nieznany
FALE ELEKTROMAGNETYCZNE id 1677 Nieznany
więcej podobnych podstron