1. PODSTAWOWE POJ

ĉCIA OBWODU

Teoria obwodów stanowi jedn

ą z dziedzin elektrotechniki zajmującą siĊ stroną teoretyczną

zjawisk wyst

Ċpujących w obwodach elektrycznych, w tym metodami analizy rozpáywu prądów i

rozk

áadu napiĊü w obwodzie w stanie ustalonym i nieustalonym. Przyjmuje siĊ, Īe noĞnikami

elektryczno

Ğci są cząstki elementarne: elektrony i protony wystĊpujące w atomie. W przypadku

przewodników elektrycznych najwa

Īniejszą rolĊ odgrywają elektrony swobodne, stanowiące

trwa

áe noĞniki ujemnego áadunku q, wyzwolone z przyciągania jądra atomu oraz jony ,

stanowi

ące cząsteczki naáadowane dodatnio lub ujemnie. àadunek elektryczny elektronu,

oznaczany jest liter

ą e a jego wartoĞü e=1,602

⋅ 10

-19

C.

Pr

ąd elektryczny powstaje jako uporządkowany ruch áadunków elektrycznych i jest utoĪsamiany

w teorii obwodów z poj

Ċciem natĊĪenia prądu elektrycznego. W ogólnoĞci definiowany jest jako

granica stosunku

áadunku elektrycznego przepáywającego przez przekrój poprzeczny elementu do

rozpatrywanego czasu, gdy czas ten d

ąĪy do zera. Prąd elektryczny oznaczany bĊdzie literą i

(du

Īą lub maáą). Jest wielkoĞcią skalarną a jej jednostką w ukáadzie SI jest amper (A).

Ka

Īdemu punktowi w Ğrodowisku przewodzącym prąd elektryczny moĪna przyporządkowaü

pewien potencja

á mierzony wzglĊdem punktu odniesienia. RóĪnica potencjaáów miĊdzy dwoma

punktami tego

Ğrodowiska nazywana jest napiĊciem elektrycznym. Jednostką napiĊcia

elektrycznego jest volt (V).

2. ELEMENTY OBWODU ELEKTRYCZNEGO

Za obwód elektryczny uwa

Īaü bĊdziemy takie poáączenie elementów ze sobą, Īe istnieje

mo

ĪliwoĞü przepáywu prądu w tym poáączeniu. Obwód jest odwzorowywany poprzez swój

schemat, na którym zaznaczone s

ą symbole graficzne elementów oraz sposób ich poáączenia ze

sob

ą, tworzący okreĞloną strukturĊ.

Na struktur

Ċ obwodu elektrycznego poza elementami skáadają siĊ równieĪ gaáĊzie, wĊzáy i oczka.

Ga

áąĨ obwodu jest tworzona przez jeden lub kilka elementów poáączonych ze sobą w okreĞlony

sposób. W

Ċzáem obwodu jest zacisk bĊdący koĔcówką gaáĊzi do którego moĪna doáączyü

nast

Ċpną gaáąĨ lub kilka gaáĊzi. GaáąĨ obwodu tworzą elementy ograniczone dwoma wĊzáami.

Oczko obwodu to zbiór ga

áĊzi poáączonych ze sobą i tworzących drogĊ zamkniĊtą dla prądu

elektrycznego. Oczko ma t

Ċ wáaĞciwoĞü, Īe po usuniĊciu dowolnej gaáĊzi ze zbioru pozostaáe

ga

áĊzie nie tworzą drogi zamkniĊtej. W obwodzie o zadanej strukturze istnieje ĞciĞle okreĞlona

liczba w

Ċzáów, natomiast liczba oczek jest wprawdzie skoĔczona ale bliĪej nieokreĞlona.

Element jest cz

ĊĞcią skáadową obwodu niepodzielną pod wzglĊdem funkcjonalnym bez utraty

swych cech charakterystycznych. Na elementy obwodu sk

áadają siĊ Ĩródáa energii elektrycznej

oraz elementy akumuluj

ące energiĊ lub rozpraszające ją. W kaĪdym elemencie mogą zachodziü

dwa lub nawet wszystkie trzy wymienione tu procesy, cho

ü jeden z nich jest zwykle dominujący.

Element jest idealny je

Ğli charakteryzuje go tylko jeden rodzaj procesu energetycznego.

Elementy posiadaj

ące zdolnoĞü akumulacji oraz rozpraszania energii tworzą klasĊ elementów

pasywnych. Nie wytwarzaj

ą one energii a jedynie ją przetwarzają. NajwaĪniejsze z nich to

rezystor, kondensator oraz cewka. Elementy maj

ące zdolnoĞü generacji energii nazywane są

Ĩródáami. Zaliczamy do nich niezaleĪne Ĩródáo napiĊcia i prądu oraz Ĩródáa sterowane.

Ka

Īdy element obwodu moĪe byü opisany równaniami algebraicznymi lub róĪniczkowymi,

wi

ąĪącymi prąd i napiĊcie na jego zaciskach. Element jest liniowy, jeĞli równanie opisujące go

jest liniowe. W przeciwnym wypadku element jest nieliniowy.

Rezystor, zwany równie

Ī opornikiem naleĪy do klasy elementów pasywnych rozpraszających

energi

Ċ. W teorii obwodów rezystor uwaĪa siĊ za element idealny i przypisuje mu tylko jedną

cech

Ċ (parametr), zwaną rezystancją lub oporem. W dalszej czĊĞci rozwaĪaü bĊdziemy

wy

áącznie rezystor liniowy. RezystancjĊ (opornoĞü) oznaczaü bĊdziemy literą R a jej odwrotnoĞü

jest nazywana konduktancj

ą i oznaczana literą G, przy czym R=1/G. Symbol graficzny rezystora

liniowego przedstawiony jest na rys. 1.1.

Opis matematyczny rezystora wynika z prawa Ohma, zgodnie z którym

(2.1) Rezystor

Rys. 1.1 Oznaczenie rezystora liniowego

Spadek napi

Ċcia na rezystorze liniowym jest proporcjonalny do prądu przepáywającego przez

niego a wspó

áczynnik proporcjonalnoĞci jest równy rezystancji R. WartoĞü rezystancji rezystora

liniowego przyjmuje warto

Ğü staáą. Jednostką rezystancji jest om (Ω ) a konduktancji siemens (S).

W realizacji praktycznej opornik jest wykonywany najcz

ĊĞciej z drutu metalowego o dáugoĞci l,

polu przekroju poprzecznego S i rezystancji w

áaĞciwej r. Rezystancja takiego opornika jest

wprost proporcjonalna do l i ρ a odwrotnie proporcjonalna do S, R=ρl/S.

Cewka zwana równie

Ī induktorem naleĪy równieĪ do klasy elementów pasywnych. Ma zdolnoĞü

gromadzenia energii w polu magnetycznym. Cewce idealnej przypisuje si

Ċ tylko jedną

w

áaĞciwoĞü, zwaną indukcyjnoĞcią wáasną (w skrócie indukcyjnoĞcią) L. W przypadku cewki

liniowej indukcyjno

Ğü definiuje siĊ jako stosunek strumienia Ψ skojarzonego z cewką do prądu

p

áynącego przez nią, to znaczy

Strumie

Ĕ skojarzony Ψ cewki o z zwojach jest równy sumie strumieni wszystkich zwojów cewki,

to jest

(φ - strumie

Ĕ skojarzony z jednym zwojem cewki, z - liczba zwojów). Jednostką

indukcyjno

Ğci jest henr (H), przy czym 1H=1Ω s. NapiĊcie cewki wyraĪone jest jako pochodna

strumienia wzgl

Ċdem czasu

W przypadku cewki liniowej, dla której strumie

Ĕ jest iloczynem prądu i indukcyjnoĞci L,

, relacja napi

Ċciowo-prądowa upraszcza siĊ do postaci

Na rys. 1.2 przedstawiono symbol graficzny cewki liniowej o indukcyjno

Ğci L.

Zauwa

Īmy, Īe przy staáej wartoĞci prądu cewki napiĊcie na niej jest równe zeru, gdyĪ pochodna

warto

Ğci staáej wzglĊdem czasu jest równa zeru. Stąd cewka w stanie ustalonym obwodu przy

(1.1)

(2.2) Cewka

(1.2)

(1.3)

(1.4)

Rys. 1.2 Symbol graficzny cewki liniowej

pr

ądzie staáym zachowuje siĊ jak zwarcie.

Interesuj

ące zjawiska powstają w ukáadzie dwu cewek poáoĪonych blisko siebie, w których

zachodzi wzajemne przenikanie si

Ċ strumieni magnetycznych. JeĞli dwie cewki o

indukcyjno

Ğciach wáasnych i

s

ą tak usytuowane, Īe strumieĔ wytworzony przez jedną z

nich jest skojarzony z drug

ą to takie cewki nazywamy sprzĊĪonymi magnetycznie. Na rys. 1.3

przedstawiono oznaczenie cewek sprz

ĊĪonych magnetycznie. Punktami oznaczono początki

uzwoje

Ĕ kaĪdej cewki.

Obok indukcyjno

Ğci wáasnej wprowadza siĊ dla nich pojĊcie indukcyjnoĞci wzajemnej M, jako

stosunek strumienia magnetycznego wytworzonego w cewce pierwszej i skojarzonego z cewk

ą

drug

ą do prądu páynącego w cewce pierwszej, a wiĊc

gdzie

oznacza strumie

Ĕ skojarzony z cewka drugą wytworzony przez prąd páynący w cewce

pierwszej. Jednostk

ą indukcyjnoĞci wzajemnej jest równieĪ henr.

Istnienie sprz

ĊĪenia magnetycznego powoduje indukowanie siĊ napiĊü na cewce wskutek zmian

pr

ądu páynącego w cewce drugiej. Zgodnie z prawem indukcji elektromagnetycznej napiĊcie

wytworzone na skutek indukcji wzajemnej okre

Ğlone jest wzorem

Znak plus lub minus wyst

Ċpujący we wzorze jest uzaleĪniony od przyjĊtego zwrotu prądu

wzgl

Ċdem początku uzwojenia cewki. Przyjmuje siĊ znak plus jeĞli prądy w obu elementach

sprz

ĊĪonych magnetycznie mają jednakowe zwroty wzglĊdem zacisków oznaczających początek

uzwojenia (oznaczone na rysunku gwiazdk

ą). Przy zwrotach przeciwnych przyjmuje siĊ znak

minus. Z zale

ĪnoĞci powyĪszych widaü, Īe w elementach sprzĊĪonych magnetycznie energia

elektryczna mo

Īe byü przekazywana z jednego elementu do drugiego za poĞrednictwem pola

magnetycznego. Co wi

Ċcej, nawet przy braku przepáywu prądu przez cewkĊ, moĪe na niej

Rys. 1.3 Oznaczenie cewek sprz

ĊĪonych magnetycznie

(1.5)

(1.6)

(1.7)

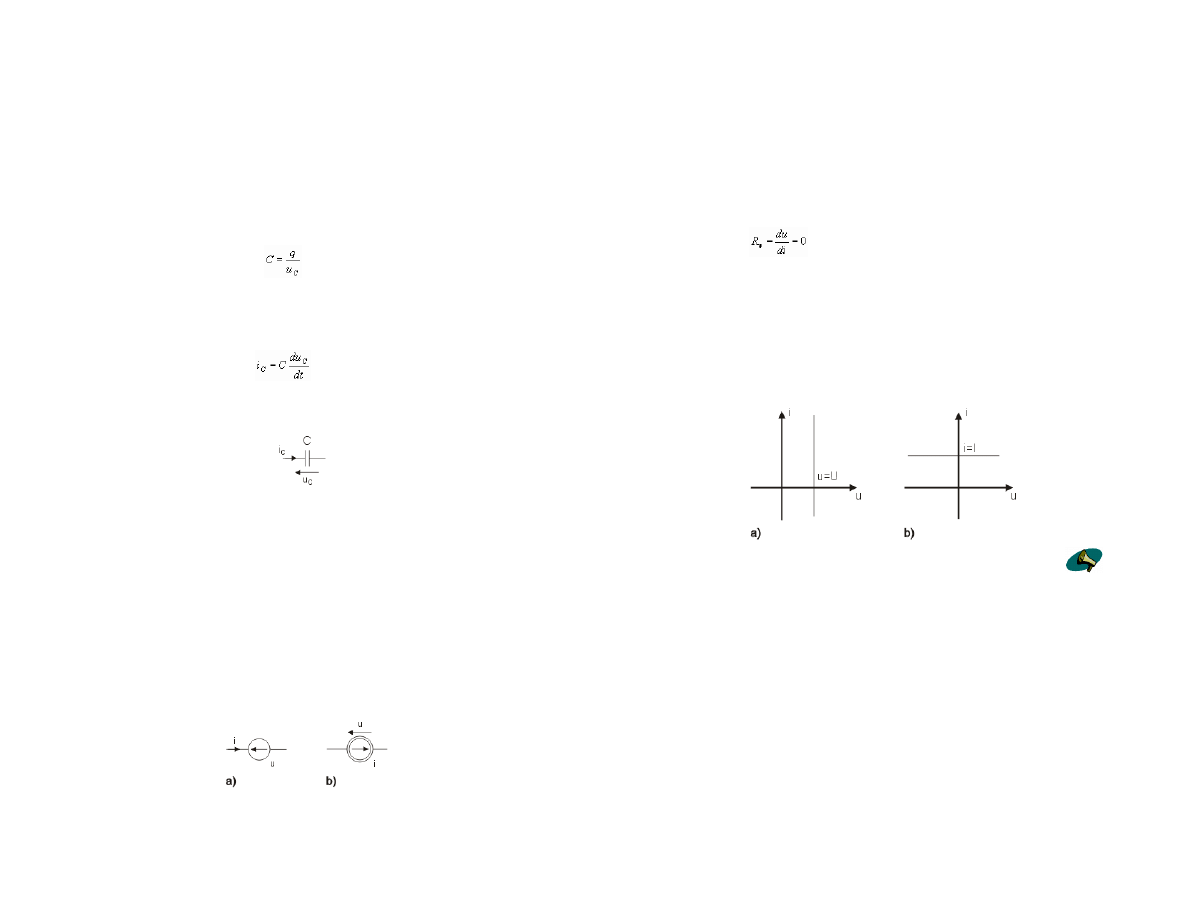
pojawi

ü siĊ napiĊcie pochodzące ze sprzĊĪenia magnetycznego od cewki drugiej.

Kondensator jest elementem pasywnym w którym istnieje mo

ĪliwoĞü gromadzenia energii w polu

elektrycznym. Kondensatorowi idealnemu przypisuje si

Ċ tylko jedną wáaĞciwoĞü zwaną

pojemno

Ğcią C. W przypadku kondensatora liniowego pojemnoĞü C jest definiowana jako

stosunek

áadunku q zgromadzonego w kondensatorze do napiĊcia miĊdzy okáadzinami tego

kondensatora

W uk

áadzie SI jednostką áadunku jest kulomb ( C ), a pojemnoĞci farad (F), przy czym 1 F=1

C/V. Zale

ĪnoĞü wiąĪąca napiĊcie i prąd kondensatora dana jest w postaci równania

ró

Īniczkowego

Symbol graficzny kondensatora przedstawiony jest na rys. 1.4.

Podobnie jak w przypadku cewki, je

Ğli napiĊcie na zaciskach kondensatora jest staáe, jego prąd

jest równy zeru (pochodna warto

Ğci staáej wzglĊdem czasu jest zerem). Kondensator zachowuje

si

Ċ wtedy jak przerwa (pomimo istnienia napiĊcia prąd nie páynie).

ħródáo niesterowane prądu bądĨ napiĊcia, zwane w skrócie Ĩródáem pradu i Ĩródáem napiĊcia,
jest elementem aktywnym, generuj

ącym energiĊ elektryczną, powstającą zwykle z zamiany

innego rodzaju energii, na przyk

áad z energii mechanicznej, sáonecznej, jądrowej itp. W teorii

obwodów rozwa

Īaü bĊdziemy Ĩródáa idealne naleĪące do klasy Ĩródeá napiĊciowych bądĨ

pr

ądowych. Symbol idealnego niesterowanego Ĩródáa napiĊcia przedstawiony jest na rys. 1.5a,

natomiast

Ĩródáa prądu na rys. 1.5.b.

(2.3) Kondensator

(1.8)

(1.9)

Rys. 1.4 Symbol graficzny kondensatora

(2.4) Niesterowane

ďródáo napiĊcia i pr±du

Niesterowane

Ĩródáa prądu i napiĊcia mają nastĊpujące wáaĞciwoĞci.

z

Napi

Ċcie na zaciskach idealnego Ĩródáa napiĊcia nie zaleĪy od prądu przepáywającego

przez to

Ĩródáo, a zatem nie zaleĪy od jego obciąĪenia.

z

Przy sta

áym napiĊciu u panującym na zaciskach oraz prądzie i wynikającym z obciąĪenia,

rezystancja wewn

Ċtrzna idealnego Ĩródáa napiĊciowego, definiowana w postaci zaleĪnoĞci

ró

Īniczkowej

. St

ąd idealne Ĩródáo napiĊcia charakteryzuje siĊ rezystancją

wewn

Ċtrzna równą zeru (zwarcie z punktu widzenia rezystancyjnego).

z

Pr

ąd idealnego Ĩródáa prądu nie zaleĪy od obciąĪenia tego Ĩródáa, a wiĊc od napiĊcia

panuj

ącego na jego zaciskach.

z

Przy sta

áym prądzie páynącym przez idealne Ĩródáo prądowe i dowolnym (bliĪej

nieokre

Ğlonym) napiĊciu panującym na jego zaciskach rezystancja wewnĊtrzna idealnego

Ĩródáa prądowego jest równa nieskoĔczonoĞci. Stąd idealne Ĩródáo prądowe z punktu
widzenia rezystancyjnego reprezentuje sob

ą przerwĊ.

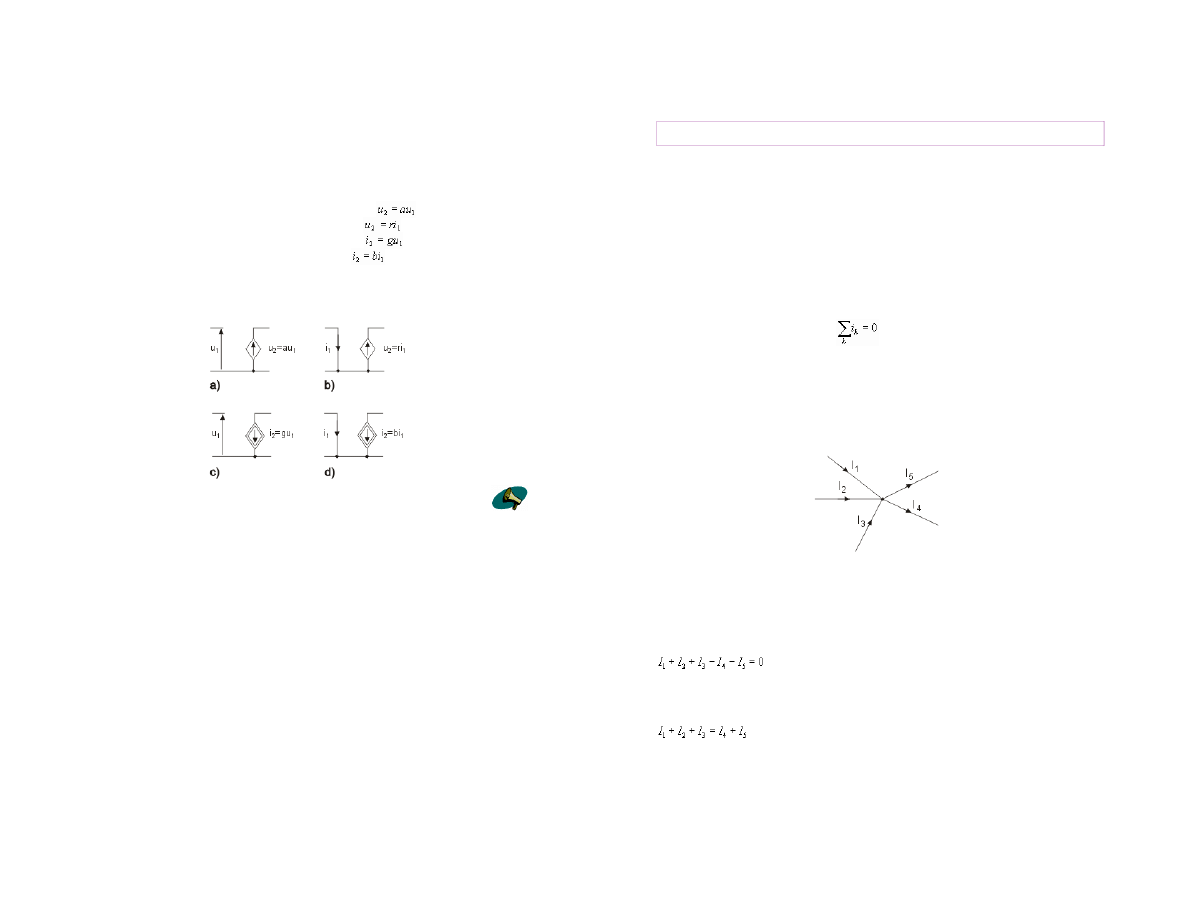
Rys. 1.6 przedstawia charakterystyki pr

ądowo-napiĊciowe obu rodzajów idealnych Ĩródeá

niesterowanych: napi

Ċcia (rys. 1.6a) i prądu (rys. 1.6b).

Dla

Ĩródáa napiĊciowego charakterystyka jest równolegáa do osi prądowej (wartoĞü napiĊcia u

sta

áa), a dla Ĩródáa prądowego równolegáa do osi napiĊciowej (wartoĞü prądu i staáa). Tak podane

charakterystyki odnosz

ą siĊ do Ĩródeá staáych. W przypadku Ĩródeá sinusoidalnych idealnoĞü jest

rozumiana jako sta

áoĞü parametrów Ĩródáa (amplituda, faza początkowa oraz czĊstotliwoĞü

niezale

Īna od obciąĪenia).

Przyk

áadami Ĩródáa napiĊcia staáego jest akumulator, Ĩródáa napiĊcia zmiennego - generator

synchroniczny,

Ĩródáa prądowego - elektroniczny zasilacz prądowy o stabilizowanym,

niezale

Īnym od obciąĪenia prądzie, itp.

W odró

Īnieniu od Ĩródeá niesterowanych, których prąd lub napiĊcie (bądĨ parametry

charakteryzuj

ące je, np. amplituda i czĊstotliwoĞü) byáy staáe, ustalone na etapie wytworzenia,

Rys. 1.5 Symbole graficzne niesterowanego

Ĩródáa a) napiĊcia, b) prądu

Rys. 1.6 Charakterystyki pr

ądowo-napiĊciowe idealnych Ĩródeá niesterowanych: a) Ĩródáo

napi

Ċcia, b) Ĩródáo prądu

(2.5) ¬ród

áa sterowane pr±du i napiĊcia

Ĩródáa sterowane z definicji zaleĪą od wielkoĞci sterujących, którymi mogą byü prąd lub
napi

Ċcie dowolnego innego elementu w obwodzie.

ħródáo sterowane jest wiĊc elementem czterozaciskowym i charakteryzuje siĊ tym, Īe napiĊcie
lub pr

ąd na jego zaciskach wyjĞciowych jest proporcjonalny do napiĊcia lub prądu związanego z

druga par

ą zacisków sterujących. WyróĪniü moĪna cztery rodzaje Ĩródeá sterowanych:

z

Ĩródáo napiĊcia sterowane napiĊciem, opisane równaniem

z

Ĩródáo napiĊcia sterowane prądem, opisane równaniem

z

Ĩródáo prądu sterowane napiĊciem, opisane równaniem

z

Ĩródáo prądu sterowane prądem, opisane równaniem

Schematy graficzne wszystkich wymienionych tu rodzajów

Ĩródeá sterowanych prądu i napiĊcia

przedstawione s

ą na rys. 1.7.

Wielko

Ğci r, g oraz a i b stanowią wspóáczynniki proporcjonalnoĞci miĊdzy wielkoĞcią sterującą i

sterowan

ą tych Ĩródeá. Przyjmują one najczĊĞciej wartoĞci rzeczywiste, choü w róĪnego rodzaju

modelach mog

ą byü równieĪ opisane funkcją zespoloną. NaleĪy nadmieniü, Īe Ĩródáa sterowane

stanowi

ą bardzo popularne modele wielu elementów elektrycznych i elektronicznych, takich jak

transformatory idelane, maszyny elektryczne, tranzystory bipolarne i polowe, wzmacniacze
operacyjne napi

Ċciowe i prądowe, itp.

Rys. 1.7 Schematy graficzne

Ĩródeá sterowanych

3. PRAWA KIRCHHOFFA

Pod poj

Ċciem analizy obwodu elektrycznego rozumie siĊ proces okreĞlania rozpáywu prądów i

rozk

áadu napiĊü w obwodzie przy zaáoĪeniu, Īe znana jest struktura obwodu oraz wartoĞci

wszystkich jego elementów. Podstaw

Ċ analizy obwodów elektrycznych stanowią prawa

Kirchhoffa, podane przez niemieckiego fizyka Gustawa Kirchhoffa w dziewi

Ċtnastym wieku.

Wyró

Īnia siĊ dwa prawa okreĞlające rozpáyw prądów i rozkáad napiĊü w obwodzie. Pierwsze

prawo Kirchhoffa kojarzy si

Ċ zwykle z bilansem prądów w wĊĨle obwodu elektrycznego a drugie

z bilansem napi

Ċü w oczku.

Suma pr

ądów w kaĪdym wĊĨle obwodu elektrycznego jest równa zeru

Sumowanie dotyczy wszystkich pr

ądów które dopáywają lub odpáywają z danego oczka, przy

czym wszystkie pr

ądy wpáywające do wĊzáa brane są z jednakowym znakiem a wszystkie prądy

wyp

áywające z wĊzáa ze znakiem przeciwnym (nie jest istotne czy znak plus dotyczy prądów

wp

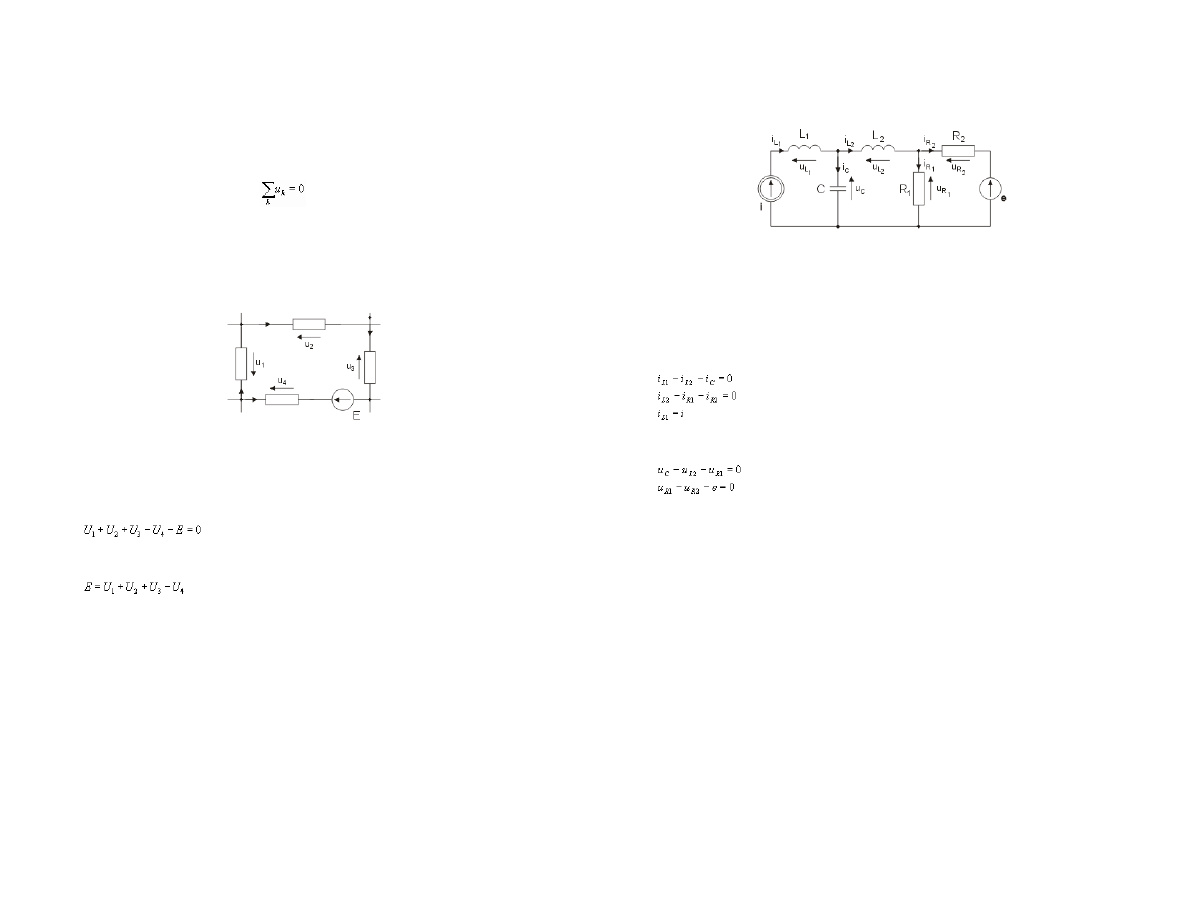
áywających czy wypáywających). Sposób tworzenia równania prądowego Kirchhoffa

zilustrujemy dla jednego w

Ċzáa obwodu przedstawionego na rys. 1.8

Prawo Kirchhoffa dla tego w

Ċzáa z uwzglĊdnieniem kierunków prądów w wĊĨle zapiszemy w

postaci

Mo

Īna je równieĪ zapisaü jako bilans prądów dopáywających i odpáywających od wĊzáa w

postaci

Dla ka

Īdego obwodu moĪna napisaü dokáadnie n-1 niezaleĪnych równaĔ prądowych, gdzie n

oznacza ca

ákowitą liczbĊ wĊzáów a (n-1) liczbĊ wĊzáów niezaleĪnych. Bilans prądów w

pozosta

áym n-tym wĊĨle obwodu wynika z równaĔ prądowych napisanych dla n-1 wĊzáów (jest to

w

Ċzeá zaleĪny zwany wĊzáem odniesienia). Wybór wĊzáa odniesienia jest caákowicie dowolny.

(3.1) Prawo pr±dowe

(1.10)

Rys. 1.8 Przyk

áad wĊzáa obwodu elektrycznego

Suma napi

Ċü w kaĪdym oczku obwodu elektrycznego jest równa zeru

Sumowanie dotyczy napi

Ċü gaáĊziowych wystĊpujących w danym oczku zorientowanych

wzgl

Ċdem dowolnie przyjĊtego kierunku odniesienia. NapiĊcie gaáĊziowe zgodne z tym

kierunkiem jest brane z plusem a przeciwne z minusem. Sposób pisania równa

Ĕ wynikających z

prawa napi

Ċciowego Kirchhoffa pokaĪemy na przykáadzie oczka obwodu przedstawionego na

rys. 1.9

Uwzgl

Ċdniając kierunki napiĊü gaáĊziowych równanie napiĊciowe Kirchhoffa dla tego oczka

przyjmie posta

ü

Mo

Īna je równieĪ zapisaü jako bilans napiĊü Ĩródáowych i odbiornikowych w postaci

Dla ka

Īdego obwodu moĪna napisaü tyle równaĔ oczkowych ile oczek wyodrĊbnimy w tym

obwodzie, przy czym cz

ĊĞü równaĔ oczkowych bĊdzie równaniami zaleĪnymi (wynikającymi z

liniowej kombinacji innych równa

Ĕ). Liczba równaĔ oczkowych branych pod uwagĊ w analizie

jest wi

Ċc równa liczbie oczek niezaleĪnych.

Napiszemy równania Kirchhoffa dla obwodu z rys. 1.8.

(3.2) Prawo napi

Ċciowe

(1.11)

Rys. 1.9 Przyk

áad oczka obwodu z oznaczeniami napiĊü gaáĊziowych

(3.3) Przyk

áad 1.1

Rozwi

ązanie

Zgodnie z prawami Kirchhoffa równania obwodu przyjm

ą nastĊpującą postaü.

Równania pr

ądowe:

Równania napi

Ċciowe:

Napisany tu uk

áad równaĔ jest wystarczający do uzyskania wszystkich innych wielkoĞci

pr

ądowych bądĨ napiĊciowych w obwodzie. NaleĪy go jedynie uzupeániü o równania definicyjne

wi

ąĪące prąd i napiĊcie kaĪdego elementu. Po takim uzupeánieniu uzyskuje siĊ peány opis

obwodu a jego rozwi

ązanie pozwala wyznaczyü rozpáyw prądów i rozkáad napiĊü w obwodzie.

Szczególnie proste zale

ĪnoĞci otrzymuje siĊ dla obwodu rezystancyjnego, zawierającego oprócz

Ĩródeá wymuszających jedynie rezystory oraz (ewentualnie) Ĩródáa sterowane o rzeczywistych
wspó

áczynnikach sterowania. Dla takich obwodów równania elementów rezystancyjnych są dane

w postaci zale

ĪnoĞci algebraicznych, które wstawione do równaĔ Kirchhoffa pozwalają utworzyü

uk

áad równaĔ algebraicznych o liczbie zmiennych równych liczbie równaĔ. Sposób tworzenia

takiego uk

áadu równaĔ pokaĪemy na przykáadzie obwodu z rys. 1.11.

Nale

Īy okreĞliü rozpáyw prądów i rozkáad napiĊü w obwodzie rezystancyjnym o strukturze

przedstawionej na rys. 1.11. Warto

Ğci elementów są nastĊpujące: R

1

=2Ω , R

2

=2Ω , R

3

=3Ω ,

R

4

=4Ω , e=10V, i

z1

=2A, i

z2

=5A.

Rys. 1.10 Schemat obwodu poddanego analizie w przyk

áadzie 1.1

(3.4) Przyk

áad 1.2

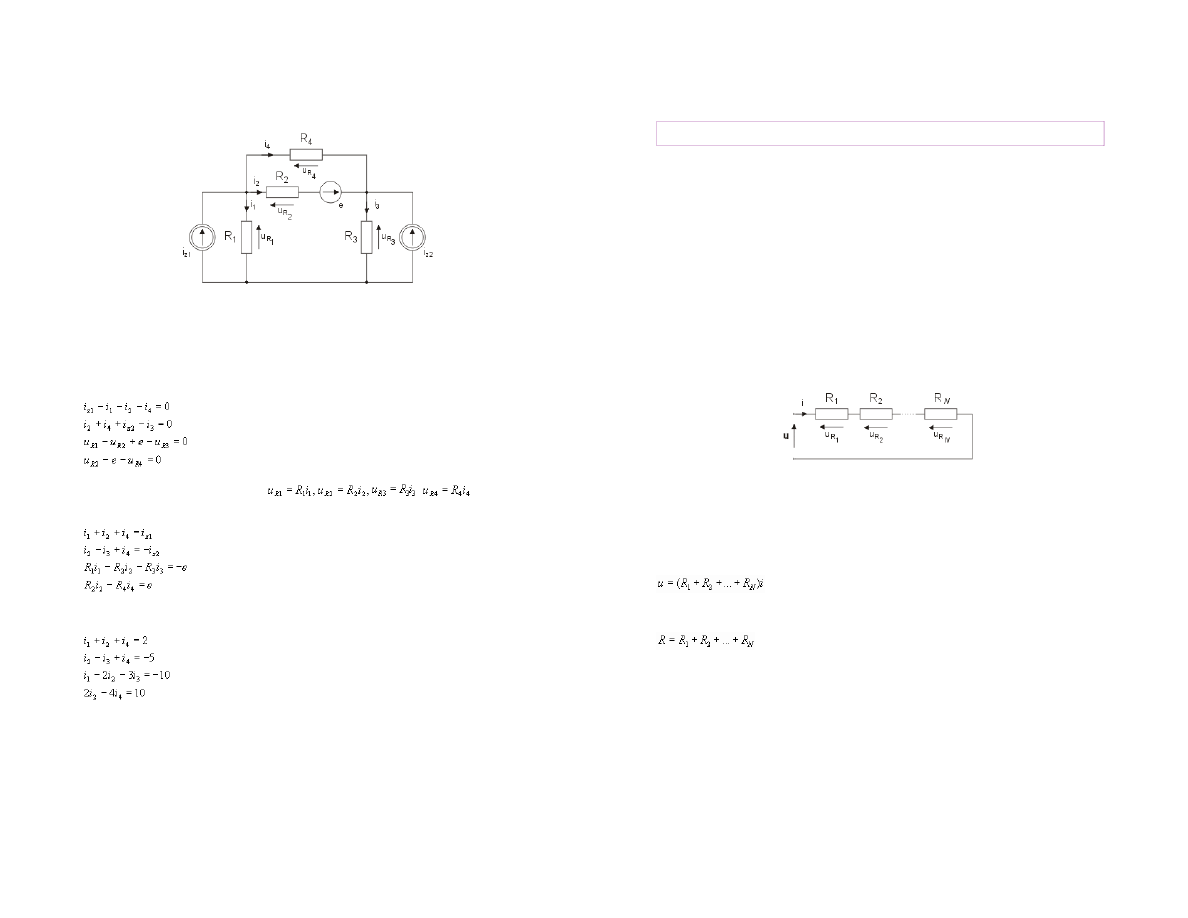
Rozwi

ązanie

Z równa

Ĕ Kirchhoffa otrzymuje siĊ

Równania elementów rezystancyjnych :

,

tworz

ą

wspólnie z równaniami Kirchhoffa nast

Ċpujący ukáad równaĔ algebraicznych:

Po wstawieniu danych liczbowych do powy

Īszych równaĔ otrzymuje siĊ:

W wyniku rozwi

ązania tego ukáadu równaĔ otrzymuje siĊ: i

1

=3,187A, i

2

=0,875A, i

3

=3,812A

oraz i

4

=-2,062A.

àatwo sprawdziü przez podstawienie obliczonych wartoĞci do ukáadu równaĔ Īe

bilans pr

ądów w kaĪdym wĊĨle oraz bilans napiĊü w kaĪdym oczku obwodu jest zerowy.

Rys. 1.11 Struktura obwodu poddanego analizie w przyk

áadzie 1.2

4. PRZEKSZTA

àCENIA OBWODÓW

W analizie obwodów elektrycznych wa

Īną rolĊ odgrywa upraszczanie struktury obwodu,

polegaj

ące na zastĊpowaniu wielu elementów poáączonych szeregowo lub równolegle poprzez

jeden element zast

Ċpczy. UmoĪliwia to zmniejszenie liczby równaĔ w opisie obwodu i

uproszczenie etapu rozwi

ązania tych równaĔ. WyróĪniü moĪna cztery podstawowe rodzaje

po

áączeĔ elementów, do których stosuje siĊ przeksztaácenie. Są to:

z

po

áączenie szeregowe

z

po

áączenie równolegáe

z

po

áączenie gwiazdowe

z

po

áączenie trójkątne.

W po

áączeniu szeregowym elementów koniec jednego elementu jest bezpoĞrednio poáączony z

pocz

ątkiem nastĊpnego. Rys. 1.12 przedstawia schemat ogólny poáączenia szeregowego

rezystorów.

Pr

ąd kaĪdego elementu obwodu jest jednakowy i równy i, natomiast napiĊcie na zaciskach

zewn

Ċtrznych obwodu jest równe sumie napiĊü poszczególnych elementów tworzących

po

áączenie. NapiĊciowe równanie Kirchhoffa dla obwodu z rys. 1.12 przyjmuje wiĊc postaü

Przy oznaczeniu sumy rezystancji przez R

otrzymuje si

Ċ transformacjĊ N rezystorów poáączonych szeregowo do jednego rezystora

zast

Ċpczego o rezystancji R opisanej wzorem (1.13). Rezystancja wypadkowa poáączenia

szeregowego rezystorów jest równa sumie rezystancji poszczególnych elementów tworz

ących to

po

áączenie.

W po

áączeniu równolegáym początki i koĔce wszystkich elementów są ze sobą bezpoĞrednio

po

áączone, jak to pokazano dla elementów rezystancyjnych na rys. 1.13.

(4.1) Uk

áad poá±czenia szeregowego elementów

Rys. 1.12 Po

áączenie szeregowe elementów

(4.2) Uk

áad poá±czenia równolegáego elementów

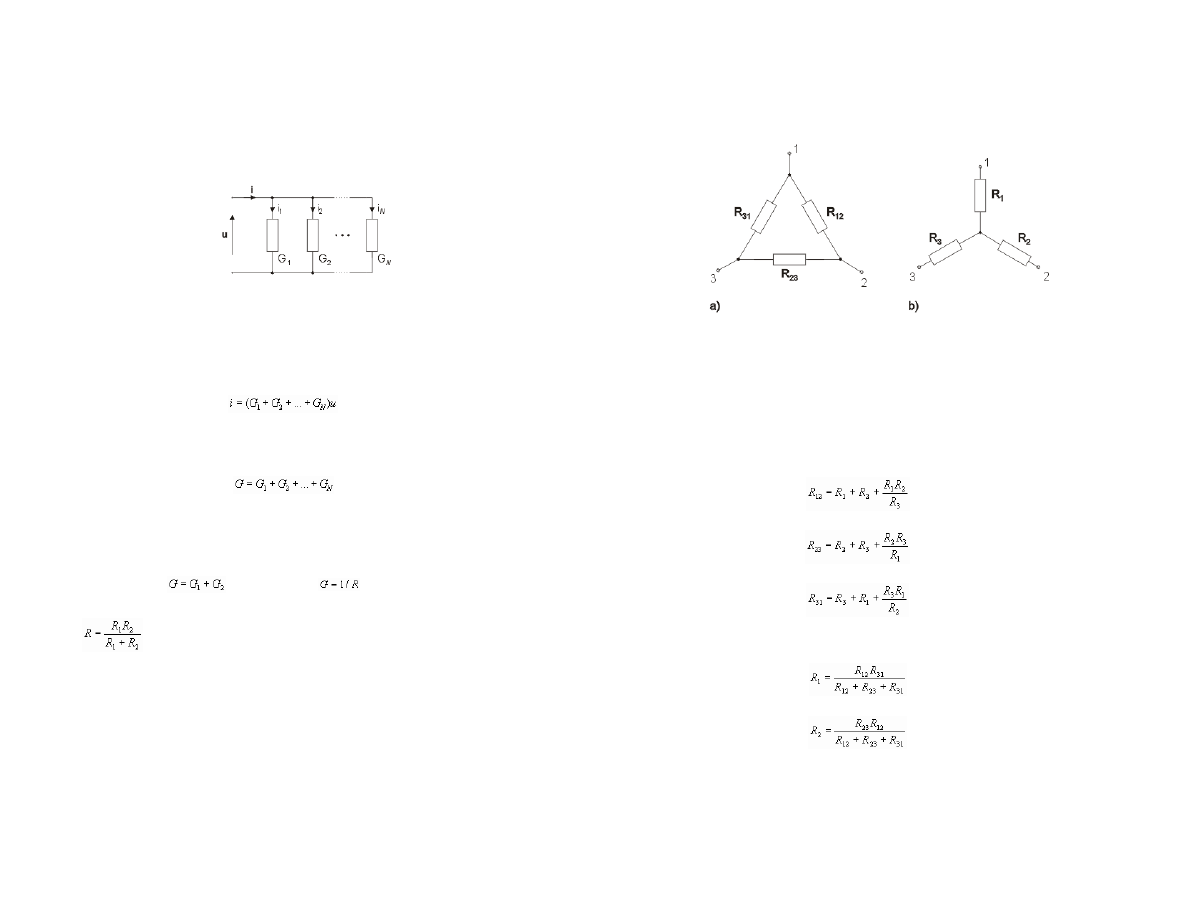
Z po

áączenia tego wynika Īe napiĊcie na wszystkich elementach jest jednakowe a prąd

wypadkowy jest równy sumie pr

ądów wszystkich elementów obwodu. Prądowe prawo

Kirchhoffa dla obwodu z rys. 1.13 mo

Īna wiĊc zapisaü w postaci

przy czym G

i

(i = 1, 2, ..., N) stanowi

ą konduktancje rezystorów, G

i

=1/R

i

. Przy oznaczeniu sumy

konduktancji przez G, gdzie

otrzymuje si

Ċ transformacjĊ N rezystorów poáączonych równolegle do jednego rezystora

zast

Ċpczego o konduktancji G opisanej wzorem (1.12). Jak widaü w poáączeniu równolegáym

rezystorów konduktancja wypadkowa jest równa sumie konduktancji poszczególnych rezystorów.

Szczególnie prosty jest wzór na rezystancj

Ċ zastĊpczą dla 2 rezystorów poáączonych równolegle.

W tym przypadku

. Uwzgl

Ċdniając, Īe

, po prostych przekszta

áceniach

otrzymuje si

Ċ

.

Nale

Īy jednak podkreĞliü tu, Īe przy trzech (i wiĊcej) elementach poáączonych równolegáe

wygodniejsze jest operowanie na konduktancjach a przej

Ğcie na rezystancjĊ zastĊpczą wykonuje

si

Ċ w ostatnim kroku po ustaleniu wartoĞci sumy konduktancji.

Operowanie uproszczonym schematem wynikaj

ącym z poáączenia szeregowego i równolegáego

elementów jest najwygodniejszym sposobem redukcji obwodu. W przypadku gdy nie ma
elementów po

áączonych szeregowo czy równolegle moĪliwe jest dalsze uproszczenie przez

zastosowanie przekszta

ácenia gwiazda-trójkąt lub trójkąt-gwiazda. Oznaczenia elementów

Rys. 1.13 Po

áączenie równolegáe elementów

(1.11)

(1.12)

(4.3) Transfiguracja gwiazda-trójk±t i trójk±t -gwiazda

obwodu trójk

ąta i gwiazdy są przedstawione na rys. 1.14.

Transfiguracja trójk

ąta na gwiazdĊ lub gwiazdy na trójkąt polega na przyporządkowaniu danej

konfiguracji elementów konfiguracji zast

Ċpczej, równowaĪnej jej z punktu widzenia zacisków

zewn

Ċtrznych (te same prądy przy tych samych napiĊciach miĊdzyzaciskowych). Dla uzyskania

niezmienionych pr

ądów zewnĊtrznych obwodu gwiazdy i trójkąta rezystancje miĊdzy parami

tych samych zacisków gwiazdy i trójk

ąta powinny byü takie same. Zostaáo udowodnione, Īe

warunki powy

Īsze są automatycznie speánione, jeĞli przy zamianie gwiazdy na trójkąt speánione

s

ą nastĊpujące warunki na rezystancje

Podobnie przy zamianie trójk

ąta na gwiazdĊ rezystancje gwiazdy muszą speániaü warunki

Rys. 1.14 Po

áączenie trójkątne i gwiazdowe elementów

(1.13)

(1.14)

(1.15)

(1.16)

(1.17)

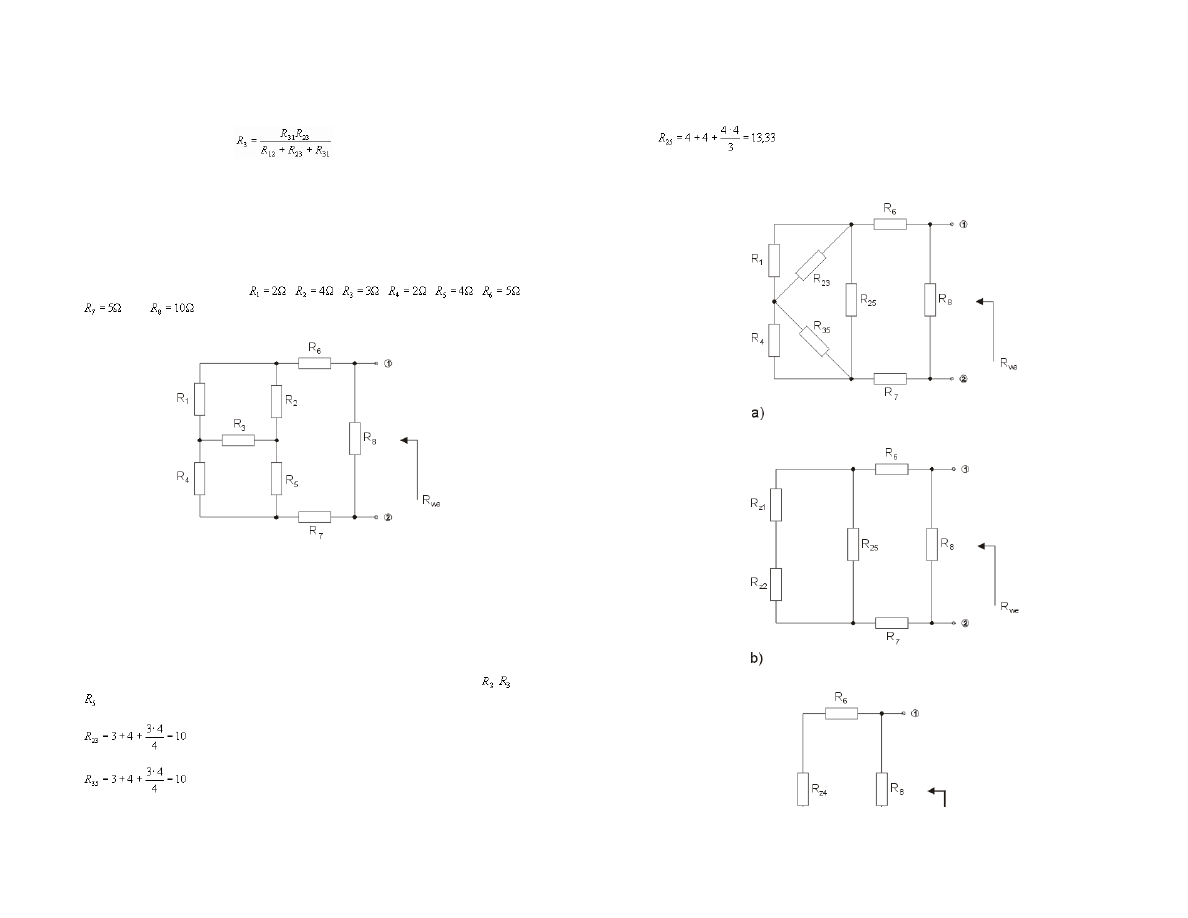
Przekszta

ácenia równowaĪne obwodu wykorzystujące reguáy poáączenia szeregowego,

równoleg

áego oraz przeksztaácenia gwiazda-trójkąt i trójkąt-gwiazda umoĪliwiają dalszą redukcjĊ

tego obwodu i po wykonaniu odpowiedniej liczby przekszta

áceĔ sprowadzenie go do

pojedynczego elementu zast

Ċpczego.

Okre

Ğliü rezystancjĊ zastĊpczą obwodu przedstawionego na rys. 1.15, widzianą z zacisków 1-2.

Warto

Ğci rezystancji są nastĊpujące:

,

,

,

,

,

,

oraz

.

Rozwi

ązanie

Z punktu widzenia zacisków wej

Ğciowych w obwodzie nie moĪna wyróĪniü Īadnego poáączenia

szeregowego czy równoleg

áego elementów. Dla uproszczenia struktury tego obwodu konieczne

jest wi

Ċc zastosowanie przeksztaácenia gwiazda-trójkąt lub trójkąt-gwiazda w stosunku do

rezystorów po

áoĪonych najdalej od wĊzáów wejĞciowych (w wyniku przeksztaácenia nie mogą

ulec likwidacji w

Ċzáy wejĞciowe obwodu). Zamieniając gwiazdĊ záoĪoną z rezystorów

,

i

na równowa

Īny jej trójkąt otrzymuje siĊ

(1.18)

(4.4) Przyk

áad 1.3

Rys. 1.15 Struktura obwodu do przyk

áadu 1.3

Schemat obwodu po przekszta

áceniach przedstawiony jest na rys. 1.16.

W obwodzie tym mo

Īna juĪ wyróĪniü poáączenia równolegáe elementów R

1

i R

23

oraz R

4

i R

35

.

Wykorzystuj

ąc reguáĊ upraszczania elementów poáączonych równolegle otrzymuje siĊ

Rezystory R

z1

i R

z2

s

ą poáączone szeregowo. Ich rezystancja zastĊpcza jest równa

R

z3

=R

z1

+R

z2

=3,333.

Jest ona po

áączona równolegle z rezystorem R

25

. St

ąd rezystancja zastĊpcza tego poáączenia

wynosi

.

Rezystory R

6

, R

z4

i R

7

s

ą poáączone szeregowo. Ich rezystancja zastĊpcza wynosi wiĊc

R

z5

=R

6

+R

z4

+R

7

=12,667Ω .

Rezystancja ta jest z kolei po

áączona równolegle z rezystancją R

8

tworz

ąc wypadkową

rezystancj

Ċ obwodu widzianą z zacisków zewnĊtrznych. Stąd caákowita rezystancja zastĊpcza

obwodu wyra

Īa siĊ wzorem

Jak wida

ü w powyĪszym przykáadzie przeksztaácenie gwiazda-trójkąt umoĪliwiáo dalsze

uproszczenie obwodu i otrzymanie ostatecznego wyniku na rezystancj

Ċ widzianą z zacisków

wej

Ğciowych. NaleĪy jednak zaznaczyü, Īe przeksztaácenia gwiazda-trójkąt i trójkąt-gwiazda są

bardziej z

áoĪone obliczeniowo w stosunku do reguáy upraszczania poáączenia szeregowego i

równoleg

áego. Stosuje siĊ je tylko wtedy gdy w obwodzie nie da siĊ wyróĪniü Īadnych poáączeĔ

Rys. 1.16 Schematy obwodu z rys. 1.15 po przekszta

áceniu gwiazda-trójkąt