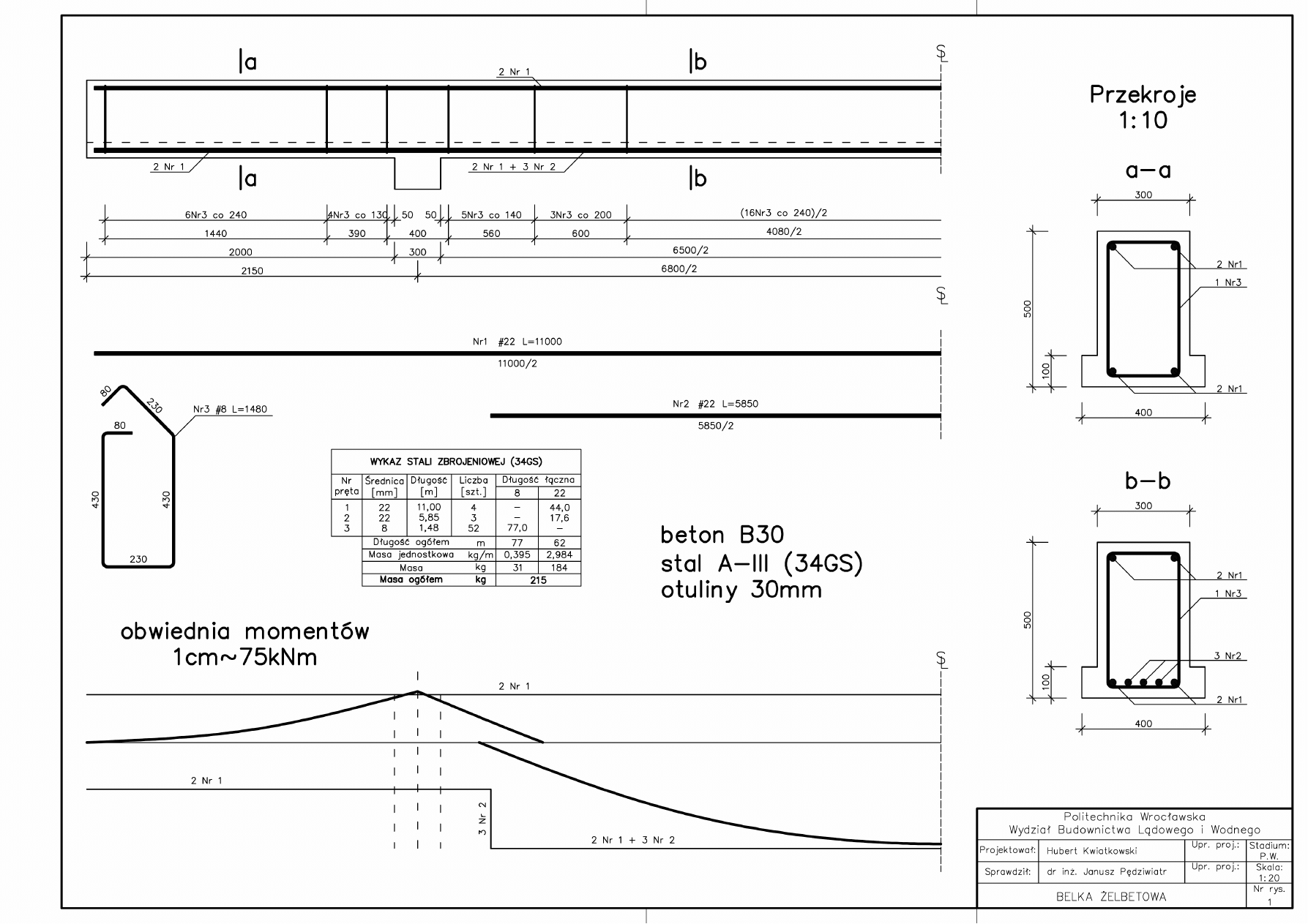
1. Belka żelbetowa

1.1 Wstępne przyjęcie przekroju belki

Obciążenia belki żelbetowej:

g

k

=

4,55 kPa⋅5 m=22,75 kN

m

q

k

=

3,00 kPa⋅5m=15,00 kN

m

Warianty obciążeń belki:

I:

1,05 q

k

+ 1,35 g

k

= 44,46

kN

m

II:

1,50 q

k

+ 1,15 g

k

= 48,66

kN

m

III

0,00 q

k

+ 1,00 g

k

= 22,75

kN

m

Przyjęcie długości obliczeniowych przęsła i wsporników:

l

eff 1

2,00 m0,15m=2,15m

l

eff

2

6,50 m2⋅0,15 m=6,80m

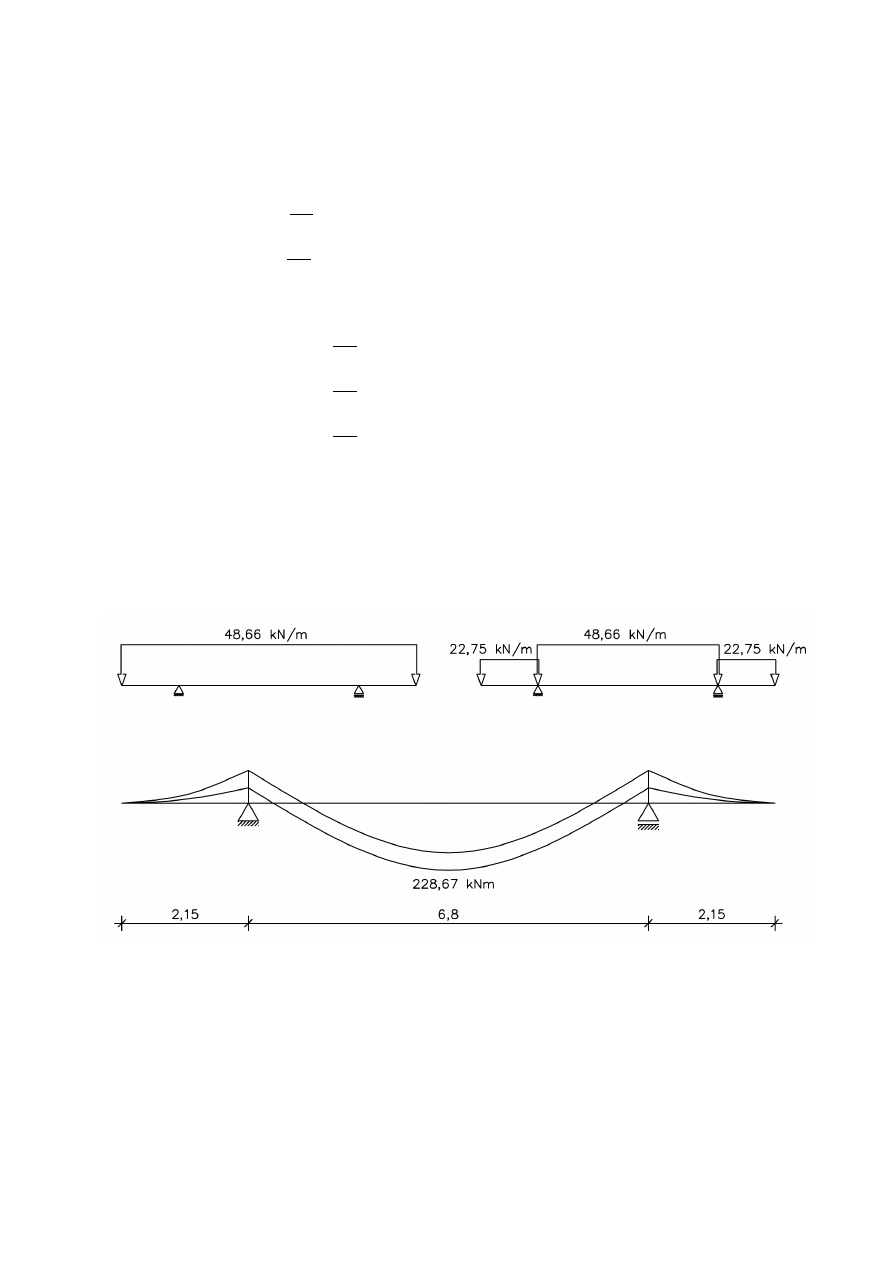
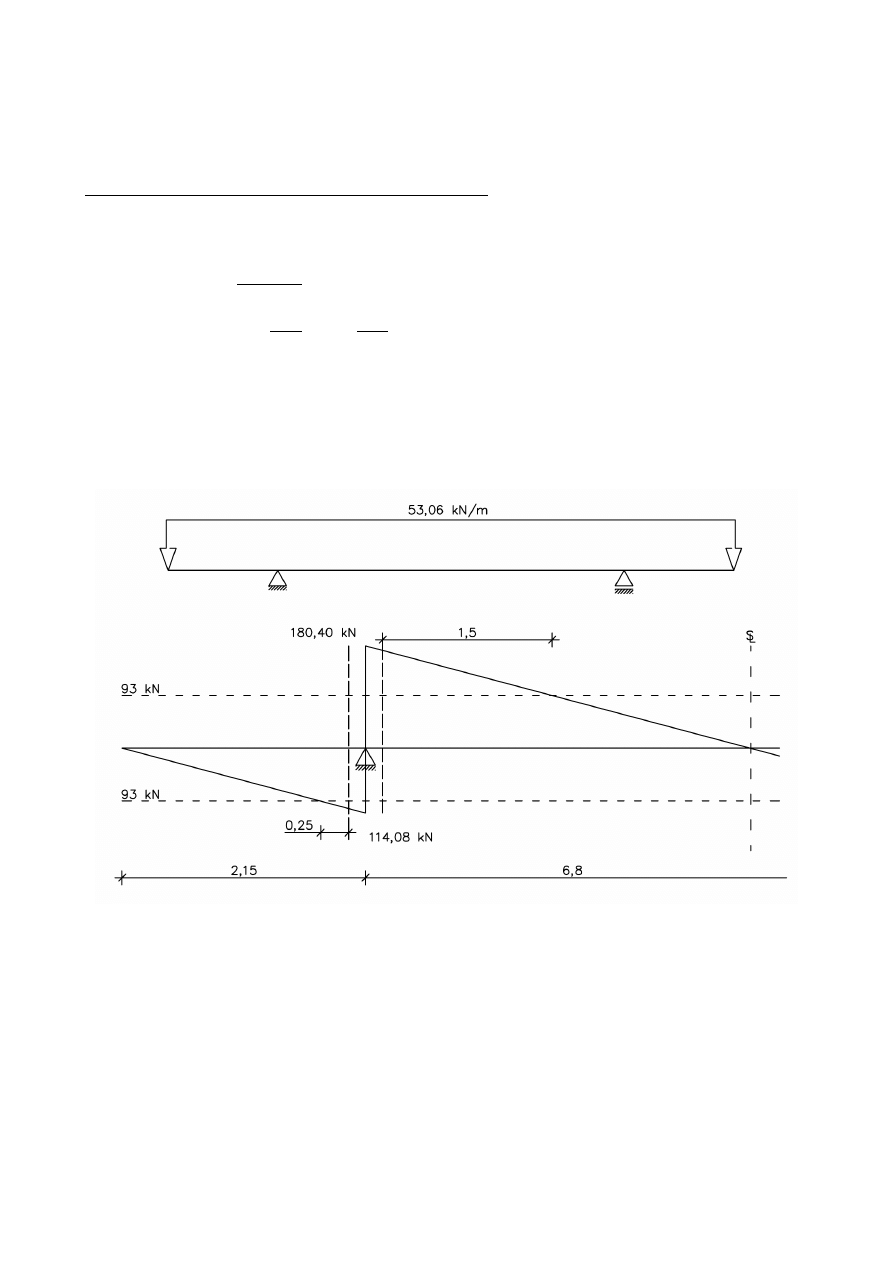
Obwiednia momentów gnących dla przyjęcia przekroju wstępnego:

1

Wstępne wymiary przekroju obliczamy dla momentu gnącego w przęśle (M

sd

= 228,67kN)

przyjmując:

Beton B30:

f

cd

=16,7 MPa

Stal zbrojeniowa A-III (34GS):

f

yd

=350 MPa

Stopień zbrojenia:

ρ=2,00%

, stąd: A=0,3318

Stosunek b

w

:d :

b

w

:d = 3:5

Stąd:

A=

M

sd

f

cd

⋅

b⋅d

2

=

M

sd

f

cd

⋅

0,6⋅d

3

⇒

d=

3



M

sd

f

cd

⋅

A⋅0,6

=

3



228,67

16,7⋅0,3318⋅0,6

=

0,41m

Ostatecznie przyjęto:
Wysokość obliczeniowa belki:

d = 0,45m

Wysokość całkowita belki:

h = 0,50m

Szerokość środnika:

b

w

= 0,30m

Szerokość półki:

b

eff

= 0,40m

Wysokość półki:

h

f

= 0,10m

Ciężar własny belki:



g

k

=

0,3⋅0,40,4⋅0,1⋅25=4 kN

m

Skorygowane warianty obciążeń:

I:

44,46 + 1,10·4 = 48,86

kN

m

II:

48,66 + 1,10·4 = 53,06

kN

m

III:

22,75 + 1,00·4 = 26,75

kN

m

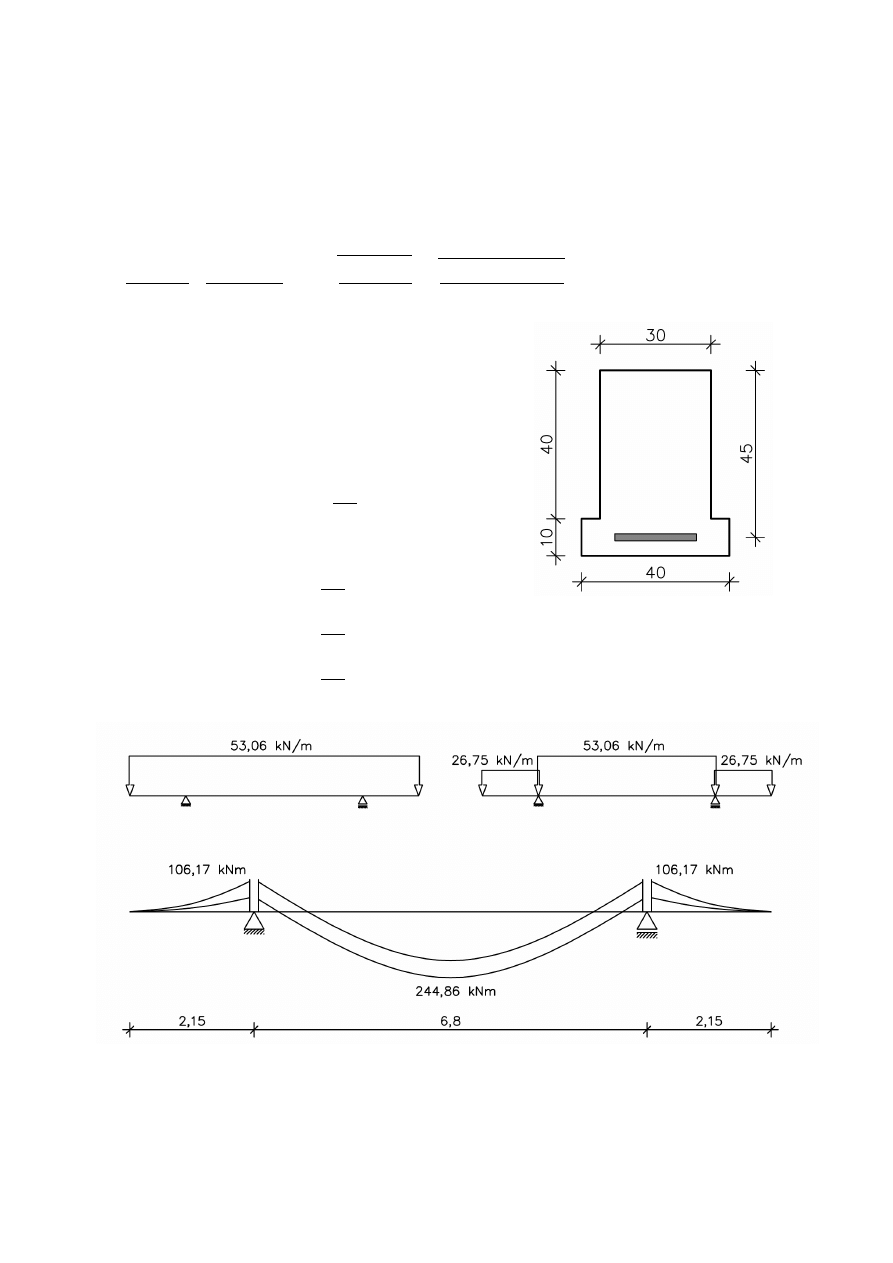
Obwiednia momentów gnących dla wymiarowania belki:

2

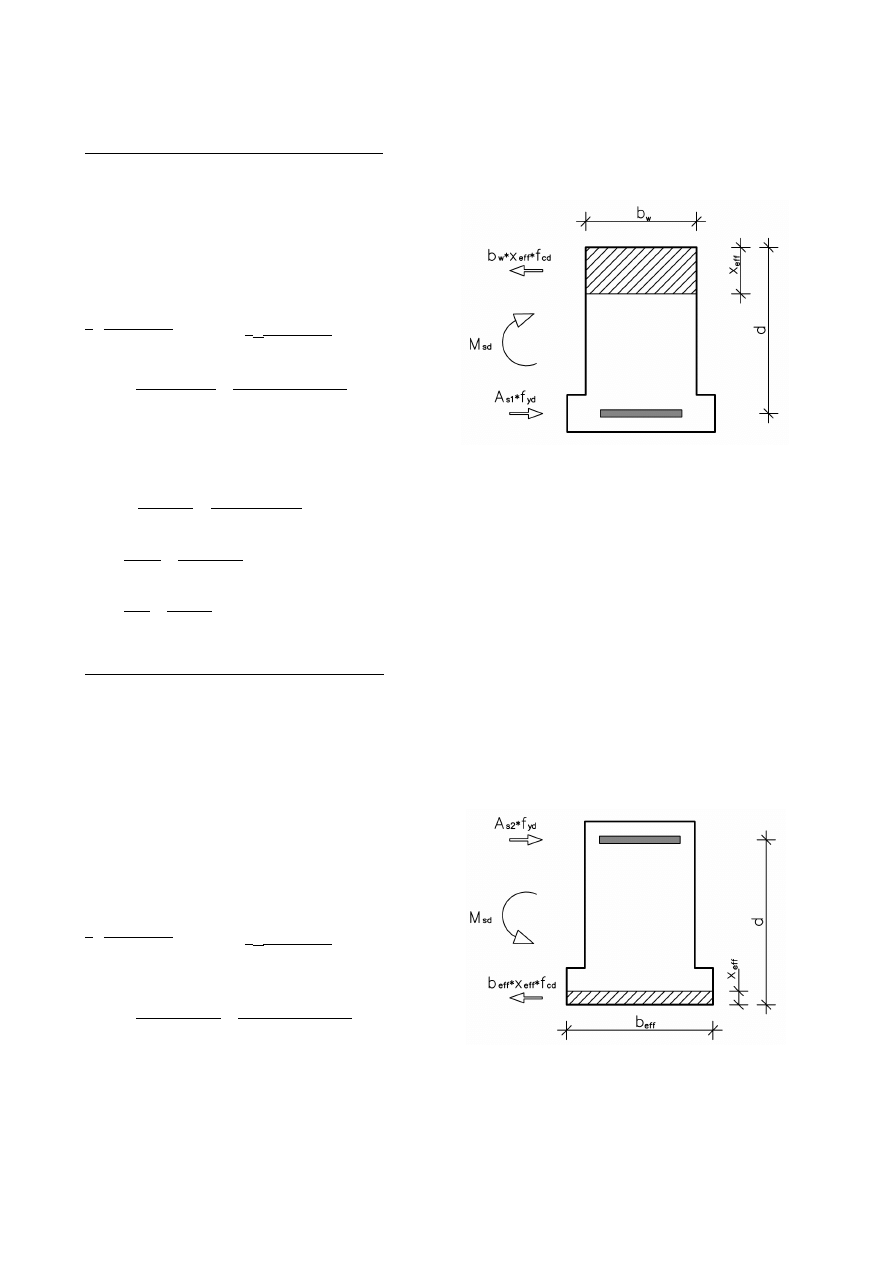
1.2 Wymiarowanie belki ze względu na zginanie

Wymiarowanie zbrojenia pasa dolnego

Przyjęto do obliczeń:

M

sd

=0,24486 MNm

M

sd

=

f

cd

⋅

b

w

⋅

x

eff

⋅

d−0,5⋅x

eff



0,24486=16,7⋅0,3⋅x

eff

⋅

0,45−0,5⋅x

eff



2,505⋅x

eff

2

−

2,2545⋅x

eff



0,24486=0

x

eff

=0,774m lub

x

eff

=0,126m

f

cd

⋅

b

w

⋅

x

eff

=

A

s1

⋅

f

yd

A

s1

=

f

cd

⋅

b

w

⋅

x

eff

f

yd

=

16,7⋅0,3⋅0,126

350

=

18,09cm

2

Przyjęto zbrojenie 2Ф22:

A

s1

=

5⋅1,1

2

⋅

3,14=19,00cm

2



18,04cm

2

x

eff

=

A

s1

⋅

f

yd

f

cd

⋅

b

w

=

0,0019⋅350

16,7⋅0,3

=

0,133m

=

A

s1

b

w

⋅

d

=

0,0019

0,3⋅0,45

=

1,41%

=

x

eff

d

=

0,133

0,45

=

0,300,53

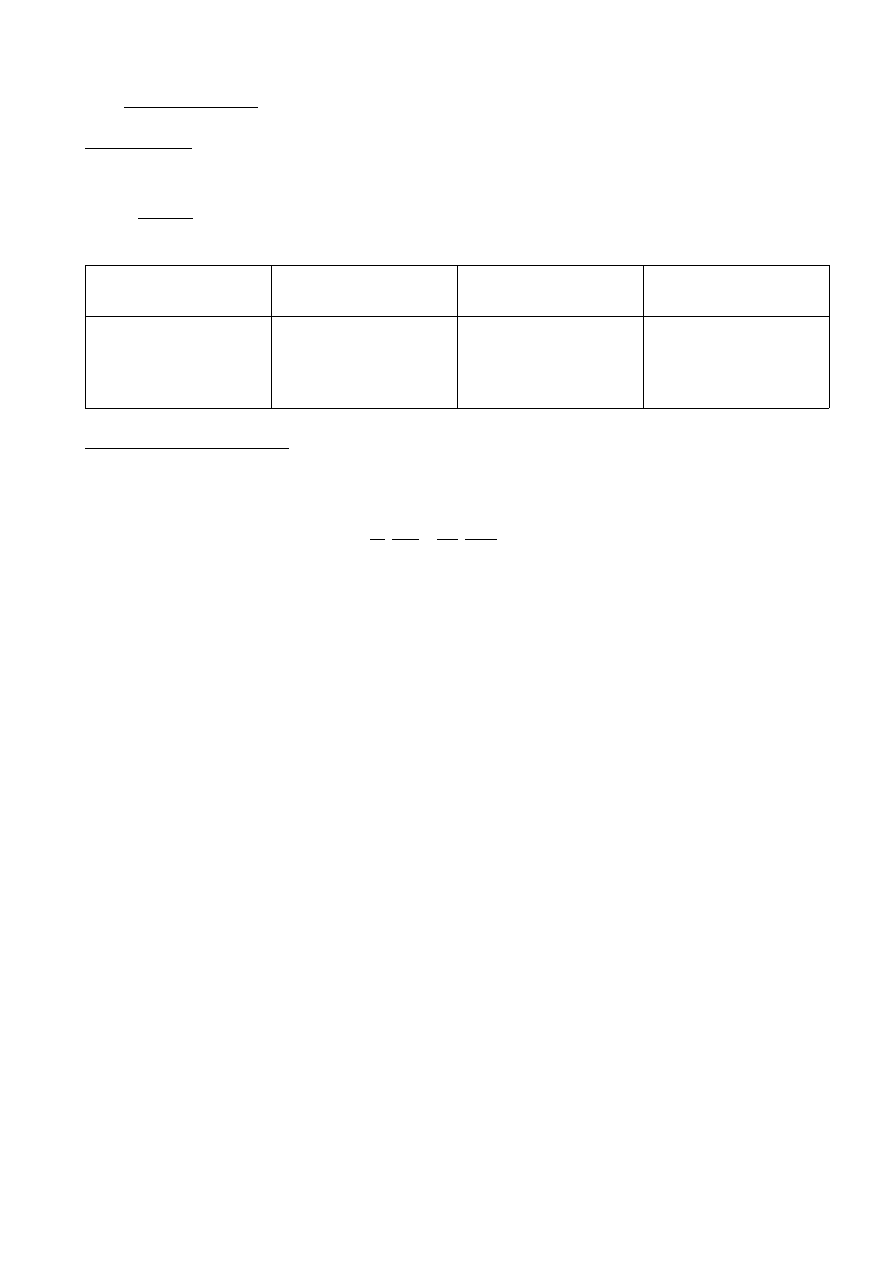
Wymiarowanie zbrojenia pasa górnego

Przyjęto do obliczeń:

M

sd

=0,10617MNm

M

R ,lim

=

b

eff

⋅

h

f

⋅

f

cd

⋅

d−0,5⋅h

f

=

0,4⋅0,1⋅16,7⋅0,45−0,5⋅0,1=0,26MNm0,11MNm

Przekrój jest pozornie teowy.

M

sd

=

f

cd

⋅

b

eff

⋅

x

eff

⋅

d−0,5⋅x

eff



0,10617=16,7⋅0,4⋅x

eff

⋅

0,45−0,5⋅x

eff



3,34⋅x

eff

2

−

3,006⋅x

eff



0,10617=0

x

eff

=0,863m lub

x

eff

=0,037m

f

cd

⋅

b

eff

⋅

x

eff

=

A

s2

⋅

f

yd

A

s2

=

f

cd

⋅

b

eff

⋅

x

eff

f

yd

=

16,7⋅0,4⋅0,037

350

=

7,06cm

2

Przyjęto zbrojenie 2Ф22:

A

s2

=

2⋅3,14⋅1,1

2

=

7,60 cm

2



7,06cm

2

3

Całkowity stopień zbrojenia belki:

=

0,00190,00076

0,45⋅0,3

=

1,97 %

Nośność belki

Nośność została wyliczona według poniższych wzorów i zestawiona w tabeli:

x

eff

=

A

s1

⋅

f

yd

b

w

⋅

f

cd

, oraz M

Rd

=

b

w

⋅

x

eff

⋅

f

cd

⋅

d−0,5⋅x

eff



Pręty

A

s

[cm

2

]

x

eff

[m]

M

rd

[kNm]

5Ф22

2Ф22

2Ф22

19,00

7,60

7,60

0,133

0,053

0,040

255,54

112,45

114,90

Długość zakotwienia pręta

Dla prętów żebrowanych Ф22 i betonu klasy B30 podstawowa długość zakotwienia pręta
wynosi:

l

b

=



4

⋅

f

yd

f

bd

=

22

4

⋅

350

2,7

=

713mm

4

1.3 Wymiarowanie belki ze względu na ścinanie

Przyjęto strzemiona Ф8 ze stali AIII (f

yd

=350MPa)

Znalezienie odcinków pierwszego i drugiego rodzaju

f

ctd

=1,20MPa

k=1,6-0,45=1,15



L

=

7,60

0,45⋅0,3

=

0,56 %

=

0,5−

f

ck

250

=

0,5− 25

250

=

0,4

V

Rd1

=

0,35⋅k⋅f

ctd

⋅

1,240⋅

L

⋅

b

w

⋅

d=0,35⋅1,15⋅1,2⋅1,240⋅0,0056⋅0,3⋅0,45=0,093MN

V

Rd2

=

0,5⋅⋅f

cd

⋅

b

w

⋅

z=0,5⋅0,4⋅16,7⋅0,3⋅0,9⋅0,45=0,406MN

Dopuszczalne długości podziału odcinków drugiego rodzaju:

l

t ,min

=

z⋅ctg =0,45⋅0,9⋅1=0,405m

l

t , max

=

z⋅ctg =0,45⋅0,9⋅2=0,81m

5

Wymiarowanie wspornika

Długość odcinka drugiego rodzaju:

l

t



0,15

0,11408−0,093

=

2,15

0,11408

⇒

l

t

=

0,25 m

Siła tnąca w licu:

V

Sd

2,15−0,15

=

0,11408

2,15

⇒

V

Sd

=

0,10612MN

Dla przyjętego l

t

=0,405m rozstaw strzemion wynosi:

s=

A

sw1

⋅

f

ywd1

⋅

l

t

V

Sd

=

1,0048⋅350⋅0,405

0,10612

=

0,134 m

Przyjęto: 4 strzemiona Ф8 co 13cm, dalej strzemiona Ф8 co 24cm.

Nośność odcinka drugiego rodzaju:

l

t

=

4⋅0,13 m=0,52m

V

Rd

=

A

sw1

⋅

f

ywd1

⋅

l

t

s

=

1,0048⋅350⋅0,52

0,13

=

0,141MN

Wymiarowanie przęsła

Długość odcinków drugiego rodzaju:

l

t



0,15

0,18040−0,093

=

3,4

0,18040

⇒

l

t

=

1,50 m

Przyjmujemy podział odcinka na długości l

1

=0,7m oraz l

2

=0,8m

Siły tnące na początkach odcinków:

V

Sd1

3,4−0,15

=

0,18040

3,4

⇒

V

Sd1

=

0,17244MN

V

Sd2

3,4−0,85

=

0,18040

3,4

⇒

V

Sd2

=

0,13530MN

Rozstaw strzemion:

s

1

=

A

sw1

⋅

f

ywd1

⋅

l

1

V

Sd1

=

1,0048⋅350⋅0,7

0,17244

=

0,143m

s

2

=

A

sw1

⋅

f

ywd1

⋅

l

2

V

Sd2

=

1,0048⋅350⋅0,8

0,13530

=

0,208m

Przyjęto: 5 strzemion Ф8 co 14 cm, 4 strzemiona Ф8 co 20 cm, dalej strzemiona Ф8 co 24cm.

Nośność odcinków drugiego rodzaju:

l

1

=

5⋅0,14 m=0,7m

V

Rd1

=

A

sw1

⋅

f

ywd1

⋅

l

1

s

1

=

1,0048⋅350⋅0,7

0,14

=

0,176 MN

l

2

=

4⋅0,20 m=0,8 m

V

Rd2

=

A

sw1

⋅

f

ywd1

⋅

l

2

s

2

=

1,0048⋅350⋅0,8

0,20

=

0,141 MN

6

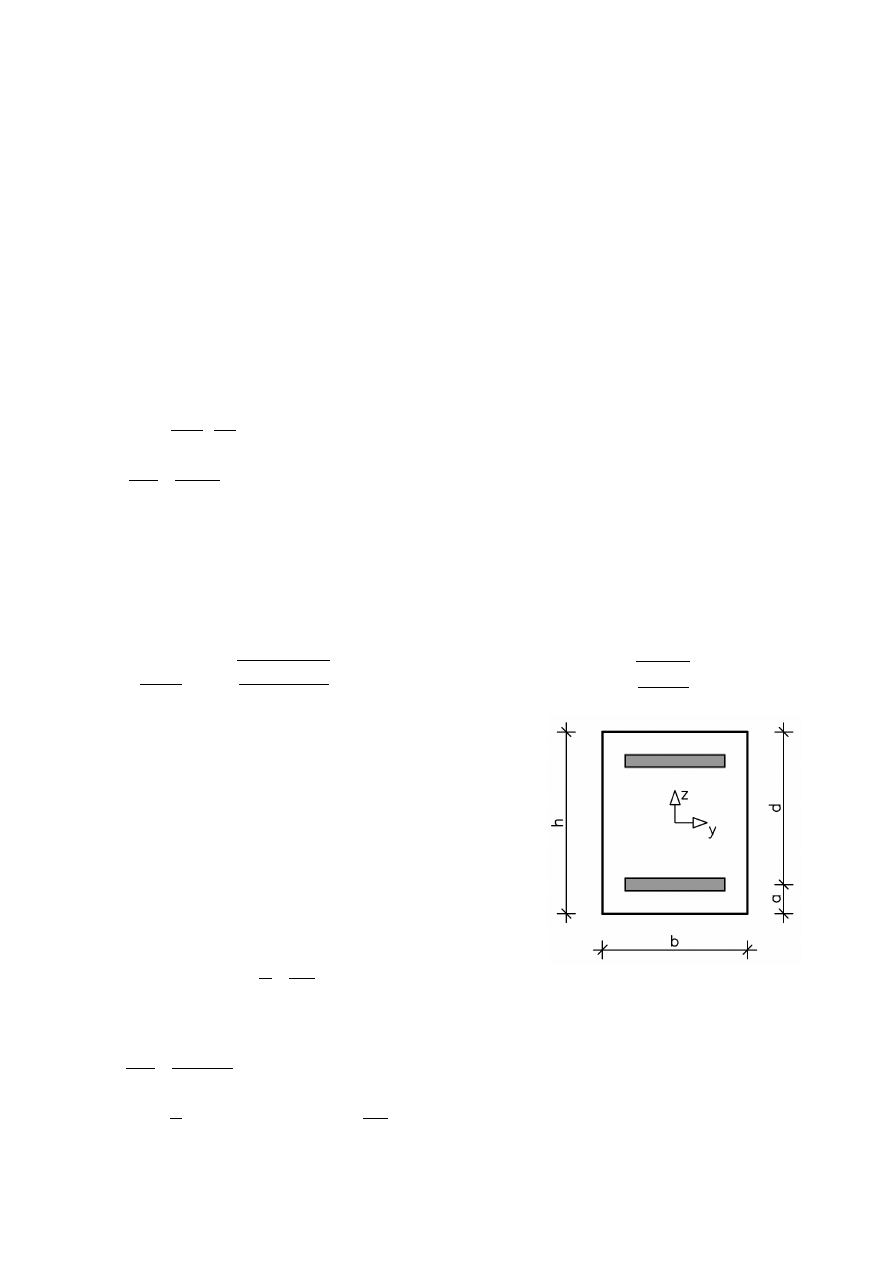
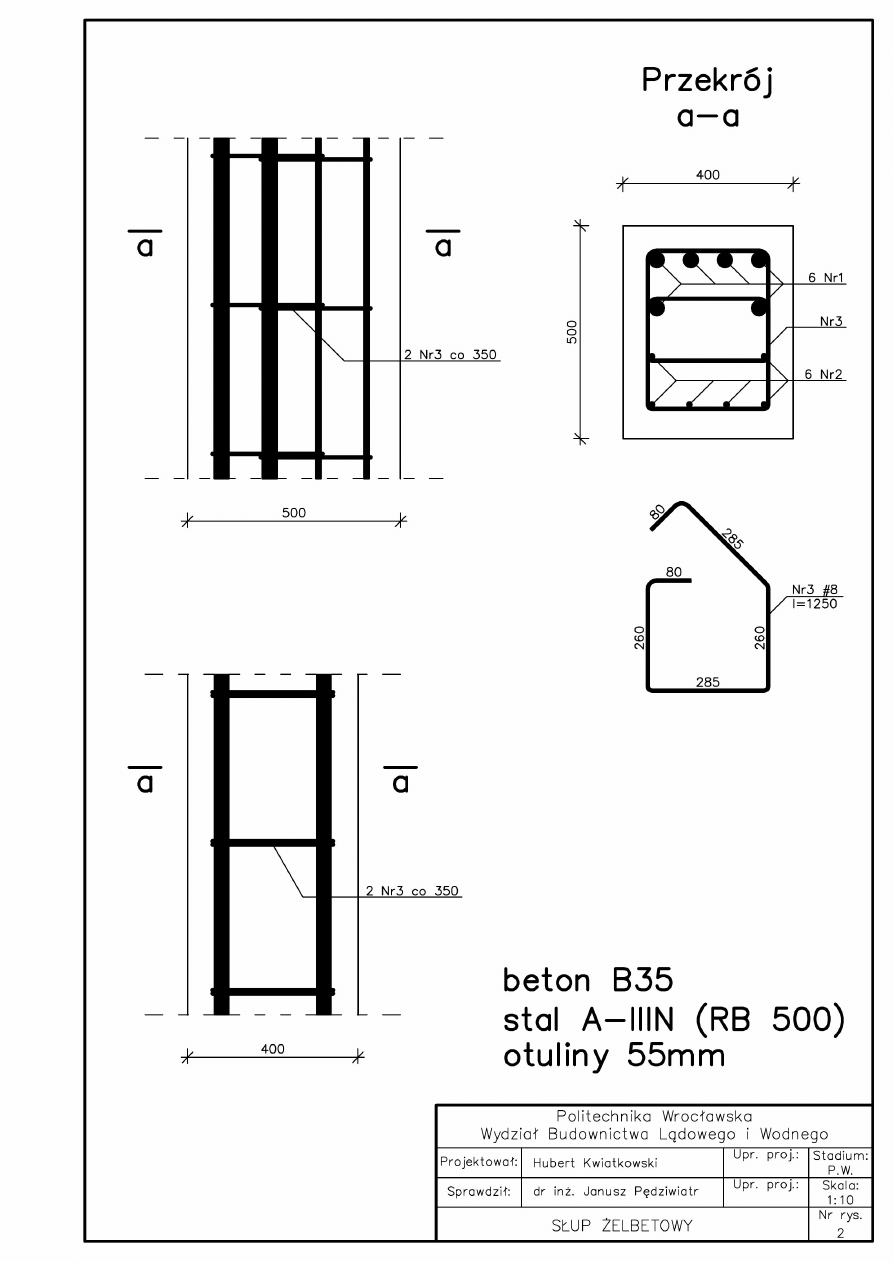
2. Słup żelbetowy

2.1 Wstępne przyjęcie przekroju słupa

Dane:

l

o

=5,5m

N

Sd

=5,0MN

M

Sd

=0,150MNm

N

Sd,lt

/N

Sd

=0,39

Przyjęto beton B35 oraz stal A-IIIN:
f

cd

=20MPa

f

yd

=420MPa

E

cm

=32GPa

E

s

=205GPa

Mimośród statyczny i niezamierzony:

e

a

=

max

{

l

col

600

,

h

30

,20mm

}

=

{

9mm , ≃17mm ,10mm

}

≈

0,02m

e

e

=

M

Sd

N

Sd

=

0,150

5

=

0,03 m

Mimośród początkowy:

e

o

=

0,02 m0,03m=0,05m

Dla niewielkiego mimośrodu lub spodziewanej całej strefy ściskanej możemy przyjąć:

=

2,5%

b/d=1/1,2

bd

2

=

2 M

Sd

f

yd



⇒

d=

3



2⋅0,150⋅1,2

420⋅0,025

=

0,32 m

b=0,27m

, lub

b=h

N

Sd

=

0,9 bh f

cd

⇒

h=



5

0,9⋅20

=

0,53 m

Przyjmujemy:

b=0,40m
d=0,42m
h=0,50m
a=0,08m

2.2.Wymiarowanie słupa w płaszczyźnie xz

Smukłość słupa:

l

o

h

=

5,5
0,5

=

117 , należy uwzględnić efekty drugiego rzędu.

Momenty bezwładności stali i betonu:

I

c

=

b h

3

12

=

0,4⋅0,5

3

12

=

4,1667⋅10

−

3

m

4

I

s

=

bd 



h
2

−

a



2

=

0,4⋅0,42⋅0,025⋅



0,5

2

−

0,08



2

=

0,1214⋅10

−

3

⋅

m

4

7

Współczynnik oddziaływania długotrwałego:

k

l t

=

10,5

N

Sd , l t

N

Sd

⋅ ∞

, t

0

=

10,5⋅0,39⋅2=1,39

Siła krytyczna:

N

crit

=

9

l

o

2

[

I

c

E

cm

2k

l t



0,11

0,1e

o

/

h



0,1





E

s

I

S

]

e

o

h

=

max

{

e

o

h

; 0,5−0,01⋅

l

o

h

−

0,01 f

cd

; 0,05

}

=

max {0,1 ; 0,19 ; 0,05}

N

crit

=

9

5,5

2

[

4,1667⋅10

−

3

⋅

32000

2⋅1,39



0,11

0,10,19



0,1





205000⋅0,1214⋅10

−

3

]

=

14,24kN

=

1

1−

N

Sd

N

crit

=

1

1−

5,00

14,24

=

1,54

Mimośród końcowy:

e

tot

=

e

o

=

0,05⋅1,54=0,077m

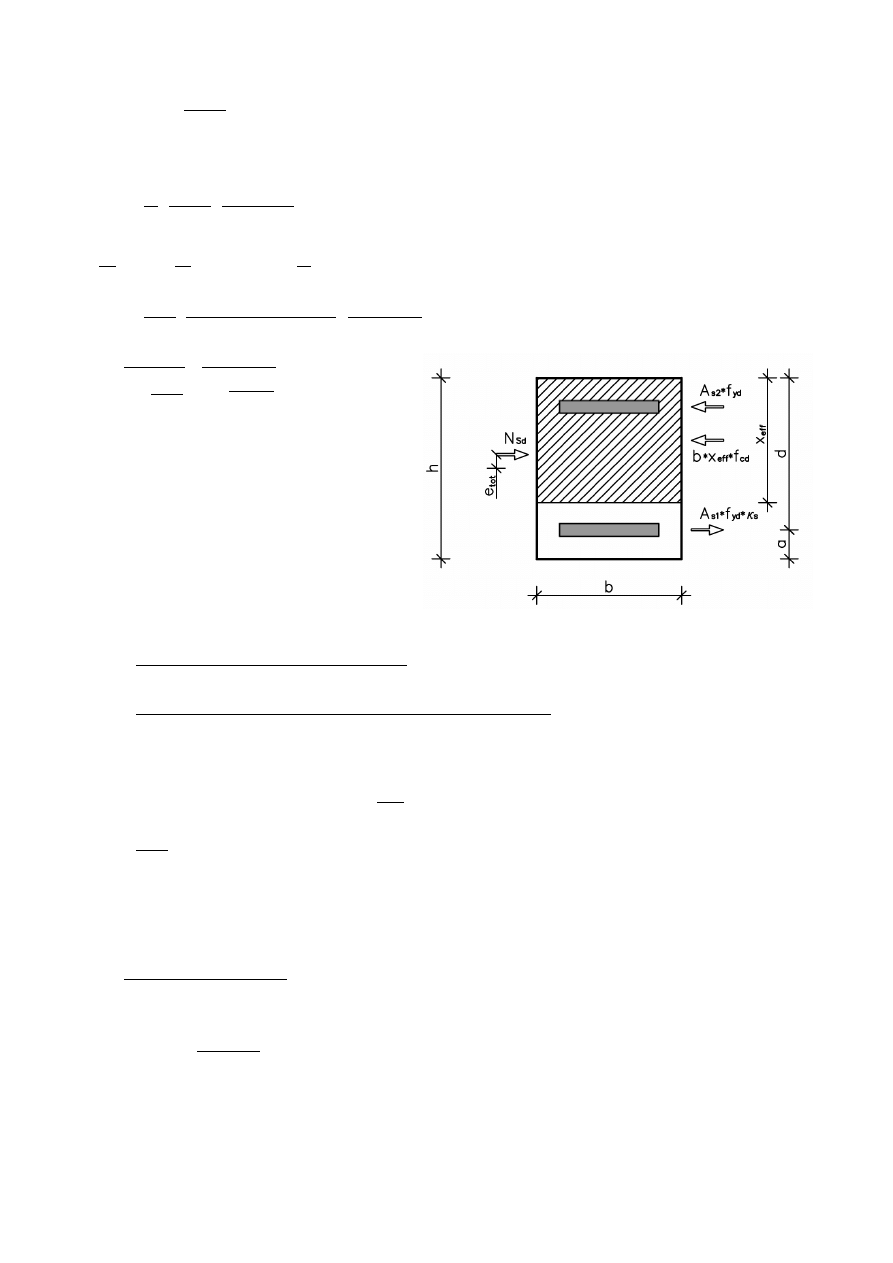
Do obliczeń założono mały mimośród:



s

=−

1 x

eff

=

d

Zbrojenie A

s2

:

N

Sd



e

tot



h/2−a= f

cd

bdd−0,5 d A

s2

f

yd



d−a

A

s2

=

N

Sd



e

tot



h/2−a− f

cd

bd d−0,5 d

f

yd



d−a

A

s2

=

50,0770,5⋅0,5−0,08−20⋅0,4⋅0,420,42−0,5⋅0,42

4200,42−0,08

=

37,07cm

2

Zbrojenie A

s1

:

N

Sd

=

A

s2

f

yd



A

s1

⋅

f

yd



f

cd

bd ⇒ A

s1

=

1

f

yd



N

Sd

−

A

s2

f

yd

−

f

cd

bd

A

s1

=

1

420



5−0,003707⋅420−20⋅0,5⋅0,42=1,98cm

2

Przyjęto:

4 pręty Φ35: A

s2

=38,48cm

2

4 pręty Φ12: A

s1

=4,52cm

2

=

0,0038480,000452

0,4⋅0,42

⋅

100%=2,56%4 %

A

s ,min

=

max

{

0,15 N

Sd

f

yd

;0,3 %

}

=

max

{

0,18% ;0,3 %

}

≤

2,56%

8

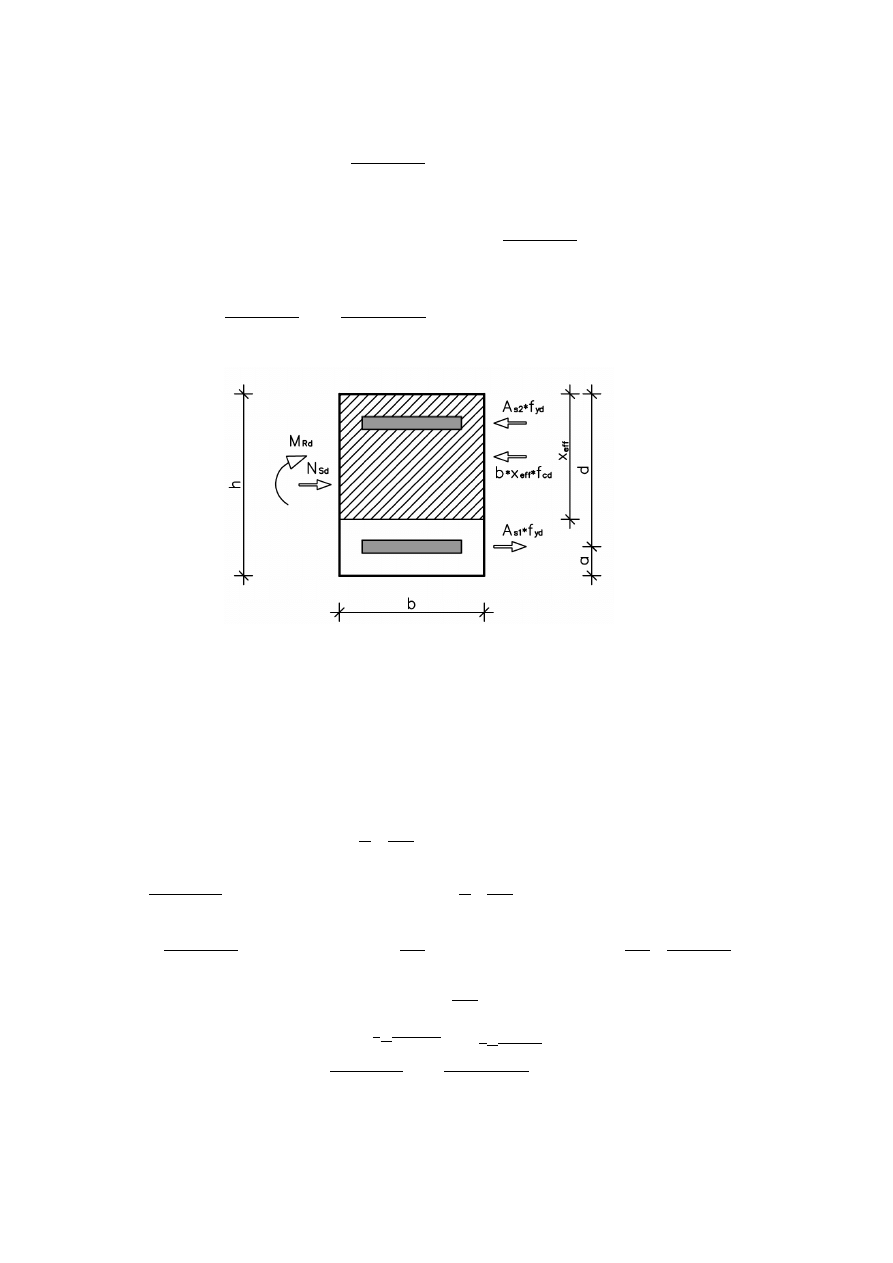
2.3 Nośność w płaszczyźnie xz

Zasięg strefy ściskanej nośności na zginanie:

N

Sd

=

A

s2

f

yd



f

cd

bd 

eff

−

A

s1

f

yd

[

21−

eff



1−

eff,lim

−

1

]

5=0,003848⋅42020⋅0,4⋅0,42⋅

eff

−

0,000452⋅420⋅

[

2 1−

eff



1−0,5

−

1

]



eff

=

0,96



s

=

21−

eff



1−

eff,lim

−

1=

21−0,96

1−0,5

−

1=−0,84



s

∈〈−

1 ; 1〉

Moment graniczny:

M

Rd



N

Sd



h/2−a= f

cd

bd

2



eff



1−0,5 

eff



A

s2

f

yd



d−a

M

Rd

=

f

cd

bd

2



eff



1−0,5

eff



A

s2

f

yd



d−a−N

Sd



h/2−a

M

Rd

=

20⋅0,4⋅0,42

2

⋅

0,961−0,5⋅0,960,000452⋅4200,42−0,08−50,5⋅0,5−0,08

M

Rd

=

0,40MNmM

Sd

=

0,15MNm

Zasięg strefy ściskanej nośności na ściskanie:

M

Sd

=

s

f

yd

A

s1



h/2−a f

cd

b x

eff



h
2

−

x

eff

2





f

yd

A

s2



h/2−a

M

Sd

=

[

21−

eff



1−

eff,lim

−

1

]

f

yd

A

s1



h/2−a f

cd

b x

eff



h

2

−

x

eff

2





f

yd

A

s2



h/2−a

0,150=

[

21−

eff



1−0,5

−

1

]

⋅

420⋅0,000452⋅



0,5

2

−

0,08





20⋅0,4⋅0,42⋅

eff



0,5

2

−

0,42⋅

eff

2







420⋅0,003848



0,5

2

−

0,08



ξ

eff

=-0,25

ξ

eff

=1,26



s

=

2 1−

eff



1−

eff, lim

−

1= 2



1−1,26

1−0,5

−

1=−2,04

9

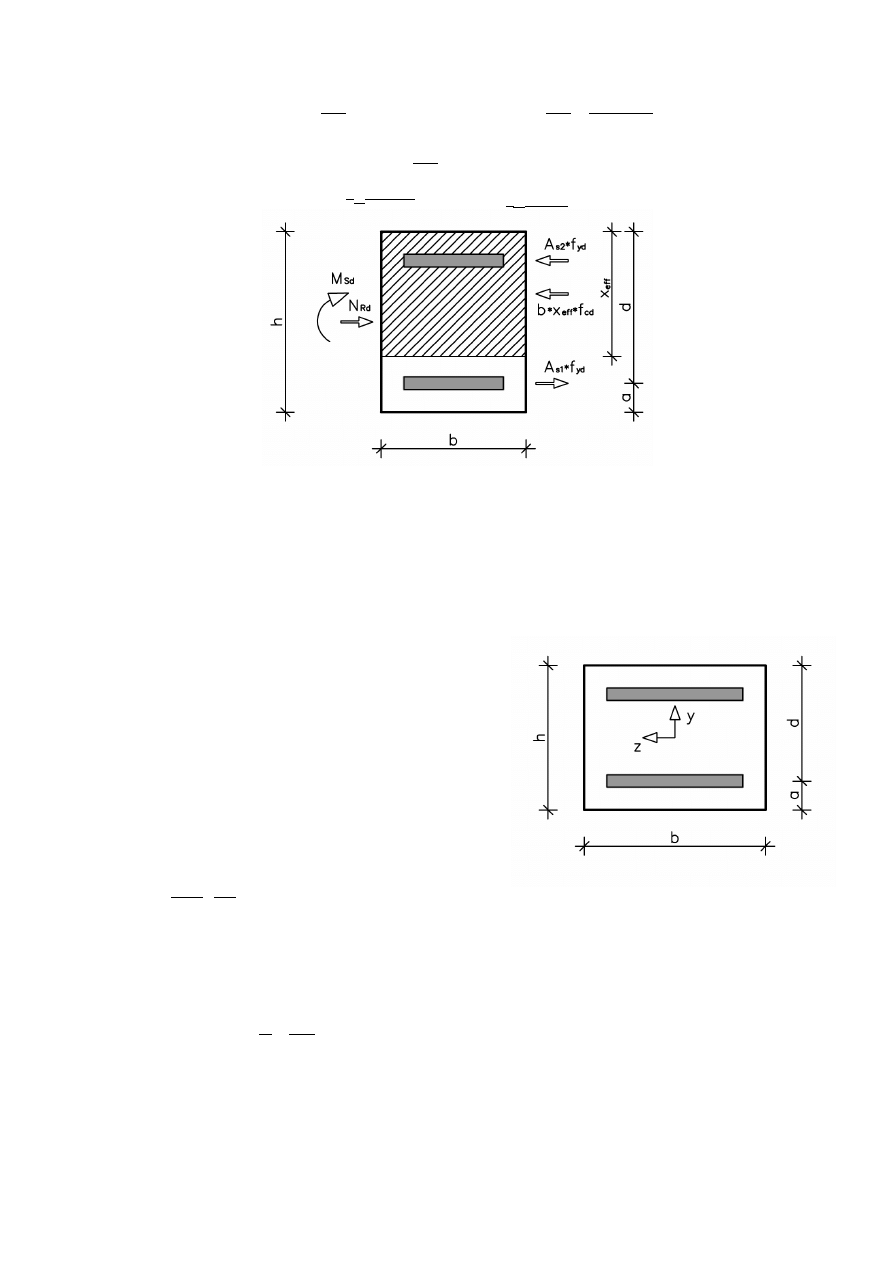
Dla κ

s

= -1:

0,150=−1⋅420⋅0,000452⋅



0,5

2

−

0,08





20⋅0,4⋅0,42⋅

eff



0,5

2

−

0,42⋅

eff

2







420⋅0,003848



0,5

2

−

0,08



ξ

eff

=-0,10

ξ

eff

=1,29

Graniczna siła ściskająca:

N

Rd

=

A

s2

f

yd



f

cd

b d 

eff

−

A

s1

f

yd



s

=

420⋅0,00384820⋅0,4⋅0,42⋅1−0,000452⋅420⋅−1=

=

5,166MNm

N

Rd

=

5,166MNmN

Sd

=

5,0 MNm

2.4 Wymiarowanie w płaszczyźnie xy

b=0,50m
d=0,32m
h=0,40m
a=0,08m

Zakładamy zbrojenie symetryczne A

s

Mimośród statyczny i niezamierzony:

e

e

=

0

e

a

=

max

{

l

col

600

, b

30

,10mm

}

=

9mm , 13mm , 20mm=0,01 m

Mimośród początkowy:

e

o

=

e

e



e

a

=

0,01m

Smukłość słupa:

l

o

b

=

5,5
0,4

=

13,757 , należy uwzględnić efekty drugiego rzędu.

10

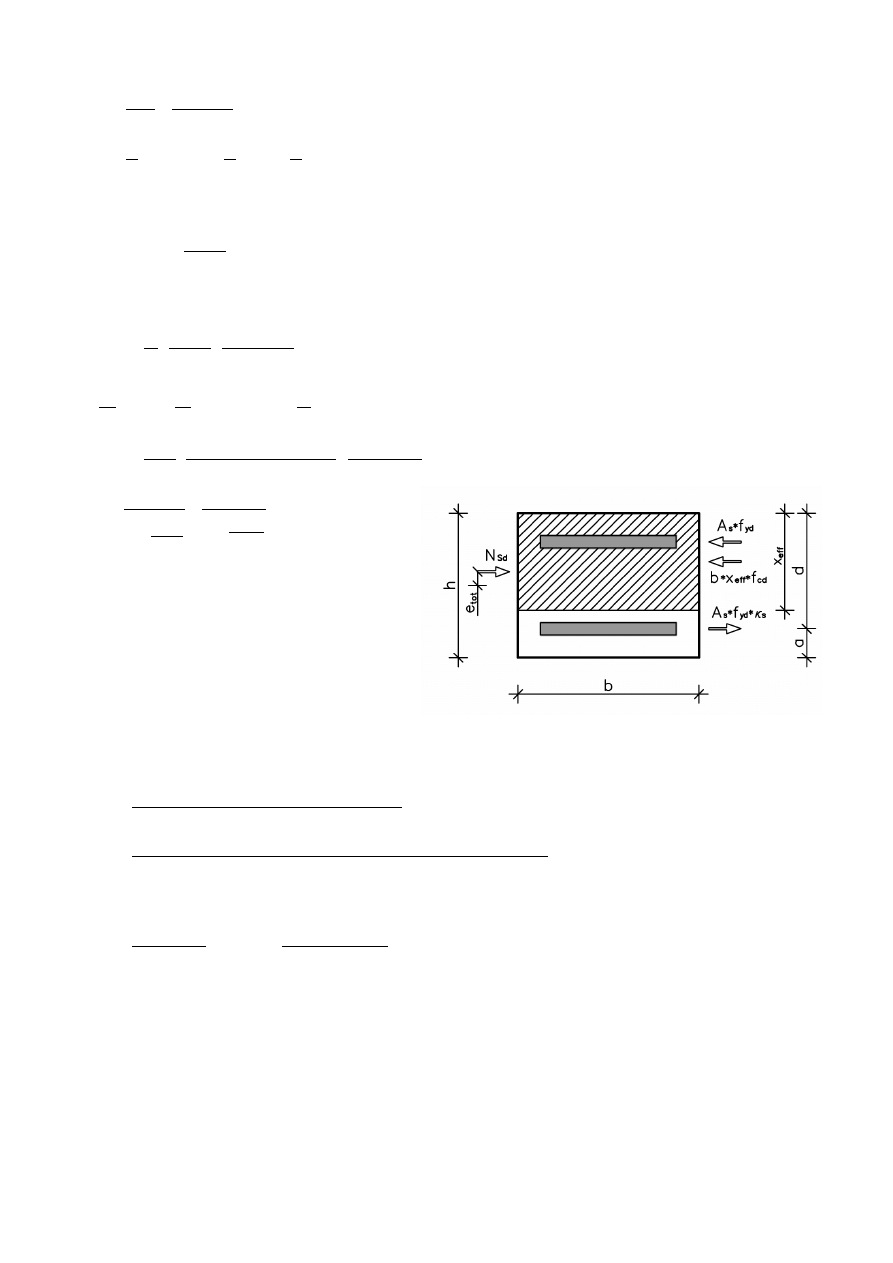
Momenty bezwładności betonu i stali:

I

c

=

b h

3

12

=

0,5⋅0,4

3

12

=

2,6667⋅10

−

3

m

4

I

s

=

1
2



A

s1



A

s2





h
2

−

a



2

=

1
2



0,0038480,0004520,2−0,08

2

=

0,03096⋅10

−

3

m

4

Współczynnik oddziaływania długotrwałego:

k

l t

=

10,5

N

Sd , l t

N

Sd

⋅ ∞

, t

0

=

10,5⋅0,39⋅2=1,39

Siła krytyczna:

N

crit

=

9

l

o

2

[

I

c

E

cm

2k

l t



0,11

0,1e

o

/

h



0,1





E

s

I

S

]

e

o

h

=

max

{

e

o

h

; 0,5−0,01⋅

l

o

h

−

0,01 f

cd

; 0,05

}

=

max {0,03 ; 0,16 ; 0,05}

N

crit

=

9

5,5

2

[

2,6667⋅10

−

3

⋅

32000

2⋅1,39



0,11

0,10,16



0,1





205000⋅0,03096⋅10

−

3

]

=

6,67 kN

=

1

1−

N

Sd

N

crit

=

1

1−

5,00
6,67

=

3,99

Mimośród końcowy:

e

tot

=

e

o

=

0,01⋅3,99=0,04m

Założono do obliczeń mały mimośród:



s

=−

1 x

eff

=

d

N

Sd



e

tot



h/2−a= f

cd

bdd−0,5 d A

s

f

yd



d−a

Zbrojenie A

s

:

A

s

=

N

Sd



e

tot



h/2−a− f

cd

bd d−0,5d 

f

yd



d−a

A

s

=

50,0240,4⋅0,5−0,08−20⋅0,5⋅0,320,32−0,5⋅0,32

4200,32−0,08

=

20,63 cm

2

Brakujące zbrojenie:

A

s

−



A

s1



A

s2



4

=

20,63−38,484,52

4

=

9,88cm

2

Przyjęto 1Φ12 oraz 1Φ35 (10,75cm

2

)

Dla prętów 2Φ12 oraz 2Φ35 :

A

s

=

21,5cm

2

11

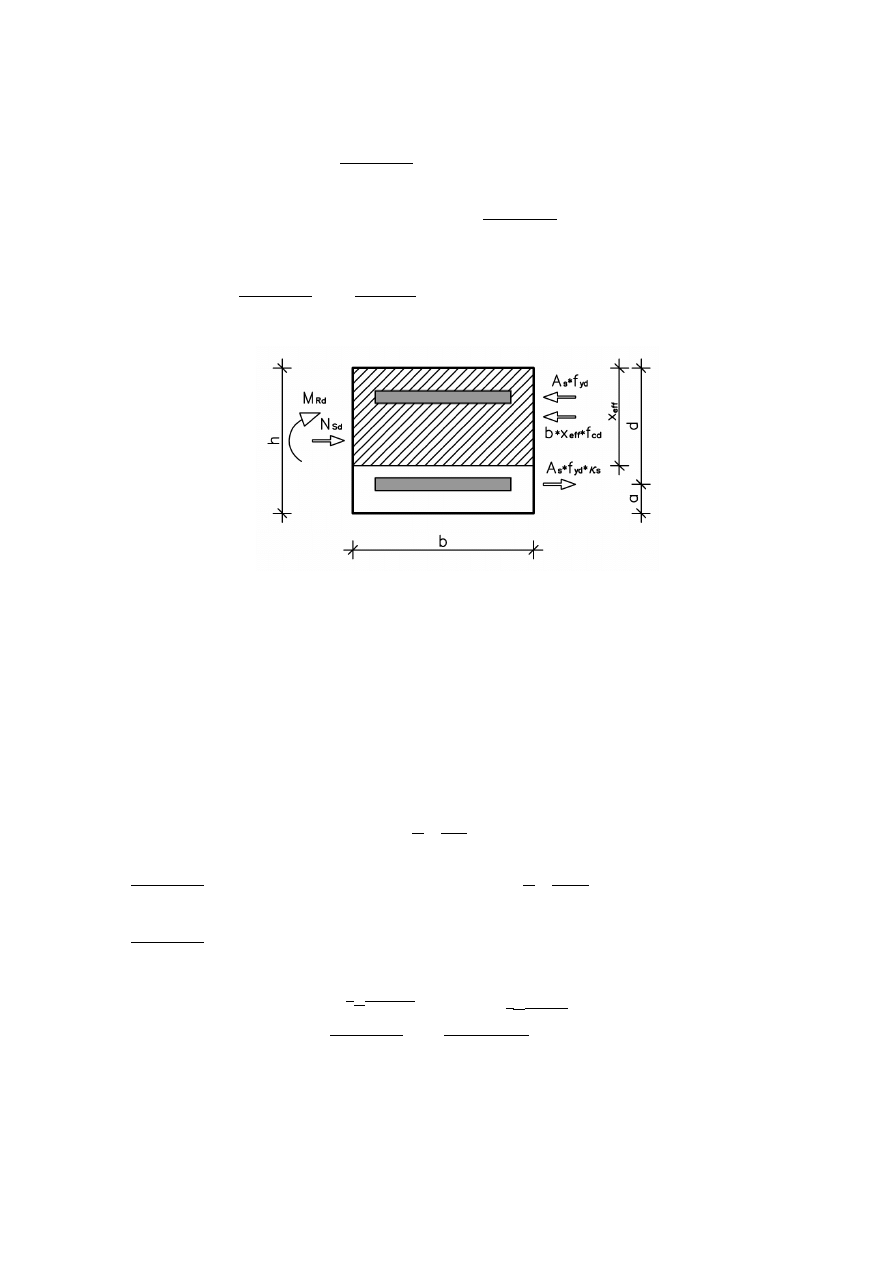
2.5 Nośność w płaszczyźnie xy

Zasięg strefy ściskanej na zginanie:

N

Sd

=

A

s

f

yd



f

cd

bd 

eff

−

A

s

f

yd

[

21−

eff



1−

eff,lim

−

1

]

5=0,00215⋅42020⋅0,5⋅0,32⋅

eff

−

0,00215⋅420⋅

[

21−

eff



1−0,5

−

1

]



eff

=

1



s

=

21−

eff



1−

eff,lim

−

1=

21−1

1−0,5

−

1=−1



s

∈〈−

1 ;1〉

Graniczny moment gnący:

M

Rd



N

Sd



h/2−a= f

cd

bd

2



eff



1−0,5 

eff



A

s

f

yd



d−a

M

Rd

=

f

cd

bd

2



eff



1−0,5

eff



A

s

f

yd



d−a−N

Sd



h/2−a

M

Rd

=

20⋅0,5⋅0,32

2

⋅

11−0,5⋅10,00215⋅4200,32−0,08−50,4⋅0,5−0,08

M

Rd

=

0,129 MNm

Zasięg strefy ściskanej nośności na ściskanie:

0=

s

f

yd

A

s



e

tot



h/2−a− f

cd

b x

eff



e

tot

−

h
2



x

eff

2



−

f

yd

A

s



e

tot

−

h/2a

0=

[

21−

eff



1−

eff,lim

−

1

]

f

yd

A

s



e

tot



h/2−a− f

cd

bd 

eff



e

tot

−

h

2



d 

eff

2



−

f

yd

A

s



e

tot

−

h/2a

0=

[

21−

eff



1−0,5

−

1

]

420⋅0,002150,0240,2−0,08−20⋅0,5⋅0,32

eff



0,024−0,20,16

eff



−

−

420⋅0,002150,024−0,20,08

ξ

eff

=-0,92

ξ

eff

=1,01



s

=

2 1−

eff



1−

eff, lim

−

1= 21−1,01

1−0,5

−

1=−1,04

12

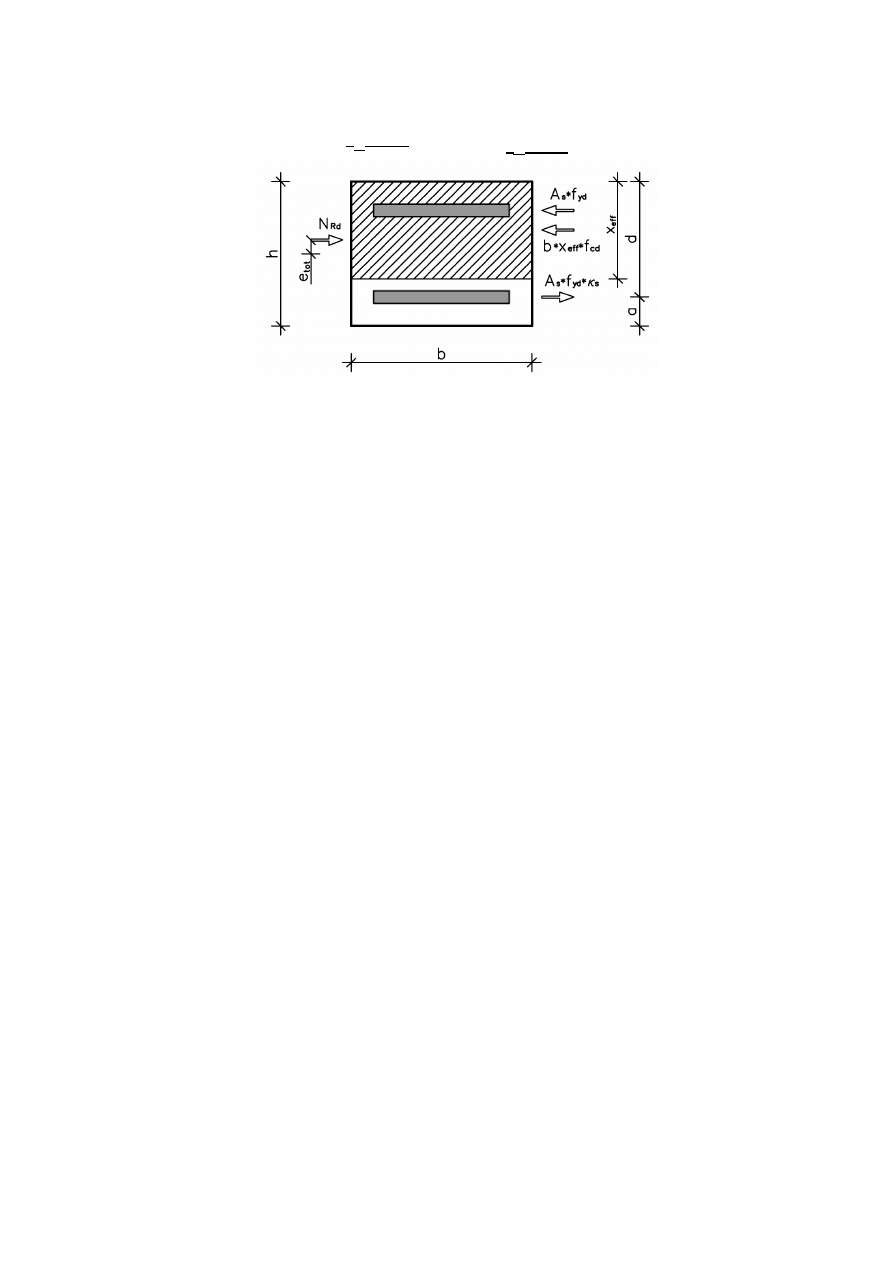
Dla κ

s

= -1:

0=−1⋅420⋅0,002150,0240,2−0,08−20⋅0,5⋅0,32 

eff



0,024−0,20,16

eff



−

−

420⋅0,002150,024−0,20,08

ξ

eff

=0,08

ξ

eff

=1,02

Graniczna nośność na ściskanie

N

Rd

=

A

s

f

yd



f

cd

bd 

eff

−

A

s

f

yd



s

=

420⋅0,0021520⋅0,5⋅0,32⋅1−0,00215⋅420⋅−1=

=

5,01 MNm

N

Rd

=

5,01 MNmN

Sd

=

5,0 MNm

2.6 Rozstaw strzemion

Rozstaw:

s

1

{

≤

15≤3%

≤

10≥3%

≤

b≤h

≤

400mm

, zatem s

1

{

≤

350mm

≤

400mm

≤

400mm

Przyjęto podwójne strzemiona z prętów Φ8 co 350mm.

13