Kolokwium 1 – podejście 2

 {odpowiedzi} 

grupa I

 

Zadanie 1: Podać część rzeczywistą i urojoną następujących liczb: 

1.   

  

 

 

  

 

  

  

      

  

    

   

 

       

   

 

 

  

   

    

    

    

 

       

    

 

   

 

 

 

   

           

 

 

                

 

 

                

 

 

           

 

 

                    

         ,             

2. 

  

 

      

 

 

       

 

 

 

 

Trzy pierwiastki (     ): 

1.:    

 

 

      

 

       

 

 

      

 

     

 

 

       

 

 

 

  

 

 

 
 

    

    

  

 

,       

 
 

 

2.:    

 

 

      

 

       

 

 

      

 

     

  

 

       

  

 

   

  

 

 

 
 

   

      

  

 

,       

 
 

 

3.:    

 

 

      

 

       

 

 

      

 

     

  

 

       

  

 

      

      ,           

3. 

 

    

 

 
 

 

 
 

  

Zadanie 2: Narysować na płaszczyźnie liczb zespolonych: 

1.             
Niech            . Wtedy               
                              
       

 

2.                     

 

   

 

 

 

 

      

 

  przesunięty o wektor        

 

     

 

             

 

             

 

 

   i                    

 

 

     

 

 

 

          

 

 

   i  

  

 

          

  

 

 

oraz udowodnić 

3.   

 

   

 

     

 

 

 

       

 

Niech  

 

   

 

   

 

  oraz  

 

   

 

   

 

 . 

 

 

   

 

      

 

   

 

 

              

 

   

 

 

                 

 

   

 

    

 

   

 

      

 

 

 

   

 

 

 

    

 

 

 

   

 

 

 

  

   

 

 

 

   

 

 

 

    

 

 

 

   

 

 

 

  

                                           

 

   

 

    

 

   

 

  

                              

 

 

 

       

Zadanie3: W zbiorze  

 

 par liczb rzeczywistych określone jest działanie: 

                                     

Sprawdzić, czy    

 

     jest grupą. 

Rozwiązanie:  

1. łączność ( 

 

 

  

 

  

 

  

 

   

 

   

 

     

 

   

 

    

 

   

 

 ) 

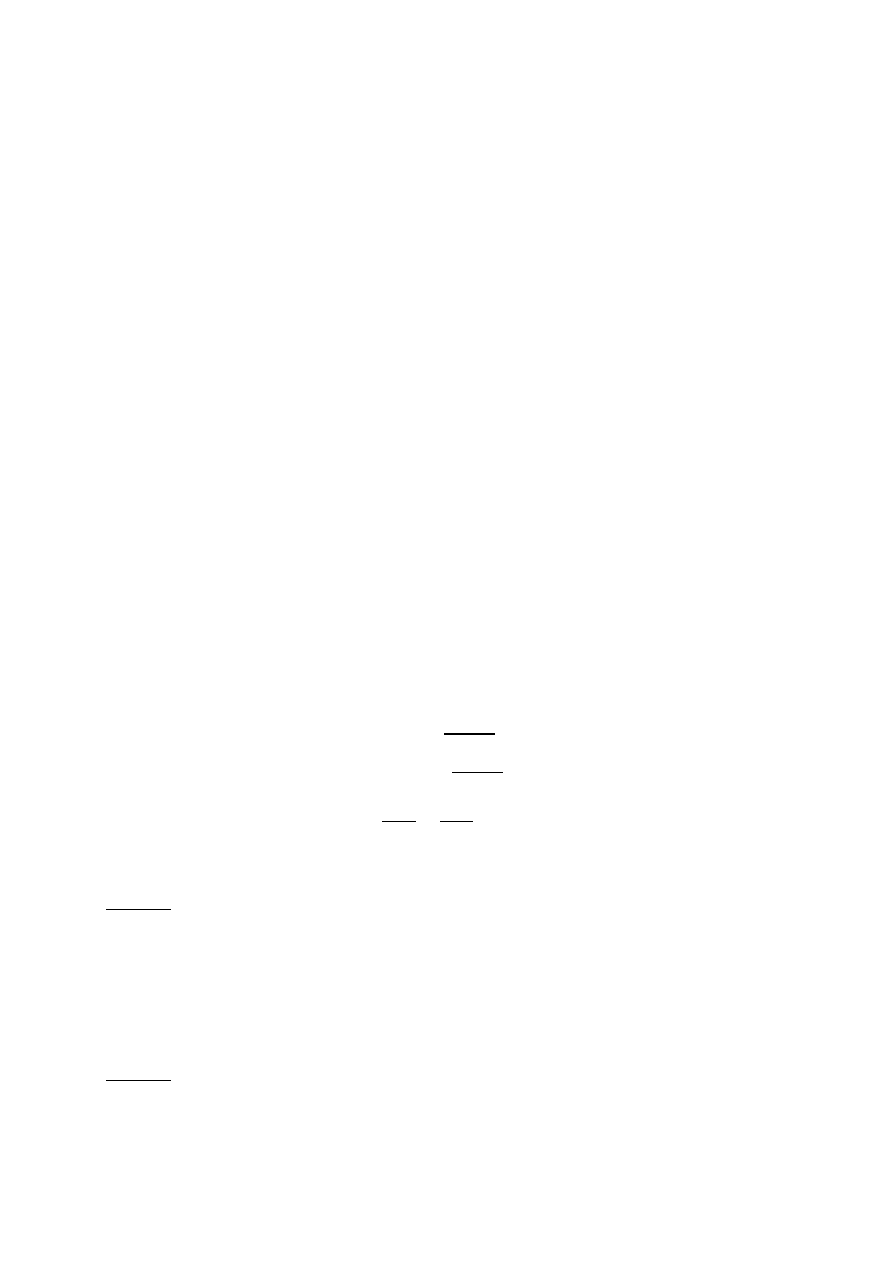
Niech  

 

    

 

   

 

 ,  

 

    

 

   

 

 ,  

 

    

 

   

 

   

  

 

   

 

     

 

     

 

   

 

      

 

   

 

       

 

   

 

      

 

 

 

   

 

 

 

    

 

 

 

   

 

 

 

      

 

   

 

 

     

 

 

 

   

 

 

 

  

 

    

 

 

 

   

 

 

 

  

 

     

 

 

 

   

 

 

 

  

 

    

 

 

 

   

 

 

 

  

 

 

    

 

 

 

 

 

   

 

 

 

 

 

   

 

 

 

 

 

   

 

 

 

 

 

    

 

 

 

 

 

   

 

 

 

 

 

   

 

 

 

 

 

   

 

 

 

 

 

  

 

 

    

 

   

 

      

 

   

 

       

 

   

 

      

 

   

 

       

 

   

 

      

 

 

 

   

 

 

 

    

 

 

 

   

 

 

 

 

    

 

  

 

 

 

   

 

 

 

     

 

  

 

 

 

   

 

 

 

      

 

 

 

   

 

 

 

  

 

    

 

 

 

   

 

 

 

  

 

 

    

 

 

 

 

 

   

 

 

 

 

 

   

 

 

 

 

 

   

 

 

 

 

 

    

 

 

 

 

 

   

 

 

 

 

 

   

 

 

 

 

 

   

 

 

 

 

 

  

Zatem   

 

   

 

     

 

   

 

    

 

   

 

 , czyli    

 

     jest łączna. 

 

2. element neutralny 

Niech               

 

. Szukamy       

 

   

 

 , które należałoby do  

 

 i spełniało równość: 

          

           

 

   

 

       

 

    

 

    

 

    

 

           

 

  

 

    

 

   

  

 

    

 

   

  

 

 

 

   

 

 

   

  

Zatem element neutralny istnieje i jest to          . 

 

3. element odwrotny 

Niech               

 

  Dla każdego   szukamy       

 

   

 

 , które należałoby do  

 

 i 

spełniało równość: 

          

           

 

   

 

       

 

    

 

    

 

    

 

          

 

  

 

    

 

   

  

 

    

 

   

  

 

 

 

 

 

 

 

   

 

 

 

   

 

 

 

   

 

  

Zatem       

 

   

 

  istnieje:      

 

 

 

  

 

   

 

 

 

  

 

 . 

Z 1., 2. i 3. wnioskujemy, że    

 

     jest grupą. 

Zadanie 4: Uzasadnić, że zbiór W jest podprzestrzenią liniową przestrzeni liniowej  :  

          

 

                                    ,      

 

    

Rozwiązanie: Niech  

 

,  

 

   . Trzeba sprawdzić, czy ich kombinacja liniowa również należy do  . 

Niech      będzie tą kombinacją liniową. Wystarczy pokazać, że      spełnia własność podaną w 
definicji zbioru  . 

        

 

 

 

       

 

 

 

       

 

   

 

        

 

   

 

          

 

 

 

       

 

 

 

             

Zadanie 5: Zbadać liniową niezależność wektorów          ,        ,            w  

 

. 

Rozwiązanie: Jeśli są liniowo niezależne, to  

 

             

 

           

 

                 tylko dla 

 

 

   

 

   

 

   . Sprawdzamy: 

  

 

     

 

    

 

      

 

      

 

       

 

     

 

   

 

            

  

 

   

 

   

 

     

 

    

 

    

 

   

 

   

 

            

 

 

 

   

 

   

 

   

   

 

    

 

   

  

 

   

 

   

 

   

  

 

 

 

   

 

   

 

   

 

 

    

 

  

 

   

 

   

 

   

  

 

 

    

 

 wstawiamy do równania pierwszego i trzeciego. Otrzymujemy: 

 

   

 

   

 

   

   

 

   

 

   

  

Czyli mamy nieskończenie wiele rozwiązań, gdzie:  

 

 

    

 

 

 

    

 

 . Na przykład dla  

 

   ,  

 

     i 

 

 

   . A zatem  

 

             

 

           

 

                 dla  

 

,  

 

 i  

 

 innych niż same zera, 

czyli układ wektorów jest liniowo zależny.