Omówienie zagadnien

* Celem synchronizacji jest kontrola przyznawania zasobów do procesów tak, aby dopuszczalne stały się
jedynie instrukcje zgodne z zamysłem programisty.
* Synchronizacja na najniższym poziomie polega na wykonaniu specjalnych instrukcji, które powodują
zatrzymanie postępu przetwarzania.
* Synchronizacja na wyższym poziomie polega na użyciu specjalnych konstrukcji programotwórczych, lub
odpowiednich definicji struktur danych.
Sekcja krytyczna w programowaniu współbieżnym fragment kodu programu, w którym korzysta się z
zasobu dzielonego, a co za tym idzie w danej chwili może być wykorzystywany przez co najwyżej jeden
wątek. System operacyjny dba o synchronizację, jeśli więcej wątków żąda wykonania kodu sekcji krytycznej,
dopuszczany jest tylko jeden wątek, pozostałe zaś są wstrzymywane.

Środki synchronizacji procesów(sekcji krytycznej):

1. Semafory mogą być wykorzystywane tam, gdzie zasób dzielony jest na ograniczoną ilość

użytkowników. Jest zmienną całkowitą, do której dostęp można uzyskać (poza inicjalizacją) jedynie

za pomocą dwóch specjalnych operacji: czekaj i sygnalizuj. Pierwsza sprawdza, czy semafor ma

wartość większą od zera. Jeśli tak, to zmniejsza ją o jeden, jeśli nie, to czeka aż tę wartość osiągnie i

dopiero wtedy ją zmniejsza. Druga polega na zwiększeniu wartości semafora o jeden. Istnieją różne

wersje semaforów, takie które przyjmują jedynie dwie wartości nazywa się semaforami binarnymi

bądź muteksami. Istnieją dwa sposoby implementacji operacji czekaj. Pierwszy z nich wymaga

aktywnego oczekiwania na podniesienie semafora. Drugi sposób polega na umieszczeniu

wszystkich procesów czekających na podniesienie semafora w kolejce oczekiwania na to zdarzenie.

Kiedy semafor osiągnie wartość większą od zera uaktywniany jest jeden z tych procesów i on może

opuścić semafor.

2. Regiony w językach programowania (głównie proceduralnych) wprowadzono instrukcje pozwalające

tworzyć tzw. regiony krytyczne. Słowo kluczowe shared pozwala na określenie zmiennej, jako
współdzielonej przez kilka procesów, natomiast instrukcja “region zmienna współdzielona do
operacja” gwarantuje, że operacja wykonana na zmiennej współdzielonej będzie niepodzielna.
Regiony można zagnieżdżać, jednak należy robić to ostrożnie, by nie doprowadzić do zakleszczenia.

3. Monitory są środkiem synchronizacji właściwym dla języków obiektowych, choć zostały opracowane

niezależnie od techniki obiektowej. Monitor można określić jako obiekt, którego wszystkie pola są
prywatne, a ich wartości osiągalne tylko za pomocą metod obiektu, wykonywanych w sposób
niepodzielny.

Algorytm piekarniany – algorytm rozwiązujący wykluczanie się w sekcji krytycznej dla dowolnej N liczby
procesów.

2. Warunki powstania zakleszczeń.

[powrót]

4. Zakleszczenie to zbiór procesów będących w impasie wywołanym przez to, że każdy proces

należący do tego zbioru przetrzymuje zasoby potrzebne innym procesom z tego zbioru, a
jednocześnie czeka na zasoby przydzielone innym procesom.

Warunki powstania zakleszczeń:

● Wzajemne wykluczanie w jednej chwili z jednego zasobu może korzystać co najwyżej jeden proces.
● Przetrzymywanie i oczekiwanie proces przetrzymujący co najmniej jeden zasób czeka na przydział

dodatkowych zasobów, które są przydzielone innym procesom.

● Brak wywłaszczania procesy zwalniają zasoby dobrowolnie po zakończeniu swojego zadania. Nie

można odebrać procesowi przydzielonego zasobu, którego ten nie ma ochoty zwolnić.

● Czekanie cykliczne istnieje zbiór czekających procesów {P(1), P(2), ...,P(n)}, takich, że:

o proces P(i1) czeka na zasób przydzielony procesowi P(i)
o proces P(n) czeka na zasób przydzielony procesowi P(1)

3. Metody unikania zakleszczeń.

[powrót]

Metody zapobiegania zakleszczeniom wiążą się bezpośrednio z warunkami powstawania
zakleszczeń:

● Wzajemne wykluczenie zasoby lokalne i przeznaczone tylko do odczytu nie muszą być objęte

warunkiem wzajemnego wykluczania. Inaczej jest z zasobami niepodzielnymi, muszą być
użytkowane na zasadzie wyłączności, dlatego warunek wzajemnego wykluczania jest przy nich
niezbędny.

● Przetrzymywanie i oczekiwanie aby zapewnić że ten warunek nigdy nie będzie spełniony, należy

wymusić na procesach, aby zamawiały zasoby, tylko wtedy, gdy nie są w posiadaniu innych zasobów

● Brak wywłaszczeń brak spełnienia tego warunku można zapewnić na dwa sposoby:

○ jeśli proces zamawiający zasób musi czekać na jego przydział, to system operacyjny

niejawnie odbiera mu wszystkie zasoby jakie są w jego posiadaniu i niejawnie dopisuje je do
listy jego zamówień. Proces jest budzony z oczekiwania dopiero wtedy, gdy można przydzielić
mu wszystkie te zasoby

○ jeśli proces zamawia zasób, który jest w posiadaniu innego procesu, który czeka na przydział

innych zasobów, to temu ostatniemu procesowi zasób jest odbierany i przydzielany
pierwszemu

● Czekanie cykliczne można zagwarantować niespełnienie warunku czekania cyklicznego nadając

każdemu zasobowi określony, unikatowy numer porządkowy (liczbę naturalną) i wymuszając na
procesach zamawianie zasobów, według rosnącej numeracji

Ponieważ zapobieganie zakleszczeniom polega na ograniczaniu przydziału zasobów procesom, to jego

niekorzystnym skutkiem ubocznym może być zmniejszenie wykorzystania tych zasobów, co z kolei prowadzi

do obniżenia przepustowości systemu. Istnieją jednak inne metody, które można stosować zamiast

zapobiegania zakleszczeniom. Jedną z tych metod jest unikanie zakleszczeń. Jednym z algorytmów

pozwalających na unikanie zakleszczeń jest algorytm bankiera.

Algorytm bankiera algorytm służący do unikania zakleszczeń; polega na utrzymywaniu systemu w stanie

bezpiecznym, tj. na zapewnianiu, że system będzie mógł zawsze przydzielić zasoby procesom w określonej

kolejności z puli zasobów aktualnie dostępnych, powiększonej o zasoby chwilowo utrzymywane przez

procesy. Algorytm bankiera nie dopuszcza do sytuacji, w której zabrakłoby zasobów do przydziału.

Stosowanie algorytmu bankiera jest ograniczone ze względu na jego znaczną złożoność obliczeniową.
Algorytm grafowy w systemach, w których występuje tylko jeden egzemplarz wszystkich typów zasobów

można zastosować prostszy algorytm o mniejszej złożoności. Jest to algorytm grafowy, a graf na którym

przeprowadzane są operacje jest zmodyfikowanym grafem przydziału zasobów.

4. Architektura von Neumanna.

[powrót]

Pierwszy rodzaj architektury komputera, opracowano

przez

Johna von Neumanna, Johna W. Mauchly’ego oraz

Johna

Presper Eckerta w 1945 roku. Cechą charakterystyczną

tej

architektury jest to, że dane przechowywane są wspólnie z instrukcjami, co sprawia, że są kodowane w
ten sam sposób.

W architekturze tej komputer składa się z czterech głównych komponentów:

● pamięci komputerowej przechowującej dane programu oraz instrukcje programu; każda komórka

pamięci ma unikatowy identyfikator nazywany jej adresem

● jednostki sterującej odpowiedzialnej za pobieranie danych i instrukcji z pamięci oraz ich

sekwencyjne przetwarzanie

● jednostki arytmetycznologicznej odpowiedzialnej za wykonywanie podstawowych operacji

arytmetycznych.

● urządzeń wejścia/wyjścia służących do interakcji z operatorem

Jednostka sterująca wraz z jednostką arytmetycznologiczną tworzą procesor.

System komputerowy zbudowany w oparciu o architekturę von Neumanna powinien:

● mieć skończoną i funkcjonalnie pełną listę rozkazów
● mieć możliwość wprowadzenia programu do systemu komputerowego poprzez urządzenia

zewnętrzne i jego przechowywanie w pamięci w sposób identyczny jak danych

● dane i instrukcje w takim systemie powinny być jednakowo dostępne dla procesora
● informacja jest tam przetwarzana dzięki sekwencyjnemu odczytywaniu instrukcji z pamięci komputera

i wykonywaniu tych instrukcji w procesorze.

1. Podane warunki pozwalają przełączać system komputerowy z wykonania jednego zadania

(programu) na inne bez fizycznej ingerencji w strukturę systemu, a tym samym gwarantują jego
uniwersalność.

2. System komputerowy von Neumanna nie posiada oddzielnych pamięci do przechowywania danych i

instrukcji. Instrukcje jak i dane są zakodowane w postaci liczb.

3. Bez analizy programu trudno jest określić czy dany obszar pamięci zawiera dane czy instrukcje.
4. Wykonywany program może się sam modyfikować traktując obszar instrukcji jako dane, a po

przetworzeniu tych instrukcji – danych – zacząć je wykonywać.

5. Model komputera wykorzystującego architekturę von Neumanna jest często nazywany przykładową

maszyną cyfrową (PMC).

5. Cykl rozkazowy komputera.

[powrót]

Cykl rozkazowy składa się z 2 faz:

Pobierania:

1. Wartość licznika rozkazów > Szynę adresową > Pobranie adresu rozkazu > Szyna danych
2. Szyna danych > rejestru rozkazów
3. Zwiększenie licznika rozkazów o jeden (następny rozkaz)

Wykonania:
4. Rejestr rozkazów > dekoder > wynik wykonania rozkazu (np. sygnał sterujący)

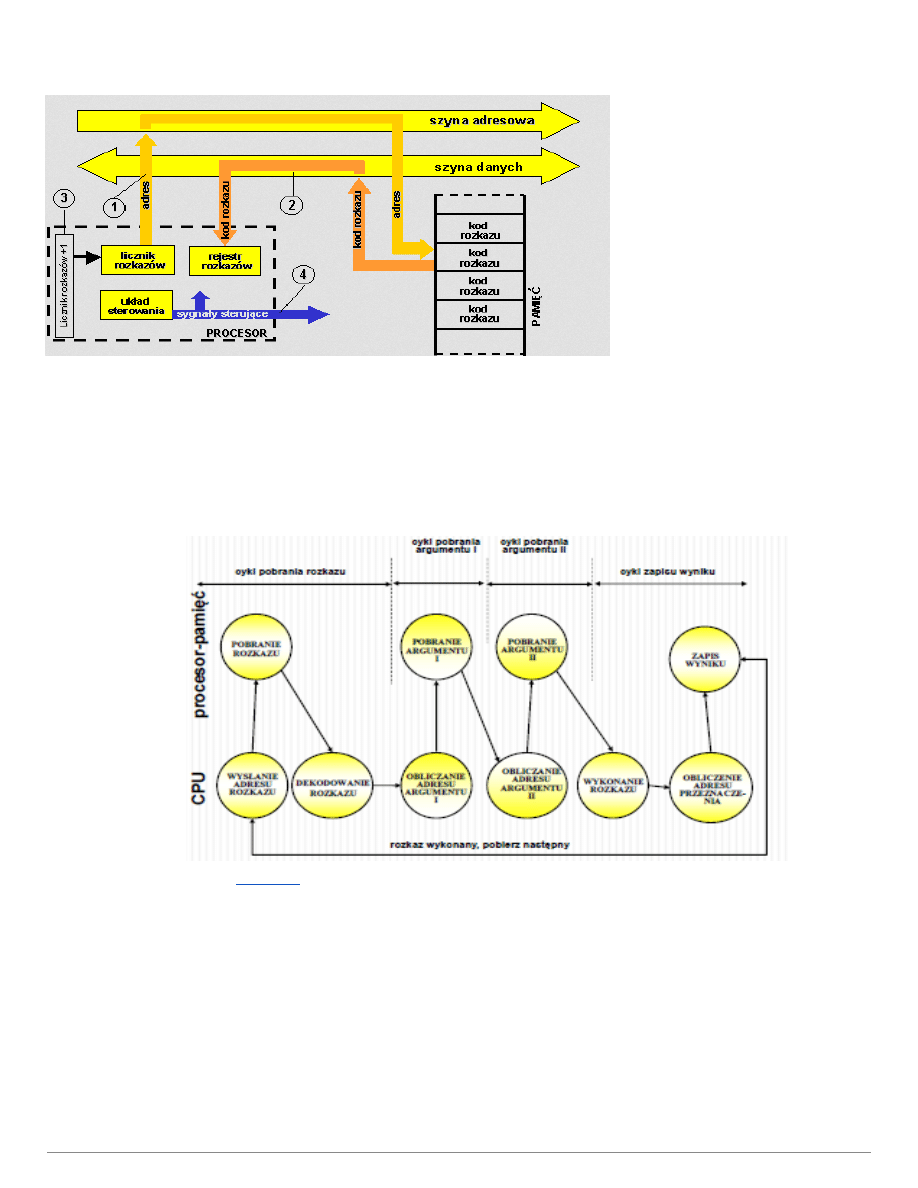
Cykl 14 nazywamy cyklem Neumana

Z punktu logicznego cykl instrukcyjny wygląda tak:

1. Pobranie instrukcji
2. Dekodowanie instrukcji
3. Obliczanie adresu argumentów
4. Pobranie argumentów
5. Wykonywanie instrukcji
6. Zapamiętanie wyników

6. Tryby adresowania.

[powrót]

Rozkaz składa się z kodu operacji (którą należy wykonać) oraz jej argumentów.
Tryby adresowania określają miejsce przechowywania argumentu operacji (rozkazu), np. w kodzie,
rejestrach, pamięci.

W zależności gdzie ten argument jest, wyróżniamy adresowanie:

Natychmiastowe

● Argument zawarty jest w kodzie rozkazu (jest częścią rozkazu)
● Musi być on znany w podczas pisania programu

Nie trzeba się odwoływać do pamięci, bo argument jest od razu częścią rozkazu i nie trzeba nic pobierać

Argument może przechowywać mało informacji (mały rozmiar pola)

Rejestrowe

● Rozkaz zawiera odniesienie do rejestru, w którym jest argument operacji

Rejestrów nie jest dużo, więc odniesienie do rejestru (pole adresowe) ma od 3 do 6 bitów (szybkość
pobierania)

No właśnie rejestrów nie jest za dużo.

Bezpośrednie

● Rozkaz zawiera adres do komórki pamięci, w której jest argument operacji
● Należy zarezerwować adres podczas pisania programu

Jedno odniesienie do pamięci. Nie wymaga żadnych obliczeń

Nieprzenośność programu. Ograniczenie adresacji wielkością pola adresowego (tego co trzyma w rozkazie
adres do komórki)

Pośrednie

● Rozkaz zawiera odniesienie do rejestru, a w rejestrze jest adres komórki pamięci, w której jest

argument.

Duża przestrzeń adresowa. Małe pole adresowe w rozkazie wskazuje na miejsce gdzie jest zapisany pełny
adres.

Wolniej, niż przy jednym odniesieniu do pamięci

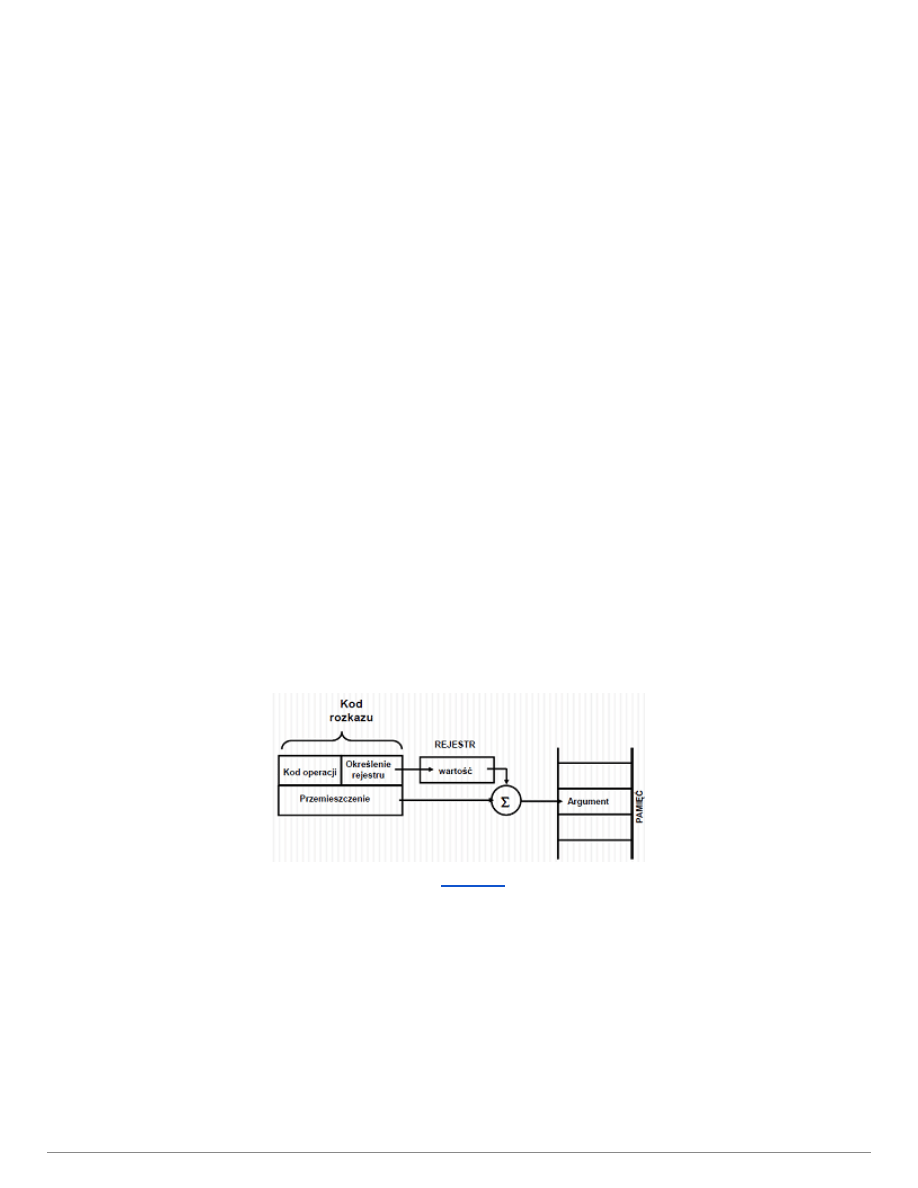
Indeksowe z przemieszczeniem

● Rozkaz zawiera dwa pola: odniesienie do rejestru i przemieszczenie. Argument jest w komórce

pamięci, której adres obliczany jest jako suma przemieszczenia (w rozkazie) i wartości w rejestrze.

Zastosowanie przy adresowaniu względnym.

7. Zwiększanie efektywności pracy procesora.

[powrót]

Rejestr instrukcji przechowuje instrukcje do wykonania.

ALU jednostka arytmetycznologiczna. Taka część procesora, co wykonuje obliczenia.

Ponieważ szybkość pobierania instrukcji z rejestru zależy od:

● Trybu adresowania
● Liczby argumentów
● Czasu dostępu do pamięci
● Czasu wykonywania instrukcji

● Obciążenia szyn danych

I czasem ALU lub szyna danych nie wyrabia i coś musi czekać bezczynnie na drugie.

Aby zwiększyć efektywnosć, zastępuje się rejestr instrukcji > wielopozycyjnym buforem z kolejką
instrukcji.
Dzięki temu, gdy ALU działa wolniej, a szyna dostarcza instrukcji szybciej, to są one odkładane w kolejkę.
Następnie gdy ALU działa szybciej w stosunku do szyny, nie musi na nią czekać, tylko pobiera instrukcje z
kolejki.

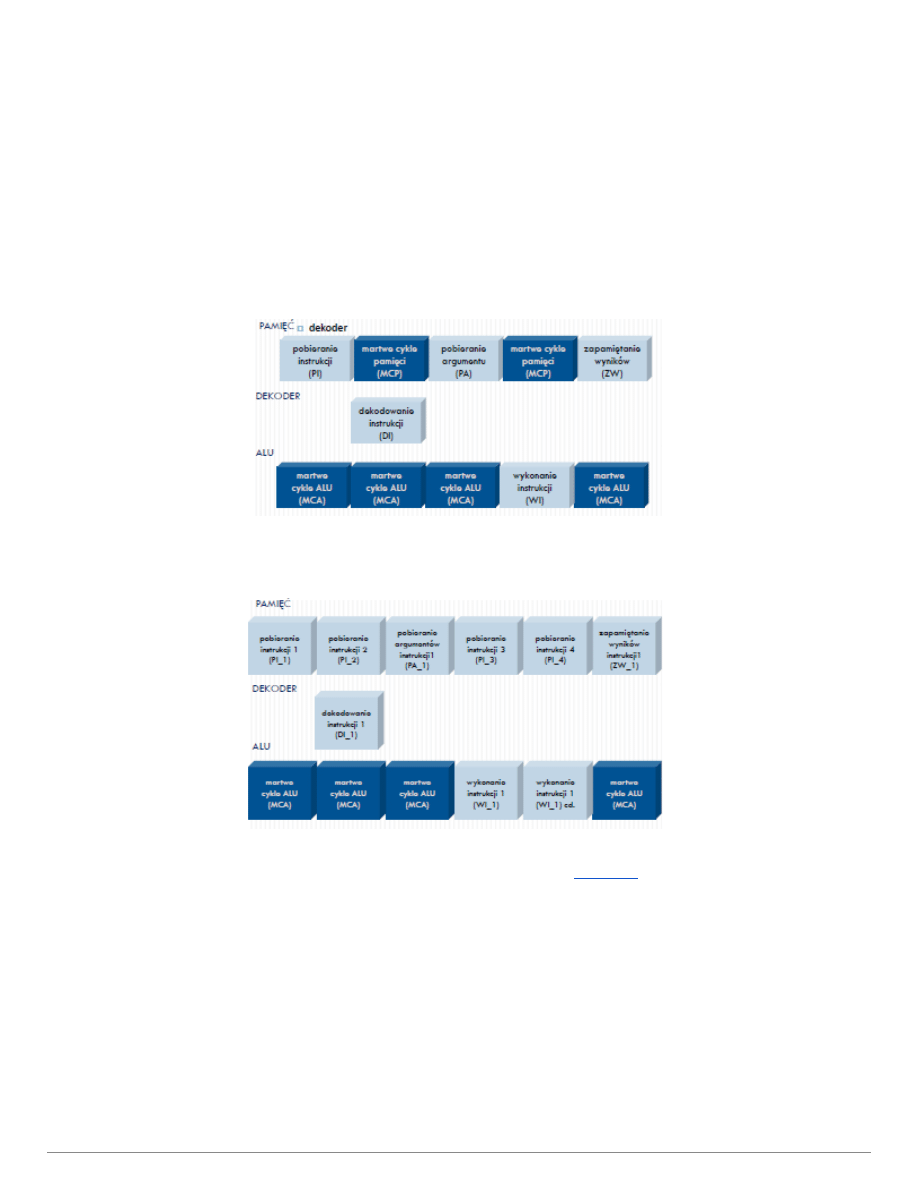
Normalnie cykl pobierania i wykonywani instrukcji wygląda tak:

Po zwiększeniu efektywności procesora, w chwili gdy ALU liczy, pamięć nie czeka i pobiera kolejne
instrukcje do kolejki:

8. Maszyny Turinga – deterministyczna i niedeterministyczna.

[powrót]

Deterministyczna Maszyna Turinga (DTM) to piątka {Q, S, d, q0, F}, gdzie:
Q - zbiór stanów sterowania maszyny,
S - alfabet (zbiór symboli) taśmy,
d - funkcja przejścia:
d: Q x S -> Q x S x {R, L, N}
q0 - początkowy stan sterowania,
F - zbiór końcowych stanów sterowania.
Działanie maszyny:
- Startujemy z pewnego miejsca na taśmie i ze stanu sterowania q0.

- Czytamy symbol s z taśmy.
- Na podstawie tych dwóch danych (stan q = q0, symbol s) za pomocą funkcji d
obliczamy:
- nowy stan q’,
- nowy symbol s’, który zapisujemy na taśmie, oraz
- jeden z symboli: R, L lub N, odpowiadający kierunkowi przemieszczenia się czytnika na
taśmie.
- Operację powtarzamy do momentu, gdy maszyna znajdzie się w stanie sterowania
należącym do zbioru F.
Mimo prostoty sformułowania maszyna Turinga dysponuje bardzo dużymi możliwościami
obliczeniowymi. Jest przy tym na tyle ściśle zdefiniowana, że można z jej pomocą
dokładnie określić, jaka jest złożoność czasowa danego algorytmu - jest to dokładnie
liczba pojedynczych kroków maszyny. To nas uniezależnia od takich drobiazgów
technicznych, jak zastanawianie się nad konkretnym rodzajem procesora i efektami
kompilacji programu (w celu ścisłego policzenia liczby kroków algorytmu).

Niedeterministyczna maszyna Turinga

(NDTM) jest zdefiniowana dokładnie w ten sam

sposób, co deterministyczna, jednak funkcja przejścia d(q,s) może mieć kilka różnych
wartości (efektywnie powodując rozwidlenie działania programu na kilka możliwych
ścieżek). Wynik obliczeń jest pozytywny, jeśli choć jedna z możliwych dróg działania
maszyny doprowadzi do sukcesu.
Możemy sobie wyobrażać NDTM jako maszynę o nieskończonej możliwości klonowania się
i wykonywania wszystkich ścieżek na raz. Możemy też zamiast tego przyjąć, że NDTM
podczas wykonywania "programu" potrafi w magiczny sposób przewidzieć, jakiego
dokonać wyboru (np. czy zapisać na taśmie 1, czy 0), by doprowadzić do pozytywnego
wyniku (o ile jest to w ogóle możliwe). W takim razie jej działanie będzie z zewnątrz
przypominało pracę DTM.
O ile DTM może być z dobrym przybliżeniem utożsamiana ze zwykłymi komputerami, to
NDTM nie udało się jeszcze nikomu zbudować. Mimo tego pojęcie NDTM ma bardzo
pożyteczne własności w teorii złożoności obliczeniowej.

9. Cechy poprawności algorytmu.

[powrót]

a) skończoność  wykonuje się w skończonej liczbie kroków
b) określoność  operacje i ich porządek wykonywania są ściśle określone, brak miejsca na dowolną
interpretację
c) ogólność  algorytm nie ogranicza się do jednego szczególnego przypadku, ale odnosi do pewnej klasy
zadań
d) efektywność  algorytm prowadzi do rozwiązania jak najprostszą drogą
e) kompletność  uwzględnia wszystkie przypadki, realizuje algorytm zgodnie z instrukcjami
przewidzianymi na każdy przypadek
f) jednoznaczność  niezależność działania programu od momentu jego wykonania, innych programów
działających w systemie oraz od sprzętu

10. Zapis liczb w systemie pozycyjnym.

[powrót]

Każdą liczbę przedstawiamy w postaci wyrażenia:

gdzie p jest podstawą systemu liczenia, zaś liczby oznaczone literą c z indeksami, nazywamy cyframi. Cyfry
wyrażają liczbę użytych jednostek rzędu, przy której występują

Przykład:

11. Zapis liczb w systemie zmiennopozycyjnym

[powrót]

Zapis zmiennopozycyjny – liczba w tym zapisie składa się z trzech części: liczby stałoprzecinkowej, podstawy

systemu i potęgi zwanej wykładnikiem lub cechą

(Przykład od krupińskiej, w liczeniu oczywiście błąd, ale wyniki dobre)

L=m*p^c

m - mantysa, część ułamkowa

p - podstawa systemu,

c – cecha, wykładnik potęgowy.

12. Zapis liczby w kodzie U2

[powrót]

Kod uzupełnień U2 - Pozycja znakowa (najstarszy bit) posiada swoją wagę i uczestniczy w wartości liczby jak

każda inna pozycja.

Wartość liczby U2 obliczamy: cyfry mnożymy przez wagi pozycji, na których się znajdują i dodajemy otrzymane

iloczyny. Waga bitu znakowego jest ujemna.

gdzie b - bit, cyfra dwójkowa 0 lub 1; n - liczba bitów w zapisie liczby

Przykład:

13. Liczba przeciwna w kodzie U2

[powrót]

1. Przejść do pierwszego od prawej strony bitu zapisu liczby.
2. Do wyniku przepisać kolejne bity 0, aż do napotkania bitu o wartości 1, który również przepisać.
3. Wszystkie pozostałe bity przepisać zmieniając ich wartość na przeciwną.

Przykład:

● Analizę liczby rozpoczynamy od ostatniej cyfry zapisu liczby. Przesuwamy się w lewą stronę. Do

wyniku przepisujemy wszystkie kolejne bity o wartości 0, aż do napotkania bitu 1.

● Napotkany bit 1 również przepisujemy do wyniku bez zmian:
● Pozostałe bity przepisujemy zmieniając ich stan na przeciwny

Liczba U2

1100100010111010111010010100001000000

Liczba przeciwna U2

001101110100010100010110101111

1000000

14. Przeliczanie liczb dziesiętnych na liczby w kodzie U2

[powrót]

Dla liczb dodatnich nie ma problemu z przeliczaniem na kod U2. Wystarczy znaleźć reprezentację dwójkową
danej wartości liczbowej, a następnie uzupełnić ją bitami 0 do długości formatu kodu U2
Przykład:

Wyznaczyć 8-mio bitowy kod U2 dla liczby dziesiętnej 27(10).

27(10) = 16 + 8 + 2 + 1 = 11011(2) = 00011011(U2).

W przypadku wartości ujemnej postępujemy tak:

1. Wyznaczamy zapis dwójkowy liczby przeciwnej (czyli dodatniej).

2. Otrzymany kod dwójkowy uzupełniamy w miarę potrzeb do rozmiaru formatu U2
3. Wyznaczamy liczbę przeciwną za pomocą opisanej wcześniej metody

15. Zapis liczby w kodzie U1

[powrót]

Kod uzupełnień U1 - W systemie tym wszystkie bity zapisu liczby posiadają swoje wagi. Najstarszy bit jest bitem

znaku i ma wagę równą (-2^(n-1)+1). Pozostałe bity posiadają wagi takie jak w naturalnym systemie dwójkowym.

Wartość liczby U1 obliczamy zgodnie z zasadami - cyfry mnożymy przez wagi pozycji, na których się znajdują i

dodajemy otrzymane iloczyny:

gdzie b - bit, cyfra dwójkowa 0 lub 1; n - liczba bitów w zapisie liczby

Może by kto trzasnął jakiś przykładzik?

16. Standard zapisu zmiennoprzecinkowego IEEE 754

[powrót]

IEEE 754 standard zapisu liczb zmiennoprzecinkowych, określający ich zapisu.
Liczba zapisywana jest na 32 bitach. Istnieje też liczba podwójnej precyzji na 64 bitach.

● 1 bit Bit znaku. 0= liczba dodatnia. 1 = liczba ujemna
● 8 bitów Wykładnik (cecha). Wartości od <127,128>
● 23 bity Mantysa. A właściwie jej część ułamkowa. Jest to liczba od 1 do 2. W bitach jest

zapisywane tylko to, co jest po przecinku, więc przy dekodowaniu należy dodać 1.

Oprócz liczby można zapisać tam specialne wartości:

● Nieskończoność wykładnik=same 1 , mantysa=same 0. Pojawia się np. przy dzieleniu przez 0
● NaN not a number. wykładnik=same 1 , mantysa=kod błędu. Pojawia się jako wynik jakiegoś błędu.
● 0+ Wszystkie bity=0
● 0 Bit znaku=1, reszta=0

Liczbę L odczytujemy za pomocą wzoru:

http://lidiajs.kis.p.lodz.pl/Systemy_Liczbowe/standard_754_teoria.php

17. Notacja nadmiarowa

[powrót]

18.Złożoność algorytmów

[powrót]

Ilość zasobów niezbędnych do wykonania algorytmu można rozumieć jako jego złożoność. W zależności od
rozważanego zasobu mówimy o złożoności czasowej czy też pamięciowej. W większości wypadków ilość
potrzebnych zasobów będzie się różnić w zależności od danych wejściowych z zakresu danego
zagadnienia.
Im większe rozmiary danych wejściowych, tym więcej zasobów (czasu, procesorów, pamięci) jest
koniecznych do wykonania danych obliczeń. Złożoność algorytmu jest więc funkcją rozmiaru danych
wejściowych.
Zadaniem analizy algorytmu jest określenie tej złożoności, a co za tym idzie realizowalności algorytmu.

Ogólnie:
Złożoność obliczeniowa nie zależy od architektury i konfiguracji sprzętowej komputerów (wyznaczamy ją dla
maszyny z pamięcią o dostępie swobodnym), ale zależy od rozmiaru i uporządkowania danych
wejściowych. Wyznaczając złożoność obliczeniową algorytmu badamy 3 przypadki: optymistyczny,
pesymistyczny i średni.

W skrócie:

Złożoność czasowa

liczba "podstawowych operacji", jakie musi wykonać dany

algorytm rozwiązujący zadanie.

Złożoność pamięciowa

liczba "podstawowych jednostek pamięci", które zajmuje

program podczas pracy.

19. Rodzaje języków programowania

[powrót]

Język programowania – zbiór zasad określających, kiedy ciąg symboli tworzy program (czyli ciąg symboli
opisujący obliczenia) oraz jakie obliczenia opisuje. Język programowania pozwala na precyzyjny zapis
algorytmów oraz innych zadań, jakie komputer ma wykonać.
Rodzaje języków:

● Poziom języka:

o Języki wysokiego poziomu – rozbudowana składnia, czytelna dla programisty. (np. C++, Java)

o Języki niskiego poziomu (asemblery) - posługują się składnią zbliżoną do elementarnych operacji

procesora i adresów symbolicznych reprezentujących jego rejestry; łatwo przekształcalne do kodu

maszynowego

● Sposób wykonywania:

o Kompilowane, gotowe do wykonywania przez system operacyjny (np. C++)

o Interpretowane, wykonywane przez tzw. interpretery (np. matlab, html)

(html to nie język programowania!!!) (php, ruby, perl etc.)

● Paradygmat programowania:

o Proceduralne

o Strukturalne

o Obiektowe

20. Problemy NP i NPzupełne

[powrót]

Problem NP (niedeterministycznie wielomianowy, ang. nondeterministic polynomial) to problem
decyzyjny, dla którego rozwiązanie można zweryfikować w czasie wielomianowym. Równoważna definicja
mówi, że problem jest w klasie NP, jeśli może być rozwiązany w wielomianowym czasie na

niedeterministycznej maszynie Turinga

Różnica pomiędzy problemami P i NP polega na tym, że w przypadku P znalezienie rozwiązania ma mieć
złożoność wielomianową, podczas gdy dla NP sprawdzenie podanego z zewnątrz rozwiązania ma mieć
taką złożoność.

Przykładowo rozważmy problem:

Czy jakikolwiek niepusty podzbiór zadanego zbioru (np. {2,6,3,72,10,11}) sumuje się do zera ?

Trudno znaleźć rozwiązanie tego zagadnienia w czasie wielomianowym. Nasuwający się algorytm
sprawdzenia wszystkich możliwych podzbiorów ma złożoność wykładniczą ze względu na liczebność zbioru.
Nie wiadomo zatem, czy problem ten jest klasy P. Na pewno natomiast uzyskawszy z zewnątrz kandydata
na rozwiązanie (np. {2,6,3,10,11}) możemy w liniowym (a zatem wielomianowym) czasie sprawdzić, czy
sumuje się do zera. Jest to zatem problem NP.
Problem NPzupełny (NPC) czyli problem zupełny w klasie NP ze względu na redukcje wielomianowe, to
problem, który należy do klasy NP oraz dowolny problem należący do NP może być do niego zredukowany
w czasie wielomianowym. Czasami zamiast redukcji w czasie wielomianowym używa się redukcji w
pamięci logarytmicznej. Pytanie, czy są to definicje równoważne pozostaje pytaniem otwartym. Taka
definicja problemów NPzupełnych implikuje fakt, że jeśli tylko potrafimy rozwiązać jakikolwiek problem

NPzupełny w czasie wielomianowym, to potrafimy rozwiązać w czasie wielomianowym wszystkie problemy
NP. Problemy NPzupełne można więc traktować jako najtrudniejsze problemy klasy NP (z punktu widzenia
wielomianowej rozwiązywalności).

Pierwszym problemem, którego NPzupełność wykazano, był problem SAT, czyli problem spełnialności
formuł zdaniowych. Udowodnił to w 1971 roku Stephen Cook.

Pytanie związane z problemami NPzupełnymi ma szczególne znaczenie w kryptografii rozwiązanie
któregokolwiek problemu NPzupełnego w czasie wielomianowym (a zatem rozwiązanie ich wszystkich)
umożliwiłoby między innymi szybkie łamanie szyfru RSA (jednego z najbardziej popularnych szyfrów
aktualnie stosowanych) opiera się on na założeniu, że problem podziału dowolnej liczby na czynniki
pierwsze nie jest problemem wielomianowym. Problem ten jest w NP, ale nie udowodniono jego
NPtrudności.

(źródło:

http://pl.wikipedia.org/wiki/Problem_NPzupe%C5%82ny

)

Wyszukiwarka

Podobne podstrony:
byt-opracowanie-pytan, byt-omowienia-zagadnien
miernicto omówienie zagadnień kontrolnych
32 opis zagadnien, OMÓWIENIE ZAGADNIEŃ TEORETYCZNYCH
Ekonomia omówienie zagadnień
Erystyka - omówienie zagadnienia, Retoryka i erystyka
Polityka gospodarcza - omówienie zagadnień, Ekonomia, ekonomia
Makroekonomia omówienie zagadnień
Polityka gospodarcza omówienie zagadnień
Ekonomia - omówienie zagadnień, Ekonomia, ekonomia
Psychologia-omowienie zagadnien, Studia, Psychologia
Postać literacka - omówienie zagadnienia, Poetyka

więcej podobnych podstron