1

Geologia górnicza – kolokwium II

Oprac. Adam 

Zakres – statystyczny opis zmienności parametrów złożowych oraz ocena zasobów złoża bilansowego.

I. Błędy (1) – Błędy rzecz ludzka, często się zdarzają, a potem jest problem z interpretacją. Poniżej
wypisze i krótko scharakteryzuje te podstawowe (właściwie to ostatni temat poprzedniego kolosa,
ale jest tu pewien związek i z tym):
Błędy mogą być związane z pobraniem próbki ze złoża, z przygotowaniem jej do analizy lub z samą
analizą. I tak wyróżniamy:

a) błędy przypadkowe

pobór próbki – niedokładne pobranie, rozrzut materiału, zanieczyszczenie

przygotowanie próbki – zły schemat przygotowania, złe oczyszczenie urządzeń

analiza – mało staranna, słabe doświadczenie, błędy urządzeń

b) błędy systematyczne

pobór próbki – wykruszenie się niektórych minerałów / ich wietrzenie

przygotowanie próbki – wietrzenie w przypadku złego opakowania

analiza – zła metodyka, zanieczyszczenia, słabe wymieszanie materiału

c) błędy grube (pomyłkowe)

pobór próbki – błędy w numerowaniu próbek, niewłaściwy sposób poboru, opr. tendencyjne

przygotowanie próbki – błędy w numerowaniu, zanieczyszczenie mat. obcym

analiza – znowu pomyłki w numeracji, ogólnie zła metodyka

Teraz warto tylko przypomnieć co to jest błąd systematyczny i losowy.
Błąd systematyczny to taki błąd, gdzie wartość różnicy pomiędzy wartością rzeczywistą, a
pomierzoną jest stała. Błąd losowy - wartość ta jest zmienną losową.

2

Błąd systematyczny liczymy ze wzoru:

Przy czym n to liczba pomiarów sparowanych, Xi to analizy kontrolne, Yi – podstawowe.
Oczywiście aby otrzymać z tego błąd systematyczny względny, wynik dzielimy przez średnią
arytmetyczną i mnożymy przez 100%.

Błąd losowy liczymy ze wzoru

To samo aby otrzymać błąd względny.

Istnieje również tzw. wzór Karolewa, mówiący żeby jeśli podana niżej nierówność nie jest spełniona
to występuje błąd systematyczny:

II. Statystyczny opis zmienności

Co to jest statystyczny opis zmienności?* (kol)

Statystyczny opis zmienności polega na wykorzystaniu aparatu matematycznego, a konkretniej
rozkładu prawdopodobieństwa, do opisu całego zbioru zwanego populacją. Wnioskowanie o całej
populacji jest możliwe używając tylko jej części – tzw. próby statystycznej. Przez próbę statystyczną z
kolei należy rozumieć zestaw wyników pomiarów parametrów złożowych, przyporządkowanych
odpowiednim próbom geologicznym.
Cała populacja daje nam opis własności złoża, co jest celem geologii górniczej.

Zbiór czy zestaw wyników pomiarowych, możemy przedstawić/opisać za pomocą 4 grup miar
statystycznych:

Jakie mamy miary rozkładu?

1) miary położenia (tendencji rozkładu)

średnia arytmetyczna - wiadomo
mediana – wartość środkowa (przy nieparzystej ilości danych, średnia arytmetyczna dwóch
środkowych wyrazów).

moda – wartość najczęstsza (może ich być kilka)

Poza tym wyróżniamy szereg pozycyjny – gdzie wartości są ułożone od najmniejszej do największej
oraz szereg rozdzielczy, gdzie wartości są posegregowane w odpowiednie klasy.

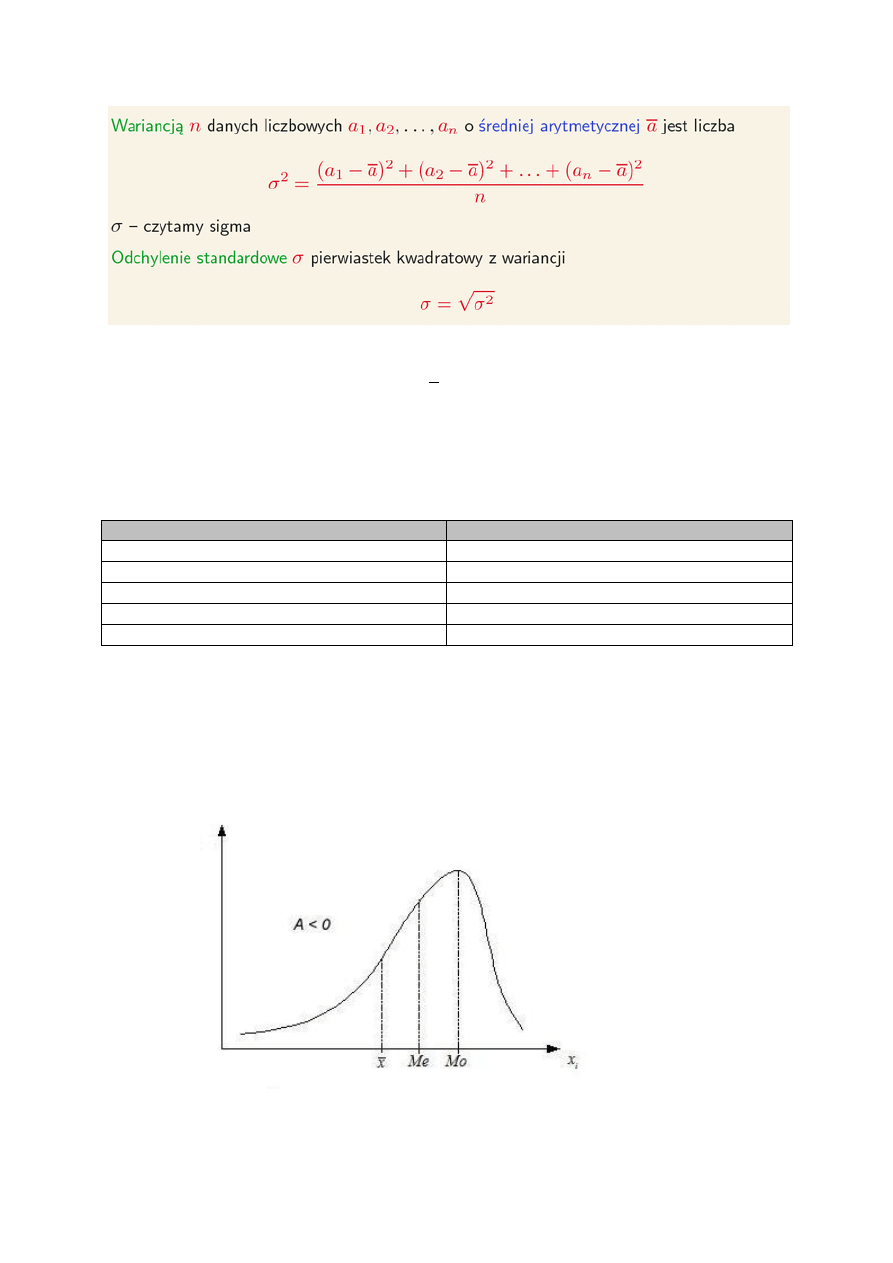
2) miary rozproszenia

odchylenie standardowe

wariancja

współczynnik zmienności

Poniżej jest wytłumaczone co i jak:

3

Współczynnik zmienności z kolei oznaczamy literką V i obliczamy go jako:

UWAGA: σ=s (różne oznaczenia)
x – średnia arytmetyczna

Mając już współczynnik zmienności możemy określić charakter zmienności, a zrobić to możemy za
pomocą tej tabeli:

V – współczynnik zmienności [%]

Zmienność

0 - 20

Mała

20 - 40

Przeciętna

40 - 100

Duża

100 - 150

Bardzo duża

powyżej 150

Skrajnie duża

3) miary asymetrii (skośności)

współczynnik asymetrii (wzór zbyt skomplikowany)

rozkład lewoasymetryczny (ujemny)

jak widać x<Me<Mo

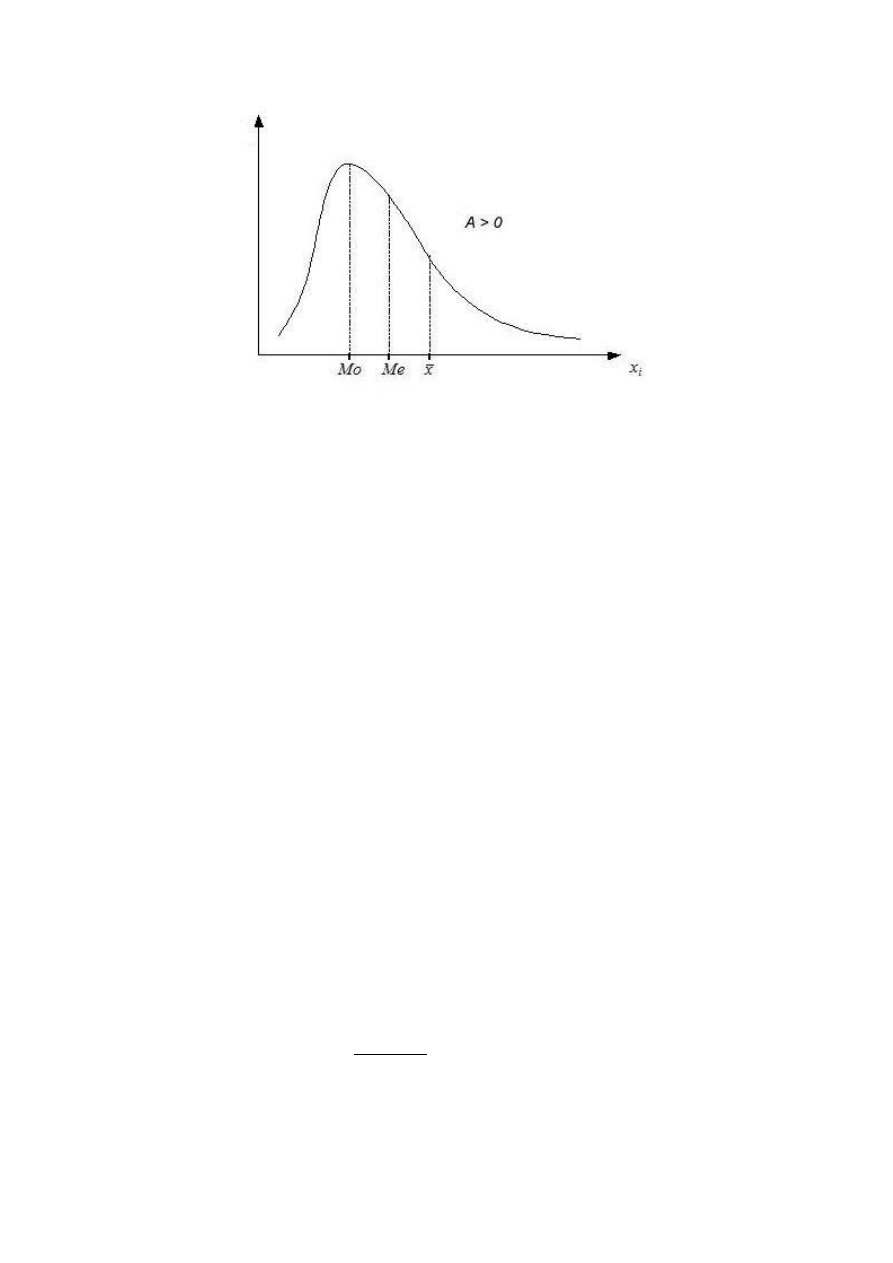
rozkład prawoasymetryczny (dodatni)

4

x>Me>Mo – średnia arytmetyczna może zawyżać/zaniżać wartość parametru

Współczynnik asymetrii wspomaga wizualną ocenę asymetrii rozkładu. Obliczając go, możemy

posłużyć się poniższą klasyfikacją i ocenić stopień asymetrii:

0 – 0,5 – symetria

0,5 -1 – asymetria słaba

1 – 2 – asymetria umiarkowana

2 – 4 – asymetria silna

powyżej 4 – asymetria skrajnie silna

[wszystko w wartości bezwzględnej, bo może wyjść ujemny]

4) miary spłaszczenia (ekscesu)

współczynnik spłaszczenia (-||-)

rozkład może być zbliżony do normalnego  klasyczny dzwon

może być taki, że współczynnik spłaszczenia > 0  wykres b.wypukły ku górze
może być taki, że współczynnik spłaszczenia <0  wykres bardzo słabo wypukły, o
dużym rozprzestrzenieniu.

Ważnym typem wykresu jest histogram. Jest to wykres słupkowy wykreślony w prostokątnym
układzie współrzędnych, na którym na osi odciętych (x) znajdują się poszczególne przedziały klasowe,
natomiast na osi rzędnych (y) – ich liczebności bądź udziały procentowe, czyli częstości. Histogram
może być 1/2/polimodalny oraz może być symetryczny lub wykazywać asymetrię. Mogą się też
pojawić wartości anomalne – widoczne gołym okiem na wykresie.

Istnieje kilka wskazówek dotyczących tworzenia histogramu:


- liczba klas od 7 do 15
- dobrze jest obliczyć liczbę przedziałów lub szerokość przedziału

liczba przedziałów  m = 1 + 3,3 log(n) – gdzie n to liczebność próbki/ilość pomiarów

szerokość przedziału  ΔX =

- należy zaokrąglać wartości, tj. jeśli na przykład x

min

= 0,34, przyjmijmy 0,3, itd.

Poza wymienionymi miarami, można jeszcze mówić o kwartylach (dolnym i górnym)

kwarty dolny (q

1

) – 25 % wartości mniejszych lub równych jego wartości.

5

kwartyl górny (q

3

) – 75% wartości mniejszych lub równych jego wartości.

Ocena przedziałowa zmienności parametrów:

W statystyce wykorzystuje się właściwie 2 metody oceny średnich wartości parametrów:

a) metodę punktową – wykorzystującą wartość średniej arytmetycznej, która najlepiej pozwala
poznać przybliżenie wartości nieznanego parametru, jednak z uwagi na błędy analizy chemicznej,
błędy opróbowania oraz naturalną zmienność parametrów – jest to metoda bardzo ryzykowna.

b) metodę przedziałową – tutaj zakłada się, że wartość średnia nieznanego parametru (m) leży w
pewnym przedziale z określonym prawdopodobieństwem. Wyznacza się przedziały ufności.

jeśli ilość punktów rozpoznania (czy też ilość próbek) > 30  rozkład średniej arytmetycznej jest
zbliżony do normalnego (dzwon).

Wzór do oceny przedziałowej:

dolna granic liczba górna granica

przedziału danych przedziału

Oznaczenia:

x – średnia arytmetyczna
s – odchylenie standardowe
z – współczynnik ufności wyznaczony z tablic rozkładu dla danego α
n – ilość punktów rozpoznania
m – szukana, rzeczywista średnia wartość danego parametru
α – poziom istotności – dopełnienie tej wartości do jedności informuje o prawdopodobieństwie P
wypełnienia relacji zaznaczonej we wzorze nawiasami.

Dodatkowe objaśnienie do α: Jeżeli mamy prawdopodobieństwo P na założonym poziomie 95%, tzn.,
że poziom istotności α = 5%, a mówiąc inaczej, ryzyko popełnienia błędu wynosi tylko 5%.

Wyróżniamy kilka najczęściej zakładanych poziomów P:

1) P=0,68 (68%) – najwęższy przedział, ale największe ryzyko błędu – inaczej prawdopodobieństwo
standardowe.

2) P=0,95 (95%) – pośredni przedział i ryzyko błędu (5%)

3) P =0,99 (99%) – prawie zerowe ryzyko błędu, ale z kolei najszerszy możliwy przedział ufności.

Założenia:

Wzory na przedziały ufności można zastosować jedynie wtedy, kiedy zmienność parametrów jest
losowa. Nie może również występować tzw. autokorelacja – czyli jakakolwiek zależność dwóch
parametrów (dla przykładu – w złożu Cu-Ag rośnie nam gęstość przestrzenna skały goszczącej, a w
związku z tym, rośnie również zawartość procentowa Cu w tej skale).

6

Zastosowanie statystycznego opisu zmienności w geologii górniczej:

- szacowanie średnich wartości parametrów złożowych
- wyznaczanie gęstości sieci rozpoznawczej (g

S

=

)

- obliczanie zasobów danego złoża (z wykorzystaniem metod, które będą opisane niżej)
- obliczanie minimalnej ilości punktów rozpoznania n

Wracając do sieci rozpoznawczej. Co to jest sieć reprezentacyjna?

Jest to sieć, o takiej gęstości, która gwarantuje uzyskanie z góry zadanej dokładności rozpoznania z
pewnym, z góry zadanym prawdopodobieństwem (P).
Dokładność rozpoznania = dokładność oceny średniej wartości parametrów złożowych
Dokładność rozpoznania powinna być osiągnięta oczywiście możliwie najniższym nakładem
finansowym.

Tutaj stosujemy wzór:

Do tego oblicza się błąd bezwzględny, czyli dopuszczalny, bezwzględny błąd oceny średniej wartości
parametru:

=

(względny – podzielić na średnią * 100%)

Teraz, aby wyznaczyć z tego minimalną liczbę punktów rozpoznania , należy wyznaczyć n, a prawą

stronę podzielić przez Z (PROBLEM OZNACZEŃ, U NAS X – średnią arytmetyczną zawartość składnika

użytecznego) oraz pomnożyć * 100%

wartość

wówczas zamieni się na na

ε

w

czyli błąd względny oraz będziemy mieli też współczynnik

zmienności V = s/x.

Kategorie rozpoznania:

A  10%
B  20%
C-130% BŁĘDU [%]
C-2 40%

Metody wyznaczania zasobów złoża + parametry bilansowości dla siarki

Parametr

Wymagania/Kryteria

Maksymalna głęb. spągu

400 [m]

Minimalna zawartość S próbce konturującej złoże

10 [%]

Minimalna średnia zawartość S w serii złożowej

10 [%]

Minimalna zasobność jednostkowa złoża

75 [Mg/m

2

]

Przypomnijmy co to była zasobność jednostkowa:

7

q

j

= M * Z * γ * 0,01 [Mg/m

2

]

M – miąższość [m]
Z – średnia zawartość składnika użytecznego [%]
γ – gęstość przestrzenna skały goszczącej [Mg/m

3

] lub [kg/m

3

]

Możemy też policzyć zasobność liniową:

q

l

= M * Z [m%]

Czyli jest to zasobność złoża w jednostce jego długości.

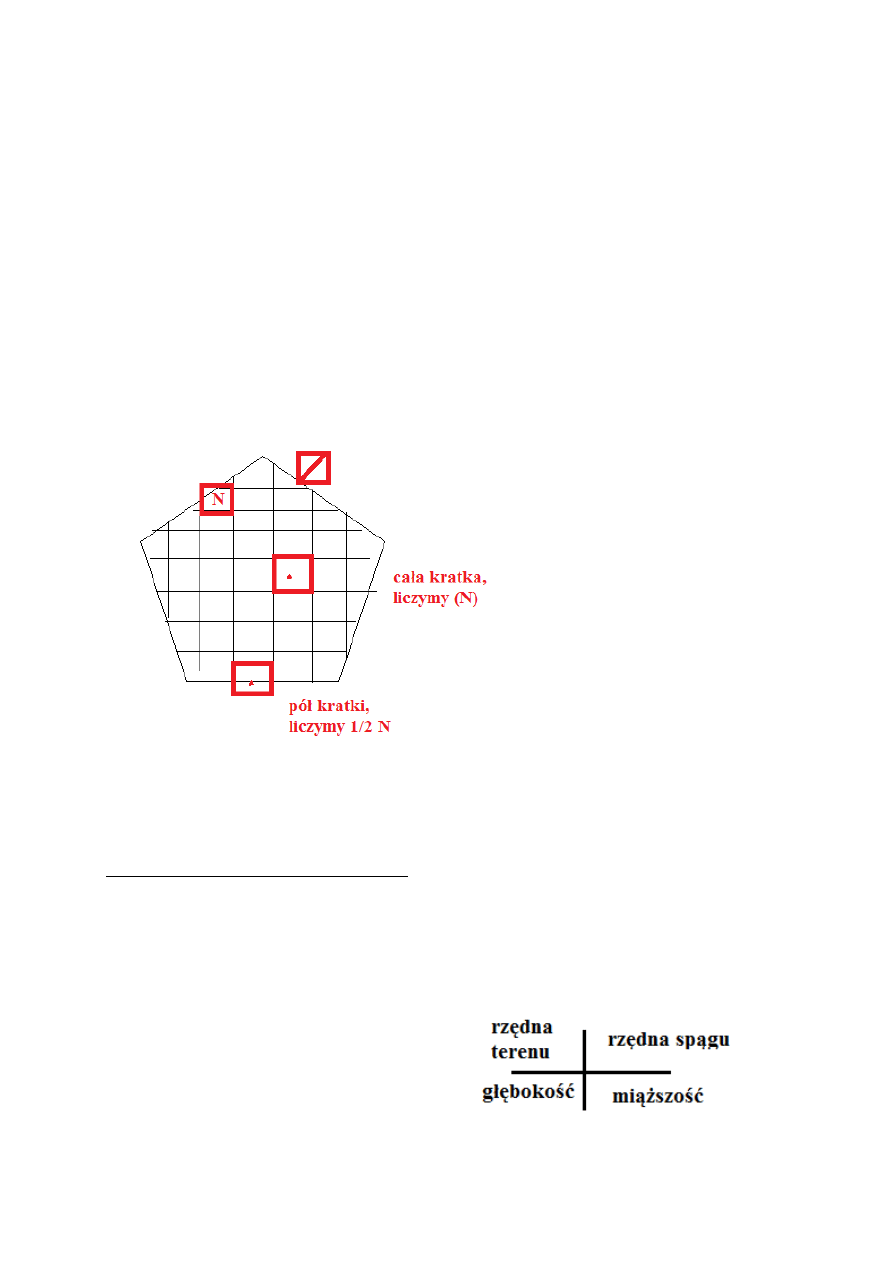
Jeśli nie dysponujemy żadnym programem, który szybko policzy za nas pole okonturowanego przez
nas złoża, można posłużyć się metodą paletki:

Później zliczone elementy podstawia się do wzoru na pole:

F = N * a

2

+ ½ N

pół

*a

2

i mamy pole (a oznacza bok małego kwadratu – kratki)

Z jakimi rodzajami map możemy się spotkać?

1) Mapa sytuacyjno – wysokościowa fragmentu złoża

Co na niej jest?

numer otworu

rzędna spągu oraz stropu

miąższość złoża

rzędna terenu

głębokość otworu

średnia zawartość składnika użytecznego

grubość nadkładu

głębokość spągu

zasobność liniowa [m%]

gęstość przestrzenna

8

2) Mapa obliczenia zasobów bilansowych metodą średniej zasobności
3) Mapa obliczenia zasobów bilansowych metodą wieloboków

Co na niej jest?

informacje o q

i

podane powierzchnie (F

i

) i zasoby (Q

i

) wieloboków

łączne zasoby dla całej granicy

No dobra, ale jak obliczyć te zasoby?

1) Metody geometryczno – statystyczne (!)

metoda średniej arytmetycznej

metoda średniej zasobności

metoda wieloboków

2) Metody geometryczno – geologiczne

metoda przekrojów

metoda izolinii (gridding)

metoda bloków

Zanim zacznę omawiać poszczególne metody, należy również zwrócić uwagę, że każda mapa
zasobów musi posiadać (poza elementami podstawowymi wymienionymi wyżej):

granice obszaru dokumentowanego i wyinterpretowane granice złoża

kontur obszaru obliczenia zasobów

granice wydzielonych rodzajów / kategorii złóż

kontur pól obliczeniowych (parceli) z wewnętrzną informacją o

średniej zasobności jednostkowej

powierzchni takiej parceli

zasobach tej parceli

Teraz konkrety (jak liczyć?)

METODA ŚREDNIEJ ARYTMETYCZNEJ

METODA ŚREDNIEJ ZASOBNOŚCI

Q = M * Z (nie dla węgla) * γ * P * 0,01 * F [Mg]=[t]

M – miąższość
Z – średnia arytmetyczna zawartość składnika
użytecznego
γ – gęstość przestrzenna
P – średnia zawartość %-wa składnika użytecznego

Co jeszcze trzeba wiedzieć?
- metodę można stosować zarówno dla rozpoznania
wiertniczego jak też górniczego
- musi występować zmienność losowa
- nie może występować autokorelacja (wyżej)
- należy określić wielkość błędy oszacowania
zasobów.

Q = M * Z (-||-) * γ * 0,01 * F [Mg]=[t]
lub prościej
Q = q

j

* F

gdzie q

j

to oczywiście zas. jednostkowa.

Co jeszcze trzeba wiedzieć?
- metodę można stosować zarówna dla
rozpoznania wiertniczego jak też górniczego.
- musi być zmienność losowa
- MOŻE występować autokorelacja
- konieczna ocena błędu oszac. zasobów

9

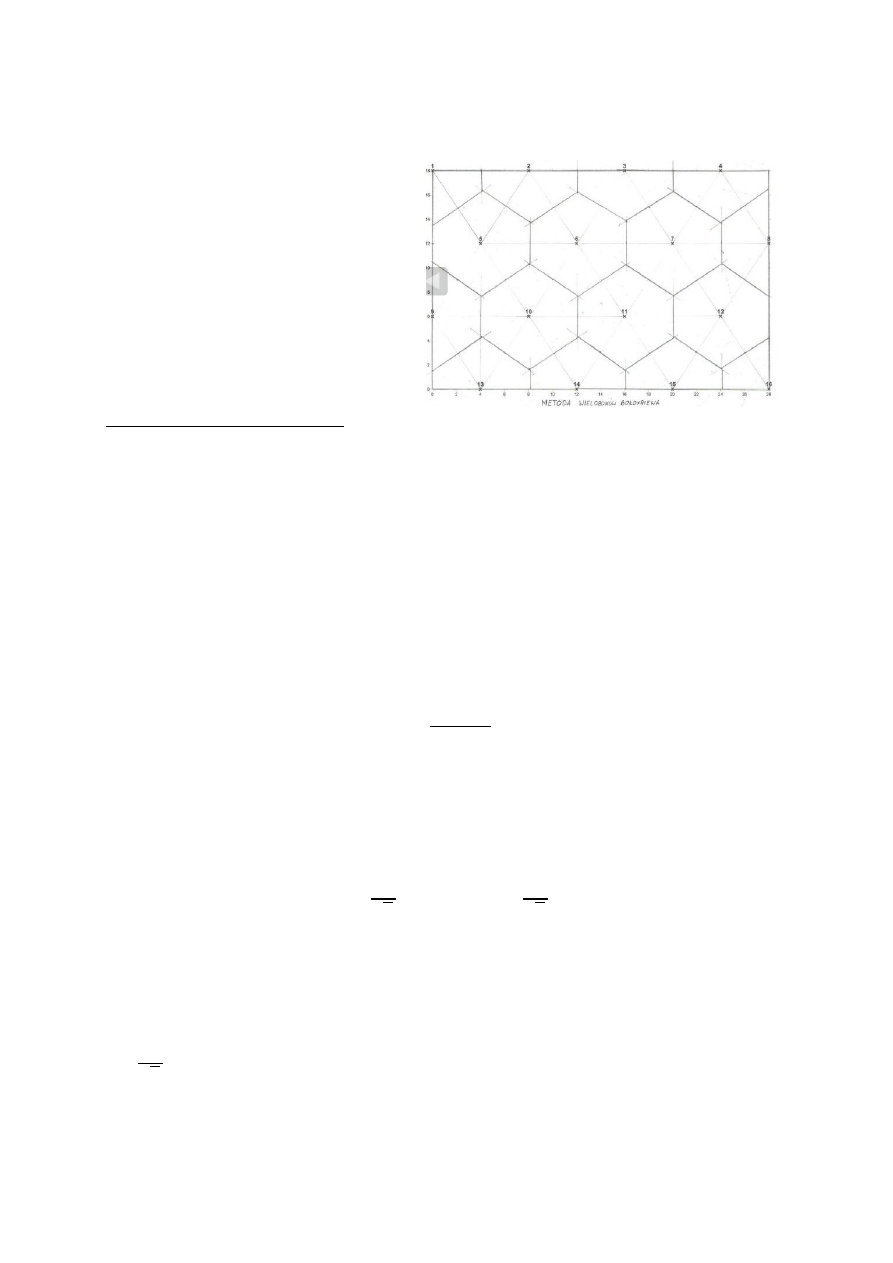
METODA WIELOBOKÓW:

- Inaczej zwana metodą najbliższego
sąsiedztwa Bołdyriewa. Polega na stworzeniu
wieloboków, które w rzeczywistości stanowią
tylko podstawy graniastosłupów o wysokości
= M lub q

j

. Następnie szkicuje się symetralne

wewnętrznych odcinków łączących
poszczególne otwory i na przecięciu
symetralnych powstaje nowa figura –
wielobok. Tak postępujemy ze wszystkimi
otworami.

Zasoby liczone dla i-tego wieloboku

Q

i

= F

i

* q

i

Q =

Ostatnim krokiem jest kontrola poprawności obliczenia zasobów:

Przede wszystkim należy najpierw porównać wyniki osiągnięte wszystkimi zastosowanymi

metodami (na ćwiczeniach była to metoda średniej zasobności oraz metoda wieloboków).

Jeżeli metodę średniej zasobności przyjmiemy za metodę podstawową i oznaczymy tak

obliczone zasoby przez Q

P

, a metodę wieloboków za kontrolną (Q

k

), to mamy:

R

W

=

R

W

≤ 5%

(nie może wyjść więcej różnicy względnej)

I już na sam koniec ocena przedziałowa zasobów:

Założenie: N<30 (mało pkt rozpoznania)+ normalność rozkładu+ P=0,95 (95%)

(P) { [F * (q –

)] < Q

RZ

< F * (q +

)] = 1 – α}

Wzór podobny do poprzedniego (patrz ocena przedziałowa, wyżej) – po prostu został

przekształcony pod parametr takie jakie średnia zasobność jednostkowa (q) oraz zasoby (Q)

Liczymy błąd oszacowania zasobów

ε

q

=

 ε

q

*F = ε

Q

 ε

Q

/Q

P

* 100% = ε

QW

(BŁĄD WZGLĘDNY OSZACOWANIA ZASOBÓW) [%]

Współczynnik „t” odczytuje się z tablic, biorąc pod uwagę N i P (u nas ≈2).