/40
Imi Nazwisko
nr indeksu
pkt
ocena
ARYTMETYKA – KOLOKWIUM 2
27 stycznia 2006
Janusz Biernat
Errata rozwi
ązań opublikowanych 27.01.2006 (poprawki naniesione w tekście na następnych stronach)
G2/4: Jest 15 ma by
ć 13
G4/6: Jest 1,643
7
ma by
ć 1,656
2
G5/6: Jest 2
–54
ma by
ć 2
54
G5/7a: Skutkiem „literówki” był bł
ędny zapis przekodowanego mnożnika i całego mnożenia.
Wszystkie sensowne rozwi
ązania zadania 2a i 2b były akceptowane (choć niekoniecznie ocenione na
maksymaln
ą liczbę punktów). Poniżej rozwiązania podane 27.01, alternatywne rozwiązania w tekście.
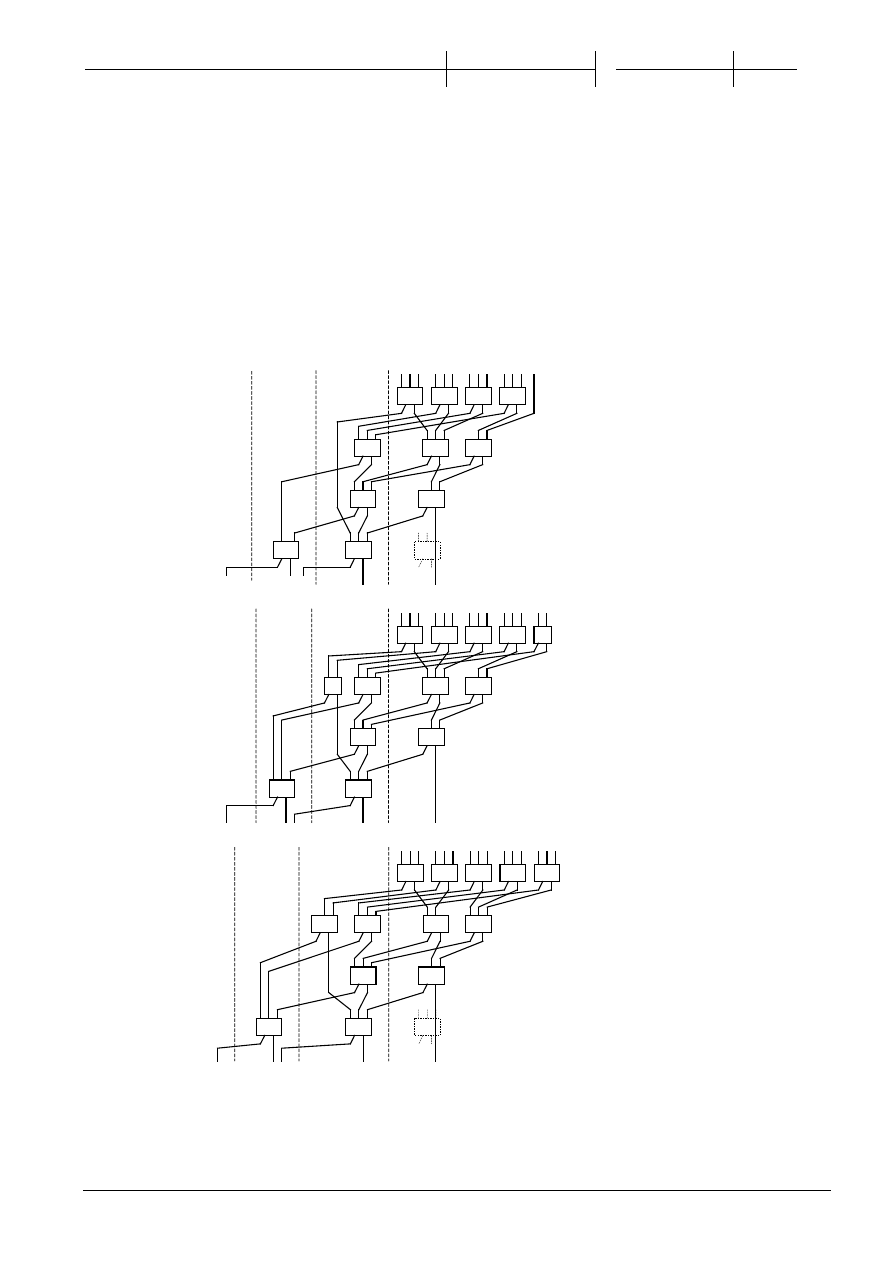
Zad. G1/2
(inne rozwi
ązanie)
Zad. G2/2
(inne rozwi
ązanie)
Zad. G3/2
(inne rozwi
ązanie)
/40
Imi Nazwisko
nr indeksu
pkt
ocena
1
ARYTMETYKA – KOLOKWIUM 2
27 stycznia 2006
Janusz Biernat
1.(4p) Dodanie 53 liczb 64-bitowych w kodzie NB wymaga
.
9-poziomowego drzewa CSA. Zawiera ono 3264
(51x64) sumatorów, a minimalny całkowity czas dodawania wynosi T
CSA
+2log
2
n=48 (9x4+2x6)
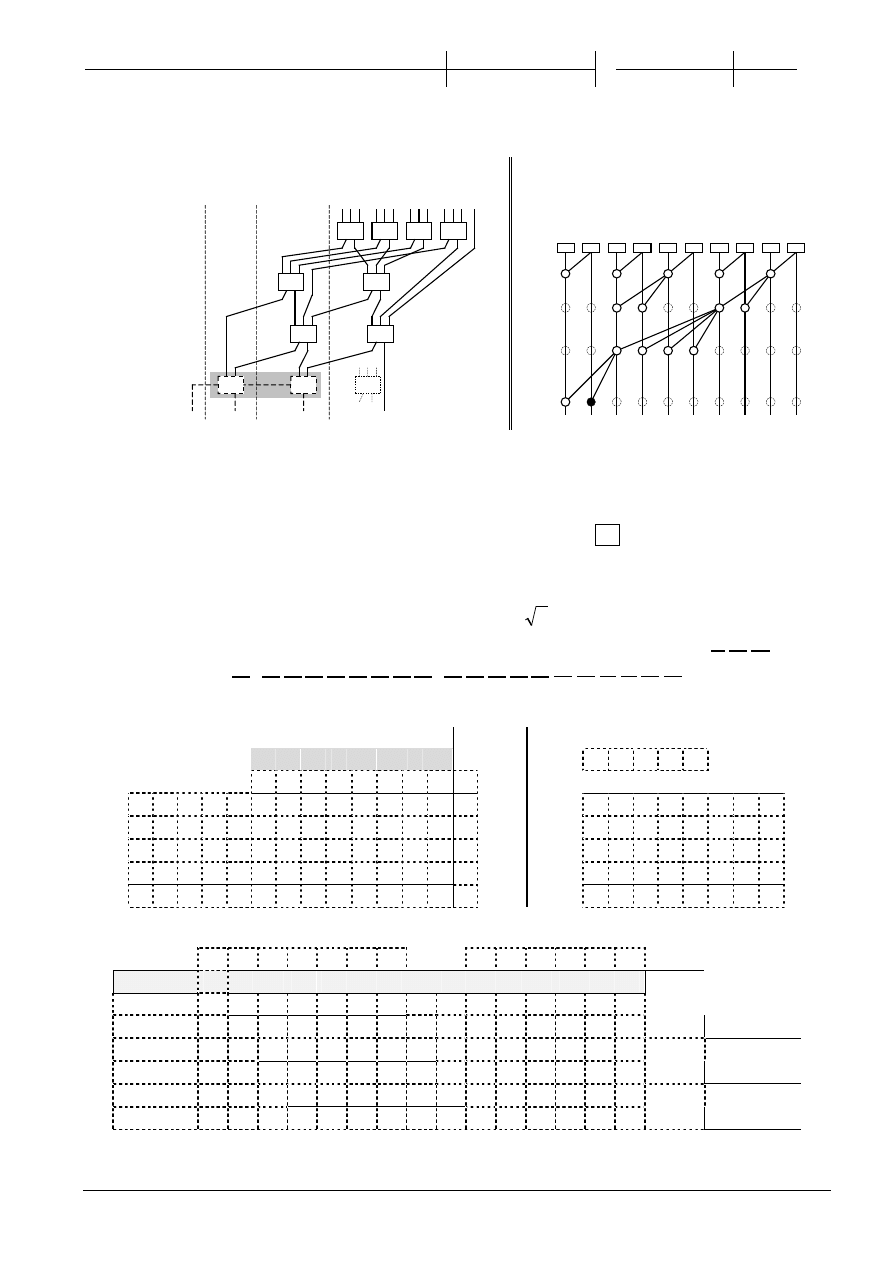
2.
(5p) Uzupełnij schemat drzewa CSA zliczaj
ącego jedynki
sumator ko cowy
(4p) Uzupełnij poni
ższy graf prefiksowy.
Zaznacz w
ęzeł wytwarzający G
0,8
(0)
(9)
3.(4p) W systemie RNS (4, 5, 7) warto
ścią liczby {1, 1, 2}+{1, 2, 3}*{1, 2, 4}={2, 0, 0}jest 70
4.(4p) Oblicz: 64
124
mod 33 = (2
⋅
33–2)
124 mod (2
⋅
10)
mod 33 = (–2)
4
mod 33 = 16
6
–1
mod 37 = 31 (–6)
5.(3p) W 8-bitowym dodawaniu liczb 11010100
U2
+ 01010111
U2
nadmiar nie wyst
ąpi, a logiczne warto
ści
funkcji generacji przeniesienia wynosz
ą G
3,6
=1 oraz G
0,7
= 1.
6.(6p) Ci
ąg 0 1010 1110 0111 0101 1110 1101 0101 111 jest zmiennoprzecinkową znormalizowaną
reprezentacj
ą liczby x (wykładnik w kodzie „+127”). Oblicz x i zapisz go w tym samym formacie
z zaokr
ągleniem do 5. cyfry ułamka. Wartość dziesiętna pierwiastka wynosi około 1,| 6 | 8 | 7
5
|
×
2
23
.
| 0 | | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | | 1 | 0 | 1 | 1 | 0 | 0 | 0 |… …| 0 | 0 |
7.
(4p) Oblicz, stosuj
ąc przekodowanie Booth’a-McSorley’a
(2p) oblicz w systemie U10
A
U2
1 0 1 1 0 1
X
U2
××××
1 0 0 1 0 0 1 1
9 9 9 9 9 8 3 7
X
SD
-1 0
0
1
0
1
0
-1
××××
9 7 2 3
0 0 0 0 0 0 0
0 1 0 0 1 1
9 9 9 9 9 5 1 1
1 1 1 1 1
1 0 1 1 0 1
9 9 9 9 6 7 4
1 1 1
1 0 1 1 0 1
9 9 8 8 5 9
0 1 0 0 1 1
0 0 1 6 3
0 1 0 0 0 0 0 0 1 0 1 1 1
0 0 0 4 5 1 5 1
8.(4p) Wykonaj z dokładno
ścią do 3 cyfr znaczących dzielenie nieodtwarzające liczb danych w kodzie NB
1 0, 1 0 1 1
====
−−−−
D
X =
0
1
0 0, 1 0
:
0 1, 0 1 0 1
====
++++
D
k=-2
-D
1 0, 1 0 1 1
1
1
1
0
1
0
q
0
= 0
0
1
0
1
0
1
0
0
1
1
1
1
0
q
1
= 1
1 0, 1 0 1 1
0
0
1
0
0
1
q
2
= 1
Iloraz jest równy Q = 0,11...
2
⋅
2
2
/40
Imi Nazwisko
nr indeksu
pkt
ocena
2
ARYTMETYKA – KOLOKWIUM 2
27 stycznia 2006
Janusz Biernat
1.(4p) Dodanie 64 liczb 32-bitowych w kodzie NB wymaga 10-poziomowego drzewa CSA. Zawiera 1984
(62x32)
sumatorów, a minimalny całkowity czas dodawania wynosi T
CSA
+2log
2
n= 50 (10x4+5x2).
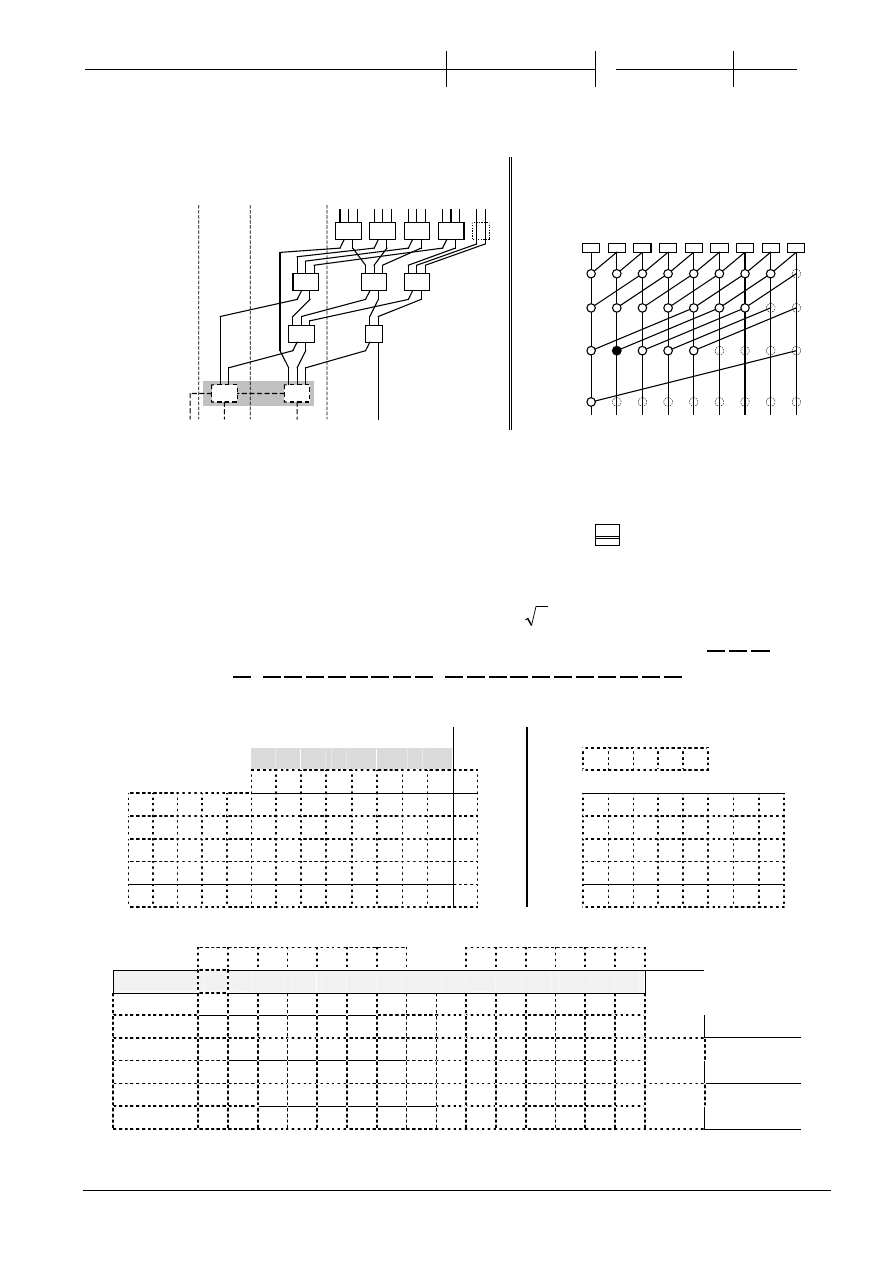
2.
(5p) Uzupełnij schemat drzewa CSA zliczaj
ącego jedynki
sumator ko cowy
(4p) Uzupełnij poni
ższy graf prefiksowy.
Zaznacz w
ęzeł wytwarzający G
0,7
(0)
(8)
3.(4p) W systemie RNS (5, 6, 7) warto
ścią liczby {3, 2, 3}+{2, 2, 3}*{1, 2, 2}={0, 0, 2} jest
.
30
4.(4p) Oblicz: 40
159
mod 21 = (2
⋅
21–2)
159 mod (2
⋅
6)
mod 21 = (–2)
3
mod 21 = 13 (–8)
5
–1
mod 41 = 33 (–8)
5.(3p) W 8-bitowym dodawaniu liczb 11010100
U2
+ 10010001
U2
nadmiar nie wyst
ąpi, a logiczne warto
ści
funkcji generacji przeniesienia wynosz
ą G
2,5
= 0 oraz G
0,6
=.0.
6.(6p) Ci
ąg 0 1110 1100 0100 0101 1110 1101 0101 111 jest zmiennoprzecinkową znormalizowaną
reprezentacj
ą liczby x (wykładnik w kodzie „+127”). Oblicz x i zapisz go w tym samym formacie
z zaokr
ągleniem do 5. cyfry ułamka. Wartość dziesiętna pierwiastka wynosi około 1,| 5 | 9 | 3
7
|
×
2
54
.
| 0 | | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | | 1 | 0 | 0 | 1 | 1 | 0 | 0 |… …| 0 | 0 |
7.
(4p) Oblicz, stosuj
ąc przekodowanie Booth’a-McSorley’a
(2p) oblicz w systemie U10
A
U2
1 0 1 0 1 1
X
U2
××××
1 0 1 1 0 0 1 1
9 9 9 9 9 8 5 3
X
SD
0 -1 0
-1 0
1
0
-1
××××
6 2 1
0 0 0 0 0 0 0
0 1 0 1 0 1
9 9 9 9 9 8 5 3
1 1 1 1 1
1 0 1 0 1 1
9 9 9 9 7 0 6
0 0 0
0 1 0 1 0 1
9 9 9 1 1 8
0
0 1 0 1 0 1
0 0 1 4 7
0 0 1 1 0 0 1 0 1 0 0 0 1
0 0 0 5 5 7 1 3
8.(4p) Wykonaj z dokładno
ścią do 3 cyfr znaczących dzielenie nieodtwarzające liczb danych w kodzie NB
1
0
1
1 1, 1
====
−−−−
D
X = 0
0 1, 0 1 1 0
:
0
1
0 0 0, 1
====
++++
D
k= 2
1
0
1 1 1, 1
1
1
1
0
1
0
0
q
0
= 0
0
1
0
0
0
1
0
0
0
1
0
1
0
q
1
= 1
1
0
1
1
1
1
1
1
1
0
0
1
q
2
= 0
Iloraz jest równy Q =
.
0,10...
2
⋅
2
–2
/40
Imi Nazwisko
nr indeksu
pkt
ocena
3
ARYTMETYKA – KOLOKWIUM 2
27 stycznia 2006
Janusz Biernat
1.(4p) Dodanie 72 liczb 16-bitowych w kodzie NB wymaga
.
10-poziomowego drzewa CSA. Zawiera 1120
(70x16) sumatorów, a minimalny całkowity czas dodawania wynosi T
CSA
+2log
2
n= 48 (4x10+2x4).
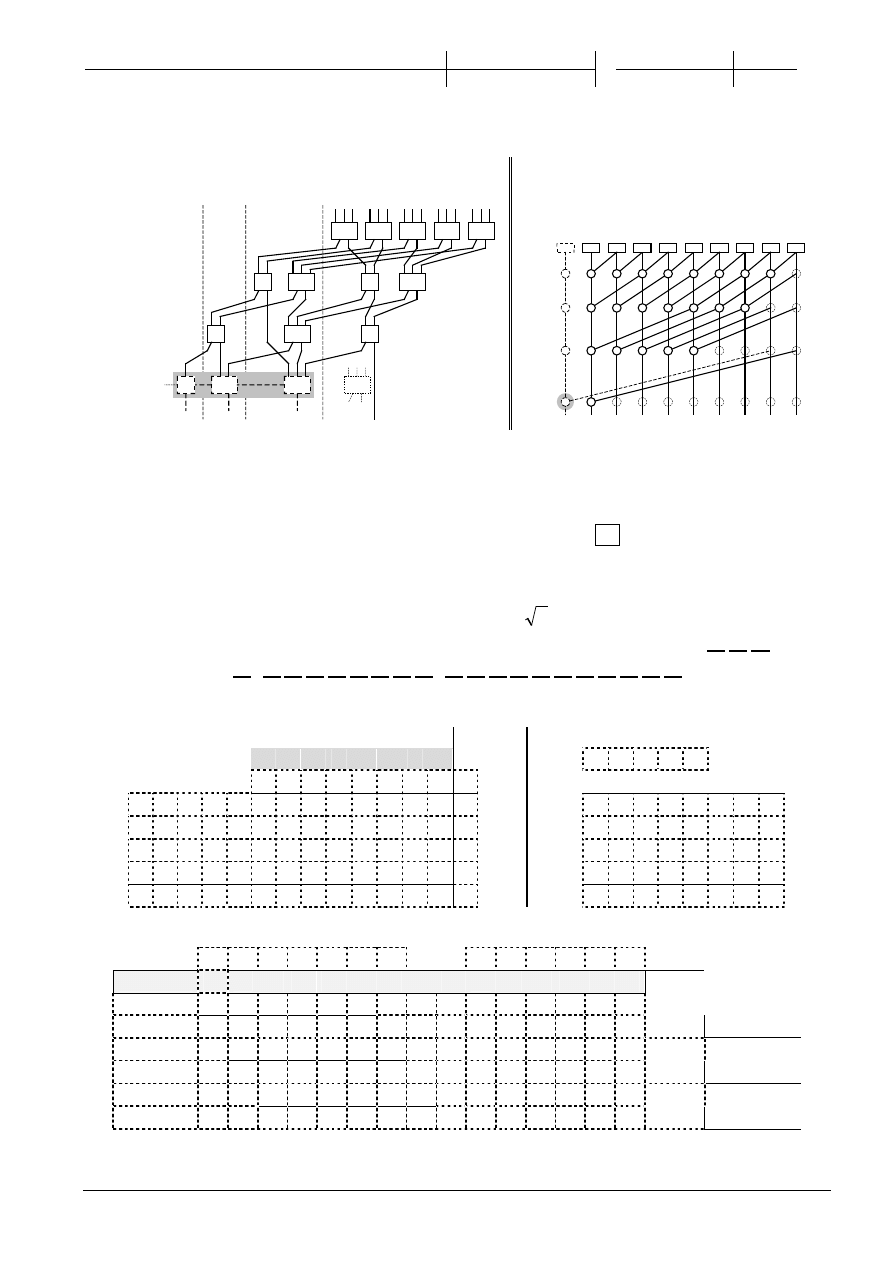
2.
(5p) Uzupełnij schemat drzewa CSA zliczaj
ącego jedynki
sumator ko cowy
(4p) Uzupełnij poni
ższy graf prefiksowy.
Zaznacz w
ęzeł wytwarzający G
0,9
(!!brak)
(0)
(8)
3.(4p) W systemie RNS (3, 5, 7) warto
ścią liczby {2, 1, 3}+{1, 4, 3}*{1, 3, 6}={0, 3, 0} jest
.
63
4.(4p) Oblicz: 67
243
mod 35 = (2
⋅
35–3)
243 mod (4
⋅
6)
mod 35 = (–3)
3
mod 35 = 8 (–27)
6
–1
mod 43 = 36 (–7)
5.(3p) W 8-bitowym dodawaniu liczb 01100100
U2
+ 10111111
U2
nadmiar nie wyst
ąpi, a logiczne warto
ści
funkcji generacji przeniesienia wynosz
ą G
1,7
= 1 oraz G
0,5
= 1.
6.(6p) Ci
ąg 0 0010 1100 1110 0101 1110 0101 1101 111 jest zmiennoprzecinkową znormalizowaną
reprezentacj
ą liczby x (wykładnik w kodzie „+127”). Oblicz x i zapisz go w tym samym formacie
z zaokr
ągleniem do 5. cyfry ułamka. Wartość dziesiętna pierwiastka wynosi około 1,| 9 | 3 | 7
5
|
×
2
–42.
.
| 0 | | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | | 1 | 1 | 1 | 1 | 0 | 0 | 0 |… …| 0 | 0 |
7.
(4p) Oblicz, stosuj
ąc przekodowanie Booth’a-McSorley’a
(2p) oblicz w systemie U10
A
U2
1 0 1 1 0 1
X
U2
××××
1 0 0 1 0 1 1 1
9 9 9 9 9 7 3 7
X
SD
-1 0
0
1
1
0
0
-1
××××
9 8 3 2
0 0 0 0 0 0 0
0 1 0 0 1 1
9 9 9 9 9 4 7 4
1 1 1 1
1 0 1 1 0 1
9 9 9 9 2 1 1
1 1 1
1 0 1 1 0 1
9 9 7 8 9 6
0 1 0 0 1 1
0 0 2 6 3
0 0 1 1 1 1 1 0 0 1 0 1 1
0 0 0 4 4 1 8 4
8.(4p) Wykonaj z dokładno
ścią do 3 cyfr znaczących dzielenie nieodtwarzające liczb danych w kodzie NB
1 0, 1 0 1 1
====
−−−−
D
X = 0
0
1
1 1, 1 0
:
0 1, 0 1 0 1
====
++++
D
k= -3
-D
1 0, 1 0 1 1
1
1
1
0
1
0
0
q
0
= 0
0
1
0
1
0
1
0
0
1
0
0
1
0
q
1
= 1
1
0
1
0
1
1
1
1
1
1
0
1
q
2
= 0
Iloraz jest równy Q =
.
0,10...
2
⋅
2
3
/40
Imi Nazwisko
nr indeksu
pkt
ocena
4
ARYTMETYKA – KOLOKWIUM 2
27 stycznia 2006
Janusz Biernat
1.(4p) Dodanie 42 liczb 64-bitowych w kodzie NB wymaga 8-poziomowego drzewa CSA. Zawiera ono 2560
(40x64) sumatorów, a minimalny całkowity czas dodawania wynosi T
CSA
+2log
2
n= 44 (8x4+2x6).
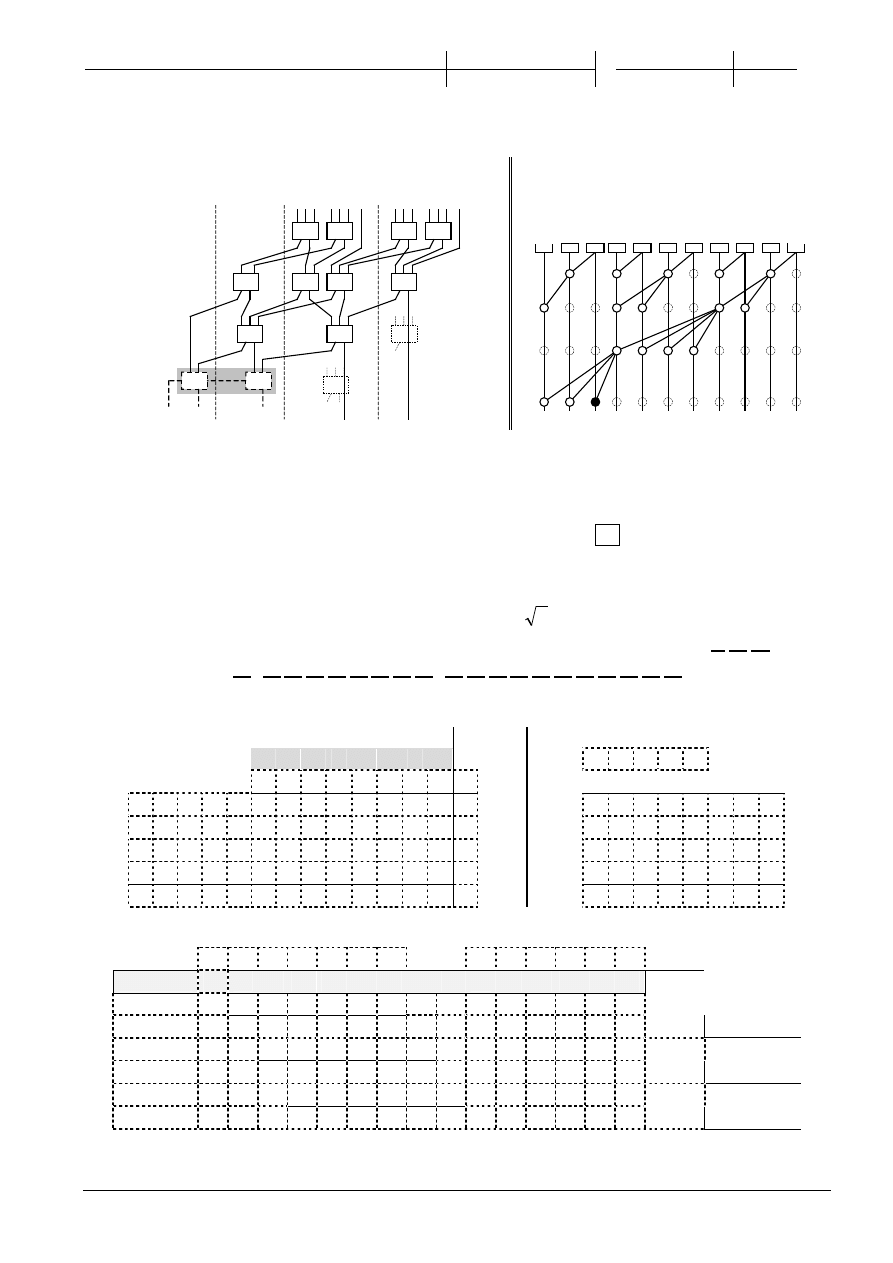
2.
(5p) Uzupełnij schemat poni
ższego sumatora CSA (7x2b)
(4p) Uzupełnij poni
ższy graf prefiksowy.
Zaznacz w
ęzeł wytwarzający G
0,8
(0)
(10)
3.(4p) W systemie RNS (3, 5, 8) warto
ścią liczby {1, 1, 1}+{1, 2, 3}*{1, 2, 5}={2, 0, 0} jest
.
80
4.(4p) Oblicz: 68
184
mod 33 = (2
⋅
33+2)
184 mod (2
⋅
10)
mod 33 = (+2)
4
mod 33 = 16
9
–1
mod 37 = 33 (–4)
5.(3p) W 8-bitowym dodawaniu liczb 11010100
U2
+ 01011111
U2
nadmiar nie wyst
ąpi, a logiczne warto
ści
funkcji generacji przeniesienia wynosz
ą G
1,6
=
1 oraz G
0,4
=.1
6.(6p) Ci
ąg 0 1010 1110 0110 0101 0001 0001 0101 111 jest zmiennoprzecinkową znormalizowaną
reprezentacj
ą liczby x (wykładnik w kodzie „+127”). Oblicz x i zapisz go w tym samym formacie
z zaokr
ągleniem do 5. cyfry ułamka. Wartość dziesiętna pierwiastka wynosi około 1,| 6 | 5 | 6
2
|
×
2
23
.
| 0 | | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | | 1 | 0 | 1 | 0 | 1 | 0 | 0 |… …| 0 | 0 |
7.
(4p) Oblicz, stosuj
ąc przekodowanie Booth’a-McSorley’a
(2p) oblicz w systemie U10
A
U2
1 0 0 0 1 1
X
U2
××××
1 0 1 1 0 1 1 1
9 9 9 9 9 8 3 7
X
SD
0 -1 0
-1 1
0
0
-1
××××
9 6 4 1
0 0 0 0 0 0 0
0 1 1 1 0 1
9 9 9 9 9 8 3 7
1 1 1 1
1 0 0 0 1 1
9 9 9 9 3 4 8
0 0 0
0 1 1 1 0 1
9 9 9 0 2 2
0
0 1 1 1 0 1
0 0 1 6 3
0 1 0 0 0 0 1 0 0 0 1 0 1
0 0 0 5 8 5 1 7
8.(4p) Wykonaj z dokładno
ścią do 3 cyfr znaczących dzielenie nieodtwarzające liczb danych w kodzie NB
1 0, 1 0 1 1
====
−−−−
D
X =
0
1
0 0, 1 0
:
0 1, 0 1 0 1
====
++++
D
k= -2
-D
1 0, 1 0 1 1
1
1
1
1
0
1
0
q
0
= 0
0
1
0
1
0
1
0
0
1
1
1
1
0
q
1
= 1
1
0
1
0
1
1
0
0
1
0
0
1
q
2
= 1
Iloraz jest równy Q =
.
0,11...
2
⋅
2
2
/40
Imi Nazwisko
nr indeksu
pkt
ocena
5
ARYTMETYKA – KOLOKWIUM 2
27 stycznia 2006
Janusz Biernat
1.(4p) Dodanie 63 liczb 32-bitowych w kodzie NB wymaga
.
9-poziomowego drzewa CSA. Zawiera ono 1952
(61x32) sumatorów, a minimalny całkowity czas dodawania wynosi T
CSA
+2log
2
n= 46 (9x4+2x5).
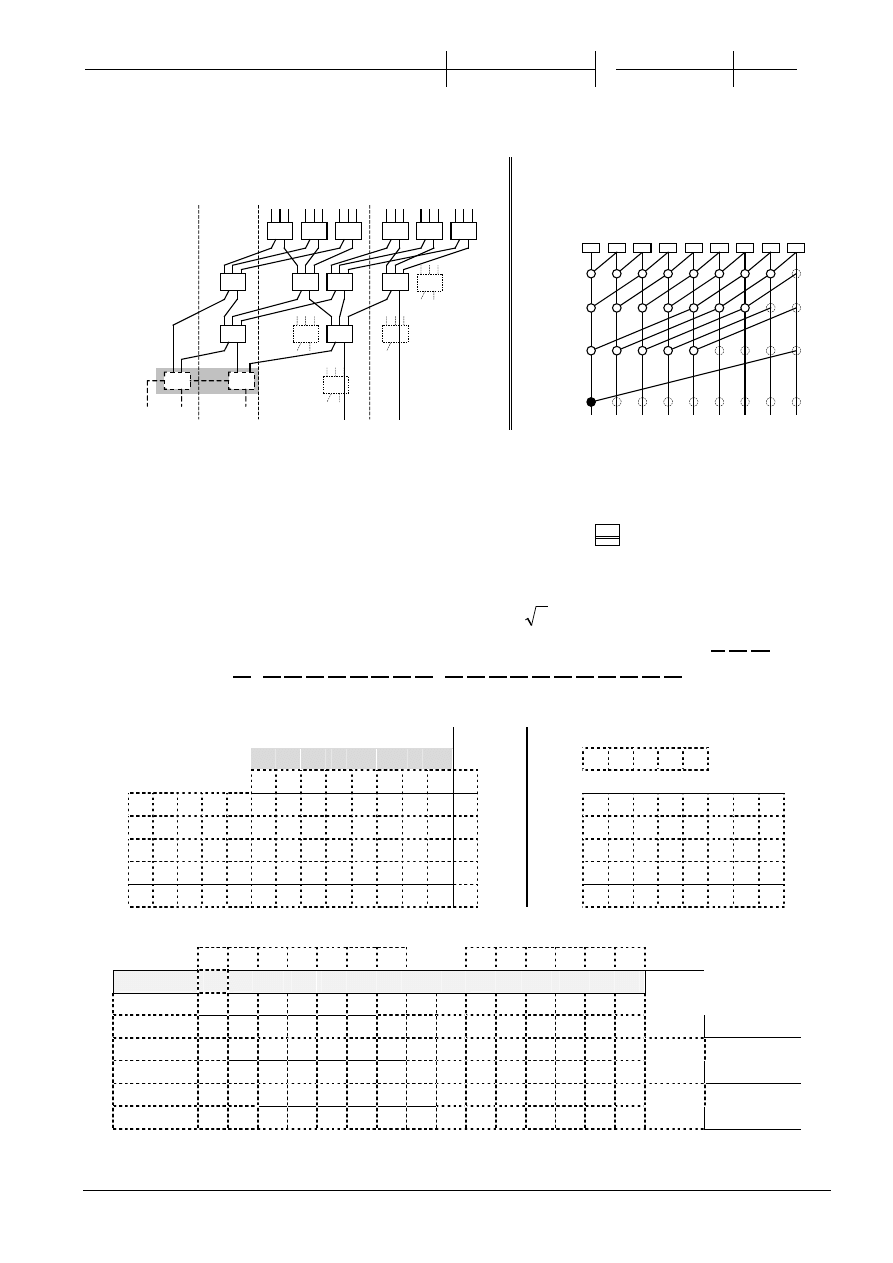
2.
(5p) Uzupełnij schemat poni
ższego sumatora CSA (9x2b)
(4p) Uzupełnij poni
ższy graf prefiksowy.
Zaznacz w
ęzeł wytwarzający G
0,8
(0)
(8)
3.(4p) W systemie RNS (5, 7, 8) warto
ścią liczby {3, 1, 2}+{2, 3, 3}*{1, 3, 2}={0, 3, 0} jest 80
4.(4p) Oblicz: 44
279
mod 21 = (2
⋅
21+2)
279 mod (2
⋅
6)
mod 33 = (+2)
3
mod 33 = 8
8
–1
mod 41 = 36 (–5)
5.(3p) W 8-bitowym dodawaniu liczb 11010100
U2
+ 10010001
U2
nadmiar nie wyst
ąpi, a logiczne warto
ści
funkcji generacji przeniesienia wynosz
ą G
2,6
=
0 oraz G
0,5
= 0.
6.(6p) Ci
ąg 0 1110 1100 0111 0111 0010 0000 0101 111 jest zmiennoprzecinkową znormalizowaną
reprezentacj
ą liczby x (wykładnik w kodzie „+127”). Oblicz x i zapisz go w tym samym formacie
z zaokr
ągleniem do 5. cyfry ułamka. Wartość dziesiętna pierwiastka wynosi około 1,| 6 | 8 | 7
5
|
×
2
54
.
| 0 | | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | | 1 | 0 | 1 | 1 | 0 | 0 | 0 |… …| 0 | 0 |
7.
(4p) Oblicz, stosuj
ąc przekodowanie Booth’a-McSorley’a
(2p) oblicz w systemie U10
A
U2
1 0 1 1 1 1
X
U2
××××
1 0 1 1 0 0 1 0
9 9 9 9 9 8 5 3
X
SD
0 -1 0
-1 0
1
-1 0
××××
7 5 1
0 0 0 0 0 0
0 1 0 0 0 1
0
!
9 9 9 9 9 8 5 3
1 1 1 1 1
1 0 1 1 1 1
9 9 9 9 2 6 5
0 0 0
0 1 0 0 0 1
9 9 8 9 7 1
0
0 1 0 0 0 1
0 0 1 4 7
0 0 1 0 1 0 0 1 0 1 1 1 0
0 0 0 3 6 6 0 3
8.(4p) Wykonaj z dokładno
ścią do 3 cyfr znaczących dzielenie nieodtwarzające liczb danych w kodzie NB
1
0
1
1
1 1
====
−−−−
D
X = 0
0 1, 0 1 1 0
:
0
1
0 0 0, 1
====
++++
D
k= 2
1
0
1 1 1, 1
1
1
1
0
1
0
0
q
0
= 0
0
1
0
0
0
1
0
0
0
1
0
1
0
q
1
= 1
1
0
1
1
1
1
1
1
1
0
0
1
q
2
= 0
Iloraz jest równy Q = 0,10...
2
⋅
2
–2
/40
Imi Nazwisko
nr indeksu
pkt
ocena
6
ARYTMETYKA – KOLOKWIUM 2
27 stycznia 2006
Janusz Biernat
1.(4p) Dodanie 41 liczb 16-bitowych w kodzie NB wymaga
.
8-poziomowego drzewa CSA. Zawiera ono 624
(39x16) sumatorów, a minimalny całkowity czas dodawania wynosi T
CSA
+2log
2
n= 40 (8x4+2x4).
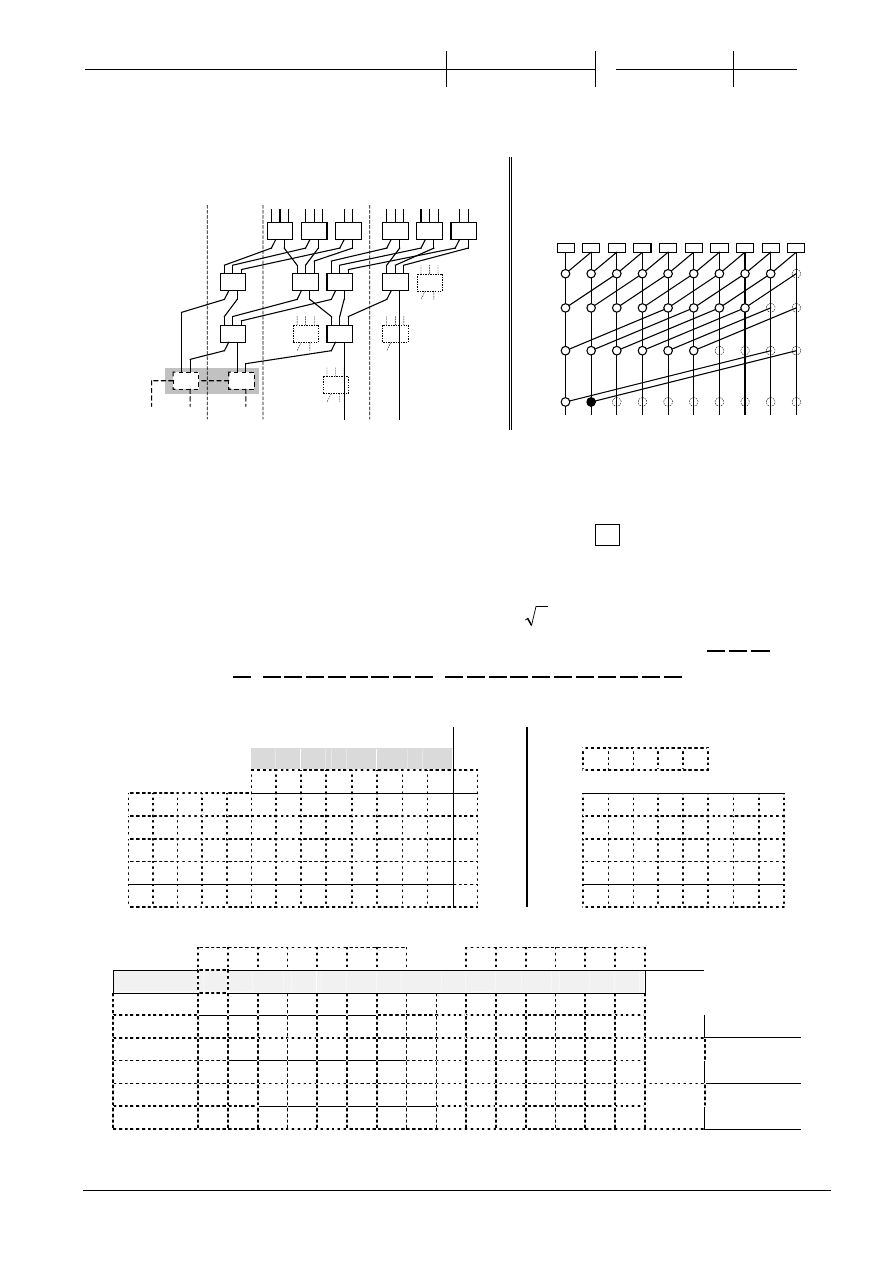
2.
(5p) Uzupełnij schemat poni
ższego sumatora CSA (8x2b)
(4p) Uzupełnij poni
ższy graf prefiksowy.
Zaznacz w
ęzeł wytwarzający G
0,8
(0)
(9)
3.(4p) W systemie RNS (3, 7, 8) warto
ścią liczby {2, 2, 3}+{1, 4, 3}*{1, 3, 5}={0, 0, 2} jest 42
4.(4p) Oblicz: 73
267
mod 35 = (2
⋅
35+3)
267 mod (4
⋅
6)
mod 35 = (+3)
3
mod 35 = 27
7
–1
mod 43 = 37 (–6)
5.(3p) W 8-bitowym dodawaniu liczb 01100100
U2
+ 10111111
U2
nadmiar nie wyst
ąpi, a logiczne warto
ści
funkcji generacji przeniesienia wynosz
ą G
1,6
= 1 oraz G
0,3
= 1.
6.(6p) Ci
ąg 0 0010 1100 1110 0100 0001 0101 1101 111 jest zmiennoprzecinkową znormalizowaną
reprezentacj
ą liczby x (wykładnik w kodzie „+127”). Oblicz x i zapisz go w tym samym formacie
z zaokr
ągleniem do 5. cyfry ułamka. Wartość dziesiętna pierwiastka wynosi około 1,| 9 | 3 | 7
5
|
×
2
–42
.
| 0 | | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | | 1 | 1 | 1 | 1 | 0 | 0 | 0 |… …| 0 | 0 |
7.
(4p) Oblicz, stosuj
ąc przekodowanie Booth’a-McSorley’a
(2p) oblicz w systemie U10
A
U2
1 0 1 1 0 1
X
U2
××××
1 0 1 1 1 0 0 1
9 9 9 9 9 7 3 7
X
SD
0 -1 0
0
-1 0
0
1
××××
6 1 4
1 1 1 1 1 1 1
1 0 1 1 0 1
9 9 9 9 8 9 4 8
0 0 0 0
0 1 0 0 1 1
9 9 9 9 7 3 7
9 9 8 4 2 2
0
0 1 0 0 1 1
0 0 2 6 3
0 0 1 0 1 0 1 0 0 0 1 0 1
0 0 1 0 1 5 1 8
8.(4p) Wykonaj z dokładno
ścią do 3 cyfr znaczących dzielenie nieodtwarzające liczb danych w kodzie NB
1 0, 1 0 1 1
====
−−−−
D
X = 0
0
1
1 1, 1 0
:
0 1, 0 1 0 1
====
++++
D
k=-3
-D
1 0, 1 0 1 1
1
1
0
1
0
0
q
0
= 0
0
1
0
1
0
1
0
0
1
0
0
1
0
q
1
= 1
1
0
1
0
1
1
1
1
1
1
0
1
q
2
= 0
Iloraz jest równy Q =
.
0,10...
2
⋅
2
3