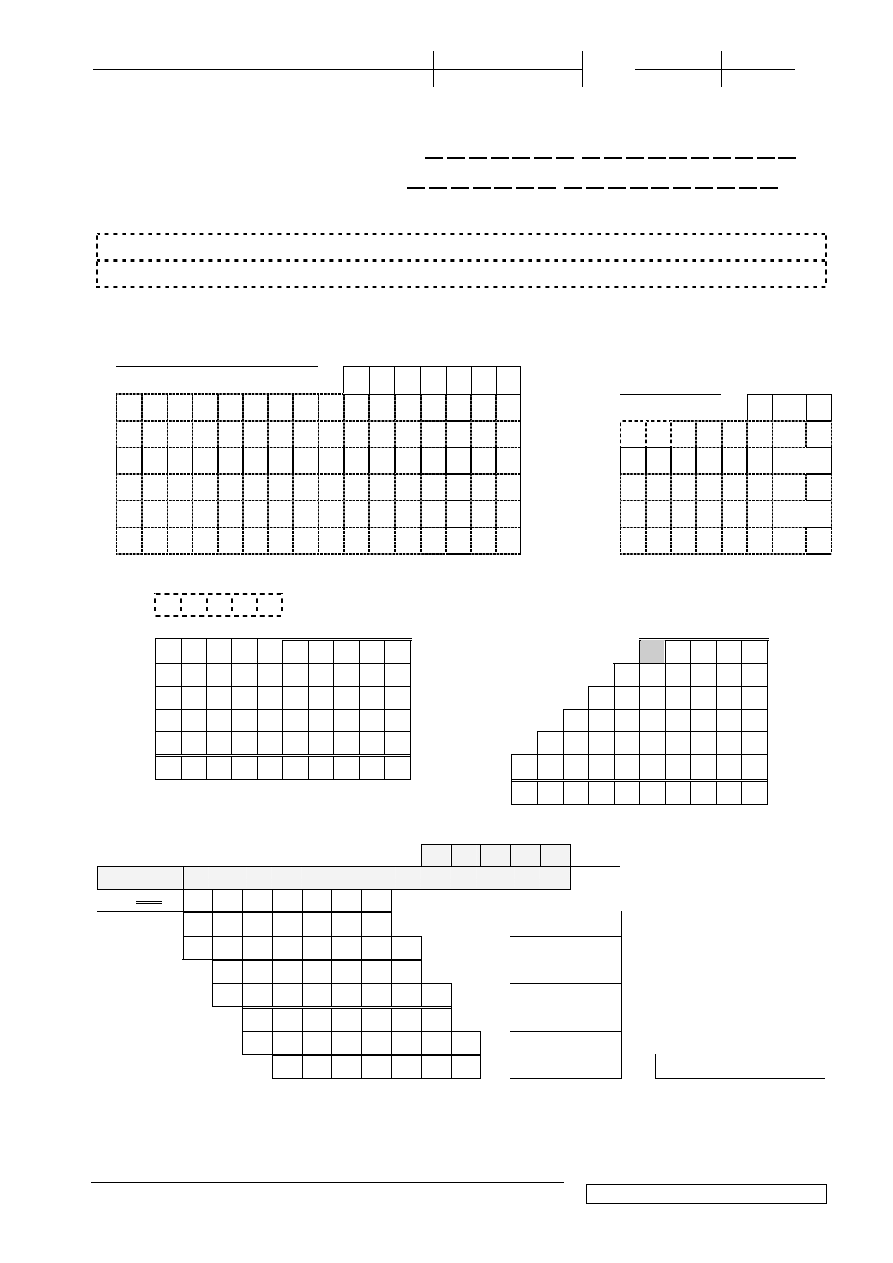
/25
Imi
ę
Nazwisko
nr indeksu
pkt
ocena
1
Arytmetyka – Kol.I
3 grudnia 2004
Janusz Biernat
10–3,0; 13–3,5; 16–4,0; 19–4,5; 21–5,0
1.(4p) Oblicz ró
ż
nic
ę
i zapisz j
ą
w systemie U2, z dokładno
ś
ci
ą
do 10 bitów cz
ę
ś
ci ułamkowej:
45
10
– 71,(13)
10
= – 26,(13)
10
=
(–32,1031...
8
) =
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |, 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
U2
(7)45
U8
– (7)71,(13)
U8
= (7)53,(64)
U8
= | 1 | 1 | 0 | 1 | 0 | 1 | 1 |, 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
U2
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
(–34640
8
*105336
8
) mod 101
8
= [(–1)*(40–46+3)*(36–53+10)]
8
mod 101
8
= (–1)*(–3)*(–5) = –17
8
(3–104
10
)*45351
10
mod 99
10
= [(–101)*(51+53+4)]
10
mod 99
10
= [(–2)*108]
10
mod 99
10
= –18
10
(2p) Oblicz: 45
122
mod 11 = (45 mod 11)
122
mod 11 = 1
122
mod 11 = 1
7
–1
mod 11 = 8
(7*8 mod 11 = 1)
3.(4p) Oblicz: z dokładno
ś
ci
ą
: do 4 cyfr znacz
ą
cych
√
0, 1 0 1 0 1 1 1
2
= 0, 1 1 0 1
do 3 cyfr znacz
ą
cych [!(..)
8
]
– 1
√
3 6 2 3
8
= 5 4, 0
1 1 0
> 1 0 1
3 1
– 1 0 1
5 2 3
124*4
0 1 1 1
< 1 1 0 1
5 2 0
0 1 1 1 1 0 > 1 1 0 0 1
2
2
=04
3
2
=11
4
2
=20
5
2
=31
6
2
=43
7
2
=61
3 0 0
1300*0
–
1 1 0 0 1
4.(4p) Wykonaj mno
ż
enie pisemne liczb w kodzie U2 u
ż
ywaj
ą
c rozszerze
ń
i bez u
ż
ycia rozszerze
ń
1 0 1 0 1
1 0 1 0 1
×
1 0 1 1 1
×
1 0 1 1 1
1 1 1 1 1 1 0 1 0 1
0 0 1 0 1
1 1 1 1 1 0 1 0 1
0 0 1 0 1
1 1 1 1 0 1 0 1
0 0 1 0 1
0 0 0
0
1 0 0 0 0
0 0 1 0 1 1
1 1 0 1 1
0 0 0 1 1 0 0 0 1 1
1
1
0 0 0 1 1 0 0 0 1 1
5.(4p) Metod
ą
nieodtwarzaj
ą
c
ą
oblicz z dokładno
ś
ci
ą
do 4 cyfr znacz
ą
cych iloraz liczb danych w kodzie U2
0, 1
0
1 1
==== −
D
X =
0, 0
1 1
1
: 1, 0
1
0 1
= +
= +
= +
= +
D
k=0
+D /– D
1, 0
1
0
1
1
1
1
0
0
0
rD >0
q
0
= 1
–D
0
1
0
1
1
0
0
0
1
1
0
rD <0
q
1
= 0
+D
1
0
1
0
1
1
1
0
1
1
0
rD >0
q
2
= 1
–D
0
1
0
1
1
Iloraz jest równy
0
0
0
0
1
rD <0
q
3
= 0
Q =1,010…
U2
6.(3p) Udowodnij,
ż
e je
ś
li k
≥≥≥≥
1, to liczby 2
3k
–1 i 2
k
+1 s
ą
wzajemnie wzgl
ę
dnie pierwsze
2
3k
–1=2
2k
(2
k
+1)–2
k
(2
k
+1)+(2
k
+1)–2, wi
ę
c NWP(2
3k
–1,2
k
+1)=NWP(2,2
k
+1)=1
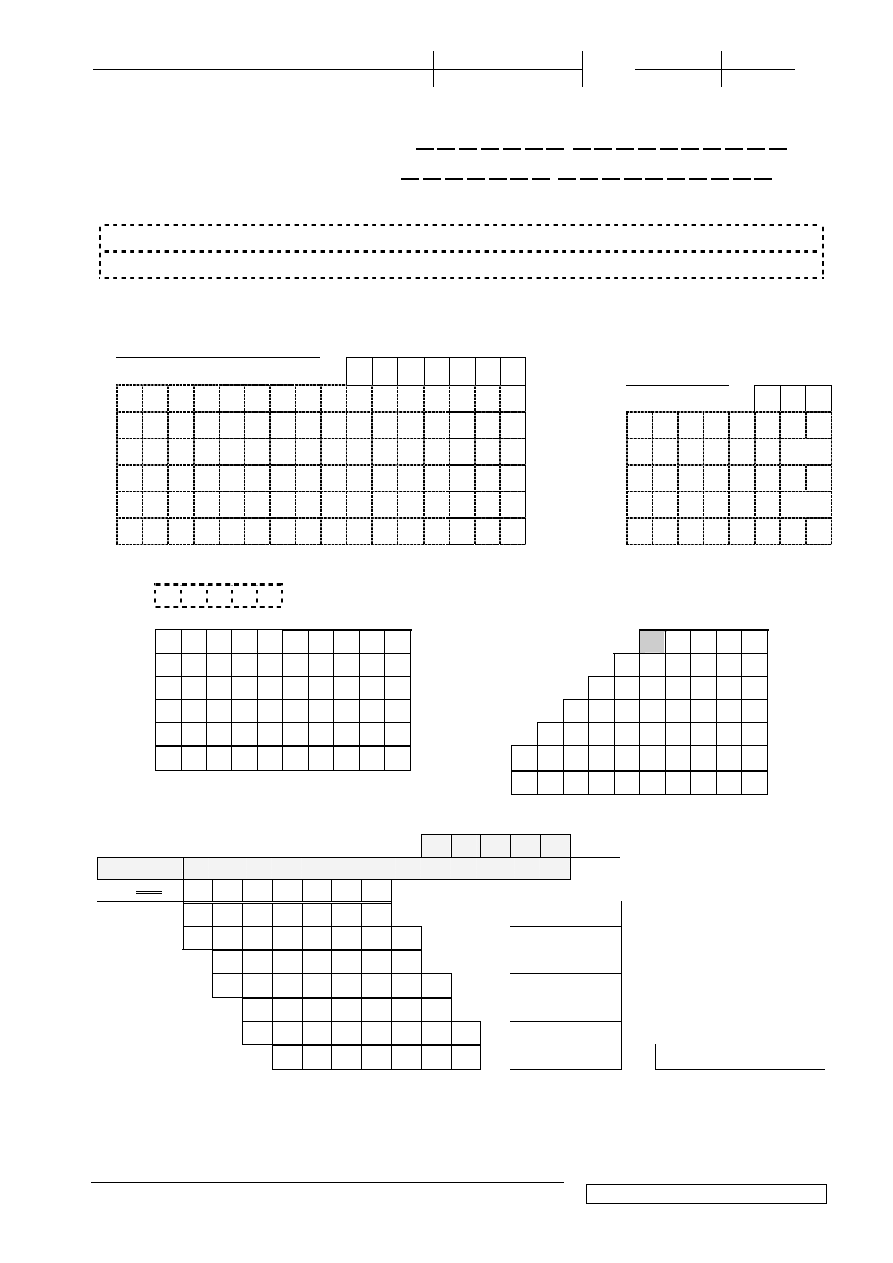
/25
Imi
ę
Nazwisko
nr indeksu
pkt
ocena
2
Arytmetyka – Kol.I
3 grudnia 2004
Janusz Biernat
10–3,0; 13–3,5; 16–4,0; 19–4,5; 21–5,0
1.(4p) Oblicz ró
ż
nic
ę
i zapisz j
ą
w systemie U2, z dokładno
ś
ci
ą
do 10 bitów cz
ę
ś
ci ułamkowej:
42
10
– 15,(74)
10
= 26,(25)
10
=
(32,2012...
8
) =
| 0 | 0 | 1 | 1 | 0 | 1 | 0 |, 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
U2
(7)42
U8
– (0)15,(74)
U8
= 724,(03)
U8
= | 1 | 0 | 1 | 0 | 1 | 0 | 0 |, 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
U2
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
(–34630
8
*103336
8
) mod 77
8
= [(–1)*(30+46+3)*(36+33+10)]
8
mod 77
8
= (–1)*2*2 = –4
8
(5–104
10
)*45351
10
mod 101
10
= [(–99)*(51–53+4)]
10
mod 101
10
= 2*2 = 4
(2p) Oblicz: 38
122
mod 13 = (38mod 13)
122
mod 11 = ( – 1)
122
mod 11 = 1
8
–1
mod 11 = 7
(8*7 mod 11 = 1)
3.(4p) Oblicz: z dokładno
ś
ci
ą
: do 4 cyfr znacz
ą
cych
√
1, 0 1 1 0 1 1 1
2
= 1, 0 0 1 1
do 3 cyfr znacz
ą
cych [!(..)
7
]
1
√
3 6 2 3
7
= 5 1, 4
0 1
< 1 0 1
3 4
0 1 1 0
< 1 0 0 1
2 2 3
131*1
1 1 0 1 1
> 1 0 0 0 1
1 3 1
– 1 0 0 0 1
2
2
=04
3
2
=12
4
2
=22
5
2
=34
6
2
=51
6 2 0 0
1324*4
1 0 1 0 1 0 > 1 0 0 1 0 1
5 6 3 2
4.(4p) Wykonaj mno
ż
enie pisemne liczb w kodzie U2 u
ż
ywaj
ą
c rozszerze
ń
i bez u
ż
ycia rozszerze
ń
1 0 0 1 1
1 0 0 1 1
×
1 0 1 1 1
×
1 0 1 1 1
1 1 1 1 1 1 0 0 1 1
0 0 0 1 1
1 1 1 1 1 0 0 1 1
0 0 0 1 1
1 1 1 1 0 0 1 1
0 0 0 1 1
0 0 0
0
1 0 0 0 0
0 0 1 1 0 1
1 1 1 0 1
0 0 0 1 1 1 0 1 0 1
1
1
0 0 0 1 1 1 0 1 0 1
5.(4p) Metod
ą
nieodtwarzaj
ą
c
ą
oblicz z dokładno
ś
ci
ą
do 4 cyfr znacz
ą
cych iloraz liczb danych w kodzie U2
0, 1
1
1 1
====
−−−−
D
X =
0, 0
1 0
1
: 1, 0
0
0 1
====
++++
D
k=1
+D /– D
1, 0
0
0
1
1
1
0
1
1
0
rD >0
q
0
= 1
–D
0
1
1
1
1
0
0
1
0
1
0
rD <0
q
1
= 0
+D
1, 0
0
0
1
1
1
0
1
1
0
rD >0
q
2
= 1
–D
0
1
1
1
1
Iloraz jest równy
0
0
1
0
1
rD <0
q
3
= 0
Q =1,1010…
U2
6.(3p) Udowodnij,
ż
e je
ś
li k
≥≥≥≥
1, to liczby 2
2k
+1 i 2
k
+1 nie maj
ą
wspólnego podzielnika ró
ż
nego od 1
2
2k
+1=(2
k
+1)(2
k
–1)+2, wi
ę
c NWP(2
2k
+1,2
k
+1)=NWP(2,2
k
+1)=1
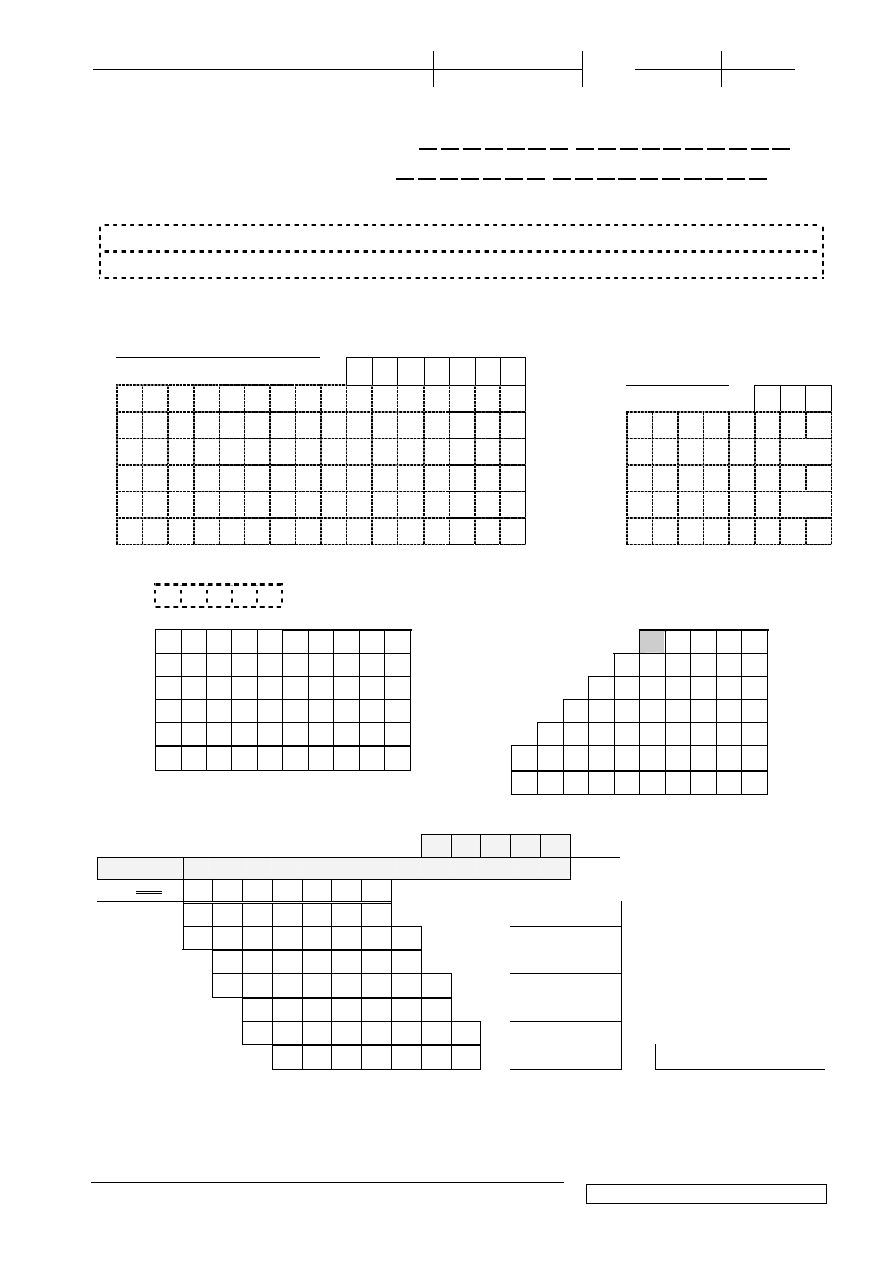
/25
Imi
ę
Nazwisko
nr indeksu
pkt
ocena
3
Arytmetyka – Kol.I
3 grudnia 2004
Janusz Biernat
10–3,0; 13–3,5; 16–4,0; 19–4,5; 21–5,0
1.(4p) Oblicz ró
ż
nic
ę
i zapisz j
ą
w systemie U2, z dokładno
ś
ci
ą
do 10 bitów cz
ę
ś
ci ułamkowej:
47
10
– 10,(71)
10
= 36,(28)
10
=
(–44,2206...
8
) =
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |, 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
U2
(7)47
U8
– (0)10,(71)
U8
= 736,(06)
U8
= | 1 | 0 | 1 | 1 | 1 | 1 | 0 |, 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
U2
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
(–23FC2
16
*9667
16
) mod 0FF
16
= [(–1)*(2+3F+C2)*(96+67)]
16
mod 0FF
16
= (–1)*4*(–2) = 8
16
(5–103
10
)*6058
10
mod 101
10
= [(–98)*(58–60)]
10
mod 101
10
= 3*(–2) = – 6
(2p) Oblicz: 35
145
mod 9 = (35 mod 9)
145
mod 9 = ( – 1)
145
mod 9 = – 1
5
–1
mod 13 = 8
(5*8 mod 13 = 1)
3.(4p) Oblicz: z dokładno
ś
ci
ą
: do 4 cyfr znacz
ą
cych
√
0, 1 1 1 0 1 0 1
2
= 0, 1 1 1 1
do 3 cyfr znacz
ą
cych [!(..)
9
]
–
1
√
3 6, 2 3
9
= 5, 6 8
1 0 1 0
< 1 0 1
– 2 7
–
1 0 1
8 2 3
116*6
1 0 1 1 0
< 1 1 0 1
– 7 1 0
–
1 1 0 1
1 1 3 0 0
1238*8
1 0 0 1 1 0 < 1 1 1 0 1
2
2
=04
3
2
=10
4
2
=17
5
2
=27
6
2
=40
7
2
=54
8
2
=71
– 1 1 2 4 1
4.(4p) Wykonaj mno
ż
enie pisemne liczb w kodzie U2 u
ż
ywaj
ą
c rozszerze
ń
i bez u
ż
ycia rozszerze
ń
1 0 1 1 1
1 0 1 1 1
×
1 0 1 0 1
×
1 0 1 0 1
1 1 1 1 1 1 0 1 1 1
0 0 1 1 1
0 0 0 0 0
0
1 0 0 0 0
1 1 1 1 0 1 1 1
0 0 1 1 1
0 0 0
0
1 0 0 0 0
0 0 1 0 0 1
1 1 0 0 1
0 0 0 1 1 0 0 0 1 1
1
1
0 0 0 1 1 0 0 0 1 1
5.(4p) Metod
ą
nieodtwarzaj
ą
c
ą
oblicz z dokładno
ś
ci
ą
do 4 cyfr znacz
ą
cych iloraz liczb danych w kodzie U2
(–X)
0, 1
0
0
1
1, 0
0
1 1
====
−−−−
D
X =
1, 0
1 1
1
: 0, 1
1
0 1
====
++++
D
k= 0
+D /– D
0, 1
1
0
1
0
0
1
0
0
0
rD >0
q
0
= 1
–D
1
0
0
1
1
1
1
0
1
1
0
rD <0
q
1
= 0
+D
0
1
1
0
1
0
0
0
1
1
0
rD >0
q
2
= 1
–D
1
0
0
1
1
Iloraz jest równy
1
1
0
0
1
rD <0
q
3
= 0
Q =1,010…
U2
6.(3p) Udowodnij,
ż
e je
ś
li k
≥≥≥≥
2, to liczby 2
2k
+1 i 2
k
–1 s
ą
wzajemnie wzgl
ę
dnie pierwsze
2
2k
+1=(2
k
+1)(2
k
–1)+2, wi
ę
c NWP(2
2k
+1,2
k
–1)=NWP(2,2
k
–1)=1
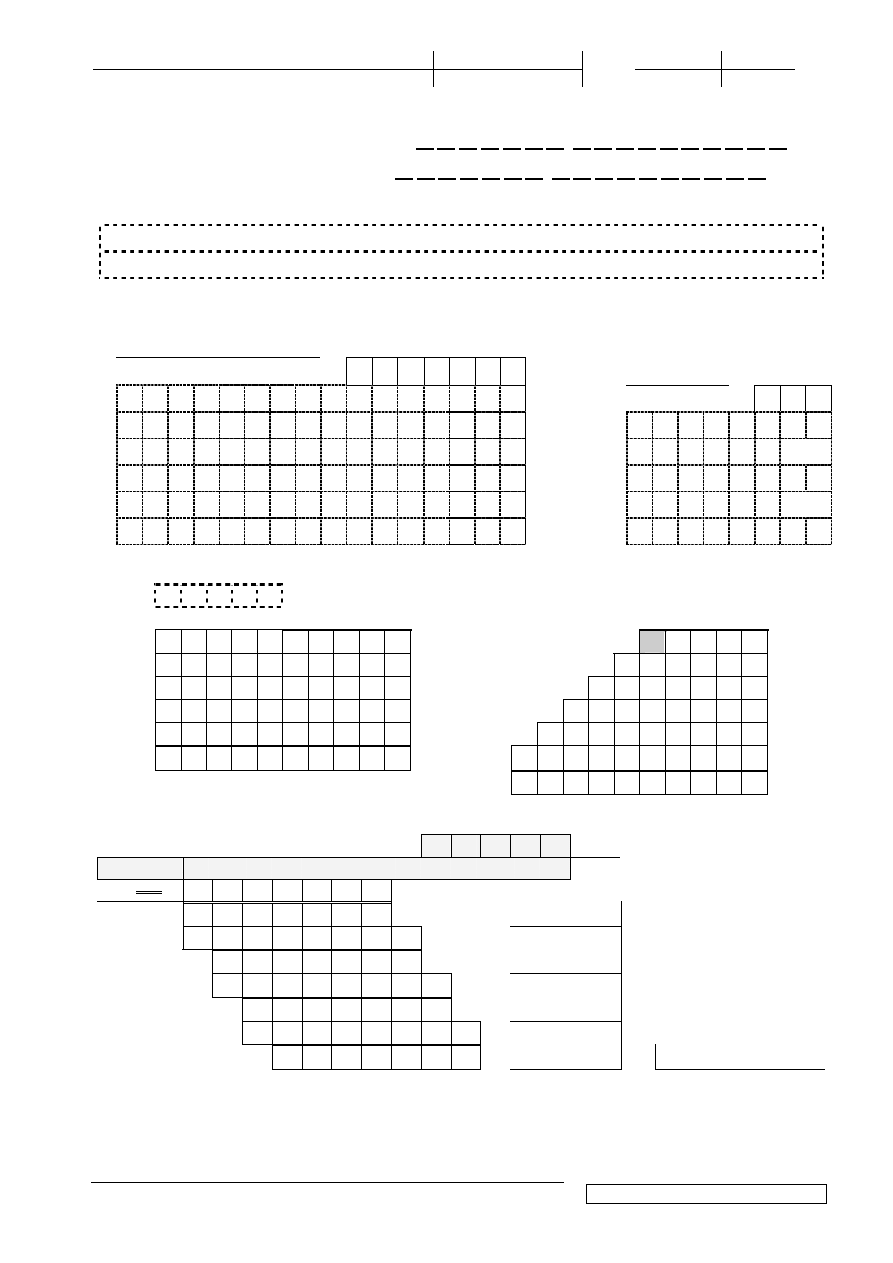
/25
Imi
ę
Nazwisko
nr indeksu
pkt
ocena
4
Arytmetyka – Kol.I
3 grudnia 2004
Janusz Biernat
10–3,0; 13–3,5; 16–4,0; 19–4,5; 21–5,0
1.(4p) Oblicz ró
ż
nic
ę
i zapisz j
ą
w systemie U2, z dokładno
ś
ci
ą
do 10 bitów cz
ę
ś
ci ułamkowej:
64
10
– 41,(67)
10
= 22,(32)
10
=
(26,2453...
8
) =
| 0 | 0 | 1 | 0 | 1 | 1 | 0 |, 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
U2
(7)64
U8
– (7)41,(67)
U8
= 022,(10)
U8
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |, 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
U2
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
(–33046
8
*331036
8
) mod 77
8
= [(–1)*(30+46+3)*(36+10+33)]
8
mod 77
8
= (–1)*2*2 = –4
8
(6–106
10
)*45153
10
mod 101
10
= [(–100)*(53–51+4)]
10
mod 101
10
= 1*6 = 6
(2p) Oblicz: 34
92
mod 7 = (34mod 7)
92
mod 7 = ( – 1)
92
mod 7 = 1
8
–1
mod 13 = 5
(8*5 mod 13 = 1)
3.(4p) Oblicz: z dokładno
ś
ci
ą
: do 4 cyfr znacz
ą
cych
√
1, 1 0 0 0 1 1 1
2
= 1, 0 0 1 1
do 3 cyfr znacz
ą
cych [!(..)
7
]
1
√
5 1, 2 4
7
= 6, 0 1
1 0
< 1 0 1
– 5 1
1 0 0 0
< 1 0 0 1
0 2 4
150*0
1 0 0 0 1 1
> 1 0 0 0 1
–
0
–
1 0 0 0 1
2
2
=04
3
2
=12
4
2
=22
5
2
=34
6
2
=51
2 4 0 0
1501*1
1 0 0 1 0 1 0 > 1 0 0 1 0 1
– 1 5 0 1
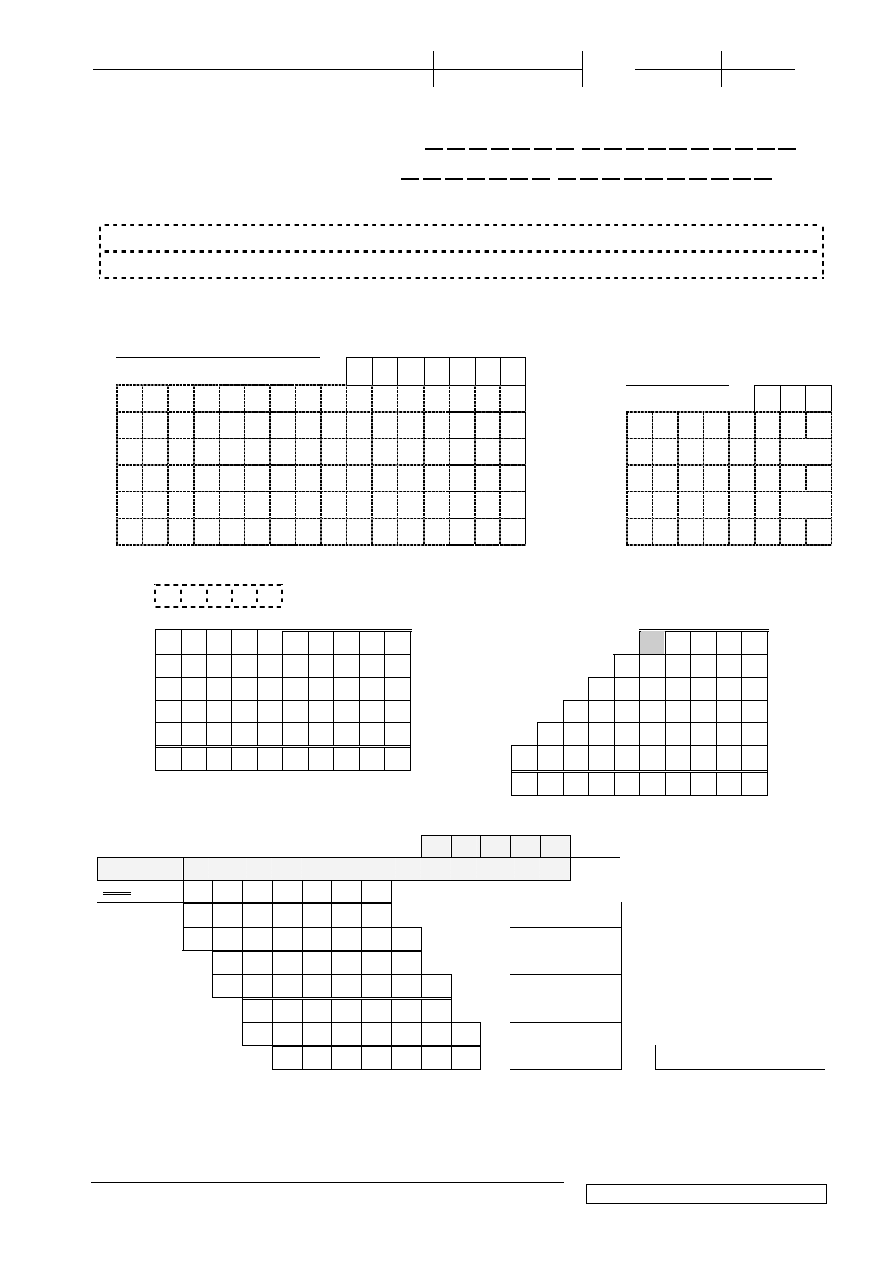
4.(4p) Wykonaj mno
ż
enie pisemne liczb w kodzie U2 u
ż
ywaj
ą
c rozszerze
ń
i bez u
ż
ycia rozszerze
ń
1 0 1 1 1
1 0 1 1 1
×
1 0 0 1 1
×
1 0 0 1 1
1 1 1 1 1 1 0 1 1 1
0 0 1 1 1
1 1 1 1 1 0 1 1 1
0 0 1 1 1
0 0 0 0
0
1 0 0 0 0
0 0 0
0
1 0 0 0 0
0 0 1 0 0 1
1 1 0 0 1
0 0 0 1 1 1 0 1 0 1
1
1
0 0 0 1 1 1 0 1 0 1
5.(4p) Metod
ą
nieodtwarzaj
ą
c
ą
oblicz z dokładno
ś
ci
ą
do 4 cyfr znacz
ą
cych iloraz liczb danych w kodzie U2
(–X)
0, 1
0
0
1
1, 0
1
0 1
====
−−−−
D
X =
1, 0
1 1
1
: 0, 1
0
1 1
====
++++
D
k= 0
+D /– D
0, 1
0
1
1
0
0
0
1
0
0
rD >0
q
0
= 1
–D
1
0
1
0
1
1
1
0
0
1
0
rD <0
q
1
= 0
+D
0
1
0
1
1
1
1
1
0
1
0
rD <0
q
2
= 0
–D
0
1
0
1
1
Iloraz jest równy
0
0
1
0
1
rD >0
q
3
= 1
Q =1,001…
U2
6.(3p) Udowodnij,
ż
e je
ś
li k
≥≥≥≥
2, to liczby 2
2k
+2 i 2
k
–1 mog
ą
mie
ć
wspólny podzielnik ró
ż
ny od 1.
2
2k
+2=(2
k
+1)(2
k
–1)+3, wi
ę
c NWP(2
2k
+2,2
k
–1)=NWP(3,2
k
–1)=3 je
ś
li k jest parzyste, bo
2
2a
–1=4
a
–1=(4–1)(4
a–1
+4
a–2
+…+4
1
+1)
/25
Imi
ę
Nazwisko
nr indeksu
pkt
ocena
5
Arytmetyka – Kol.I
3 grudnia 2004
Janusz Biernat
10–3,0; 13–3,5; 16–4,0; 19–4,5; 21–5,0
1.(4p) Oblicz ró
ż
nic
ę
i zapisz j
ą
w systemie U2, z dokładno
ś
ci
ą
do 10 bitów cz
ę
ś
ci ułamkowej:
14
10
– 27,(21)
10
= – 13,(21)
10
=
(–15,1544...
8
) =
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |, 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
U2
(0)14
U8
– (0)27,(21)
U8
= 764,(56)
U8
= | 1 | 1 | 1 | 0 | 1 | 0 | 0 |, 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
U2
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
(–33046
8
*361033
8
) mod 77
8
= [(–1)*(46+30+3)*(33+10+36)]
8
mod 77
8
= (–1)*2*2 = –4
8
(1–103
10
)*45953
10
mod 101
10
= [(–102)*(53–59+4)]
10
mod 101
10
= (–1)*(–2)= 2
(2p) Oblicz: 55
129
mod 9 = (55 mod 9)
129
mod 9 = 1
129
mod 9 = 1
3
–1
mod 17 = 6
(3*6 mod 17 = 1)
3.(4p) Oblicz: z dokładno
ś
ci
ą
: do 4 cyfr znacz
ą
cych
√
0, 1 0 1 0 1 1 1
2
= 0, 1 1 0 1
do 3 cyfr znacz
ą
cych [!(..)
8
]
1
√
5 1, 2 4
8
= 6, 3 3
1 1 0
> 1 0 1
4 4
– 1 0 1
5 2 4
143*3
1 1 1
< 1 1 0 1
4 5 1
1 1 1 1 0 > 1 1 0 0 1
2
2
=04
3
2
=11
4
2
=20
5
2
=31
6
2
=44
7
2
=61
5 3 0 0
1463*3
4 6 3 1
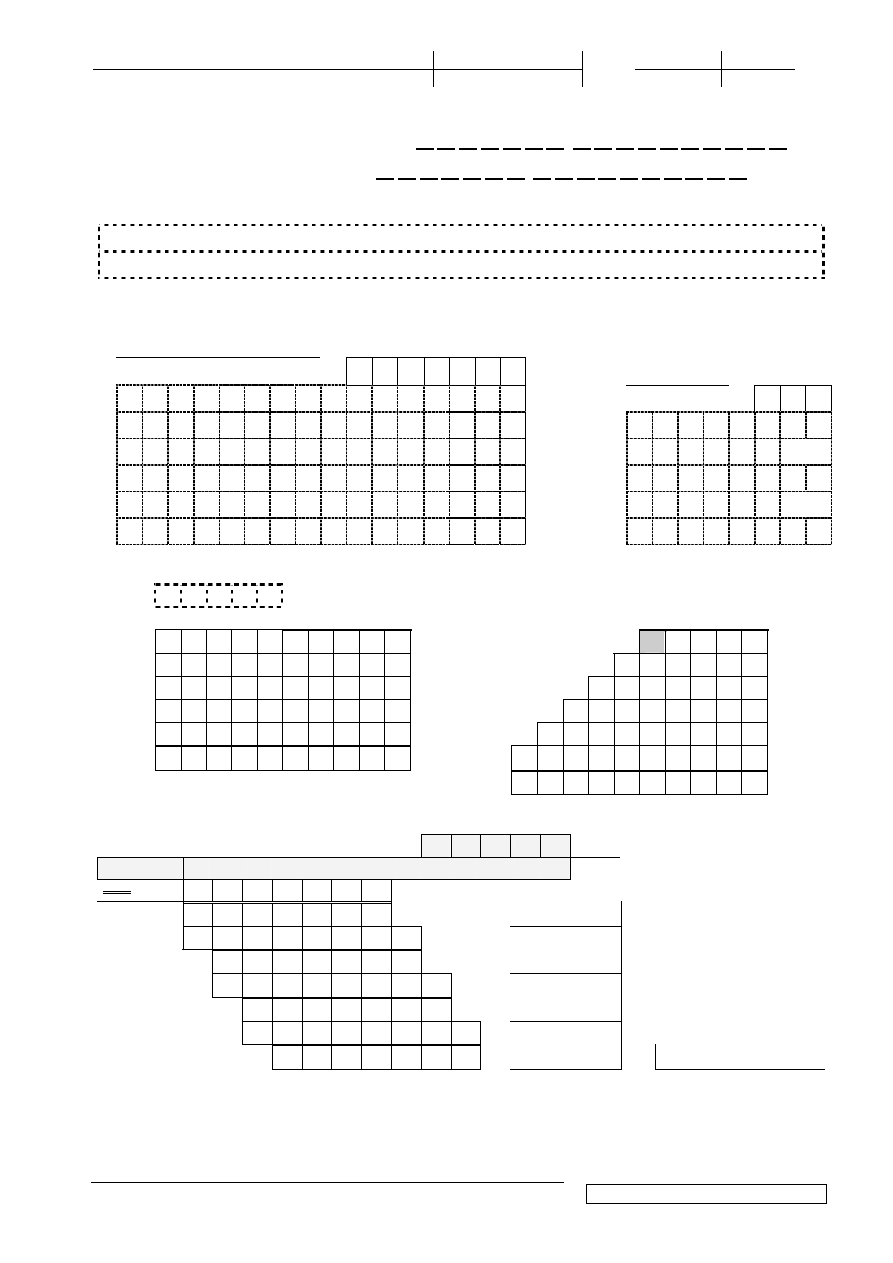
4.(4p) Wykonaj mno
ż
enie pisemne liczb w kodzie U2 u
ż
ywaj
ą
c rozszerze
ń
i bez u
ż
ycia rozszerze
ń
1 0 1 0 1
1 0 1 0 1
×
1 0 0 1 1
×
1 0 0 1 1
1 1 1 1 1 1 0 1 0 1
0 0 1 0 1
1 1 1 1 1 0 1 0 1
0 0 1 0 1
0 0 0 0
0
1 0 0 0 0
0 0 0
0
1 0 0 0 0
0 0 1 0 1 1
1 1 0 1 1
0 0 1 0 0 0 1 1 1 1
1
1
0 0 1 0 0 0 1 1 1 1
5.(4p) Metod
ą
nieodtwarzaj
ą
c
ą
oblicz z dokładno
ś
ci
ą
do 4 cyfr znacz
ą
cych iloraz liczb danych w kodzie U2
(–X)
0, 1
0
0
1
0, 1
0
1 1
====
−−−−
D
X =
1, 0
1 1
1
: 1, 0
1
0 1
====
++++
D
k= 0
+ D/–D
0, 1
0
1
1
0
0
0
1
0
0
rD <0
q
0
= 0
+D
1
0
1
0
1
1
1
0
0
1
0
rD >0
q
1
= 1
+D
0
1
0
1
1
1
1
1
0
1
0
rD >0
q
2
= 1
–D
0
1
0
1
1
Iloraz jest równy
0
0
1
0
1
rD <0
q
3
= 0
Q =0,110…
U2
6.(3p) Udowodnij,
ż
e je
ś
li k
≥≥≥≥
1, to liczby 2
ak
–1 i 2
k
+1 nie musz
ą
by
ć
wzajemnie wzgl
ę
dnie pierwsze
Je
ś
li a jest parzyste, to 2
2pk
–1=(2
pk
+1)(2
pk
–1)=(2
pk
+1)(2
k
–1)(2
(p–1)k
+2
(p–2)k
+…+2
k
+1),
wi
ę
c NWP(2
2pk
–1,2
k
+1)=2
k
+1
/25
Imi
ę
Nazwisko
nr indeksu
pkt
ocena
6
Arytmetyka – Kol.I
3 grudnia 2004
Janusz Biernat
10–3,0; 13–3,5; 16–4,0; 19–4,5; 21–5,0
1.(4p) Oblicz ró
ż
nic
ę
i zapisz j
ą
w systemie U2, z dokładno
ś
ci
ą
do 10 bitów cz
ę
ś
ci ułamkowej:
27
10
– 14,(60)
10
= 12,(39)
10
=
(14,3115...
8
) =
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |, 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
U2
27
U8
– 14,(60)
U8
= 12,(17)
U8
= | 0 | 0 | 0 | 1 | 1 | 0 | 0 |, 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
U2
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
(–4CA2F
16
*936A
16
) mod 0FF
16
= [(–1)*(4+CA+2F)*(93+6A)]
16
mod 0FF
16
= (–1)*(–2)*(–2) = –4
(8–111
10
)*16058
10
mod 101
10
= [(–103)*(58–60+1)]
10
mod 101
10
= (–2)*(–1) = 2
(2p) Oblicz: 65
131
mod 11 = (65 mod 11)
131
mod 11 = ( – 1)
131
mod 11 = – 1
7
–1
mod 17 = 5
(7*5 mod 17 = 1)
3.(4p) Oblicz: z dokładno
ś
ci
ą
: do 4 cyfr znacz
ą
cych
√
1, 1 0 1 0 1 1 1
2
= 1, 0 1 0
do 3 cyfr znacz
ą
cych [!(..)
9
]
1
√
5 1, 2 4
9
= 6, 7 1
1 0
> 1 0 1
4 0
1 0 1 0
< 1 0 0 1
1 1 2 4
137*7
1 0 0 1
1 0 8 4
1 1 1
> 1 0 1 0 1
3 0 0 0
1451*1
1 1 1 1 0
2
2
=04
3
2
=10
4
2
=17
5
2
=27
6
2
=40
7
2
=54
8
2
=71
1 4 5 1
4.(4p) Wykonaj mno
ż
enie pisemne liczb w kodzie U2 u
ż
ywaj
ą
c rozszerze
ń
i bez u
ż
ycia rozszerze
ń
1 1 0 0 1
1 1 0 0 1
×
1 0 1 1 1
×
1 0 1 1 1
1 1 1 1 1 1 1 0 0 1
0 1 0 0 1
1 1 1 1 1 1 0 0 1
0 1 0 0 1
1 1 1 1 1 0 0 1
0 1 0 0 1
0 0 0
0
1 0 0 0 0
0 0 0 1 1 1
1 0 1 1 1
0 0 0 0 1 1 1 1 1 1
1
1
0 0 0 0 1 1 1 1 1 1
5.(4p) Metod
ą
nieodtwarzaj
ą
c
ą
oblicz z dokładno
ś
ci
ą
do 4 cyfr znacz
ą
cych iloraz liczb danych w kodzie U2
(–X)
0, 1
1
0
1
0, 1
0
1 1
====
−−−−
D
X =
1, 0
0 1
1
: 1, 0
1
0 1
====
++++
D
k= –1
+ D/–D
0, 1
0
1
1
0
0
1
0
0
1
rD <0
q
0
= 0
+D
1
0
1
0
1
1
1
1
1
0
0
rD >0
q
1
= 1
–D
0
1
0
1
1
0
0
1
1
1
0
rD <0
q
2
= 0
+D
1
0
1
0
1
Iloraz jest równy
0
0
0
1
1
rD <0
q
3
= 0
Q =01,00…
U2
6.(3p) Udowodnij,
ż
e je
ś
li k
≥≥≥≥
1, to liczby 2
2k
–1 i 2
k
+1 maj
ą
wspólny podzielnik wi
ę
kszy od 1
2
2k
–1=(2
k
+1)(2
k
–1), wi
ę
c NWP(2
2k
–1,2
k
+1)=2
k
+1
Wyszukiwarka
Podobne podstrony:
2004 arytmetyka kolokwium 2 rozw
2006 arytmetyka kolokwium 2 rozw errata
2005 arytmetyka kolokwium 1 rozw
2004 arytmetyka kolokwium 2 rozwid 2 (2)
2007 arytmetyka kolokwium 2 rozw
2004 arytmetyka kolokwium 2
2008 architektura arytmetyka kolokwium
Treści zadań kolokwium?rczak+ROZW
2003 arytmetyka kolokwium 1id 21693 (2)
kolokwium rozw 1 1
2004 05 kolokwium 1
2005 arytmetyka kolokwium 1
kolokwium rozw
więcej podobnych podstron