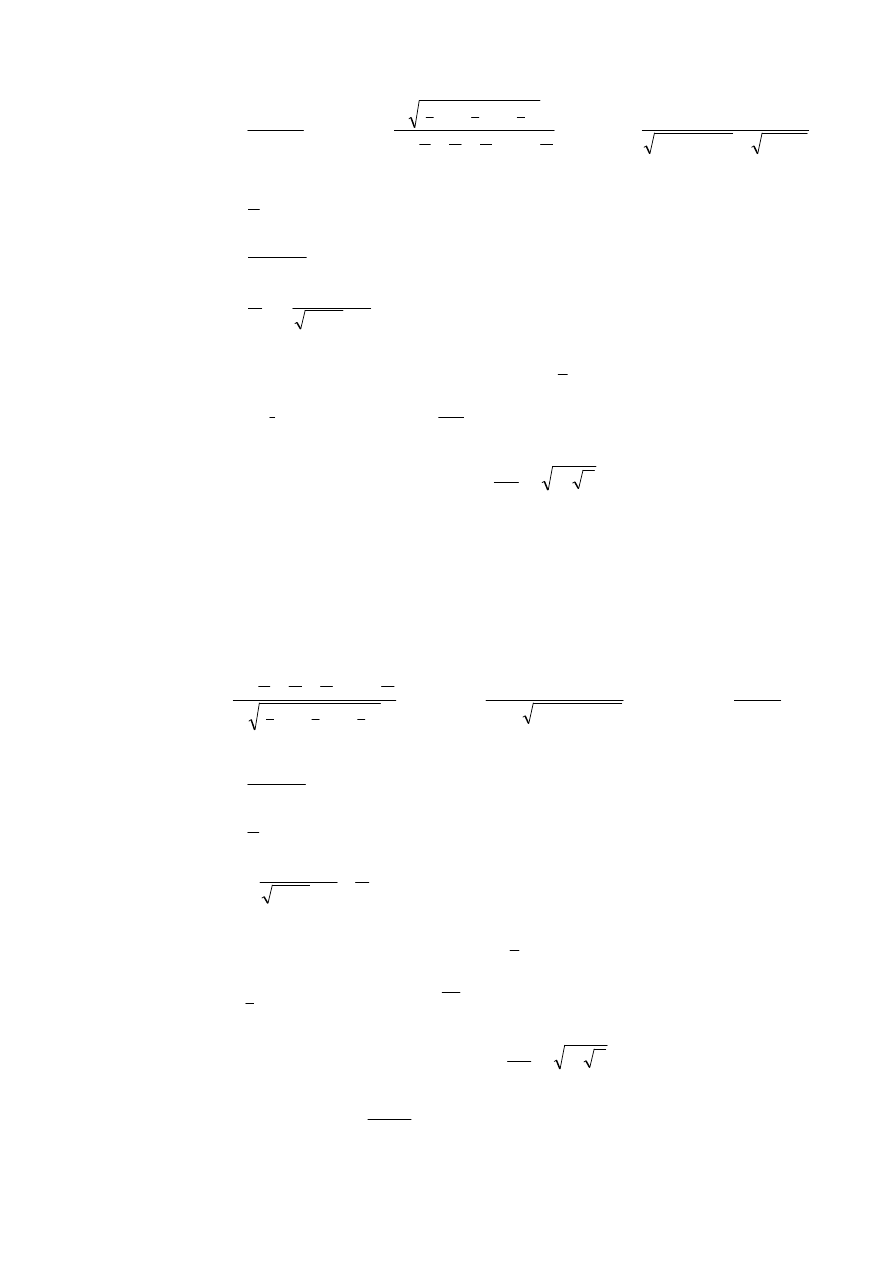
Kolokwium nr 1

Grupa 1 WILiŚ

RZĄD A 04-11-2004
Zadanie 1. Obliczyć granice następujących ciągów:

a).

3

2

2

2

ln

2

2

2

−

+

=

n

n

n

a

n

, b).

( ) ( ) ( )

n

n

n

n

n

n

a

3

1

3

1

3

1

3

1

4

3

5

4

6

5

...

1

3

2

1

+

+

+

+

+

+

+

=

, c).

3

1

5

2

2

2

+

−

−

+

=

n

n

n

a

n

.

Zadanie 2. Wyznaczyć wartość parametrów

b

a

i

tak, aby funkcja była ciągła:



















−

<

−

+

+

≤

≤

−

+

+

>

+

=

2

dla

2

6

-

4

4

0

2

dla

arctg

2

)

1

(

0

dla

)

ln

arcctg(

4

1

)

(

2

x

x

x

a

x

b

x

x

x

x

x

f

π

π

.

Zadanie 3. Wyznaczyć funkcję odwrotną

1

−

f

, dziedzinę i przeciwdziedzinę

1

i

−

f

f

gdy:

a).

1

log

)

(

2

−

=

x

x

f

, b).

2

)

1

arccos(

)

(

π

+

−

=

x

x

f

.

Zadanie 4. Korzystając z reguły de L’Hospitala obliczyć podane granice:

a).

)

1

(

1

−

−∞

→

x

e

x

lim

x

, b).

x

x

lim

x

ln

2

1

6

0

+

+

→

.

Zadanie 5. Obliczyć pochodne podanych funkcji:

a).

e

x

y

x

+

=

3

ln

)

2

(sin

, b).

( )

3

4

2

1

3

arctg

x

x

y

x

x

+

=

+

.

T: Podać definicję ciągu ograniczonego. Sformułować jedno z twierdzeń dotyczących zbieżności ciągów

ograniczonych i podać przykład ilustrujący wybrane twierdzenie.

Kolokwium nr 1

Grupa 1 WILiŚ

RZĄD B 04-11-2004
Zadanie 1. Obliczyć granice następujących ciągów:

a).

( ) ( ) ( )

n

n

n

n

n

n

a

4

3

5

4

3

2

2

1

2

1

2

1

2

1

...

1

3

2

1

+

+

+

+

+

+

+

=

, b).

1

6

9

3

6

2

+

+

−

=

n

n

n

a

n

, c).

1

1

2

3

2

ln

+













−

+

=

n

n

n

n

a

.

Zadanie 2. Wyznaczyć wartość parametrów

b

a

i

tak, aby funkcja była ciągła:



















−

<

+

−

+

>

+

≤

≤

−

+

+

=

2

dla

4

2

6

-

4

0

dla

)

ln

arcctg(

4

1

0

2

dla

arctg

2

)

1

(

)

(

2

x

x

x

a

x

x

x

b

x

x

x

f

π

π

.

Zadanie 3. Wyznaczyć funkcję odwrotną

1

−

f

, dziedzinę i przeciwdziedzinę

1

i

−

f

f

gdy:

a).

2

2

)

(

+

=

−

x

x

f

, b).

1

)

sin(

arc

)

(

2

−

+

=

π

x

x

f

.

Zadanie 4. Korzystając z reguły de L’Hospitala obliczyć podane granice:

a).

)

ctg

(

1

x

lim

x

o

x

−

−

→

, b).

1

2

3

1

−

+

→

x

x

lim

x

.

Zadanie 5. Obliczyć pochodne podanych funkcji:

a).

π

+

=

x

x

y

2

ln

)

3

(cos

, b).

( )

4

3

1

3

4

arcctg

x

x

y

x

x

+

=

−

.

T: Podać definicję ciągu monotonicznego. Sformułować twierdzenie o ciągu monotonicznym i ograniczonym.

Zbadać monotoniczność ciągu

1

3

1

2

+

+

=

n

n

n

a

.